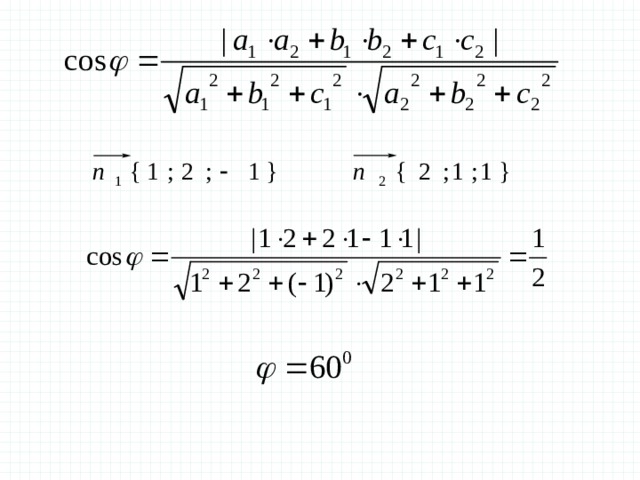Метод координат при решении 14 задачи егэ по стереометрии

Координаты вектора

Вектор – отрезок, имеющий длину и указывающий направление.

На самом деле, понимать, что такое вектор для решения задач методом координат необязательно. Можно просто использовать это понятие, как необходимый инструмент для решения задач по стереометрии. Любое ребро или отрезок на нашей фигуре мы будем называть вектором.

Для того, чтобы определить координаты вектора, нужно из координат конечной точки вычесть координаты начальной точки. Пусть у нас есть две точки (Рис. 4) :
$$ т.А(x_A,y_A,z_A); $$
$$ т.B(x_B,y_B,z_B); $$
Тогда координаты вектора (vec{AB}) можно определить по формуле:
$$ vec{AB}={x_B-x_A,y_B-y_A,z_B-z_A}. $$

Скрещивающиеся прямые

И так, мы научились находить координаты точек, и при помощи них определять координаты векторов. Теперь познакомимся с формулой нахождения косинуса угла между скрещивающимися прямыми (векторами). Пусть даны два вектора:
$$ a={x_a,y_a,z_a};$$
$$ b={x_b,y_b,z_b}; $$
тогда угол (alpha) между ними находится по формуле:
$$ cos{alpha}=frac{x_a*x_b+y_a*y_b+z_a*z_b}{sqrt{{x_a}^2+{y_a}^2+{z_a}^2}*sqrt{{x_b}^2+{y_b}^2+{z_b}^2}}. $$

Уравнение плоскости

В задачах №14 (С2) ЕГЭ по профильной математике часто требуется найти угол между прямой и плоскостью и расстояние между скрещивающимися прямыми. Но для этого вы должны уметь выводить уравнение плоскости. В общем виде уравнение плоскости задается формулой:
$$ A*x+B*y+C*z+D=0,$$
где (A,B,C,D) – какие-то числа.

Если найти (A,B,C,D), то мы мы найдем уравнений плоскости. Плоскость однозначно задается тремя точками в пространстве, значит нужно найти координаты трех точек, лежащий в данной плоскости, а потом подставить их в общее уравнение плоскости.

Например, пусть даны три точки:

$$ K(x_K,y_K,z_K);,L(x_L,y_L,z_L);,P(x_P,y_P,z_P). $$

Подставим координаты точек в общее уравнение плоскости:

$$begin{cases} A*x_K+B*y_K+C*z_K+D=0,\ A*x_L+B*y_L+C*z_L+D=0, \ A*x_P+B*y_P+C*z_P+D=0.end{cases}$$

Получилась система из трех уравнений, но неизвестных 4: (A,B,C,D). Если наша плоскость не проходит через начало координат, то мы можем (D) приравнять (1), если же проходит, то (D=0). Объяснение этому простое: вы можете поделить каждое ваше уравнения на (D), от этого уравнение не изменится, но вместо (D) будет стоять (1), а остальные коэффициенты будут в (D) раз меньше.

Теперь у нас есть три уравнения и три неизвестные – можем решить систему:

Пример 3

Найти уравнение плоскости, проходящей через точки
$$ K(1;2;3);,P(0;1;0);,L(1;1;1). $$
Подставим координаты точек в уравнение плоскости (D=1):
$$begin{cases} A*1+B*2+C*3+1=0,\ A*0+B*1+C*0+1=0, \ A*1+B*1+C*1+1=0.end{cases}$$
$$begin{cases} A+2*B+3*C+1=0,\ B+1=0, \ A+B+C+1=0.end{cases}$$
$$begin{cases} A-2+3*C+1=0,\ B=-1, \ A=-C.end{cases}$$
$$begin{cases} A=-0.5,\ B=-1, \ C=0.5.end{cases}$$
Получаем искомое уравнение плоскости:
$$ -0.5x-y+0.5z+1=0.$$

Расстояние от точки до плоскости

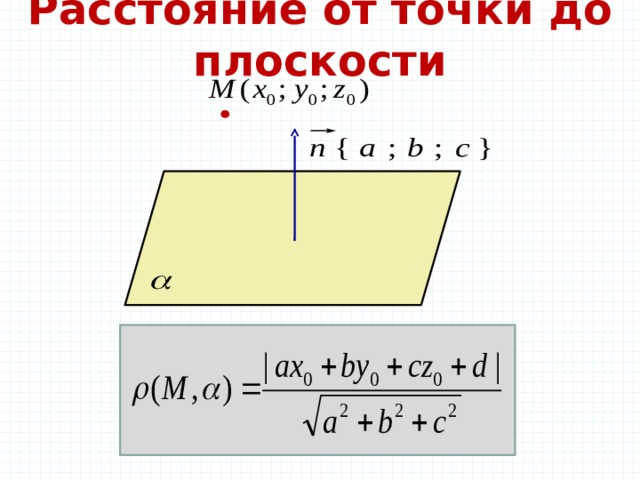
Зная координаты некоторой точки (M(x_M;y_M;z_M)), легко найти расстояние до плоскости (Ax+By+Cz+D=0:)
$$ rho=frac{|A*x_M+B*y_M+C*z_M+D|}{sqrt{A^2+B^2+C^2}}. $$

Пример 4

Найдите расстояние от т. (H (1;2;0)) до плоскости, заданной уравнением
$$ 2*x+3*y-sqrt{2}*z+4=0.$$

Из уравнения плоскости сразу находим коэффициенты:
$$ A=2,,B=3,,C=-sqrt{2},,D=4.$$
Подставим их в формулу для нахождения расстояния от точки до плоскости.
$$ rho=frac{|2*1+3*2-sqrt{2}*0+4|}{sqrt{2^2+3^2+{-sqrt{2}}^2}}. $$
$$ rho=frac{12}{sqrt{16}}=3.$$

Расстояние между скрещивающимися прямыми

Расстояние между скрещивающимися прямыми – это расстояние от любой точки одной из прямых до параллельной ей плоскости, проходящей через вторую прямую.

Таким образом, если требуется найти расстояние между скрещивающимися прямыми, то нужно через одну из них провести плоскость параллельно второй прямой. Затем найти уравнение этой плоскости и по формуле расстояния от точки до плоскости найти расстояние между скрещивающимися прямыми. Точку на прямой можно выбрать произвольно (у которой легче всего найти координаты).

Пример 5

Рассмотрим задачу из досрочного ЕГЭ по математике 2018 года.

Дана правильная треугольная призма (ABCFDE), ребра которой равны 2. Точка (G) — середина ребра (CE).

• Докажите, что прямые (AD) и (BG) перпендикулярны.
• Найдите расстояние между прямыми (AD) и (BG).

Решение:

Решим задачу полностью методом координат.

Нарисуем рисунок и выберем декартову систему координат. (Рис 5).

Всего: 117    1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

Всего: 117    1–20 | 21–40 | 41–60 | 61–80 …

МБОУ «Раздорская СОШ им. А.П.Гужвина

Решение задач №14 ЕГЭ по математике координатно-векторным методом

Методические рекомендации

Серия «Школьник —
школьнику»

С.С.Уразалиева

Решение заданий
№14 ЕГЭ по математике координатно-векторным методом

Методические
рекомендации.

   С помощью
данных методических рекомендаций можно научиться решать задачи на вычисление
углов и расстояний в стереометрии с помощью координатно-векторного метода. Для
учеников 10-11 классов самой главной проблемой является подготовка к ЕГЭ.
Причем не все ученики уверенно решают задания II части , а
некоторые и не берутся за их решение.         

   Координатно-векторный 
метод  основан  на введении   прямоугольной системы координат и создании
геометрически-алгебраической модели решения задач, тем самым упрощая 
громоздкие и достаточно сложные преобразования и выкладки.

   Достоинство
метода координат состоит в том, что его применение избавляет от необходимости
прибегать к наглядному представлению сложных пространственных конфигураций.

   Выражаю
огромную благодарность своим ученикам 11 класса 2016 – 2017 учебного года:  Комаровой
Ангелине, Тарбаеву Наилю, Бекмурзаеву Тимуру, Утегеновой Аимгуль, Абылхатаевой
Карине, Кункашевой Арине, Юсуповой Аделине, Успанову Гелиму, которые
сыграли большую роль в создании данного методического сборника

Уважаемые ребята!

   Если у вас
имеются серьезные проблемы с пониманием определений, с  чтением или построением
сложного стереометрического рисунка, если вам  никак не удается подобрать
необходимые дополнительные построения, мне кажется, что стоит заняться
изучением координатно-векторного метода. Особенно это актуально в условиях
экстренной помощи, когда до ЕГЭ остается всего лишь 2-3 месяца.

   Данный курс не
претендует на научность, а является небольшим   методическим пособием при
подготовке к ЕГЭ для выпускника, нацеленного на высокий балл при сдаче
экзамена. Курс является кратким, в нем рассмотрены лишь наиболее часто
встречающиеся типы заданий, как в сборниках, так и в контрольно-измерительных
материалах.

   Метод координат
— это довольно несложный способ, но в настоящих задачах №14 никаких координат и
векторов нет. Поэтому их придется вводить: указать начало отсчета, единичный
отрезок и направление осей x, y и z.

   Самое
замечательное свойство этого метода заключается в том, что не имеет никакого
значения, как именно вводить систему координат. Если все вычисления будут
правильными, то и ответ будет правильным.

   Успехов!

§1.
Основные понятия.

   Метод координат
—эффективный и универсальный способ нахождения любых углов или расстояний между
стереометрическими объектами в пространстве.  Данный метод заключается во
введении  декартовой системы координат, а затем – нахождение образующихся
векторов (их длин и углов между ними). Достоинство метода координат состоит в
том, что его применение избавляет от необходимости прибегать к наглядному
представлению сложных пространственных конфигураций. Алгоритм применения метода
координат к решению геометрических задач сводится к следующему:

—  Выбираем в
пространстве систему координат

—  Находим
координаты необходимых, по условию задачи, точек.

 —  Решаем задачу,
используя основные задачи метода координат.

 — Переходим от
аналитических соотношений к геометрическим.

    Для начала
разбора метода координат для стереометрических задач рассмотрим, что же
представляет собой прямоугольная (декартова) система координат в пространстве.
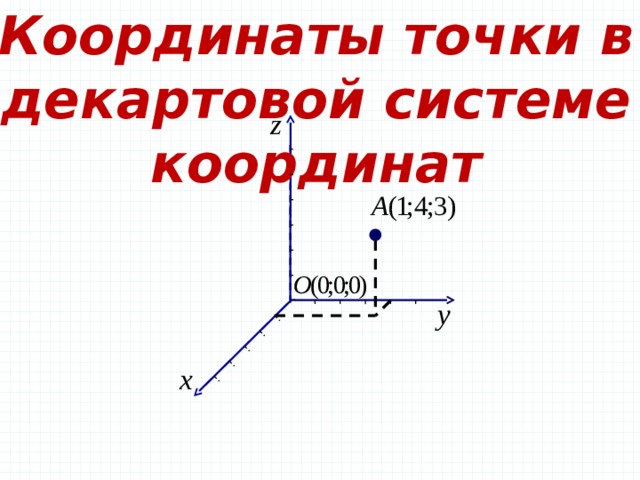
Прямоугольная (декартова) система координат в пространстве – совокупность точки
О (называемой началом координат), единицы измерения и трёх попарно
перпендикулярных прямых Ox, Oy иOz (называемых осями координат: Ox – ось
абсцисс, Oy – ось ординат, Oz – ось аппликат), на каждой из которых указано
направление положительного отсчёта. Плоскости хОу, уОz и zOx называют
координатными плоскостями. Каждой точке пространства ставится в соответствие
тройка чисел, называемых её координатами.

  
                             z

                                  
0                                     у   

                     
х

Для того чтобы
использовать метод координат, надо хорошо знать формулы:

1. Нахождение
расстояния между двумя точками, заданными своими координатами.

 , где

D=AB,
A(x₁;y₁;z₁), B(x₂;y₂;z₂)

2. Нахождение
координат середины отрезка

A(x₁;y₁;z₁),
B(x₂;y₂;z₂)  
      

3. Нахождение
косинуса угла между векторами

 , где

4. Координаты x, y, z точки М, которая делит отрезок ,
ограниченный точками А(х₁, у₁,z₁ ) и B(x₂,y₂,z₂ ), в отношении , определяется по формулам

5. Расстояние от точки до плоскости

   Для решения задач необходимо научиться находить координаты вершин
основных многогранников при помещении их в прямоугольную систему координат.

   Ниже представлены координаты вершин некоторых многогранников,
помещенных в систему координат.

Координаты
куба

Это
самый простой многогранник, все двугранные углы которого равны 90°.

Система
координат также вводится очень просто:

1.        
Начало координат —
в точке A;

2.        
Чаще всего ребро куба не указано,
поэтому принимаем его за единичный отрезок;

3.        
Ось x направляем
по ребру AB, y — по ребру AD, а ось z —
по ребру AA₁.

Обратите
внимание: ось z направляется вверх! После двумерной системы координат это
несколько непривычно, но на самом деле очень удобно и логично.

Итак, теперь у каждой вершины куба
есть координаты. Соберем их в таблицу — отдельно для нижней
плоскости куба:

Точка	A	B	C	D
Координаты	(0; 0; 0)	(1; 0; 0)	(1; 1; 0)	(0; 1; 0)

И для верхней:

Точка	A1	B1	C1	D1
Координаты	(0; 0; 1)	(1; 0; 1)	(1; 1; 1)	(0; 1; 1)

Несложно заметить, что точки верхней плоскости отличаются от
соответствующих точек нижней только координатой z. Например,
B = (1; 0; 0), B₁ = (1; 0; 1).

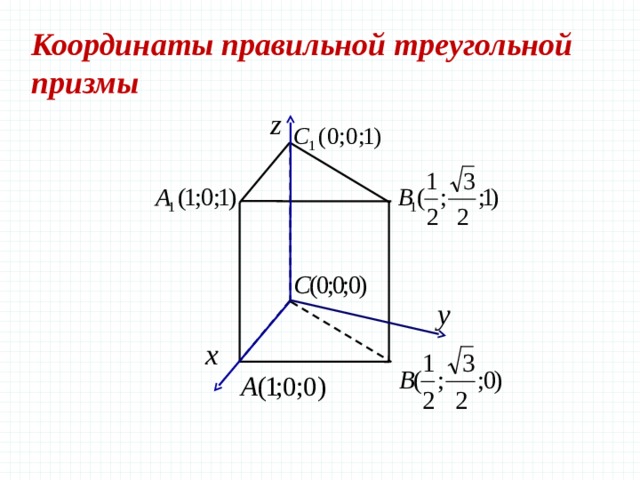
Координаты 
правильной треугольной призмы

При правильном подходе достаточно
знать координаты только нижнего основания — верхнее будет считаться
автоматически.

В задачах №14
встречаются исключительно правильные трехгранные призмы (прямые призмы,
в основании которых лежит правильный треугольник). Для них система
координат вводится почти так же, как и для куба.

Вводим
систему координат:

1.        
Начало координат —
в точке A;

2.        
Сторону призмы принимаем за единичный
отрезок, если иное не указано в условии задачи;

3.        
Ось x направляем
по ребру AB, z — по ребру AA₁, а ось y
расположим так, чтобы плоскость OXY совпадала с плоскостью
основания ABC.

Получаем
следующие координаты точек:

Как
видим, точки верхнего основания призмы снова отличаются от соответствующих
точек нижнего лишь координатой z. Основная проблема — это
точки C и C₁. У них есть иррациональные координаты, и
для того чтобы довольно просто решить задание №14 эти иррациональные координаты
надо просто запомнить. Или можно вывести.

Координаты
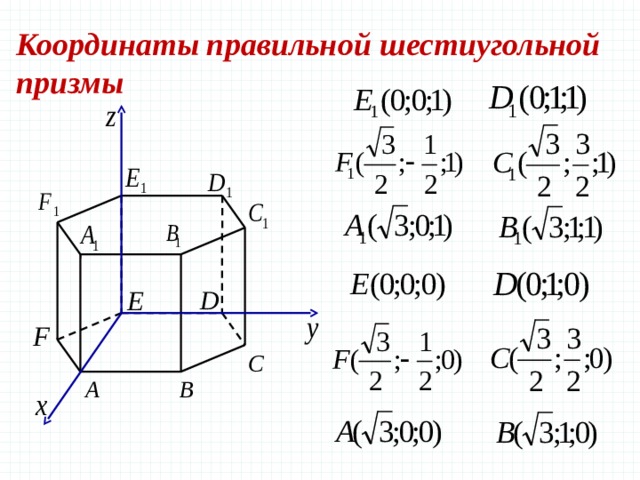
 правильной шестиугольной призмы

Шестиугольная
призма — это «клонированная» трехгранная. Можно понять, как это
происходит, если взглянуть на нижнее основание — обозначим его
ABCDEF. Проведем дополнительные построения: отрезки AD, BE и CF.
Получилось шесть треугольников, каждый из которых (например,
треугольник ABO) является основанием для трехгранной призмы.

Теперь
введем систему координат. Начало координат — точку O — поместим
в центр симметрии шестиугольника ABCDEF. Ось x пойдет
вдоль FC, а ось y — через середины отрезков AB
и DE. Получим такую картинку:

Нужно
обратить внимание на то, что  начало координат не совпадает с вершиной
многогранника. На самом деле, при решении настоящих задач выясняется, что
это очень удобно, поскольку позволяет значительно уменьшить объем вычислений. Осталось
добавить ось z. Проводим ее перпендикулярно плоскости OXY
и направляем вертикально вверх. Получим картинку:

Запишем
теперь координаты точек. Предположим, что все ребра нашей правильной
шестигранной призмы равны 1. Итак, координаты нижнего основания:

Координаты
верхнего основания сдвинуты на единицу по оси z:

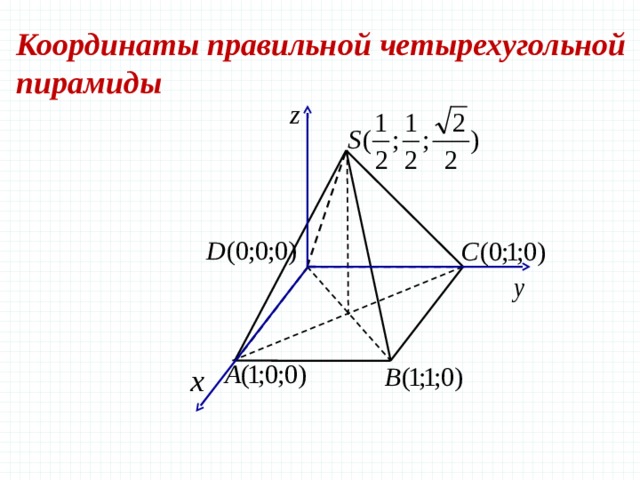
Координаты
 правильной четырехугольной пирамиды

Итак,
правильная четырехугольная пирамида. Обозначим ее SABCD,
где S — вершина. Введем систему координат: начало
в точке A, единичный отрезок AB = 1, ось x направим
вдоль AB, ось y — вдоль AD, а ось z — вверх,
перпендикулярно плоскости OXY. Для дальнейших вычислений нам потребуется
высота SH — вот и построим ее. Получим следующую картинку:

Теперь
найдем координаты точек. Для начала рассмотрим плоскость OXY. Здесь все
просто: в основании лежит квадрат, его координаты известны. Проблемы
возникают с точкой S. Поскольку SH — высота
к плоскости OXY, точки S и H отличаются лишь
координатой z. Длина отрезка SH — это и есть
координата z для точки S, поскольку
H = (0,5; 0,5; 0).

Заметим,
что треугольники ABC и ASC равны по трем сторонам
(AS = CS = AB = CB = 1,
а сторона AC — общая). Следовательно, SH = BH.
Но BH — половина диагонали квадрата ABCD, т.е.
BH = AB · sin 45°. Получаем координаты всех точек:

Ниже
представлено, как найти определитель третьего порядка по правилу Саррюса,
составить уравнение плоскости и найти вектор нормали.

§2
Практическая часть

Ниже представлены
задачи:

— на нахождение
угла между прямыми;

— угла между
прямой и плоскостью; 

— угла между плоскостями;

— расстояния от
точки до прямой;

— расстояния от
точки до плоскости.

Эти
задачи решили мои ученики 11 класса

Вариант 13. Задача
№14 по сборнику Ф.Ф.Лысенко

В кубе ABCDA₁B₁C₁D₁,
ребро которого равно 4, точка М является серединой отрезка BC₁.
Найдите расстояние между прямыми А₁В и АМ.

Задача №14 по
сборнику ФИПИ 2016

В правильной
шестиугольной призме ABCDEFA₁B₁C₁D₁
E₁F₁
все рёбра равны 1. Найдите расстояние от точки В до прямой C₁F_.

Задача №14 по
сборнику ФИПИ 2017

Дана правильная четырёхугольная
призма ABCDA₁B₁C₁D₁.
Найдите расстояние от точки B₁ 
до плоскости AD₁
C ,
если АВ равно 5, АА₁равно 6.

Задача №14 ЕГЭ по
сборнику ФИПИ 2017

В правильной
шестиугольной призме ABCDEFA₁B₁C₁D₁
E₁F₁
все рёбра равны 4.

а) Докажите, что
угол между прямыми АD₁
и DC₁
равен 90⁰.

б) Найдите угол
между плоскостями FAC₁
 и AA₁D.

Задача №14 ЕГЭ по
сборнику ФИПИ 2017

Вывод

Мы изучили метод координат на более
высоком уровне по сравнению со школьной программой по геометрии.  Познакомились
и научились применять новые формулы: на нахождение расстояния от точки до
плоскости, от точки до прямой, угла между прямыми, угла между прямой и
плоскостью, угла между плоскостями. Мы узнали, что для
составления уравнения плоскости можно использовать матрицу и определитель
третьего порядка, который можно посчитать правилом Саррюса.

Мы
пришли к выводу, что использование метода координат требует от ученика
внимательности, хороших вычислительных навыков. Мы убеждены в том, что   координатно-векторный метод в школьном
курсе геометрии необходимо изучать на глубоком уровне и увеличить количество
часов на изучение данной темы.

 Нами
подобраны задания из сборников ФИПИ 2016г и 2017г, которые мы самостоятельно решили
и которые помогут отработать полученные навыки, и тем самым более качественно
подготовиться к сдаче экзамена.

Мы
надеемся, что изложенная в работе информация поможет выпускникам решать задание
№14 и достичь более высоких результатов на ЕГЭ по математике

Список литературы

1.     ЕГЭ
2017. Математика. И.В. Ященко. 36 вариантов. Профильный уровень

2.   ru.wikipedia.org – Система
координат.

3.   Смирнова, И.М. C50         Геометрия.
Расстояния и углы в пространстве: учебно-методическое пособие  / И.М. Смирнова,
В.А. Смирнов. – 2-е изд., перераб. И доп. – М.: Издательство «Экзамен», 2009. –
158, [2]
с.
(Серия «ЕГЭ. 100 баллов»)

4.   Геометрия, 10 – 11
: Учеб. Для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б.
Кадомцев и др. – 13-е изд. – М.: Просвещение, 2014. – 206 с.: ил.

5.   Корянов А.Г,
Прокофьев А.А. Многогранники: виды задач и методы их решения. МАТЕМАТИКА
ЕГЭ 2013 (типовые задания С2) «Многогранники: виды задач
и методы их решения» www.alexlarin.narod.ru

6.   Корянов А.Г, «
Расстояния и углы в пространстве» МАТЕМАТИКА ЕГЭ 2010 (типовые задания С2) www.alexlarin.narod.ru

7.      В.В.
Леваков «Решение задач координатно-векторным методом»

Метод координат… Что же это такое и зачем он нужен? Можно ли без него обойтись при сдаче ЕГЭ? Можно, безусловно! Все стереометрические задачи второй части профильного ЕГЭ по математике решаются и без привязки фигур к системе координат. Но…  координатный метод может значительно упростить решение самых сложных вопросов, таких, как определение расстояний и углов между прямыми и плоскостями в пространстве, так как там все эти расчеты сводятся, практически, к одной формуле.

       Будем разбираться!

Вспомните, как вас знакомили с системой координат и объясняли, что положение каждой точки в системе координат можно определять координатами х и у.   Это точки M(x_m; y_m)   и N(x_n; y_n)

Как известно, прямую можно провести через две точки, и при том, только одну. Задача по определению уравнения прямой на плоскости, проходящей через две точки, координаты которых известны, решалась очень просто. В этом случае в уравнение прямой y=kx+b подставляли сначала координаты точки М, затем – точки N.

Получали систему двух линейных уравнений относительно неизвестных коэффициентов k и b, которые находили при решении  этой системы.

Но уравнение прямой на плоскости можно задать и по-другому:

Ax + By + C = 0,       (A² + B² ≠ 0)

И суть от этого не изменится, изменятся только коэффициенты. Условие в скобках означает, что А и В не могут быть равны нулю одновременно.

Стереометрия рассматривает фигуры в пространстве, где каждая точка описывается уже тремя координатами – (x, y, z).

Привязка фигур к  системе координат позволяет не только определять координаты точек, но и записать уравнение плоскости. Как известно, на трех точках можно построить плоскость, притом, только одну. Соответственно, можно и записать плоскость уравнением. Выглядит это уравнение следующим образом:

  Ax + By + Cz + D = 0

 Очень похоже на вторую запись уравнения прямой на плоскости. Значит, и коэффициенты  А, В, С и D мы будем находить также, как и коэффициенты для прямой на плоскости, по точкам.

Это действие сродни тому, что вы производили, определяя уравнение прямой, проходящей через две точки, заданные координатами.

Прямую можно провести через две точки, и мы составляли два уравнения для двух точек.

Плоскость можно провести через три точки, значит, и уравнений будет три!

Но уравнений три, а неизвестных – четыре! Ну, и что! Мы же можем разделить все уравнения на D, при этом они не изменятся, будут равнозначны первоначальным! Так и будем поступать! Тогда   вместо D   будет единица, а все остальные коэффициенты будут делиться на D,  назовем их также, А, В, С. И это уже вполне решаемая система!

Здесь значения всех x, y и z известны, это координаты точек, принадлежащих данной плоскости.

Итак, точку описать можем, прямую описать можем, плоскость –  можем. Осталось вспомнить сами векторы и их координаты, они нам тоже пригодятся при решении задач.

Векторы и их координаты

          Вектор – это математический объект, характеризующийся величиной и направлением. Например, в геометрии и в естественных науках вектор есть направленный отрезок прямой.

Мы можем «привязать» вектор к системе координат, т.е. мы можем его определять в пространстве координатами его проекций на координатные плоскости.

Если даны две точки в пространстве А(x_a; y_a; z_a) и B(x_b; y_b; z_b), то дан и вектор

, где а_х, а_у и а_z – координаты вектора.  Осталось определить значения а_х, а_у и а_z. Определяем:

а_х = x_b – x_a

а_у = y_b – y_a

а_z = z_b  –  z_а

       Теперь, зная длины проекций вектора, мы можем легко найти длину вектора, которая, как видно из чертежа, есть не что иное, как диагональ параллелепипеда, сторонами которого являются координаты этого вектора. Его длина, модуль вектора, будет равна:

А что есть длина вектора, как не расстояние между двумя точками: началом и концом вектора? То есть выведенная формула определяет расстояние между двумя точками в декартовой системе координат.

Метод координат

Примеры решения задач →

Стереометрия

Метод координат

в задачах № 14 ЕГЭ

Координаты точки в декартовой системе координат

Координаты вектора

=

Координаты середины отрезка

Угол между прямыми

— направляющий вектор прямой а

— направляющий вектор прямой b

— угол между прямыми

Уравнение плоскости, проходящей

через три заданных точки

-нормальный

вектор плоскости

Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору

-нормальный

вектор плоскости

, где

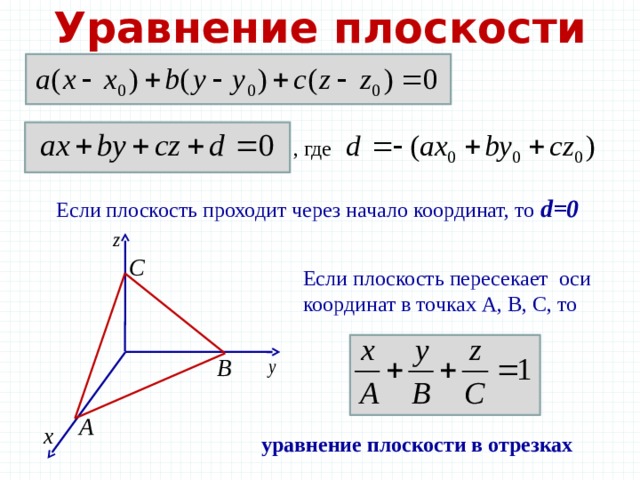
Уравнение плоскости

, где

Если плоскость проходит через начало координат, то d=0

Если плоскость пересекает оси координат в точках А, В, С, то

уравнение плоскости в отрезках

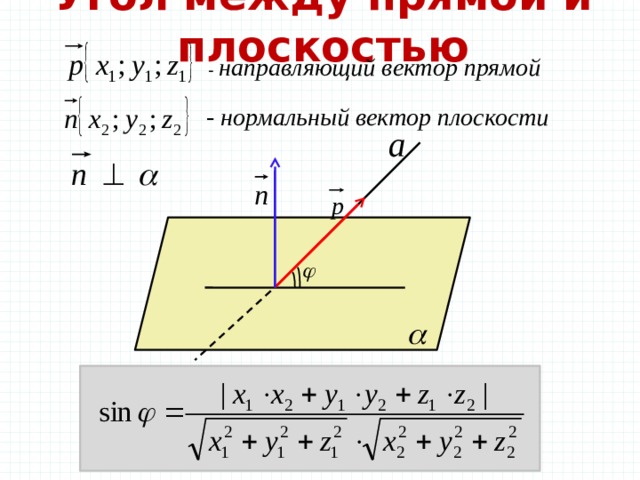
Угол между прямой и плоскостью

— направляющий вектор прямой

— нормальный вектор плоскости

Угол между плоскостями

Вектор нормали плоскости

Вектор нормали плоскости

Расстояние от точки до плоскости

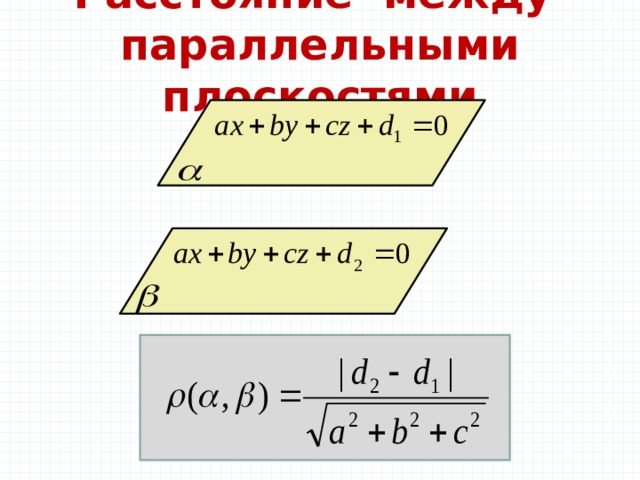
Расстояние между параллельными плоскостями

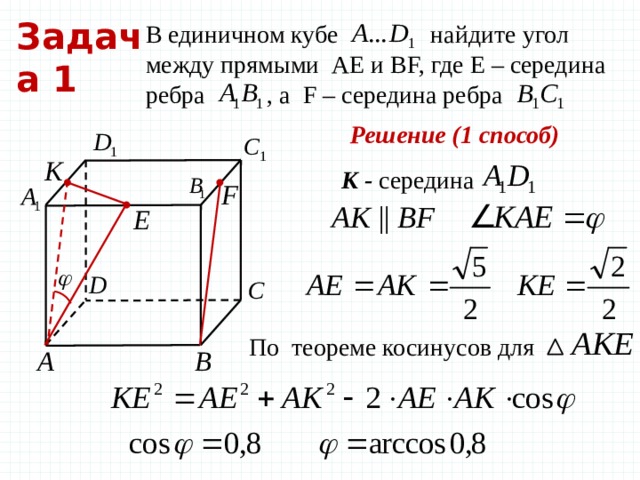
Задача 1

В единичном кубе найдите угол между прямыми AE и BF, где Е – середина ребра , а F – середина ребра

Решение (1 способ)

К — середина

По теореме косинусов для

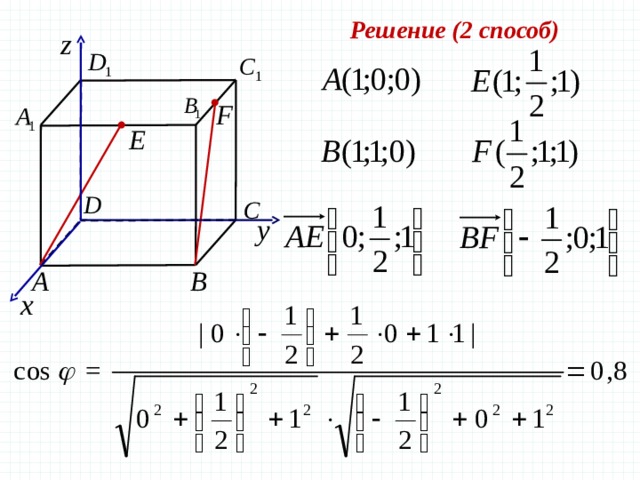
Решение (2 способ)

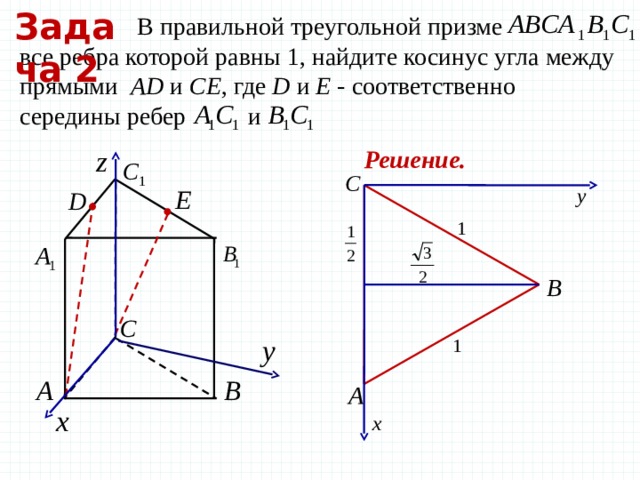
Задача 2

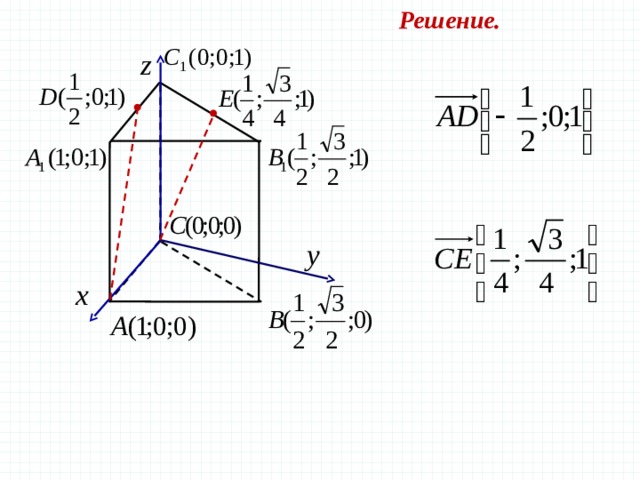
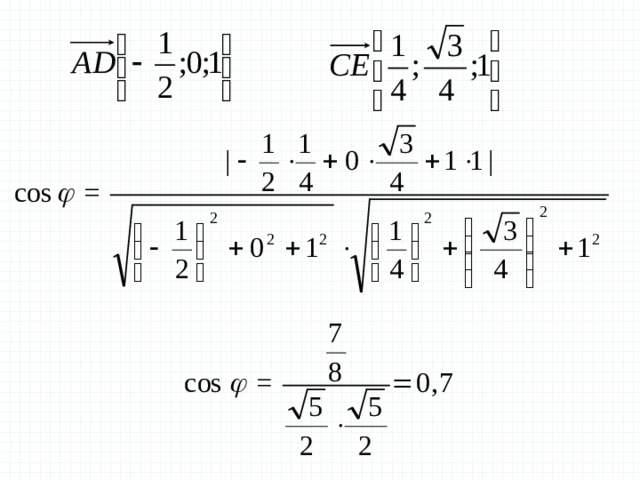
В правильной треугольной призме все ребра которой равны 1, найдите косинус угла между прямыми AD и CE , где D и E — соответственно середины ребер и

Решение.

Координаты правильной треугольной призмы

Решение.

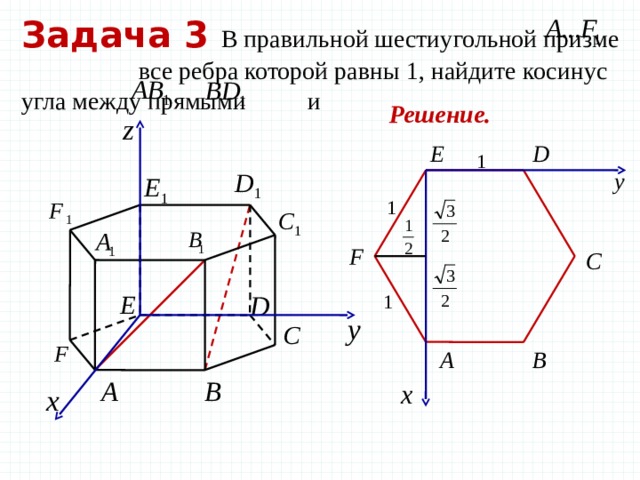
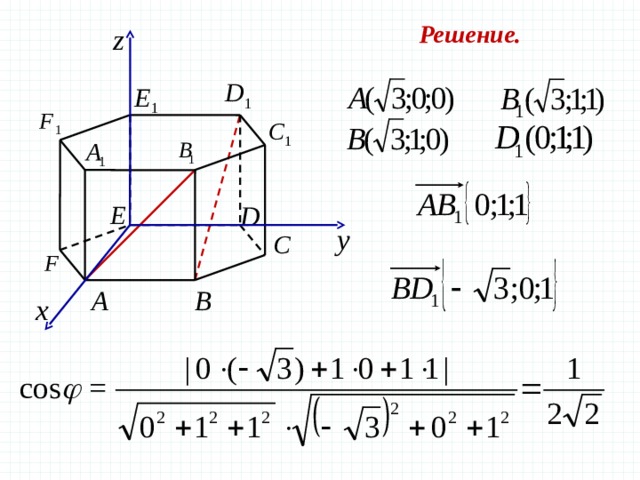
Задача 3 В правильной шестиугольной призме все ребра которой равны 1, найдите косинус угла между прямыми и

Решение.

Координаты правильной шестиугольной призмы

Решение.

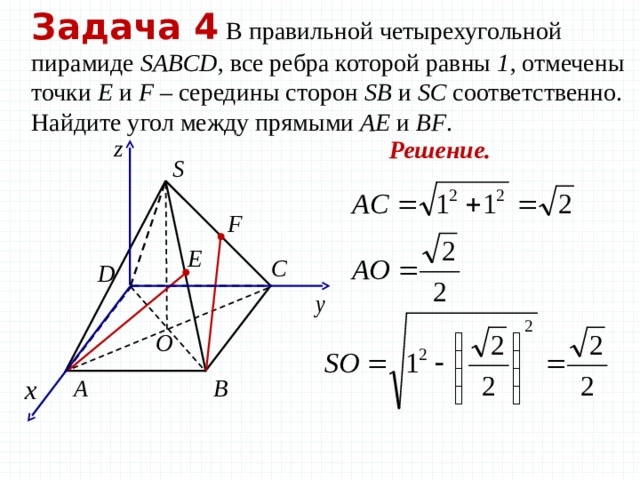
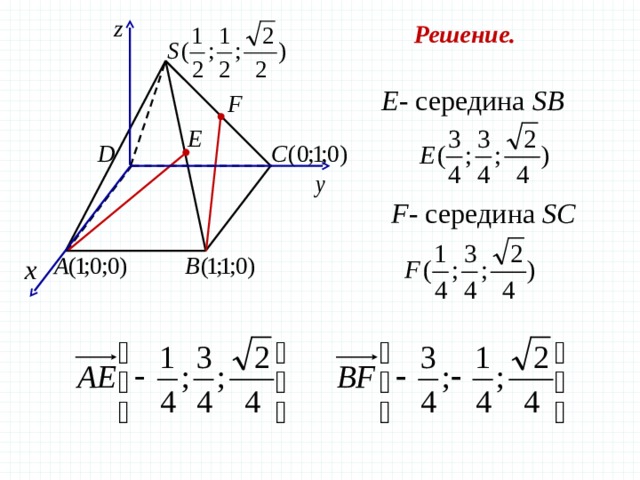
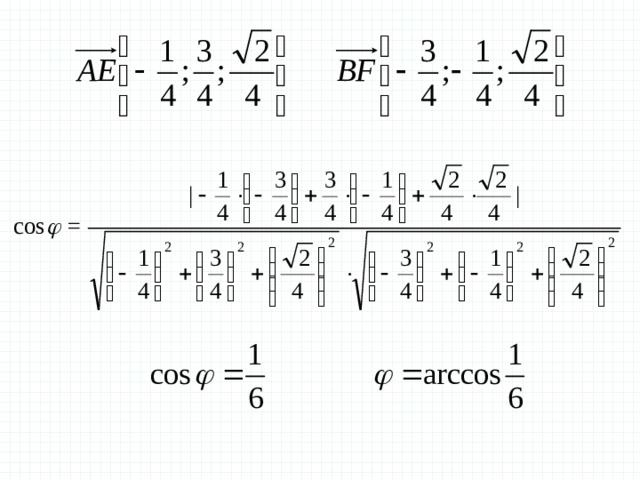
Задача 4 В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1 , отмечены точки Е и F – середины сторон SB и SC соответственно. Найдите угол между прямыми AE и BF .

Решение.

Координаты правильной четырехугольной пирамиды

Решение.

Е — середина SB

F — середина SC

Задача 5 Составить уравнение плоскости, проходящей через точки А(-2;3;5), В(4;-3;0), С(0;6;-5) и найти координаты вектора нормали.

Решение.

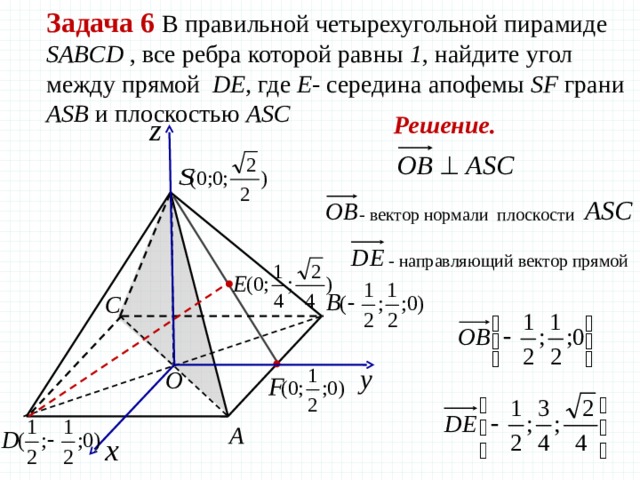
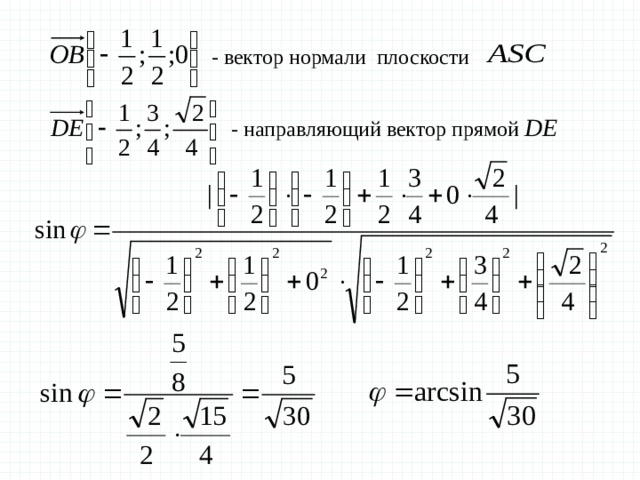
Задача 6 В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1 , найдите угол между прямой DE, где Е — середина апофемы SF грани ASB и плоскостью ASC

Решение.

— вектор нормали плоскости

— направляющий вектор прямой

— вектор нормали плоскости

— направляющий вектор прямой DE

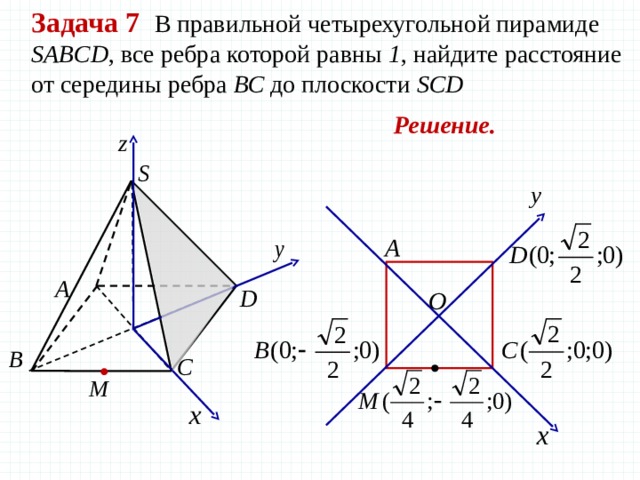
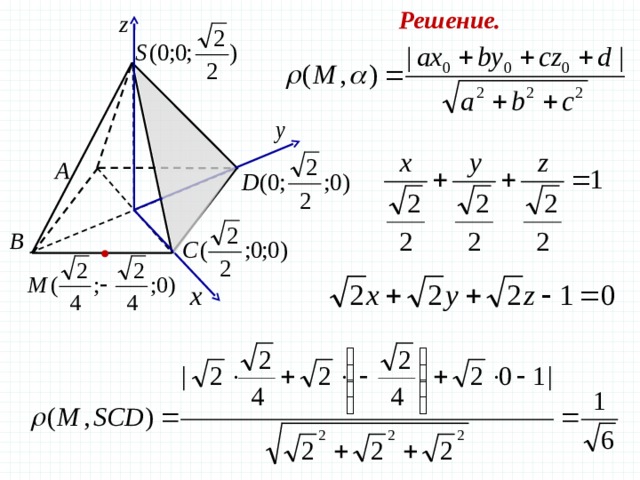
Задача 7 В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1 , найдите расстояние от середины ребра ВС до плоскости SCD

Решение.

Решение.

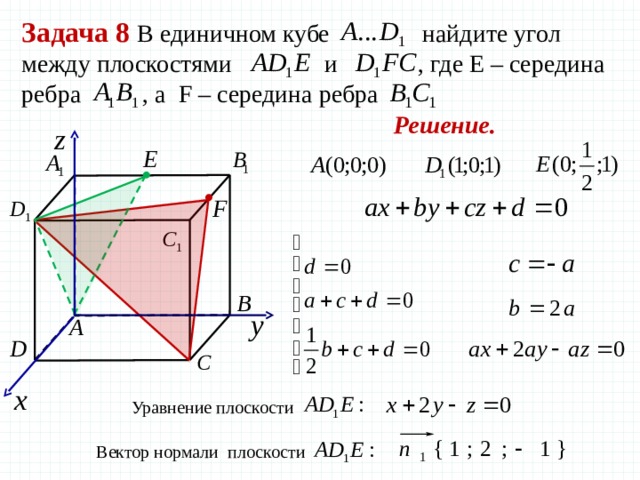
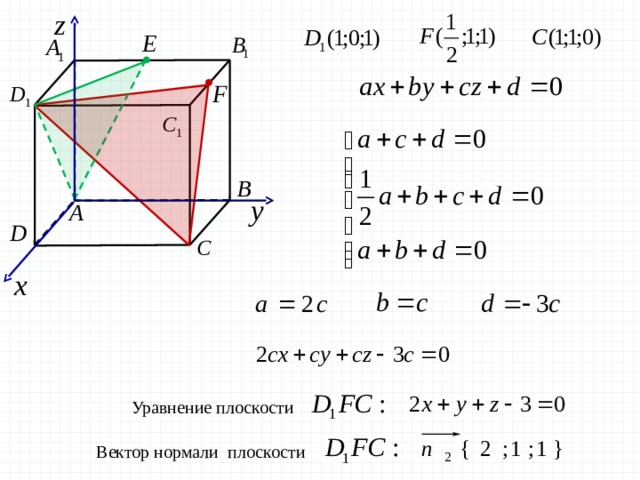
Задача 8 В единичном кубе найдите угол между плоскостями и , где Е – середина ребра , а F – середина ребра

Решение.

Уравнение плоскости

Вектор нормали плоскости

Уравнение плоскости

Вектор нормали плоскости

Задачи для самостоятельного решения

• В правильной четырёхугольной пирамиде SABCD с основанием

ABCD точка М – середина ребра SA, точка К – середина ребра SC.

Найдите угол между плоскостями МВК и АВС, если АВ=4, SC=7.

2. Основанием пирамиды SABC является равносторонний треугольник ABC, сторона которого равна 2√2. Боковое ребро SC перпендикулярно плоскости основания и равно 1. Найдите угол между скрещивающимися прямыми, одна из которых проходит через точку S и и середину ребра ВC, а другая проходит через точку C и середину ребра AB.

8 ноября 2020

В закладки

Обсудить

Жалоба

С помощью данных методических рекомендаций можно научиться решать задачи на вычисление углов и расстояний в стереометрии координатно-векторным методом.

Координатно-векторный метод основан на введении прямоугольной системы координат и создании геометрически-алгебраической модели решения задач, тем самым упрощая громоздкие и достаточно сложные преобразования и выкладки.

Достоинство метода координат состоит в том, что его применение избавляет от необходимости прибегать к наглядному представлению сложных пространственных конфигураций.

→ 14kvm.doc
→ Другое пособие по теме
→ Пособие к 14 задаче
→ Экзаменационные задачи

Муниципальное бюджетное

 общеобразовательное учреждение

«Средняя общеобразовательная школа № 1»

«Решение задач 14

из   заданий

 ЕГЭ – 2016

методом координат»

                                                                     Автор:

                                                                    Шахмарданова Наиля Тимуровнва

                                                                    Россия, Республика Дагестан,

                                                                    г. Каспийск

                                                                    МБОУ «СОШ № 1», 10 «А» класс.

                                                                    Научный руководитель:

                                                                    Шахмарданова Роза Санидиновна,

                                                                   учитель математики

                                                                   МБОУ «СОШ №1», г. Каспийск.

                        Каспийск – 2017

«Решение задач 14 из заданий ЕГЭ – 2016 методом координат»

Автор: Шахмарданова Наиля Тимуровна, Россия, Республика Дагестан,

г. Каспийск, МБОУ «СОШ № 1», 10 «А» класс.

                                                               Наука не является и никогда не будет

                                                               являться законченной книгой.

                                                                                       А. Эйнштейн

        Шахмарданова Наиля Тимуровна – ученица 10 «А» класса «СОШ № 1»     г. Каспийска.

     Представляю Вашему вниманию проект на тему «Решение задач 14 из заданий ЕГЭ – 2016 методом координат».  

                                         Аннотация.    

    Целью моего проекта является определить виды стереометрических задач, включённых в Единый Государственный Экзамен, и методы их решения.

 Объектом исследования являются сами стереометрические задачи.

Предмет исследования: методы решения этих задач.

Планируемый результат: найти более рациональный метод решения стереометрических задач и научиться его применять.

     При написании проекта я изучала различную литературу для подготовки к итоговой аттестации и выяснила, что задачи по стереометрии встречаются в ЕГЭ в блоке повышенного уровня сложности, т.е. в задании 14.  

     Решать такие задачи – по сути задачи аналитической геометрии – можно методом координат.

                                      Введение.

       Немного из истории координатного метода.

      В настоящее время уже очень большое число специалистов из разных областей науки имеют представление о прямоугольных декартовых координатах на плоскости, так как эти координаты дают возможность наглядно при помощи графика изобразить зависимость одной величины от другой. Название «декартовы координаты» наводит на ложную мысль о том, что эти координаты были открыты Декартом. В действительности прямоугольные координаты использовались в геометрии еще до нашей эры. Древний математик александрийской школы Аполлоний Пергский (живший в III-II веке до н. э.) уже фактически пользовался прямоугольными координатами. Он определял и изучал с их помощью хорошо известные в то время кривые: параболу, гиперболу и эллипс.

      Декарт внес в прямоугольные координаты очень важное усовершенствование, введя правила выбора знаков. Но главное, пользуясь прямоугольными координатами, он построил аналитическую геометрию на плоскости, связав этим геометрию и алгебру. Нужно сказать, однако, что одновременно с Декартом построил аналитическую геометрию и другой французский математик, Ферма.

       Сущность метода координат как метода решения задач состоит в том, что, задавая фигуры уравнениями и выражая в координатах различные геометрические соотношения, мы можем решать геометрическую задачу средствами алгебры. Обратно, пользуясь координатами, можно истолковывать алгебраические и аналитические соотношения и факты геометрически и таким образом применять геометрию к решению алгебраических задач.

        Метод координат – это универсальный метод. Он обеспечивает  тесную связь между алгеброй и геометрией, которые, соединяясь, дают «богатые плоды», какие они не могли бы дать, оставаясь разделенными.

        В отношении школьного курса геометрии можно сказать, что в некоторых случаях метод координат дает возможность строить доказательства и решать многие задачи более рационально, красиво, чем чисто  геометрический способ.                

                                   Основная часть.

Итак, задачи 14 из ЕГЭ – 2016. Какие же это задачи?

 Я бы хотела показать Вам разбор задач типа 14 двумя методами: вычислительно-аналитическим и векторно-координатным.

1. Задача на нахождение угла между двумя скрещивающимися прямыми.

• Углом между двумя пересекающимися прямыми называется наименьший из углов, образованных при пересечении прямых.

• 0˚ < ∠(a;b)≤ 90˚ .

• Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся.

• Две прямые называются перпендикулярными,

если угол между ними равен 90˚ .

• Угол между параллельными прямыми считается равным нулю.

• При нахождении угла между прямыми используют:

1) формулу  cosφ  =   для нахождения углаφ  между прямыми m и l , если стороны а и b треугольника АВС соответственно параллельны этим прямым;

1. формулу  cosφ  =   или в координатной форме

cosφ =

для нахождения угла φ между прямыми m и l , если векторы  (х1;у1;z1) и (х2;у2;z2) параллельны соответственно этим прямым; в частности, для того чтобы прямые m и l были перпендикулярны, необходимо и достаточно, чтобы = 0 или x1·x2 + y1·y2+z1·z2 = 0.

Пример.

В кубе ABCDA1B1C1D1 найдите угол  между прямыми A1D и D1E , где Е – середина  ребра CC1 .

Решение.

1-й способ.  

 Пусть F – середина ребра  ВВ1 , а –ребро куба, φ — искомый угол.

Так как A1 F ǁ D1 E  , то φ — угол при вершине  A1 в треугольнике A1FD.

Из треугольника BFD имеем

FD2 = BD2 + BF2 = 2a2 +  = ,

 а из треугольника A1B1F  получаем

A1 F 2 = A1B12 + B1F 2 = a2 + = , откуда

A1F =

Далее в треугольнике A1FD используем теорему косинусов

FD2 = A1D 2 + A1F 2 –2 A1D · A1Fcosφ,

 = 2а2 +—  2 · · cosφ ,  откуда

cosφ =    и  φ = arccos  .

Ответ:  arccos  .

2-й способ.

Введем прямоугольную систему координат, как указано на рисунке.

Не нарушая общности задачи, обозначим длину ребра куба а.

Тогда А1(0; а; а), D(а; а; 0), D1(а; а; а),

 Е(а; 0;  ).

Найдём координаты направляющих векторов прямых A1D и D1E

= , = .

Тогда

сosφ =  =  = .

cosφ =    и  φ = arccos  .

Ответ:  arccos  .

2) Задача на нахождение угла между прямой и плоскостью.

• Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость.

• 0˚ < ∠(a;α ) < 90˚ .

• Угол между взаимно перпендикулярными прямой и плоскостью равен 90˚ .

• Если прямая параллельна плоскости (или лежит в ней), то угол между ними считается равным 0˚ .

   Угол между прямой l и плоскостью α можно вычислить:

1) если этот угол удается включить в прямоугольный треугольник в качестве одного из острых углов;

2) по формуле  sinφ =  или в координатной форме

sin φ =   , где

(x1 ; y1 ; z1) — вектор нормали плоскости α ,

(x2 ; y2 ; z2) — направляющий вектор прямой l;

• прямая l и плоскость α параллельны тогда и только тогда, когда

 x1 x2 + y1 y2 + z1 z2 = 0 .

Пример.

В кубе ABCDA1 B1 C1 D1 точка Е – середина ребра  A1 В1 . Найдите синус угла между прямой АЕ и плоскостью  ВDD1 .

Решение.

1-й способ.

     Угол между прямой АЕ и плоскостью ВDD1 будем искать как угол  между данной плоскостью и прямой DЕ1, параллельной прямой АЕ.

Из точки Е1 опустим перпендикуляр Е1Е2 на прямую В1D1.

Искомый угол – это угол между прямыми DE2 и DE1.

Пусть сторона куба равна а. 

А1С1 =  а.

Е1Е2 = · А1С1 =  · а =  .

DE1 =  = .

=  =  :   =     =  = .

Ответ:  .

2-й способ.

Введем прямоугольную систему координат, как указано на рисунке.

Не нарушая общности задачи, обозначим длину ребра куба а.

За вектор нормали плоскости ВDD1 возьмем вектор

Найдём координаты нужных точек.

А(0; 0; 0), Е(0;  ; а), С(а; а; 0).

Тогда = , = .

sin φ =   =  =  .

Ответ:  .

3)  Задача на нахождение угла между двумя плоскостями.

• Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру.

• Величина двугранного угла принадлежит промежутку (0˚ ;180˚ ).

• Величина угла между пересекающимися плоскостями принадлежит промежутку (0˚ ;90˚ ].

• Угол между двумя параллельными плоскостями считается равным 0˚ .

Угол между пересекающимися плоскостями можно вычислить:

1) как угол между прямыми, лежащими в этих плоскостях и перпендикулярными к линии их пересечения;

2) как угол треугольника, если удается включить линейный угол в некоторый треугольник;

3) как угол между перпендикулярными им прямыми;

4) по формуле 

  или в координатной форме

где  (

 

Пример.

Основание прямой четырехугольной призмы ABCDA1B1C1D1 — прямоугольник ABCD, в котором АВ = 12, AD =  . Найдите косинус угла между плоскостью основания призмы и плоскостью, проходящей через середину ребра AD перпендикулярно прямой  BD1, если расстояние между прямыми AC и  B1D1 равно 5.

Решение.

 1-й способ.

    Решение этой задачи вычислительно-аналитическим методом очень громоздкое и сложное, даже выполнить чертеж к этой задаче крайне сложно, поэтому я его не привела, а методом координат эта задача решается легко и просто.  

2-й способ.

   Легко видеть, что этот угол равен углу между нормалями к этим плоскостям.

 Вектор – вектор нормали плоскости основания.

А вектором нормали плоскости, проходящей через середину ребра АD перпендикулярно прямой ВD1 будет вектор.

   Введем прямоугольную систему координат, как указано на рисунке.

Найдём координаты нужных точек, т.е. точек А, А1, В, D1.

А (0; 0; 0), А1(0; 0; 5), В(0; 12; 0),

 D1(; 0; 5).

Тогда   = , = .

=  =  =

 =  =  .

Ответ:  .

                                       Заключение.

     Я прорешала множество задач типа 14 из литературы, для подготовки к Единому Государственному Экзамену, и выяснила, что стереометрические задачи на нахождение углов в пространстве можно разделить  на три группы:

1. это задачи на нахождение угла между скрещивающимися прямыми,
2. задачи на нахождение угла между прямой и плоскостью и
3.   на нахождение угла между двумя плоскостями.

    Так как, я считаю, что векторно-координатный метод является более рациональным, то я сформулировала алгоритмы решения стереометрических задач данным методом по озвученной теме.

     Алгоритм нахождения угла между скрещивающимися прямыми:

1) мы ввели прямоугольную систему координат,

 2) нашли координаты нужных точек,

3) затем нашли координаты направляющих векторов прямых и

4) вычислили косинус угла между ними.

     Следующий алгоритм несущественно отличается от предыдущего.

Алгоритм нахождения угла между прямой и плоскостью.

Третьим шагом мы должны ввести нормальный вектор к плоскости и найти его координаты, а затем вычислить синус искомого угла. Он равен косинусу угла между направляющим вектором прямой и вектором нормали  к плоскости. 

     При решении задачи на нахождение угла между двумя плоскостями, необходимо найти координаты нормальных векторов к заданным плоскостям и вычислить по формуле модуль косинуса угла между этими векторами.

    Таким образом, я определила виды стереометрических задач на нахождение углов в пространстве, включённых в ЕГЭ. Выявила и освоила более рациональный метод их решения.

      С этой работой я выступила перед учителями нашего города на заседании городского методобъединения. Многих учителей эта работа заинтересовала.

     Изучив различную литературу для подготовки к ЕГЭ, я выяснила, что в блоке задач 14 встречаются задачи на нахождение расстояния между геометрическими фигурами. В дальнейшем я планирую применить векторно-координатный метод к решению задач данного типа. Так как считаю, что этот способ решения более рациональный из изученных мною.

      Написание проекта стало своеобразной подготовкой к итоговой аттестации. Я думаю, что результатом проделанной работы будет верное решение задания повышенного уровня сложности такого типа на итоговой аттестации.

         Собственные достижения:

1. обработка банка заданий 14, разбивка их на группы;
2. выявление и освоение более рационального метода их решения;
3. создание алгоритма решения;
4. использование знаний вне школьной программы.

                                          Литература

1. Газета «Математика» №8, 2016 г, издательский дом «Первое сентября».
2. Математика ЕГЭ – 2016, задания 14, Корянов А.Г., г Брянск.
3. Семенов А.Л, Ященко И.В. ЕГЭ – 2016. Типовые тестовые задания, МИОО, «Экзамен», 2016.