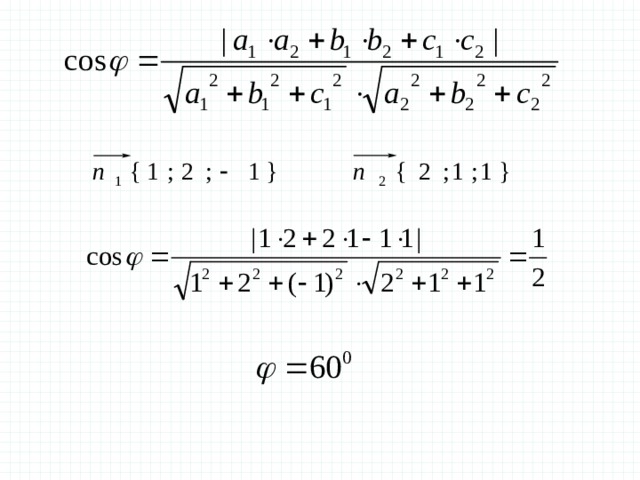1. Готовимся к ЕГЭ. Задача С2. Координатный метод (ключевые задачи).
МБОУ г. Мурманска гимназия №3
Шахова Татьяна Александровна
2.
Координатный метод может быть использован
для нахождения:
1)
2)
3)
4)
5)
6)
7)
длины отрезка (расстояния между точками);
расстояния между прямыми;
расстояния от точки до прямой и плоскости;
угла между прямыми;
угла между прямой и плоскостью;
угла между плоскостями;
нахождения площади сечения.
Первоначальные сведения
о прямоугольной системе координат
смотри по адресу:
http://le-savchen.ucoz.ru/load/4-1-0-183
3.
Ключевые задачи.
1) Нахождение координат точки.
2) Нахождение угла между прямыми.
3) Вывод уравнения плоскости.
4) Нахождение расстояния от точки до плоскости.
5) Нахождение угла между плоскостями.
6) Нахождение угла между прямой и плоскостью.
7) Нахождение расстояния между прямыми.
4.
Определение координат точки.
Справочные материалы.
Как вычислить координаты
внутренней точки
С отрезка АВ, если АС=СВ?
x A xB y A yB z A z B
С
;
;
2
2
2
С
А
Вывод формулы и тренировочные
упражнения с самопроверкой
смотри по адресу:
http://le-savchen.ucoz.ru/load/4-1-0-196
Как вычислить координаты
внутренней точки
С отрезка АВ, если АС:СВ=k?
x A kxB yA kyB z A kz B
С
;
;
k 1
k 1
k 1
В
В
А
С
Назад
5.
Определение координат точки.
Тренировочные упражнения.
Прямоугольный параллелепипед
Правильная шестиугольная призма
Правильная четырехугольная пирамида
Правильная треугольная пирамида
6.
Определение координат точки.
ABCDA1B1C1D1 – прямоугольный параллелепипед. AB=2,
AD=4, AA1=2, А1К=КВ1, АМ:МС=2:3, KL=LM .
Определите координаты точек A, C, А1, В1, К, М, L.
Z
С1
D1
К
А1
2
X
Задачи
C(?;?;?)
C(0;2;0)
B1(?;?;?) B1(4;2;2)
К(?;?;?) К(4;1;2)
M(?;?;?) ?
x kxC y A kyC z A kzC
M A
;
;
k 1
k 1
k 1
Y
М
А
А1(?;?;?) А1(4;0;2)
С
D
4
А(4;0;0)
В1
L
2
А(?;?;?)
В
2
2
2
4
0
0
2
0
0
3 ;
3 ;
3 12 ; 4 ;0
2
2
2 1
5
5
1
1
3
3
3
7.
Определение координат точки.
ABCDA1B1C1D1 – прямоугольный параллелепипед. AB=2,
AD=4, AA1=2, А1К=КВ1, АМ:МС=2:3, KL=LM .
Определите координаты точек A, C, А1, В1, К, М, L.
Z
К(4;1;2)
С1`
D1
L(?;?;?) ?
К
А1
С
D
4
2
X
Задачи
Y
М
А
xK xM yK yM z K zM
L
;
;
2
2
2
В1
L
2
12 4
M ; ;0
5 5
В
12
4
1
4
2 0
5
5
;
;
2
2
2
22 9
; ;1
10 10
8.
Определение координат точки.
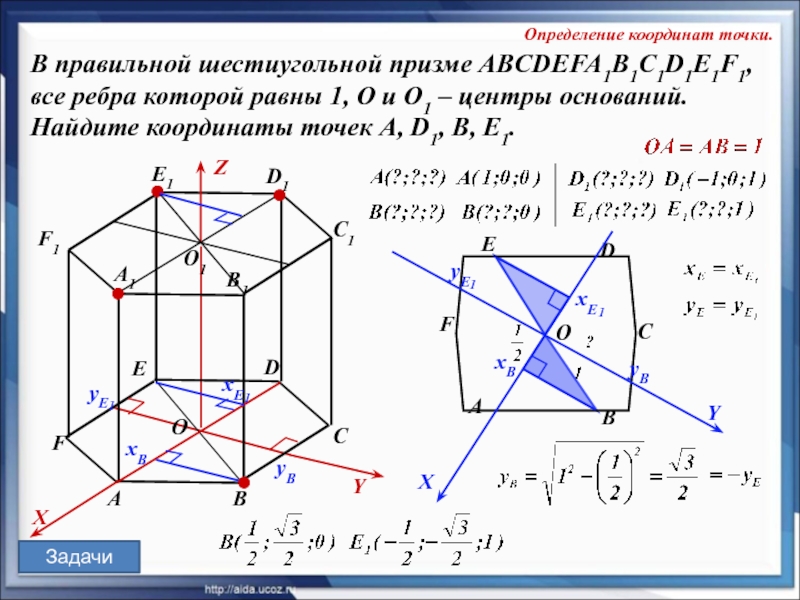
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1,
все ребра которой равны 1, O и О1 – центры оснований.
Найдите координаты точек А, D1, B, E1.
Z
E1
F1
A1
О1
А(?;?;?) А( 1 ;0 ;0 )
D1
C1
В(?;?;?) В(?; ?;0 )
Е
D
yЕ1
B1
хЕ 1
yЕ1
F
X
хB
A
Задачи
1
2
хB
D
A
О
C
yB
x E x E1
хЕ 1
F
E
OA AB 1
D1 (?;?;?) D1 ( 1;0 ;1 )
Е1 (?;?;?) Е1 (?;?;1 )
О ?
y E y E1
C
yB
1
Y
B
2
Y
X
3
1
уЕ
уВ 12
2
2
B
1
3
1 3
В( ;
;0 ) Е 1 ( ;
;1 )
2
2
2 2
9.
Определение координат точки.
SABCD – правильная пирамида, все ребра которой равны 1.
SL=LC, SK:KO=1:2, KM=MC .
Определите координаты точек C, S, O, L, К, M.
Z
C(?;?;?) C(0;1;0)
S(?;?;?) S(?;?;1)
О(?;?;?) О(?;?;0)
S
D
Y
xO(xS )
М
D
X
С
L
К
А
yO(yS )
С
Y
А
X
O
В
O
В
1 1
O ; ;0
2 2
1 1
S ; ;1
2 2
L(?;?;?) ?
1
1
1
0
1
0
1 3 1
x S xC y S yC z S zC 2
2
2
; ;
;
;
L
;
;
4 4 4
2
2
2
2
2 2
10.
Определение координат точки.
SABCD – правильная пирамида, все ребра которой равны 1.
SL=LC, SK:KO=1:2, KM=MC .
Определите координаты точек C, S, O, L, К, M.
Z
1 1 O 1 ; 1 ;0
S ; ;1
2 2
2 2
S
K(?;?;?) ?
L
К
М
D
А
X
Задачи
x S kxO y S kyO z S kzO
K
;
;
k 1
k 1
k 1
С
Y
O
1
1 1 1 1 1 1
1
0
В
2 1 ;1 ;2
2 2 2 ;2 2 2 ;
1
1
1 1
2
2
3
1
1
2
2
2
11.
Определение координат точки.
SABCD – правильная пирамида, все ребра которой равны 1.
SL=LC, SK:KO=1:2, KM=MC .
Определите координаты точек C, S, O, L, К, M.
Z
1 1 2
K ; ;
2 2 3
S
C(0;1;0)
M(?;?;?) ?
L
К
М
D
А
X
Задачи
xC x K yC y K zC z K
M
;
;
2
2
2
С
Y
O
В
2
1
1
0
0
1
1 3 1
3
2
2
; ;
;
;
2
2 4 4 3
2
12.
Определение координат точки.
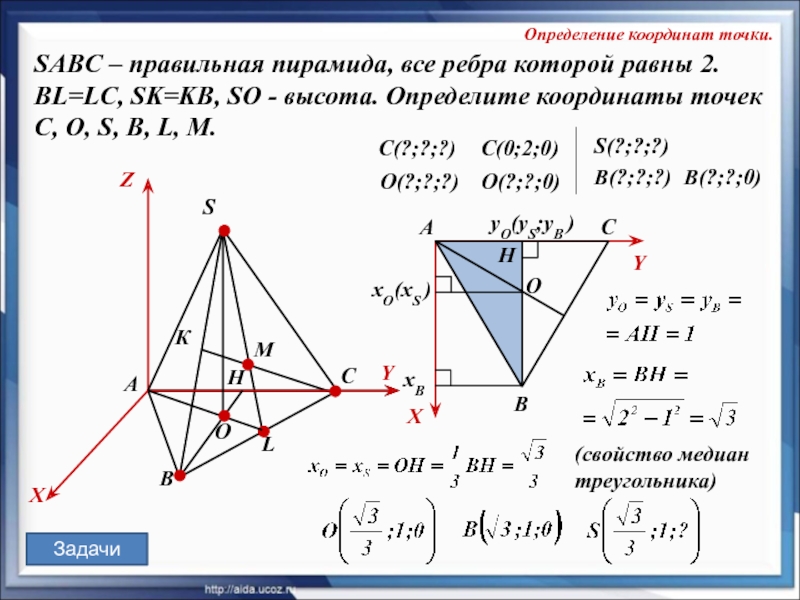
SABC – правильная пирамида, все ребра которой равны 2.
BL=LC, SK=KB, SO — высота. Определите координаты точек
C, О, S, В, L, M.
C(?;?;?) C(0;2;0)
О(?;?;?) О(?;?;0)
Z
S
yO(yS;уВ )
H
O
А
xO(xS )
К
O
В
X
Задачи
С
Y
yO yS уВ
хВ BH
Y x
В
В
X
L
С
AH 1
М
H
А
S(?;?;?)
В(?;?;?) В(?;?;0)
xO xS ОН
3
O
;1 ;0
3
2 2 12 3
1
3
BH
3
3
В 3 ;1;0
(свойство медиан
треугольника)
3
S
;1 ;?
3
13.
Определение координат точки.
SABC – правильная пирамида, все ребра которой равны 2.
BL=LC, SK=KB, SO — высота. Определите координаты точек
C, О, S, В, L, M.
3
S
;1 ;?
3
Z
S
ВО
BH 3
zS SO
2
2 3
ВН
3
3
Из треугольника ВОS
К
С
А
O
В
X
Задачи
2
М
Y
X
L
2 3
2 6
z S SO 2
3
3
2
3
2 6
S
;1 ;
3
3
14.
Определение координат точки.
SABC – правильная пирамида, все ребра которой равны 2.
BL=LC, SK=KB, SO — высота. Определите координаты точек
C, О, S, В, L, M.
C(0;2;0)
Z
B
3 ;1;0
S
L(?;?;?) (середина отрезка ВС) ?
x xC yB yC z B zC
L B
;
;
2
2
2
К
М
С
А
O
В
X
Задачи
Y
X
L
3 0 1 2 0 0
;
;
2
2
2
3 3
L
; ;0
2 2
15.
Определение координат точки.
SABC – правильная пирамида, все ребра которой равны 2.
BL=LC, SK=KB, SO — высота. Определите координаты точек
C, О, S, В, L, M.
3
2 6
S
;1 ;
3
3
Z
S
3 3
L
2 ; 2 ;0
М(?;?;?)
К
М
С
А
O
В
X
Задачи
М – точка пересечения медиан
треугольника BSC => SМ:ML=2:1 ?
Y
X
L
x S kx L y S ky L z S kz L
M
;
;
k 1
k 1
k 1
3
3
3 2 6
2
2 0 4 3 4 2 6
1 2
2 ;
2; 3
; ;
3
2 1
2 1
2 1 9 3 9
16.
Нахождение угла между прямыми.
Алгоритм.
1 ) АВ xB x A ; yB yA ; zB z A
СD x D xC ; yD yC ; z D zC
направляющие векторы
D
2 ) АВ CD x x y y z z
AB
CD
AB
CD
3)
С
2
2
AB
AB
AB
В
CD
А
АВ x y z
2
AB
CD x 2 y2 z 2
CD
CD
CD
AB CD
4 ) cos ( AB; CD )
AB CD
Назад
17.
C(0;2;0) В 3 ;1;0
Нахождение угла между прямыми.
Найдите угол между
прямыми CВ и OS.
3
2 3
O
;1 ;0 S
;1; 3
3
3
СВ
3 0 ;1 2;0 0 3 ; 1;0
2 3
3
OS
;1 1; 3 0
3
3
3
3
( 1 ) 0 0
3
CB OS
cos ( СB; OS )
3
3
0 2 ( 3 )2
( 3 ) ( 1 ) 0
3
1 0 0
1
3
30
1
10
2 10
20
3 1 0
0 3
2
3
3
CB OS
2
3
;0 ; 3
3
2
2
( СB; OS ) arccos
2
30
20
Алгоритм
18.
Вывод уравнения плоскости ax+by+cz+d=0.
Алгоритм.
1) Подставить в уравнение плоскости
координаты точек А,В и С.
А
В
ax A byA cz A d 0
ax B byB cz B d 0
ax by cz d 0
C
C
C
С
2) Решить систему — выразить а, b и с через d; либо а, b и d через с;
либо а, с и d через b, либо c, b и d через a в зависимости от
составленной системы.
3) Подставить выраженные коэффициенты в исходное
уравнение и преобразовать к удобному виду.
Назад
19.
А 3;1;1
В 3;1;3
С 2;3;2
Вывод уравнения плоскости.
Запишите уравнение плоскости (АВС)
3a b c d 0
2с 0 с 0
3a b 3c d 0
2 a 3b 2 c d 0
3a b d 0
а 2b 0 a 2b
2 a 3b d 0
ax by cz d 0
2 bx by 0 z 7 b 0 b
2x y 7 0
6 b b d 0 7 b d 0 d 7 b
Алгоритм
20.
Вывод уравнения плоскости.
1 3 1 3
;0
А ;
;0 С ;
Запишите уравнение плоскости (АВС)
2 2
2 2
В 1;0 ;1
1
3
a
b 0 c d 0
3
2
2
3b 2 d 0 d
b
2
1
3
b 0 c d 0
a
2
2
1 a 0 b 1 c d 0
ax by cz d 0
3
3
0 x by
bz
b 0
1
3
3
2
2
a
b
b 0 a 0
2
2
2
3
3
y
z
0 2
3
2
2
c
b 0 c 3 b
2
2
2 y 3z 3 0
b
Алгоритм
21.
Нахождение расстояния от точки до плоскости.
Алгоритм.
А
Если плоскость α задана уравнением
ax by cz d 0 ,
то расстояние от точки А до
плоскости α можно найти
по формуле:
( A; )
α
ax A byA cz A d
a2 b2 c 2
Назад
22.
: 2 x 3 y 3z 3 0
1 3
А ;
; 2
2 2
2
( A; )
Расстояние от точки плоскости.
Найдите расстояние от точки А
до плоскости α.
1
3
3
3 ( 2 ) 3
2
2
2 2 ( 3 )2 ( 3 )2
1
3
2 3 3
2
4 3 3
5
3 3
3 3 2 ,5
2
10
10
Алгоритм
23.
Нахождение угла между плоскостями.
Алгоритм.
α
Если плоскости α и β заданы уравнениями
a1 x b1 y c1z d1 0 и a2 x b2 y c2 z d2 0
β
соответственно, то
a a1 ; b1 ; c1 — вектор нормали (перпендикуляра) плоскости α,
b a2 ; b2 ; c2 — вектор нормали плоскости β.
Угол между плоскостями равен углу
между нормалями этих плоскостей.
cos ( ; ) cos ( a ; b )
Алгоритм
Назад
24.
Угол между плоскостями.
: 2 x 3 y 3z 3 0
Найдите угол между плоскостями α и β.
: x 2 3 y 3z 7 0
b 1;2
a 2; 3 ; 3
3 ; 3
— нормали плоскостей α и β.
a b
cos ( ; )
a b
2 6 3
4 3 3 1 3 3
2 1 3 2 3 3 ( 3 )
2 ( 3 ) ( 3 ) 1 ( 3 ) ( 3 )
2
2
5
10 7
( ; ) arccos
2
2
2
2
5
5 70
70
70
14
70
70
14
Алгоритм
25.
Нахождение угла между прямой и плоскостью.
Алгоритм.
Если плоскость α задана уравнением
ax by cz d 0 ,
А
a a ; b ; c — вектор нормали плоскости α,
В
?
направляющий
вектор прямой
АВ b имеет координаты p; q; r ,
то угол между прямой АВ и
плоскостью α можно по
формуле:
b
α
sin ( AB ; ) cos a b
a b
a b
Назад
26.
Угол между прямой и плоскостью.
: 2 x 3 y 3z 3 0
А 3; 1; 1 В 3;1;3
a 2; 3 ; 3
Найдите угол между плоскостямью α
и прямой АВ.
— вектор нормали плоскости α
AB 3 3 ;1 ( 1 ); 3 ( 1 ) 0 ;2;4 — направляющий вектор прямой АВ
a b
sin
a b
2 0 2 3 4 3
2 ( 3 ) ( 3 ) 0 2 4
2
2
6 3
4 3 3 0 4 16
2
2
2
2
6 3
6 3
6 3
3 3 3 6
10
10 20
200 10 2 5 2
( ; AB ) arcsin
3 6
10
Алгоритм
27.
Нахождение расстояния между прямыми.
Алгоритм.
1) Определить координаты
М
направляющих векторов AB и CD .
B
Пусть MK AB , CD , тогда
выполнено
AB MK 0
C
условие: CD MK 0.
К
2) Из системы определить
координаты MK , затем найти MK ( a ; b )
А
a
b
D
Замечание: для записи координат точек М и К воспользоваться
формулой:
x A kx B y A kyB z A kz B
;
;
k 1
k 1
k 1
Если АМ:МВ=k, то M
Назад
28.
A 0 ;0 ;0 В 0 ;1;0
С 0 ;1;1 D 1;0 ;1
Нахождение угла между прямыми.
Найдите расстояние между
C
прямыми AC и BD.
М
AC 0 0 ;1 0 ;1 0 0 ;1;1
B
А
К
BD 1 0 ;0 1;1 0 1; 1;1
Пусть MK AB, CD, АМ:МС=k, BK:KD=n, тогда:
k
k
x A kxC yA kyC z A kzC
;
M
;
;
0;
k 1
k 1 k 1 k 1
k 1
x nxD yB nyD z B nzD
K B
;
;
n 1
n 1
n 1
1
n
n
;
;
n
1
n
1
n
1
D
k
p
k 1
Если
n
q,
n 1
то M 0 ; p; p , K q;1 q; q , MK q ;1 q p ; q p .
AС MK 0 0 q 1 ( 1 q p ) 1 ( q p ) 0
MK AB, CD
BD MK 0. 1 q ( 1 ) ( 1 q p ) 1 ( q p ) 0.
Алгоритм
29.
A 0 ;0 ;0 В 0 ;1;0
С 0 ;1;1 D 1;0 ;1
Нахождение угла между прямыми.
Найдите расстояние между
C
прямыми AC и BD.
М
MK q ;1 q p ; q p
B
0 q 1 ( 1 q p ) 1 ( q p ) 0
1 q ( 1 ) ( 1 q p ) 1 ( q p ) 0.
1 q p q p 0
q 1 q p q p 0
1 2 p 0
1 3q 0
1 1 1
1
MK ;1 ;
3 2 3
3
1 1 ; 1 ; 1
2 3 6 6
2
2
D
1
p
1 2 p 0
2
1 3q 0
1
q
3
2
1 1 1
MK ( AC ; BD )
3 6 6
А
1
1
9
81
Алгоритм
30.
При создании презентации использовано
пособие:
http://www.alleng.ru/d/math/math784.htm
15.04.2017
30
Аннотация:
Данная презентация продолжает рассказ о координатном методе решения задач С2 на ЕГЭ, предназначена ученикам 11-х классов и будет полезна при подготовке к экзамену. Данную разработку можно использовать при дистанционном обучении. В презентации рассматриваются такие темы, как «Угол между прямыми», «Угол между прямой и плоскостью», «Угол между плоскостями».
Целевая аудитория: для 11 класса
Автор: Лещенко Светлана Ивановна
Место работы: МБОУ СОШ № 8 г. Туапсе
Добавил: ячс1319
Уважаемые коллеги! Автор ждёт Ваши отзывы! Оставьте своё мнение о разработке!
Всего комментариев: 4
Порядок вывода комментариев:

Физкультминутки
Физкультминутки обеспечивают кратковременный отдых детей на уроке, а также способствуют переключению внимания с одного вида деятельности на другой.

В помощь учителю
Уважаемые коллеги! Добавьте свою презентацию на Учительский портал и получите бесплатное свидетельство о публикации методического материала в международном СМИ.
Для добавления презентации на портал необходимо зарегистрироваться.
Конкурсы
Диплом и справка о публикации каждому участнику!
© 2007 — 2023 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.
Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.
Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.
Фотографии предоставлены
Слайд 1
Метод координат при решении задач по подготовке к ЕГЭ
Слайд 2
Координаты многогранников. Учитель ГБОУ Школа № 1897 Шаповалова Е.Д.
Слайд 3
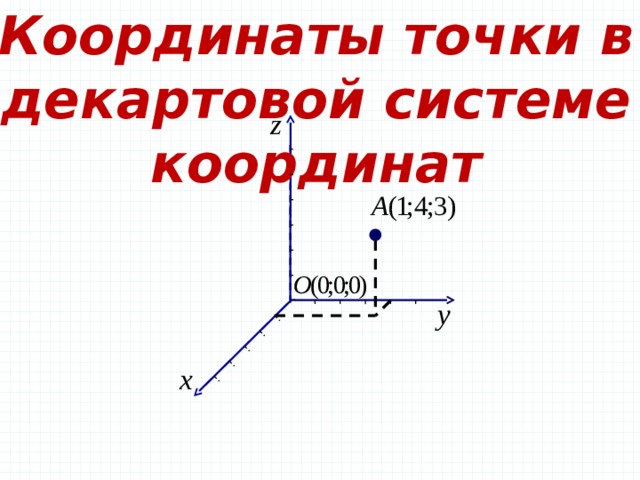
Единичный куб. х у z D (0; 0; 0) A (1; 0; 0) C (0; 1; 0) B (1; 1; 0 ) D 1 (0; 0; 1) A 1 (1; 0; 1) C 1 (0; 1 ; 1) B 1 (1; 1; 1)
Слайд 4
Прямоугольный параллелепипед. х у z D (0; 0; 0) A (a; 0; 0) C (0; b; 0) B (a; b ; 0) D 1 (0; 0; c) A 1 (a; 0; c) C 1 (0; b; c ) B 1 (a; b ; c ) a b c
Слайд 5
Правильная шестиугольная призма. х у C F D E B A a a C (a; 0;0) F (- a; 0;0) х у z C 1 (a; 0;c) F 1 (- a; 0;c) a c
Слайд 6
Правильная треугольная призма. С 1 А В С А 1 В 1 c a х у z O
Слайд 7
Правильная треугольная пирамида. х y O z H h
Слайд 8
Правильная четырехугольная пирамида. a h х y z h
Слайд 9
Правильная шестиугольная пирамида. х y z a h C (a; 0;0) F (- a; 0;0)
Слайд 10
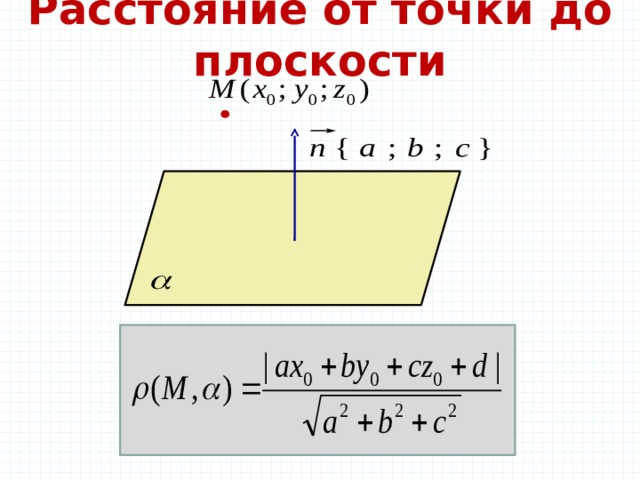
Расстояние от точки до плоскости.
Слайд 11
Расстояние от точки М( x 0 ;y 0 ;z 0 ) до плоскости ax + by + cz + d = 0 . Например:
Слайд 12
Уравнение плоскости, проходящей через три точки. Уравнение плоскости имеет вид Числа a, b, c находим из системы уравнений
Слайд 13
Например: Написать уравнение плоскости, проходящей через точки — уравнение плоскости, проходящей через три данные точки.
Слайд 14
№ 1 В единичном кубе АВС DA 1 B 1 C 1 D 1 найдите расстояние от точки А 1 до плоскости (BDC 1 ) . х у z A 1 (1; 0; 1) D (0; 0; 0) B (1; 1; 0 ) C 1 (0; 1 ; 1) Запишем уравнение плоскости DBC 1 .
Слайд 15
A 1 (1; 0; 1) Найдем искомое расстояние по формуле Ответ:
Слайд 16
х у z № 2. В правильной шестиугольной призме все ребра равны 1. Найдите расстояние от точки А до плоскости (DEF 1 ) F 1 (- 1; 0;1) Запишем уравнение плоскости DC 1 F 1 . C 1 (1; 0;1) 1 1
Слайд 18
Найдем искомое расстояние по формуле Ответ:
Слайд 19
Расстояние между скрещивающимися прямыми.
Слайд 20
Расстоянием между скрещивающимися прямыми называется расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через вторую прямую, параллельно первой. b c A B
Слайд 21
№ 1. В единичном кубе найдите расстояние между прямыми А D 1 и В D . х у z
Слайд 22
A (1; 0; 0 ) D (0; 0; 0 ) B (1; 1; 0 ) C 1 (0; 1; 1) Запишем уравнение плоскости BDC 1 . Найдем искомое расстояние по формуле
Слайд 23
A (1; 0; 0 ) Ответ:
Слайд 24
№ 2. В правильной четырехугольной пирамиде SABCD все ребра равны 1. Найдите расстояние между прямыми А S и ВС. х y z 1 1 h O
Слайд 25
Запишем уравнение плоскости ADS .
Слайд 26
Найдем искомое расстояние по формуле Ответ:
Слайд 27
Литература : Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения. МАТЕМАТИКА ЕГЭ 2011 (типовые задания С2) 18.02.2011 www.alexlarin.narod.ru
1
2
Исследование выполнил: ученик 11 а класса сш 177 САБИРОВ ИЛЬДАР Научный руководитель: учитель математики высшей категории Хабибуллина А.Я Научный руководитель: учитель математики высшей категории Хабибуллина А.Я
3
Координатный метод решения заключается во введении (привязке к исследуемым фигурам) декартовой системы координат, а затем – исчислении образующихся векторов (их длин и углов между ними). Мы уже хорошо знакомы с векторами, координатами и их свойствами. Цель моей работы: научиться применять знания для решения задач стереометрии (С2).
4
Алгоритм применения метода координат к решению геометрических задач сводится к следующему: Выбираем в пространстве систему координат из соображений удобства выражения координат и наглядности изображения. Выбираем в пространстве систему координат из соображений удобства выражения координат и наглядности изображения. Находим координаты необходимых для нас точек. Находим координаты необходимых для нас точек. Решаем задачу, используя основные задачи метода координат. Решаем задачу, используя основные задачи метода координат. Переходим от аналитических соотношений к геометрическим. Переходим от аналитических соотношений к геометрическим.
5
В задании С2 чаще всего требуется найти: угол между двумя скрещивающимися прямыми, угол между двумя скрещивающимися прямыми, угол между прямой и плоскостью, угол между прямой и плоскостью, угол между двумя плоскостями, угол между двумя плоскостями, расстояние между двумя скрещивающимися прямыми, расстояние между двумя скрещивающимися прямыми, расстояние от точки до прямой, расстояние от точки до прямой, расстояние от точки до плоскости. расстояние от точки до плоскости.
6
Углом между скрещивающимися прямыми называется угол между двумя прямыми, параллельными им и проходящими через произвольную точку. При нахождении угла между прямыми используют формулу или в координатной форме При нахождении угла между прямыми используют формулу или в координатной форме для нахождения угла φ между прямыми m и l, если векторы и параллельны соответственно этим прямым; в частности, для того чтобы прямые m и l были перпендикулярны, необходимо и достаточно, чтобы или.
7
Задача на нахождение угла между скрещивающимися прямыми. Сторона основания правильной четырехугольной призмы ABCDA1B1C1D1 равна 2, высота 4. Точка E середина отрезка CD, точка F середина отрезка AD. Найдите угол между прямыми CF и B1E.
8
Решение х С у А F D E B z B 1 C 1 A 1 D 1 Поместим параллелепипед в прямоугольную систему координат, как показано на рисунке, и найдём искомый угол как угол между векторами. Выпишем координаты точек B1, E, C, F в этой системе координат:B1 (0; 0; 4), E(1; 2; 0), C (0; 2; 0), F (2; 1; 0). Поместим параллелепипед в прямоугольную систему координат, как показано на рисунке, и найдём искомый угол как угол между векторами. Выпишем координаты точек B1, E, C, F в этой системе координат: B1 (0; 0; 4), E(1; 2; 0), C (0; 2; 0), F (2; 1; 0). Тогда {2; -1; 0}, {1; 2; -4}. Найдём угол между этими векторами по формуле: То есть искомый угол α=90˚. Ответ: 90˚.
9
Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и её проекцией на данную плоскость. Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и её проекцией на данную плоскость. Угол между прямой l и плоскостью α можно вычислить: 1) по формуле ; 2) по формуле или в координатах, где — вектор нормали к плоскости α, — направляющий вектор прямой l
10
Задача на нахождение угла между прямой и плоскостью. В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра АВ и АА1 равны 1, а ребро АD=2. Точка Е – середина ребра В1С1. Найдите угол между прямой ВЕ и плоскостью АВ1С.
11
Решение Для решения этой задачи необходимо воспользоваться уравнением плоскости, имеющим общий вид ах+by+cz+d=0, где a, b и c – координаты нормали к плоскости. Чтобы составить это уравнение, необходимо определить координаты трёх точек, лежащих в данной плоскости: А(1; 0; 0), В1(0;0;1), С(0;2;0). Решая систему находим коэффициенты а, b и с уравнения ах+by+cz+d=0: а=-d, b=, c=-d. Таким образом, уравнение примет вид или, после упрощения, 2 х+у+2z-2=0. Значит нормаль n к этой плоскости имеет координаты.
12
Длину вектора легко найти геометрически: Но его координаты нам всё равно необходимы. Из простых вычислений находим, что. Найдем угол между вектором и нормалью к плоскости по формуле скалярного произведения векторов: Ответ: 45˚
13
Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру. Угол между двумя пересекающимися плоскостями можно вычислить: 1)по формуле 2) как угол между нормалями по формуле или в координатной форме где — вектор нормали плоскости А1 х+В1 у+С1z+D1=0, — вектор нормали плоскости A2x+B2y+C2z+D2=0. — вектор нормали плоскости A2x+B2y+C2z+D2=0.
14
Задача на нахождение угла между двумя плоскостями. В единичном кубе АВСDA1В1С1D1 найдите угол между плоскостями АD1 Е и D1FC, где точки Е и F- середины ребер А1В1 и В1С1.
15
Решение. Введём прямоугольную систему координат. Тогда А(0;0;0), С(1;1;0), D1(1;0;1), E(0;0,5;1), F(0,5;1;1). 1) Решая систему составляем уравнение плоскости АD1E: x+2y-z=0. 2) плоскость CFD1: отсюда находим уравнение 2x+y+z-3=0. Найдём искомый угол как угол между нормалями плоскостей:, откуда φ=60˚ Ответ: 60˚
16
Расстояние между точками А и В можно вычислить: 1) по формуле, где A(x1; y1; z1), B(x2; y2; z2); 2) по формуле.
17
Задача на нахождение расстояния между двумя точками. В основании пирамиды SABCD лежит ромб со стороной 2 и острым углом в 60˚. Боковое ребро SA перпендикулярно основанию пирамиды и равно 4. Найдите расстояние от середины Н ребра SD и серединой М ребра ВС.
18
Решение. Поместим пирамиду в прямоугольную систему координат, как показано на рисунке. Найдём координаты точки Н как координаты середины отрезка SD: S(0; 0; 4), D(0; 2; 0). Чтобы найти координаты точек В и С, найдём координаты их проекций на оси. АВх=ACx=2·cos30˚=, ABy=ACу–2=2·cos60˚=1. Отсюда В( ;1;0), С( ;3;0). Тогда координаты точки М равняются: Теперь находим расстояние между точками, заданными своими координатами: Ответ:
19
Задача. В единичном кубе АВСDA1В1С1D1 точки Е и К – середины ребер АА1 и СD соответственно, а точка М расположена на диагонали В1D1 так, что В1М = 2МD1. Найдите расстояние между точками Q и L, где Q – середина отрезка ЕМ, а L – точка отрезка МК такая, что ML=2LK.
20
Решение. Введём декартову систему координат. E(1;0;0,5), K(0,5;1,0), В1(0;0;1), D1(1;1;1). Чтобы вычислить координаты т.М, воспользуемся формулой для нахождения координат точки, которая делит отрезок B1D1 в отношении λ=2:1: Аналогично находим координаты точки L:
21
Координаты точки Q находим по формуле координат середины отрезка:. Ответ:.
22
Расстояние от точки до плоскости, не содержащей эту точку, есть длина отрезка перпендикуляра, опущенного из этой точки на плоскость. Расстояние от точки М до плоскости α 1)вычисляется по формуле, где ρ=ρ(М;α), ρ1=ρ(М1;α), ОМ=r, ОМ1=r1, ММ1 α=0; в частности, ρ=ρ1, если r=r1: прямая m, проходящая через точку М, пересекает плоскость α в точке О, а точка М1 лежит на прямой m; вычисляется по формуле, 2) вычисляется по формуле, где М(х 0;у 0;z0), плоскость α задана уравнением ax+by+cz+d=0;
23
Задача на нахождение расстояния от точки до плоскости. В кубе АВСDA1B1C1D1 проведена диагональ B1D. В каком отношении, считая от вершины B1, плоскость А1BC1 делит диагональ B1D?
24
Решение. Составим уравнение плоскости А1BC1 и найдём расстояние от этой плоскости до каждой из точек B1 и D. Пусть l – ребро куба. В(0;0;0), А1(l;0;l), С1(0;l;l). Решив систему определяем, что уравнение плоскости имеет вид: x+y–z=0 а=1, b=1, c= –1. B1(0;0;1), D(1;1;0). Теперь найдём расстояние от каждой точки до плоскости по формуле Ответ: 2:1.
25
Задача. Основание прямой призмы АВСА1В1С1 – равнобедренный треугольник АВС, основание АС и высота ВD которого равны 4. Боковое ребро равно 2. Через середину К отрезка В1С проведена плоскость, перпендикулярная к этому отрезку. Найдите расстояние от вершины А до этой плоскости. Задача. Основание прямой призмы АВСА1В1С1 – равнобедренный треугольник АВС, основание АС и высота ВD которого равны 4. Боковое ребро равно 2. Через середину К отрезка В1С проведена плоскость, перпендикулярная к этому отрезку. Найдите расстояние от вершины А до этой плоскости.
26
Решение. Выберем систему координат как показано на рисунке и выпишем координаты вершин данной призмы и точки К в этой системе координат: А(0;–2;0), В(0;0;0), С(0;2;0), В1(4;0;2), К(2;1;1). Тогда. Этот вектор перпендикулярен плоскости, значит, он является его нормалью. К тому же плоскость проходит через точку К. То есть уравнение плоскости имеет вид –2(x–2)+2(у–1)–2(z–1)=0 или, после упрощения, 2x–y+z-4=0. Теперь находим расстояние от т.А(0;-2;0) до плоскости: Ответ:.
27
Как вы видите, все те соотношения, которые при решении традиционным методом даются с большим трудом (через привлечение большого количества вспомогательных теорем), координатным методом получаются в ходе несложных алгебраических вычислений. Нам не нужно задумываться, к примеру, как проходит та или иная плоскость, как упадет перпендикуляр, опущенный из данной точки на плоскость, каким образом скрещивающие прямые перенести, чтобы они были пересекающимися и т.д. Нам просто надо поместить тело в прямоугольную систему координат, определить координаты точек, векторов или плоскостей и воспользоваться формулой.
28
Благодарим за внимание!
Егорова Елена 
Отзыв о товаре ША PRO Анализ техники чтения по классам
и четвертям
Хочу выразить большую благодарность от лица педагогов начальных классов гимназии
«Пущино» программистам, создавшим эту замечательную программу! То, что раньше мы
делали «врукопашную», теперь можно оформить в таблицу и получить анализ по каждому
ученику и отчёт по классу. Великолепно, восторг! Преимущества мы оценили сразу. С
начала нового учебного года будем активно пользоваться. Поэтому никаких пожеланий у
нас пока нет, одни благодарности. Очень простая и понятная инструкция, что
немаловажно! Благодарю Вас и Ваших коллег за этот важный труд. Очень приятно, когда
коллеги понимают, как можно «упростить» работу учителя.
Наговицина Ольга Витальевна 
учитель химии и биологии, СОШ с. Чапаевка, Новоорский район, Оренбургская область
Отзыв о товаре ША Шаблон Excel Анализатор результатов ОГЭ
по ХИМИИ
Спасибо, аналитическая справка замечательная получается, ОГЭ химия и биология.
Очень облегчило аналитическую работу, выявляются узкие места в подготовке к
экзамену. Нагрузка у меня, как и у всех учителей большая. Ваш шаблон экономит
время, своим коллегам я Ваш шаблон показала, они так же его приобрели. Спасибо.
Чазова Александра 
Отзыв о товаре ША Шаблон Excel Анализатор результатов ОГЭ по
МАТЕМАТИКЕ
Очень хороший шаблон, удобен в использовании, анализ пробного тестирования
занял считанные минуты. Возникли проблемы с распечаткой отчёта, но надо ещё раз
разобраться. Большое спасибо за качественный анализатор.
Лосеева Татьяна Борисовна 
учитель начальных классов, МБОУ СОШ №1, г. Красновишерск, Пермский край
Отзыв о товаре Изготовление сертификата или свидетельства конкурса
Большое спасибо за оперативное изготовление сертификатов! Все очень красиво.
Мой ученик доволен, свой сертификат он вложил в портфолио.
Обязательно продолжим с Вами сотрудничество!
Язенина Ольга Анатольевна 
учитель начальных классов, ОГБОУ «Центр образования для детей с особыми образовательными потребностями г. Смоленска»
Отзыв о товаре Вебинар Как создать интересный урок:
инструменты и приемы
Я посмотрела вебинар! Осталась очень довольна полученной
информацией. Всё очень чётко, без «воды». Всё, что сказано, показано, очень
пригодится в практике любого педагога. И я тоже обязательно воспользуюсь
полезными материалами вебинара. Спасибо большое лектору за то, что она
поделилась своим опытом!
Арапханова Ашат 
ША Табель посещаемости + Сводная для ДОУ ОКУД
Хотела бы поблагодарить Вас за такую помощь. Разобралась сразу же, всё очень
аккуратно и оперативно. Нет ни одного недостатка. Я не пожалела, что доверилась и
приобрела у вас этот табель. Благодаря Вам сэкономила время, сейчас же
составляю табель для работников. Удачи и успехов Вам в дальнейшем!
Дамбаа Айсуу 
Отзыв о товаре ША Шаблон Excel Анализатор результатов ЕГЭ по
РУССКОМУ ЯЗЫКУ
Спасибо огромное, очень много экономит времени, т.к. анализ уже готовый, и
особенно радует, что есть варианты с сочинением, без сочинения, только анализ
сочинения! Превосходно!
Слайд 1Готовимся к ЕГЭ.
Задача С2.
Координатный метод
(ключевые задачи).
МБОУ г. Мурманска
гимназия №3
Шахова Татьяна Александровна

Слайд 2Координатный метод может быть использован для нахождения:
длины отрезка (расстояния между
точками);
расстояния между прямыми;
расстояния от точки до прямой и плоскости;
угла между прямыми;
угла между прямой и плоскостью;
угла между плоскостями;
нахождения площади сечения.
http://le-savchen.ucoz.ru/load/4-1-0-183
Первоначальные сведения
о прямоугольной системе координат
смотри по адресу:

Слайд 3 Нахождение координат точки.
Нахождение угла между прямыми.
Вывод уравнения плоскости.
Нахождение расстояния от точки до плоскости.
Нахождение угла между плоскостями.
Нахождение угла между прямой и плоскостью.
Нахождение расстояния между прямыми.
Ключевые задачи.

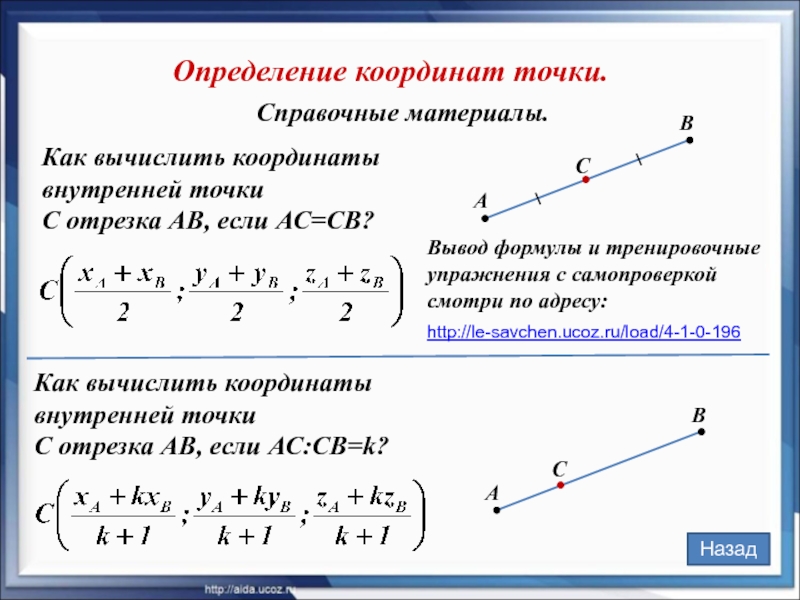
Слайд 4Справочные материалы.
Как вычислить координаты внутренней точки
С отрезка АВ, если АС:СВ=k?
Как вычислить координаты внутренней точки
С отрезка АВ, если АС=СВ?
Определение координат точки.
Вывод формулы и тренировочные
упражнения с самопроверкой
смотри по адресу:
http://le-savchen.ucoz.ru/load/4-1-0-196
Назад
А
В
С
А
В
С
Слайд 5Тренировочные упражнения.
Прямоугольный параллелепипед
Правильная шестиугольная призма
Правильная четырехугольная пирамида
Правильная треугольная пирамида
Определение координат точки.

Слайд 6L
К
А
В
С
D
А1
D1
С1
В1
X
Y
Z
Y
А1(4;0;2)
2
2
4
B1(?;?;?)
B1(4;2;2)
М
К(?;?;?)
C(?;?;?)
C(0;2;0)
К(4;1;2)
А1(?;?;?)
А(?;?;?)
А(4;0;0)
M(?;?;?)
ABCDA1B1C1D1 – прямоугольный параллелепипед. AB=2, AD=4, AA1=2, А1К=КВ1, АМ:МС=2:3, KL=LM .
Определите координаты точек A, C, А1, В1, К, М, L.
?
?
Определение координат точки.
Задачи

Слайд 7L
К
А
В
С
D
А1
D1
С1`
В1
X
Y
Z
Y
2
2
4
М
L(?;?;?)
К(4;1;2)
Определение координат точки.
ABCDA1B1C1D1 – прямоугольный параллелепипед. AB=2, AD=4, AA1=2, А1К=КВ1, АМ:МС=2:3,
KL=LM .
Определите координаты точек A, C, А1, В1, К, М, L.
?
Задачи

Слайд 8
B
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, O
и О1 – центры оснований. Найдите координаты точек А, D1, B, E1.
A
A1
B1
C
C1
D1
D
E
F1
F
E1
F
A
B
C
D
Е
X
Y
Z
X
Y
хЕ
yЕ
хB
yB
хB
хЕ
yB
yЕ
О
О1
Определение координат точки.
О
1
1
1
1
Задачи
Слайд 9O
К
А
SABCD – правильная пирамида, все ребра которой равны 1. SL=LC, SK:KO=1:2,
KM=MC .
Определите координаты точек C, S, O, L, К, M.
В
С
D
S
L
X
Y
Z
Y
М
S(?;?;?)
C(?;?;?)
C(0;1;0)
S(?;?;1)
X
Y
O
yO(yS )
L(?;?;?)
xO(xS )
D
А
В
С
?
Определение координат точки.
О(?;?;?)
О(?;?;0)

Слайд 10O
К
А
В
С
D
S
L
X
Y
Z
Y
М
K(?;?;?)
?
SABCD – правильная пирамида, все ребра которой равны 1. SL=LC, SK:KO=1:2,
KM=MC .
Определите координаты точек C, S, O, L, К, M.
Определение координат точки.
Задачи

Слайд 11O
К
А
В
С
D
S
L
X
Y
Z
Y
М
C(0;1;0)
M(?;?;?)
?
SABCD – правильная пирамида, все ребра которой равны 1. SL=LC, SK:KO=1:2,
KM=MC .
Определите координаты точек C, S, O, L, К, M.
Определение координат точки.
Задачи

Слайд 12
O
К
А
SABC – правильная пирамида, все ребра которой равны 2. BL=LC, SK=KB,
SO — высота. Определите координаты точек C, О, S, В, L, M.
В
С
А
S
L
X
Z
Y
М
C(0;2;0)
C(?;?;?)
X
Y
O
xO(xS )
yO(yS;уВ )
В
С
H
H
(свойство медиан
треугольника)
О(?;?;?)
S(?;?;?)
Определение координат точки.
xВ
О(?;?;0)
В(?;?;?)
В(?;?;0)
Задачи
Слайд 13
O
К
А
В
С
S
L
X
Z
Y
М
X
SABC – правильная пирамида, все ребра которой равны 2. BL=LC, SK=KB,
SO — высота. Определите координаты точек C, О, S, В, L, M.
Определение координат точки.
Из треугольника ВОS
Задачи

Слайд 14O
К
А
В
С
S
L
X
Z
Y
М
C(0;2;0)
X
(середина отрезка ВС)
L(?;?;?)
?
SABC – правильная пирамида, все ребра которой равны 2.
BL=LC, SK=KB, SO — высота. Определите координаты точек C, О, S, В, L, M.
Определение координат точки.
Задачи

Слайд 15O
К
А
В
С
S
L
X
Z
Y
М
X
М – точка пересечения медиан
треугольника BSC =>
М(?;?;?)
SМ:ML=2:1
?
SABC – правильная пирамида,
все ребра которой равны 2. BL=LC, SK=KB, SO — высота. Определите координаты точек C, О, S, В, L, M.
Определение координат точки.
Задачи

Слайд 16Алгоритм.
Нахождение угла между прямыми.
Назад
А
В
С
D
направляющие векторы

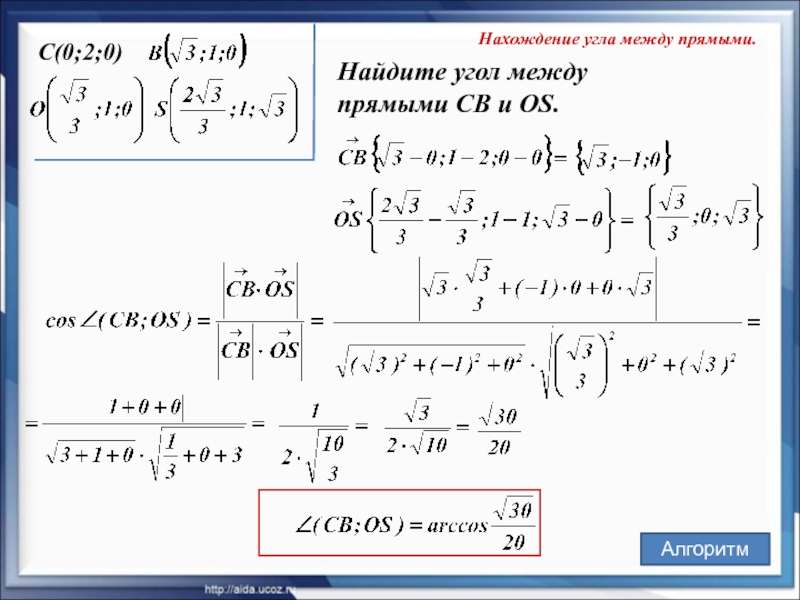
Слайд 17Нахождение угла между прямыми.
C(0;2;0)
Найдите угол между
прямыми CВ и OS.
Алгоритм
Слайд 18
Алгоритм.
Вывод уравнения плоскости ax+by+cz+d=0.
Назад
А
В
С
Подставить в уравнение плоскости
координаты точек А,В и С.
Решить
систему — выразить а, b и с через d; либо а, b и d через с;
либо а, с и d через b, либо c, b и d через a в зависимости от
составленной системы.
3) Подставить выраженные коэффициенты в исходное
уравнение и преобразовать к удобному виду.

Слайд 19Вывод уравнения плоскости.
Запишите уравнение плоскости (АВС)
Алгоритм

Слайд 20Вывод уравнения плоскости.
Запишите уравнение плоскости (АВС)
Алгоритм

Слайд 21
Алгоритм.
Нахождение расстояния от точки до плоскости.
Назад
А
α
Если плоскость α задана уравнением
то расстояние
от точки А до
плоскости α можно найти
по формуле:

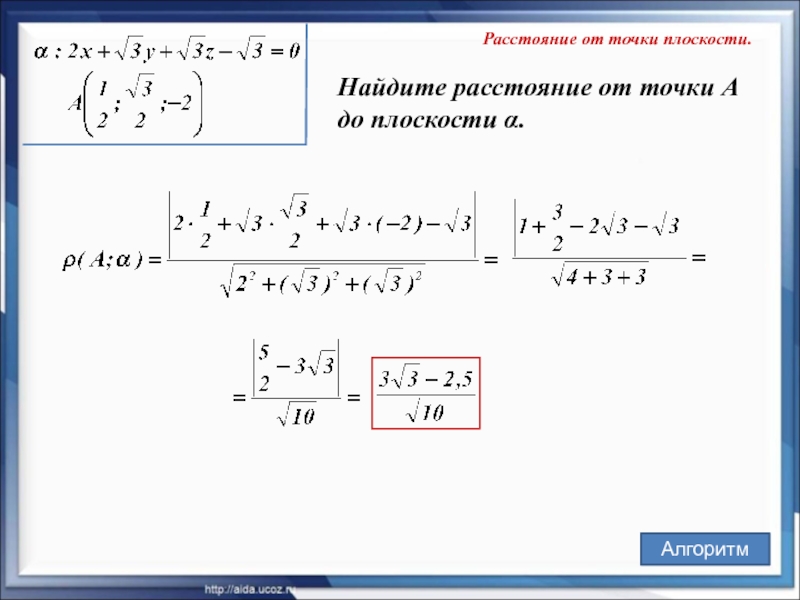
Слайд 22Расстояние от точки плоскости.
Найдите расстояние от точки А
до плоскости α.
Алгоритм
Слайд 23
Алгоритм.
Нахождение угла между плоскостями.
Назад
Если плоскости α и β заданы уравнениями
β
α
соответственно, то
и
—
вектор нормали (перпендикуляра) плоскости α,
— вектор нормали плоскости β.
Угол между плоскостями равен углу
между нормалями этих плоскостей.
Алгоритм

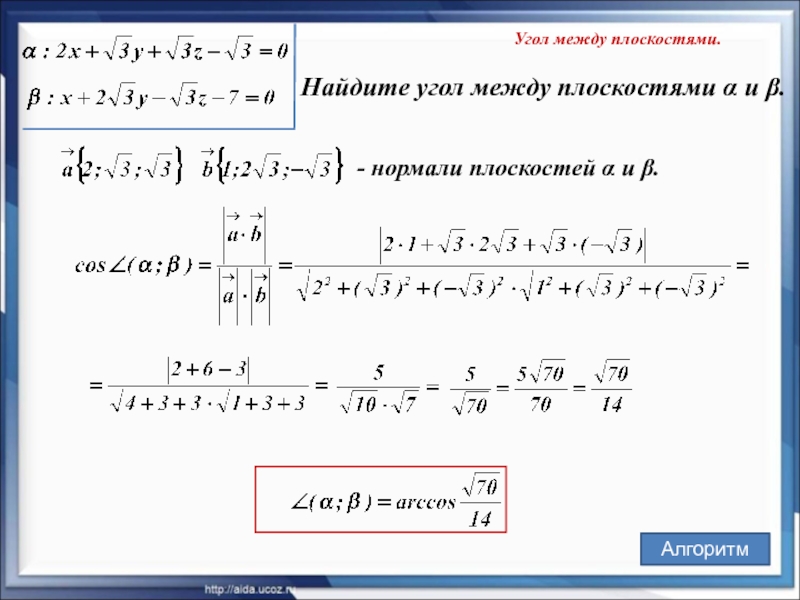
Слайд 24Угол между плоскостями.
Найдите угол между плоскостями α и β.
Алгоритм
— нормали плоскостей
α и β.
Слайд 25
Алгоритм.
Нахождение угла между прямой и плоскостью.
Назад
А
α
Если плоскость α задана уравнением
направляющий вектор
прямой
АВ имеет координаты
В
— вектор нормали плоскости α,
то угол между прямой АВ и
плоскостью α можно по формуле:
?

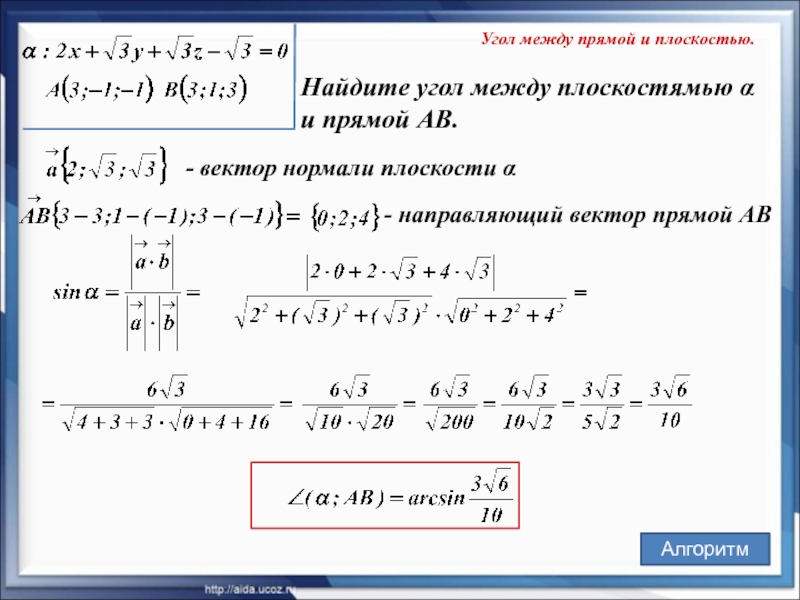
Слайд 26Угол между прямой и плоскостью.
Найдите угол между плоскостямью α
и прямой
АВ.
Алгоритм
— вектор нормали плоскости α
— направляющий вектор прямой АВ
Слайд 27Пусть
, тогда выполнено
условие:
Алгоритм.
Нахождение расстояния между прямыми.
Назад
B
C
А
D
М
К
1) Определить координаты направляющих векторов и .
2) Из системы определить координаты , затем найти
Замечание: для записи координат точек М и К воспользоваться формулой:
Если АМ:МВ=k, то

Слайд 28Нахождение угла между прямыми.
Найдите расстояние между
прямыми AC и BD.
Алгоритм
B
C
А
D
М
К
Пусть
АМ:МС=k, BK:KD=n,

Слайд 29Нахождение угла между прямыми.
Найдите расстояние между
прямыми AC и BD.
Алгоритм
C
А
D
М
B

Слайд 30*
При создании презентации использовано пособие:
http://www.alleng.ru/d/math/math784.htm
Стереометрия
Метод координат
в задачах № 14 ЕГЭ
Координаты точки в декартовой системе координат
Координаты вектора
=
Координаты середины отрезка
Угол между прямыми
— направляющий вектор прямой а
— направляющий вектор прямой b
— угол между прямыми
Уравнение плоскости, проходящей
через три заданных точки
-нормальный
вектор плоскости
Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
-нормальный
вектор плоскости
, где
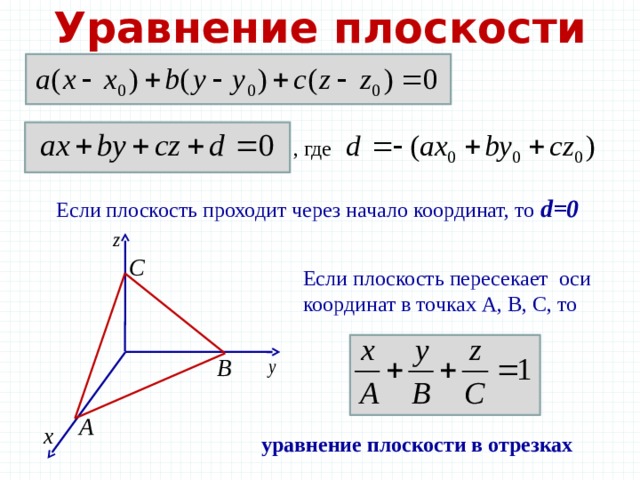
Уравнение плоскости
, где
Если плоскость проходит через начало координат, то d=0
Если плоскость пересекает оси координат в точках А, В, С, то
уравнение плоскости в отрезках
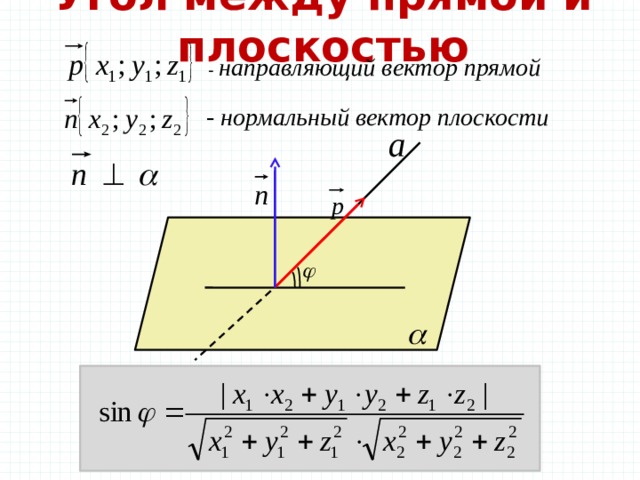
Угол между прямой и плоскостью
— направляющий вектор прямой
— нормальный вектор плоскости
Угол между плоскостями
Вектор нормали плоскости
Вектор нормали плоскости
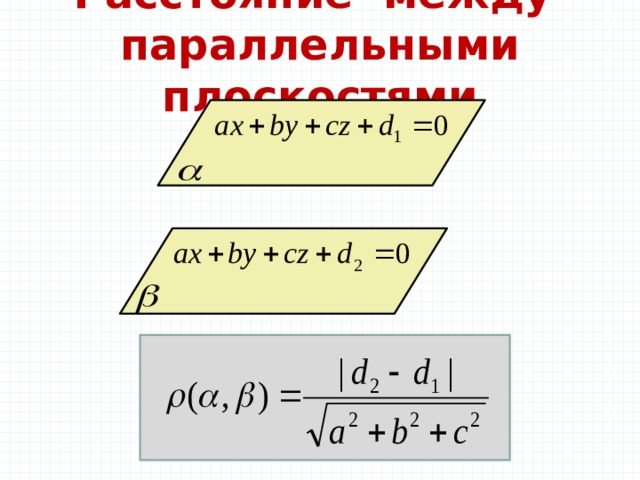
Расстояние от точки до плоскости
Расстояние между параллельными плоскостями
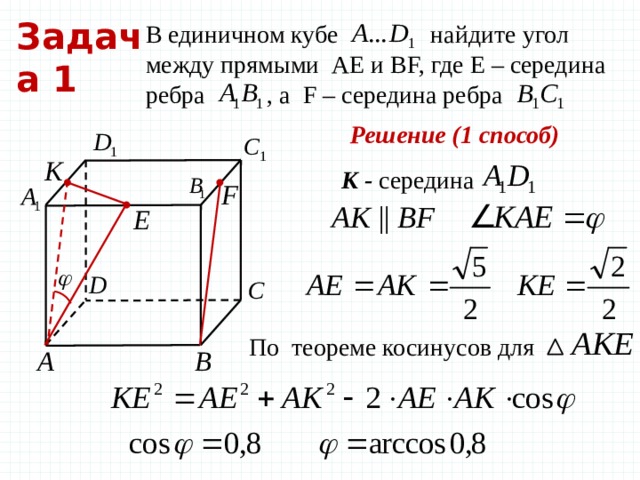
Задача 1
В единичном кубе найдите угол между прямыми AE и BF, где Е – середина ребра , а F – середина ребра
Решение (1 способ)
К — середина
По теореме косинусов для
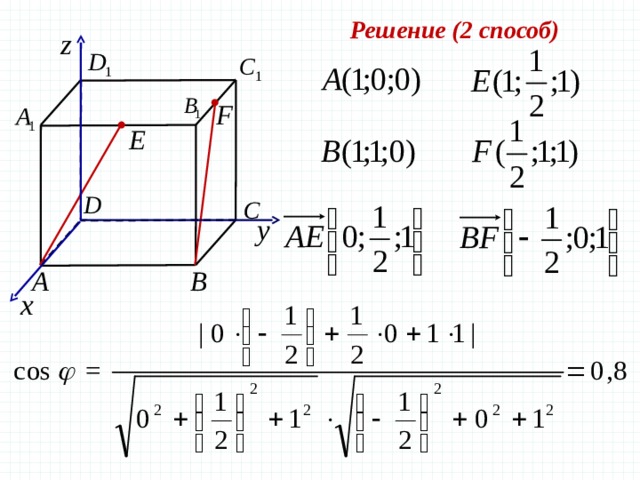
Решение (2 способ)
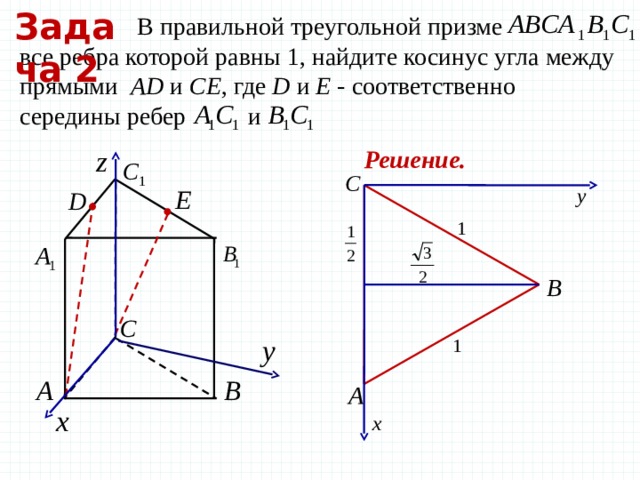
Задача 2
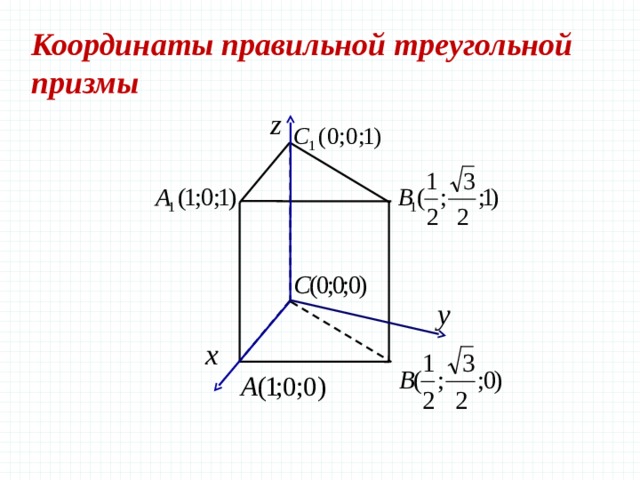
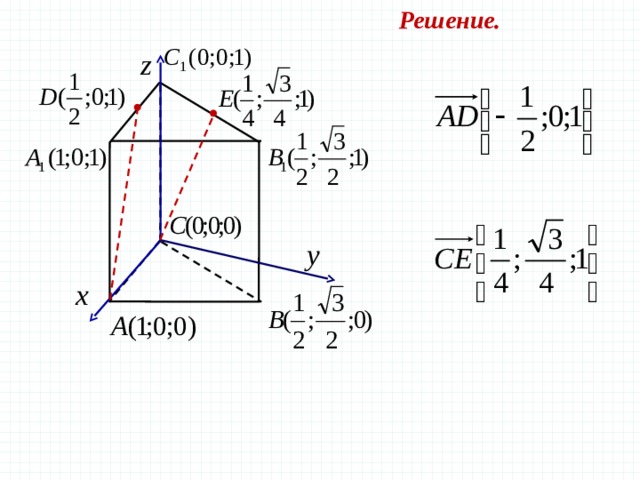
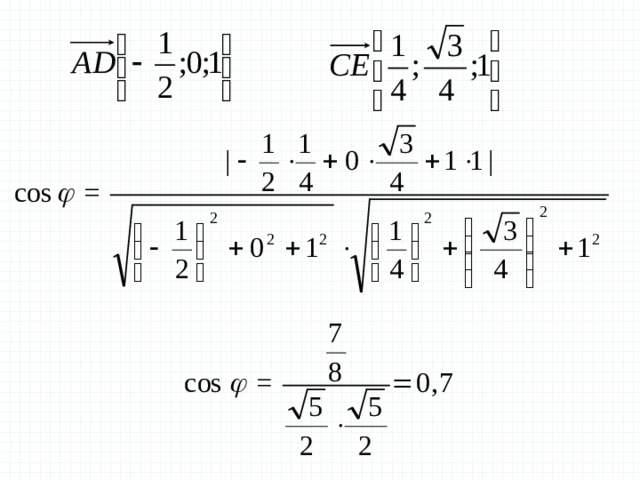
В правильной треугольной призме все ребра которой равны 1, найдите косинус угла между прямыми AD и CE , где D и E — соответственно середины ребер и
Решение.
Координаты правильной треугольной призмы
Решение.
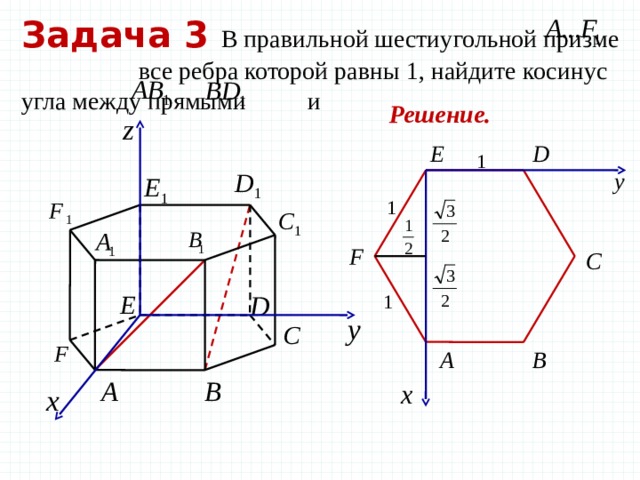
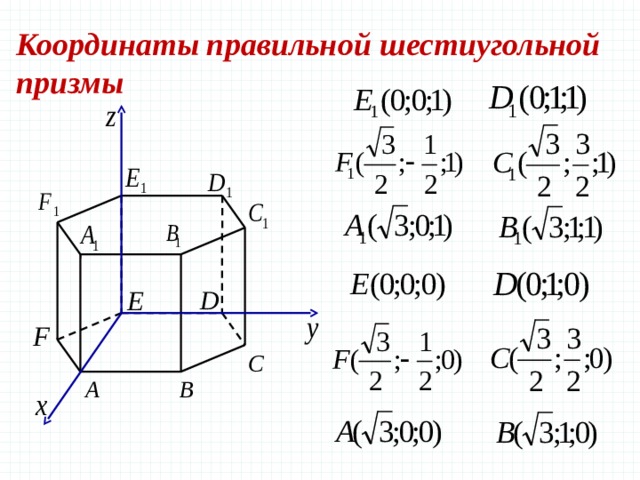
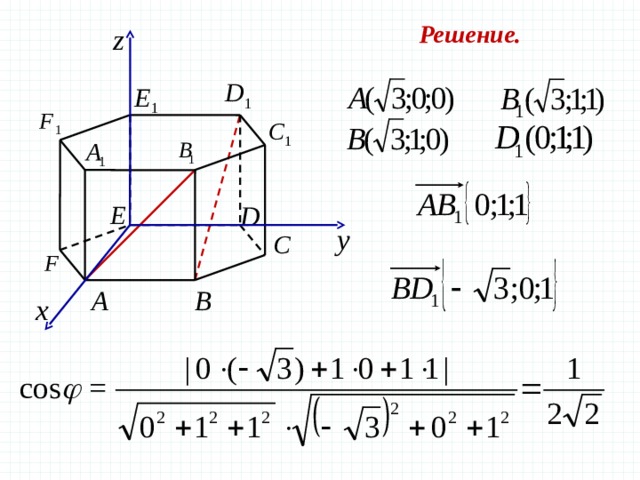
Задача 3 В правильной шестиугольной призме все ребра которой равны 1, найдите косинус угла между прямыми и
Решение.
Координаты правильной шестиугольной призмы
Решение.
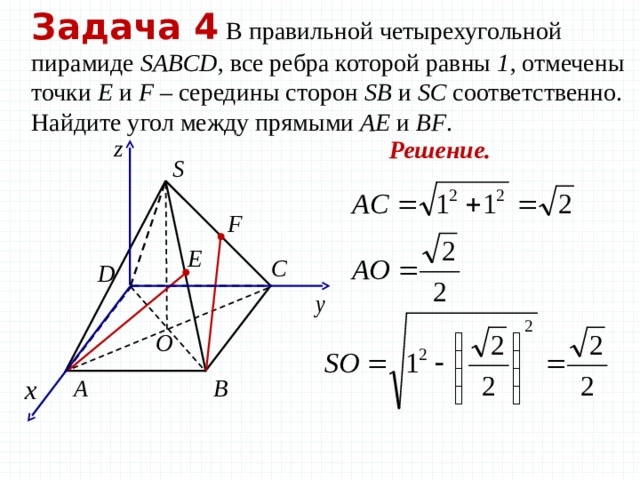
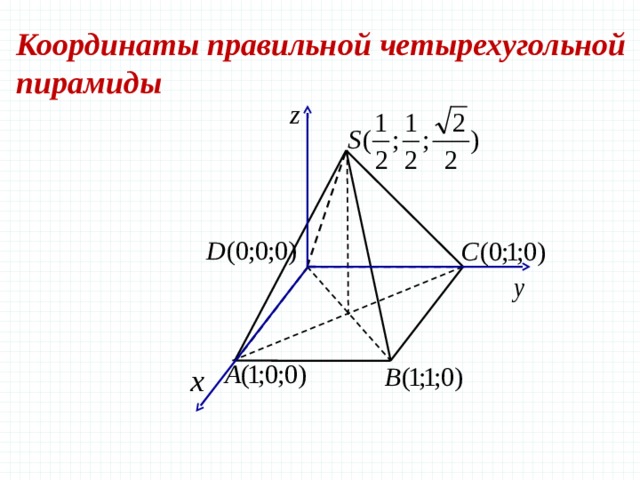
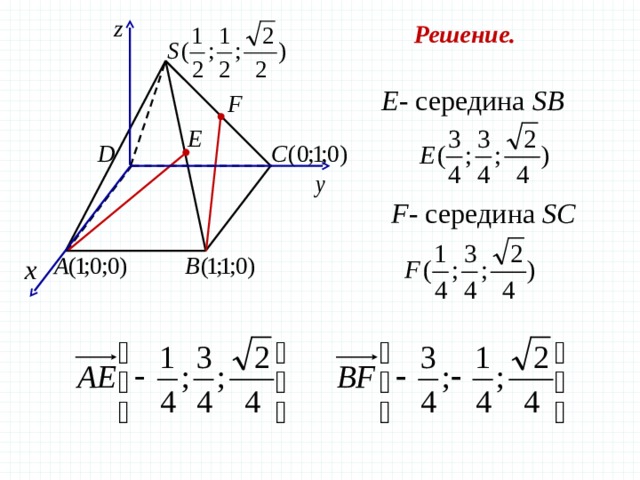
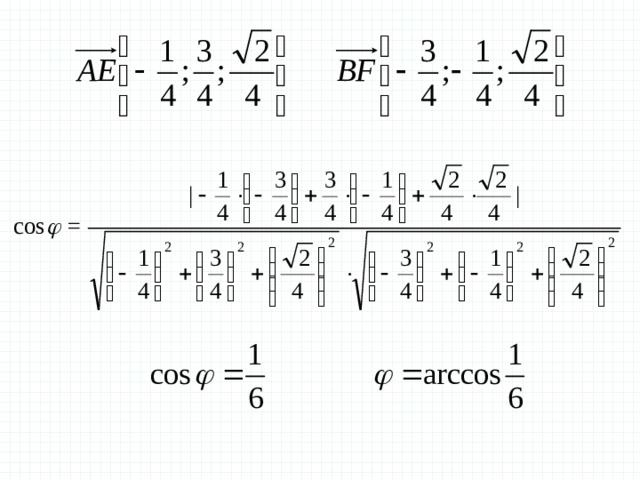
Задача 4 В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1 , отмечены точки Е и F – середины сторон SB и SC соответственно. Найдите угол между прямыми AE и BF .
Решение.
Координаты правильной четырехугольной пирамиды
Решение.
Е — середина SB
F — середина SC
Задача 5 Составить уравнение плоскости, проходящей через точки А(-2;3;5), В(4;-3;0), С(0;6;-5) и найти координаты вектора нормали.
Решение.
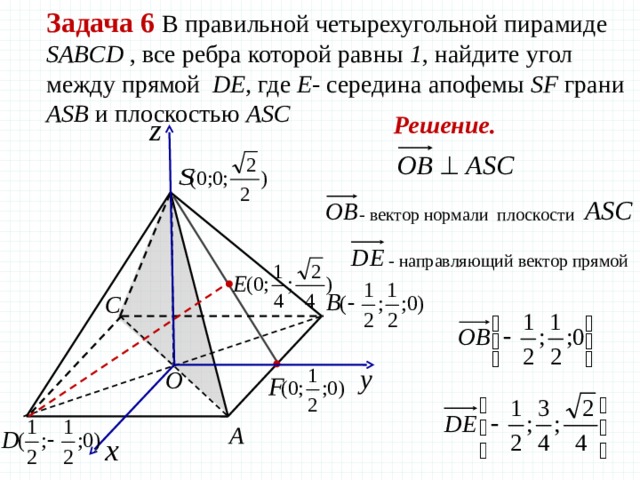
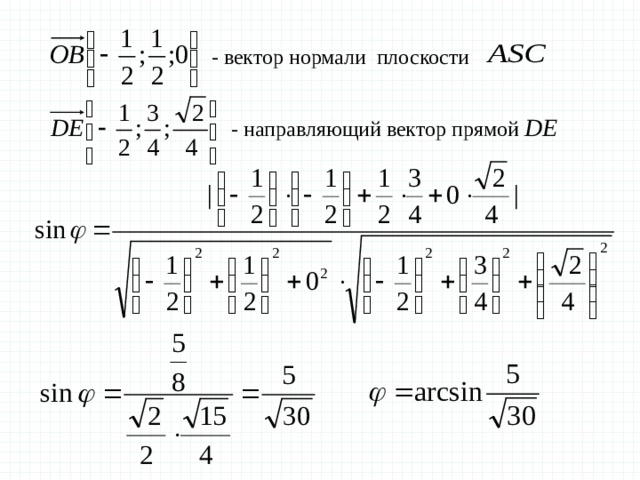
Задача 6 В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1 , найдите угол между прямой DE, где Е — середина апофемы SF грани ASB и плоскостью ASC
Решение.
— вектор нормали плоскости
— направляющий вектор прямой
— вектор нормали плоскости
— направляющий вектор прямой DE
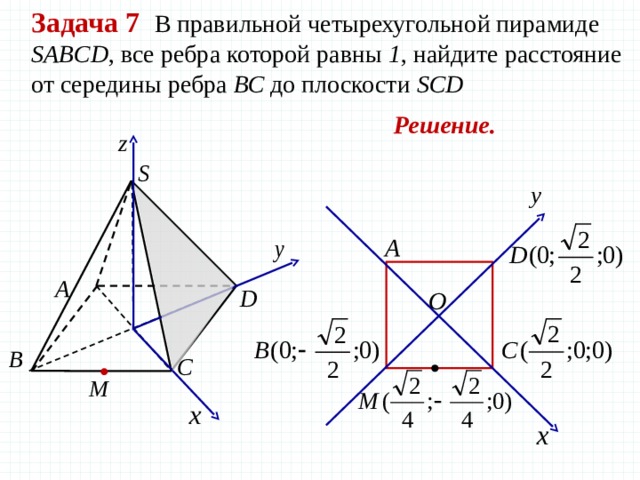
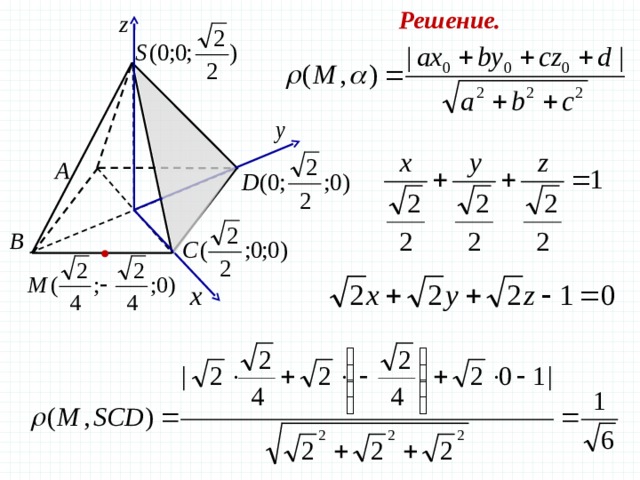
Задача 7 В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1 , найдите расстояние от середины ребра ВС до плоскости SCD
Решение.
Решение.
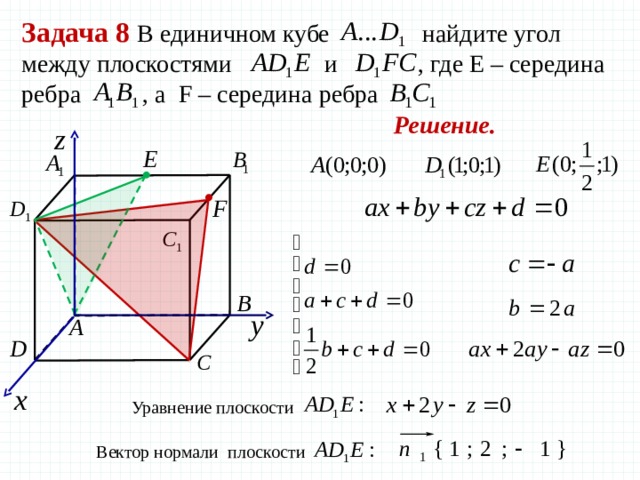
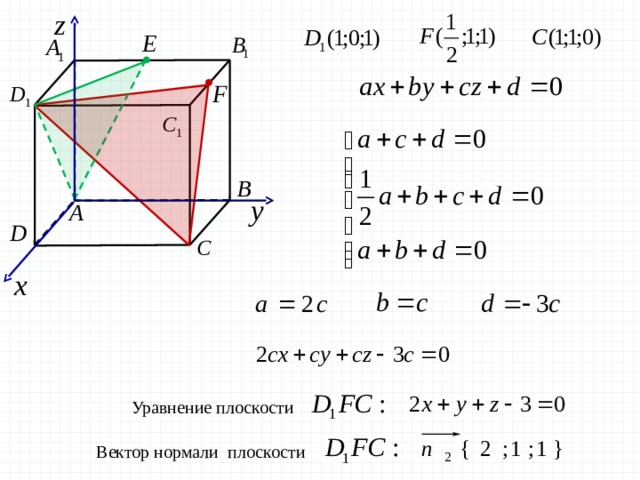
Задача 8 В единичном кубе найдите угол между плоскостями и , где Е – середина ребра , а F – середина ребра
Решение.
Уравнение плоскости
Вектор нормали плоскости
Уравнение плоскости
Вектор нормали плоскости
Задачи для самостоятельного решения
- В правильной четырёхугольной пирамиде SABCD с основанием
ABCD точка М – середина ребра SA, точка К – середина ребра SC.
Найдите угол между плоскостями МВК и АВС, если АВ=4, SC=7.
2. Основанием пирамиды SABC является равносторонний треугольник ABC, сторона которого равна 2√2. Боковое ребро SC перпендикулярно плоскости основания и равно 1. Найдите угол между скрещивающимися прямыми, одна из которых проходит через точку S и и середину ребра ВC, а другая проходит через точку C и середину ребра AB.