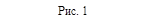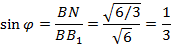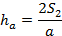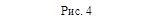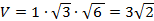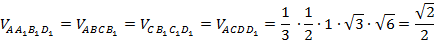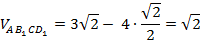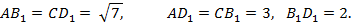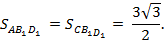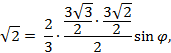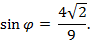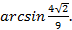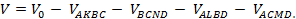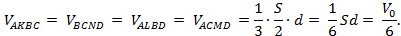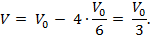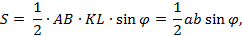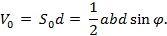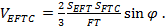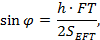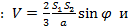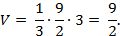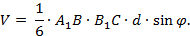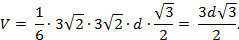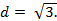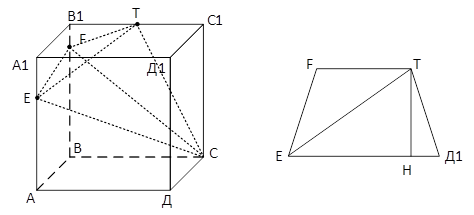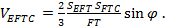Метод объемов егэ математика профиль - Помощь в подготовке к экзаменам и поступлению

Метод объемов в задачах по стереометрии

Метод объемов применяется, когда мы хотим найти расстояние от точки до плоскости.

Или расстояние между двумя скрещивающимися прямыми. Или расстояние между двумя параллельными плоскостями.

Метод объемов состоит в том, чтобы, записав двумя разными способами объем какой-либо треугольной пирамиды и приравняв эти выражения, найти нужную нам величину.

Вот как он применяется в задачах ЕГЭ:

9. В правильной треугольной призме $ABCA_{1}B_{1}C_{1}$ сторона AB основания равна 12, а высота призмы равна 2. На рёбрах $B_{1}C_{1}$ и AB отмечены точки P и Q соответственно, причём $PC_{1}=3$ , а AQ=4. Плоскость $A_{1}PQ$ пересекает ребро BC в точке M.

а) Докажите, что точка M является серединой ребра BC.

б) Найдите расстояние от точки B до плоскости $A_{1}PQ.$

Построим сечение призмы плоскостью A_1PQ.

Проведём $QM parallel {A}_1P$ в плоскости ABC, точка M лежит на ребре BC.

Мы пользуемся здесь тем, что линии пересечения параллельных плоскостей третьей плоскостью параллельны. Трапеция $QMPA_{1}$ — искомое сечение.

а) Покажем, что M — середина BC.

Пусть P_1 — проекция точки P на плоскость ABC, P_1C=3. Тогда

Пусть $BM = x, triangle QBMsim triangle { }A{BP}_1$ (по двум углам)

$frac{BQ}{AB}=frac{BM}{{BP}_1};$

$frac{8}{12}=frac{x}{9}$

Отсюда x = 6 и M — середина BC.

б) Найдем расстояние от точки B до плоскости A_1PQ, пользуясь методом объемов.

Выразим двумя способами объем треугольной пирамиды A_1QMB. $V_{A_1QMB}=frac{1}{3}S_{triangle { QMB}}cdot h_1=frac{1}{3}S_{triangle { }A_1{ QM}}cdot h_2{, }$ где h_1 — расстояние от точки $A_{1}$ до плоскости QMB, то есть до плоскости основания призмы.

Оно равно высоте призмы, то есть h_1=2.

h_2 — искомое расстояние от точки B до плоскости $A_1{ QM.}$

$S_{triangle { QMB}}=frac{1}{2}cdot BQcdot BMcdot sin60^circ =frac{1}{2}cdot 8cdot 6cdot frac{sqrt{3}}{2}=12sqrt{3;}$

Из по теореме косинусов:

${QM}^2={BQ}^2+{BM}^2-2BQcdot BMcdot cos60^circ,$

${QM}^2=64+36-2cdot 8cdot 6cdot frac{1}{2}=100-38=52;$

Из $triangle { }AA_1Q:$

$A_1Q=sqrt{{AQ}^2+{AA_1}^2}=sqrt{16+4}=2sqrt{5}.$

Точка M — середина BC, $AM=frac{12sqrt{3}}{2}=6sqrt{3}.$

Из прямоугольного треугольника ${{ A}}_{{ 1}}AM$ найдем $A_1M = 4sqrt{7}.$

Рассмотрим треугольник A_1QM , в котором мы знаем все стороны.

По теореме косинусов:

$20= 112+52 - 2cdot 8cdot sqrt{7}cdot sqrt{13}cdot cosangle A_1MQ;$

$cosangle A_1MQ=frac{9}{sqrt{91}}$

Тогда $sinangle A_1MQ=sqrt{frac{10}{91}}$

$S_{triangle { }A_1QM}=frac{1}{2}QMcdot A_1Mcdot sinangle A_1MQ=$

$=frac{1}{2}cdot 2sqrt{13}cdot 4sqrt{7}cdot sqrt{frac{10}{91}}=4sqrt{10};$

Объем пирамиды $A_1QBMV_{{ }A_1QBM}=frac{1}{3}S_{triangle { }QBM}cdot AA_1=frac{1}{3}S_{{ }A_1QM}cdot h_2,$

Отсюда

$h_2=frac{S_{triangle { }QBM}cdot { A}A_1}{S_{{ }A_1QM}}=frac{12sqrt{3}cdot 2}{4sqrt{10}}=frac{3sqrt{30}}{5}.$

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Метод объемов в задачах по стереометрии» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Авторы
Файлы
Ключевые слова
Литература

Ушаков Р.А.

1 МОУ «Архангельская СШ»

исследовательская

работа

математика

геометрия

метод объемов

1. Готман Э.Г. Стереометрические задачи и методы их решения.— М.: МЦНМО, 2006.—160 с.: ил.

2. Демонстрационные варианты контрольных измерительных материалов для проведения в 2018 году единого государственного экзамена по математике [Электронный ресурс]. – Москва: ФИПИ, 2015 Режим доступа: www.fipi.ru, свободный.

3. Интернет — ресурсы: http://coko29.info/; http://alexlarin.net/; http://www.ege.edu.ru/.

4. Корянов А.Г., Прокофьев А.А. Математика. ЕГЭ – 2018. Многогранники: типы задач и методы их решения (типовые задания С2) [Электронный ресурс]. – Режим доступа: http: alexlarin.net/, свободный.

5. Спецификация контрольных измерительных материалов для проведения в 2018 году единого государственного экзамена по математике [Электронный ресурс]. – Москва: ФИПИ, 2018 Режим доступа: www.fipi.ru, свободный.

6. Яковлев И. В. Материалы по математике. Метод объёмов. [Электронный ресурс] http://mathus.ru/

При решении геометрических задач, как правило, алгоритмов нет, и выбрать наиболее подходящую к данному случаю теорему из большого количества теорем не просто. А ещё это связано с тем, что редко какая задача в геометрии может быть решена с использованием определенной формулы. При решении большинства задач не обойтись без привлечения разнообразных фактов теории, доказательства тех или иных утверждений, справедливых лишь при определенном расположении элементов фигур.

Особые затруднения вызывают стереометрические задачи, в которых требуется построить сечение многогранника плоскостью, найти площадь сечения, угол между скрещивающимися прямыми, угол между прямой и плоскостью, двугранные углы между плоскостями. Перечисленные задания в демонстрационном варианте ЕГЭ по математике составляют содержание задач уровня №14. Эта тема актуальна всем тем, кому предстоит сдавать профильный экзамен по математике. Согласно статистике, у большинства сдающих ЕГЭ по математике возникают трудности при решении стереометрических задач под №14. Материалом исследования послужили книга Э.Г. Готмана «Стереометрические задачи и методы их решения» и статья И.В. Яковлева «Метод объёмов».

В центре внимания исследовательской работы положен метод объёмов.

Объект исследования: стереометрические задачи, требующие нахождения расстояния между прямой и плоскостью; угла между прямой и плоскостью; угла между плоскостями; расстояния между скрещивающимися прямыми.

Предмет исследования: метод объёмов.

Гипотеза: метод объёмов в некоторых случаях позволяет получить результат, который при других способах решения получается гораздо сложнее.

Цель работы: изучение применения метода объёмов при решении стереометрических задач.

Задачи:

1. Проанализировать различные аспекты изучения данной темы. (Осуществить поиск и отбор информации о методе объёмов, изучить и доказать теоремы, позволяющие применять данный метод при решении стереометрических задач).

2. Проанализировать и выявить факты, подтверждающие возможность применение метода объёма при решении задач по математике на ЕГЭ.

3. Организовать сбор задач, из вариантов ЕГЭ по математике, при решении которых может применяться метод объёмов.

4. Научиться применять метод объёмов при решении стереометрических задач.

5. Оформить результаты исследования.

Результатом исследования должна стать презентация по теме, которая поможет выпускникам познакомиться с методом объёмов и покажет возможность применения этого метода для решения заданий №14 на ЕГЭ по математике и подборка задач из ЕГЭ по математике, при решении которых применялся метод объёмов. Подборка задач может быть применена и преподавателями математики в качестве раздаточного материала при подготовке к ЕГЭ.

Метод объёмов при решении стереометрических задач

При изучении литературы по теме «Решения стереометрических задач» можно встретить различную классификацию методов решений.

Существует три основных метода решения задач №14. Условно назовем их «методом построений», «векторно-координатным методом» и «методом объемов». Каждый из них удобен в том или ином случае, поэтому лучше знать и уметь использовать все три.

Объём треугольной пирамиды можно посчитать несколькими разными способами. Методом объёмов мы называем приравнивание двух подходящих выражений для объёма, в результате чего удаётся вычислить искомую величину (расстояние или угол). Метод объёмов можно использовать, вычисляя:

расстояние от точки до плоскости;
угол между прямой и плоскостью;
угол между плоскостями;
расстояние между скрещивающимися прямыми.

С идейной точки зрения метод объёмов весьма прост. Всё, что здесь нужно, — это найти подходящую треугольную пирамиду и аккуратно провести вычисления. Правда, вычислений обычно получается несколько больше, чем в методах, рассмотренных выше. Но тут уж ничего не поделаешь — за простоту метода приходится платить. [3,с.1]

1.1 Расстояние от точки до плоскости

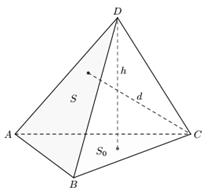
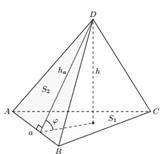
Треугольная пирамида замечательна тем, что для вычисления её объёма, за основание можно выбрать любую её грань. Этот факт можно использовать при нахождении расстояния от точки до плоскости; нужно лишь представить искомое расстояние как высоту подходящей пирамиды. Рассмотрим пример. Дана треугольная пирамида ABCD (рис.1). Нужно найти расстояние от некоторой точки С до некоторой плоскости ABD. Тогда искомое расстояние – это высота d данной пирамиды, проведённой из вершины C.

Пусть S0 – площадь грани ABC, h – высота, опущенная на эту грань, S – площадь грани АВД. С одной стороны, объём пирамиды ABCD может быть найден по формуле:

(1)

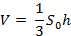
С другой стороны, за основание можно принять грань ABD, и тогда

(2)

Приравниваем правые части формул (1) и (2), получаем:

(3)

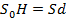
Из соотношения (3) находим искомую величину d.Пример решения стереометрической задачи на нахождение расстояния от точки до плоскости приведён в приложении № 2.Метод объёмов позволяет найти высоту без построения перпендикуляра, опущенного из точки на плоскость. Освоив столь мощный метод нахождения расстояния от точки до плоскости, мы в качестве «дополнительной опции» немедленно получаем метод вычисления угла между прямой и плоскостью [7, с.3].

1.2 Угол между прямой и плоскостью

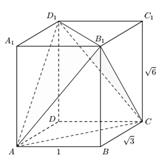
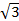
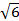
ABCDA1B1C1D1 (рис 2) известны рёбра: AB = 1, AD= , AA1 = . Найдите угол между прямой BB1 в прямоугольном параллелепипеде и плоскостью AB1C.

Искомый угол φ.

(4)

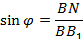
где BN – расстояние от точки В до плоскости АВ1С находим методом объёмов по формуле:

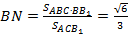
Далее подставляем полученный результат в формулу (4).

Ответ:

1.3 Угол между плоскостями

При вычислении угла между плоскостями может оказаться полезной следующая формула для объёма треугольной пирамиды:

(5)

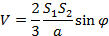
Здесь S1 и S2 — площади двух граней пирамиды, a- общее ребро этих граней, 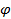— угол между плоскостями этих граней (рис 3).

Рассмотрим вывод формулы (5). Пусть S1 и S2 — площади треугольников ABC и ABD соответственно, a= AB, 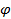— угол между плоскостями ABC и ABD.

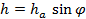
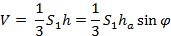
Из вершины D проведём высоту пирамиды h и высоту грани h_a грани ABD. Легко видеть, что . Тогда для объёма пирамиды имеем:

(6)

С другой стороны, запишем формулу для площади S2:

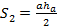
Откуда

Это выражение нужно подставить в (6):

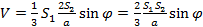
Что и нужно было получить.

Рассмотрим решение задачи:

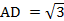
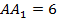
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны рёбра: AB = 1, , . Найдите угол между плоскостями AB1D1 и CB1D1. Решение. Делаем чертёж (рис. 4). Искомый угол Φ будем вычислять с помощью треугольной пирамиды AB1CD1.

Согласно формуле (5) имеем:

(7)

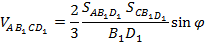
Объём тетраэдра AB1CD1 мы найдём, «отрезая» от исходного параллелепипеда четыре равнообъёмных «куска»:

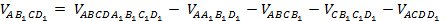
Следовательно,

Теперь найдём площади граней AB1D1 и CB1D1. Имеем:

Таким образом, треугольники AB1D1 и CB1D1 имеют стороны 2,3 и .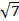

Находим их площадь по формуле Герона. Получаем:

Подставляем найденные величины в формулу (7):

откуда

Ответ:

1.2 Расстояние между скрещивающимися прямыми

При нахождении расстояния между скрещивающимися прямыми может помочь следующая формула для объёма тетраэдра:

(8)

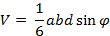
Здесь a и b – скрещивающиеся рёбра тетраэдра, d и 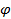— соответственно расстояние, и угол между ними (точнее, между прямыми, содержащими эти рёбра).

Дадим вывод этой формулы.

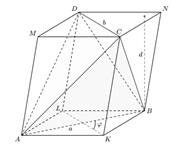
На рисунке мы видим тетраэдр ABCD, достроенный до параллелепипеда AKBLMCND следующим образом: через каждое ребро тетраэдра проведена плоскость, параллельная ребру, скрещивающемуся с данным ребром. Покажем, что объём V тетраэдра ABCD равен одной третьи объёма V0 получившегося параллелепипеда.

Отрезаем от параллелепипеда четыре тетраэдра:

Все эти тетраэдры имеют одинаковый объём. В самом деле, если S и d – соответственно площадь основания и высота параллелепипеда, то

Тогда

Пусть a = AB, b = CD. Расстояние между прямыми, проходящими через рёбра a и b, являются расстоянием между параллельными плоскостями AKB и MCN, то есть высотой d нашего параллелепипеда. Угол между рёбрами a и b – это угол 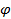между прямыми AB и KL.

Для площади основания параллелепипеда имеем:

Находим объём параллелепипеда:

Объём тетраэдра ABCD меньше в три раза, тем самым, получаем нужную формулу (8).Применение данной формулы и метода объёмов рассмотрено на примере решения задачи «В кубе ABCDA1B1C1D1 найдите расстояние между прямыми A1B и B1C. Ребро куба равно 3.» представлено в приложении № 2.

Метод объёмов помог, не производя построений, найти расстояние между скрещивающими прямыми. Что значительно облегчает решение задачи.

Решение стереометрических задач из ЕГЭ по математике методом объемов

Содержание и структура экзаменационной работы дают возможность проверить усвоение курсов математики 5—6-го классов, алгебры 7—9-го классов, алгебры и начал анализа 10-11-го классов и геометрии 7—11-го классов. При этом, в частности, проверяются умения использовать полученные знания в практической деятельности и в повседневной жизни, а также умения строить и исследовать математические модели.Задача №14. Стереометрия. Построение сечения. Нахождение каких-либо величин через заданные [6, с.2].

2.1. Характеристика стереометрических задач №14 из ЕГЭ по математике

В задаче 14 рассматриваются многогранники, на основе которых, как правило, нужно найти одну из следующих величин:

1. Угол между скрещивающимися прямыми — это угол между двумя прямыми, которые пересекаются в одной точке и параллельны данным прямым.

2. Угол между прямой и плоскостью — это угол между самой прямой и ее проекцией на данную плоскость.

3. Угол между двумя плоскостями — это угол между прямыми, которые лежат в данных плоскостях и перпендикулярны линии пересечения этих плоскостей. [6, с.5]

Прямые всегда задаются двумя точками на поверхности или внутри многогранника, а плоскости — тремя. Сами многогранники всегда задаются длинами своих граней.

В школьном курсе стереометрии упор делается на дополнительные построения, которые позволяют выделить искомый угол, а затем рассчитать его величину.

Здесь уместно вспомнить задачи на построение сечений многогранников, которые рассматриваются в 10 классе и у многих вызывают трудности. Существование формального алгоритма для таких построений совершенно не облегчает задачу, поскольку каждый случай достаточно уникален, а любая систематизация лишь усложняют процесс.

Именно поэтому задача 14 оценивается в два балла. Первый балл дается за правильные построения, а второй — за правильные вычисления и собственно ответ.

Преимущества традиционного решения:

1. Высокая наглядность дополнительных построений, которые подробно изучаются на уроках геометрии в 10-11 классах;

2. При правильном подходе значительно сокращается объем вычислений.

Недостатки:

1. Необходимо знать большое количество формул из стереометрии и планиметрии;

2. Дополнительные построения каждый раз приходится придумывать «с нуля». И это может оказаться серьезной проблемой даже для хорошо подготовленных учеников.

Вот в таких трудных случаях, когда «метод построений» не даёт нужного результата, на помощь приходят два метода — это «векторно-координатным метод» и «методом объемов».

2.2. Решение задач №14 из ЕГЭ по математике

Покажем применение метода объёмов при решении стереометрических задач из ЕГЭ по математике.На ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка E так, что A1E : EA =1: 2 , на ребре BB1 — точка F так, что B1F : FB =1:5 , а точка T — середина ребра B1C1 . Известно, что AB = 4, AD = 2, AA1 = 6.

а) Докажите, что плоскость EFT проходит через вершину D1.

б) Найдите угол между плоскостью EFT и плоскостью BB1C1

Доказательство приведено в приложении № 3.

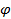
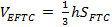
Рассмотрим нахождение угла между плоскостью EFT и плоскостью BB1C1. Обозначим искомый угол между плоскостями через . Рассмотрим треугольную пирамиду EFTC. Вычислим объём этой пирамиды двумя способами:

И уравняв правые части, выразим 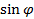, получим формулу:

где h – высота пирамиды, опущенная из вершины E. Полное решение приведено в приложении № 3.

Вывод: при использовании метода объёмов получили много вычислений, но преимущество данного метода в отсутствии построения угла между плоскостями. На практике такое построение часто вызывает затруднения.

Заключение

В ходе исследования был изучен метод объёмов при решении стереометрических задач и сделан вывод: метод объёмов в некоторых случаях позволяет получить результат, который при других способах решения получается гораздо сложнее.

Таким образом, гипотеза подтвердилась.В заключение следует отметить, что выведенные, в ходе исследования, формулы

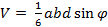
значительно обогатят багаж математических знаний, обучающихся 11 класса и расширят возможности в нахождении способов решения стереометрических задач, а по мнению Р.К. Гордина эти формулы входят в перечень основных знаний по стереометрии. [1, с. 23]

Задачи по стереометрии — прекрасные упражнения, способствующие развитию пространственных представлений, умения логически мыслить, способствующие развитию творческих способностей на уровне, необходимом для продолжения образования и для самостоятельной деятельности в области математики и ее приложений в будущей профессиональной деятельности.

Приложение 1

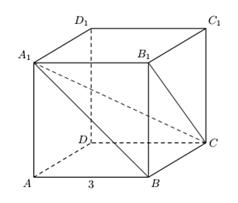
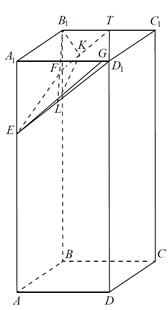
В кубе ABCDA1B1C1D1 найдите расстояние между прямыми A1B и B1C. Ребро куба равно 3.

Объём V данного тетраэдра легко найти, приняв за основание грань BCB1. Тогда:

С другой стороны, согласно формуле (8) имеем:

Здесь

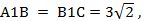
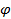
угол между прямыми A1B и B1C равен 600, так что имеем:

Остаётся приравнять выражения для объёма и найти требуемое расстояние:

Приложение 2

Задача№14 из вариант МА10107 (профильный) Математика. 11 класс, ноябрь 2015 года.На ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка E так, что A1E : EA =1: 2 , на ребре BB1 — точка F так, что B1F : FB =1:5 , а точка T — середина ребра B1C1 . Известно, что AB = 4, AD = 2, AA1 = 6.

а) Докажите, что плоскость EFT проходит через вершину D1.

Решение: a) В плоскости AA1D1 проведём через точку E прямую, параллельную TF. Пусть она пересекает ребро AD1 или его продолжение точке G . Плоскость EFT проходит через точку G . Треугольник EGA1 подобен равнобедренному треугольнику FTB1 , в котором FB1 = B1T =1. Отсюда EA1 = A1G = 2 , значит, точка G совпадает с точкой D1 .

б) Найдите угол между плоскостью EFT и плоскостью BB1C1

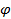
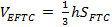
б) Обозначим искомый угол между плоскостями через . Рассмотрим треугольную пирамиду EFTC. Вычислим объём этой пирамиды двумя способами:

И уравняв правые части, выразим 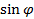, получим формулу:

где h – высота пирамиды, опущенная из вершины E. FT находим из прямоугольного треугольника FB1T, 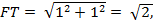а площадь треугольника EFT по формуле

Имеем:

Библиографическая ссылка

Ушаков Р.А. МЕТОД ОБЪЁМОВ ПРИ РЕШЕНИИ СТЕРЕОМЕТРИЧЕСКИХ ЗАДАЧ // Старт в науке. – 2020. – № 1.
;

URL: https://science-start.ru/ru/article/view?id=1833 (дата обращения: 11.03.2023).

Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»

(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)

Источник

Как подготовиться к решению заданий ЕГЭ № 14 по стереометрии | 1С:Репетитор

Как показывают результаты профильного экзамена по математике, задачи по геометрии — в числе самых сложных для выпускников. Тем не менее, решить их, хотя бы частично, а значит заработать дополнительные баллы к общему результату возможно. Для этого необходимо, конечно, знать достаточно много о «поведении» геометрических фигур и уметь применять эти знания для решения задач. Здесь мы постараемся дать некоторые рекомендации, как подготовиться к решению задачи по стереометрии.

Эта задача обычно состоит из двух частей:

доказательной, в которой вас попросят доказать некоторое утверждение для заданной конфигурации геометрических тел;

вычислительной, в которой нужно найти некоторую величину, опираясь на то утверждение, которое вы доказали в первой части задачи.

За решение данной задачи на экзамене по математике в 2018 году можно получить максимум два первичных балла. Допускается решить только «доказательную» или только «вычислительную» часть задачи и заработать в этом случае один первичный балл.

Многие школьники на экзамене даже не приступают к решению задачи №14, хотя она значительно проще, например, задачи № 16 — по планиметрии.

В задачу № 14 традиционно включается лишь несколько вопросов из всех возможных для стереометрических задач:

нахождение расстояний в пространстве;

нахождение углов в пространстве;

построение сечения многогранников плоскостью;

нахождение площади этого сечения или объемов многогранников, на которые эта плоскость поделила исходный многогранник.
В соответствии с этими вопросами строится и подготовка к решению задачи.

Сначала, разумеется, нужно выучить все необходимые аксиомы и теоремы, которые понадобятся для доказательной части задачи. Помимо того, что знание аксиом и теорем поможет вам на экзамене непосредственно при решении задачи, их повторение позволит систематизировать и обобщить ваши знания по стереометрии вообще, то есть создать из этих знаний некую целостную картину.

Итак, что же нужно выучить?

Способы задания плоскости в пространстве, взаимное расположение прямых и плоскостей в пространстве.

Определения, признаки и свойства параллельных прямых и плоскостей в пространстве.

Определения, признаки и свойства перпендикулярных прямых и плоскостей в пространстве.

После того как вы повторили теорию, можно приступать к рассмотрению методов решения задач. В курсе «1C:Репетитор» представлены все необходимые материалы для подготовки: видеолекции с теорией, тренажеры с пошаговым решением задач, тесты для самопроверки, интерактивные модели, позволяющие ученикам 10-х и 11-х классов наглядно рассмотреть методы решения задач по стереометрии, в том числе на примерах задач ЕГЭ 2017 года.

Мы рекомендуем решать задачи в такой последовательности:

Углы в пространстве (между скрещивающимися прямыми, между прямой и плоскостью, между плоскостями);
Расстояния в пространстве (между двумя точками, между точкой и прямой, между точкой и плоскостью, между скрещивающимися прямыми);
Решение многогранников, то есть нахождение углов между ребрами и гранями, расстояний между ребрами, площадей поверхностей, объемов по заданным в условии задачи элементам;
Сечения многогранников — методы построения сечений (например, метод следов) и нахождения площадей сечений и объемов получившихся после построения сечения многогранников (например, использование свойств перпендикулярной проекции и метод объемов).

Для всех указанных типов задач существуют различные методы решения:

классический (основанный на определениях и признаках);

метод проекций;

метод замены точки;

метод объемов.

Эти методы нужно знать и уметь применять, так как есть задачи, которые довольно сложно решаются одним методом и гораздо проще — другим.

При решении стереометрических задач более эффективным по сравнению с классическим методом нередко оказывается векторно-координатный. Классический метод решения задач требует отличного знания аксиом и теорем стереометрии, умения применять их на практике, строить чертежи пространственных тел и сводить стереометрическую задачу к цепочке планиметрических. Классический метод, как правило, быстрее приводит к искомому результату, чем векторно-координатный, но требует определенной гибкости мышления. Векторно-координатный метод представляет собой набор готовых формул и алгоритмов, но при этом требует более длительных расчетов; тем не менее, для некоторых задач, например, для нахождения углов в пространстве, он предпочтительнее классического.

Многим абитуриентам не позволяет справиться со стереометрической задачей неразвитое пространственное воображение. В этом случае мы рекомендуем использовать для самоподготовки интерактивные тренажеры с динамическими моделями пространственных тел. Такие тренажеры есть на портале «1С:Репетитор» (для перехода к их использованию необходимо зарегистрироваться): работая с ними, вы не только сможете «выстроить» решение задачи «по шагам», но и на объемной модели увидеть все этапы построения чертежа в различных ракурсах.

С помощью таких же динамических чертежей мы рекомендуем учиться строить сечения многогранников. Кроме того, что модель автоматически проверит правильность вашего построения, вы сами сможете, рассматривая сечение с разных сторон, убедиться, верно или неверно оно построено, и если неправильно, то в чем именно ошибка. Построение сечения на бумаге, с помощью карандаша и линейки, конечно, таких возможностей не дает. Посмотрите пример построения сечения пирамиды плоскостью с использованием такой модели (Нажмите на картинку, что бы перейти к тренажеру):

Последний вопрос, на который надо обратить внимание, — это нахождение площадей сечений или объемов, получившихся после построения сечения многогранников. Здесь также существуют подходы и теоремы, которые позволяют в общем случае существенно сократить трудозатраты на поиск решения и получение ответа. В курсе «1С:Репетитор» мы знакомим вас с этими приемами.

Если вы следовали нашим советам, разобрались со всеми вопросами, которые здесь затронуты, и решили достаточное количество задач, то велика вероятность, что вы практически готовы к решению задачи по стереометрии на профильном ЕГЭ по математике в 2018 году. Дальше необходимо только поддерживать себя «в форме» до самого экзамена, то есть решать, решать и решать задачи, совершенствуя свое умение применять изученные приемы и методы в разных ситуациях. Удачи!

Регулярно тренируйтесь в решении задач

Чтобы начать заниматься на портале «1С:Репетитор», достаточно зарегистрироваться.
Вы можете:

Начать заниматься бесплатно.
Получить доступ ко всей теории и тренажерам задачи №14. Это стоит всего 990 рублей.
Купить доступ к этой задаче в составе экспресс-курса «Геометрия» и научиться решать задачи №14 и №16 на максимальный балл.

Все курсы состоят из методически правильной последовательности теории и практики, необходимой для успешного решения задач. Включают теорию в форме текстов, слайдов и видео, задачи с решениями, интерактивные тренажеры, модели, и тесты.

Остались вопросы? Позвоните нам по телефону 8 800 551-50-78 или напишите в онлайн-чат.

Здесь ключевые фразы, чтобы поисковые роботы лучше находили наши советы:
Как решать задание 14 на экзамене ЕГЭ, задачи по геометрии, решение задач, по стереометрии, методы решения задач, тренажеры, видео, КИМ ЕГЭ 2017, подготовка к ЕГЭ, профиль математика, математика профильного уровня, решение задачи по наклонной треугольной призме, грани, взаимно перпендикулярно, общее ребро, плоскости, точки, ребро равно, боковая поверхность, решение задач на сечение многогранника, перпендикулярное сечение, вычислить объем фигуры, в основании прямой треугольной призмы лежит, признаки равенства и подобия треугольников, примеры решения задач ЕГЭ по геометрии, вычисление сечения, задачи по математике профильного уровня, применение методов сечения, решение задач на площадь, задачи ЕГЭ 2017 по стереометрии, подготовка к ЕГЭ, выпускникам 11 класса, в 2018 году, поступающим в технический вуз.

Источник