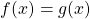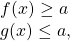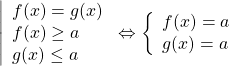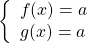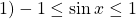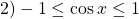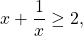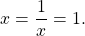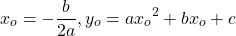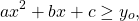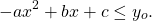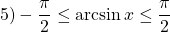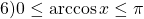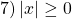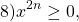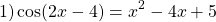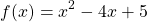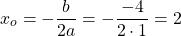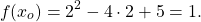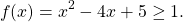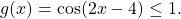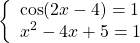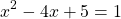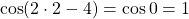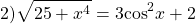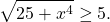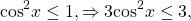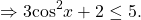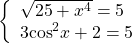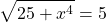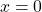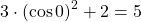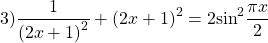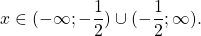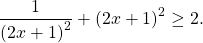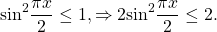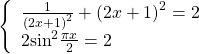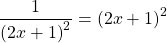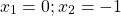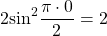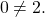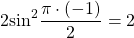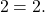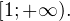Метод оценки егэ математика

В этой статье мы рассмотрим мощный метод, который применяется, когда в левой и правой частях уравнения или неравенства стоят функции разных типов. Для того чтобы лучше его запомнить, расскажем историю о том, как птичка и рыбка полюбили друг друга.

Еще раз: в левой и правой частях уравнения находятся функции разных типов. Мы помним, что в математике существует 5 типов элементарных функций: степенные, показательные, логарифмические, тригонометрические и обратные тригонометрические. Подробно о них — в статье «Элементарные функции и их графики».

Мы знаем из курса алгебры, что уравнения, которые мы решаем, обычно относятся к одному из этих пяти типов. Показательные и логарифмические, квадратные и тригонометрические уравнения — для каждого типа есть свои характерные приемы и способы решения. И основаны они на тех или иных свойствах функций. Для тригонометрических уравнений — свои способы решения, для логарифмических — свои.

Но сейчас мы рассмотрим уравнение, в левой и правой частях которого находятся функции разных типов. Вот оно:

Такое уравнение бесполезно возводить в квадрат или делать с ним арифметические действия. Бесполезно брать логарифмы от обеих частей — от этого оно станет только хуже.

Что же с ним делать? Упростим его, насколько возможно.

Посмотрим на правую часть этого уравнения. Очевидно,

Интересно — а какой же будет левая часть? Давайте оценим и ее тоже.

Поскольку получим, что

Значит,

Получается, что при всех значениях х левая часть уравнения не меньше, чем 8, а правая часть не больше, чем 8. И это значит, что решением уравнения могут быть только такие значения переменной х, когда и левая, и правая часть равны 8. Тогда они равны друг другу. В этом и состоит метод оценки.

Метод оценки применяется для уравнений и неравенств, где функции, стоящие в левой и правой части, могут быть равны друг другу только в определенной точке, причем одна из них принимает в этой точке наименьшее значение, а другая — наибольшее. 

Вот как это выглядит:

А чтобы лучше запомнить суть метода, рассказываем историю.

Глубоко-глубоко в море жила маленькая рыбка. А высоко-высоко в небе жила маленькая птичка. И однажды они полюбили друг друга! А встретиться они могли только в одной точке, на границе моря и неба, до которой рыбке надо подняться, а птичке — спуститься! 

Смотри видео о том, как птичка и рыбка полюбили друг друга и что из этого получилось

О чем эта история? О нашем уравнении, конечно! В левой и правой его частях находятся функции разных типов. И при определенном значении х они оказались равны друг другу. Легко заметить, что значения выражения в левой части всегда больше либо равны восьми («птичка»), значения выражения в правой части — меньше либо равные восьми («рыбка»). И возможно, есть такая точка, где у одной из этих функций будет минимум, а у другой — максимум, причем значение каждой из них станет равно восьми.

Нам осталось только проверить, что эта точка действительно есть. Приравняем правую часть к восьми.

Подставив в левую часть, получим, что и она равна восьми при этом значении x. Значит, является единственным корнем данного уравнения.

Ответ:

Вот еще одна задача на метод оценки.

Умножим обе части данного неравенства на положительную величину:

В левой и правой частях полученного неравенства оказались функции разных типов. Метод оценки!

Выделим под логарифмом полный квадрат:

Неравенство примет вид:

Наибольшее значение выражения под логарифмом равно 2. Стало быть, наибольшее значение логарифма равно
, то есть 1, и достигается оно при единственном значении x = 3.

В то же время, наименьшее значение выражения также равно 1, и достигается оно при том же единственном значении x= 3.

Поэтому последнее неравенство будет выполнено лишь в одном-единственном случае: когда обе его части равны 1, т. е. при x = 3. Решением данного неравенства служит единственное число!

Ответ: x= 3.

Мы обещали задачи с параметрами, которые решаются методом оценки. Вот, пожалуйста:

18. Найдите все значения а, при которых уравнение

имеет ровно два решения.

Обозначим Уравнение примет вид:

Мы видим, что левая часть этого уравнения не меньше единицы, а правая часть — не больше единицы. Равенство может быть, только если обе они равны единице.

Это классическая задача на метод оценки.

В нашем случае функция f в левой части уравнения и функция g в правой части «встречаются», когда одна из них принимает свое наименьшее значение, равное единице, а другая — свое наибольшее значение, также равное единице.

Получим:

Второе уравнение означает, что частное — целое число.

В первом уравнении сделаем замену

Получим:

Обозначим а — 6 = b и найдем, сколько корней имеет уравнение при неотрицательных z и различных b.

Нам нужно, чтобы исходное уравнение относительно х имело два корня.

Это происходит, когда уравнение имеет единственный положительный корень , которому соответствуют и

Заметим, что так как если то и двух корней не получится.

График функции — парабола с вершиной М(3;-9)

1) Если , то уравнение имеет единственный корень , которому соответствуют два корня исходного уравнения: и

Поскольку , в этом случае . Это значение удовлетворяет и второму уравнению системы: — целое.

2) Уравнение > имеет единственное положительное решение также при , при этом и

Но если , условию удовлетворяет только

Ответ: или

Слайд 1

М етод мажорант при решении задач с параметрами Николаева Ирина Николаевна

Слайд 2

Применим для задач в которых множества значений левой и правой частей уравнения или неравенства имеют единственную общую точку, являющуюся наибольшим значением для одной части и наименьшим для другой. Эту ситуацию хорошо иллюстрирует график. Как начинать решать такие задачи ? Привести уравнение или неравенство к виду Сделать оценку обеих частей. Пусть существует такое число М , из области определения такое что Решить систему уравнений: МЕТОД МАЖОРАНТ

Слайд 3

1 3

Слайд 4

Пример 1 . Решить уравнение При х = 0 второе уравнение обращается в тождество, значит х = 0 корень уравнения. Ответ: х = 0. Графическая иллюстрация

Слайд 5

1 5

Слайд 6

Ответ: нет корней. Пример 2 . Решите уравнение Графическая иллюстрация х = 0 не удовлетворяет второму уравнению, полученная система не имеет решений

Слайд 7

Применим для задач в которых множества значений левой и правой частей уравнения или неравенства имеют единственную общую точку, являющуюся наибольшим значением для одной части и наименьшим для другой. Эту ситуацию хорошо иллюстрирует график. Как начинать решать такие задачи ? Привести уравнение или неравенство к виду Сделать оценку обеих частей. Пусть существует такое число М , из области определения такое что Решить систему уравнений: МЕТОД МАЖОРАНТ

Слайд 8

1 8

Слайд 9

1 9 Задача 1. Найти все значения параметра а при которых уравнение имеет решение. Задача 2. Найти все значения параметра при каждом из которых существует хотя бы одно число x , удовлетворяющее уравнению .

Слайд 10

Выводы: 1 10 Внешним признаком использования метода оценок является наличие функций различной природы, что затрудняет или делает невозможным использование стандартных методов. Иногда оценка одной из частей уравнения (неравенства) может быть легко сделана, тогда следует попытаться получить противоположную оценку для другой части уравнения (неравенства). Но решающим фактором успешного применения метода оценок остается знание свойств элементарных функций.

Слайд 11

Задача 3. Найти все значения параметра а , при каждом из которых уравнение имеет решения. Найдите эти решения. При всех значениях х выражение При всех значения х выражения Поэтому Следовательно, левая часть уравнения не меньше 4, а правая часть – не больше 4. Получаем систему: Ответ: при Решение. Перепишем уравнение в виде

Слайд 12

1 12 Пример. Решить уравнение:

Решение уравнений методом оценки

Решение уравнений методом оценки основано на сравнении области значений функций, стоящих в левой и правой части уравнения.

Если в уравнении

то равенство возможно тогда и только тогда, когда и f(x) и g(x) одновременно равны a:

При этом, если максимальное значение функции, стоящей в одной части уравнения, равно минимальному значению функции, стоящему в другой части уравнения, и эти значения достигаются для обеих функций при x=x0, то xo — корень уравнения.

Графически это можно проиллюстрировать так:

Если максимальное значение функции, стоящей в одной части уравнения, равно минимальному значению функции, стоящему в другой части уравнения, но эти значения достигаются при разных x0, то уравнение не имеет корней:

Получив систему уравнений

достаточно решить одно из уравнений (которое проще), а затем проверить, являются ли найденные корни корнями другого уравнения.

Чаще всего при решении уравнений методом оценки правой и левой части используют следующие соображения:

причём равенство достигается при

4) Квадратичная функция в вершине параболы (x0; y0)

при a>0 принимает своё наименьшее значение:

при отрицательном коэффициенте a при x² — наибольшее значение:

где n — натуральное число.

Примеры решения уравнений методом оценки левой и правой части.

— квадратичная функция. График — парабола ветвями вверх. Наименьшее значение принимает в вершине

С другой стороны

Следовательно, исходное уравнение равносильно системе уравнений

Корень второго уравнения:

x=2. Проверяем, является ли 2 корнем первого уравнения:

— верно. Следовательно, x=2 — единственный корень.

Так как x⁴≥0, то 25+ x⁴≥25, а значит,

С другой стороны,

Следовательно, исходное уравнение равносильно системе уравнений

Решаем первое уравнение

Проверяем, является ли x=0 корнем второго уравнения:

— верно. Значит, x=0 — корень данного уравнения.

Так как сумма взаимно-обратных положительных чисел не меньше двух,

Так как сумма положительных взаимно-обратных чисел равна 2, если эти числа равны между собой, то

Проверяем, являются ли эти корни корнями второго уравнения.

Таким образом, исходное уравнение имеет единственный корень x= -1.

Метод оценки области значений

Самостоятельная работа №2

Тема: «Решение уравнений. Способы решения уравнений»

Метод разложения на множители

Суть данного метода в том, чтобы путем равносильных преобразований представить левую часть исходного уравнения, содержащую неизвестную величину в какой-либо степени, в виде произведения двух выражений, содержащих неизвестную величину в меньшей степени. При этом справа от знака равенства должен оказаться ноль. Проще всего уяснить эту идею на конкретном примере.

Пример: решите уравнение методом разложения на множители: 2,5x^2+4x = 0.

Решение. Осуществим разложение на множители (представим исходное выражение в виде произведения). Для этого вынесем переменную x за скобки: x(2,5x+4) = 0.

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. Следовательно, x=0 или 2,5x+4 =0. Из последнего уравнения получаем: 2,5x = -4 или x=-1,6.

Метод замены переменной

Цель данного метода в том, чтобы удачным образом заменить сложное выражение, содержащее неизвестную величину, новой переменной, в результате чего уравнение принимает более простой вид. Далее полученное уравнение решается относительно новой переменной, после чего происходит возврат к исходной переменной. Все эти идеи проще осознать на конкретном примере.

Решите уравнение методом замены переменной:

Решение. Такие уравнения называются биквадратными. Перепишем его в виде: Введем новую переменную Тогда исходное уравнение примет следующий простой вид: Решая полученное квадратичное уравнение, получаем, что или

Возвращаемся теперь к старой переменной (обратная замена): или Решений у первого уравнения нет, поскольку не существует такого действительного числа, квадрат которого был бы отрицателен. Второе уравнение имеет два корня

Метод оценки области значений

Суть данного метода в сравнении областей значений выражений, входящих в уравнение. Часто такой анализ позволяет легко решать сложные уравнения, содержащие различные выражения (рациональные, тригонометрические, логарифмические, показательные и др.). Разберем это на конкретном примере.

Пример:Решите уравнение, используя метода оценки области значений:

Решение. Рассмотрим функцию Известно, что поэтому Итак, функция может принимать значения только из промежутка

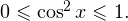
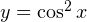
Рассмотрим теперь функцию Графиком данной функции является парабола, ветви которой направлены вверх, а вершина расположена в точке

График соответствующей квадратичной функции

То есть область значений данной функции (те значения, которые может принимать переменная ) представляет собой промежуток

Таким образом выражения, стоящее справа и слева от знака равенства в исходном уравнении, могут оказаться равными, только если их значения окажутся равными 1, причем при одном и том же значении Непосредственной подстановкой убеждаемся, что это условие выполняется при Действительно, и При всех остальных значениях функция больше 1 (см. график). Значит — единственный корень уравнения.

Ответ: 0.

4. Приведение подобных членов.

Переход от уравнения

f(x) + m(x) — m(x) = g(x) (5)

f(x) = g(x) (6),
называют приведением подобных слагаемых.

Прежде чем рассматривать переход от уравнения (5) к уравнению (6), сделаем следующее замечание. Согласно сказанному в предыдущем пункте уравнеПрежде чем рассматривать переход от уравнения (5) к уравнению (6), сделаем следующее замечание. Согласно сказанному в предыдущем пункте уравнение (5) равносильно уравнению

f(x) + m(x) = g(x) + m(x) (7).

Поэтому переход от уравнения (1) к уравнению (2) означает то же самое, что и переход от уравнения (7) к уравнению (2), т. е. во всех рассуждениях уравнение (1) можно заменять равносильным ему уравнением (7). Таким образом, сказанное в этом пункте будет относиться не только к приведению подобных членов в одной части уравнения, но и к вычеркиванию (взаимному уничтожению) одинаковых слагаемых в левой и правой частях. Прежде чем сформулировать общее утверждение, относящееся к переходу от уравнения (1) к уравнению (2) или, что то же самое, от

уравнения (7) к уравнению (2), рассмотрим следующие примеры.

Пример: . слагаемого — х и — 2 получается равносильное уравнение х 4 = х 2 .

5. Умножение обеих частей уравнения на одно и то же выражение.

Переход от уравнения

f(x) = g(x) (8)
к уравнению

f(x) p(x) = g(x) p(x). (9)
называют умножением обеих частей уравнения на одно и тоже выражение.

По поводу этого перехода можно высказать следующие утверждения:

1) Если в каждой точке, где определены обе функции f(x), g(x) определена также и функция p(x) (иначе говоря, Если в каждой точке, где определены обе функции f(x), g(x) определена также и функция p(x)), то уравнение (9) является следствием уравнения (8) или (8) (9)

2) Если в каждой точке, где определены обе функции f(x), g(x) определена также и функция p(x) и в каждой точке указанного множества функция p(x) отлична от нуля, то уравнения (8) и (9) равносильны, т. е. (8) (9).

Заметим, что в общем случае переход от уравнения (9) к уравнению (8) может привести как к появлению посторонних корней, так и к потере корней.

Рассмотрим уравнение x 2 — x = 0. Умножив обе части этого уравнения на , мы получим уравнение = 0, которое не является следствием исходного. В самом деле, исходное уравнение имеет корни х₁ = 0, х₂ = 1, а уравнение = 0 — лишь корень х = 1. Потеря корня связана с тем, что функция — не определена при. х = 0, а как раз это значение х является корнем заданного уравнения.

6. Метод замены неизвестного. Метод замены неизвестного применяется при решении уравнений вида f(g(x)) = 0.

Он основывается на следующей теореме.

Теорема 3. Рассмотрим уравнение f(t) = 0, где t — вспомогательное неизвестное, и пусть t₁, t₂,₃. t_k — все корни уравнения. Тогда для решения уравнения f(g(x)) = 0 достаточно найти все корни каждого из уравнений g(x) = t_m (m = l, 2, . k) и объединить множества корней этих уравнений.

Иначе говоря, f(g(x)) = 0 g(x) = t₁, g(x) = t₂, . g(x) = t_k.

Эта теорема позволяет свести решение уравнения вида f(g(x))= 0 к решению нескольких более простых уравнений f(t) = 0, g(x) = t_k, где k = 1, 2. m.

Обычно эта теорема применяется следующим образом.

Дано некоторое уравнение f(x) = 0. Задача заключается в том, чтобы умело подобрать функцию g(x), позволяющую ввести новое неизвестное t = g(x), и затем выразить функцию f(х) через t, т. е. представить ее в виде f(x) = h(g(x)). В результате данное уравнение запишется в виде h(g(x))= 0, и для его решения можно будет применить доказанную теорему. Такой прием решения уравнений и называется методом замены неизвестного (поскольку вначале решается уравнение f(t) = 0, в котором неизвестное х заменено новым, вспомогательным неизвестным t.

7. Способ сложения

Алгоритм решения системы линейных уравнений с двумя неизвестными способом сложения.

1. Если требуется, путем равносильных преобразований уравнять коэффициенты при одной из неизвестных переменных в обоих уравнениях.

2. Складывая или вычитая полученные уравнения получить линейное уравнение с одним неизвестным

3. Решить полученное уравнение с одним неизвестным и найти одну из переменных.

4. Подставить полученное выражение в любое из двух уравнений системы и решить это уравнение, получив, таким образом, вторую переменную.

Применение метода оценки к решению уравнений
методическая разработка на тему

Применение метода оценки к решению уравнений

Урок — творческая лаборатория

Математика всегда была неотъемлемой и существенной составной частью человеческой культуры, она является ключом к познанию окружающего мира, базой научно-технического прогресса и важной компонентой развития личности. Творческая деятельность учащихся не ограничивается лишь приобретением нового. Работа будет творческой, когда в ней проявляется собственный замысел учащихся, ставятся новые задачи, и они самостоятельно решаются при помощи приобретенных знаний, при активном участии в проектной и исследовательской деятельности. Это позволяет развивать познавательную активность учащихся, творческие способности и сообразительность. В процессе такой работы ребята учатся работать с дополнительной литературой, историческим материалом, устанавливать внутрипредметные и межпредметные связи. Всё это будет проявляться ярче, быстрее и качественнее, если на уроках применяются современные информационные и педагогические технологии.

Технические средства способствуют активизации учебного процесса, помогают нам эффективно проводить уроки, организовывать быстрый доступ к запланированной информации, решать задачи практического содержания, выполнять исследовательскую работу. Больше внимания уделить математической речи, формированию познавательного интереса к предмету и творческой активности, отработки вычислительных навыков, и навыков анализа и сравнения, исследовательской деятельности. На данном уроке-творческой лаборатории по теме «Применение метода оценки к решению уравнений» благодаря предварительной работе с дополнительной литературой, интернетом, подготовке презентаций, а самое главное исследовательской деятельности обучающихся, расширяется кругозор, повышается познавательная активность. Эпиграфом нашего урока стало высказывание С. Коваля: «Решение уравнений это золотой ключ, открывающий все сезамы». Урок проведен был для учащихся 10 и 11 классов. Для 10 класса это был урок обобщения и систематизации знаний по теме «Решение уравнений и неравенств» и в тоже время некоторый материал был для них новым и ранее не изученным. Для 11 класса этот урок был одним из этапов подготовки к ЕГЭ. После урока обучающиеся высказали свое мнение о проведенном совместном занятии. Такой подход к изучению математики вызвал интерес у учащихся и они выразили желание проводить такие уроки чаще.

Широкое применение таких технологий при изучении математики даёт возможность реализовать принцип «учение с увлечением». И это очень важно, ведь всем понятно, что учебная успешность школьника определяется не только и не столько его способностями, сколько желанием учиться, то есть мотивацией. Познавательные мотивы в самом широком смысле – это желание ребёнка освоить новые знания или способы получения новых знаний. Все это в совокупности позволило повысить информативность урока, эффективность обучения, придать уроку динамизм и выразительность. Известно, что в среднем с помощью органов слуха усваивается лишь 15% информации, с помощью органов зрения 25 %. А если воздействовать на органы восприятия комбинированно, усвоенными окажутся около 65 % информации. Уроки с применением современных педагогических технологий в купе с креативным подходом позволяет решить старую проблему — низкую степень индивидуализации обучения, усилить темп умственной деятельности, обеспечивает творческий рост, как учащихся, так и учителя.

Скачать:

Вложение	Размер
urok.docx	61.72 КБ
refleksiya_domashnee_zadanie_kartochki.docx	23.4 КБ
prezentaciya1.ppt	229 КБ
prezentaciya_microsoft_powerpoint.pptx	2.25 МБ

Предварительный просмотр:

Муниципальное образовательное учреждение

средняя общеобразовательная школа с углубленным изучением отдельных предметов

Применение метода оценки к решению уравнений

Урок — творческая лаборатория

учитель математики МОУ СОШ №21

учитель математики МОУ СОШ №21

Учитель математики и информатики

2011-2012 учебный год

Современные педагогические технологии как средство решения математических задач

Математика всегда была неотъемлемой и существенной составной частью человеческой культуры, она является ключом к познанию окружающего мира, базой научно-технического прогресса и важной компонентой развития личности. Творческая деятельность учащихся не ограничивается лишь приобретением нового. Работа будет творческой, когда в ней проявляется собственный замысел учащихся, ставятся новые задачи, и они самостоятельно решаются при помощи приобретенных знаний, при активном участии в проектной и исследовательской деятельности. Это позволяет развивать познавательную активность учащихся, творческие способности и сообразительность. В процессе такой работы ребята учатся работать с дополнительной литературой, историческим материалом, устанавливать внутрипредметные и межпредметные связи. Всё это будет проявляться ярче, быстрее и качественнее, если на уроках применяются современные информационные и педагогические технологии.

Технические средства способствуют активизации учебного процесса, помогают нам эффективно проводить уроки, организовывать быстрый доступ к запланированной информации, решать задачи практического содержания, выполнять исследовательскую работу. Больше внимания уделить математической речи, формированию познавательного интереса к предмету и творческой активности, отработки вычислительных навыков, и навыков анализа и сравнения, исследовательской деятельности. На данном уроке-творческой лаборатории по теме « Применение метода оценки к решению уравнений » благодаря предварительной работе с дополнительной литературой, интернетом, подготовке презентаций, а самое главное исследовательской деятельности обучающихся, расширяется кругозор, повышается познавательная активность. Эпиграфом нашего урока стало высказывание С. Коваля: «Решение уравнений это золотой ключ, открывающий все сезамы». Урок проведен был для учащихся 10 и 11 классов. Для 10 класса это был урок обобщения и систематизации знаний по теме «Решение уравнений и неравенств» и в тоже время некоторый материал был для них новым и ранее не изученным. Для 11 класса этот урок был одним из этапов подготовки к ЕГЭ. После урока обучающиеся высказали свое мнение о проведенном совместном занятии. Такой подход к изучению математики вызвал интерес у учащихся и они выразили желание проводить такие уроки чаще.

Широкое применение таких технологий при изучении математики даёт возможность реализовать принцип «учение с увлечением». И это очень важно, ведь всем понятно, что учебная успешность школьника определяется не только и не столько его способностями, сколько желанием учиться, то есть мотивацией. Познавательные мотивы в самом широком смысле – это желание ребёнка освоить новые знания или способы получения новых знаний. Все это в совокупности позволило повысить информативность урока, эффективность обучения, придать уроку динамизм и выразительность. Известно, что в среднем с помощью органов слуха усваивается лишь 15% информации, с помощью органов зрения 25 %. А если воздействовать на органы восприятия комбинированно, усвоенными окажутся около 65 % информации. Уроки с применением современных педагогических технологий в купе с креативным подходом позволяет решить старую проблему — низкую степень индивидуализации обучения, усилить темп умственной деятельности, обеспечивает творческий рост, как учащихся, так и учителя.

Тема: Применение метода оценки к решению уравнений.

Урок – творческая лаборатория для учащихся 10 и 11 классов.

• Повторить основные методы решения уравнений:

1. Разложение на множители.
2. Введение новой переменной.
3. Понижение степени.
4. Возведение обеих частей в степень
5. Умножение обеих частей уравнения на выражение, не принимающее значение- равное нулю.

• Систематизировать и обобщить применение метода оценки:

1. Использование монотонности функции
2. Использование ограниченности функции
3. Использование ОДЗ
4. Применение неравенства Коши
5. Неравенство Бернулли и его применение

• Активизировать творческую активность учащихся;самостоятельность при работе с дополнительной литературой, отборе практического материала по заданной теме.
• Развивать вариативность мышления, логику, анализ, ораторские способности.

Оборудование: Проектор, презентация к уроку, программа «Живая математика», компьютер, карточки с заданиями.

Предварительная подготовка: Задания старшим групп и консультации по данной теме: Лазарева С.И. (10 класс) — неравенство Коши и его применение, Суханова Н.А.(11 класс) — неравенство Бернулли и его применение, Ульянова Н.В.(10-11 классы) — создание презентаций.

1. Учитель математики 10 класса ( слайд №1 ).

Мы приветствуем всех любителей математики в нашей творческой лаборатории. Тема нашего занятия «Применение метода оценки к решению уравнений», а эпиграфом мы выбрали слова: «Решение уравнений это золотой ключ, открывающий все сезамы». Сегодня мы рассмотрим несколько нестандартных методов решения задач по математике. Незнание и непонимание таких методов существенно уменьшает область успешно решаемых задач. Тем более, что имеющая место тенденция к усложнению заданий ЕГЭ по математике стимулирует появление новых оригинальных (нестандартных) подходов к решению математических задач.

И в 10, и в 11 классах мы решали достаточно много разных видов уравнений, используя при этом различные способы и приемы решения ( слайд №2 ). На заседании нашей творческой лаборатории мы обобщим и систематизируем полученные ранее знания. Кроме того мы попытаемся подняться на более высокую ступеньку знаний, получив ещё один инструмент решения уравнений: методом оценки. Итак, остановимся на рассмотрении приема «Метод оценки», который включает в себя:

1. Использование монотонности функций
2. Использование ограниченности функций
3. ОДЗ
4. Неравенство Коши
5. Неравенство Бернулли

Рассмотрим решение уравнения несколькими способами и оценим рациональность какого-либо метода.

1. А) Ученица 10 класса показывает решение уравнения двумя способами.

1 способ (по алгоритму): (слайд №3).

2 способ (использование монотонности функции): ( слайд№4 )

Т.к. y 1 (x)=X – 2 – возрастающая функция,

y 2 (x)= — убывающая функция, то если корень существует, то он единственный ( Если функция непрерывна и возрастает (убывает) на отрезке , а функция непрерывна и убывает (возрастает) на этом же отрезке, то уравнение на отрезке может иметь не более одного корня .)

Из уравнения очевидно, что x=2. (на слайде №4 графическая интерпретация). Это решение достойно внимания, запишите его в тетрадь.

Б) Учитель математики 10 класса : «Чтобы решить уравнение,
Корни его отыскать,
Нужно немного терпенья,
Ручку, перо и тетрадь»

Предлагаю выполнить задания по группам с последущей проверкой.

1. 2 x = 6 – x
2. 8 — x=

1. Использование ограниченности функций

А) Учитель математики 11 класса. Одним из эффективных методов решения уравнений или неравенств является метод, основанный на использовании ограниченности функций. К наиболее известным ограниченным функциям относятся, например, некоторые тригонометрические функции; обратные тригонометрические функции; функции, содержащие модуль, степень, корень с четной степенью и т.д. Ученик 11 класса покажет применение этого метода на примере решения уравнения. Так как для учащихся 10 класса, я думаю, такое решение будет открытием, то его надо записать в тетради.

Рассмотрим функции y 1 (x) = , y 2 (x)= . Обе функции ограничены:

E (y 1 ) = [-1;1], E(y 2 ) = [1;  ]. То есть уравнение имеет решение в случае:

Ни при как значениях n (целых), корни уравнений не совпадут, значит исходное уравнение не имеет решения (на слайде №5 графическая интерпретация).

Б) Т. к «Усердие все превозмогает» давайте решим уравнение на данный метод (по парам)

|x+2| = — (x+2) 2 (Ответ: -2)

А) Учитель математики 10 класса приглашает ученицу 10 класса для решения уравнения:

1 способ: Это уравнение решается традиционным способом, возведением последовательно дважды в квадрат. Решение громоздкое и не рациональное. 2 способ . Я предлагаю более изящное решение этого уравнения. Предлагаю записать его в тетрадь. ( слайд №5, ссылка с графической интепретации )

Очевидно, чтобы решение существовало необходимо потребовать, чтобы x+2>x+5, тогда 2>5 не верно => уравнение решений не имеет.

Б) Ученик 10 класса предлагает два способа решения уравнения:

1 способ. Предлагаю вам план стандартного решения.

1. ОДЗ [-3;0)  (0;3]
2. При приведении к общему знаменателю получаем уравнение

, которое решается по алгоритму. Вывод: решение очень громоздкое

2 способ решения более рациональный (с использованием неравенства Коши) ( слай №7, №8, №9 ).

По неравенству Коши получаем

Так как равенство достигается лишь в случае равенства слагаемых (следствие из неравентсва Коши: )

Так как y , то 3+y , получаем

Так как , то или

Проще и красивее. А как думаете вы? (Решение даётся учащимся на карточке)

4. Учитель математики 11 класса. Для решения следующего уравнения красивым, удобным методом является метод, основанный на использовании ОДЗ. А) Ученик 11 класса предлагает решение уравнения:

Решение: ( слайд №10, №11 )

Оценим слагаемые на ОДЗ. С учетом верхней границы и нижней границы ОДЗ.

Очевидно, что , значит , т.е. уравнение не имеет решений.

Очень красивое решение получается при применеии неравенства Бернулли. Б) Ученик11 класса знакомит с краткой биографией Я. Бернулли ( слайд№12, №13 )

В) Ученик 11 класса знакомит с обобщённым неравенством Бернулли и показывает решение предыдущего уравнения с его применением ( слайд №14, №15, №16 )

Используем обобщенное неравенство Бернулли: если , то

т.к. x > -1, p=0,25, то

– не верно, значит уравнение не имеет решений.

Г) Ученик 11 класса предлагает решение уравнения:

( слайд № 17 ). Решение даётся учащимся на карточке.

5.Итог урока: Слайд №2, Следует отметить, что знание нестандартных методов и приемов решения задач по математике способствует развитию нового, нешаблонного мышления, которое можно успешно применять также и в других сферах человеческой деятельности (кибернетика, вычислительная техника, экономика, радиофизика, химия и т.д.).

«Теория без практики мертва и бесплодна, практика без теории невозможна и пагубна. Для теории нужны знания, для практики, сверх того, и умение.» ( слайд №18 )

Учите теорию, применяйте полученные знания на практике, и перед вами откроется огромный мир непостижимого и прекрасного.

Отметки за урок.

6. «Результат учения равен
произведению способности на старательность.
Если старательность равна нулю,
то и произведение равно нулю.
А способности есть у каждого.» Предлагаем проявить способности и старательность при выполнении домашнего задания, которое вы можете увидеть на карточке. В наших классах много творческих личностей, способных к самостоятельным исследованиям, поэтому мы надеемся, что вы сможете использовать один из приёмов решения рассмотренных на уроке, а, быть может, кто-то из вас откроет новый приём.

А на перемене взять интервю у учащихся 10 и 11 классов.

Применяем неравенство Бернулли к каждому слагаемому