16. Задачи по планиметрии
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи, решаемые методом площадей
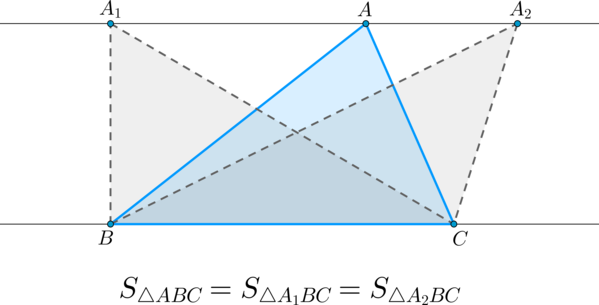
(blacktriangleright) Если вершину треугольника перемещать по прямой, параллельной противолежащей стороне, то площадь при этом останется прежней.
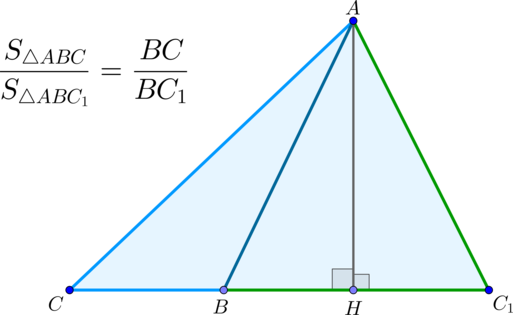
(blacktriangleright) Если два треугольника имеют равные высоты (общую высоту), то их площади относятся как основания, к которым эти высоты проведены.
(blacktriangleright) Если два треугольника имеют одинаковые стороны (общую сторону), то их площади относятся как высоты, которые к этим сторонам проведены.
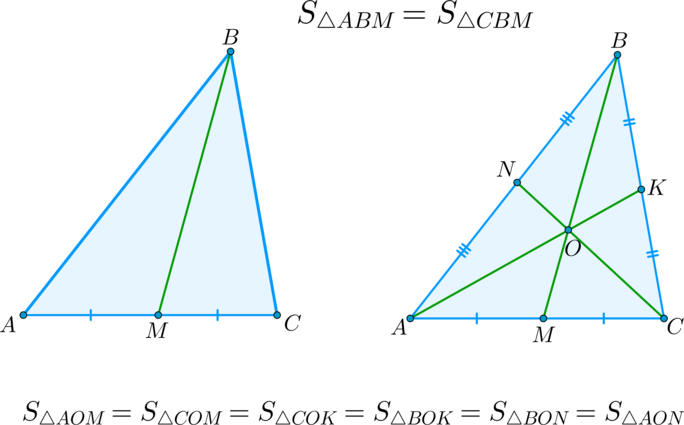
(blacktriangleright) Следствие: медиана треугольника делит его на два треугольника, равных по площади.
(blacktriangleright) Следствие: все три медианы треугольника делят его на шесть треугольников, равных по площади.
(blacktriangleright) Если два треугольника имеют по равному углу (общему углу), то их площади относятся как произведения сторон, образующих эти углы.
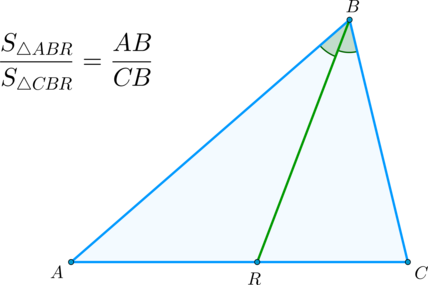
(blacktriangleright) Следствие: биссектриса угла треугольника делит его на два треугольника, площади которых относятся как стороны, образующие этот угол.
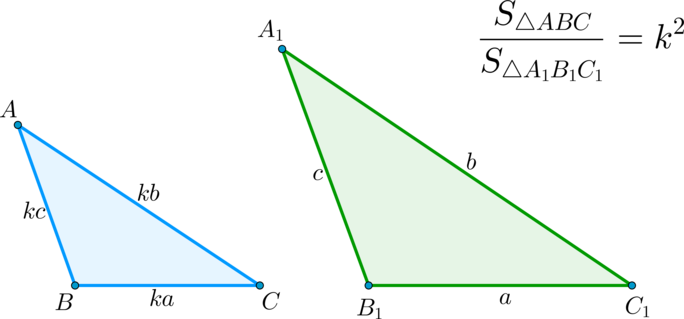
(blacktriangleright) Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
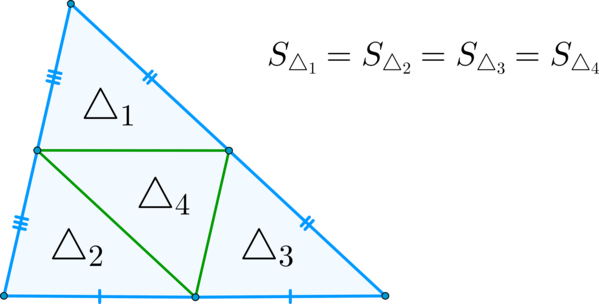
(blacktriangleright) Следствие: все три средние линии треугольника делят его на четыре равных треугольника, и, как следствие, равных по площади.
Задание
1
#2436
Уровень задания: Легче ЕГЭ
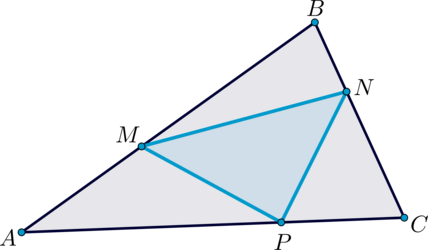
Точки (M, N, P) лежат на сторонах (AB, BC, CA) соответственно треугольника (ABC), причем (AM:AB=BN:BC=CP:CA=1:3). Площадь треугольника (MNP) равна (15). Найдите площадь треугольника (ABC).
(triangle ABC) и (triangle MBN) имеют общий угол (B), при этом (BM=frac23BA), (BN=frac13BC).
Т.к. площади треугольников, имеющих общих угол, относятся как произведения сторон, образующих этот угол, то
[dfrac{S_{MBN}}{S_{ABC}}=dfrac{frac23BAcdot frac13BC}{BAcdot BC}=
dfrac29 quad Rightarrow quad S_{MBN}=dfrac29S_{ABC}]
Аналогично рассуждая, получаем, что
[S_{MAP}=S_{PCN}=dfrac29S_{ABC}]
Следовательно, [15+3cdot dfrac29S_{ABC}=S_{ABC} quad Rightarrow
quad S_{ABC}=3cdot 15=45.]
Ответ: 45
Задание
2
#2444
Уровень задания: Легче ЕГЭ
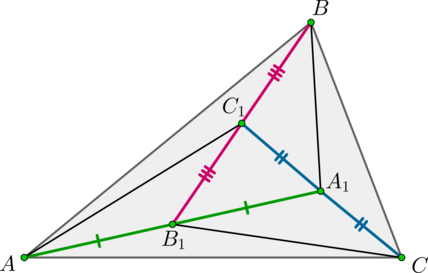
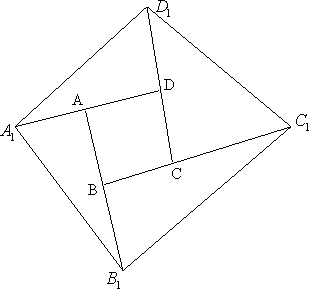
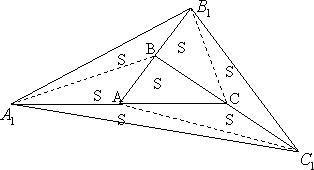
Внутри треугольника (ABC) взяты точки (A_1, B_1, C_1) так, что (B_1) – середина (AA_1), (C_1) – середина (BB_1), (A_1) – середина (CC_1). Найдите отношение площадей треугольников (A_1B_1C_1) и (ABC).
Соединим точки (A) и (C_1), (B) и (A_1), (C) и (B_1).
Т.к. медиана делит треугольник на два равновеликих треугольника, то
[S_{triangle AB_1C}=S_{triangle A_1B_1C}=S_{triangle A_1B_1C_1}.]
Аналогично,
[S_{triangle CA_1B}=S_{triangle C_1A_1B}=S_{triangle AC_1B}=S_{triangle
AC_1B_1}.]
Таким образом, все семь образовавшихся треугольников имеют одинаковые площади. Значит,
[S_{triangle A_1B_1C_1}:S_{triangle ABC}=1:7.]
Ответ:
(1:7)
Задание
3
#1760
Уровень задания: Равен ЕГЭ
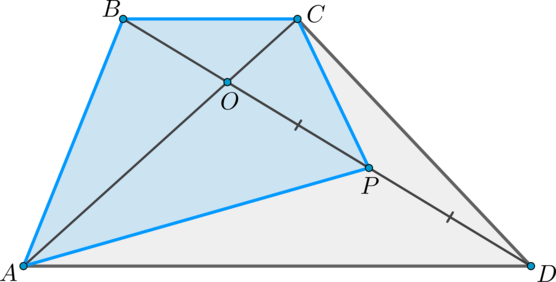
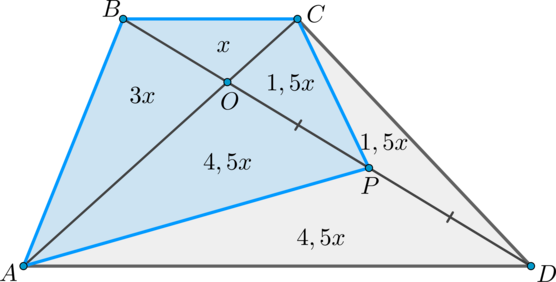
Дана трапеция (ABCD), ее основания (BC) и (AD) равны (2) и (6) соответственно. Диагонали (BD) и (AC) пересекаются в точке (O). Точка (P) – середина (OD). (S_{bigtriangleup ABO}=9). Найдите площадь четырехугольника (ABCP).
Пусть (S_{bigtriangleup BOC}=x). Заметим, что (bigtriangleup BCO
sim bigtriangleup AOD) по двум углам, так как (BCparallel AD), (angle BCA = angle CAD) как накрест лежащие и (angle BOC = angle
AOD) как вертикальные.
Следовательно, [dfrac{BC}{AD} =dfrac{BO}{OD} =dfrac{CO}{OA}
=dfrac{2}{6} =dfrac{1}{3}.]
(dfrac{S_{bigtriangleup ABO}}{S_{bigtriangleup BCO}}
=dfrac{AO}{OC} =dfrac{3}{1} Rightarrow S_{bigtriangleup
ABO}=3x), аналогично, (S_{bigtriangleup CDO}=3x).
(dfrac{S_{bigtriangleup COP}}{S_{bigtriangleup CPD}}
=dfrac{OP}{PD} =dfrac{1}{1} Rightarrow S_{bigtriangleup
COP}=S_{bigtriangleup CPD}=1,5x).
Площади подобных треугольников относятся как коэффициент подобия в квадрате, следовательно, [dfrac{S_{bigtriangleup BOC}}{S_{bigtriangleup AOD}} =left(
dfrac{1}{3} right)^2 =dfrac{1}{9} Rightarrow
S_{bigtriangleup ADO}=9x Rightarrow S_{bigtriangleup APO}=4,5x
Rightarrowqquad S_{ABCP}=10x.] Так как (3x=9), то (x=3) и, следовательно, (S_{ABCP}=30).
Ответ: 30
Задание
4
#2441
Уровень задания: Равен ЕГЭ
Внутри равностороннего треугольника со стороной (m) движется точка. Докажите, что сумма расстояний от этой точки до сторон треугольника не меняется, и найдите эту сумму.
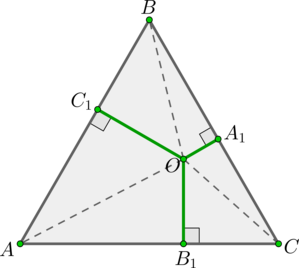
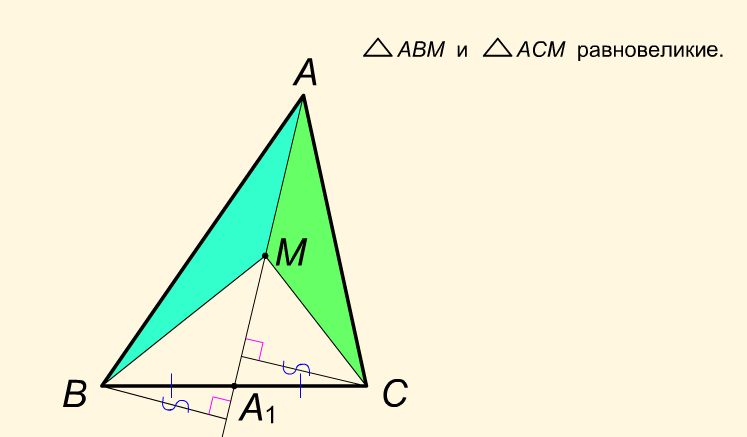
Рассмотрим равносторонний (triangle ABC), (AB=m), (O) – точка внутри треугольника, (OA_1, OB_1, OC_1) — перпендикуляры на стороны (BC, AC, AB) соответственно.
Рассмотрим (triangle AOB, triangle BOC, triangle COA). Их площади равны (0,5mcdot OC_1; 0,5mcdot OA_1; 0,5mcdot OB_1) соответственно. Тогда сумма их площадей равна площади всего (triangle ABC), следовательно:
[0,5mcdot (OC_1+OA_1+OB_1)=S_{triangle ABC}=dfrac{sqrt3}4m^2 quad
Leftrightarrow quad OC_1+OA_1+OB_1=dfrac{sqrt3}2m.]
Таким образом, мы доказали, что для фиксированного равностороннего треугольника сумма постоянна, а также нашли ее.
Ответ:
(dfrac{sqrt3}2m)
Задание
5
#1287
Уровень задания: Равен ЕГЭ
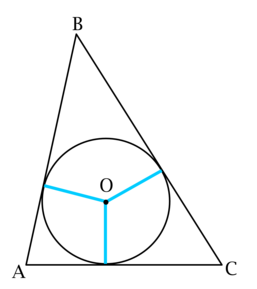
Радиус вписанной в треугольник (ABC) окружности равен трети одной из его высот.
а) Докажите, что одна из сторон треугольника (ABC) равна среднему арифметическому двух других его сторон.
б) Найдите наибольшее возможное значение периметра такого треугольника, если одна из его сторон равна (4), а две другие имеют целые длины.
а) (S_{ABC} = pcdot r), где (p) – полупериметр, а (r) – радиус вписанной в (ABC) окружности.
Пусть (h) – длина той высоты, которая равна (3r), (a) – длина стороны, высота к которой имеет длину (h), (P) – периметр треугольника (ABC).
В итоге имеем: [dfrac{1}{2}hcdot a = S_{ABC} = pcdot r = pcdotdfrac{h}{3},] откуда (a = dfrac{P}{3}), тогда (b + c = dfrac{2P}{3} = 2a), где (b) и (c) длины других сторон треугольника.
б) Длины сторон треугольника (ABC) образуют арифметическую прогрессию: если обозначить (a — c = d), то (a = c + d), (b = c + 2d).
Пусть (d > 0). Тогда (b) наибольшая сторона треугольника (ABC) и существование треугольника (ABC) с длинами сторон (a), (b) и (c) равносильно выполнению неравенства [b < a + cqquadLeftrightarrowqquad c + 2d < 2c + dqquadLeftrightarrowqquad d < c.] Так как длины всех сторон треугольника (ABC) – целые числа, то (d) – целое, следовательно, (dleq c — 1).
Так как (c) – меньшая из сторон, то (cleq 4), тогда (dleq 3), откуда (aleq 7), (bleq 10), тогда [P_{triangle ABC}leq 4 + 7 + 10 = 21.] При этом случай (c = 4), (a = 7), (b = 10) подходит, следовательно, при (d > 0) максимально возможный периметр равен 21.
При (d = 0) треугольник (ABC) равносторонний и (P_{triangle ABC} = 12 < 21).
Случай (d < 0) рассматривается аналогично (меняется только то, что (c > a > b), следовательно, достаточно в рассуждении из случая (d > 0) всюду поменять местами (b) и (c)).
Таким образом, наибольший возможный периметр треугольника (ABC) равен 21.
Ответ:
б) (21).
Задание
6
#1288
Уровень задания: Равен ЕГЭ
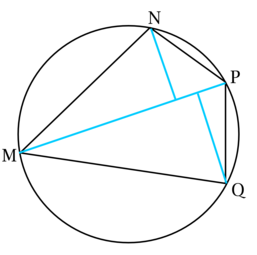
Четырёхугольник (MNPQ) вписан в окружность, причём (dfrac{MN}{PQ} = dfrac{QM}{PN}).
а) Докажите, что точки (N) и (Q) равноудалены от прямой, содержащей (MP).
б) Найдите расстояние от точки (P) до прямой, содержащей (MQ), если (MP = 4), расстояние от (N) до прямой, содержащей (MP) равно (1,5), (MQ = 3).
а) Так как (dfrac{MN}{PQ} = dfrac{QM}{PN}), то (MNcdot PN = QMcdot PQ).
Так как (MNPQ) вписанный, то (angle MNP = 180^circ — angle MQP), следовательно, (sinangle MNP = sinangle MQP).
В итоге [S_{triangle MNP} = 0,5cdot MNcdot PNcdotsinangle MNP = 0,5cdot QMcdot PQcdotsinangle MQP = S_{triangle MQP}.]
С другой стороны, у треугольников (MNP) и (MQP) общее основание, следовательно, их площади относятся как высоты, проведённые к этому основанию, тогда эти высоты равны, значит, точки (N) и (Q) равноудалены от прямой, содержащей (MP).
б) В данном случае (S_{triangle MNP} = 0,5cdot 4cdot 1,5 = 3), но (S_{triangle MNP} = S_{triangle MQP}). Обозначим расстояние от точки (P) до прямой, содержащей (MQ) через (h), тогда [S_{triangle MQP} = 3 = 0,5cdot 3cdot h,] следовательно, (h = 2).
Ответ:
б) (2).
Задание
7
#1289
Уровень задания: Равен ЕГЭ
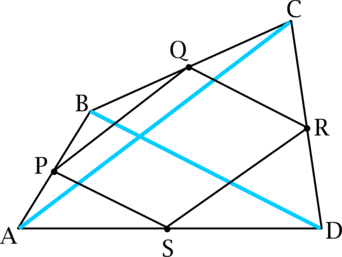
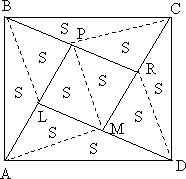
(ABCD) – выпуклый четырёхугольник, точки (P), (Q), (R) и (S) середины его сторон, причём (PQRS) тоже выпуклый четырёхугольник. (A_1B_1C_1D_1) другой выпуклый четырёхугольник с серединами сторон в точках (P), (Q), (R) и (S).
а) Докажите, что диагонали (PQRS) точкой пересечения делятся пополам.
б) Найдите максимально возможное значение величины (dfrac{S_{A_1B_1C_1D_1}}{S_{ABCD}}).
а) Проведём диагонали (AC) и (BD).
Рассмотрим треугольники (APS) и (ABD): (PS) – средняя линия в треугольнике (ABD), тогда треугольники (APS) и (ABD) подобны, причём (dfrac{PS}{BD} = dfrac{1}{2}).
Аналогично (dfrac{QR}{BD} = dfrac{1}{2}), следовательно, (PS = QR).
Аналогично доказывается равенство (PQ = RS). В итоге в выпуклом четырёхугольнике (PQRS) противоположные стороны равны, тогда (PQRS) – параллелограмм, следовательно, его диагонали точкой пересечения делятся пополам.
б) Докажем, что по взаимному расположению середин сторон выпуклого четырёхугольника его площадь восстанавливается однозначно.
Из подобия (APS) и (ABD) получаем: [dfrac{S_{APS}}{S_{ABD}} = left(dfrac{1}{2}right)^2 = dfrac{1}{4}.]
Аналогично (4S_{QCR} = S_{CBD}), (4S_{PBQ} = S_{ABC}), (4S_{SDR} = S_{ACD}). Тогда [S_{ABCD} = S_{ABD} + S_{CBD} = 4S_{APS} + 4S_{QCR}.] С другой стороны, [S_{ABCD} = S_{ABC} + S_{ACD} = 4S_{PBQ} + 4S_{SDR},] тогда [S_{ABCD} + S_{ABCD} = 4S_{APS} + 4S_{QCR} + 4S_{PBQ} + 4S_{SDR} qquadLeftrightarrow] [S_{APS} + S_{QCR} + S_{PBQ} + S_{SDR} = dfrac{1}{2}S_{ABCD}.] Но (S_{ABCD} = S_{APS} + S_{QCR} + S_{PBQ} + S_{SDR} + S_{PQRS}), откуда окончательно [S_{PQRS} = dfrac{1}{2}S_{ABCD}.]
Таким образом, по взаимному расположению точек (P), (Q), (R), (S) однозначно восстанавливается площадь параллелограмма (PQRS), а значит и площадь любого выпуклого четырёхугольника с серединами сторон в точках (P), (Q), (R) и (S).
В итоге [dfrac{S_{A_1B_1C_1D_1}}{S_{ABCD}} = 1.]
Ответ:
б) (1).
Практика показывает, что задачи на нахождение площади треугольника встречаются в ЕГЭ из года в год. Именно поэтому, если учащиеся хотят получить достойные баллы по итогам прохождения аттестационного испытания, им непременно стоит повторить эту тему и снова разобраться в материале.
Как подготовиться к экзамену?
Научиться решать задачи на нахождение площади треугольника, подобные тем, которые встречаются в ЕГЭ, вам поможет образовательный проект «Школково». Здесь вы найдете весь необходимый материал для подготовки к прохождению аттестационного испытания.
Для того чтобы упражнения по теме «Площадь треугольника в задачах ЕГЭ» не вызывали у выпускников затруднений, рекомендуем прежде всего освежить в памяти базовые тригонометрические понятия и правила. Для этого достаточно перейти в раздел «Теоретическая справка». Там представлены основные определения и формулы, которые помогут при нахождении правильного ответа.
Чтобы закрепить усвоенный материал и попрактиковаться в решении задач, предлагаем выполнить упражнения, которые подобрали специалисты образовательного проекта «Школково». Каждое задание на сайте имеет правильный ответ и подробное описание способа решения. Учащиеся могут практиковаться как с простыми, так и с более сложными задачами.
«Прокачать» свои навыки в выполнении подобных упражнений школьники могут в режиме онлайн как в Москве, так и в любом другом городе России. В случае необходимости выполненное задание можно сохранить в разделе «Избранное», чтобы в дальнейшем вернуться к нему и обсудить ход решения с преподавателем.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Тема: «Метод площадей при решении геометрических задач второй части ОГЭ».
Цель: Рассмотрение теоретических основ;
Формирование представления о методе площадей;
Использование метода площадей при решении планиметрических (второй части ОГЭ и
некоторых конкурсных) задач.
Актуальность
Предмету геометрия отведено по учебному плану меньше
часов, чем алгебре. Учащиеся испытывают трудности при выполнении геометрических
заданий. Это задачи повышенной трудности, в модуле «Геометрия» на ОГЭ. Тема
«Метод площадей» — актуальна в связи с решением таких задач на экзамене (как
№24, №25, №26)
и на различных олимпиадах и конкурсах.
План
I.
Введение
II. Основная
часть.
1. Метод площадей.
2. Определение метода площадей. Характеристики метода.
3. Основные свойства площадей и ключевые задачи.
4. Практический диапазон применимости метода площадей к решению
задач
III. Выводы
IV. Заключение
V. Приложение. Причины ошибок. Классификация
I. Введение
Определение проблемы: необходимость
разбора решения геометрических задач из второй части экзаменационной работы по
выбранному методу.
Задачи
1. Изучение научно-методической литературы по проблеме
исследования.
Изучение метода площадей и после определения проблемы
научиться применять свойства площадей для составления соотношений, связывающих
ключевые задачи с неизвестными, используя различные приёмы.
2. Анализ различных учебных пособий с целью изучения и
описания метода площадей.
3.
Рассмотрение некоторого диапазона применимости метода
площадей к решению задач.
4. Рассмотрение на примерах структуры процесса решения
таких задач и развитие умения самостоятельно анализировать и конструировать
свои знания; классифицировать задачи.
5.
Умение ориентироваться в планиметрическом пространстве и нахождение путей
решения.
Трудности решения геометрических задач обусловлены следующими
факторами:
Неалгоритмичность задач.
Необходимость выбора метода решения задачи и теоремы для решения конкретной
задачи из большого набора известных фактов.
Обсуждение методов исследования. Метод
конкретных ситуаций (следование принципу «процесс обсуждения важнее самого
решения»), самостоятельное изучение и подготовленное в письменном виде решение
проблемы.
Результаты исследования.
Сбор, анализ полученных данных, систематизация
решенных задач, корректировка их. Оформление результатов
исследовательской работы в электронном виде.
II. Основная
часть
1. Метод площадей.
В школьном курсе математики, самыми трудными считаются
геометрические
задачи. Как научиться решать геометрические задачи,
особенно
сложные, конкурсные? При решении геометрических задач, как
правило,
алгоритмов нет, и выбирать наиболее подходящую к данному
случаю
теорему не просто.
В данной работе рассматривается один из самых распространенных
алгоритмов
решения геометрических задач – метод площадей. Значимость метода
площадей заключается в том, что он является предметом изучения и одновременно
средством для изучения последующего материала.
Рассмотрим
в нашем исследовании метод площадей.
2. Определение
метода площадей. Характеристики метода.
Из
названия следует, что главным объектом данного метода является площадь.
Для
ряда фигур, например для треугольника, площадь довольно просто выражается через
разнообразные комбинации элементов фигуры.
1. Весьма эффективным оказывается прием, когда сравниваются различные выражения
для площади данной фигуры. В этом случае возникает уравнение, содержащее
известные и искомые элементы фигуры, разрешая которое мы определяем
неизвестное.
Здесь и проявляется основная особенность метода площадей:
из геометрической задачи он «делает» её алгебраической, сводя всё к
решению уравнения (а иногда и системы уравнений).
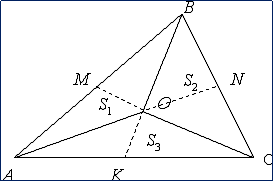
2.
Одна из разновидностей метода площадей сводится к использованию в задаче свойства
аддитивности площади: если фигура разбита на части, то ее площадь равна
сумме площадей этих частей. S=S1+S2+S3
2.
Универсального метода для решения всех задач на площади
многоугольников
нет, но существуют приемы, применимые ко многим
задачам.
Понятие площади мы используем даже при решении тех задач,
в условии которых отсутствует упоминание площади. Поэтому можно
говорить о методе площадей в геометрии.
4.
Метод площадей состоит в применении различных её свойств для нахождения
соотношений, связывающих их с неизвестными.
Остановимся
подробнее на характеристике и диапазоне применимости метода площадей.
3. Основные свойства площадей
Свойство
1.
Если вершину треугольника передвигать по прямой, параллельной основанию, то
площадь при этом не измениться.
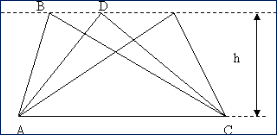
Рассмотрим
▲ABC и ▲ADC. Они
имеют
общее основание и равные
высоты,
т.к. прямые AC и BD
параллельные,
то расстояние между
ними равно h — высоте ▲ABC и ▲ADC.
Свойство
2. Если
два треугольника имеют одинаковые высоты, то отношение их
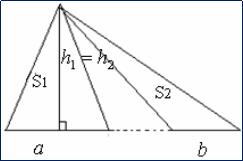
отношению длин оснований, т. е. сторон,
на которые опущены эти высоты.
Доказательство:
Пусть
h1 = h2 в двух треугольниках
с
основаниями a и b.
Рассмотрим
отношение площадей
этих
треугольников, получим:
=
.
Свойство 3
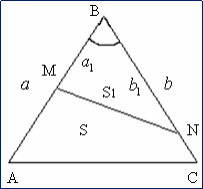
имеют общий угол, то их площади относятся
как
произведение сторон, заключающих этот угол.
Доказательство:
Рассмотрим
▲ABC и ▲MBN.
Пусть
AB = k∙MB, BC = k∙NB и ABC=MBN .
Используя
формулу площади треугольника, получим: отношение подобных площадей ▲ABC и
▲MBN.
Тогда
получим: = k2 .
Свойство
№4
Медиана
треугольника делит его на две равновеликие части.
Доказательство:
Рассмотрим
▲ABC . Пусть
медиана
— BM , тогда
AM=MC=1/2AC.
Медиана делит
треугольник
на два равновеликих с одинаковой
высотой.
Найдем площади
треугольников
▲ABM и ▲MBC. SABM = SCBM.
Свойство
№5
Медианы
треугольника делят
его
на три равновеликие части.
Аналогично
доказывается.
Медианы
треугольника делят его
на 6 равновеликих частей.
Утверждение.
Два треугольника
являются равновеликими,
если
равны их высоты и основания.
Свойство
№6
Средние
линии треугольника площади S
отсекают
от него
треугольники
площади ¼ S.
Доказательство
Рассмотрим
▲ABC. NM — средняя линия
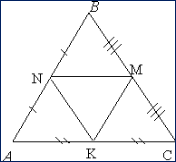
она равна половине
основания
AC.
Если
SABC = S, то можно доказать, что
площади
всех треугольников равны
одной
четвертой части площади ▲ABC.
4.
Применение свойств метода площадей к решению задач.
В
данном пункте рассмотрим систему геометрических задач, решаемых методом площадей.
Задачи построены по нарастающему уровню сложности.
№1(Задания типа № 24).
Стороны AC, AB, BC треугольника ABC равны 2,
и 2 соответственно.
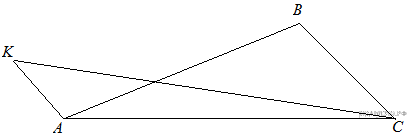
Точка K расположена вне треугольника ABC ,
причём отрезок KC пересекает сторону AB в
точке, отличной от B. Известно, что треугольник с вершинами K,
A и C подобен исходному. Найдите косинус
угла AKC, если ∠KAC >
90°. Найти площадь треугольника АВС.
Решение.
Рассмотрим подобные треугольники ABC и AKC и
установим соответствие между их углами. Против большей стороны всегда
лежит больший угол, в треугольнике ABC это
угол ABC в треугольнике ,
в свою очередь, есть тупой угол и
он является наибольшим, значит, ∠КАС = ∠АВС. Угол АСК заведомо
не может быть равен углу так
как он составляет только его часть. Следовательно, угол АСВ равен
углу АКС.
Найдём косинус угла , используя
теорему косинусов:
1)
2) S ABC = • СА• СВ•
;
Найдём: =
;
)2
= =
=
. S ABC =
Ответ: =
; S ABC =
.
Задания типа № 25.
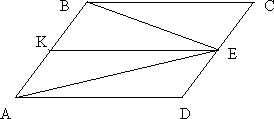
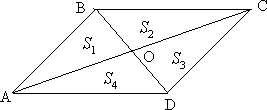
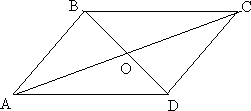
№2. В параллелограмме ABCD диагонали AC и BD пересекаются
в точке O. Докажите, что площадь параллелограмма ABCD в
четыре раза больше площади треугольника BOC.
Решение.
Проведём высоту так,
чтобы она проходила через точку О. Углы и
равны
друг другу как вертикальные. Вспомним также, что диагонали делятся точкой
пересечения пополам, следовательно, Рассмотрим
треугольники и
,
они прямоугольные, имеют равные углы и равные гипотенузы, следовательно,
эти треугольники равны, а значит, равны отрезки
и .
Таким образом,
Площадь параллелограмм
равна а
площадь треугольника
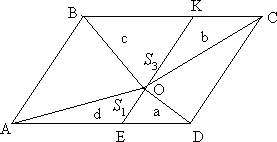
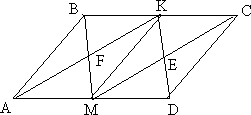
Типа №26. №3.
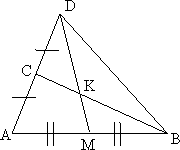
В треугольнике ABC на его медиане BM отмечена
точка K так, что BK : KM = 10 : 9.
Прямая AK пересекает сторону BC в
точке P. Найдите отношение площади четырёхугольника KPCM к
площади треугольника ABС.
Решение.
Пусть площадь
треугольника равна
Проведём прямую параллельную
Точка
—
середина следовательно,
—
средняя линия треугольника
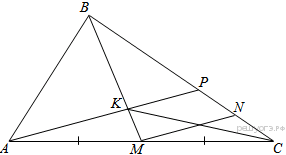
По теореме Фалеса для угла
находим:
а так как получаем,
что
Стороны треугольников и
сонаправлены,
их площади относятся как произведение отношений сонаправленных сторон,
поэтому
откуда
,
в то время как следовательно,
Тем самым, для искомого отношения площадей имеем:.
Ответ. .
Олимпиадные задачи: 9 класс.
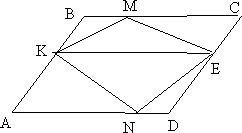
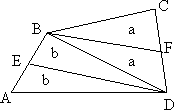
1. Сторона KP
трапеции NMКP равна 3 см. Расстояние из вершин N и М до стороны КР равны 7см и
5 см соответственно. Найдите площадь трапеции NMКP.
Решение. Сделаем чертеж. Опустим перпендикуляры из
точек N и М на сторону КР и
построим перпендикуляр KH
к стороне NP.
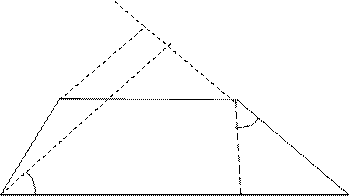 |
Обозначим ∠ANP
через α. Заметим, что ∠BMK
= ∠ANP
= α (стороны этих углов соответственно
параллельны), а также∠HKP
= ∠ANP
= α (в прямоугольных треугольниках NAP
и KHP угол с вершиной Р– общий).Тогда
имеем три подобных прямоугольных треугольника: NAP, MВK и КНР.
Значит: МК= , NP=
, КH=
. Следовательно,
SNMKP=
(MK
+ NP)KH=
= 18 (кв.см). Ответ: 18
кв.см
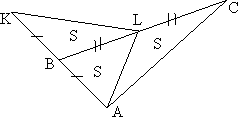
№2. 10 класс
а)
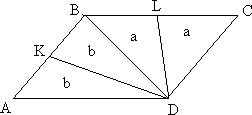
В треугольнике АВС на продолжении медианы ВМ выбрана точка К так, что МК:ВМ =
1:2. Известно, что АВ=5, ВС=3, СК=4. Найти АК.
б)
Найти площадь треугольника АВС.
Решение.
Сделаем чертёж:
В

 |
А
Обозначим ∠АМК
через α. Тогда ∠АМВ = π-α, ∠ВМС
= α, ∠СМК = π-α.
Применим
теорему косинусов к треугольникам АВМ, ВСМ, СКМ и АКМ.
КМ=
х, тогда ВМ= 2х, АМ =СМ= у.
Имеем:
25=
у2+4х2+4ху cosα,
9=
у2+4х2— 4ху cosα,
16
= у2+ х2+2ху cosα.
Решив
систему трёх уравнений с тремя неизвестными, получим:
,
,
.
Из
треугольника АКМ имеем: АК2= 12-2. Тогда АК=2
.
б)
Найти площадь треугольника АВС.
SABC
= • 2•MB
• MC• ; ∠ВМС
= α; ;
=
=
; SABC
= • 2•2•
•
= 2
=
•
Ответ:
2 . SABC
=
.
Выводы.
1. При решении геометрических задач внимательно
анализировать условие задачи, находить взаимосвязь между элементами
геометрических фигур, применять свойства и конкретные приёмы решения задач.
2. Использовать приравнивание выражений, полученных
по различным формулам площади для одной и той же фигуры, что позволит получить
зависимость между ее элементами. Полезно рассматривать отношение площадей фигур,
одна из которых (или обе) содержит в себе искомые элементы.
3. Применять также метод «вспомогательного элемента»,
который заключается во включении в решение некоторого дополнительного объекта,
прямо не фигурирующего в условии, если с его помощью можно получить новые
умозаключения и результаты с последующим исключением объекта.
4. Для развития умений самостоятельно конструировать
свои знания, рассматривая различные структуры процесса решения задач,
ориентируясь в информационном и социальном пространстве.
Заключение.
Подводя итог обзору методов решения и методов поиска решения геометрических
задач, заметим, что не все этапы в равной степени обязательно присутствуют в
решении любой задачи. Мы рассмотрели примеры, показывающие, что не всегда
приходится выявлять характерные особенности конфигурации и, наоборот, некоторые
решения одним этим этапом, по сути, и исчерпывались. Отдельно следует сказать
об анализе полученного решения. Основная функция анализа — контроль
правильности полученного решения,
Иногда
в ходе анализа необходимо провести исследование, существует ли полученная
конфигурация, не относится ли она к разряду невозможных, при каких условиях
возможно ее существование.
Изучение
методов решения геометрических задач будет более эффективным, если
рассматривать на примере одной задачи возможности использования
различных геометрических приёмов.
Приложение
1. Причины ошибок в решении геометрических задач
·
Незнание и/или непонимание аксиом, определений, теорем
·
Неумение их применять
·
Невнимательное чтение условия и вопроса задания
·
Вычислительные ошибки
·
Нарушения логики в рассуждениях
·
Принятие ошибочных гипотез. Недостатки в работе с рисунком.
2.
Классификация
задач, решаемых методом площадей
1.
В
условии задачи упоминается о площади
2. В условии задачи не упоминается о площади
3.
Задачи на выражение площади несколькими способами
4.
Задачи на использование свойства аддитивности.
5.
Задачи на использование свойств отношения площадей.
6.
Комбинированные задачи.
Слайд 2
Цель урока: повторение и обобщение знаний о методе площадей в решении задач.
Задачи:
- обучающие: обобщить и систематизировать знания о методе площадей, отработать умения применить формулы в решении задач.
- развивающие: развить познавательные умения,
- воспитательные: развить положительное отношение к знаниям.
Тип урока: урок повторения.
Ход урока
I. Актуализация знаний.
Слайд 3
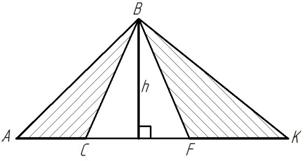
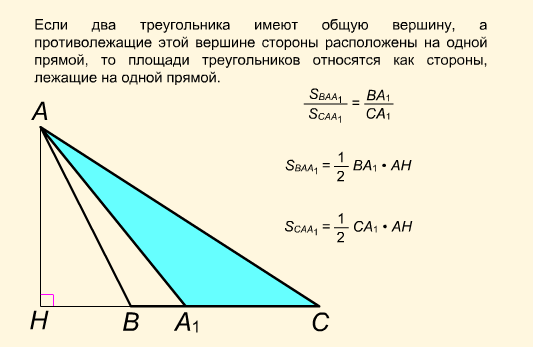
Площади треугольников, имеющих равные высоты (общую высоту), относятся как стороны соответствующие этим высотам.
Рисунок 1
Слайд 4
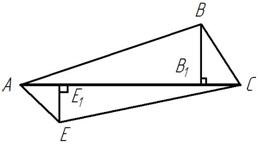
Площади треугольников, имеющих равные стороны, относятся как соответствующие этим сторонам высоты.
Рисунок 2
Слайд 5
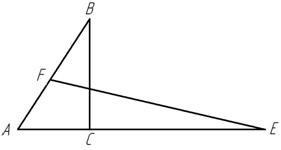
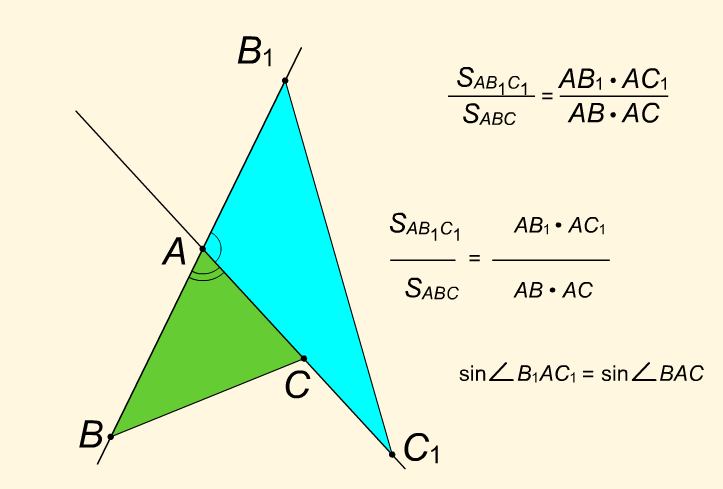
Площади треугольников, имеющих равный угол (или общий угол), относятся как произведение сторон, содержащий этот угол.
Рисунок 3
Слайд 6
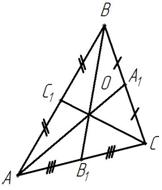
Медиана делит треугольник на два равновеликих треугольника.
Три медианы треугольника делят его на шесть равновеликих треугольников.
Рисунок 4
Слайд 7
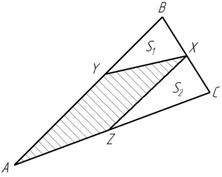
Рисунок 5
II. Устная работа.
Слайд 8
Случай, когда треугольники имеют общую высоту.
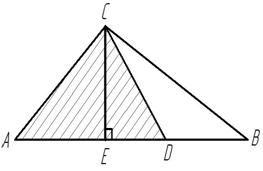
Рисунок 6
Дано:
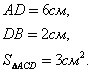
Найти:
Ответ:
Слайд 9
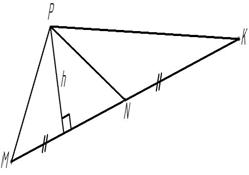
Рисунок 7
Дано:
Найти:
Ответ: 20.
Вывод:
- Отношение площадей треугольников, имеющих общую высоту равно отношению сторон, к которым проведена высота.
- Если же стороны, к которым проводится высота равны, то и площади треугольников также равны.
- Во сколько раз отношение сторон треугольников, к которым проводится высота больше (меньше), во столько раз и площади больше (меньше).
Слайд 10
Случай, когда треугольник и параллелограмм имеют общую высоту.
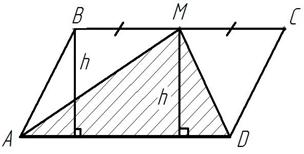
Рисунок 8
Дано:
параллелограмм,
Найти:
Ответ: 8.
Вывод: В этом случае отношение площадей треугольника и параллелограмма равно отношению их высот. Высота параллелограмма есть высота треугольника. Но в нахождении площади треугольника присутствует коэффициент , а, значит, составляя и решая данную пропорцию, получаем 8.
Слайд 11
Рисунок 9
Дано:
Найти:
Ответ:
Слайд 12
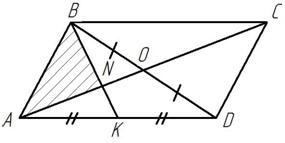
Рисунок 10
Дано:
– параллелограмм,
– медиана
– медиана
– середина
Найти:
Ответ: 10.
III. Работа на уроке.
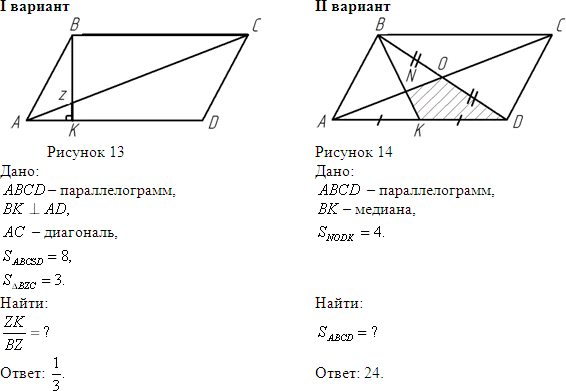
1 ряд. Работа в парах (сидят слабый ученик и ученик средних способностей).
Решает I вариант – уровень «4»,
2, 3 ряды – II вариант – уровень «4 – 5».
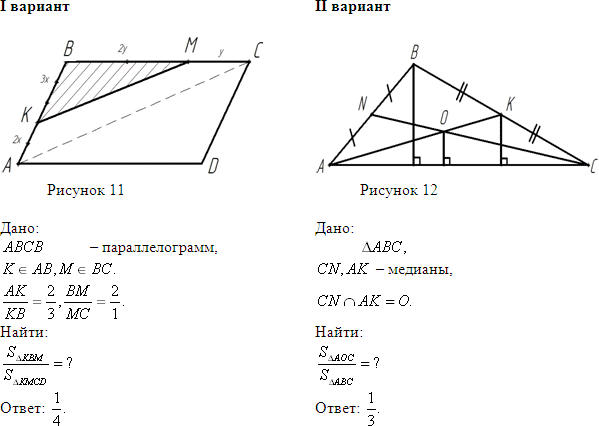
IV. Самостоятельная работа контролирующего характера (дифференцированная).
V. Итог урока.
Домашнее задание. Ученику следует выбрать для решения две любые задачи. При желании можно выполнить всё задание.
Задача 1. В треугольнике со сторонами
вписан параллелограмм
причём точки
лежат на сторонах
соответственно. Известно, что площадь параллелограмма составляет
площади треугольника
Найдите стороны параллелограмма.
Задача 2. В треугольнике на прямой
выбрана точка
так, что
Точка
середина стороны
Прямая
пересекает отрезок
в точке
Найдите площадь треугольника
если площадь треугольника
равна 120.
Задача 3. Через точку лежащую в треугольнике
проведены три прямые, параллельные всем сторонам треугольника. В результате треугольник разбился на 3 треугольника и 3 параллелограмма. Известно, что площади полученных треугольников равны соответственно 1;2,25и 4. Найдите сумму площадей полученных параллелограммов.
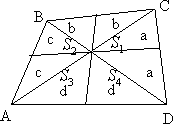
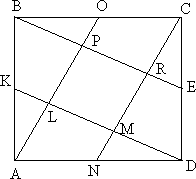
Задача 4. Площадь трапеции равна 810. Диагонали пересекаются в точке
Отрезки, соединяющие середину основания
с вершинами
и
пересекаются с диагоналями трапеции в точках
и
Найдите площадь треугольника
если одно из оснований трапеции вдвое больше другого.
Литература:
- Геометрия. 10–11 классы: учеб.для общеобразоват. учреждений: базовый и профил. уровни / [Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.]. – 22-е изд. – М.: Просвещение, 2013. – 255с.
- Геометрия в таблицах. 7–11 кл.: Справочное пособие / Авт.-сост. Л.И. Звавич, А.Р. Рязановский. – 4-е изд., стереотип. – М.: Дрофа, 2000. – 128 с.
- http://www.fipi.ru (Официальный сайт Федерального института педагогических измерений)
Разработка урока.
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
PRZ_-_shpory.docx
Скачиваний:
83
Добавлен:
25.12.2018
Размер:
9.39 Mб
Скачать
Характеристика
метода. Из названия
следует, что главным объектом данного
метода является площадь. Для ряда фигур,
например для треугольника, площадь
довольно просто выражается через
разнообразные комбинации элементов
фигуры (треугольника). Поэтому весьма
эффективным оказывается прием, когда
сравниваются различные выражения для
площади данной фигуры. В этом случае
возникает уравнение, содержащее известные
и искомые элементы фигуры, разрешая
которое мы определяем неизвестное.
Здесь и проявляется основная особенность
метода площадей – из геометрической
задачи он «делает» алгебраическую,
сводя все к решению уравнения (а иногда
системы уравнений).
Само сравнение
выражений для площади фигуры может быть
различным. Иногда площадь фигуры
представляется в виде суммы площадей
ее частей. В других случаях приравниваются
выражения, основанные на различных
формулах площади для одной и той же
фигуры, что позволяет получить зависимость
между ее элементами.
Суть
метода площадей не ограничивается
только описанным выше приемом. Иногда
бывает полезно рассмотреть отношение
площадей фигур, одна из которых (или
обе) содержит в себе искомые элементы.
В
современных учебниках, пособиях и
различного рода задачниках, к сожалению,
уделяется мало внимания психологическим
факторам, влияющим на успешность обучения
математике. А именно, воспитание у
учащихся уверенности в своих силах,
развитие умения пользоваться прошлым
опытом. В данном реферате предлагается
разработка системы математических
задач, решаемых методом площадей.
Реферат построен следующим образом.
Берутся два общеизвестных утверждения,
которые являются базовыми. На основе
этих утверждений выстраиваются две
«цепочки» задач по нарастающему уровню
сложности. Решения задач в этих «цепочках»
основаны на базовых утверждениях и на
решении предыдущих задач.
Утверждение
1. Два
треугольника являются равновеликими,
если равны их высоты и основания.
|
Задача |
|
Решение. |
|
Задача |
|
Решение. |
|
Задача |
|
Решение. Отсюда |
|
Задача |
|
Решение. |
|
Задача |
|
Решение. |
Утверждение
2. Медиана
треугольника делит его на два равновеликих
треугольника.
|
Задача |
|
Решение. Проведем |
|
Задача Докажите, |
|
Решение. |
|
Задача |
|
Решение. |
|
Задача |
|
Решение. S▲AOB |
|
Задача |
|
Решение. |
|
Задача |
|
Решение. |
|
Задача |
|
Решение. Продолжим |
|
Задача |
|
Решение. |
|
Задача |
|
Решение. Произведя |
|
Задача |
|
Решение. |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #