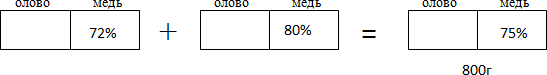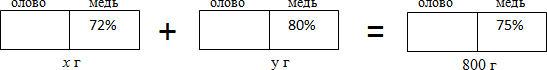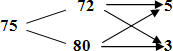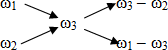Нижегородская область
администрация Шатковского муниципального района
муниципальное общеобразовательное учреждение
«Лесогорская средняя школа»
Творческая работа по математике
Решение одной задачи разными способами
|
Работу выполнил Воробьев Илья, ученик 11 класса МОУ «Лесогорская СШ» |
|
|
Руководитель Жилова Зоя Геннадьевна, учитель математики МОУ «Лесогорская СШ» |
|
|
Адрес: 607710, Нижегородская обл., Шатковский р-н, п. Лесогорск, ул. Электриков, д. 8. |
|
|
E-mail – les-mou@yandex.ru Тел. 8-831-90-4-60-80 |
2018г
СОДЕРЖАНИЕ.
Введение……………………………………………………………………………3
I. Способы и методы рационального решения задач на смеси, растворы и сплавы
1.1.Табличный способ решения задач.…………………………………………4
1.2.Решение задач «методом чаш»……………………………… ……………4
1.3. «Правило креста» или Конверт Пирсона»………………………………..4
1.4.Решение задач «Методом рыбки»………………………………………..5
1.5.Решение задач методом площадей равновеликих прямоугольников и подобия прямоугольных треугольников…………………………………………..5
II. Решение одной задачи разными способами
2.1. 1-й способ: «метод чаш»………………………………………………….6
2.2. 2-й способ: табличный……………………………………………………6
2.3. 3-й способ: метод площадей равновеликих прямоугольников………….6
2.4. 4-й способ: через подобие прямоугольных треугольников………………7
2.5. 5-й способ: «конверт Пирсона»……………………………………………7
2.6. 6-й способ: «метод рыбки»…………………………………………………7
Заключение……………………………………………………………………………9
Список литературы…………………………………………………………………10
Введение
ЗАДАЧИ НА СМЕСИ, РАСТВОРЫ И СПЛАВЫ
В данной работе я рассмотрел нестандартные, рациональные способы решения задач на смеси, сплавы и растворы, а также представил решение одной задачи разными способами.
Задачи с использованием таких понятий как концентрация, процентное содержание вещества в смеси, растворе и в сплаве часто включают в экзаменационные варианты ЕГЭ, в олимпиады по математике, физике и химии. В школьном курсе математики на решение задач отводится недостаточное количество времени. Увидев задачу на смеси, растворы и сплавы, многие сразу отказываются ее решать, считают их задачами повышенной сложности. Существуют разные способы, и методы решения задач на смеси, растворы и сплавы. В данной работе я хочу поделиться рациональными, нестандартными способами решения задач.
Цель работы: исследовать разные способы решения задач на смеси, растворы и сплавы и выявить рациональные способы.
Задачи:
- познакомиться с литературой по данной теме;
- научиться решать задачи на смеси, растворы и сплавы разными способами;
- применить полученные знания при решении задач такого типа вариантов ЕГЭ.
Объект исследования: задачи на смеси, растворы и сплавы.
Предмет исследования: способы и методы решения задач.
Методы исследования: изучение литературы по теме исследования, сравнение, анализ, систематизация способов решения.
Глава 1. Способы и методы рационального решения задач на смеси, растворы и сплавы
- Табличный способ решения задач
При решении задач рассматриваемого вида, удобно использовать таблицу, т.к. зрительное восприятие определённого расположения величин в таблице даёт дополнительную информацию, облегчающую процесс решения задачи и её про- верки.
- Решение задач «Методом чаш»
Метод состоит в следующем: необходимо изобразить каждый сплав (раствор, смесь) в виде прямоугольника, разбитого на фрагменты. После заполняем получившиеся прямоугольники в соответствии с условием задачи:
- Над каждым «маленьким» прямоугольником указываем соответствующие компоненты сплава (смеси, раствора).
- Внутри прямоугольников вписываем процентное содержание соответствующего компонента. Если сплав (смесь, раствор) состоит из двух компонентов, то достаточно указать процентное содержание одного из них. В этом случае процентное содержание второго компонента равно разности 100% и процентного содержания первого.
- Под прямоугольником записываем массу (или объем) соответствующего сплава (или компонента). И учитывая, что масса сплава (раствора, смеси) нескольких веществ равна сумме масс компонентов, составляем уравнение.
- «Правило креста» или «Конверт Пирсона»
«Конверт Пирсона» — это удобный и рациональный способ решения задач. Данный способ предложил английский математик, статистик, биолог и философ Карл Пирсон. Метод состоит в следующем: при расчетах записываем одну над другой массовые доли растворенного вещества в исходных растворах, справа между ними – его массовую долю в растворе, который нужно приготовить, и вычитаем по диагонали из большего меньшее значение. Разности их вычитаний показывают массовые доли для первого и второго растворов, необходимые для приготовления нужного раствора.
- Решение задач «Методом рыбки»
Впервые в России такой способ решения задач был описан в арифметике 18 века, автором которой был замечательный русский математик и педагог Леонтий Филиппович Магницкий. При решении задач этим способом строится схема, похожая на рыбку, вот поэтому он так и называется. Метод состоит в следующем: друг под другом записываем содержания веществ имеющихся растворов (смесей, сплавов), слева от них и примерно посередине — содержание вещества в растворе (в смеси или в сплаве), который должен получиться после смешивания. Соединяем написанные числа прямыми. В каждой паре из большего числа вычитаем меньшее, и результат записываем в конце соответствующей прямой. Получаемые массовые доли показывают, в каком отношении надо слить исходные растворы (смеси, сплавы). Записываем пропорцию и решаем её.
- Решение задач методом площадей равновеликих прямоугольников и подобия прямоугольных треугольников
В тех задачах, где одна из рассматриваемых величин является произведением двух других, целесообразно для наглядности представлять такое произведение в виде площади прямоугольника. Для решения задач необходимо построить диаграмму по заданному условию. В горизонтальном направлении откладываем массу сплава (раствора, смеси), а в вертикальном — концентрацию сплава (раствора, смеси) или число долей вещества в сплаве. Получаем равновеликие прямоугольники, составляем уравнение, приравняв их площади [3].
Глава 2. Решение одной задачи разными способами
Задача. Для приготовления торта «Воздушный» маме требуется 10 г 40% раствора лимонной кислоты. Какова масса 20% и 70% растворов лимонной кислоты, которые она смешала, чтобы получить раствор нужной концентрации?
1-й способ:
Решение: «метод чаш»
Масса лимонной кислоты в нужном растворе равна сумме масс лимонной кислоты в исходных растворах. Составляем уравнение и решаем его:
0,2х + 0,7(10 – х) = 0,4·10; 0,2х + 7 – 0,7х = 4; 0,5х = 3; х = 6 (г) – масса 20%
раствора; 1) 10 – 6 = 4 (г) – масса 70% раствора.
Ответ: 6 грамм 20% раствора и 4 грамма 70% раствора.
2-й способ:
Решение: табличный способ
|
Наименование |
% содержание лимонной кислоты |
Масса раствора (г) |
Масса лимонной кислоты (г) |
|
первый раствор |
20 % |
х |
0,2х |
|
второй раствор |
70 % |
10 – х |
0,7(10 – х) |
|
Новый раствор |
40 % |
10 |
0,4·10 |
Масса лимонной кислоты в новом растворе равна сумме масс лимонной кислоты в исходных растворах. Составляем уравнение и решаем его:
0,2х + 0,7(10 – х) = 0,4·10; 0,2х + 7 – 0,7х = 4; 0,5х = 3; х = 6 (г) – масса 20%
раствора; 1) 10 – 6 = 4 (г) – масса 70% раствора.
Ответ: 6 грамм 20% раствора и 4 грамма 70% раствора.
3-й способ:
Решение: метод площадей равновеликих прямоугольников
Прямоугольники с площадями S1 и S2 равновелики. Составляем уравнение по площадям прямоугольников: (70 – 40)х = (40 – 20)(10 – х) ; 30х = 20(10 – х); 3х = 20 — 2х; 5х = 20;
х = 4(г) — масса 70% раствора;
1)10 – 4 = 6(г) — масса 20% раствора
Ответ: 6 грамм 20% раствора и 4 грамма 70% раствора.
4-й способ:
Решение: через подобие прямоугольных треугольников
Прямоугольные треугольники подобны. Запишем равенство отношений соот
ветствующих сторон, подставив значения70−20= 10 ; 50 = 10 ; 5 =10
; 5х = 20
40−20 х 20 х 2 х
; х = 4; 1) 10 – 4 = 6(г) — масса 20% раствора.
Ответ: 6 грамм 20% раствора и 4 грамма 70% раствора.
5-й способ:
Решение: «конверт Пирсона»
Отношение массы первого раствора к массе второго раствора есть отношение разности массовых долей лимонной кислоты во втором и в новом растворах к разности соответствующих величин в новом растворе и в первом. Составляем
уравнение и решаем его: х
= 30; х
= 3; 2х = 30 – 3х; 5х = 30; х = 6 (г) – масса
10−х 20 10−х 2
20% раствора; 1) 10 – 6 = 4 (г) – масса 70% раствора.
Ответ: 6 грамм 20% раствора и 4 грамма 70% раствора.
6-й способ:
Решение: «метод рыбки»
Решение: составляем пропорцию и решаем её х
= 30 ; х
= 3; 2х = 30-3х;
10−х 20 10−х 2
5х = 30; х = 6(г) — масса 20% раствора; 1) 10 – 6 = 4(г) — масса 70% раствора.
Ответ: 6 грамм 20% раствора и 4 грамма 70% раствора.
Заключение
Я рассмотрел разные способы решения задач на смеси, растворы и сплавы, научился решать задачи всеми способами. Составил презентацию по всем способам решения задачи. В процессе решения задач выяснил, что таблицы, схемы, рисунки позволяют точнее, быстрее и проще составлять уравнения и системы уравнений к задачам, при этом вычислительный процесс не столь сложен.
Работа имеет практическое значение, так как может служить пособием при подготовке к итоговой аттестации выпускников 9 и 11 классов.
Большая часть учащихся 9 — 11 классов испытывает затруднения при решении задач на смеси, растворы и сплавы. Мало кто знает рациональные и нестандартные способы решения подобных задач и поэтому при решении таких задач на ЕГЭ и ОГЭ выпускники могут потерять «драгоценное» для себя время и баллы.
Список литературы
- Мальцев, Д.А., Мальцев, А.А., Мальцева, Л.И., Каибханова, С.З. и др. Математика 9 класс. Итоговая аттестация 2012. Предпрофильная подготовка: учебно-методическое пособие / под ред. Д.А. Мальцева. – Ростов н/Д: Издатель Мальцев Д.А.; М.: НИИ школьных технологий, 2012. – 208 с.
- Образовательный портал для подготовки к экзаменам [Электронный ресурс]. – Режим доступа: http://reshuege.ru.
- Решение задач с помощью двумерных диаграмм. Занятие элективного курса по математике 9 класс. Учитель математики Фролова А.Х. 2011-2012 учебный год. Тема: «Решение задач с помощью двумерных диаграмм» [Электронный ресурс]. – Режим доступа: http://litcey.ru/ matematika/49222/index.html.
- Сборник практико-ориентированных задач по теме «Рациональные способы решения задач на смеси, растворы и сплавы» (наша публикация) [Электронный ресурс]. – Режим доступа: http://nsportal.ru/ap/ap/nauchno-tekhnicheskoe- tvorchestvo/sbornik-praktiko-orientirovannykh-zadach-po-teme.
- Семенов, А.В. Государственная итоговая аттестация выпускников 9 классов в новой форме. Математика. 2012. Учебное пособие / А.В.Семенов, А.С. Трепа- лин, И.В. Ященко, П.И. Захаров; под. ред. И.В. Ященко; Московский центр не- прерывного математического образования. – 2-е изд., доп. – М.: Интеллект- Центр, 2012. – 112 с.
- Шевкин, А.В. Текстовые задачи. Пособие для учащихся. – М.: Просвеще- ние, 1997. – 112 с.: ил.
Математика, давно став языком науки и техники, в настоящее время всё шире проникает в повседневную жизнь и обиходный язык, всё более внедряется в традиционно далекие от неё области.
Основная задача обучения математике в школе заключается в обеспечении прочного и сознательного овладения учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности каждому члену современного общества, достаточных для изучения смежных дисциплин и продолжения образования, а также в профессиональной деятельности, требующей достаточно высокой математической культуры. Для жизни в современном обществе важным является формирование математического стиля мышления, проявляющего в определённых умственных навыках.
Тема «Проценты» является универсальной в том смысле, что она связывает между собой многие точные и естественные науки, бытовые и производственные сферы жизни. Обучающиеся встречаются с процентами на уроках физики, химии, при чтении газет, просмотре телепередач. Умением грамотно и экономно проводить элементарные процентные вычисления обладают далеко не все обучающиеся. Практика показывает, что очень многие окончившие школу не только не имеют прочных навыков обращения с процентами в повседневной жизни, но даже не понимают смысла процентов, как доли от некоторой заданной величины. Происходит это потому, что проценты изучаются на первом этапе основной школы, в 5-6 классах, когда учащиеся в силу возрастных особенностей ещё не могут получить полноценные представления о процентах, об их роли в повседневной жизни.
В последнее же время в контрольно-измерительные материалы экзамена по математике, проводящегося в форме ЕГЭ, включают и задачи на проценты, смеси и сплавы.
ЗАДАНИЯ ИЗ ВАРИАНТОВ ЕГЭ
- В сосуд, содержащий 5 литров 12% водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?
- Смешали некоторое количество 15% раствора некоторого вещества с таким же количеством 19% раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
- Смешали 4 литра 15% водного раствора некоторого вещества с 6 литрами 25% водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
- Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
- Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
- Смешав 30% и 60% растворы кислоты и добавив 10 кг чистой воды, получили 36% раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50% раствора той же кислоты, то получили бы 41% раствор кислоты. Сколько килограммов 30% раствора использовали для получения смеси?
- Имеются два сосуда. Первый содержит 30 кг, а второй — 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
ЗАДАНИЯ ИЗ ВСТУПИТЕЛЬНЫХ ЭКЗАМЕНОВ В МГУ
МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ. Имеются три металлических слитка. Первый весит 5 кг, второй – 3 кг, и каждый из этих двух слитков содержит 30% меди. Если первый слиток сплавить с третьим, то получится слиток, содержащий 56% меди, а если второй слиток сплавить с третьим, то получится слиток, содержащий 60% меди. Найти вес третьего слитка и процент содержания меди в нём.
ХИМИЧЕСКИЙ ФАКУЛЬТЕТ. Сосуд вместимостью 8 л наполнен смесью кислорода и азота. На долю кислорода приходится 16% вместимости сосуда. Из сосуда выпускают некоторое количество смеси и впускают такое же количество азота, после чего опять выпускают такое же, как в первый раз, количество смеси и опять добавляют столько же азота. В новой смеси кислорода оказалось 9%. Какое количество смеси каждый раз выпускалось из сосуда?
ЭКОНОМИЧЕСКИЙ ФАКУЛЬТЕТ. Банк планирует вложить на 1 год 40% имеющихся у него средств клиентов в проект Х, а остальные 60% – в проект Y. В зависимости от обстоятельств проект Х может принести прибыль в размере от 19 до 24% годовых, а проект Y – от 29 до 34% годовых. В конце года банк обязан вернуть деньги клиентам и выплатить им проценты по заранее установленной ставке. Определить наименьший и наибольший возможный уровень %-ой ставки по вкладам, при которых чистая прибыль банка составит не менее 10 и не более 15% годовых от суммарных вложений в проекты Х и Y.
СОЦИОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ. В дошкольном учреждении провели опрос. На вопрос: «Что Вы предпочитаете, кашу или компот?» – большая часть ответила: «Кашу», меньшая: «Компот», а один респондент: «Затрудняюсь ответить». Далее выяснили, что среди любителей компота 30% предпочитают абрикосовый, а 70% – грушевый. У любителей каши уточнили, какую именно кашу они предпочитают. Оказалось, что 56,25% выбрали манную кашу, 37,5% – рисовую, и лишь один ответил: «Затрудняюсь ответить». Сколько детей было опрошено?
В связи с этим появилась необходимость в усилении практической направленности обучения, включении в работу с учащимися соответствующих заданий на проценты, пропорции, графики реальных зависимостей, текстовые задачи с построением математических моделей реальных ситуаций. В процессе подготовки приходится искать различные пути решения таких типов задач как задачи «на движение», «на работу», «процентное содержание», «смеси и сплавы»…
Тема «Проценты» на самом деле достаточно обширна и сегодня я хотела бы остановиться на одном из ее разделов – задачах на смеси и сплавы, тем более что при решении задач на смеси и сплавы очевидны межпредметные связи с химией, физикой и экономикой, знание этого повышает учебную мотивацию учащихся по всем предметам.
Ведь, если человек талантлив в одном, он обычно талантлив во многом.
В частности хочу поделиться уже опробованным приёмом для решения задач на «смеси и сплавы». По отзывам школьников, рассматриваемая модель соответствует их представлениям о процессе сплавления, выпаривания и др., позволяет компактно и наглядно представить эти процессы, упрощает составление уравнения. Он появился и нашел свое применение после знакомства с различной литературой.
Но первым делом необходимо вспомнить некоторые теоретические основы решения задач на смеси и сплавы (Слайд 5).
В процессе поиска решения этих задач полезно применить очень удобную модель и научить школьников пользоваться ею. Изображаем каждую смесь (сплав) в виде прямоугольника разбитого на фрагменты, количество которых соответствует количеству составляющих эту смесь (этот сплав) элементов.
В качестве примера рассмотрим следующую задачу.
Задача 1. Имеется два сплава меди и олова. Один сплав содержит 72% меди, а другой 80% меди. Сколько нужно взять каждого сплава, чтобы получилось 800г сплава, содержащего 75% меди?
Изобразим каждый из сплавов в виде прямоугольника, разбитого на два фрагмента по количеству входящих элементов. Кроме того на модели отобразим характер операции – сплавление. Для этого между первым и вторым прямоугольниками поставим знак «+», а между вторым и третьим прямоугольниками поставим знак «=». Этим мы показываем, что третий сплав получен в результате сплавления первых двух. Полученная схема имеет следующий вид:
Теперь заполним получившиеся прямоугольники в соответствии с условием задачи.
Над каждым прямоугольником укажем соответствующие компоненты сплава. При этом обычно бывает достаточно использовать первые буквы их названия (если они различны). Удобно сохранять порядок соответствующих букв.
Внутри прямоугольников впишем процентное содержание (или часть) соответствующего компонента. Если сплав состоит из двух компонентов, то достаточно указать процентное содержание одного из них. В этом случае процентное содержание второго равно разности 100% и процентного содержания первого.
Под прямоугольником запишем массу (или объем) соответствующего сплава (или компонента).
Рассматриваемый в задаче процесс можно представить в виде следующей модели-схемы:
Решение.
1-й способ. Пусть х г – масса первого сплава. Тогда, (800 – х) г – масса второго сплава. Дополним последнюю схему этими выражениями. Получим следующую схему:
Сумма масс меди в двух первых сплавах (то есть слева от знака равенства) равна массе меди в полученном третьем сплаве (справа от знака равенства): .
Решив это уравнение, получаем При этом значении х выражение
. Это означает, что первого сплава надо взять 500 г, а второго – 300 г.
Ответ:500 г, 300 г.
2-й способ. Пусть х г и у г – масса соответственно первого и второго сплавов, то есть пусть исходная схема имеет вид:
Легко устанавливается каждое из уравнений системы двух линейных уравнений с двумя переменными:
Решение системы приводит к результату: Значит, первого сплава надо взять 500 г, а второго – 300 г.
Ответ:500 г, 300 г.
Рассмотренная модель облегчает учащимся процесс перехода от условия задачи к ее непосредственной реализации стандартными путями: в виде уравнений или систем уравнений.
Особый интерес представляют два других способа, сводящие решение этих задач к тривиальному варианту, опирающемуся на арифметику и понятие пропорции.
Старинный способ решения
Таким способом можно решать задачи на смешивание (сплавление) любого числа веществ. Задачам подобного типа уделялось значительное внимание в старинных рукописях и «Арифметике» Леонтия Филипповича Магницкого (1703 г). (Лео́нтий Фили́ппович Магни́цкий (при рождении Телятин; 9 (19) июня 1669, Осташков — 19 (30) октября 1739, Москва) — русский математик, педагог. Преподаватель математики в Школе математических и навигацких наук в Москве (с 1701 по 1739), автор первой в России учебной энциклопедии по математике).
Данный способ позволяет получить правильный ответ за очень короткое время и с минимальными усилиями.
Решим предыдущую задачу 1 старинным способом.
Друг под другом пишутся процентные содержания меди в имеющихся сплавах, слева от них и примерно посередине – процентное содержание меди в сплаве, который должен получиться после сплавления. Соединив написанные числа черточками, получим такую схему:
Рассмотрим пары 75 и 72; 75 и 80. В каждой паре из большего числа вычтем меньшее, и результат запишем в конце соответствующей стрелочки. Получится такая схема:
Из нее делается заключение, что 72%-ного сплава следует взять 5 частей, а 80%-ного – 3 части (800:(5 + 3) = 100 г приходится на одну часть.) Таким образом, для получения 800 г 75%-ного сплава нужно взять 72%-ного сплава 100·5 = 500 г, а 80%-ного – 100·3 = 300 г.
Ответ:500г, 300г.
Задача 2. В каких пропорциях нужно сплавить золото 375-й пробы с золотом 750-й пробы, чтобы получить золото 500-й пробы?
Ответ: Нужно взять две части 375-й пробы и одну часть 750-й пробы.
Правило креста или квадрат Пирсона
(Карл (Чарлз) Пирсон (27 марта 1857, Лондон — 27 апреля 1936, там же) — выдающийся английский математик, статистик, биолог и философ; основатель математической статистики, автор свыше 650 опубликованных научных работ).
Очень часто при решении задач приходится встречаться со случаями приготовления растворов с определенной массовой долей растворенного вещества, смешением двух растворов разной концентрации или разбавлением крепкого раствора водой. В некоторых случаях можно провести достаточно сложный арифметический расчёт. Однако это малопродуктивно. Чаще для этого лучше применить правило смешения (диагональную модель «квадрата Пирсона», или, что тоже самое, правило креста).
Допустим, нужно приготовить раствор определенной концентрации, имея в распоряжении два раствора с более высокой и менее высокой концентрацией, чем нужно нам. Тогда, если обозначить массу первого раствора через m1, а второго – через m2, то при смешивании общая масса смеси будет складываться из суммы этих масс. Пусть массовая доля растворённого вещества в первом растворе – 1, во втором –
2, а в их смеси –
3. Тогда общая масса растворённого вещества в смеси будет складываться из масс растворённого вещества в исходных растворах:
m1∙
1 + m2∙
2 =
3(m1 + m2). Отсюда m1(
1 –
3) = m2(
3 –
2),
.
Видно, что отношение массы первого раствора к массе второго раствора есть отношение разности массовых долей растворённого вещества в смеси и во втором растворе к разности соответствующих величин в первом растворе и в смеси.
При решении задач на растворы с разными концентрациями чаще всего применяют диагональную схему правила смешения. При расчётах записывают одну над другой массовые доли растворённого вещества в исходных растворах, справа между ними – его массовую долю в растворе, который нужно приготовить, и вычитают по диагонали из большего меньшее значение. Разности их вычитаний показывают массовые доли для первого и второго растворов, необходимые для приготовления нужного раствора.
ω1, ω2 – массовые части первого и второго растворов соответственно.
Для пояснения этого правила сначала решим простейшую задачу.
Задача 3. Морская вода содержит 5% соли (по массе). Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составила 1,5%?
Ответ: 7 килограммов.
Данный метод может использоваться и при решения задач на смеси и сплавы. Отлили часть раствора, отрезали кусок сплава. При этой операции остается неизменной концентрация веществ.
В заключение разговора о решении задач на смеси и сплавы, отмечу, что при внешнем различии сюжета задачи на сплавы, смеси, концентрации, на соединение либо на разделение различных веществ, решаются по общей схеме. (См. примеры решения задач в Презентации).
Таким образом, дополнительная работа по развитию и совершенствованию навыка решения задач на проценты имеет значимость не только для будущих абитуриентов, которые возможно встретятся с такими заданиями на ЕГЭ, но и для всех учащихся, так как современная жизнь неминуемо заставит в своей повседневности решать задачи на проценты.
Жизнь украшается двумя вещами: занятием математикой и ее преподаванием!
С. Пуассон
Слайд 1Способы решения задач на смеси и сплавы
Автор: Понукарина Юлия Сергеевна
Класс: 9
ОУ:

Слайд 2Цель:
Выбор оптимального способа решения задач на смеси и сплавы
Задачи:
Найти необходимую литературу и изучить её.
Научиться решать задачи этими способами.
Выбрать наиболее удобный способ решения задач
Научить одноклассников использовать эти способы.
Создать презентацию.
Выпустить сборник способов решения задач

Слайд 3Объект исследования:
Способы решения задач
Предмет Исследования:
Алгоритм решения задач
Методы исследования:
Работа с
литературой;
Анализ;
Обобщение;
Сравнение.
Гипотеза: Я предполагаю, что существуют разные способы решения задач на смеси и сплавы и среди них можно найти наиболее удобный способ решения задач на смеси и сплавы, в том числе и предлагаемых на ОГЭ и ЕГЭ.

Слайд 4Способы решения задач на смеси и сплавы
Решение задач с помощью формулы
Решение
задач с помощью модели- схемы
Старинный метод «рыбки» из учебника Магницкого
Способ креста
Геометрический

Слайд 5Решение задач с помощью формулы
Масса смеси * концентрацию = количество чистого
вещества
Пример 1:
В сосуд, содержащий 5 литров 26-процентного водного раствора некоторого вещества, добавили 5 литров воды. Сколько процентов составляет концентрация получившегося раствора?
Решение.
Применяем формулу: Масса смеси * концентрацию = количество чистого вещества
5*0,26=1,3 масса чистого вещества в растворе
После того, как добавили 5 л воды, масса раствора стала 10 л, а масса чистого вещества не изменилась. Пусть х –концентрация нового раствора.
10*х=1,3
Х=1,3:10
Х=0,13*100%
Х= 13% концентрация нового раствора.
Ответ: 13%

Слайд 6Пример 2:
Имеется два сплава меди и свинца. Один сплав содержит 15%
меди, а другой 65% меди. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?
Решение.
Применяем формулу: Масса смеси * концентрацию = количество чистого вещества
Пусть х(г) –масса первого сплава, у(г) – масса второго сплава
Х+у =200
0,15х+ 0,65у=200*0,3
0,15(200-у)+0,65у=60
30-0,15у+0,65у=60
0,5у=30
У=60(г) масса второго сплава
200-60=140(г) масса первого сплава
Ответ: 140(г), 60(г)

Слайд 7Табличный
Для того, чтобы решить данный вид задач с помощью таблицы надо:
— составить и заполнить таблицу, согласно условию задачи
— составить и решить уравнение (между первой и второй строкой последнего столбца ставим знак +, а между второй и третьей строкой последнего столбца таблицы ставим равно)
Таблица для решения задач имеет вид.

Слайд 8Пример:
Имеется два сплава меди и свинца. Один сплав содержит 15%
меди, а другой 65% меди. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?
Решение:
Составим уравнение
0,15х +0,65(200-х)=60
0,15х+130-0,65х=60
-0,5х= -70
Х=140
Масса первого сплава 140г, масса второго сплава 200-х=200-140=60(г)
Ответ: 140г, 60г

Слайд 9Решение задач с помощью модели-схемы
Изобразим каждый из сплавов в
виде прямоугольника, разбитого на два фрагмента (по числу составляющих элементов). Кроме того, на модели отобразим характер операции – сплавление, поставим знак «+» между первым и вторым прямоугольниками. Поставив знак «=» между вторым и третьим прямоугольниками, мы тем самым показываем, что третий сплав получен в результате сплавления первых двух. Полученная схема имеет следующий вид:

Слайд 10Теперь заполняем получившиеся прямоугольники в соответствии с условием задачи:
Над каждым прямоугольником
(«маленьким») указываем соответствующие компоненты сплава. При этом обычно бывает достаточно использовать первые буквы их названия (если они различны). Удобно сохранять порядок соответствующих букв.
Внутри прямоугольников вписываем процентное содержание (или часть) соответствующего компонента. Понятно, что если сплав состоит из двух компонентов, то достаточно указать процентное содержание одного из них. В этом случае процентное содержание второго компонента равно разности 100% и процентного содержания первого.
Под прямоугольником записываем массу (или объем) соответствующего сплава (или компонента).

Слайд 11Пример:
В 4кг сплава меди и олова содержится 40% олова. Сколько
килограммов олова надо добавить к этому сплаву, чтобы его процентное содержание в новом сплаве стало равным 70%?
Решение:
0,4*4+х=0,7(4+х)
1,6+х=2,8+0,7х
0,3х=1,2
Х=4
Ответ:4кг

Слайд 12Старинный способ решения задач на смеси и сплавы («метод рыбки»)
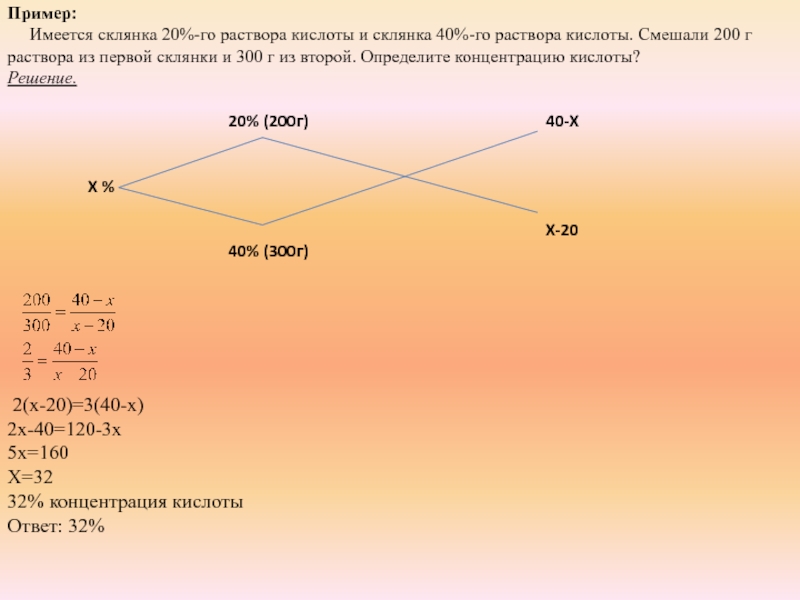
Слайд 13Пример:
Имеется склянка 20%-го раствора кислоты и склянка 40%-го
раствора кислоты. Смешали 200 г раствора из первой склянки и 300 г из второй. Определите концентрацию кислоты?
Решение.
20% (200г) 40-X
X %
X-20
40% (300г)
2(х-20)=3(40-х)
2х-40=120-3х
5х=160
Х=32
32% концентрация кислоты
Ответ: 32%
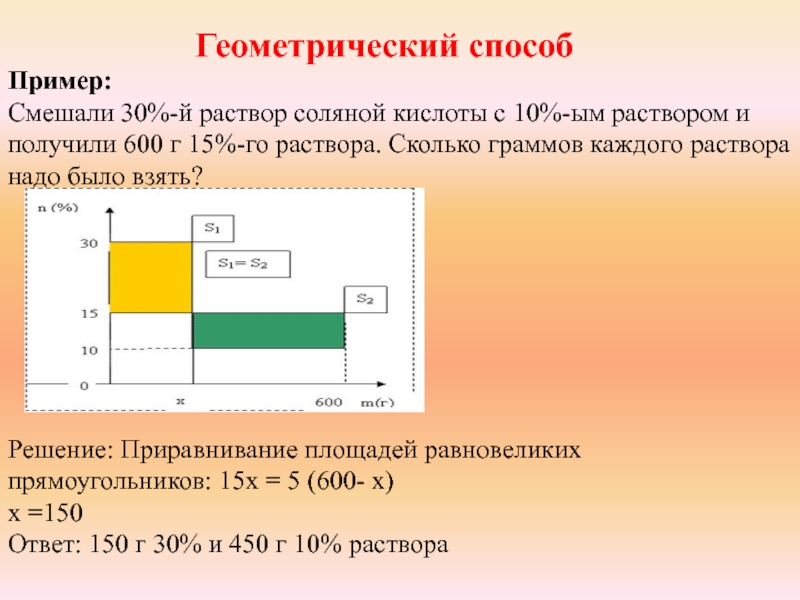
Слайд 14Геометрический способ
Пример:
Смешали 30%-й раствор соляной кислоты с 10%-ым раствором и получили
600 г 15%-го раствора. Сколько граммов каждого раствора надо было взять?
Решение: Приравнивание площадей равновеликих прямоугольников: 15x = 5 (600- x)
x =150
Ответ: 150 г 30% и 450 г 10% раствора
Слайд 16Пример:
Смешали некоторое количество 11-процентного раствора некоторого вещества с таким же количеством
17-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение.
х-11=17-х
2х=28
х=14%-концентрация полученного раствора
Ответ: 14%
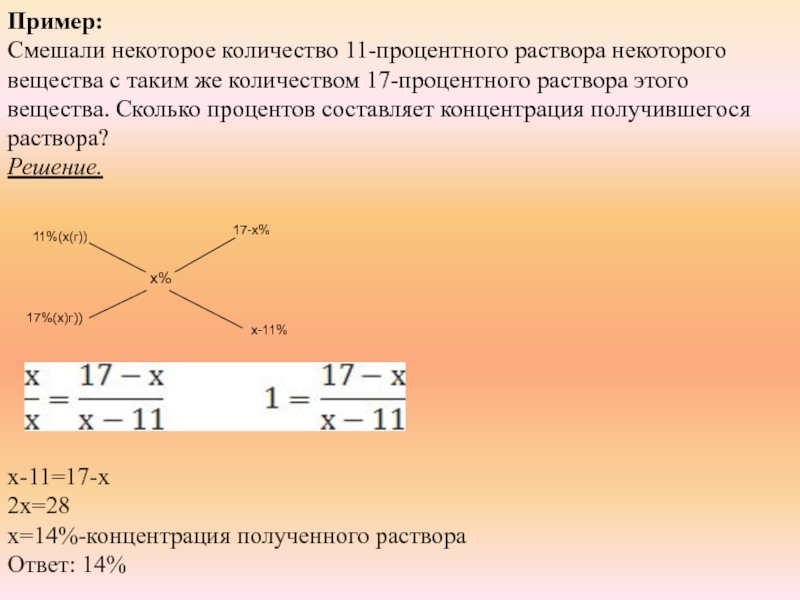
Слайд 17№ 99573. Смешали 4 литра 15–процентного водного раствора некоторого вещества с 6
литрами 25–процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
1 способ
6(y-25)=4(15-y)
6y-150=60-4y
10y=210
y=21%
Ответ: 21%-концентрация получившегося раствора.
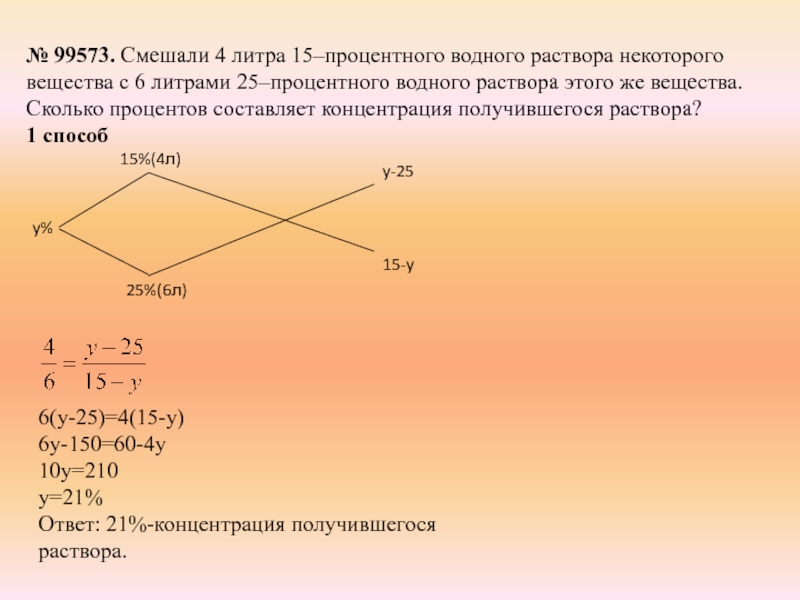
Слайд 182 способ
0,15*4+0,25*6=10y
0,6+1,5=10y
2,1=10y
y=0,21*100%=21%
Ответ: 21%-концентрация получившегося раствора.

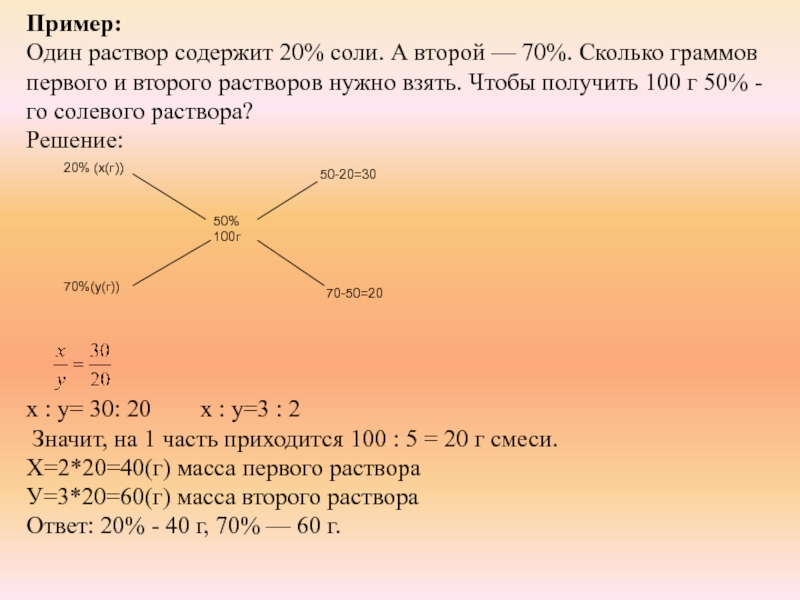
Слайд 19Пример:
Один раствор содержит 20% соли. А второй — 70%. Сколько граммов
первого и второго растворов нужно взять. Чтобы получить 100 г 50% — го солевого раствора?
Решение:
х : у= 30: 20 х : у=3 : 2
Значит, на 1 часть приходится 100 : 5 = 20 г смеси.
Х=2*20=40(г) масса первого раствора
У=3*20=60(г) масса второго раствора
Ответ: 20% — 40 г, 70% — 60 г.
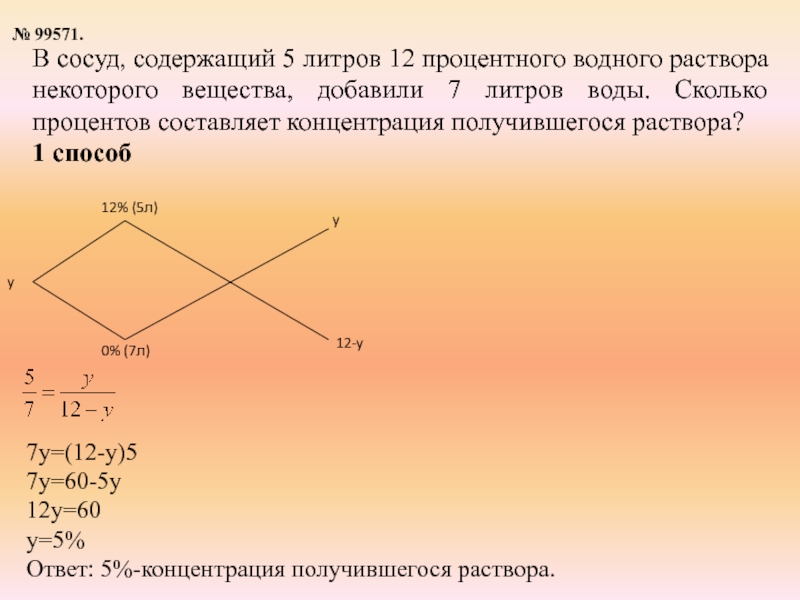
Слайд 20
№ 99571.
В сосуд, содержащий 5 литров 12 процентного водного раствора
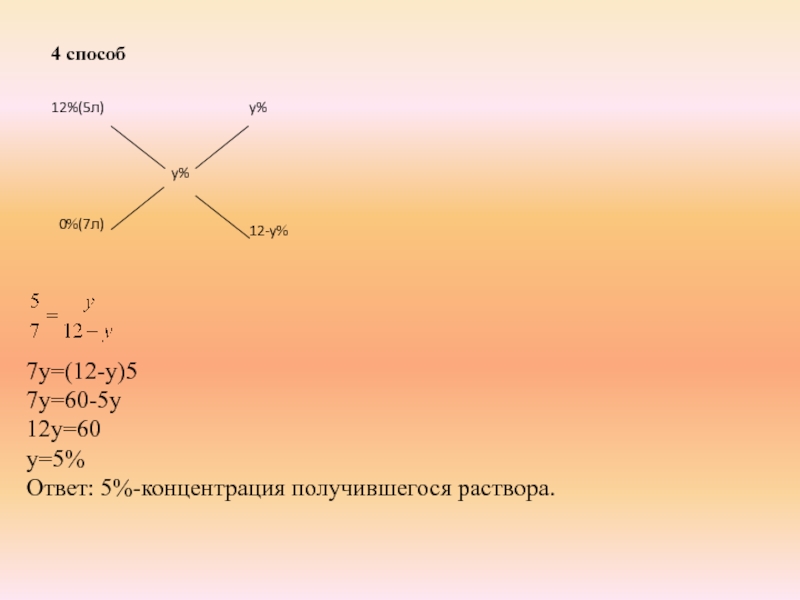
некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?
1 способ
7y=(12-y)5
7y=60-5y
12y=60
y=5%
Ответ: 5%-концентрация получившегося раствора.
Слайд 21
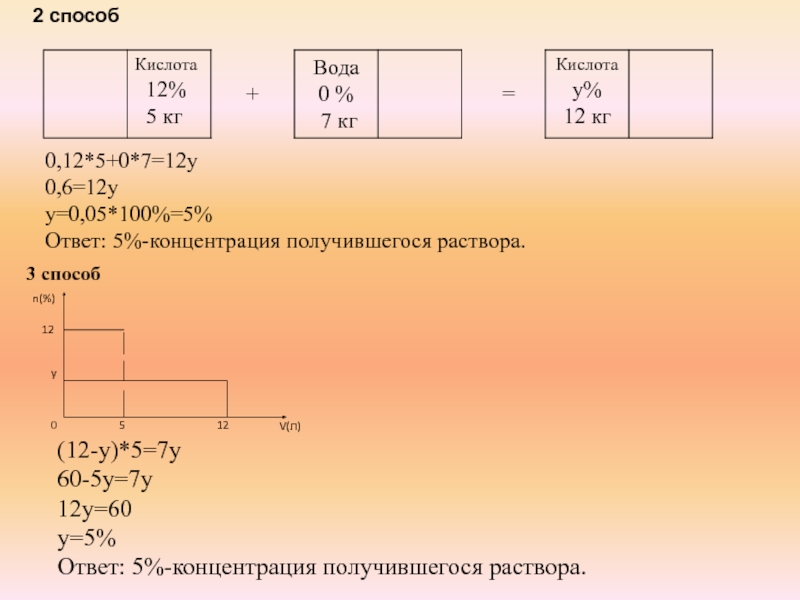
0,12*5+0*7=12y
0,6=12y
y=0,05*100%=5%
Ответ: 5%-концентрация получившегося раствора.
2 способ
(12-y)*5=7y
60-5y=7y
12y=60
y=5%
Ответ: 5%-концентрация получившегося раствора.
3 способ
Слайд 227y=(12-y)5
7y=60-5y
12y=60
y=5%
Ответ: 5%-концентрация получившегося раствора.
4 способ