Метод скользящего экзамена

Скорректированный скользящий экзамен, соклассификаторы, фрактальные классификаторы и локальная вероятность ошибки

Время на прочтение
5 мин

Количество просмотров 2.4K

В данной работе даются элементы введения в классификацию с обучением на малых выборках — от удобной системы обозначений до специальных оценок надежности. Постоянное наращивание быстродействия вычислительных устройств и малые выборки, позволяют пренебречь значительным объемом вычислений, необходимым при получении некоторых из этих оценок.

Определения и обозначения

Пусть задано некоторое исходное разбиение множества image объектов image на два подмножества (класса) image, таких, что
image, image.
(1)

Будем отождествлять двухклассовый классификатор с бинарной функцией вида
image
(2)

где image — случайные выборки-подмножества image из классов image, image -исследуемый объект, который необходимо отнести к одному из классов. Значения этой функции будут истолковываться в качестве «решений» в соответствии с правилом

(3)

В зависимости от того, соответствуют или нет решения классификатора исходному разбиению image на классы, будем считать их соответственно «правильными» или «ошибочными». Договоримся также -ые элементы выборок image обозначать , так, что соответственно:
,
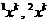
(4)

где image — объемы обучающих выборок. Полагаем множество image «погруженным» в image -мерное правостороннее евклидово пространство image. Тогда все элементы классов image, включая, естественно, и элементы обучающих выборок и исследуемый объект, можно рассматривать как его точки. Координаты объектов-точек из множества image будем помечать правым нижним индексом image. Координаты объектов обучающих выборок запишутся как , исследуемого объекта image как —image. В зависимости от контекста, image понимается либо как имя объекта, либо как радиус-вектор.
Исходим из отсутствия проверочной последовательности, а оценки вероятности ошибки классификации image осуществим в режиме скользящего экзамена
image,
(5)

где
image,
(6)

image.
(7)

Объекты image обучающих выборок, классифицируемые в режиме скользящего экзамена, будем в дальнейшем называть квазиэкзаменируемыми.

Скорректированный скользящий экзамен

Скользящий экзамен, как известно, отличает ряд недостатков. Эти недостатки могут быть в какой-то мере устранены через коррекцию скользящего экзамена. Скорректированные оценки, помечаемые левым штрихом, запишутся следующим образом
image,
(8)

image,
(9)

image.
(10)

К недостаткам скорректированного скользящего экзамена следует отнести возрастание количества операций и в тот факт, что эта оценка проводится на обеих выборках на единицу меньшего объема. Таким образом при малых выборках оценка вероятности ошибки оказывается несколько завышенной, однако с возрастанием объема выборок этот эффект утрачивает значение.

Соклассификатор

Вследствие большой трудоемкости скорректированного скользящего экзамена, представляет интерес метод бинарной оценки надежности классификации – соклассификатор. Как и скользящий экзамен, он может базироваться и исключительно на информации из обучающих выборок, но может использоваться и при наличии проверочных последовательностей.
Введем выборки image объектов, соответственно правильно и ошибочно отнесенных классификатором (2) в режиме скользящего экзамена
image,
(11)

image.
(12)

Тогда решение соклассификатора первого порядка классификатора (2), определяемого как
image,
(13)

истолковывается следующим образом
если image то классификатор (2) принял правильное решение относительно image,
если image, то классификатор(2) принял ошибочное решение относительно image.
(14)

При этом будем считать, что выборки извлечены из неких классов объектов, потенциально правильно либо ошибочно отнесенных классификатором (2).

При определении (13) предполагается, что объем выборки image не слишком мал. Таким образом, если располагаем лишь материалом обучающих выборок, а проверочные последовательности отсутствуют, то использовать соклассификатор рекомендуется в условиях, когда классификатор (2) допускает значительное количество ошибок. Если все же использовать соклассификатор в условиях малой выборки image, то его следует выбирать в достаточно простой форме. Например, если соклассификатор фишеровского типа, можно предположить диагональность ковариационной матрицы или даже ее единичность.

Подобно adaptive boosting, композиция классификаторов может рассматриваться как коллективный классификатор, организованный существенно более нелинейно по сравнению с предложенными в [1].

Остановимся на вопросах, связанных с выбором конкретной формы соклассификатора. Пусть, например, выборки image извлечены из классов image с плотностями распределений image, причем классы сильно перекрываются. В этом случае зачастую может оказываться, что выборочные плотности имеют близкие средние значения. В этом случае соклассификатор может быть выбран, например, в форме линейного фишеровского классификатора, модифицированного с использованием процедуры Петерсона-Маттсона [2,3].

Фрактальный классификатор

Процесс синтеза соклассификаторов более высоких порядков может быть продолжен в рамках рекуррентной процедуры, когда первоначально осуществляется подстановка
,
(15)

затем, повторяя вышеописанный алгоритм, получаем на выходе соклассификатор второго порядка
image.
(16)

и продолжаем эту процедуру. Императивный останов наступает при построении соклассификатора такого порядка 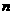image, при котором image или даже image. В результате получаем итерированную систему классификаторов – фрактальный классификатор. Этот коллективный классификатор не следует, разумеется, смешивать с классификаторами изображений, использующими для их обработки фрактальные и вейвлетные преобразования.

На практике нам приходилось использовать лишь соклассификаторы первого порядка. Они были разработаны нами много лет назад и зарекомендовали себя в качестве полезных инструментов при решении различных практических задач, в частности, при анализе отраженных радиосигналов для установок поиска пластиковых противопехотных мин [4], а также при создании системы LEKTON. Эта система позволила полностью автоматически проверять подлинность подписей на чеках, векселях и других документах и явилась первой реально используемой в банке системой такого типа.

Локальная вероятность ошибки

В практических исследованиях хорошо себя зарекомендовали локальные image — оценки вероятности ошибки классификации. Пусть классификатор (2) может быть представлен в форме
image,
(17)

где image — оценки плотностей image по выборкам image соответственно. Тогда локальная image — оценка вероятности ошибки этого классификатора может быть определена как
image,
(18)

где image.
Введем специальную 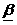image — оценку, которая может рассматриваться в качестве «размытого» классификатора
image
(19)

где image. Тогда будем считать, что истолковывается как решение размытого классификатора, что image, image — как решение, что image. При этом, чем ближе image к нулю либо к единице, тем соответственные решения размытого классификатора более заслуживают доверия.

На основе оценки (19) можно обобщить определение классификатора (2), введя зону отказа либо зоны отказа. Обозначая ширину этих зон соответственно image, представим их в следующей форме
image
(20)

где image — границы зон. При отсутствии асимметрии в требованиях к зонам выбирается image.

Литература:

1. Archipov G. F. Collectives of determinative rules: optimal solutions and some of the characteristics of reliability of classification. – In the Collection of articles “Statistical problems of control”, Vilnius, 1983, vol.61, pp. 130-145.
2. Мясников В.В. O модификациях метода построения линейной дискриминантной функции, основанного на процедуре Петерсона-Маттсона. computeroptics.smr.ru/KO/PDF/KO26/KO26211.pdf.
3. Фукунага К. Введение в статистическую теорию распознавания образов. М. «Наука» 1979. стр. 105-130.
4. Archipov G., Klyshko G., Stasaitis D., Levitas B., Alenkowicz H., Jefremov S. Research of Metallic and Dielectric Underground Objects on the Basis of Original Computer Recognition Technique of Reflected Radio Signals. MIKON-2000., XII International Conference on Microwaves, Radar and Wireless Communications, Volume 2, pp. 495-498./>

Источник

…птимальный вектор  параметров размытости для непараметрической оценки уравнения разделяющей поверхности допускает упорядочение в виде неравенств:

То v-я компонента вектор x имеет наименьшее влияние на точность восстановления уравнения разделяющей поверхности в данном наборе признаков.

В случае зависимых признаков правило формирования обучающей выборки  информативных признаков и состоит из следующих этапов:

1) в пространстве вектора исходных признаков проводится оптимизация непараметрической оценки уравнения разделяющей поверхности по вектору.

2) Составляется вариационный ряд из коэффициентов размытости и исключается из обучающей выборки признак соответствующий максимальному значению.

3) В пространстве оставшихся признаков вновь проводится оптимизация, и неинформативные признаки исключаются по правилу.

4) Процедура формирования выборки из информативных признаков продолжается до тех пор, пока число оставшихся признаков после отбрасывания неинформативных не будет равным заданному количеству.

20. Гибридные модели в задаче восстановления стохастических зависимостей.

 Пусть при восстановлении однозначной зависимости  кроме выборки  известны частичные сведения (либо принимается гипотеза)  о виде преобразования  с точностью до набора параметров .

Увеличение объема априорной информации и требование наиболее полного его использования в задаче восстановления  позволяют расширить область применения принципов теории обучающихся систем. Один из эффективных подходов решения указанной проблемы состоит в предварительном исследовании аппроксимационных свойств параметрической модели  зависимости  путем организации вычислительного эксперимента на статистических данных V с формированием выборки расхождений (невязок)  . По ней восстанавливается зависимость  представляющая собой функцию невязки между  и .    с помощью непараметрической процедуры. Гибридная модель формируется как некоторая комбинация  и , зависящая от введенного преобразования q .

Строим модель корректирующей функции (преобразование q) в виде непараметрической регрессии

Гибридная модель записывается в виде  

На основании двух моделей можно построить коллектив

Второй этап

, уточняем  и строим корректирующую функцию .

где  — расхождение между новыми экспериментальными данными и первой гибридной выборкой;

 — корректирующая функция второго этапа в виде непараметрической регрессии;

 — гибрид второго этапа.

21. Многоуровневые системы принятия решений в обработке разнотипных данных

Имеется обучающая выборка

V=(xi, ui, vi,δ(i), i=1,k);

Vx=(xi, δ(i), i=1,n);

Vu=( ui, δ(i), iЄI/ Ω1(x)∩Ω2(x)); δ(i)=1, М – указания учителя о принадлежности ситуации xi к одному из М классов. Непрерывные и дискретные признаки являются случайными векторами с неизвестными функциями распределения.

Используется условно-последовательная процедура распознавания образов

Где алгоритм  осуществляет классификацию на j-ом этапе в пространстве однотипных признаков  при условии принадлежности  области пересечения классов.

Качество решения задачи распознавания образов определяется исходя из минимума принятой ошибки классификации.

Требуется разобрать методику синтеза и анализа системы распознавания образов на основе последовательной процедуры принятия решений m(x)={mt(x(t)),t=1,T}, характеризующейся решающими правилами mt, t=1,T, в пространстве наборов разнотипных признаков х=(x(t),t=1,T).

Последовательные методы обработки данных дают возможность разбиения на ряд задач принятия решений по ограниченным наборам признаков.

V=(xi, ui, vi,δ(i), i=1,k); Vx=(xi, δ(i), i=1,n); Vu=( ui, δ(i), iЄI/ Ω1(x)∩Ω2(x));

22. Обучающийся алгоритм формирования наборов информативных признаков

1. Получение информации для решения данной задачи.

Возьмем некоторый признак

2.

3. Анализ полученной информации

Построим информационный граф G(X,A) множество вершин Х которого соответствует множеству признаков (Х=к), а ребра между двумя вершинами  существуют, если    (достоверно с уровнем значимости β не отличается от ошибки в пространстве этих признаков). Это выполняется, когда признаки независимы.

 – это независимость.

Можно отбросить одну из групп, у которой ошибка минимальна.

4. Выделить сильные компоненты (сильно связанные подграфы – каждая пара вершин связана ребром) этого графа, провести их анализ и определить соответствующие им ошибки распознавания образов…… которому будет соответствовать сильная компонента с минимальной ошибкой.

23. Алгоритмы принятия решений в условиях малых выборок

V=(xi,i=1,n)

Восстановим зависимость по выборке

1. Разбиваем по признакам

x=(x(1)…x(T))

k – Набор признаков k1+…+kT=K

Обобщенная модель               

Веса, обозначающие значимость модели —

2. x=(x(1)…x(T)), признаки не зависят друг от друга                                           

1) Определяем интервал вокруг каждой точки         

2) Сопоставим каждому интервалу датчик СВ. с некоторым законом распределения Pj(x2) на интервале xi±β

3) Осуществим генерацию случайных чисел х2 с помощью ДСВ:

x2 имеет нулевое мат. ожидание и находится на интервале 2β, по полученной выборке построить оценку плотности вероятности P(x).

Задача продолжения случайной последовательности 

Строим ДСВ P(x) –> xi, i=1,n xi, i=1,n получить xn+1, xn+2. Выбрать случайным образом из интервала [0,n1] выбираем точку с адресом x3.

Оценка плотности вероятности  если n –> бесконечно и m тоже, то оценка сходится .

Если n конечно, то нельзя добиться асимптотической сходимости но результат можно получить

25. Статистические методы принятия решений в условиях больших выборок

Вычислительная эффективность непараметрических алгоритмов во многом зависит от объёма n статистических данных и снижается по мере его увеличения, что проявляется в росте временных затрат обработки информации. Поэтому возникает задача уменьшения объёма выборки, таким образом, чтобы не повлиять на точность оценки плотности вероятности.

n’<<n выбрать некоторые точки, остальные выбросить (из сотен тысяч выбрать тысячу)

 сжать информацию и решать задачу на основании новой выборки.

Методика синтеза оценки плотности вероятности для одномерного случая.

Имеем выборку   V=(xi,i=1,n)

1. Разобьем выборку на N равных интервалов длиной обозначим центр интервала zj, j=1,N

2. По выборке V=(xi,i=1,n) сформировать . Pj – оценка вероятности попадания СВ в интервал j, в предположении, что в этом интервале искомая плотность вероятности является равномерной. Тогда частота будет равна:

 — количество , попавших в этот интервал.

3. Зная высоту ступеньки, можем перейти от частоты к оценке плотности .

Отличается задача оптимизации

4. При оценивании плотности вероятности будем использовать модель стохастической зависимости, чтобы модель хорошо сходилась с экспериментальными данными. Возьмем в качестве модели непараметрической регрессии оценку оптимального решающего правила (условное математическое ожидание)

5. Воспользуемся данной моделью непараметрической регрессии при оценке плотности вероятности по выборке  для этого построим модификацию данной модели

 имеет равномерную плотность вероятности, т.к. находится на одинаковых расстояниях. У нормированной плотности S=1, если P(z)

 — регрессионная оценка плотности вероятности, построенная на сжатости для выбора параметра с используется критерий:   в многомерном случае оценка примет вид

26. Метод скользящего экзамена и его применение при оптимизации алгоритмов принятия решения

Пусть дана выборка  статистически независимых наблюдений случайной величины, распределённой с неизвестным законом.

       Методика формирования регрессионной оценки плотности вероятности:

       1. Разобьём область определения  на N непересекающихся интервалов длинной  таким образом, чтобы в каждый интервал попало минимум 2-3 наблюдения.

       Пусть  количество наблюдений в каждом -м интервале.

       2. Находим оценки вероятностей попадания наблюдений в каждый -й интервал по формуле:

.

       3. Предполагаем, что в каждом интервале имеет место равномерный закон распределения наблюдений. Исходя из этого, находим высоты полученных прямоугольников. Площади прямоугольников соответствуют оценкам вероятности попадания случайной величины  в j-й интервал. Так как площадь, то высота прямоугольников (оценка плотности вероятности для -го интервала) .

       4. На основе полученной информации сформируем статистическую выборку, где  — центры введённых интервалов.

В итоге после сокращений получаем формулу регрессионной оценки плотности вероятности

и если  — многомерная случайная величина, то регрессионная оценка плотности вероятности имеет вид:

Оптимизация регрессионной оценки плотности вероятности по коэффициенту размытости     

Преимущество предлагаемых в повышении вычислительной эффективности непараметрических алгоритмов, за счёт сжатия исходной обучающей выборки;

в упрощении задачи оптимизации коэффициента размытости, например, с помощью метода «скользящего экзамена» по выборке  при конкретном значении .

Оптимизация коэффициента размытости с помощью метода «скользящего экзамена».

Оптимизация регрессионной оценки плотности вероятности по коэффициентам размытости осуществляется по выборке  из условия минимума эмпирического критерия оценок плотности вероятности заключается:

.

Идея метода «скользящего экзамена» заключается в том, что каждое  наблюдение обучающей выборки подаётся на контроль и исключается из процесса обучения при оценивании плотности вероятности. Вычисляется квадратическое расхождение её значения с  оценкой плотности вероятности для каждого j-го интервала. Данная процедура повторяется для всех ситуаций обучающей выборки и формируется критерий, минимум которого определяет оптимальный коэффициент ядерной функции c.

27. Статистические методы принятия решений в условиях малых выборок

Восстановим зависимость по выборке V=(xi,yi,i=1,n); x=(xv,v=1,k); n/k<30 искусственно наращиваем выборку

1)        Используя принцип индексации 2) используя принцип декомпозиции систем (метод

группового учета аргументов МГУА)

Этапы:

1. Выбрать некоторых 2 признака из исходного набора (xv,xj,) сформировать из них выборку V=(xiv, xij, yi ,i=1,n)

2. По этой выборке построить модель в пространстве этих признаков, когда отношение n/2>>30 (искусственное повышение отношения n/k методом декомпозиции) модель строим т.о., чтобы минимизировать критерий отражающий качество аппроксимации:

3. Повторить этап 2 для всех сочетаний (xv,xj) (число сочетаний равно  по два признака из k)

4. Выбрать некоторую модель  из условия, что,  которая в пространстве двух признаков дает минимальную ошибку из всех возможных сочетаний

5. Сформировать выборку формируем в процессе проведения вычислительного эксперимента с моделью .

6. Построить модель по выборке  . Вычисляем критерий

7. Повторить этап 6 для

8. Выбрать модель , для которой справедливо такой признак  , который в паре с  дает наилучшую аппроксимацию исходной зависимости.

9. Сформировать выборку

10. По выборке  строим модель ,  вычисляем для нее ошибку аппроксимации и выбираем такой признак, который в паре с  дает наименьшую аппроксимацию исходной зависимости

Условия прекращения: 1. Когда использовали все k признаков 2. Когда результат приемлемый (одновременно выбираем наиболее приемлемые признаки)

28. Принятие решений в пространстве дискретных признаков

Заменяем в булевой системе 0 и 1 на a1a2 и т.д.

Надо ввести меру близости

Каждому признаку присваивается коэффициент

1) a1+a5+a7

2) a1+a6+a7

Алгоритм распознавания образов в условиях дискретных признаков

Vu=(ui,s(i), i=1,n) u=(001101)

Чтобы оценить вероятности надо исследовать признаки uv,v=1,m на их независимость и на этой основе оценить искомые вероятности.

Предположим, что признаки независимы, тогда  — частота встречаемости значений признака uv в первом классе .

29. Непараметрические алгоритмы автоматической классификации

Задача: разбить эти точки на группы, когда количество групп неизвестно.

Существует 3 группы алгоритмов автоматической классификации:

  1. Эвристические, т.к. не обоснована процедура формирования параметра r (алгоритм Форель, Взаимного поглощения)
  2. Алгоритмы основанные на понятии класса (метод профессора Васильева)
  3. Оптимизационные методы

Обобщенный непараметрический алгоритм автоматической классификации

  1. Выделяем центры классов  и

Для выделения центров классов назначим   — некоторый уровень совместной плотности вер-ти.

Из выборки V выбрать точки, для которых  (сюда входят точки, которые принадлежат центрам классов)

  1. Используя базовый алгоритм, проводим классификацию точек.

Базовый алгоритм

Из выборки берем некоторую точку , условие, что расстояние между классами  и

Проводим классификацию оставшихся точек (n-1) в соответствии с алгоритмом:

Обозначим через  — множество номеров точек отнесенных алгоритмом  к классу j и  точку, а через — обозначим множество номеров точек 

— количество точек отнесенных к j-ому классу

Проводим классификацию в соответствии с алгоритмом

Продолжаем до тех пор, пока на S-ом этапе значение функции обратится в 0 во всех точках, оставшимся точкам присвоить значение.

Т.к. на втором этапе классы не выделяются, переходим к первому и назначаем уровень , здесь классы выделяются, но т.е. не соблюдается условие базовой классификации.

Переходим к  и т.д., при некотором значении  получим границу между классами:

На основе этой границы строим решающее правило:

Продолжается пока не будут идентифицированы все точки. Данный закон хорошо работает, пока законы распределения симметричны.

—  проверяется на однородность, т.к. это может быть совокупностью классов, а не один класс.

30. Синтез байесовских решающих функций

Рассмотрим объект с входом , который может быть вектором , и выходом y – скаляр. Выходная переменная y является дискретной случайной величиной.

Рис. 4.1. Объект исследования.

Существует некоторая неизвестная зависимость между входом и выходом . Необходимо оценить данную зависимость, построив модель

Пусть дана выборка  статистически независимых наблюдений случайной величины x, распределённых с неизвестной плотностью – «указания учителя» о принадлежности ситуации  к тому либо иному классу .

Под классом понимается совокупность наблюдений, связанных между собой каким либо свойством или целью.

Необходимо построить решающее правило,  позволяющее в  автоматизированном режиме принимать решение о принадлежности новых ситуаций  к классам .

При наличии двух классов y принимает значения  и. Если классифицируемые объекты характеризуются двумя признаками, то двухальтернативная задача распознавания образов иллюстрируется, где  – разделяющая поверхность (решающая функция) между классами  и . В результате преабразований оптимальная граница находится в точке пересечения двух классов. Полученная разделяющая поверхность между классами называется байесовской решающей функцией и имеет вид

Исходя из этого, решающее правило будет иметь вид:

Решающее правило, соответствующее данной байесовской разделяющей поверхности, называется правилом максимального правдоподобия.

       Далее рассмотрим ситуацию когда, априорные вероятности  классов разные. Пусть n – общее количество наблюдений; n1– количество наблюдений первого класса; n2– количество наблюдений второго класса.

Найдём минимум суммарной ошибки по границе  и получим байесовскую разделяющую поверхность

.

       Тогда решающее правило, соответствующее данной разделяющей поверхности, будет иметь вид

и называется правилом  максимума  апостериорной  вероятности.

31.  Метод взаимного поглощения.

Пусть имеются точки, вокруг которых построены гиперсферы с радиусом .   – гиперсферы;  – их пересечение. Они имеют область взаимного поглощения, если в область пересечения попадает как точка , так и точка :

Рисунок 2. Область взаимного поглощения

Класс образуют те точки, которые попадают в область взаимного поглощения.

Алгоритм:

1) Вокруг каждой точки построить гиперсферу радиуса .

2) Определить область взаимного поглощения с максимальным количеством точек (они относятся к первому классу).

3) Отбросить эти точки из выборки, и из оставшихся точек найти область взаимного поглощения с максимальным количеством точек и так далее.

Значение радиуса  берем равным максимальному расстоянию между точками.

32. Принятие решений в пространстве разнотипных признаков.

Лингвистические переменные – переменные, которые выражаются в виде словесных инструментов.

υ=(хорошо, не хорошо, очень хорошо)

Необходимо использовать многоуровневую систему принятия решения и свести признаки к дискретному виду:

Порядковые и номинальные признаки можно свести к булевым.

33. Алгоритм «Форель».

Он предполагает:

1. Ввести параметр r (как среднее расстояние между точками) окрестности для каждой точки xi.

2. Взять xi из исходной выборки V и отнести эту точку к исходному классу Ώ1, xv -> Ώ1.

3. Проводим классификацию оставшихся точек в соответствии с алгоритмом m1(xj): xj Ώ1, если xjDi, j=1,n;j≠i

Точки из выборки, которые попадают в окрестность r, относятся к тому же классу что и центральные xi.

4. Провести классификацию оставшихся точек в соответствии с алгоритмом:

m2(xj): xj Ώ1, если xjUDt, tI1, j=II11

I12 – множество точек которые на четвертом этапе были отнесены  к первому классу.

m3(xj): xj Ώ1, если xjUDt, tI12, j=II11U I12

Эта процедура продолжается пока на некотором S-ом этапе к первому классу не будет отнесена ни одна из оставшихся точек, т.е. первый класс сформирован.

Точки первого класса исключаем из выборки V. Из оставшихся точек выбираем любую и относим ее ко второму классу. Далее процесс классификации точек аналогичен процедуре формирования первого класса. Далее третий класс и т.д.

34. Оптимизация непараметрических и гибридных моделей стохастических зависимостей.

35. Метод группового учета аргументов в задачах восстановления стохастических зависимостей.

Входные параметры — y=φ(x), v=(xi,yi,i=1,n) n/k<30

  1. Выбираем из исходного набора два признака (xv,xj), vvj=(xvi, xji, i=1,n)
  2. , т.е. искусственно повышаем отношение n/k за счет декомпозиции
  1. Повторить этап 2 для всех сочетаний xv,xj. Это число различных сочетаний по два признака из k (c2k).
  2. Выбираем некоторую модель  из условия, что W1(μ,q)=minW(v,j),   .
  3. Сформировать выборку , она является частью v.

Для определения  — организовать вычислительный эксперимент с моделью:

  1. По выборке v2 построить модель
  2. Повторить этап 6 для v=1,k; v≠μ; v≠q. При построении модели на этапе 6 вычисляется критерий:
  1. Выбрать модель  для которой справедливо

W2(r)=minW2(v); v=1,k; v≠μ; v≠q

Это значит, что мы выбираем такой признак, который в паре с y1 дает наилучшую аппроксимацию исходной зависимости.

  1. Аналогично этапу 5

Формируем . v3 часть v.

  1.   . v4 часть v.

И так идет усложнение, пока ошибка аппроксимации W не станет нас удовлетворять или пока мы не используем все k признаков.

36. Непараметрические коллективы решающих правил в задачах распознавания образов.

37. Асимптотические свойства непараметрических алгоритмов принятия решений.

1.   Асимптотическая несмещенность

2.   Сходимость среднеквадратического

3.   Состоятельность

38. Непараметрические модели временных процессов коллективного типа

Рассматриваются непараметрические модели временных зависимостей, являющихся основными элементами структуры пространственно распределённых временных систем. Представляемые модели развивают результаты научных исследований, опубликованных в работах.

Синтез непараметрических моделей временных зависимостей.

Пусть V(xt, yt, t=1,n) — выборка наблюдений стохастического процесса y(t)=ψ(x(t)), измеряемых в дискретном времени t = 1,n. При этом объем исходной выборки n сопоставим с размерностью пространства p входных признаков. Случайные величины xt, yt в каждый момент времени t распределены с неизвестными плотностями вероятности p(xt, yt) и p(xt)> 0 . Априори вид нелинейной стохастической зависимости y(t)=ψ(x(t)) не задан.

Для инерционных процессов, когда y(t) зависит от x(t) и предыдущих значений выходной переменной, в предлагаемом методе изменяется лишь размерность пространства входных факторов.

Для восстановления временных зависимостей в условиях малых выборок предлагаются непараметрические модели коллективного типа.

В многомерном случае, наряду с линейными, в качестве опорных также могут быть использованы нелинейные опорные функции. Однако, при формировании подобных опорных функций необходим больший объем времени по сравнению с линейными, что существенно влияет на вычислительные характеристики непараметрического коллектива.

39. Нелинейные непараметрические коллективы в задаче восстановления стохастических зависимостей.

Идея предлагаемого подхода состоит в декомпозиции исходной задачи, построении семейства локальных решающих функций на основании однородных частей обучающей выборки и последующей их организации в едином нелинейном решающем правиле с помощью методов непараметрической статистики. Однородная часть обучающей выборки содержит её элементы, удовлетворяющие одному или нескольким требованиям, таким как наличие однотипных признаков (непрерывные, дискретные, лингвистические и др.), отсутствие либо наличие пропусков данных, что порождает широкий круг условий синтеза непараметрических решающих правил. Однородные части обучающей выборки могут отличаться размерностью и количеством элементов.

На основании однородных частей обучающей выборки сформируем наборы признаков (х(j), j=1,m)  из исходных x =( x1 ,K , xk ) и построим семейство частных моделей φ(j)( х(j), j=1,m) на основании обучающих выборок Vj =( xi (j) yi ,i=1, n) j=1, m.

 Интеграция частных моделей в нелинейном коллективе решающих правил осуществляется в соответствии с процедурой:

Где  — модели частных зависимостей и объединяющего их нелинейного оператора. Структура предлагаемого коллектива решающих правил при восстановлении многомерной стохастической зависимости представлена на рисунке:

При построении частных моделей  могут быть использованы известные методы аппроксимации, включая непараметрическую регрессию

Обобщение частных моделей в едином решающем правиле осуществляется с помощью непараметрической статистики

Оптимизация непараметрического коллектива  по коэффициентам размытости ядерных функций производится в режиме «скользящего экзамена» из условия минимума эмпирического критерия 

40. Двойное коллективное оценивание

Объектом исследования является временная зависимость:

Где преобразование  при каждом  имеет, по крайней мере, две первые ограниченные производные по . Такой класс преобразований будем обозначать через .

Априорная информация о временной зависимости представлена в выборке статически независимых наблюдений . Причем вид плотности вероятности   неизвестен.

Для восстановления зависимости воспользуемся модифицированной методикой синтеза непараметрических моделей коллективного типа, основанной на построении системы упрощенных аппроксимаций, и последующим объединением их в коллективе решающих правил. В предлагаемом подходе система упрощенных аппроксимаций формируется последовательно в двух направлениях от начального  и от конечного  условий, что позволяет в два раза увеличить их количество. Причем организация полученных аппроксимаций в обобщенной модели осуществляется с помощью двойного коллективного оценивания (непараметрического и параметрического).

Данная идея реализуется следующим алгоритмом:

1. Принять t=1.

2.  Сформировать выборку

3. Построить упрощенную аппроксимацию  зависимости с учетом условий:

В соответствии с приведенными условиями упрощенная аппроксимация  проходит через точку  и близка в среднеквадратическом ко всем последующим ситуациям

4. Если , перейти к этапу 2 при , в противном случае – к этапу 5.

5. Построить непараметрическую модель коллективного типа зависимости в виде статистики:

6. Принять t=n.

7. Сформировать выборку

8. Построить упрощенную аппроксимацию , проходящую через точку  при , параметры которой удовлетворяют условию:

9.  t>k, перейти к этапу 7 при t=t-1, иначе – к этапу 10.

10. Систему упрощенных аппроксимаций  организовать в непараметрический коллектив

11. Построить обобщенную коллективную модель зависимости в соответствии с процедурой

Где параметр  определяется из условия минимума эмпирического критерия:

Изложенный метод основан на двойном коллективном оценивании.

41. Нелинейные непараметрические коллективы в задаче распознавания образов

Так же как и в 54 вопросе! (?).

42. Асимптотические свойства непараметрической оценки уравнения разделяющей поверхности.

1. Асимптотическая несмещенность

2. Сходимость среднеквадратического

43. Статистические модели пространственно распределенных временных систем в однородных условиях.

Непараметрические модели однородных процессов. Идея разработанного подхода состоит в построении статистических моделей вре­менных процессов

соответствующих пространственным координатам  на­блюдении за процессом  и последующей их интеграции в единой решающей функции с помощью не параметрической оценки услов­ного математического ожидания.

Для восстановления временных зависимостей предлагается использовать методику синтеза непараметрических моделей коллек­тивного типа, обеспечивающих наиболее полный учет информации обучающих выборок  на основе сочетания преимуществ параметрических и локальных аппроксимаций [1].

Поставим в соответствие каждому наблюдению  подвыборку  и линейный полином, параметры которого удовлетворяют условиям

в виде непараметрической модели коллективного типа [2]

Ф(-) — ядерные функции, удовлетворяющие условиям положитель­ности, симметричности и нормированности [3].

Непараметрическая модель коллективного типа характери­зуется высоким уровнем помехозащищенности, что обеспечивается двойным сглаживанием при формировании системы упрощенных аппроксимаций , и путем их усреднения в соответ­ствии с процедурой.

Оптимизация непараметрической модели по параметрам размытости — оценки среднеквадратических отклонений осуществляется из условия минимума эмпирического критерия

отражающего меру близости между экспериментальными данными  и результатами их оценивания по модели (6.3).

Выбор параметров с осуществляется в режиме «скользящего эк­замена»: ситуация представляемая на контроль, ис­ключается из процесса обучения в процедуре (6.3), что выполняется  .

Для построения обобщенной статистической модели процесса в однородных условиях воспользуемся оператором условного математического ожидания в пространстве z, непараметрическая оценка которого имеет вид:

44. Методы формирования “опорных” ситуаций в непараметрических коллективах решающих правил.

Предлагаются два подхода формирования системы опорных точек в процессе синтеза структуры непараметрической модели коллективного типа.

Первый подход основан на моделировании опорных точек с законом распределения, соответствующим значениям восстанавливаемой зависимости. Второе направление базируется на итерационной процедуре последовательного формирования упрощённых аппроксимаций, минимизирующих на каждом этапе относительную эмпирическую ошибку расхождения между восстанавливаемой зависимостью и её коллективной моделью.

Моделирование системы опорных точек.

Пусть  — исходная обучающая выборка, а  — система опорных точек,  . Мощность множества  . Плотность вероятности опорных точек  , соответствующая y(x), минимизирует главный член дисперсии коллективной модели.

Отсюда следует, что одно из возможных направлений формирования системы опорных точек состоит в их случайном выборе с законом распределения . При этом основной проблемой является построение соответствующего датчика случайных величин.

На оси случайных чисел  с равномерным законом распределения определим интервалы:

для каждой точки   обучающей выборки. Нетрудно заметить, что длина такого интервала пропорциональна значению восстанавливаемой зависимости, а их сумма равна 1.

Для снижения влияния помех на вероятностные свойства целесообразно предварительно сгладить значения экспериментальных данных, тогда алгоритм выбора системы опорных точек представляется следующей последовательностью действий:

1. Принять j=1.

2. Обратиться к датчику случайных величи

Источник

Макеты страниц

Как сказано в § 2.1, оценка качества построенного правила классификации является завершающей операцией ДА. Выбор конкретных показателей и методов их оценивания зависит от целей построения правила классификации, от начальных предположений и степени уверенности в них, от выбранного алгоритма и, наконец, от доступного программного обеспечения.

3.4.1. Показатели качества разделения.

В табл. 3.1 дана сводка основных показателей качества дискриминации, там же указано, где в книге можно найти соответствующие разделы. Средняя ошибка входит в две группы показателей (1.2 и 2.1). Показатели (1.3 и 3.1) так же связаны друг с другом. Их сопоставление может быть использовано для прямой проверки применимости модели Фишера. Особое место занимают показатели, требующие численной оценки отношения правдоподобия в каждой точке выборочного пространства (2.2 и 3.2). Если умеем его оценивать, то «первичная» оценка расстояния Бхатачария по обучающей выборке может выглядеть, например, следующим образом:

Таблица 3.1

Смысл слова «первичная» будет ясен из материала следующего пункта.

3.4.2. Методы оценивания.

Хорошо известно, что если применить построенное правило классификации к обучающей выборке, то оценка качества классификации будет в среднем завышена по сравнению с той же оценкой качества по не зависимым от обучения данным. Это означает, что регистрируемые на обучающей выборке значения ошибок и функции потерь будут ниже ожидаемых, а значения расстояний — больше. Укажем основные приемы борьбы с этим завышением качества.

Разбиение имеющихся данных на две части: обучающую и экзаменующую выборки. Это самый простой и убедительный метод. Им следует широко пользоваться, если данных достаточно. Тем более что, если разбиение данных произведено по какому-либо моменту времени, метод позволяет оценивать качество правила, построенного по прошлым данным, в применении к сегодняшним данным. С чисто статистической точки зрения метод разбиения данных на две части расточителен. Поэтому предложен ряд других, более сложных методов, которые полнее используют выборочную информацию.

Метод скользящего экзамена. При этом методе одно из наблюдений отделяется от выборки и рассматривается в качестве экзаменующего наблюдения.

По оставшимся наблюдениям строится правило классификации, которое применяется к выделенному наблюдению. Результат применения регистрируется и оценивается. Наблюдение возвращается в выборку, выделяется следующее наблюдение и т. д. Процесс прекращается через шагов, когда будет перебрана вся выборка. Последовательные оценки, получаемые с помощью скользящего экзамена, несмещены, однако зависимы между собой. Существенная особенность метода — -кратное построение правила классификации. В случае непараметрических оценок пп. 3.2.2 и 3.2.4 это сделать легко — достаточно просто не включать выделенное наблюдение в суммы в формулах (3.10), (3.11) или не учитывать его в окрестности . В случае использования линейной дискриминантной функции, оцениваемой через при коррекции используется формула Бартлетта для обратных симметричных матриц А

которая существенно упрощает расчеты. В общем случае, особенно при отборе переменных, метод скользящего экзамена слишком трудоемок.

Использование обучающей выборки в качестве экзаменационной с последующей поправкой на смещение. Идея метода достаточно проста. Пусть оценивается некоторый параметр . Обозначим его оценку на обучающей выборке и оценку на новой выборке . Пусть далее , а А — некоторая оценка А. Тогда

Предложены различные способы оценки А: аналитические, опирающиеся на предельные соотношения гл. 2, и эмпирические, использующие специальные вычислительные процедуры. Оба подхода описываются ниже.

3.4.3. Аналитические поправки.

Они наиболее просты в вычислительном плане, но существенно опираются на математические предположения проверяемых моделей. Поэтому их следует рассматривать только в качестве первых приближений.

Поправка для оценки расстояния Махаланобиса в модели Фишера. Пусть

Оценка смещена. Несмещенная оценка расстояния Махаланобиса [264]

Поправка для ООК. На основании теоретического рассмотрения модели Фишера и ряда результатов моделирования с различными алгоритмами Раудис Ш. [132] рекомендует при конструировании поправки использовать параметр (см. гл. 2); если — оценка ошибки классификации, полученная на обучающей выборке, то а — оценка ООК может быть приближенно оценена с помощью

3.4.4. Метод статистического моделирования (bootstrap method).

Предложен В. Эфроном [219]. В нем рекомендуется принять обучающую выборку за генеральную совокупность. Из нее производить повторные по параметру i наборы обучающих и экзаменующих выборок и для каждой пары выборок оценивать разность

Среднее арифметическое А, принимается за А. Далее используется формула (3.19).

Источник

Список выпусков > Серия «Математика».
2021.
Том 38

О точности оценок скользящего экзамена в задаче классификации

Автор(ы)

В.М. Неделько

Аннотация

Метод скользящего экзамена (K-fold cross-validation) является наиболее часто используемым методом оценивания качества решений в задачах машинного обучения. Несмотря на большое число работ, посвященных исследованию данного подхода, остается открытой проблема оценивания точности получаемых
оценок качества. В частности, в настоящее время неизвестны доверительные интервалы для оценки скользящего экзамена, существуют лишь очень грубые оценки
таких интервалов.

Основной идеей работы является схема статистического моделирования, которая позволяет использовать реальные данные для получения статистических оценок,
которые обычно получаются только при использовании модельных распределений. Предложенный подход позволяет достаточно точно вычислять как общую погрешность оценок скользящего экзамена, так и отдельные ее компоненты (смещение, дисперсию), а также оценивать связь этой погрешности с различными статистиками.

Использование повторяющегося скользящего экзамена со случайным разбиением на подвыборки также не дает принципиального выигрыша в точности. Результаты экспериментов позволяют сформулировать эмпирическую оценку, что точность оценок, полученных методом скользящего экзамена приблизительно такая же, как точность оценок, полученных по контрольной выборке, вдвое меньшего объема. Этот результат легко объяснить тем фактом, что все объекты контрольной выборки независимы, а оценки, построенные скользящим экзаменом на разных подвыборках, не являются независимыми.

Об авторах

Неделько Виктор Михайлович, канд. физ.-мат. наук, доц., старший научный сотрудник, Институт математики им. С. Л. Соболева СО РАН, Российская Федерация, 630090, г. Новосибирск, просп. Академика Коптюга, 4, тел.: +7(383) 333-27-93, email: nedelko@math.nsc.ru

Ссылка для цитирования

Nedel’ko V.M. On the Accuracy of Cross-Validation in the Classification Problem // Известия Иркутского государственного университета. Серия Математика. 2021. Т. 38. С. 84-95. https://doi.org/10.26516/1997-7670.2021.38.84

Ключевые слова

построение решающих функций, скользящий экзамен, точность статистических оценок, машинное обучение

УДК

519.246

MSC

68T10, 62H30

DOI

https://doi.org/10.26516/1997-7670.2021.38.84

Литература

  1. Bayle P., Bayle A., Janson L., Mackey L. Cross-validation Confidence Intervals for Test Error // Advances in Neural Information Processing Systems. 2020. Vol. 33. P. 16339–16350
  2. Beleites C., Baumgartner R., Bowman C., Somorjai R., Steiner G., Salzer R., Sowa M. G. Variance reduction in estimating classication error using sparse datasets // Chemometrics and Intelligent Laboratory Systems. 2005. Vol. 79, Iss. 1-2. P. 91—100. https://doi.org/10.1016/j.chemolab.2005.04.008
  3. Franc V., Zien A., Sch¨olkopf B. Support Vector Machines as Probabilistic Models // Proc. of the International Conference on Machine Learning (ICML). ACM, New York, USA, 2011. P. 665–672.
  4. Friedman J., Hastie T., Tibshirani R. Additive logistic regression: a statistical view of boosting // Annals of Statistics. 2000. Vol. 28. P. 337–407. https://doi.org/10.1214/aos/1016218223
  5. Кельманов А. В., Пяткин А. В. NP-трудность некоторых квадратичных евклидовых задач 2-кластеризации // Доклады Академии наук. 2015. Т. 464, №
    5. С. 535–538. https://doi.org/10.7868/S0044466916030091
  6. Лбов Г. С., Старцева Н. Г. Сравнение алгоритмов распознавания с помощью программной системы «Полигон» // Анализ данных и знаний в экспертных системах. Новосибирск, 1990. Вып. 134 : Вычислительные системы. С. 56–66.
  7. Лбов Г. С., Старцева Н. Г. Логические решающие функции и вопросы статистической устойчивости решений. Новосибирск : Институт математики СО РАН, 1999. 211 с.
  8. Lugosi G., Vayatis N. On the bayes-risk consistency of regularized boosting methods // Annals of Statistics. 2004. Vol. 32. P. 30–55. https://doi.org/10.1214/aos/1079120129
  9. Mease D., Wyner A. Evidence contrary to the statistical view of boosting // Journal of Machine Learning Research. 2008. Vol. 9. P. 131–156. https://doi.org/10.1145/1390681.1390687
  10. Motrenko A., Strijov V., Weber G.-W. Sample Size Determination For Logistic Regression // Journal of Computational and Applied Mathematics. 2014. Vol.
    255. P. 743–752. https://doi.org/10.1016/j.cam.2013.06.031
  11. Krasotkina O. V., Turkov P. A., Mottl V. V. Bayesian Approach To The Pattern Recognition Problem In Nonstationary Environment // Lecture Notes in Computer
    Science. 2011. Vol. 6744. P. 24–29. https://doi.org/10.1007/978-3-642-21786-9_6
  12. Красоткина О. В., Турков П. А., Моттль В. В. Байесовская логистическая регрессия в задаче обучения распознаванию образов при смещении решающего
    правила // Известия Тульского государственного университета. Технические науки. 2013. № 2. C. 177–187.
  13. Nedel’ko V. M. Misclassification probability estimations for linear decision functions. // Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics). 2004. Vol. 3138. P. 780–787. https://doi.org/10.1007/978-3-540-27868-9_85
  14. Nedel’ko V. Decision trees capacity and probability of misclassification // Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial
    Intelligence and Lecture Notes in Bioinformatics). LNAI. 2005. Vol. 3505. P. 193–199. https://doi.org/10.1007/11492870_16
  15. Неделько В. М. Регрессионные модели в задаче классификации // Сибирский журнал индустриальной математики. 2014. Т. 27, № 1. C. 86–98.
  16. Неделько В. М. К вопросу об эффективности бустинга в задаче классификации // Вестник Новосибирского государственного университета. Серия: математика, механика, информатика. 2015. Т. 15, вып. 2. C. 72–89. https://doi.org/10.17377/PAM.2015.15.206
  17. Torshin I. Yu., Rudakov K. V. On the Theoretical Basis of Metric Analysis of Poorly Formalized Problems of Recognition and Classification. Pattern Recognition and Image Analysis (Advances in Mathematical Theory and Applications). 2015. Vol. 25, N 4. P. 577–587. https://doi.org/10.1134/S1054661815040252
  18. Vanwinckelen G., Blockeel H. On estimating model accuracy with repeated crossvalidation // BeneLearn 2012: Proceedings of the 21st Belgian-Dutch Conference
    on Machine Learning. 2012. P. 39–44.
  19. Vorontsov K.V. Exact Combinatorial Bounds on the Probability of Overfitting for Empirical Risk Minimization // Pattern Recognition and Image Analysis (Advances in Mathematical Theory and Applications). 2010. Vol. 20, N 3. P. 269–285. https://doi.org/10.1134/S105466181003003X

Полная версия (english)

Источник


Ключевые слова:робастная статистика, непараметрическая статистика, регрессионный анализ, обработка данных

В современном мире все большую роль в промышленности приобретают автоматизированные системы. Для качественного управления технологическим процессом необходимо предварительное построение математической модели или идентификация и глубокое исследование процесса. Модели позволяют проводить качественный и количественный анализ объекта, а также прогнозировать его дальнейшее поведение.

Огромное влияние на адекватность будущей модели оказывают исходные данные, поэтому предварительная обработка данных приобретает особую значимость. Основная задача данного этапа — обработка аномальных измерений, выбросов (промахов), в исходной выборке. Причины появления аномальных наблюдений на практике очень разнообразны:

– сбой измерительной аппаратуры;

– искажение данных при их регистрации, передаче и хранении.

Присутствие нескольких выбросов может негативно отразиться на вычислении оценок параметров распределений и различных статистических характеристик.

Проблема обработки данных, содержащих резко выделяющиеся значения, давно известна. Даже одно такое незамеченное значение может значительно снизить точность анализа данных, а иногда и совсем его обесценить. Представление о том, какие значения считать резко выделяющимися, в большинстве случаев носят субъективный характер, так как оно основано на личном опыте исследователя. Исключение «плохих» данных по существу представляет «чистку» первичных данных перед обработкой и в ряде случаев является вполне допустимым. Однако, такая процедура тщательного просмотра данных возможна только для небольших выборок. Если объем данных велик, то их просмотр потребует столько времени и усилий, что вряд ли окажется реальным. Вместе с тем, практика обработки данных показывает, что появление резко выделяющихся значений в результатах наблюдений является скорее правилом, чем исключением. Таким образом, особое значение принимает возможность автоматизированной обработки резко выделяющихся наблюдений для больших объемов выборок.

Борьба с выбросами актуальна не только в идентификации, но и в любых вопросах, связанных со статистической обработкой данных. Проблемами определения выбросов и получения методов, устойчивых к выбросам, занимается раздел статистики называемый робастной статистикой. В статистике под робастностью понимают нечувствительность к малым отклонениям от предположений [1]. При обработке аномальных измерений были выработаны два подхода:

– исключение промахов из выборки;

– использование робастных методов обработки.

Термин «робастный» введен Джорджем Боксом в 1953 году для обозначения методов, устойчивых к малым отклонениям от предположений. Основы математической теории робастных оценок заложены Питером Хьюбером.

Выбросы (резко выделяющиеся наблюдения) — наблюдения, сильно отличающиеся от основной массы элементов выборки. Они обычно трактуются как грубые ошибки, возникающие в результате случайного просчета или неправильного чтения показаний измерительного прибора.

Робастная оценка — статистическая оценка, нечувствительная к малым изменениям исходной статистической модели. Также термин робастный переводится, как устойчивый, стабильный, помехоустойчивый.

Статистическая модель является приближением реальных процессов, если модель успешно описывает исследуемый объект, то говорят, что она адекватна, в противном случае неадекватна.

Непараметрическая статистика в самой исходной модели предполагает, что функциональный вид распределений, участвующих в задаче не известен. Приведем основные определения данного раздела статистики.

Непараметрическая задача — статистическая задача, в которой указываются только различия между классами распределений. По крайней мере, один из этих классов состоит из подчиняющихся некоторым довольно общим ограничениям, а в остальном неизвестных распределений. Такой класс распределений называется непараметрической гипотезой [3].

Непараметрическая статистика — ветвь математической статистики, занимающаяся рассмотрением непараметрических задач и связанных с ними теоретических проблем.

Непараметрические процедуры — алгоритмы решения непараметрических задач.

В непараметрическом случае оценка «параметров» возможна, если параметр есть известный функционал от неизвестного распределения. Оценка этого функционала, полученная без предположения о типе распределения, называется непараметрической.

Непараметрический факт — свойство выборки (или ее преобразований), которое не зависит от функционального вида распределения генеральной совокупности.

Методы непараметрической регрессии интенсивно развиваются в последние десятилетия. Повышенный интерес к сглаживанию обусловлен двумя причинами: статистики осознали, что параметрический подход не обладает необходимой гибкостью при оценивании, развитие вычислительной техники породило потребность в создании теории вычислительных методов непараметрического оценивания.

Регрессия описывает усредненную количественную связь между выходом и входом объекта. Методы непараметрической обработки информации работают при минимуме априорной информации, таким образом, иногда методы непараметрической регрессии применяют на начальной стадии анализа объекта для угадывания параметрического семейства зависимостей. Однако, универсальность методов компенсируется сложностью обработки исходной выборки, которую приходится хранить на протяжении всех вычислений. Вид функции регрессии может показать, для каких значений аргумента следует ожидать наибольшие значения наблюдений, также большой интерес представляют монотонность или унимодальность функции. Более того, иногда необходимо получить не функцию регрессии, а ее производные или другие функционалы.

При наличии наблюдений регрессионное соотношение может задаваться следующим образом:

(1)

где – неизвестная функция регрессии, а — ошибки наблюдения.

Цель регрессионного анализа состоит в осуществлении разумной аппроксимации неизвестной функции отклика . За счет уменьшения ошибок наблюдения становится возможным сконцентрировать внимание на важных деталях средней зависимости от при ее интерпретации. Эта процедура аппроксимации обычно называется «сглаживанием».

Главным вопросом, возникающим при построении непараметрической оценки, является степень сглаживания, которая определяется параметром сглаживания. Этот параметр управляет размером окрестности точки . Локальное усреднение по слишком большой окрестности не приводит к хорошим результатам. В этом случае происходит «чрезмерное сглаживание» кривой, приводящее к смещению оценки . Если определить параметр сглаживания так, что он будет соответствовать слишком малой окрестности, то в оценку регрессии будет вносить лишь небольшое количество точек, и мы получим грубое приближение.

Представим, что имеется процесс, общая схема которого изображена на рисунке 1.

Рис. 1. Общая схема процесса, принятая в теории идентификации: А — неизвестный оператор объекта; — выходная переменная процесса; — векторное управляющее воздействие; — векторное случайное воздействие; () — непрерывное время; — означают измерения , в дискретное время; — объем выборки; , — каналы связи, соответствующие различным переменным; , — случайные помехи измерений соответствующих переменных процесса

На вход объекта подается контролируемое воздействие , затем с помощью некоторого оператора преобразования получаем выходную переменную . Контроль переменных осуществляется через интервал времени через каналы связи и , то есть — выборка измерений переменных процесса . Случайные воздействия могут наблюдаться как в каналах связи, так и воздействовать на сам объект, поэтому аномальные измерения могут быть обнаружены, как при измерении входных, так и выходных данных. Таким образом, при исследовании объекта мы располагаем текущей информацией в виде выборки измерений , а также априорной информации о нем. В дальнейшем будем считать, что имеется объект с аддитивным шумом, помехи в каналах связи отсутствуют.

Пусть даны наблюдения случайных величин , распределенных с неизвестными плотностями вероятности ( — область значений ), тогда непараметрическая оценка регрессии будет иметь следующий вид [2]:

(2)

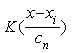
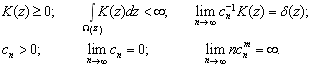
где — точка, в которой восстанавливается функция регрессии или , при расчете не используется точка , — коэффициент размытости, главным образом определяющий степень сглаживания весовой функции , удовлетворяет некоторым условиям сходимости:

(3)

На рисунке 2 приведены наиболее распространенные ядерные функции [2].

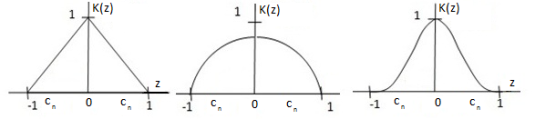
Рис. 2. Виды ядерных функций

(4)

(5)

(6)

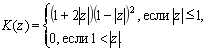
В классическую непараметрическую регрессию 2 добавим весовую функцию , которая будет выполнять сглаживание по выходу .

Полученная робастная регрессия будет выглядеть следующим образом:

(7)

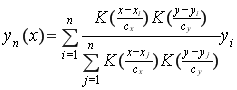
Таким образом, оценка регрессии в точке будет строиться с учетом значений выходов соседних точек. Если точка, в которой восстанавливается значение, будет сильно отличаться от соседних, то такая точка является аномальной, и ядро будет равняться нулю.

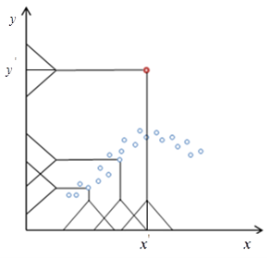
Рис. 3. Принцип работы алгоритма

На рисунке 3 красная точка является аномальной, значение сильно превосходит соседние точки в интервале , поэтому ни одна точка не попадает под весовую функцию , из чего следует, что оценка регрессии в точке будет равна нулю.

Параметр размытости определяется путем решения задачи минимизации квадратичного показателя соответствия выхода объекта и выхода модели, основанного на «методе скользящего экзамена», когда при построении модели не учитывается i-я пара измерений:

(8)

В многомерном случае, если каждой компоненте вектора соответствует компонента вектора , то во многих практических задачах можно принять скалярной величиной, если предварительно привести компоненты вектора , по выборке наблюдений, к одному и тому же интервалу, например, использовать операции центрирования и нормирования.

Настройку коэффициента размытости можно выполнять методом скользящего экзамена для обратной оценки регрессии.

В данной статье представлен алгоритм полного исключения выброса из исходной выборки. Если при изучении процесса имеется необходимое количество измерений, то при полном исключении точки из исходной выборки возможно более точное исследование.

Литература:

  1. Хьюбер П. Робастность в статистике. — М.: Мир, 1984. — 303 с.
  2. Рубан А. И. Методы анализа данных: учебное пособие. — 2-е изд. — Красноярск: ИПЦ КГТУ, 2004. — 319 с.
  3. Тарасенко Ф. П. Непараметрическая статистика. — Томск: изд. ТГУ, 1976. — 294 с.

Основные термины (генерируются автоматически): исходная выборка, канал связи, весовая функция, компонент вектора, непараметрическая регрессия, непараметрическая статистика, оценка регрессии, априорная информация, класс распределений, регрессионный анализ.

Источник

Понравилась статья? Поделить с друзьями:
  • Метод потенциалов физика егэ
  • Медаль посвящена экспедиции которую возглавлял крузенштерн корабли русского флота егэ
  • Мгту га результаты вступительных экзаменов
  • Материалы для подготовки к экзамену по истории россии
  • Квизлет литература егэ