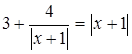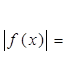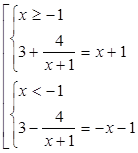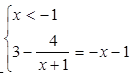Доклад на тему: «Теоретические и методические особенности
подготовки к ЕГЭ по математике».
Основная задача, которая стоит перед каждым учителем, это как
можно лучше подготовить учащихся к сдаче ЕГЭ. Потому что результаты, полученные
выпускниками на ЕГЭ, это и оценка работы учителя. И учащиеся, и их учителя все
больше заинтересованы в получении как можно лучших результатов. Поэтому каждый
педагог ищет и применяет в своей работе наиболее эффективные методы, формы и
технологии обучения. Ведущая идея моего опыта — повышение качества
математической подготовки школьников на основе использования различных форм и
технологий.
Работа над этой
проблемой у меня началась несколько лет назад. Первоначально это было
знакомство с нормативно-правовыми документами, изучение КИМ разных лет, опыта
работы других учителей по этой проблеме. Затем начался поиск и отбор форм и
методов обучения, которые мне казались эффективными.
Наша основная цель: подготовить всех учащихся к успешной
сдаче ЕГЭ с хорошим качеством. А для этого необходимо:
— Учителю обладать
необходимыми компетенциями (самому уметь решать все задачи ЕГЭ)
-Совершенствовать
структуру и содержание учебного материала в ходе подготовки к ЕГЭ
— Систематизировать
повторение программного материала
— Отработать тестовые
технологии в ходе работы с контрольно- измерительными материалами через
личностно-ориентированный подход.
Можно выделить шесть вида
направления деятельности учителя математики по подготовке учащихся к ЕГЭ :
1) психологическая подготовка
учащихся;
2) методическая
подготовка учителя к ЕГЭ;
3) организация вводного,
текущего и итогового повторения;
4) создание банка
тестовых заданий;
5) организация
самостоятельной работы учащихся;
6) диагностика и анализ
качества ЗУН учащихся по материалам ЕГЭ.
1.Методическая
подготовка учителя к ЕГЭ- то есть учитель знакомиться с нормативными
документами по проведению ЕГЭ через районное методическое объединение и
администрацию школы,
Повышает свой уровень
профессиональной грамотности.
2. Психологическая
подготовка — учащихся-это обучение жёсткому самоконтролю времени, оценке трудности заданий
и разумному выбору этих заданий, обучение прикидке границ результатов и
минимальной подстановке как способам проверки результатов.
3. Организация
повторения-это
вводное, текущее и итоговое повторение и повторение, ориентированное на
индивидуальный уровень подготовки учащихся.
4. Создание банка
тестовых заданий- создание тестов по основным темам курса,
тренировочных тестов, итоговых тестов, тестов прошлых лет, тестов пробных
экзаменов.
5. Организация
самостоятельной работы учащихся- то есть организация работы
учащихся по сборникам подготовки к ЕГЭ и организация самостоятельной работы по
материалам в интернете.
6. Анализ качества ЗУН
учащихся—
осуществляется при помощи тематических тестов по основным разделам курса,
контрольных зачётов и пробных ЕГЭ по линии администрации.
С целью повышения
эффективности работы педагога при подготовке учащихся к сдаче ЕГЭ по математике
применяются информационно- компьютерные технологии (ИКТ).
Компьютерные (новые
информационные) технологии
обучения — это процесс подготовки и передачи
информации обучаемому, средством осуществления которого является компьютер.
При применение ИКТ на
уроках имеются и преимущества, и недостатки.Преимущества в том что:
— индивидуализация
обучения;
-интенсификация
самостоятельной работы;
-рост объема выполненных
на уроке заданий;
-возможность получения
различного рода материалов;
-Возможность учителю
переложить часть своей
работы на ПК;
-Получение объективной
картины уровня усвоения
изучаемого материала.
Имеются и
недостатки:
— Недостаточно времени
для подготовки к ИКТ уроку;
-Недостаточная
компьютерная грамотность учителя;
-Отсутствие
демонстрационного центра;
-Сложность интегрирования
в поурочную структуру;
-Отсутствие в рабочем
графике времени для исследования возможностей Интернет.
Существуют различные
аппаратные средства ИКТ при подготовке к ЕГЭ:
1.
Применение
сети компьютеров-позволяет
:
— усилить мотивацию
ребенка;
— полностью устранить
одну из важнейших причин отрицательного отношения к учебе – неуспех;
— получить возможность
довести решение задачи до конца, опираясь на необходимую помощь;
— наглядное пособие
(качественно нового уровня с возможностями мультимедиа); тренажер; средство
диагностики и контроля;
— выполнить самопроверку.
2. Использование
интерактивной доски SMART Board-её преимущества
использования :
-Экономия времени урока;
-Наглядность и
интерактивность;
-Многократное
использование;
-Повышение уровня
компьютерной компетенции учителя и учащихся;
-Учиться становиться
интересно и увлекательно.
3.Работа с
документ-камерой-при
её помощи осуществляется:
— Решение задач по
готовым чертежам по геометрии для устной работы;
— фронтальная проверка по
готовому решению;
— оперативный анализ
контрольной или самостоятельной работы;
— оперативная проверка
блоков домашнего задания по заданиям
из сборника ЕГЭ, работа с
бланками ЕГЭ
— документ-камера
помогает при рассмотрении реальных объектов и их проекций, демонстрируемых на
экране.
— В условиях подготовки
ребят к сдаче независимых экзаменов в форме ГИА или ЕГЭ, когда работы (большую
часть) проверяет машина — использование интерактивной системы опроса оказывает
неоценимую помощь не только в качественной подготовке к самому экзамену, но и
моральному настрою на то, что надеяться надо на свои знания и стараться их
показать.
6.Использование сети
Интернет– это:
-Использование Цифровых
образовательных ресурсов при подготовке к ЕГЭ;
-Применение компьютерных
презентаций;
— Применение обучающих
программ, тренажеров, интерактивных тестов.
В
современных условиях модернизации математического образования одним из приоритетных
направлений преподавания математики является изменение акцентов в учебной
деятельности учащихся, усиление самостоятельности школьников, более широкое
использование в обучении видов деятельности, направленных на подготовку
учащихся к новым формам контроля – к сдаче ЕГЭ.
Идеального
варианта подготовки к ЕГЭ не существует, как и не существует идеального
отчаяния. 4 года мои ученики сдавали ЕГЭ. Были и успехи, и отчаяния. В своем докладе,
а просто хочу поделиться опытом своей работы по подготовке учащегося к сдаче
ЕГЭ.
При
подготовке к ЕГЭ у выпускника появляются новые трудности. Главное отличие ЕГЭ
от выпускного экзамена состоит в том, что при подготовки придется повторить
весь материал, изучаемый, начиная с 5 по 11 класс. ЕГЭ
предлагает выпускнику сразу 20 заданий на 3 часа базового уровня. При этом
школьнику предлагается самому выбирать задания, с которыми он может справиться.
Но ведь это уже очень трудная задача для учащегося, который привык стараться
справиться с тем, что задано учителем. К ЕГЭ надо готовиться и по предмету, и
психологически. Это связано еще с тем, что задания ЕГЭ сформулированы в
непривычной для учащегося форме, и кроме того, большинство школьников должны
смириться с тем, что все задачи они не решат в отведенное время.
Сконцентрироваться надо на понятных для них задачах, решать их спокойно и до
конца. Для того, чтобы учащиеся не растерялись перед заданиями ЕГЭ и решили
правильно больше задач, их нужно готовить не в конце учебного года 11 класса, а
намного раньше – начиная с 5-го класса.
В
каждом классе 3-4 раза в год я провожу уроки-путешествия в «мир ЕГЭ». Раздаю
учащимся готовые варианты с заданиями ЕГЭ 9-х и 11-х классов и прошу, чтобы они
выбрали те задания, которые могут решить. В конце учебного года в 5-ом, 6-ом
классах, после изучения тем «Формула площади прямоугольника», «Проценты»,
«Десятичные дроби» сильные ученики могут решить некоторые текстовые задачи из
ЕГЭ 9-го и 11-го класса. В 7-ом, 8-ом классах они решают большинство заданий
ЕГЭ 9-го класса. И у многих учащихся появляется интерес к тестам. После чего
контрольные работы, зачеты в виде тестов (некоторые с ответами), а некоторые
задания без готовых ответов они решают с желанием.
Можно
составить разно уровневые тесты, можно задать домашнее задание, самим
составить тесты с готовыми ответами из нескольких заданий.
Хочу
вернуться к началу выступления. Не существует идеального отчаяния. Каковы
бывают отчаяния у учащихся и у учителя после сдачи пробного ЕГЭ? Тот, кто хотел
получить высокие баллы — получил низкие, тот, кто был уверен в сдаче ЕГЭ — не
сдал. У каждого ученика ограничен круг возможностей. Будет неправильно, если во
время подготовки не будем учитывать возможности учащегося. В течение всей 4-ой
четверти 11 класса я стараюсь прогнать весь пройденный материал, который есть в
ЕГЭ и при этом изучать новые темы. Во время осенних каникул провожу пробный ЕГЭ
на школьном уровне и по результатам выявляю и возможности учащегося и те темы,
которые надо повторить с классом. После этого, учитывая и желание ученика, я
разделяю класс на 3 группы: 1-ая группа — те, которые просто хотят
сдать ЕГЭ, 2-ая группа – те, которые на средние баллы и 3-я группа – те,
которые хотят получить высокие баллы т.е. (профильную). Когда работаю с одной
группой, 2 другие группы решают самостоятельно или при помощи сильного ученика.
В течение 5 лет по традиции школы проводила консультации в 9-ом, 11-ом классах,
начиная с начала учебного года. Так как по учебному плану на алгебру отводится
3 часа + 1 школьный компонент, этих часов практически не хватает для усвоения
программного материала и подготовки к ЕГЭ. Но представьте, какая нагрузка
для учителя 2 раза в неделю по 2-3 часа готовить к экзаменам. Поэтому в конце
10-го класса я начинаю проходить материал 11-го класса, и к первому полугодию
11-го класса завершаю материал, а во втором полугодии готовлю учеников к ЕГЭ.
Еще можно использовать часы геометрии. В 2018-2019 учебном году все выпускники
получили аттестаты, хотя класс был не из сильных. Успеваемость -100%, качество
по математике 76 %. Есть дети, для которых математика – это «темный лес», подготовка
этих учащихся только по заданиям 1-8, может дать результат.
Для качественной
подготовки к ЕГЭ созданы сайты, обеспечивающие поддержку работы учителя и
самостоятельную работу учащихся по подготовке к сдаче экзамена.
Опасность кроется в том,
что демонстрационный вариант ЕГЭ по математике может сильно отличаться от того
варианта, который даётся на экзамене. Экзаменационный вариант может быть
сложнее демонстрационного, а многие задачи могут не соответствовать тем, к
которым готовился ученик. Поэтому выпускнику необходимо заниматься
самостоятельно, помимо школьной программы, и не просто “натаскаться” на задачах
демонстрационного материала, но и изучить принципы и методы решения различных
задач, а также научиться думать нешаблонно, сформировав цельную картину
изучаемого предмета.
Экзамен не должен стать
для выпускников испытанием на прочность нервной системы. Чем раньше начнется
подготовка к экзамену, тем легче пройдет сдача экзамена. Подготовка к экзамену
– означает изучение программного материала с включением заданий в формах,
используемых при итоговой аттестации. Кроме того, необходимо ликвидировать
пробелы в знаниях и постараться решить общие проблемы, хорошо известные каждому
учителю: отсутствие культуры вычислений и несформированность приемов
самопроверки.
Спасибо
за внимание!
Методические рекомендации учителям математики по подготовке к ЕГЭ.
Подготовила учитель математики
Куликова Е.Г.
Основная подготовка выпускников к ЕГЭ по математике осуществляется не только в течение учебных лет в старшей школе, но и раньше, начиная с 7-9 класса.
Исключительно важным становится целенаправленная и специально планируемая подготовка школьников к ЕГЭ. Безусловно, на последний год обучения в школе приходится максимальная нагрузка на учащихся. При этом возрастает роль и ответственность в подготовительной работе и учителя и самого ученика.
ЕГЭ (единый государственный экзамен) основан на тестовых технологиях. Тестирование как новая форма экзамена накапливает свой опыт и требует предварительной подготовки всех участников образовательного процесса. Учителям следует активнее вводить тестовые технологии в систему обучения, ведь не зря говорят, что «нельзя научиться плавать, стоя на берегу». Особый интерес в этом плане представляют впервые издаваемые Центром тестирования РФ сборники тематических тестов. Эти тесты разработаны для учащихся с 5 по 11 класс, с их помощью можно оценивать уровень усвоения материала и отработать навык их выполнения.
Такие тренировки в выполнении тестовых заданий позволят реально повысить тестовый балл. Зная типовые конструкции тестовых заданий, ученик практически не будет тратить время на понимание инструкции. Во время таких тренировок формируются соответствующие психотехнические навыки саморегуляции и самоконтроля. При этом основную часть работы желательно проводить заранее, отрабатывая отдельные детали при сдаче каких-нибудь зачетов и пр., т.е. в случаях не столь эмоционально напряженных. Ученые считают, что психотехнические навыки сдачи экзаменов не только повышают эффективность подготовки к экзаменам, позволяет более успешно вести себя во время экзамена, но и вообще способствуют развитию навыков мыслительной работы, умению мобилизовать себя в решающей ситуации, овладевать собственными эмоциями.
Как я осуществляю подготовку к экзамену:
- Знакомлю детей с методикой подготовки к экзаменам. Не имеет смысла зазубривать весь фактический материал, достаточно просмотреть ключевые моменты и уловить смысл и логику материала. Очень полезно делать краткие схематические выписки и таблицы, упорядочивая изучаемый материал по плану. Если они не умеют, показываю ученикам, как это делается на практике. Основные формулы и определения можно выписать на листочках и повесить над письменным столом, над кроватью, в столовой и т.д.
- Готовлю различные варианты тестовых заданий по предмету (сейчас существует множество различных сборников тестовых заданий). Большое значение имеет тренаж ребенка именно по тестированию, ведь эта форма отличается от привычных ему письменных и устных экзаменов.
- Помогаю детям распределить темы подготовки по дням.
- Советую детям во время экзамена обратить внимание на следующее:
- пробежать глазами весь тест, чтобы увидеть, какого типа задания в нем содержатся, это поможет настроиться на работу;
- внимательно прочитать вопрос до конца и понять его смысл (характерная ошибка во время тестирования — не дочитав до конца, по первым словам уже предполагают ответ и торопятся его вписать);
- если не знаешь ответа на вопрос или не уверен, пропусти его и отметь, чтобы потом к нему вернуться;
- если не смог в течение отведенного времени ответить на вопрос, есть смысл положиться на свою интуицию и указать наиболее вероятный вариант.
5. Подбадриваю детей, хвалю их за то, что они делают хорошо.
Психологическая подготовка к ЕГЭ:
- Итак, первое, что можно посоветовать начать делать уже завтра: прекратить пугать учеников предстоящим ЕГЭ, и начать формировать у них твердое убеждение в том, что, если очень постараться, то можно получить вполне приличный балл: время для подготовки еще не полностью потеряно. Конечно, не следует «перегибать палку» и внушать школьникам, что ЕГЭ – это легко и просто. Но не нужно и внушать им мысль о полной безнадежности. Начните с вопроса: «Что каждый из Вас хочет получить на ЕГЭ?» Таким образом, сразу определится планируемый результат обучения. Важно, чтобы школьник сам его честно сформулировал для себя. Этот разговор дает возможность учитывать «актуальный потолок» обучаемого. Это не значит, что следует его занижать, или этот «потолок» неизменен и, однажды его наметив, на него следует постоянно ориентироваться.
В этой связи, уровень сложности заданий в некоторых случаях следует объявлять заранее, а в некоторых – только после его выполнения: «Как вы думаете, из какого раздела было это задание» Из раздела В! (или С!) И вы его сделали! Кому оно показалось невероятно трудным? Никому! Молодцы! Идем дальше: из какого раздела хотите следующее задание?» Понятно, что это психологически продуманная игра, но при спланированном подборе заданий она приводит к очень значительному сдвигу, как в самооценке школьника, так и в его чувстве уверенности в себе, а также к некоторым положительным подвижкам в качестве его знаний и умения их применять. А главное, в умении «технично» сдавать тест, используя всевозможные вспомогательные приемы и соображения.
- Следует учить школьника технике сдачи теста. Эта техника включает следующие моменты:
- обучение постоянному жесткому самоконтролю времени;
- обучение оценки объективной и субъективной трудности заданий и соответственно разумному выбору этих заданий;
- обучение прикидке границ результатов и минимальной подстановке как проверки, проводимой сразу после решения задания;
- обучение приему «спирального движения» по тесту.
Прием «спирального движения» находится в полном несоответствии с действующей методикой обучения школьника математике. Но он является первым необходимым приемом для успешного написания задания типа «тест с ограничением времени». Он состоит в следующем: ученик сразу просматривает тест от начала до конца и отмечает для себя то, что кажется ему простым, понятным и легким. Именно эти задания школьник выполняет первыми. Я говорю так: «Начинайте с того, что вы можете выполнить сходу, без особых раздумий. Пробегите глазами по разделу В и отметьте два-три задания, которые поняли сразу.. Просмотрите раздел С – один пример в этом разделе всегда решаем без особого напряжения (это действительно так). Отметьте то, что вы попробуете решить, когда закончите с разделом В. Ученик может сделать так несколько раз (двигаясь по спирали и выбирая то, что «созрело» к данному моменту). Если он ориентируется на тройку, то после того, как решил все, что мог из раздела В, он попробует решить что-то из раздела С.
Педагогическая система подготовки учащихся к ЕГЭ по математике.
I. Подготовительный этап – включает в себя: повторение ранее изученного материала, необходимого для успешной сдачи ЕГЭ; формирование некоторого комплекса умений, навыков и способов деятельности, необходимых на начальном этапе, чтобы приступить к решению той или иной задачи содержания ЕГЭ; рассмотрение основных методов и приемов, применение которых поможет при решении ряда нестандартных и исследовательских задач; изучение внепрограммного материала необходимого для решения задач ЕГЭ рассчитанных на поступление в вуз; накопление знаний в процессе формирования индивидуального справочника учащегося.
Алгебра и начала анализа:
· восполнение пустот вычислительной культуры учащихся;
· отработка основных умений и навыков, необходимых учащимся для выполнения упражнений и задач, связанных с преобразованиями выражений;
· классификация тестовых задач по темам и методам их решения;
· формирование индивидуального справочника учащегося по основным разделам алгебры.
Геометрия:
· выделение основных типажей условий геометрических задач содержания ЕГЭ и приемов работы с каждым типом;
· выделение для учащихся основных требований к построению чертежа по условию геометрической задачи, с учетом специфики разделов: планиметрии и стереометрии;
· рассмотрение основных методов, применение которых необходимо при решении геометрических задач части В и С ЕГЭ;
· поиск и выделение опорных задач по планиметрии и стереометрии двух видов: вспомогательных задач-теорем и задач-методов;
· формирование индивидуального справочника учащегося по основным разделам геометрии.
II. Практический этап – включает в себя:
· отработку навыков решения элементарных задач;
· решение задач по отдельным темам и разделам;
· отработку навыков применения отдельных методов и приемов при решении задач различных уровней сложности;
· определение темы разделов алгебры и геометрии и метода решения, применимых к рассматриваемой задаче;
· решение задач как отдельно по уровням В и С, так и рассмотрение наборов задач, включающих в себя в любом порядке задачи различных уровней сложности;
· обмен опыта учащихся по применению методов и приемов при решении задач ЕГЭ по математике;
· формирование навыков нахождения учащимися различных способов решения тех или иных задач, совместно с одноклассниками их рассмотрение и взаимообмен.
III. Диагностический этап включает:
· в обязательном порядке входящий и итоговый контроль измерителями, составленными на основе КИМов, используемых при сдаче ЕГЭ по математике прошлых лет;
· тематический контроль;
· проведение итоговых обобщающих занятий по отдельным разделам алгебры и геометрии;
· рассмотрение с учащимися ряда исследовательских задач для выявления у них способностей применения полученных знаний на практике и при решении нестандартных задач;
· отслеживание учебных достижений учащихся на основе требований к уровню подготовки выпускников в течение всего времени подготовки к ЕГЭ.
Во время подготовки необходимо уделить особенное внимание изучению таких разделов и тем, как:
МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ ПОДГОТОВКИ СТАРШЕКЛАССНИКОВ
К СДАЧЕ ЕГЭ ПО МАТЕМАТИКЕ
Т.А. Медведева (КамчатГТУ, БГАРФ)
Проведен анализ результатов сдачи Единого государственного экзамена по математике школьниками области. Показаны причины, по которым результаты сдачи оказались ниже общего федерального уровня. Предлагается методика подготовки школьников выпускных классов к сдаче экзамена по математике.
The analysis of UST (Unified State Test) mathematics results among the schoolchildren of Kamchatka region was carried out. The author defines the reasons, which caused lower results than the results of general federal level and offers methods ofpreparation to math graduation exam.
Третий год продолжается эксперимент по проведению итоговой аттестации выпускников школ в форме Единого государственного экзамена (ЕГЭ). Отношение к нему среди преподавателей, школьников и их родителей неоднозначно. Согласно опросу Фонда общественного мнения «Единый государственный экзамен», 24% одобряют ЕГЭ, 20% не одобряют, 25% не определились, какую сторону принять (данные по состоянию на 19.06.2003 г.). А эксперимент тем временем «набирает обороты», и в 2005 г. Министерство образования и науки РФ планирует «перевод ЕГЭ из разряда экспериментального в разряд обязательного экзамена на всей территории России» (брифинг по результатам ЕГЭ от 01.07.2004 г.).
По данным информационного центра «Образование», статистика такая: в 2001 г. в эксперименте приняли участие 5 регионов; в 2002 г. — 16; в 2003 г. — 47; в 2004 г. — 65. Общее количество участников эксперимента составило 821 184 человека, из них 2 874 выпускника школ Камчатской области писали ЕГЭ по математике. Информация о результатах ЕГЭ в 2004 г. приведена в таблице.
Средний тестовый балл Оценки по пятибалльной шкале, %
2 3 4 5
Камч. обл. Россия Камч. обл. Россия Камч. обл. Россия Камч. обл. Россия Камч. обл. Россия
47,4 49,89 19,6 19,4 41,7 34 31,7 35,42 7,1 11,09
Таким образом, по сравнению с 2003 г. увеличилось количество тестируемых, получивших неудовлетворительные оценки. Руководитель Федеральной службы по надзору в сфере образования и науки Виктор Болотов объясняет это тем, что к сегодняшним выпускникам предъявлены слишком высокие требования.
Как видим из сравнения статистических данных, количество неудовлетворительных оценок по Камчатской области выше, чем в среднем по России. Среди камчатских выпускников лидируют «троечники» со значительным отрывом от среднестатистического ученика по России. Что же касается хороших и отличных оценок, то здесь все наоборот. Выводы, которые напрашиваются сами собой, не радуют: на Камчатке средний уровень подготовки выпускника по математике ниже, чем по России, а значит, основная цель введения ЕГЭ — обеспечение равных условий для поступления в вузы выпускников центра и регионов не достигнута.
Причин тому, на наш взгляд, несколько. Одна из них — психологического свойства. Как показывает опыт работы с абитуриентами, большинство из них не готовы сдавать ЕГЭ чисто психологически. У выпускников нет должного положительного настроя и уверенности в своих силах. Для них непривычны также и работа по заполнению материалов теста, и сам факт необходимости зарабатывать баллы. Поэтому, на наш взгляд, воспитание положительного отношения, психологическая поддержка учителями своих воспитанников необходимы ничуть не меньше, чем твердые, качественные знания.
Другая причина — это, естественно, качество и глубина полученных в школе знаний. Экзаменационная работа мо математике (ЕГЭ 2004 г.) охватывает большой объем учебного материала, требующего не просто умения применять отработанные алгоритмы решения типовых задач, но и высокого уровня «интеллектуальной культуры обучаемых».
Первый уровень интеллектуальной культуры — учащиеся «обладают довольно обширными предметными знаниями …, но с трудом выделяют взаимосвязи однородных базовых понятий, … применяют знания для решения задач на уровне известных алгоритмов …» [1, 2], что вполне соответствует выполнению первой части работы, с которой справились большинство выпускников. Это свидетельствует о достаточной степени усвоения базового материала школьной
программы и соответствует оценке «удовлетворительно».
Второй уровень интеллектуальной культуры — учащиеся «владеют сложными синтезированными методами восхождения от абстрактного к конкретному, дифференцированноинтегрального расчленения и синтеза» [1, 2]. Этот уровень соответствует второй части экзаменационного задания, с которой справились лишь около трети выпускников школ Камчатской области, что показывает отсутствие у большинства из них глубины в знаниях, наличие формализма, привычки алгоритмического усвоения материала.
Третий уровень интеллектуальной культуры — «учащиеся владеют дедуктивным методом познания, … применяют при решении практических задач эвристические, индивидуальнотворческие способы составления алгоритмов, синтезируя при этом свой опыт нахождения аналогов, теоретических обобщений, математических моделей …» [1, 2]. Всего лишь 7,1% камчатских выпускников достигли за 11 лет обучения такого уровня.
Чтобы добиться третьего, самого высокого уровня, необходима большая и специфическая работа в течение всего периода обучения плюс эффективное повторение материала перед экзаменом. По утверждению психологов, учащиеся, усваивающие новый материал, сопоставляют его с уже имеющимися знаниями. Если отсутствует какое-либо звено в цепи последовательного изучения материала, то разорвана и вся цепь. Следовательно, для успешного повторения при подготовке к экзаменам необходимо актуализировать, откорректировать школьную базу, устранить имеющиеся пробелы.
Рассмотрим предэкзаменационное повторение на примере раздела «Тригонометрия», материал которого традиционно включают в экзаменационные работы, причем есть он во всех уровнях сложности ЕГЭ по математике 2004 г. Важность глубоких знаний этого раздела элементарной математики трудно переоценить. Тригонометрия активно используется в курсе высшей математики: в теории пределов, интегральном исчислении, теории функций комплексной переменной, рядах Фурье и т. д.
Примерный план интенсивного повторения
Первая часть включает в себя составление базового конспекта по теории и содержит следующие вопросы:
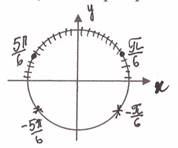
1. Определение тригонометрических функций через соотношения в прямоугольном треугольнике и через координаты точки единичной окружности.
2. Связь между градусом и радианом.
3. Значения тригонометрических функций некоторых углов. (Обратить внимание учащихся на то, что запоминанию подлежат только значения тригонометрических функций углов 30о, 45о, 60о. Значения же для углов 0о, 90о, 180о, 270о, 360о полезнее уметь находить, зная определения тригонометрических функций и используя единичную окружность.)
4. Знаки значений тригонометрических функций по четвертям. (Не нужно запоминать схему с кругами, достаточно знать базовые определения sin а и cos а как ординату и абсциссу точки единичной окружности.)
5. Четность, нечетность. (Здесь вспомнить определения четных и нечетных функций, свойства их графиков.)
6. Периодичность. (Полезно провести аналогию между периодическими явлениями в природе и наличием периода у всех тригонометрических функций.)
7. Основные тригонометрические тождества. (Эту часть повторения учащиеся могут законспектировать дома, используя любой справочник по элементарной математике или школьный учебник. Следует обратить внимание на такие группы тождеств, как «Формулы понижения степени», которые часто применяются для решения довольно сложных тригонометрических уравнений, используются в курсе высшей математики в разделах «Интегральное исчисление функции одной переменной», «Выражение тригонометрических функций через тангенс половинного аргумента», которые также используются в курсе высшей математики (интегрирование способом универсальной тригонометрической подстановки). Кроме того, применение этих формул часто приводит к сужению области допустимых значений выражения.)
8. Формулы приведения. (Сформулировать мнемоническое правило, сразу отработать его на простейших примерах, предложить учащимся дома доказать любую из формул.)
9. Графики тригонометрических функций. (Напомнить построение с использованием единичной
окружности, указать на соразмерность единиц масштаба горизонтальной и вертикальной осей. Повторить построение графиков вида: У = А sin(rax + B) + C в зависимости от значений параметров
А,В,С,ш ; У = |f (х)|, У = f|х| .)
10. Обратные тригонометрические функции. (Обратить внимание на область их определения. Полезно сделать соответствующий рисунок. Напомнить, как находить значения arcsin(-a), arccos(-a), arctg(-a), arcctg(-a), предложить учащимся дома построить графики обратных тригонометрических функций, зная графики тригонометрических функций и используя свойство графиков взаимно-обратных функций.)
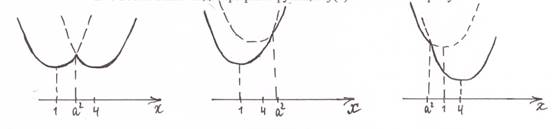
11. Решение простейших тригонометрических уравнений. (Особо отметить частные случаи для уравнений вида sin t = a,cos t = a . Провести аналогию с решением более сложных задач с параметрами: исследование правой части уравнения и, в зависимости от этого, применение соответствующей простейшей формулы.)
Как показывает опыт организации работы итогового повторения с абитуриентами, составление конспекта занимает не более 1,5 академических часов и приносит огромную пользу при решении задач любого уровня сложности по этой теме.
Вторая часть — это решение тренировочных задач, требующих алгоритмического воспроизведения. В зависимости от уровня подготовленности группы эта часть занимает от 20 минут до 1,5 часов.
Третья часть — решение задач, требующих у учащихся наличия «второго интеллектуального уровня». (Дать классификацию способов решения тригонометрических уравнений. Особое внимание обратить на возможность решения одного и того же уравнения разными способами и несовпадения при этом формы записи ответа; отбор корней из заданного интервала и с учетом области допустимых значений уравнения. Рассмотреть примеры решения уравнений, содержащих обратные тригонометрические функции).
Четвертая часть — решение задач повышенной сложности, требующих у учащихся наличия третьего интеллектуального уровня.
Опыт показывает, что организация итогового повторения по этой схеме «на выходе» дает неплохой результат.
В заключение отметим, что наблюдается устойчивое падение интереса российских школьников к точным наукам. По данным исследования PISA, Россия занимает 22 место в мире по математике (для сравнения: Южная Корея — 1, США, славящиеся своим низким образовательным уровнем — 19, Великобритания — 8, Франция — 10). Станет Единый государственный экзамен по математике обязательным или нет — неизвестно, но проблему повышения интереса к точным наукам, а следовательно, качество математической подготовки выпускников придется все равно решать.
Методика подготовки к ЕГЭ по математике. Автор: Анна Георгиевна Малкова.
-
Основные принципы методики Анны Малковой:
-
Программа Полного курса подготовки к ЕГЭ по математике для учащихся групп «М-100».
-
Сентябрь.
-
Текстовые задачи на ЕГЭ по математике.
-
Октябрь.
-
Геометрия и стереометрия на ЕГЭ по математике, часть 1.
-
Октябрь — ноябрь.
-
Алгебра на ЕГЭ по математике, часть 1.
-
Тригонометрия на ЕГЭ по математике.
-
Декабрь.
-
Производная функции. Геометрический смысл производной.
-
Стереометрия на ЕГЭ по математике.
-
Январь.
-
Неравенства на ЕГЭ по математике.
-
Февраль.
-
Геометрия на ЕГЭ по математике. Задача С4.
-
Задачи с экономическим содержанием на ЕГЭ по математике.
-
Март.
-
Задачи с параметрами на ЕГЭ по математике.
-
Апрель.
-
Нестандартные задачи на ЕГЭ по математике (С6).
-
Май.
-
Повторение всех тем и решение вариантов ЕГЭ.
-
Рекомендуемый хронометраж для учащихся, претендующих на 90-100 баллов ЕГЭ:
-
Дополнения к Авторской методике Анны Малковой:
-
Приложение к методике: Обучающие комплекты видеокурсов Анны Малковой «Получи пятерку» и «Премиум».
-
Авторское право.
Внимание! Методика подготовки к ЕГЭ Анны Георгиевны Малковой защищена законом об авторских правах. Все материалы, находящиеся в данном файле, не подлежат воспроизведению в какой-либо форме или каким-либо образом без предварительного письменного разрешения ООО «ЕГЭ-Студия» и Анны Георгиевны Малковой. © 2017.
Методика подготовки к профильному ЕГЭ по математике Анны Малковой является результатом многолетнего опыта репетиторской и преподавательской работы. Анна Малкова преподает математику более 25 лет и за это время разработала целостную систему, включающую эффективные приемы объяснения той или иной темы школьной программы, пошаговое повышение мотивации учащихся и контроль достигнутых ими успехов.
Методика Анны Малковой рассчитана на обычного среднестатистического школьника и позволяет ему получить результат 90-100 баллов на ЕГЭ по математике профильного уровня за один учебный год подготовки.
Методика Анны Малковой предназначена для учителей, выпускающих 11 класс, преподавателей курсов подготовки к ЕГЭ и репетиторов, готовящих к ЕГЭ по математике.
Рассмотрим основные цели и задачи, стоящие перед репетитором-математиком (учителем, преподавателем), который готовит ученика к ЕГЭ или дополнительным вступительным экзаменам в вузы.
— Глобальная цель: пройти с учеником весь курс математики 10-11 класса. При необходимости – повторить отдельные темы или весь курс математики 5-9 класса.
Часто говорят, что репетитор «натаскивает» перед экзаменом, то есть сообщает, в каких задачах какие именно механические действия надо сделать, чтобы магическим образом получить ответ. Этот миф о репетиторах не имеет с реальностью ничего общего, и таким способом подготовить к экзамену невозможно.
Задача репетитора – не «натаскать перед экзаменом», а передать ученику полное и целостное понимание всего курса школьной математики. Не показать разрозненные приемы решения отдельных задач, а научить решать творчески и при этом математически грамотно любую экзаменационную задачу.
— При работе с учеником репетитору необходимо выявить пробелы, возникшие при изучении тех или иных тем в школе, и проработать эти темы наиболее тщательно.
К сожалению, старшеклассник, обучающийся в среднестатистической школе, практически всегда имеет такие пробелы и не скрывает, что некоторых тем в математике не понимает совсем.
Это связано с тем, что в разных школах преподавание математики ведется по различным программам, часто не состыкованным друг с другом. Смена учителя и тем более смена школы ведет к еще большей несогласованности пройденных тем.
— Одна из задач репетитора — дать навыки решения простых задач ЕГЭ быстро и без калькулятора.
Как показывает статистика, большая часть ошибок на ЕГЭ связана с арифметическими вычислениями. Именно из-за ошибок в вычислениях выпускник часто теряет драгоценные баллы и получает результат ниже, чем рассчитывал. Связано это с тем, что на уроках в школе и тем более при выполнении домашних заданий школьник привыкает пользоваться калькулятором, при этом часто забывая, как «в столбик» поделить одно число на другое.
— Следующая задача репетитора (преподавателя) — научить выпускника рассчитывать время на экзамене.
Профильный ЕГЭ по математике – фактически два экзамена в одном. Это и относительно простые 12 (в 2015 году — 14) задач части 1, или части В, которые можно считать выпускным экзаменом за курс средней школы, и 7 задач части 2 (которую еще недавно называли «Часть С»), которые по уровню сложности и требованиям к оформлению близки к традиционным задачам вступительных экзаменов в вузы. На все эти задачи дается 3 часа 55 минут. Это значит, что у ученика нет времени «изобретать» решение задачи на экзамене. Ему необходимо заранее знать все алгоритмы и нюансы решения каждой задачи, уметь доводить решение до результата, не бросая на полпути, уметь адекватно оценивать и проверять результат, а также следить за временем, зная, сколько минут можно потратить на решение тех или иных задач.
— Одна из важнейших задач репетитора (учителя, преподавателя курсов подготовки к ЕГЭ) — дать абитуриенту базу для дальнейшего освоения высшей математики и других связанных с математикой дисциплин при учебе в вузе.
Как правило, с поступлением абитуриента в вуз работа репетитора (учителя, преподавателя курсов подготовки к ЕГЭ) счастливо завершается, но на этом не заканчивается знакомство его ученика с математикой. Чем более качественной была подготовка к ЕГЭ, тем проще учащемуся, теперь уже студенту, будут даваться математический анализ, аналитическая геометрия, дифференциальные уравнения, математическая статистика и другие изучаемые в вузе науки.
Методика Анны Малковой отвечает всем этим требованиям.
к оглавлению ▴
Основные принципы методики Анны Малковой:
— Любую тему школьной математики можно объяснить просто и понятно, сохраняя при этом необходимую математическую строгость изложения. Это особенно важно при изучении таких традиционно трудных для школьников понятий, как понятия алгебраических преобразований, арифметического квадратного корня, модуля числа, степени с действительным показателем, обратной функции и многих других.
— Изучение каждой темы начинается с основных понятий, определений, связи этих понятий с уже пройденными темами, иными словами – с нуля. Любой новый термин, который вводится в курсе, объясняется через уже известные ученику.
— Курс математики изучается как целостная система. При этом репетитор (преподаватель) знает, какое место займет данная тема в общей математической картине учащегося, когда она понадобится в будущем и как связана с темами, которые еще предстоит пройти.
— Каждая тема в авторском курсе Анны Малковой занимает свое определенное место, в соответствии с Авторской программой подготовки к ЕГЭ Анны Малковой. Перестановка тем, пропуск тем или разделов или добавление других тем являются отступлением от методики. Такой порядок тем обусловлен необходимостью построить систему знаний, прежде всего понятную для ученика, где каждый новый «уровень» логически опирается на предыдущие.
— Основа мотивации учащихся – небольшие ежедневные успехи в освоении математики и отсутствие «провалов», то есть непонятных или неподъемных тем. Программа Анны Малковой построена так, чтобы ученик, независимо от предыдущего уровня подготовки, видел результаты занятий с первых же пройденных тем. Тогда его мотивация становится выше, самооценка растет, и за счет этого недавний троечник, занимающийся по методике Анны Малковой, выходит на уровень 80-90 баллов ЕГЭ.
— Один из основных принципов методики Анны Малковой – понимание вместо зубрежки. Большинство математических понятий, которые в школе бессмысленно заучиваются, вводятся на понятном уровне, причем не изолированно, а как элементы системы, связанные и с пройденным ранее материалом, и с тем, который будет в дальнейшем.
— Освоение каждой темы предполагает решение 50-100 практических задач по данной теме. Часть из этих задач разбирается на занятиях, часть задается на дом или изучается самостоятельно по видеоматериалам и Годовому онлайн-курсу Анны Малковой.
— Методика подготовки к ЕГЭ Анны Малковой основана на традициях советской математической школы и прежде всего на системе обучения, принятой в МФТИ, и полностью адаптирована к задаче подготовки к ЕГЭ.
— Методика Анны Малковой рассчитана на учащихся общеобразовательной школы и отличается от обычной школьной программы прежде всего системностью и практичностью, при этом без ущерба для математической культуры и грамотности.
— Для качественного освоения методики Анны Малковой каждая тема сопровождается авторскими методическими материалами:
1) Книга «ЕГЭ по математике. Полный курс подготовки».
2) Полный онлайн-курс подготовки к ЕГЭ по математике (включает 9 мастер-классов по 8 часов + домашние задания).
3) Полный видеокурс для подготовки к ЕГЭ по математике (12 дисков на физических или электронных носителях).
к оглавлению ▴
Программа Полного курса подготовки к ЕГЭ по математике для учащихся групп «М-100».
Программа рассчитана на учащихся 11 класса, которые готовятся к ЕГЭ 1 год, с сентября по май, 4 часа в неделю на занятиях + самостоятельная подготовка. Начальный уровень – около 50-60 баллов. Начальный уровень определяется на входном тестировании. Результат по окончании курса: 80-100 баллов. Программа расписана по занятиям, из расчета: 2 занятия в неделю. Праздничные дни при этом являются учебными, каникулы с 30 декабря по 5 января.
к оглавлению ▴
Сентябрь.
Текстовые задачи на ЕГЭ по математике.
1. Задачи на проценты на ЕГЭ по математике.
2. Текстовые задачи на движение и работу.
3. Задачи на сплавы, смеси, растворы.
4. Задачи на движение протяженных тел, на среднюю скорость и движение по окружности.
5. Алгебраические задачи с физическим содержанием.
6. Теория вероятностей на ЕГЭ по математике.
7. Задачи с экономическим содержанием (подготовительные занятия).
8. Знакомство с нестандартными задачами на ЕГЭ по математике (С6).
Дополнительно: приемы быстрого счета без калькулятора. Приемы решения алгебраических уравнений и систем уравнений. Алгебраические преобразования.
Первый блок Полного курса подготовки к ЕГЭ традиционно посвящен алгебре. Курс начинается с тем «Задачи на проценты» и «Текстовые задачи». Это материал 5-8 класса, который чаще всего к 11 классу оказывается благополучно забытым.
Почему именно эти темы рекомендованы для старта в методике Анны Малковой?
Цели такой компоновки следующие:
— Повторить и улучшить основные математические навыки учащихся.
— Вспомнить (или заново освоить) навыки составления и решение уравнений. Построение математических моделей.
— Освоить навыки быстрого счета и проверки ответа. На ЕГЭ пользоваться калькулятором не разрешается, поэтому выпускнику надо уметь считать быстро без калькулятора.
— Повторить основные темы алгебры: арифметические действия, порядок действий, десятичные и обыкновенные дроби и действия с ними, решение квадратных и дробно-рациональных уравнений.
Темы «Текстовые задачи» и «Задачи на проценты» являются выгодными для репетитора и преподавателя. Их освоение сразу дает быстрые результаты. Здесь не требуется сложного математического аппарата. Достаточно нескольких простых правил, которые школьнику легко запомнить. Таким образом, уже с первых уроков работы по данным темам ученик получает заметный, измеримый результат. Даже если у него «никогда и ничего не получалось» или «ненавидел математику» — первый результат помогает учащемуся поверить в себя и повысить самооценку. При этом также растет авторитет преподавателя – поскольку объяснил то, что раньше было недоступным.
Задачи на сплавы, смеси, растворы – также выигрышная тема для преподавателя или репетитора. Из курса химии у старшеклассника эта тема чаще всего остается непонятной. Несколько простых приемов помогают освоить эту тему.
Задачи на движение протяженных тел, на среднюю скорость и движение по окружности – приятный бонус: решаются за счет знания нескольких «репетиторских секретов», которые трудно найти в учебниках. Такие «секреты» особенно любят и ценят школьники.
Теория вероятностей – тема, отсутствующая в большинстве школьных учебников и совсем недавно появившаяся в программе ЕГЭ по математике. Авторский курс Анны Малковой по теории вероятностей, свободно доступный в Интернете, на сегодняшний день наиболее популярный среди школьников и учителей по данной теме.
Задачи с физическим содержанием – тема, которую учащиеся 11 класса признают страшной. За исключением учащихся физмат школ, старшеклассники боятся «физики», часто не знают основных физических законов и от любых физических формул приходят в ужас. Конечно, включение задач с физическим содержанием в курс математики не может восполнить пробел в знаниях по физике, зато на примере этой темы можно отлично проиллюстрировать понятие функции как зависимости одной физической величины от другой по определенному закону. Часто такие задачи решаются с помощью графиков функций.
И наконец, на первом этапе репетитор (преподаватель) знакомит учащегося с отдельными и специально подобранными сложными задачами из части 2. Это задачи с экономическим содержанием, недавно появившиеся в ЕГЭ по математике, и нестандартные задачи (С6). Следует помнить, что это только первое знакомство, подготовительные занятия, которые тем не менее повышают самооценку ученика и помогают ему получить баллы за эти задачи на первом сентябрьском пробном ЕГЭ по математике.
к оглавлению ▴
Октябрь.
Геометрия и стереометрия на ЕГЭ по математике, часть 1.
1. Планиметрия, основные формулы. Вычисление площадей фигур на клетчатой бумаге. Вывод формулы площади прямоугольника, параллелограмма, треугольника, трапеции.
2. Тригонометрия на ЕГЭ по математике. Определения синуса, косинуса, тангенса угла в прямоугольном треугольнике.
3. Внешний угол треугольника – как найти его синус, косинус и тангенс. Понятие смежных углов. Высота в прямоугольном треугольнике.
4. Определения медианы, биссектрисы, высоты. Простые геометрические построения. Сумма углов треугольника.
5. Краткий курс геометрии. Программа здесь.
6. Векторы на плоскости.
7. Стереометрия. Формулы объема и площади поверхности многогранников и тел вращения.
8. Все задачи по стереометрии из Первой части ЕГЭ по математике.
Планиметрия и тем более стереометрия – темы, по которым даже школьные хорошисты в начале курса подготовки к ЕГЭ показывают практически нулевые знания.
Геометрии и стереометрии в школьной программе по математике уделяется значительно меньше внимания, чем алгебре. Уроки геометрии и стереометрии учителя часто заменяют алгеброй, поскольку отдельного обязательного экзамена по геометрии в школе теперь нет.
Особенно катастрофически сказалось на изучении геометрии и стереометрии в школе то, что из школьной программы исчез такой предмет, как черчение, и только в первом-втором классе сохранилось рисование. При этом школьная программа по геометрии и стереометрии никак не скорректирована и не адаптирована к этим изменениям.
Изучение планиметрии в школьной математике в 7 классе начинается с аксиом и доказательства очевидных для ученика утверждений. Как правило, ученик уже на этом этапе перестает что-либо понимать. В 10 классе, опять с непонятных аксиом, начинается стереометрия.
Школьные учебники по геометрии и стереометрии авторов Погорелова и Атанасяна в целом лучше, чем учебники по алгебре. Однако они не рассчитаны на то мизерное количество часов, которое в школе отводится на изучение этих дисциплин. В них не всегда можно выделить главные, ключевые моменты, и сделать это может только высококвалифицированный учитель.
В авторском курсе Анны Малковой изучение геометрии начинается с темы «площади фигур». Формулы для площадей прямоугольника, параллелограмма, треугольника, трапеции иллюстрируются простыми и наглядными примерами.
К сожалению, большая часть наших старшеклассников не понимает, что такое «длина отрезка» и как посчитать площадь квадрата. Методика Анны Малковой учитывает этот нулевой уровень владения навыками и помогает освоить геометрию начиная с самых основ.
Обязательным для изучения и запоминания является авторский комплект «шпаргалок», своего рода краткий конспект с рисунками, содержащий определения, формулы, основные свойства геометрических фигур.
Весь этот теоретический материал сразу же применяется на практике, при решении задач части 1 ЕГЭ.
На этом этапе вводятся также понятия синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике, основные формулы тригонометрии в прямоугольном треугольнике, формулы для тригонометрических функций смежных углов.
Подбор задач осуществлен строго по уровню сложности, для того чтобы результатом каждого занятия становился рост понимания и уверенности учащегося.
В этом же блоке, после изучения тригонометрии в прямоугольном треугольнике и основ геометрии, дается тема «Векторы на плоскости», традиционно сложная для школьников.
Аналогичным образом в методике Анны Малковой происходит изучение стереометрии.
Изучение стереометрии начинается со знакомства с основными типами многогранников и тел вращения, понятия объема и площади поверхности, формулы для вычисления объемов и площадей поверхности.
На этом этапе используются для наглядности объемные модели многогранников и тел вращения. То, что можно подержать в руках, повернуть и рассмотреть с разных сторон, оказывается для начинающего более понятным и применимым, чем оперирующие отвлеченными понятиями аксиомы.
В блоках «Геометрия, часть 2, задача С4» и «Стереометрия, часть 2, задача С2» эта тема получит дальнейшее развитие. Основное внимание в решении задач по геометрии и стереометрии части 2.
ЕГЭ по математике в методике Анны Малковой уделяется строгим математическим доказательствам и корректному решению и оформлению задач.
к оглавлению ▴
Октябрь — ноябрь.
Алгебра на ЕГЭ по математике, часть 1.
9. Корни и степени.
10. Понятие функции. Исследование графика функции. Понятия возрастания и убывания функции, нулей функции, промежутков знакопостоянства, точек максимума и минимума функции, четности и нечетности функции.
11. Квадратичная функция и квадратичные неравенства.
12. Дробно-рациональная функция и метод интервалов. Решение дробно-рациональных неравенств.
13. Модуль числа. Уравнения и неравенства с модулем.
14. Показательная функция. Показательные уравнения (часть 1 + задачи из классических сборников).
15. Логарифмы. Преобразования логарифмических выражений. Логарифмические уравнения (часть 1 + задачи из классических сборников).
16. Логарифмическая функция. Понятие обратной функции.
17. Задачи с физическим содержанием по пройденным темам.
Этот блок методики Анны Малковой посвящен понятию функции в математике – ключевому в курсе алгебры 10-11 класса.
В школьной программе тема «Функции» дана фрагментарно, начиная с линейной и квадратичной функций в 7 классе, причем семиклассники чаще всего воспринимают эту тему поверхностно, не понимая, зачем она нужна. Далее, при изучении других типов функций, в школе самому определению функции уже не уделяется достаточного внимания, поскольку формально его «прошли» в 7 классе. В итоге абитуриент, закончив общеобразовательную школу и став студентом, обычно не готов к изучению математического анализа и тоже заучивает его формально, чтобы только сдать сессию.
В методике Анны Малковой определение функции считается одним из важнейших во всей школьной программе. Оно дается несколькими способами, раскрывающими различные грани этого понятия. Показано практическое применение того или иного определения, а также их взаимосвязь.
После изучения показательных и логарифмических функций учащийся получает представление о 5 типах элементарных функций, с каждым из которых связаны определенные способы решения уравнений, о сложной и обратной функции, а также о построении (пока без производной) и преобразованиях графиков функций.
Темы этого блока методики Анны Малковой содержат максимальное, по сравнению с другими, количество строгих определений и математических формулировок, без знания которых ученик не может понять последующий материал. Это, например, определения модуля, арифметического квадратного корня, логарифма, точек максимума и минимума функции. К сожалению, большинство учителей и репетиторов либо пропускает эти определения, считая, что школьник «и так их знает», либо дает их в неточной формулировке.
Очевидно, что учитель (преподаватель, репетитор) обязан дать все эти формулировки, не пропуская и не модифицируя их, так же, как учитель русского языка должен передать ученику правила русского языка без собственных добавок и видоизменения.
Это определяет высокие требования к уровню математической культуры учителей и преподавателей, работающих по данной методике.
И закреплением темы являются задачи с физическим содержанием, теперь уже включающие в себя показательные, логарифмические и степенные зависимости одной величины от другой.
к оглавлению ▴
Тригонометрия на ЕГЭ по математике.
18. Определения синуса, косинуса, тангенса для произвольного угла.
19. Тригонометрический круг. Тригонометрические функции.
20. Формулы тригонометрии.
21. Тригонометрические преобразования. Простейшие тригонометрические уравнения.
22. Обратные тригонометрические функции и их графики.
23. Тригонометрические уравнения (часть 2).
Тема «Тригонометрия» базируется на знаниях, полученных в теме «Геометрия и стереометрия на ЕГЭ по математике. Часть 1» и начинается с повторения понятий тригонометрических функций острого угла в прямоугольном треугольнике. Для введения определений тригонометрических функций произвольного угла используется Тригонометрический круг – авторская разработка Анны Малковой. Конечно, тригонометрический круг не изобретен Анной Малковой, он существовал и раньше. Авторскими являются сам рисунок тригонометрического круга, порядок объяснения, иллюстрация с помощью тригонометрического круга основных закономерностей тригонометрии.
Особое внимание уделяется тому, что тригонометрический круг изображен в привычной школьнику декартовой системе координат, а также пониманию того, что уже известные тригонометрические функции острого угла в прямоугольном треугольнике являются частным случаем тригонометрии для произвольного угла. С помощью тригонометрического круга объясняются понятия и правила, которые в школьной программе ученику часто приходится бессмысленно зубрить (или писать по ним шпаргалки). Эта удобная иллюстрация заменяет десяток таблиц.
Один из основных принципов методики Анны Малковой – минимум зубрежки, максимум понимания. В методике Анны Малковой такие понятия, как четность и нечетность тригонометрических функций, их периодичность, знаки тригонометрических функций в координатных четвертях не заучиваются бессмысленно, а объясняются с помощью тригонометрического круга.
По сравнению с другими методиками и особенно по сравнению с распространенными в интернете шпаргалками, в методике Анны Малковой дается минимальное количество (порядка 25 штук) формул тригонометрии, причем формулы разделены по смысловым блокам. Для тренировки в применении этих формул, кроме типичных заданий ЕГЭ на вычисление или преобразование тригонометрических выражений, даются также задачи из классических сборников – Сканави и других.
Особая тема – решение простейших тригонометрических уравнений и обратные тригонометрические функции. Здесь также применяется принцип методики Анны Малковой — минимум зубрежки, максимум понимания. В частности, формулы для решения простейших тригонометрических уравнений не заучиваются, как заклинания, а выводятся из простых соображений и определений. Тема «Обратные тригонометрические функции» является логическим продолжением темы «Обратная функция», пройденной в блоке 3 (Алгебра).
Завершение темы – решение тригонометрических уравнений. Здесь рекомендуется не ограничиваться только задачами ЕГЭ по тригонометрии и использовать также классические сборники для поступающих в вузы. Количество способов решения тригонометрических уравнений здесь больше, чем в программе общеобразовательной школы: кроме способов замены переменной, разложения на множители, сведения к квадратному уравнению и частных случаев введения дополнительного угла, дается также метод решения однородных уравнений, метод введения дополнительного угла в общем виде, метод оценки, универсальная тригонометрическая замена и другие методы. Все эти методы пригодятся учащемуся позже, при решении задач с параметрами (С5).
В последние годы в сборниках вариантов ЕГЭ по математике появились комбинированные задачи по тригонометрии, включающие в себя и показательные, и логарифмические, и тригонометрические компоненты. Это дает возможность повторить пройденные ранее темы «Показательные и логарифмические уравнения».
к оглавлению ▴
Декабрь.
Производная функции. Геометрический смысл производной.
24. Производная функции. Исследование функции с помощью производной.
25. Первообразная функции.
Тема «Производная функции» закономерно изучается после того, как учащемуся уже знакомы тригонометрические функции. Точнее, к этому моменту учащийся уже знаком со всеми пятью типами элементарных функций: степенными, показательными, логарифмическими, тригонометрическими и обратными тригонометрическими, знает особенности их графиков, а также знаком с основными характеристиками поведения функции, такими, как возрастание и убывание функции, точка минимума и точка максимума, наибольшее и наименьшее значение функции на отрезке. Также к этому моменту ученик владеет методом интервалов и знает, как находить промежутки закон постоянства дробно-рациональной функции.
В общеобразовательной школе понятие производной обычно вводится как «предел отношения приращения функции к приращению аргумента при приращении аргумента, стремящемся к нулю». Естественно, обычный старшеклассник (а иногда и учитель) всего этого заклинания запомнить не может, смутно представляет себе, что такое приращение, вообще не понимает, что такое предел, а в итоге как-то укладывает в свою голову, что «производная – это штрих» и худо-бедно зазубривает таблицу производных.
В методике Анны Малковой понятие производной функции дается на основе геометрического смысла производной – как скорость изменения функции и как тангенс угла наклона, или угловой коэффициент касательной. Здесь также действует принцип «Понимание вместо зубрежки». Понятие предела функции при этом не вводится, поскольку эта непростая тема требует более высокого, чем у среднего старшеклассника, уровня математической подготовки.
Особое внимание уделяется связи поведения функции с поведением производной. Часто ученик не понимает, что это два разных объекта, и на этом построено множество задач-ловушек в вариантах ЕГЭ. Исследование поведения функции на отрезке, нахождение наибольших и наименьших значений функции – здесь везде есть свои нюансы, которые преподавателю, работающему по методике Анны Малковой, необходимо соблюдать в точности.
к оглавлению ▴
Стереометрия на ЕГЭ по математике.
26. Программа по стереометрии.
27. Классический метод решения задач по стереометрии.
28. Векторы в пространстве. Векторно-координатный метод.
Задача С2 (стереометрия) традиционно считается одной из самых сложных для учащихся 11 класса, и многие школьники за нее даже не берутся.
В методике Анны Малковой тема «Стереометрия, часть 2» начинается с подготовительной работы – изучения авторского краткого курса стереометрии, то есть основных определений, аксиом, теорем. Все разделы этого курса сопровождаются авторскими иллюстрациями, которые выдаются учащимся также в виде таблиц. Для наглядности дополнительно используются объемные модели многогранников и тел вращения.
Следующая подготовительная тема – методы построения сечений объемных тел и развитие пространственного мышления учащихся. При этом важно не просто нарисовать сечение, а описать его построение и положение вершин сечения относительно исходного объемного тела.
Для решения задач С2 в методике Анны Малковой даются два способа – классический и векторно-координатный.
В классическом способе особое внимание уделяется грамотному и математически корректному оформлению решения, строгому доказательству каждого утверждения, построению дополнительных чертежей и пошаговому сведению объемной, стереометрической задачи – к планиметрической.
Векторно-координатный способ дается в объеме школьной программы, без использования вузовских приемов аналитической геометрии, причем особое значение также имеет грамотное и математически корректное оформлению решения.
Учащиеся получают рекомендации по применению каждого из методов в тех или иных задачах.
к оглавлению ▴
Январь.
Неравенства на ЕГЭ по математике.
29. Неравенства на ЕГЭ по математике.
30. Показательные и логарифмические неравенства. (часть 2 ЕГЭ по математике).
31. Метод рационализации (замены множителя). Метод оценки.
Тема «Неравенства» (задача С3 на ЕГЭ по математике) отличается обманчивой легкостью и рекордным количеством ошибок среди абитуриентов, причем они даже не подозревают, где именно их делают. Именно здесь возникает больше всего ситуаций типа «Я все сделал правильно и получил 0 баллов».
Именно здесь проходит граница между «неплохо сдал ЕГЭ» и «поступил в престижный вуз». Задача С3 многим открывает дорогу в вузы с профильной математикой и может считаться критерием профессионализма репетитора или учителя.
Без С3 становится недоступной и более сложная С5 (задача с параметрами).
В методике Анны Малковой даются приемы решения неравенств различных типов: иррациональных неравенств, неравенств с модулем, логарифмических и показательных неравенств. Показывается правильное оформление решений, что особенно важно для тех, кто сдает ЕГЭ и ДВИ на высокие баллы.
Особое внимание уделяется разбору типичных ошибок и отработке навыков правильного решения и оформления.
к оглавлению ▴
Февраль.
Геометрия на ЕГЭ по математике. Задача С4.
32. Что такое математическое доказательство. Задачи на доказательство.
33. Задачи части 2 ЕГЭ, Геометрия.
К решению задачи С4 (Геометрия, часть 2) учащиеся, занимающиеся по методике Анны Малковой, уже подготовлены. Ведь уже пройдены темы «Геометрия на ЕГЭ по математике, часть 1» и «Стереометрия на ЕГЭ по математике».
Перед тем, как перейти непосредственно к экзаменационным задачам, необходим подготовительный период – решение задач на доказательство. Для этого разработан специальный материал «Доказательство полезных фактов», где задачи на доказательство расположены по возрастанию сложности. Каждая из таких задач является схемой для решения реальных экзаменационных. Особое внимание уделяется методам доказательства и решения, таким, как удвоение медианы, перестроение чертежа, задаче о трех точках, лежащих на одной прямой, применению равенства и подобия треугольниках в задачах.
Геометрия многим учащимся представляется сложнее алгебры, потому что здесь нет готовых алгоритмов решения (как в теме 1 – текстовых задачах). Зато намного большее значение имеет система ассоциаций и умение комбинировать различные приемы решения.
к оглавлению ▴
Задачи с экономическим содержанием на ЕГЭ по математике.
34. Задачи с экономическим содержанием на ЕГЭ по математике.
35. Арифметическая и геометрическая прогрессии.
36. Формулы для решения задач с экономическим содержанием.
Задачи с экономическим содержанием появились в ЕГЭ по математике совсем недавно, и даже многие учителя не знают, как к ним подойти.
Однако задачи такого типа считаются традиционными на олимпиадах по экономике, а также на 1 курсе экономического факультета МГУ и других вузов. Методика Анны Малковой дает способы решения таких задач, а также готовые формулы и приемы. Методические материалы по этой теме, как и по другим, постоянно дорабатываются, чтобы находиться в соответствии с последними тенденциями ЕГЭ по математике.
к оглавлению ▴
Март.
Задачи с параметрами на ЕГЭ по математике.
37. Элементарные функции и их графики.
38. Преобразования графиков функций.
39. Множества точек на плоскости. «Базовые» схемы решения. Окружность, круг, полуокружность, ромбик, сумма модулей, полуплоскость, полоса, отрезок.
40. Тренировочные задачи с параметрами.
41. Квадратичные уравнения и неравенства с параметрами.
42. Графический метод решения задач с параметрами.
43. Метод симметрии, параметр как переменная и другие методы.
Методика Анны Малковой позволяет за короткие сроки научить абитуриентов решать такую традиционно сложную задачу, как С5 (задача с параметрами). Эта задача – из тех, о которых не пишут в школьных учебниках.
Необходимая подготовительная работа в изучении данной темы – это типы элементарных функций и их графики (5 типов), преобразования графиков функций (сдвиги, растяжения-сжатия, инверсии по горизонтали и вертикали), построение графиков сложных функций. Весь этот материал в программе средней школы дается фрагментарно и факультативно, или же не дается совсем.
От привычных функций одной переменной и их графиков происходит плавный переход к неявным функциям, задающих множества точек на плоскости. Учащийся знакомится с такими базовыми схемами решения задач с параметрами, как окружность, круг, полуокружность, ромбик, сумма модулей, полуплоскость, полоса, отрезок, и с уравнениями, задающими эти объекты на плоскости.
Методика Анны Малковой включает около 15 различных методов решения задач с параметрами, и все они изучаются в течение курса. Это и метод оценки, и критерии единственности решения квадратного уравнения, и метод симметрии, и многие другие.
к оглавлению ▴
Апрель.
Нестандартные задачи на ЕГЭ по математике (С6).
44. Делимость. Признаки делимости. Деление с остатком.
45. Метод «Оценка плюс пример».
46. Реальные нестандартные задачи на ЕГЭ по математике.
Задача С6, последняя в вариантах ЕГЭ по математике, считается самой необычной. В учебниках для 10-11 класса нет даже намеков на существование таких задач.
Долгое время и школьники, и учителя просто боялись таких задач и не приступали к ним. О методах их решения не говорилось ничего, кроме «как-нибудь попробуйте догадаться сами». При этом методы решения задачи С6 существуют и успешно могут быть освоены, о чем свидетельствуют высокие результаты учеников Анны Малковой и других преподавателей, занимающихся этими задачами. Теоретической основной решения задачи С6 являются признаки делимости, приемы записи для деления с остатком, знание об арифметической и геометрической прогрессиях, в том числе целочисленных, основная теорема алгебры (о каноническом разложении натурального числа на множители).
Среди методов одним из основных является «Оценка плюс пример». Сложность С6 еще и в том, что эта задача подразумевает умение выражать свои мысли точным математическим языком, требует определенной математической культуры. Методика Анны Малковой дает ученику возможность решить С6 и понять, что это не задача для избранных, а реальный источник баллов на ЕГЭ.
к оглавлению ▴
Май.
Повторение всех тем и решение вариантов ЕГЭ.
Методика Анны Малковой отличается от многих других еще и тем, что решение вариантов ЕГЭ происходит на заключительном этапе, как итоговая тренировка. На первых этапах подготовки, пока большая часть тем еще не освоена, решение вариантов ЕГЭ может привести лишь к разочарованию учащихся в своих способностях. Это часто и бывает, когда ученик начинает занятия самостоятельно «по интернету» или занимается с неопытным репетитором.
Пробные ЕГЭ для учащихся, занимающихся по методике Анны Малковой, проводятся 1 раз в месяц, причем задачи, не пройденные к данному моменту, не обязательны для решения. На заключительном этапе подготовки обязательны все задачи.
Заключительная часть подготовки к ЕГЭ по методике Анны Малковой нацелена на тренировку решения варианта ЕГЭ без ошибок и в точно отведенное время. Не следует приступать к решению нескольких задач одновременно, так как результат при этом чаще всего нулевой.
к оглавлению ▴
Рекомендуемый хронометраж для учащихся, претендующих на 90-100 баллов ЕГЭ:
1. 20-25 минут – решение, проверка и запись ответов задач части 1 (1-12).
2. 50-60 минут – решение и оформление на чистовике задач 13-15 (С1, С2 и С3).
3. Теперь, когда обязательная программа выполнена, рекомендуется из задач №16-19 выбрать наиболее простую и знакомую, решить ее, проверить и полностью оформить. После этого переходить к решению следующей из оставшихся по тому же принципу.
к оглавлению ▴
Дополнения к Авторской методике Анны Малковой:
1. Программа синхронизирована с Годовым курсом подготовки к ЕГЭ по математике.
2. Каждая тема завершается контрольной работой или зачетом.
3. Материалы и ресурсы для подготовки:
1) Мастер-классы Анны Малковой;
2) Видеокурсы Анны Малковой;
3) Материалы для подготовки бесплатно;
5) Полезные сайты:
www.ege-study.ru — сайт Образовательной компании «ЕГЭ-Студия». В разделе «Материалы ЕГЭ» — полный курс математики. Просто, понятно, без «воды». Вся теория и разбором задач ЕГЭ по математике.
www.reshuege.ru — дистанционная обучающая система для подготовки к ЕГЭ по математике «РЕШУ ЕГЭ». Автор — Дмитрий Гущин. Тысячи заданий ЕГЭ с решениями и ответами.
www.alexlarin.net — сайт Александра Ларина, на котором постоянно публикуются варианты пробных и реальных ЕГЭ. Тренировочные варианты ЕГЭ с разбором на форуме.
к оглавлению ▴
Приложение к методике: Обучающие комплекты видеокурсов Анны Малковой «Получи пятерку» и «Премиум».
Видеокурсы «Получи пятерку» и «Премиум» являются авторскими методическими разработками Анны Малковой. Задача автора видеокурсов — объяснить каждую тему так, чтобы ученик понял, запомнил и смог применять на практике полученные знания.
1. Ученик, который смотрит видеокурс, не может задать автору вопрос, как на уроке. Это означает, что видеокурс должен быть для него максимально понятным. Для этого применены следующие принципы:
1) Чтобы максимально приблизиться к атмосфере урока (или занятия с репетитором), Анна Малкова пользуется обычной белой маркерной доской. Принцип «Учитель в кадре» считается предпочтительным.
2) При этом условия задач, как правило, выводятся на экран на специальных текстовых «плашках».
3) Монтаж видео позволяет оставить «за кадром» моменты написания на доске объемных математических преобразований или наоборот, стирания решенной задачи с доски. Это придает видеокурсу необходимую динамичность.
4) В видеокурсах Анны Малковой используются также средства компьютерной графики и анимации. Например, в ряде видеокурсов появляются забавные мультипликационные персонажи.
2. Есть также ряд чисто методических принципов, по которым построены видеокурсы. Вот некоторые из них:
1) Каждая задача в видеокурсе подобрана так, чтобы лучше всего проиллюстрировать определенную тему, или теорему, или математический прием.
2) Принцип «Одна сложность – в одну единицу времени». Например, при объяснении новой и сложной темы дается задача с максимально простыми вычислениями, чтобы внимание ученика было сконцентрировано именно на новой теме.
3) Еще один принцип. Вводя новое понятие или новый термин, обязательно объясняется, что он значит. Иначе непонятное слово оказывается барьером в восприятии.
4) Для того чтобы усвоить новую тему, необходимо повторение, причем не однократно, а несколько раз.
5) Комплект видеокурсов Анны Малковой построен по определенному принципу – каждая тема является фундаментом для следующей. При этом постоянно отмечаются взаимосвязи между различными разделами математики.
6) Особое внимание уделяется вычислительным приемам. Поскольку на ЕГЭ недопустимо пользоваться калькулятором, в первом же видеокурсе дается ряд приемов быстрого счета без калькулятора. Этими приемами Анна Малкова пользуется в каждом видеокурсе, специально акцентируя на них внимание.
7) Одной из основных проблем старшеклассников является неумение оформить решение задачи части С (части 2) так, как это необходимо для получения высокого балла на ЕГЭ по математике. В видеокурсах даются не только методы решения задач, но и полное, как на экзамене, математически грамотное оформление решения.
Для подготовки видеокурсов использованы как задачи ЕГЭ прошлых лет, так и множеством «классических» задач из сборников для поступающих в вузы. Результатом является полный спектр приемов и «инструментов» для успешного решения любой задачи ЕГЭ по математике.
Внимание! Методика подготовки к ЕГЭ Анны Георгиевны Малковой защищена законом об авторских правах. Все материалы, находящиеся в данном файле, не подлежат воспроизведению в какой-либо форме или каким-либо образом без предварительного письменного разрешения ООО «ЕГЭ-Студия» и Анны Георгиевны Малковой. © 2017.
к оглавлению ▴
Авторское право.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Методика подготовки к ЕГЭ по математике. Автор: Анна Георгиевна Малкова.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.03.2023
Основные
аспекты методики подготовки школьников к ЕГЭ
по математике в средней школе»
Содержание:
Введение…………………………………………………………………………….3
Глава 1.
«Психолого-педагогические проблемы при подготовке к ЕГЭ»
1.1 Причины волнения и трудности при
сдаче ЕГ по математике…………..…5
1.2 Психологическое сопровождение
ЕГЭ……………………….……….….….6
Глава 2. «Методические
особенности при подготовке к ЕГЭ по математике»
2.1Особенности процесса подготовки ЕГЭ………………..………………..……8
2.2Формы подготовки к ЕГЭ и их
характеристика ….…….……………..…..….9
2.3Этапы разработки программы подготовки
к ЕГЭ по математике………….10
Глава 3. «Методика работы с
задачным материалом при подготовке школьников к ЕГЭ по математике»
3.1 Организация повторения курса
математики………………..…..……………12
3.2 Группы задач для подготовки к ЕГЭ
………………….…………………..…15
·
Задачи типа №7……………………………………………..……………..…15
·
Задачи типа №11…………………………………………………………..….16
·
Задачи типа №13………………………………………………….….………17
Заключение…………………………………………………………….……….…17
Библиографический список…………………………………………….….…….18
Приложение №1. Задачи для устного счета к заданию №1
…………….………20
Приложение №2. Задачи для повторения при изучении стереометрии
………21
Приложение №3. Задачи по теме «Геометрический смысл
производной»..…24
Приложение №4 . Решение неравенств методом
интервалов……….………….26
Приложение №5. Задания по теме «Модуль числа»…………………….…..….30
Приложение №6. Задания типа №7…………………………………………..….32
Приложение №7. Группа задач типа №11……………………………………….36
Приложение №8. Группа задач типа №12……………………………………….39
Приложение №9. Задачи на отработку способов отбора
корней…………..….41
Приложение №10. Задачи типа №13…………….……………………………….45
Приложение №11. Факультативный курс по математике «Решение
уравнений с модулем»………………………………………………………..….47
Введение.
|
Единый Государственный Экзамен по математике направлен на ЕГЭ по математике является, с одной стороны, одним из двух Руководитель
Несмотря · · Низкие результаты на ЕГЭ по математике волнуют и учеников, · · Школьные учителя видят несколько причин в скромных |
||||||||||||||||||||
|
За время моей работы по подготовке обучающихся к ЕГЭ я Для достижения поставленной цели необходимо решить следующие ü ü ü ü |
Глава1.
ПСИХОЛОГО-ПЕДАГОГИЧЕСКИЕ ПРОБЛЕМЫ ПРИ ПОДГОТОВКЕ К ЕГЭ.
1.1. Причины
волнения и трудности при сдаче ЕГЭ по математике.
Проблемы
подготовки к ЕГЭ – это поле деятельности не только педагогов, но и психологов.
В настоящее время проблема методического сопровождения предметной подготовки к
ЕГЭ в целом достаточно освещена.
Подготовка к единому
государственному экзамену является одной из основных проблем выпускников. По
своей сути ЕГЭ является своеобразной проверкой знаний, социальной и
психологической готовности школьников к постоянно меняющимся условиям
современной реальности. В этой связи, психологическая устойчивость
старшеклассников является одной из основных характеристик, способствующих
успешной аттестации в форме ЕГЭ.
Подготовка
к ЕГЭ, как правило, должна проходить на протяжении 4-5 последних лет обучения.
Учителя стараются подготовить школьников с помощью дополнительных занятий.
Кроме того, старшеклассники посещают курсы, знакомятся с различными пособиями
для подготовки к ЕГЭ, некоторые занимаются с репетиторами. Но степень тревожности,
напряжения у выпускников не снижается. В свою очередь, повышенный уровень
тревоги учащихся на экзамене приводит к дезорганизации деятельности, снижению
концентрации внимания, работоспособности. Совершенно очевидно, что перед
психологами, педагогами и родителями встает проблема охраны психического
здоровья школьников, для решения которой необходима продуманная система
мероприятий, предусматривающая создание стабильной благоприятной атмосферы,
уменьшение вероятности возникновения стрессовых ситуаций и повышение
функциональных возможностей школьников.
По
результатам тестирования наших выпускников, наиболее значимыми причинами
волнения выпускников являются:
ü сомнение
в полноте и прочности знаний;
ü сомнение
в собственных способностях: умении анализировать, концентрировать и
распределять внимание;
ü психофизические
и личностные особенности: быстрая утомляемость, тревожность, неуверенность в
себе;
ü стресс
незнакомой ситуации;
ü стресс
ответственности перед родителями и школой.
Таким
образом, условно можно выделить три группы трудностей ЕГЭ для детей:
·
познавательные – связанные с особенностями
переработки информации в ходе ЕГЭ, недостаточным объемом знаний, неспособностью
гибко оперировать системой учебных понятий предмета (эти трудности являются
результатом всего периода обучения в школе!);
·
личностные – обусловленные особенностями восприятия
учеником ситуации экзамена, его субъективными реакциями и состояниями,
отсутствием возможности получить поддержку взрослых;
·
процессуальные – связанные с самой
процедурой единого государственного экзамена и отсутствием четкой стратегии
деятельности.
1.2. Психологическое
сопровождение ЕГЭ.
Для
целенаправленной подготовки к ЕГЭ необходимо создание благоприятных
психологических, организационных и методических условий подготовки к ЕГЭ еще
задолго до того, как ученик начнет целенаправленно готовиться к итоговой
аттестации.
По опыту моей работы предметную подготовку
к сдаче ЕГЭ по математике целесообразно осуществлять задолго до 11 класса для
выработки соответствующей базы знаний, умений и практического опыта. Начиная с
5-6 класса я нацеливаю ребят на ЕГЭ. Темам уроков, которые входят в кодификатор
ЕГЭ, я уделяю особое внимание. Одно и тоже задание стараюсь сформулировать
по-разному, решить одну и ту же задачу несколькими способами. Это позволяет
психологически настроить ребят на то, что в КИМах ЕГЭ можно встретить
формулировку задания отличную от учебника. Заблаговременная работа также дает
возможность перераспределить дополнительную нагрузку, не связанную с подготовкой
к ЕГЭ.
Одним из существенных аспектов психолого-педагогического
сопровождения выпускника, на мой взгляд, является ознакомление родителей со
способами правильного общения с ним, оказания ему психологической поддержки,
создания в семье благоприятного психологического климата.
Работа с родителями нацелена на повышение осведомленности
родителей и формирование реалистичной картины экзамена, снижение родительской
тревоги.
В начале
учебного года, я посещаю первое родительское собрание. На этих собраниях:
· знакомлю родителей с планом работы по математике на
предстоящий учебный год;
· разъясняю позицию Министерства РФ по проблеме ЕГЭ,
· характеризую структуру контрольно измерительных
материалов (КИМов) по математике;
· рассказываю о формах заданий и поясняю подходы к
оценке результатов выполнения заданий разной формы;
· анализируя содержание проверяемых на экзамене разделов
и тем школьного курса математики, обращаю внимание родителей какими знаниями,
умениями и навыками должен обладать каждый ученик;
· знакомлю родителей с формами подготовки к ЕГЭ.
Психологическая
подготовка к экзаменам способствует повышению уровня информированности,
психологической готовности учащихся, родителей, педагогов в режиме подготовки и
проведения ЕГЭ, если это – большая, длительная работа не только психолога с
детьми, но и всего педагогического коллектива и родителей.
Глава2. МЕТОДИЧЕСКИЕ
ОСОБЕННОСТИ
ПРИ ПОДГОТОВКЕ
К ЕГЭ ПО МАТЕМАТИКЕ.
Математика является не
только очень важным учебным предметом общеобразовательной школы, но и весьма
сложным, так как математическими способностями обладают не многие школьники, а
обучать математической грамоте необходимо всех и единый экзамен по математике
сдают все. Кроме того, значительная часть обучающихся 10-11 классов после
окончания школы хотят поступить в ВУЗы, в которых предъявляются достаточно
высокие требования к математической подготовке абитуриентов и студентов.
В соответствии с
вышесказанным можно выделить главную цель, к которой должен стремиться учитель:
наряду с формированием новых знаний, умений и навыков включать ранее
сформированные знания в деятельность ученика с целью повторения и
систематизации знаний для подготовки к единому государственному экзамену.
Исходя из ведущей цели я
определила следующие, важные, на мой взгляд, задачи:
ü систематизировать
знания и умения за курс средней школы;
ü вооружить
учащихся определенным кругом знаний, необходимых для поступления и обучения в
ВУЗах;
ü систематизировать
приемы решения различных уравнений и неравенств, систем уравнений;
ü научить
выделять главное при решении задач, учить мыслить.
ü развивать
творческие возможности ученика, привить умение самостоятельно пополнять знания;
ü
развивать следующие качества: целеустремленность,
самостоятельность, аккуратность, честность, трудолюбие, умение доводить начатое
дело до конца, развивать и поддерживать устойчивый интерес к математике.
2.1
Особенности процесса подготовки ЕГЭ.
Подготовка к ЕГЭ — ответственное мероприятие, к которому нужно
отнестись со всей серьезностью, ведь на карту поставлено многое. В случае
неудовлетворительных результатов ЕГЭ сразу по двум обязательным предметам
(русский язык, математика) учащийся не допускается к пересдаче в резервные дни
и может получить лишь справку об обучении в школе.
Следует отметить, что в решении проблем с подготовкой к
экзаменам не стоит уповать на школьного учителя, поскольку он вынужден
одновременно заниматься с целым классом. Учебный материал имеет свои
особенности, ученики усваивают его с разными скоростями и, не поняв чего-то
сразу, часто не выясняют этого позже. В результате образуются «пробелы» в
знаниях, не формируются необходимые умения и навыки по применению знаний и сдача
будущих экзаменов может оказаться под угрозой.
На мой взгляд, залогом успеха на экзамене является именно
комплексный подход к подготовке, в котором в качестве составляющих можно
выделить три важных момента:
1) Организационный.
Как
правило, подготовка к ЕГЭ занимает у учащихся достаточно много времени и
требует, кроме умственных усилий еще и решение организационных вопросов (подача
заявлений на сдачу экзаменов по выбору, подбор литературы для подготовки к ЕГЭ,
поиск репетиторов и т.д.) Для этого целесообразно составить план подготовки, в
котором нужно отразить ее основные этапы и сроки их реализации.
2) Образовательный.
Безусловно,
самое главное в процессе подготовки к экзаменам — получить необходимые знания,
умения и навыки по предмету. Школьная учебная литература достаточно полно
раскрывает тематику предмета, но также нужно использовать и дополнительную
литературу, отражающую специфику предстоящего экзамена. К ней относятся
контрольно-измерительные материалы (КИМ-ы), методические разработки, учебные
пособия, электронные учебные курсы, множество сайтов для подготовки к ЕГЭ,
курсы довузовской подготовки и многое другое.
3) Психологический.
ЕГЭ
отличается непривычным для учащихся форматом проведения. Продолжительность
экзамена — четыре часа, все бланки экзаменационных документов должны
заполняться специальным образом, существуют определенные правила поведения на
экзамене, при невыполнении которых организаторы могут удалить участника с
экзамена. Всё это, в совокупности с большим значением результатов экзамена для
выпускника, может обусловливать излишнее волнение на экзамене и, как следствие,
потерю сосредоточенности, ослабление уверенности в своих силах из-за страха
совершить ошибку. Поэтому при подготовке к ЕГЭ очень важно уделять внимание изучению
процедуры проведения экзамена, правил заполнения бланков и периодически
практиковаться на экзаменационных материалах прошлых лет в условиях,
приближенных к реальному экзамену.
2.2.
Формы подготовки к ЕГЭ и их характеристика.
Своим ученикам я предлагаю следующие формы подготовки к
экзаменам:
1) Самоподготовка.
Учащийся
самостоятельно принимает все решения относительно количества занятий, их
частоты и объема изучаемого материала. Данный способ имеет самый высокий риск
недостижения экзаменационной цели. Действительно, большинство учащихся 11-х
классов сами не смогут правильно выстроить систему подготовки к экзаменам.
Кроме этого, процесс самостоятельного устранения «пробелов» в знаниях или
усвоения нового материала стоит больших моральных и умственных усилий.
Электронные обучающие системы и видеокурсы подготовки к ЕГЭ, методические
пособия, онлайн-тесты, тематические группы в социальных сетях частично
облегчают труд учащегося при самоподготовке.
2) Занятия
на подготовительных курсах.
Такие курсы могут организовываться ВУЗами,
школами и негосударственными образовательными учреждениями.
В учебном плане 10-11 классов нашей школы имеется
1 дополнительный час в неделю учебных элективных занятий в рамках подготовки к
ЕГЭ по математике. Кроме того, создан график дополнительных консультативных
занятий по математике. Причем, дети подразделяются на группы по уровню знаний
(базовый и профильный). Посещаемость учащимися этих занятий контролирует
классный руководитель и преподаватель. Выясняются причины отсутствия ученика на
занятии, сведения доводятся до родителей. Таким образом происходит сотрудничество
классного руководителя – учителя-предметника – родителя.
Некоторые наши ученики посещают курсы организованные ВУЗами,
в который они планируют поступить. В нашем городе один раз в месяц работает
«Школа абитуриента». Занятия в этой школе проводят учителя-математики из разных
школ города. Мои ученики, по мере возможности, посещают данные занятия.
Серьезным недостатком занятий на подготовительных курсах
является невозможность для ученика получить от преподавателя индивидуальный
подход, чтобы ликвидировать собственные «пробелы» в знаниях. Кроме этого, если
говорить о вузовских курсах, то преподаватели высшей школы зачастую переносят
специфику преподавания в ВУЗах на учащихся школ. Это усложняет процесс усвоения
учащимися необходимой информации, что в совокупности с недостаточным контролем
в процессе обучения может приводить к невысоким результатам ЕГЭ.
3) Занятия
с репетитором.
Подготовка к
единому государственному экзамену требует индивидуального, личностно-ориентированного
подхода.
Для
реализации такого подхода идеально подходят занятия с репетитором, которые могут
проводиться в двух режимах: индивидуальные занятия и в мини-группах. К
сожалению, очень мало моих учеников могут позволить данные занятия, так как
материальный уровень большинства семей наших выпускников ниже среднего и
низкий.
2.3 Этапы разработки программы подготовки к ЕГЭ по
математике.
В
начале учебного года мы с ребятами разрабатываем программу подготовки к ЕГЭ по
математике. Каждый ученик определяет свои возможности и способности для себя,
так как они у всех ребят разные. Охарактеризую основные этапы разработки
программы подготовки к ЕГЭ с учетом особенностей аспектов: организационного,
образовательного и психологического.
1этап.
Определить цели подготовки.
При
составлении программы я объясняю ребятам, чтобы они не ставили перед собой
цель, например, «научиться решать такие-то задачи» или «выучить такие-то темы»,
а сформулировали их в виде желаемого результата экзамена. Например, сдать ЕГЭ
«не меньше чем на 70 баллов», «хотя бы на 60 баллов» и пр. Данный подход
позволяет сразу сориентироваться на круг рассматриваемых вопросов по математике
и представить себе за счет каких типов заданий будут набираться желаемые баллы.
2этап.
Собрать максимум информации о предстоящем экзамене.
В
кабинете математики оформляется тематический стенд «Готовимся к ЕГЭ», на
котором имеется вся необходимая информация о структуре, порядке и сроках проведения,
важные особенности и методика оценивания ЕГЭ по математике. Ежегодно в каждом
выпускном классе проходят классные собрания, на которых рассматриваются вопросы
сдачи ЕГЭ. На дополнительных занятиях мы с ребятами разбираем кодификатор ЕГЭ
с целью выявления пробелов в знаниях. По результатам изучения собранной
информации учащийся должен ясно представлять себе как проходит экзамен, какие
виды заданий используются, каковы критерии оценивания результатов экзамена. Сюда
же относится и подбор методической литературы — это могут быть
разнообразные учебные пособия, подборки контрольно-измерительных материалов
экзаменов прошлых лет и пр. Много подобной литературы для ознакомительных целей
представлена в Интернете и доступна для свободного скачивания. Большой подбор
методической литературы имеется в кабинете математики школы.
3этап.
Приступить к выбору формы подготовки.
После того как ученики определились с целью и подробно узнали о
предстоящем экзамене, я, как учитель, предлагаю своим ученикам формы подготовки
к ЕГЭ по математике: самоподготовка, занятия на подготовительных курсах и
занятия с репетитором.
Наиболее распространенной формой у наших ребят являются занятия
на подготовительных курсах, организованных в нашей школе. Так как занятия с
репетитором и на курсах довузовской подготовки требуют финансовых затрат, наши
выпускники пользуются этой услугой крайне редко.
4
этап. Определить сколько времени имеет учащийся на подготовку к экзаменам.
Вся
первая половина дня у учеников проходит в школе, а после нее многие посещают
еще и различные спортивные секции, музыкальные школы и прочие подобные
заведения. Кроме того, нужно еще выполнять домашнее задание и уделять время
полноценному отдыху. Таким образом, при ближайшем рассмотрении получается, что
времени на подготовку не так уж и много, как может показаться на первый взгляд.
Тем не менее, слишком частые занятия тоже не приведут к цели, так как очень
быстро может наступить эмоциональная и умственная «перегрузка» ученика. Для
того, чтобы этого не произошло я своим ученикам задаю дифференцированные
домашние задания, организую дополнительные задания для более сильных учеников.
5
этап. Контролировать ход процесса подготовки к экзаменам.
Здесь
на первый план выходит не контроль за прохождением занятий, а контроль
продвижения вперед, освоения предмета. В течение учебного года выпускного
класса ребята очень много пишут различных диагностических работ МИОО
«СтатГргад» и пробных ЕГЭ по математике, проводимых Департаментом образования
ТМР. Я, как учитель математики, провожу мониторинг: веду карту выполнения работ
на каждого ученика и класса в целом. Это позволяет увидеть системные ошибки,
пробелы в знаниях конкретных учеников и скорректировать мою работу, как
учителя-предметника.
Глава3. МЕТОДИКА РАБОТЫ С ЗАДАЧНЫМ
МАТЕРИАЛОМ ПРИ ПОДГОТОВКЕ ШКОЛЬНИКОВ К ЕГЭ ПО МАТЕМАТИКЕ.
В структуре ЕГЭ содержится указание на то, как можно выстроить
подготовку: существующий кодификатор позволяет разбить материал на несколько
крупных тематических блоков. Повторение можно выстроить по содержательным: вычисления,
буквенные выражения, уравнения, неравенства; и функциональным линиям: все
функции и элементы математического анализа. Такой подход будет способствовать
формированию более прочных знаний и, как следствие, более уверенному поведению
выпускника на экзамене.
Неотъемлемым элементом подготовки к ЕГЭ является обучение
заполнению бланков. Эту работу я, как учитель-предметник, веду с 10 класса.
3.1.Организация
повторения курса математики.
Единый государственный экзамен по математике, привнесенный в российское образовательное пространство, имеет свои сильные и слабые стороны. Чтобы минусы обратить в плюсы,
учителю, который готовит школьников к экзамену, в первую очередь необходимо
знание о формате и структуре ЕГЭ, особенностях
процедуры его проведения. Эта информация важна в первую очередь для
учителя, который учит школьников и готовит их к экзамену. ЕГЭ помогает решать
такую важную задачу, стоящую перед учителем, как освоение технологий обучения и
организации итогового повторения, позволяющих выпускникам демонстрировать
уровень своих знаний не ниже своей годовой отметки.
Возможностей для организации эффективного обобщающего повторения
и продуктивной подготовки к экзаменам в настоящее время довольно много. Главное
— не подменять итоговое повторение бессистемным решением (и уж тем более —
бездумным заучиванием решений) того или иного числа задач. При грамотной
организации итогового обобщающего повторения удастся диагностировать проблемные
зоны в знаниях учащихся, закрыть их, овладеть общими навыками решения задач различных
типов, эффективно и продуктивно подготовить учеников к экзамену и, в конечном
счете, обеспечить их необходимым багажом для продолжения образования.
Подготовка
к ЕГЭ по математике не сводится к «натаскиванию» выпускника на выполнение
определенного типа задач, содержащихся в демонстрационной версии экзамена.
Подготовка к экзамену означает изучение программного материала с включением
заданий в формах, используемых при итоговой аттестации. Кроме того, необходимо
выявить и ликвидировать отдельные пробелы в знаниях учащихся. Одновременно надо
постоянно выявлять проблемы и повышать уровень каждого учащегося в следующих
областях (хорошо известных каждому учителю): арифметические действия и культура
вычислений, алгебраические преобразования и действия с основными функциями, работа
с неравенствами и уравнениями, понимание условия задачи, решение практических
задач, самопроверка.
Задания типа №1 проверяют
умение выполнять арифметические действия, делать прикидку и оценку. Эти задания
являются, действительно, очень простыми, что вводит учеников в заблуждение, и
они начинают искать подвох. Единственной сложностью этих заданий является то,
что, получив в результате решения дробный ответ, в бланк записывается целое
число.
При решении этого задания следует
вспомнить, что такое процент. Для устной работы на уроке можно использовать
простые задания на нахождение процента и прикидку. (Приложение №1)
При изучении стереометрии
необходимо, прежде всего, уделять внимание формированию базовых знаний курса
стереометрии (угол между прямыми в пространстве, угол между прямой и
плоскостью, угол между плоскостями, многогранники и т.д.). Для этого
необходимо использовать задачи по готовым чертежам. Их можно включить в устный
счет, повторение пройденного материала или закрепление нового материала. (Приложение
№2)
Одновременно необходимо находить
возможность восстанавливать базовые знания курса планиметрии (прямоугольный
треугольник, решение треугольников, четырехугольники и т.д.). При изучении
геометрии необходимо повышать наглядность преподавания, больше уделять внимания
вопросам изображения геометрических фигур, формированию конструктивных умений и
навыков, применению геометрических знаний к решению практических задач.
При
изучении начал анализа следует уделять
большее внимание пониманию основных идей и базовых понятий анализа:
·
определять значение функции по значению аргумента при различных
способах задания функции; описывать по графику поведение и
свойства функций, находить по графику функции наибольшие и
наименьшие значения; строить графики изученных функций
· вычислять
производные и первообразные элементарных функций,
исследовать в простейших случаях функции на монотонность,
находить наибольшие и наименьшие значения функций.
Так
как выпускники допускают много ошибок при выполнении заданий по данной теме.
Для отработки этих задач нужно применить задания с разными формулировками. (Приложение
№3)
За
два года старшей школы к изученным ранее функциям добавляются
тригонометрические функции, показательная функция и логарифмическая функция.
Именно с этими функциями, как правило, связано большинство задач ЕГЭ. Успешная
сдача экзамена невозможна без знания свойств этих функций и уверенного владения
ими применительно к задачам различных типов. Поэтому организовать обобщающее
повторение в 11-м классе можно и по функциональным линиям: «Многочлены»,
«Рациональные функции», «Иррациональные функции», «Тригонометрические функции»,
«Показательная функция», «Логарифмическая функция». В этом случае внутри
каждого функционального блока следует выделить однотипные содержательные блоки:
числовые и буквенные выражения, уравнения и системы уравнений, неравенства и
системы неравенств, производная и первообразная, исследование функций.
При
подготовке к ЕГЭ необходимо повторить метод интервалов, так как
он используется при решении многих видов неравенств: тригонометрических,
логарифмических, иррациональных, квадратных, показательных и т.д.
Метод интервалов,
используемый в решении неравенств, позволяет сделать решение более осмысленным
в их изучении. (Приложение №4)
Несмотря на то, что тема
«Модуль числа» проходит «красной нитью» через весь курс школьной и высшей
математики, для ее изучения по программе отводится очень мало времени (в 6 классе
-2 часа, в 8 классе — 4 часа).
Исходя из всего
вышесказанного, учителю необходимо находить разнообразные методические приемы,
использовать различные подходы и методы в обучении решению задач с модулем. Как показывает практика, выпускники
часто забывают, что такое модуль. Для этого необходимо на факультативных или
дополнительных занятиях повторять и отрабатывать тему «Модуль». (Приложение
№5)
Для
организации подготовки школьников к экзамену учителю рекомендуется прежде всего
выявлять целевые группы, например:
Для
каждой целевой группы можно сформулировать несколько принципов организации
подготовки к ЕГЭ.
Первая
целевая группа – учащиеся, которые поставили перед собой
цель – преодоление нижнего рубежа (базовый уровень) для получения аттестата.
Работа
должна быть построена так, чтобы за месяц до итоговой аттестации закончить
рассмотрение всех выбранных позиций заданий совмещая работу с регулярным
тематическим повторением и отработкой базовых математических навыков.
Раз в
месяц можно проводить зачетную работу (аудиторную или домашнюю, индивидуальную
или групповую) по выбранным задачам. Общая цель такой работы – отработать
решение выбранных заданий и вселить уверенность в учащихся, что нижний рубеж им
по силам.
Вторая
целевая группа – учащиеся, которые поставили перед собой
цель – получить не очень высокие баллы (на уровне 50-60 баллов по 100-балльной
шкале), но достаточные для поступления в вуз, не предъявляющий высоких
требований к уровню математической подготовки;
Для
этой группы необходимо уверенно выполнять 10-11 заданий профильного уровня.
Работа
должна быть построена так, чтобы за два месяца до итоговой аттестации закончить
рассмотрение всех позиций части 1 ЕГЭ профильного уровня, и к моменту итоговой
аттестации закончить систематическое повторение тем, соответствующих выбранным
позициям второй части .
Для
учащихся этой целевой группы желательно регулярное проведение тренировочных
работ, состоящих из заданий части 1 и выбранных позиций части 2, в частности,
формируемых на базе работ, публикуемых на сайте Открытого банка математических
задач.
Третья
целевая группа – учащиеся, которые поставили перед собой
цель – получить высокие баллы в профильном уровне (больше 60 баллов по 100
балльной шкале), необходимые для поступления в вуз, предъявляющий высокие
требования к уровню математической подготовки абитуриентов.
Для
этой группы необходимо отработать умение уверенно выполнять задания 1-15, уметь
выполнять (может, с некоторыми недочетами) задания 16-17, стараться выполнить
задания высокого уровня 18 и 19.
Чтобы
научить решать выпускников задания №13, №14, №15, необходимо сначала привести
типичные примеры вместе с их решением и комментариями и только после обсуждения
дать варианты самостоятельных работ.
3.2. Группы задач для подготовки к ЕГЭ.
Мои наблюдения показывают, что у выпускников, сдававших
профильный уровень, вызывают затруднение задания типа В8, В11, В12 и задания
повышенного уровня №13. Конечно, у детей «группы риска», т.е. слабо
подготовленных ребят затруднения вызывают и другие задания. В данной работе
невозможно проработать все виды задач, поэтому я остановилась на вышеуказанных
заданиях.
·
Задачи типа №7
Задачи группы №7 связаны с вычислением производной. С
исследованием графиков производной функции либо самой функции, определением
экстремумов по заданному графику.
Типичные
ошибки при выполнении заданий №7:
1.
Обучающие часто
путают графики функции и ее производной;
2.
Допускается много
ошибок в нахождении точек максимума и минимума. Многие считают, что если
функция убывает, значит при пересечении о осью абсцисс — это точка минимума, на
самом деле — это точка максимум, т.к. график идет с положительной области в
отрицательную область.
3.
Выпускники не
внимательно следят за промежутками, на которых требуют что-то найти. Иногда
этот промежуток никто не замечает, а значит решает задачу относительно всего
зарисованного графика, а не заданной его части. (Приложение №7)
·
Задачи типа №11
Текстовые задачи вызывают
трудности у многих школьников. Чтобы решить задачу необходимо не только
внимательно прочитать условие задачи, но и разобраться каким способ ее решать:
по действиям, уравнением, системой уравнений, а может неравенством или системой
неравенств. Необходимо разобраться, что требуется определить в задаче и
записать правильный ответ.
Процесс решения текстовых
задач включает три основных этапа:
·
Составление математической модели.
·
Работа с математической моделью.
·
Ответ на вопрос задачи.
Самым сложным для учащихся
является составление математической модели, то есть анализ текста задачи и
поиск способа ее решения.
Все текстовые задачи можно
разделить на:
·
задачи на пропорции и проценты;
·
задачи на работу;
·
задачи на движение;
·
задачи на концентрацию, смеси и сплава. (Приложение №7)
·
Задачи типа №12
Задача
очень похожа на №7, отличие заключается в том, что в №7 работали с графиками, а
в №12 с функцией.
Типичные
ошибки при выполнении заданий №12:
1.
Обучающиеся
забывают проверить на принадлежность заданному отрезку корней уравнения (точек
экстремума);
2.
Выпускники могут
перепутать максимум и минимум.
3.
Очень часто
ребята не внимательно читают условие задачи. В результате вместо наибольшего
(наименьшего) значения функции на заданном отрезке находят точку максимума
(минимума). (Приложение №8)
·
Задачи типа №13
Задание №13 повышенного уровня сложности
на умение решать тригонометрические уравнения и отбирать корни, соответствующие
определенному промежутку. Еще
одной спецификой тригонометрических уравнений является неединственность формы
записи ответа. Необходимо отработать упражнений с подобными заданиями. Для
этого надо разобрать все возможные варианты отбора корней. (Приложение №9)
Учащиеся должны уметь выделять и решать следующие виды
тригонометрических уравнений:
·
квадратные,
относительно одной из тригонометрических функций (или приводимые к ним);
·
однородные уравнения
первой и второй степени;
·
комбинированные
уравнения. (Приложение №10)
ЗАКЛЮЧЕНИЕ.
Экзамены воспитывают в
сдающем чувство ответственности, что очень важно в педагогическом отношении.
Если они и требуют большой затраты энергии и сил, причиняют воспитанникам много
волнений и беспокойства, то и в этом можно видеть прекрасную подготовку к жизни,
вовсе не усеянной розами. Однако такого взгляда на экзамены держатся далеко не
все в педагогическом мире. Особенно не согласны с ним врачи и родители. Первые
настаивают на том, что экзамены безусловно вредны для здоровья учащихся;
установлено, например, что во время экзаменов ученики теряют в весе, чаще
происходят нервные срывы у выпускников. Родители и некоторые педагоги полагают,
что контролировать учителей и учеников надо в продолжение всего учебного года и
так рационально поставить этот контроль, чтобы экзамены стали не нужны. Во
время экзамена ученик находится в совершенно особенном, ненормальном состоянии,
что вместе с краткостью времени не позволяет считать его ответ надежным
показателем его знаний. Сам характер обучения, по мнению противников экзаменов,
принимает весьма нежелательные формы, превращаясь у иных преподавателей в
сплошное натаскивание к экзаменам.
Многие обучающиеся в году
небрежно относятся к своим обязанностям, надеясь к экзаменам всё подогнать и
восполнить все пробелы; уровень познаний, таким образом, понижается, а отнюдь
не повышается, как утверждают защитники экзаменов. Решающее значение экзаменов
заставляет учеников прибегать к разным уловкам и обманам (шпаргалки и прочее),
лишь бы получить удовлетворительную отметку, и в этом смысле экзамены имеют
деморализующее влияние на учеников.
Таким образом, еще раз
подчеркну необходимость комплексного подхода при организации подготовки
обучающихся ЕГЭ. При этом желательно не оставаться «один на один» с предметом,
а воспользоваться помощью квалифицированного репетитора, который сможет
выстроить процесс подготовки с учетом вышеназванных особенностей.
Итоги
ЕГЭ предыдущих лет позволяют высказать некоторые общие рекомендации,
направленные на совершенствование процесса преподавания и подготовки учащихся
средней школы.
·
Необходимо совершенствовать методику формирования базовых
умений, составляющих основу математической подготовки выпускников средней
школы.
·
Анализ результатов выполнения базовых заданий по курсу алгебры и
начал анализа показал наличие положительной динамики в овладении материалом
раздела «Тригонометрия». В настоящее время вызывают тревогу низкие результаты
выполнения заданий на решение иррациональных уравнений и логарифмических
неравенств. Учителям в процессе обучения следует обратить внимание на
обеспечение более прочного усвоения учащимися стандартных алгоритмов решения этих
уравнений и неравенств.
·
Геометрическая подготовка выпускников школы продолжает
оставаться невысокой, поэтому по-прежнему необходимо усиленное внимание
учителей к преподаванию курса геометрии в основной и старшей школе, чтобы в
процессе обучения учащиеся не только овладевали теоретическими фактами курса,
но и приобретали умения проводить обоснованные рассуждения при решении
геометрических задач и математически грамотно записывать полученное решение.
Опыт моей работы показывает, что подготовку к ЕГЭ необходимо
начинать с 5 класса. Для успешной сдачи ЕГЭ недостаточно 5 уроков в неделю.
Необходимо работать над заданиями повышенной и высокой уровней сложности на
дополнительных занятиях и факультативах.
Целенаправленной подготовке к ЕГЭ способствуют факультативные
курсы. В приложении №11 представлен факультатив «Решение уравнений с
модулем».
Поставленные в начале работы цели и задачи решены. Материалы,
представленные в моей работе, могут быть использованы в дальнейшем при
подготовке выпускников к ЕГЭ.
Библиографический список.
1.
1.http://schoolmathematics.ru/zadanie-s1-2
2.
http://scool1-tulsky.edusite.ru/p50aa1.html
3.
http://www.fipi.ru/binaries/1084/mat11.pdf
4.
http://scepsis.ru/library/id_2480.html
5.
http://ege-ok.ru/2012/03/28/ugol-mezhdu-pryamoy-i-ploskostyu-metod-koordinat-zadanie-s2/
6.
http://festival.1september.ru/articles/591233/
7.
http://knowledge.allbest.ru/mathematics/d-2c0a65635b2bc68b5d53b88421316c27.html
8.
http://nsportal.ru/shkola/algebra/library/sistema-podgotovki-k-ege
9.
Математика: «Решение тестовых задач»: экспресс-репетитор для
подготовки к ЕГЭ / И.С.Слонимская, Л.И.Слонимский. – М.: АСТ: Астрель;
Владимир: ВКТ, 2014.
10.
Математика. Тесты к ЕГЭ / А.Г.Клово. – Ростов н/Д: Феникс, 2015.
11. http://nsportal.ru/shkola/materialy-metodicheskikh-obedinenii/library/sistema-raboty-uchitelya-matematiki-po-podgotovke
12.
Алгебра и начала анализа: учеб. Для 10-11 кл. общеобразоват.
Учреждений / [А.Н.Колмогоров, Ю.П.Дудницын и др.]; под ред. А.Н.Колмогорова. –
16-е изд. – М.: Просаещение, 2014. – 384с.
13.
Математика №5, 2012; Т.Ермишигна «Обучение поиску решения».
14. http://www.cleverstudents.ru/maximum_minimum.html
15. Корикова
Т.М., Суслова И.В. Элементарная математика. Стереометрия: учебное пособие. –
Ярославль: Изд-во ЯГПУ, 2010.-114с.
16. Математика
№5, 2011; А.Корянов, А.Прокофьев «Различные подходы к решению задач С5 ЕГЭ»
17. Математика:
тренировочные тематические задания повышенной сложности с ответами для
подготовки к ЕГЭ и к другим формам выпускного и вступительного экзаменов/ сост.
Г.И.Ковалева, Т.И.Бузулина, О.Л.Безрукова, Ю.А.Розка. – Волгоград: Учитель,
2008. -494 с.
18. ЕГЭ-2017.
Математика. Профильный уровень: типовые экзаменационные варианты: 36 вариантов
/ под ред. И.В. Ященко. – М.:Издательство «Национальное образование», 2017. –
256 с. – (ЕГЭ, ФИПИ — школе)
19. http://edj77.narod2.ru/ege/matem/
20. http://festival.1september.ru/articles/507334/
ПРИЛОЖЕНИЯ.
Приложение №1
Задачи для устного счета к заданию №1
·
Найдите 30% от 27. (8,1)
·
Какое число получиться, если 140 увеличить на 60%? (224)
·
Кафельная плитка продается коробками по 6 м2. Сколько
коробок плитки нужно купить, чтобы хватило на облицовку стен площадью 35 м2.
? (6)
·
Билеты в ботанический сад стоит 50 рублей. Сколько рублей сдачи
нужно получить с 2000 рублей, заплаченных за проход 36 человек? (200)
·
Горные лыжи стоят 16 000 рублей. Сколько рублей будут стоить
горные лыжи во время сезонной распродажи, когда на них объявлена скидка 20%?
(12800)
·
Йогурт стоит 7 рублей 60 копеек. Какое максимальное количество
йогуртов можно купить на 50 рублей? (6)
·
Шариковая ручка стоит 7 рублей. При покупке более 50 ручек на
всю покупку начинает действовать скидка 20 %. Сколько рублей нужно заплатить
при покупке 120 ручек? (672)
Приложение №2
Задачи для повторения или закрепления при изучении стереометрии.
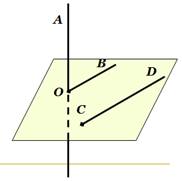
Задание №1.
Дано: ОВ ||
СD, ОА и СD – скрещивающиеся. Найти
угол между ОА и СD, если:
1)
˂АОВ=40º (40º)
2)
˂АОВ=135º (45º)
3) ˂АОВ=90º
(90º)

Задание №2 .
Треугольники АВС и
АСD лежат в разных плоскостях. РК – средняя линия
∆АDC с основанием АС. Определить взаимное расположение прямых
РК и АВ, найти угол между ними, если ˂АСВ=80º, ˂В=40º
Ответ: 1) АВ и РК –
скрещивающиеся прямые
2)60º
Задание №3.
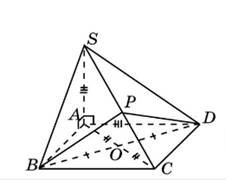
утверждений:
1)Угол между плоскостями SAB и DBC прямой;
2)Плоскости SAB и SBС перпендикулярны;
3)Плоскости SАС и DBC перпендикулярны;
4)Угол между плоскостями SDC и DBC прямой;
5)Плоскости DBC и АSР перпендикулярны;
6)Угол между плоскостями SВC и АSР прямой Ответ: 1),
3), 5)
Систематизация знаний учащихся о
нахождении расстояния между скрещивающимися прямыми может быть осуществлена с
помощью следующей таблицы:
|
Чертежи |
Основные |
|
|
1. |
|
|
2. Через одну из скрещивающихся прямых провести плоскость, |
|
|
3. Через одну из скрещивающихся прямых провести параллельные |
|
|
4. Провести плоскость, перпендикулярную одной из двух данных |
|
|
|
|
|
41. Если скрещивающиеся прямые взаимно |
|
|
|
|
|
5. Если скрещивающиеся прямые принадлежат соответственно двум |
|
|
|
|
|
6. Если на двух скрещивающихся прямых взяты точки А и В, С и D соответственно так, что |
Приложение №3
Задачи по теме «Геометрический смысл производной»
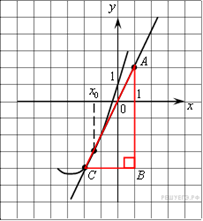
(геометрический смысл производной)
На рисунке изображён график функции и
касательная к нему в точке с абсциссой .
Найдите значение производной функции в
точке .
Ответ: 2
Задание
№2 .
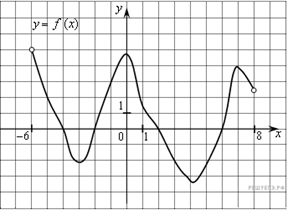
промежутков знакопостоянства производной по графику функции)
На рисунке изображен график функции ,
определенной на интервале (−6; 8). Определите количество целых
точек, в которых производная функции положительна.
Ответ: 4
Задание
№3 .
(нахождение
точек экстремума функции по ее графику)
На рисунке изображен график функции ,
определенной на интервале (-2; 12). Найдите сумму координат точек экстремума
функции .
Ответ:44
Задание
№4 .
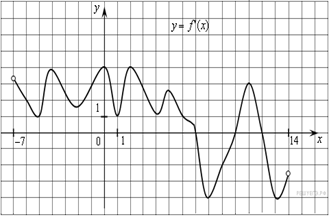
точек экстремума функции по графику производной функции)
На рисунке изображен график производной функции ,
определенной на интервале .
Найдите количество точек максимума функции на
отрезке .
Ответ: 1
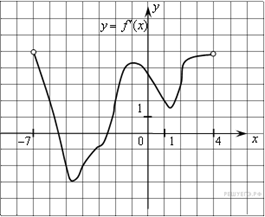
№5 .
(определение
промежутков монотонности функции по графику производной функции)
На рисунке изображен график производной функции ,
определенной на интервале .
Найдите промежутки возрастания функции . В
ответе укажите сумму координат целых точек, входящих в эти промежутки.
Ответ: -3
Приложение №4
Задачи по теме «Решение неравенств методом интервалов»
Задание №1 . Решить неравенство
Решение:
6-2х-6-3х-х=0
-6х=0
4. На координатной прямой изобразим нули
функции. Получили два промежутка
5. Определяем знак функции
на каждом из полученных интервалов подстановкой в выражении функции
какого-либо значения из соответствующего интервала: если х=-4, то
6. выберем
для ответа нужные интервалы в соответствии со знаком неравенства.
Задание №2. Решить неравенство
Решение:
Решим неравенство методом
интервалов.
Рассмотрим функцию f(x)=
и найдем множество значений
х, при которых
1) Найдем
2)
Найдем нули функции и точки, в которых функция не определена:
х-4х2 =0
х-1≠
0
х=0
х=1/4
х≠1

координатной прямой изобразим нули функции и точки, в которых функция не
определена. Получили четыре промежутка.
4)Определяем
знак функции на каждом из полученных интервалов подстановкой в выражении
функции какого-либо значения из соответствующего интервала.
5)выберем
для ответа нужные интервалы в соответствии со знаком неравенства.
Ответ:
(-∞;0] [1/4;1)
Задание №3. Решить
неравенство .
Решение:
Рассмотрим функцию f(x)=x2(2x+1)(x-3)
и найдем множество значений х , при которых
1)D(f)=R
2) Найдем нули функции:x2(2x+1)(x-3)=0
х2=0
2х+1=0 х-3=0
х1=0
х2=- х3=3
3) На координатной прямой
изобразим нули функции Получилось
четыре интервала.
4) Определяем
знак функции на каждом из полученных интервалов подстановкой в выражении
функции какого-либо значения из соответствующего интервала.
Задание №4. Решить
неравенство
Решение:
Воспользуемся методом интервалов. Рассмотрим функцию
f(x)=(3-x)log3(x+5)
и найдем множество значений х , при которых
1) Найдем D(f). Т.к. D(loga)=R+, то x+5
>0; x >-5.
2) Найдем нули функции:(3-x)log3(x+5)=0
Произведение равно нулю, если хотя бы один из множителей равен
нулю, а другие при этом не теряют смысла.
а) 3-x=0, x=3 , при этом определен второй множитель log38.
б) log3(x+5)=0, x+5=1, x=-4.
3) Отметим нули функции на координатной прямой
Ответ: (-5;4] [3;+
∞]
Приложение
№5
Задания
по теме «Модуль числа»
Задание №1. Решить
уравнение |х-5|=4.
Решение:
Исходя из определения модуля
| f(x) |= а, f(x)=а, если f(x)˃0
f(x)=-а , если f(x)˂0
произведем следующие рассуждения. Если выражение, стоящее под знаком модуля
неотрицательно, то есть х-5≥0, то уравнение примет вид х-5=4. Если
значение выражения под знаком модуля отрицательно, то по определению оно будет
равно – (х-5)=4 или х-5= -4. Решая полученные уравнения, находим: х1=9,
х2=1.
Ответ: 9; 1.
Обобщение: | f(x)
|= а ˂=˃ а≥0
f(x)=а
f(x)=-а
Задание №2 Решить
уравнение |2-х|=2х+1.
Решение:
Прежде
всего, следует установить область допустимых значений. В этом уравнении в
правой части стоит выражение с переменной, которое может быть отрицательным.
Таким образом необходимо найти область допустимых значений – это промежуток
[-½; +∞).
Найдем нуль
выражения, стоящего под знаком модуля: 2-х=0, х=2.
В первом промежутке: 2-х=2х+1, х=⅓. Это значение принадлежит ОДЗ, значит,
является корнем уравнения.
Во втором промежутке: -2+х=2х+1, х= -3. -3 не принадлежит ОДЗ, а следовательно
не является корнем уравнения.
Ответ: ⅓.
Обобщение: | f(x) |=g(х) ˂=˃ g(х)≥0
f(x) =g(х)
f(x) = —g(х)
Задание
№3 Решите уравнение: |х+3|=|2х-1|. В ответе указать целый корень.
Решение:
1 способ:
1) Чтобы решить такого вида уравнение
необходимо знать:
| f(x) |=|g(х)| ˂=˃ f(x) =g(х)
f(x) = —g(х)
2) Исходя из этого имеем:
|х+3|=|2х-1|˂=˃ х+3=2х-1
х+3=-2х+1
3) Решим полученные уравнения:
х+3=2х-1
х+3=-2х+1
х=4
х=
Ответ: 4.
2 способ:
Решение:
Для решения уравнения
воспользуемся методом возведения обеих частей уравнения в квадрат.
1) (|х+3|)2=(|2х-1|)2
2) Воспользуемся формулой сокращенного умножения а2—
в2=(а-в)(а+в) и получим: (х+3-2х+1)(х+3+2х-1)=0
3) Решим данное уравнение и получим его корни: х=4; х=
4) В ответе укажем только целый корень.
Ответ: 4
Задачи типа №7. Приложение №6
Задача1.
На рисунке изображен график функции у=f(х),определенной
на интервале (-6;6). Найдите количество точек, в которых касательная к графику
функции параллельна прямой у=-5.
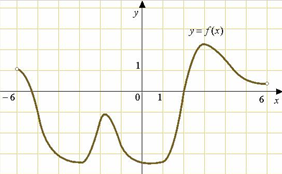
основа:
·
уравнение прямой;
·
уравнение касательной;
·
условие параллельности двух
прямых.
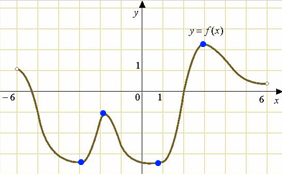
прямая у=-5 (у=kx+b, k=0) имеет коэффициент k равный нулю, то и угловой коэффициент касательной (y=f1(x0)(x—x0)-f(x0), k=f1(x0)) тоже должен быть равен нулю ( условие
параллельности двух прямых). Считаем количество экстремумов (точек максимума и
минимума) функции.
В данном
случае их количество равно 4 (синие точки).
Ответ:4.
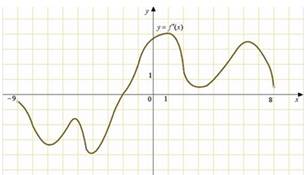
какой точке отрезка[-8,-4] f(х)
принимает наименьшее значение.
Теоретическая основа:
·
достаточный признак
возрастания и убывания функции с помощью производной;
·
правило отыскания
наибольшего и наименьшего значения непрерывной на отрезке функции.
Решение: На отрезке [-8;-4] график производной
функции лежит ниже оси ОХ, значит график функции убывает, и наименьшее значение
график принимает в точке -4 (в правом конце указанного промежутка).
Ответ: -4.
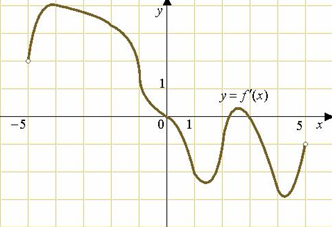
Найдите количество точек экстремума функции f(х) на отрезке [-4;4]
Теоретическая основа:
·
достаточный признак
возрастания и убывания функции с помощью производной:
ü Функция убывает на промежутке, если на этом промежутке f1(x)˂0, т.е. график производной функции расположен ниже
оси ОХ.
ü Функция возрастает на промежутке, если на этом промежутке
f1(x)˃0, т.е. график производной функции расположен выше
оси ОХ.
·
признаки максимума
и минимума функции:
ü
Если в точке х0
производная меняет знак с плюса на минус, то х0 есть точка
максимума.
ü
Если в точке х0
производная меняет знак с минуса на плюс, то х0 есть точка
минимума. [21]
Решение:
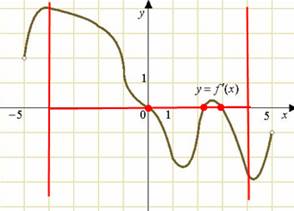
Количество точек экстремума —
есть количество точек пересечения графика производной функции с осью ОХ. Таких
точек три.
Ответ: 3
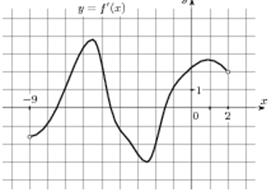
убывания функции f(х). В ответе укажите сумму целых точек,
входящих в эти промежутки.
Теоретическая основа:
Функция убывает на промежутке,
если на этом промежутке f1(x)˂0, т.е. график производной функции расположен ниже оси ОХ.
Решение:
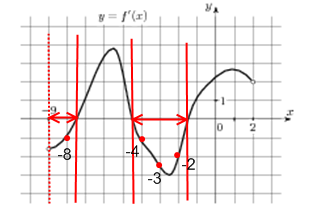
-8, а второй содержит целые точки -4, -3, -2.
Найдем их сумму: -8-4-3-2=-17
Ответ: -17
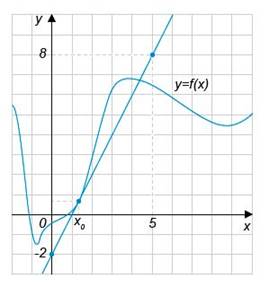
функции у=f(х) и касательная к нему в точке с
абсциссой х. Найдите значение производной функции f(х) в точке х0.
Решение: Данную задачу можно решить двумя
способами:
1.
Геометрический смысл
производной
2.
По определению
производной.
1
способ: Значение
производной в точке x0 совпадает с тангенсом угла наклона (он
же – угловой коэффициент) касательной в точке x0. Эта
касательная изображена на рисунке. Вычисление углового коэффициента облегчается
тем, что касательная проходит через два узла целочисленной решетки. Эти точки
выделены на рисунке жирным и имеют координаты (0, -2) и (5,8) соответственно.
Стороны прямоугольника, у которого эти точки являются противоположными
вершинами, имеют длины 5 – 0 = 5 (горизонтальная) и 8 – (-2) = 10
(вертикальная). Тангенс угла наклона касательной t = 10/5 = 2
2
способ:
1)
По
определению производной f!(х)=
2)
По графику находим
координаты точки А(0;-2) и точки В(5;8); значит х1=0, х2=5,
у1=-2, у2=8
3)
Подставим в
формулу значения переменных и получим
f!(х)= =2
Ответ: 2
Приложение
№7
Группа
задач типа №11.
Задача 1. Двое
рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней,
работая отдельно, выполнит эту работу первый рабочий, если он за два дня
выполняет такую же часть работы, какую второй – за 3 дня?
После зачтения задачи проводится анализ.
o
Какие величины содержатся в задаче?
o
Как связаны между собой производительность труда, время и объем
выполненных работ?
o
Сколько можно выделить в задаче различных ситуаций (событий,
случаев, фактов)?
o
Какие величины известны в каждой ситуации?
o
Какая неизвестная величина в задаче является искомой?
Выполненный анализ позволяет
осуществить запись условий и требования задачи в виде таблицы.
Решение: Составим
таблицу:
|
V (раб./день) |
T (дней) |
A(раб.) |
|
|
1 |
|
х |
1 |
|
2 |
|
у |
1 |
|
вместе |
|
12 |
1 |
По условию вместе рабочие делают часть работы, составим
первое уравнение системы +
=
.
Для второго уравнения нужна еще одна таблица:
|
V(раб./день) |
T(дней) |
A(раб.) |
|
|
1 |
|
2 |
|
|
2 |
|
3 |
|
Составим систему уравнений
с учетом данных второй таблицы:
+
=
+
=
+
=
=
х =
=20
=
=
=
=
у =
=30
Ответ: 20
Задача2. Велосипедист
выехал с постоянной скоростью из города А в город В, расстояние между которыми
равно 70 км. На следующий день он отправился обратно в А со скоростью на 3 км/ч
больше прежней. По дороге он сделал остановку на 3 часа. В результате
велосипедист затратил на обратный путь столько же времени, сколько на путь из А
в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч.
Решение: Составим
таблицу:
|
V (км/ч) |
t (ч.) |
S (км) |
|
|
Из |
х |
|
70 |
|
Из |
х+3 |
|
70 |
По условию задачи велосипедист сделал остановку на 3 часа.
Составим уравнение: + 3 =
. умножим обе части
уравнения на х(х+3)
70х+3х2+9х=70х+210 перенесем все слагаемые
в одну часть, приведем подобные слагаемые и запишем полученное квадратное
уравнение: х2+3х-70=0, корнями
которого являются числа х1=7, х2=-10.
Корень -10 не удовлетворяет условию задачи, следовательно, 7
км/ч – скорость велосипедиста.
Ответ: 7.
Задача3. Из пункта А в пункт В
вышел товарный поезд. Спустя 3 часа вслед за ним вышел пассажирский поезд,
скорость которого на 30 км/ч больше скорости товарного поезда. Через 15 часов
после своего выхода пассажирский поезд оказался впереди товарного на 300 км.
Определите скорость товарного поезда.
Решение: Составим таблицу:
|
Скорость (км/ч) |
Время |
Расстояние(км.) |
|
|
Товарный поезд |
Х |
(15+3) |
18х |
|
Пассажирский поезд |
(х+30) |
15 |
15(х+30) |
Так
как пассажирский поезд прошел на 300 км больше товарного, получаем уравнение:
15(х+30)-18х=300
15х+450-18х=300
3х=150; х=50 км/ч
Ответ:
50
Задача4. Сплавили
300 г сплава олова и меди, содержащего60% олова, и 900 г сплава олова и меди,
содержащего 80% олова. Сколько процентов олова в получившемся сплаве?
Решение:
Масса
олова в первом сплаве равна 0,6*300=180 г
Масса
олова во втором сплаве равна 0,8*900=720 г
Масса
олова в новом сплаве равна 180+720=900 г
Масса
нового сплава равна 300+901200 г
Процентное
содержание олова в новом сплаве равно =75%
Ответ:
75.
Приложение №8
Группа задач типа №12.
Задача 1. Найдите наибольшее значение функции y=9cosx+16x−8 на отрезке [−3π/ 2 ;0]
Решение:
1.
Найдем
производную функции y=9cosx+16x−8
f ′ (x)=9⋅(−sinx)+16=−9sinx+16
2.
Найдем критически
точки функции: f ′ (x)=0
−9sinx+16=0
sinx=16/ 9
Это уравнение не имеет решений, так как функция синус принимает значение от -1
до 1.
У функции f(x)=9cosx+16x−8 нет критических точек.
3.
Найдем значение f(x) на концах отрезка [−3π/ 2 ;0] и выберем
наибольшее.
f(−3π/ 2 )=9cos(−3π/ 2 )−16⋅3π 2 −8=−8(3π+1)⇒f(−3π /2 )<0.
f(0)=9cos0+16⋅0−8=9−8=1⇒f(0)>0
f(0)>f(−3π/ 2 ).
Наибольшее значение функции f(x)=9cosx+16x−8 на отрезке [−3π/ 2 ;0] равно 1.
Ответ: 1.
Задача 2. Найдите наибольшее значение
функции на
отрезке
Решение.
Найдём производную заданной функции:
.
Из
уравнения найдем
нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции
На отрезке [−2; 0] функция убывает, поэтому она достигает
своего наибольшего значения в точке x = −2. Найдём это наибольшее
значение:
Ответ: 1.
В итоге
работы с заданиями типа №12 учащиеся должны усвоить алгоритм нахождения наибольшего
и наименьшего значения непрерывной функции на отрезке [а;в]:
1)
Найти область определения функции и проверить содержится ли в ней отрезок
[а;в].
2) Найти
производную данной функции.
3)
Решить уравнение f1(x)=0 и отобрать только
те корни уравнения, которые принадлежат отрезку [а;в]
4) Вычисляем значения функции в отобранных
стационарных точках (если таковые имеются), а также при x = a и x = b.
5) Из полученных значений функции выбираем
наибольшее и наименьшее — они и будут искомыми.
Данный
алгоритм будет служить основой для решения других задач на нахождение
наибольшего или наименьшего значения функции на отрезке.
Приложение №9
Задачи на отработку способов отбора корней.
При отборе корней
в процессе решения тригонометрических уравнении обычно используют один из
следующих способов:
●
Арифметический
способ:
а)
решение двойного неравенства, относительно целочисленного п;
б)
перебор значений целочисленного параметра и вычисление корней.
●
Геометрический
способ
а)
изображение корней на тригонометрической окружности с последующим отбором с
учетом имеющихся ограничений;
б)
изображение корней на числовой прямой с последующим отбором с учетом
имеющихся
ограничений.
Чтобы учитывать
область допустимых значений учащиеся должны уметь решать простейшие
тригонометрические неравенства с помощью тригонометрического круга и графиков
тригонометрической функции.
Для повторения можно использовать
следующие задания:
Задание №1. Решите
неравенство .
Решение:
Нарисуем тригонометрическую окружность и отметим на ней точки, для которых
ордината превосходит .
Для
решением данного неравенства будут
. Ясно также, что если некоторое
число будет отличаться от
какого-нибудь числа из указанного интервала на ,
то также будет не меньше
. Следовательно, к концам
найденного отрезка решения нужно добавить .
Окончательно, получаем, что решениями исходного неравенства будут все .
Отве:. .
Другой
подход решения тригонометрических неравенств: с помощью числовой прямой.
Задание №2 .Решить неравенство .
1
способ.
Решение:
Рассмотрим график функции
Выберем
из промежутка на оси
значения аргумента
, которым соответствуют точки
графика, лежащие выше оси . Таким
промежутком является интервал .
Учитывая периодичность функции все
решения неравенства можно записать
так: .
Ответ.
.
2
способ.
Решение:
Используем
тригонометрический круг.
Задание №3. Решить уравнение
Решение. Данное уравнение равносильно следующей системе
Далее имеем
Рассмотрим окружность. Отметим на ней
корни каждой системы и отметим дугой ту часть окружности, где выполняется
неравенство
Получаем, что не может быть
решением исходного уравнения.
Ответ:
Задание №4 . Решить уравнение 2sin 2x -3cosx – 3=0
Найти все корни уравнения, принадлежащие
отрезку [π;3π].
Решение:
1) Воспользуемся основным тригонометрическим
тождеством. Получим
уравнение: 2(1- cos 2x)-3
cosx-3=0
2)Раскроем
скобки: 2-2 cos 2x-3
cosx-3=0
3)Приведем
подобные слагаемые: -2 cos 2x-3 cosx-1=0
4)
Разделим все слагаемые уравнения на (-1): 2 cos 2x+3 cosx+1=0
5)Выполним
замену cosx=а и получим квадратное уравнение: 2а2+3а+1=0
6)Решая
данное уравнение получим корни: а1=-1; а2=-1/2
7)Вернемся
к замене: cosx1=-1 cosx2=-
х1=π+2πп

Проверим какие корни принадлежат отрезку [π;3π].
1) π≤ +2πп
≤ 3π
1≤
+
2п ≤3 ; 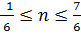
;
п
п=1 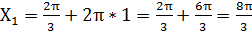
2)
π≤ — +2πп
≤ 3π
1≤ — +2п≤
3
≤
2п≤ ;
≤
п ≤
п
п=1 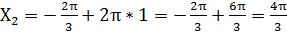
3) π ≤ π+2πп ≤
3π
1 ≤ 1+2п ≤ 3
0 ≤ 2п ≤ 2 ; п=1; п=0
п
п=1
п=0
Ответ: х1= ;
х2= ;
х3=;
х4=
Приложение №10
Задачи типа №13.
Задача 1. Решите уравнение . Укажите его корни,
принадлежащие отрезку [-π;]
Решение.
1) Данное
уравнение является однородным второй степени. Разделим каждое слагаемое
уравнения на ()
2) Получим:
tg2х-2 tg х-3=0
3) Сделаем
замену: tg х=а
4) Получим
квадратное уравнение а2-2а-3=0, корнями которого являются числа 3 и
-1
5) Вернемся
к замене и получим tg х=3 и
tg х=-1
х=arctg 3+πп и х=- +πп
6) С
помощью числовой прямой определим какие корни принадлежат промежутку [-π;]
Ответ: х1=-
; х2=arctg 3-π; х3=arctg 3
Задача 2. Решите уравнение -2х)=0 и
укажите корни, принадлежащие промежутку [-π;]
Решение:
1) С помощью формул приведения получим:
2) С помощью основных тригонометрических формул получим: -2
=0
3) вынесем
за скобки: (
— 2
)=0
4) Решим полученное уравнение: =0 или
( — 2
)=0
х=πk, kΖ;
cos2х=
х=+
, k
Ζ
5) Отметим решения на единичной окружности.
6) Выберем
корни, которые принадлежат промежутку [-π;] :
-π; —; —
; 0;
.
Ответ: -π; —; —
; 0;
.
Задача 3. Решите уравнение .
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решение.
Решим уравнение:
с помощью числовой
окружности отберём корни, принадлежащие отрезку .
Это
числа : .
Ответ:
а) .
б) .
Приложение №11
Факультативный курс по
математике «Решение уравнений с модулем»
Пояснительная
записка
Понятие
абсолютной величины (модуля) является одной из важнейших характеристик числа как
в области действительных, так и в области комплексных чисел.
Это
понятие широко применяется не только в различных разделах школьного курса
математики, но и в курсах высшей математики, физики и технических наук,
изучаемых в вузах. Например, в теории приближенных вычислений используются
понятия абсолютной и относительной погрешностей приближенного числа. В механике
и геометрии изучаются понятия вектора и его длины (модуля вектора). В
математическом анализе понятие абсолютной величины числа содержится в определениях
таких основных понятий, как предел, ограниченная функция и др. Задачи,
связанные с абсолютными величинами, часто встречаются на математических
олимпиадах, вступительных экзаменах в вузы и на ЕГЭ.
Владение
решением уравнений и неравенств с модулем будет служить пропедевтикой изучения
математического анализа в ВУЗе. В частности таких понятий как непрерывность
функции, предел функции, производная и др.
Программой
школьного курса математики не предусмотрены обобщение и систематизация знаний о
модулях, их свойствах, полученных учащимися за весь период обучения. Это и
позволит сделать элективный курс «Решение уравнений с модулем».
Курс
рассчитан на учащихся 9-11 классов общеобразовательных школ, проявляющих
интерес к изучению математики.
Курс
позволит школьникам систематизировать, расширить и укрепить знания, связанные с
абсолютной величиной, подготовиться для дальнейшего изучения тем, использующих
это понятие, научиться решать разнообразные задачи различной сложности,
способствует выработке и закреплению навыков работы на компьютере.
Учителю
курс поможет наиболее качественно подготовить учащихся к математическим
олимпиадам, сдаче ЕГЭ и экзаменов при поступлении в вузы.
Программа
факультативного курса предполагает знакомство с теорией и практикой рассматриваемых
вопросов и рассчитана на 34 часа: 7,5 часов лекций и 26,5 часов практических
занятий.
Содержание
курса состоит из восьми разделов, включая введение и итоговое занятие. Учитель,
в зависимости от уровня подготовки учащихся, уровня сложности изучаемого
материала и восприятия его школьниками, может взять для изучения не все темы,
увеличив при этом количество часов на изучение других. Учитель также может
изменить уровень сложности представленного материала.
Программа
содержит темы творческих работ и список литературы по предложенным темам.
В
процессе изучения данного курса предполагается использование различных методов
активизации познавательной деятельности школьников, а также различных форм
организации их самостоятельной работы.
Результатом
освоения программы курса является представление школьниками творческих
индивидуальных и групповых работ на итоговом занятии.
Цели
курса:
обобщение
и систематизация, расширение и углубление знаний по теме «Абсолютная величина»;
обретение практических навыков выполнения заданий с модулем; повышение уровня
математической подготовки школьников.
Задачи
курса:
· вооружить учащихся
системой знаний по теме «Абсолютная величина»;
· сформировать
навыки применения данных знаний при решении разнообразных задач различной
сложности;
· подготовить
учащихся к ЕГЭ;
· сформировать
навыки самостоятельной работы, работы в малых группах;
· сформировать
навыки работы со справочной литературой, с компьютером;
· сформировать
умения и навыки исследовательской работы;
· способствовать
развитию алгоритмического мышления учащихся;
· способствовать
формированию познавательного интереса к математике.
Требования
к уровню усвоения учебного материала
В
результате изучения программы факультативного курса «Решение уравнений с
модулем» учащиеся получают возможность знать и понимать:
· определение
абсолютной величины действительного числа;
· основные операции
и свойства абсолютной величины;
· правила построения
графиков уравнений (в т.ч. функций), содержащих знак абсолютной величины;
· алгоритмы решения
уравнений, неравенств, систем уравнений и неравенств, содержащих переменную под
знаком модуля.
Уметь:
· применять
определение, свойства абсолютной величины действительного числа к решению
конкретных задач;
· читать и строить
графики функций, аналитическое выражение которых содержит знак абсолютной
величины;
· решать уравнения,
неравенства, системы уравнений и неравенств, содержащих переменную под знаком
модуля.
Содержание
курса
(1
ч в 2 недели, всего 17 ч)
1.
Введение (1 ч).
Цели
и задачи факультативного курса. Вопросы, рассматриваемые в курсе и его
структура. Знакомство с литературой, темами творческих работ. Требования,
предъявляемые к участникам курса. Аукцион «Что я знаю об абсолютной величине?».
2.
Абсолютная величина действительного числа а (2 ч).
Абсолютная
величина действительного числа а. Модули противоположных чисел. Геометрическая
интерпретация понятия модуля а. Свойства модуля. Операции над абсолютными
величинами. Упрощение выражений, содержащих переменную под знаком модуля.
Применение свойств модуля при решении задач.
3.
Графики уравнений (в т.ч. функций), аналитическое выражение которых содержит
знак абсолютной величины (3 ч).
Правила
и алгоритмы построения графиков уравнений, аналитическое выражение которых
содержит знак модуля. Графики уравнений
Графики
некоторых простейших функций, заданных явно и неявно, аналитическое выражение
которых содержит знак модуля. Графики уравнений (в т.ч. функций), аналитическое
выражение которых содержит знак абсолютной величины в олимпиадных заданиях.
4.
Уравнения, содержащие абсолютные величины (8 ч).
Основные
методы решения уравнений с модулем. Раскрытие модуля по определению, переход от
исходного уравнения к равносильной системе, возведение в квадрат обеих частей
уравнения, метод интервалов, графический метод, использование свойств
абсолютной величины. Уравнения вида
Метод
замены переменных при решении уравнений, содержащих абсолютные величины. Метод
интервалов при решении уравнений, содержащих абсолютные величины. Уравнения
вида
Способ
последовательного раскрытия модуля при решении уравнений, содержащих «модуль в
модуле». Графическое решение уравнений, содержащих абсолютные величины.
Использование свойств абсолютной величины при решении уравнений. Уравнения с
параметрами, содержащие абсолютные величины. Защита решенных олимпиадных
заданий.
5.
Модуль в заданиях ЕГЭ ( 3 часа)
Учебно-тематический план.
|
№ занятия |
Тема занятия |
Основная цель занятия |
Вид занятия |
|
1. |
Введение |
Познакомить |
Лекция |
|
Абсолютная величина |
|||
|
2 |
Абсолютная величина действительного числа. Модули противоположных чисел. Геометрическая |
Систематизировать |
Изучение нового материала. Практикум. |
|
3. |
Свойства модуля. Операции над абсолютными величинами. |
Рассмотреть |
Изучение нового материала. Практикум |
|
Графики |
|||
|
4. |
Правила и алгоритмы построения графиков функций, содержащих |
Рассмотреть основные правила построения графиков функций, |
Изучение нового материала |
|
5. |
Построение графиков вида |
Научить обучающихся строить графики вида |
Практикум |
|
6. |
Построение графиков вида |
Научить обучающихся строить графики вида |
Практикум |
|
Уравнения, содержащие абсолютные |
|||
|
7. |
Решение уравнений Решение уравнений вида |f(x)|= g (x); |
Практикум |
|
|
8. |
Решение уравнений |
Практикум |
|
|
9. |
Метод замены переменных при решении уравнений с модулем. |
Изучение нового материала. Практикум |
|
|
10. |
Метод интервалов при решении уравнений с модулем. |
Практикум |
|
|
11. |
Графический метод решения уравнений с модулем. |
Практикум |
|
|
12. |
Решение уравнений вида |
Изучение нового материала. Практикум |
|
|
13. |
Решение уравнений, содержащих абсолютную величину различными |
Практикум |
|
|
14 |
Решение дрорбно-рациональных уравнений, содержащих модуль. |
Изучение нового материала. Практикум |
|
|
Модуль |
|||
|
15. |
Модуль в заданиях ЕГЭ типа С1 |
Практикум |
|
|
16. |
Модуль в заданиях ЕГЭ типа С5 |
Практикум |
|
|
17. |
Итоговое занятие. Защита ученических проектов и творческих |
Разработка
занятия факультативного курса
«Решение уравнений с модулем»
по теме: «Решение уравнений вида различными
способами.»
Тема: «Решение
уравнений, содержащих абсолютную величину различными способами».
Обучающая
цель: 1. Сформировать умения решать
уравнения с модулем различными способами.
2.
Формировать представление о методах математики, как науки (общекультурная
компетенция).
Развивающая
цель: Развивать:
1.
умения сравнивать, анализировать, строить аналогии (учебно-познавательная
компетенция);
2.умение
находить различные способы решения одного уравнения,
содержащего абсолютную величину;
3.
умение ставить цель и планировать деятельность, реализовывать план
(учебно-познавательная компетенция);
4.
умение слушать (коммуникативная компетенция).
Воспитательная
цель: 1. Развивать навыки контроля и самоконтроля
(компетенция личностного самосовершенствования).
2.
Воспитывать ответственность (социально-трудовая компетенция).
Тип занятия: практическая работа.
Ход занятия
Считается, что чем больше способов решения
существует у задачи, тем она интереснее с математической точки зрения. Поэтому уравнения
с модулями можно смело назвать интересными. Рассмотрим пример.
1.
Решить уравнение:
(разобрать пример)
Решение. Постараемся найти как можно
большее количество решений данного уравнения.
Способ №1. «Возведение обеих частей
уравнения в квадрат»
Решение :
1)Возведем обе части уравнения в квадрат.
1) Путем прямой
подстановки в исходное уравнение проверим нет ли посторонних корней.
а) если х=0, то
|2*0+1|=1; |1|=1
б) если х=1, то
|2*1+1|=3; |3|=3
3) Убедились, что
посторонних корней нет.
Ответ: 0; 1.
Способ №2. «Снятие
модуля с помощью числовой прямой».
1)
Для
решения данным методом потребуется найти значение переменной при котором
подмодульное выражение обращается в ноль:
2) Наносим данную точку
на числовую прямую и определяем знаки подмодульного выражения на полученных
промежутках.
2) Раскроем знак
модуля на каждом промежутке в соответствии с полученными данными:
2х(х-1)=0
х=0 х=1
3) Проверим все ли
полученные корни принадлежат данному промежутку. Убедились, что корни уравнения
и
принадлежат
промежутку
Ответ:
0;
1.
Способ №3. «Замена
уравнения смешанной системой».
1) Известно, что:
2) Раскроем модуль: 2х2
+1≥0
2х+1=2х2 +1
2х+1= — (2х2 +1)
1) Неравенство
выполняется при любом значении Следовательно, в
составе системы на него вообще можно не обращать внимания.
2) Решим совокупность
двух упавнений:
Ответ: 0;
2. Упражнения для фронтальной и
самостоятельной работы:
а) |2х-1|=х-3
д) х+|х+1|=11
б) |х-3|=х-2 е)
х-4-|2-х|= -2
в) 3х+1=|х-4 ж)
|х+1| — 2=3
г) |3х+1|+х=9
Разработка
занятия факультативного курса
«Решение уравнений с модулем»
тема: «Решение дрорбно-рациональных уравнений, содержащих модуль»
Обучающая
цель: 1. Сформировать умение решать
дробно-рациональные уравнения, содержащие модуль.
2.
Формировать представление о методах математики, как науки (общекультурная
компетенция).
Развивающая
цель: Развивать 1. умения сравнивать,
анализировать, строить аналогии (учебно-познавательная компетенция);
2.
умение ставить цель и планировать деятельность, реализовывать план
(учебно-познавательная компетенция);
3.
умение слушать, работать в паре (коммуникативная компетенция).
Воспитательная
цель: 1. Развивать навыки контроля и самоконтроля
(компетенция личностного самосовершенствования).
2.
Воспитывать ответственность (социально-трудовая компетенция).
Ход
занятия:
При решении уравнений, содержащих переменную под
знаком модуля, чаще всего применяются следующие методы:
1)раскрытие модуля по определению;
1) метод
интервалов;
2) возведение
обеих частей уравнения в квадрат.
Задание №1. Решить
уравнение
Решение:
если f (x) >0
если f (x) =0
если f (x) <0
Решим данное
уравнение методом раскрытия модуля по определению:
1) Раскроем модуль по определению:
2) Решим
каждую систему в совокупности отдельно:
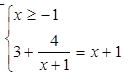
или

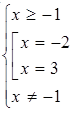
3) Выберем
решение каждой из систем совокупности:
х=3;
х=-5
Ответ:
-5;
3.
Задание
№2. Решить уравнение:
Решение:
Если˂0,
то данное уравнение решений не имеет, так как |х-2|˃0
при любых значениях х.
Если
˃ 0 (х˃0), то
обе части уравнения неотрицательны.
Воспользуемся
методом возведения обеих частей уравнения в квадрат.

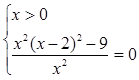
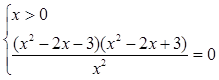
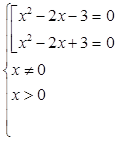
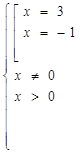
Ответ:
3.
2. Упражнения
для самостоятельной работы:
а)
б)
|х+3|=
в)
|х+4|=
Дидактические материалы для проведения занятия по теме
«Модуль в заданиях ЕГЭ типа №18».
Задание №1. Найдите все
значения a, при каждом из которых уравнение x2 + (a + 4)2
= | x + a + 4 | + | x – a – 4 | имеет единственный корень.
Решение:
При каждом
конкретном значении параметра a функции f(x)
= x2 + (a + 4)2 и g(x) = | x
+ a + 4 | + | x – a – 4 |, входящие в левую и правую
части уравнения, являются четными, поскольку выполняются следующие условия:
1) они определены
на всей числовой прямой (области определения симметричны относительно начала
координат);
2) f(–x)
= (–x)2 + (a + 4)2 = x2 + (a + 4)2 = f(x),
g(–x) = | –x
+ a + 4 | + | –x – a – 4 | = | x – a – 4
| + | x + a + 4 | = g(x).
Следовательно, если число x0
— корень уравнения f(x) = g(x), то число –x0
также будет являться корнем этого уравнения. Условие единственности
будет выполняться, если x = 0 — корень уравнения f(x) = g(x)
и других корней нет.
Подставив в исходное уравнение значение x
= 0,получим уравнение относительно параметра a:
(a
+ 4)2 = | a + 4 | + | –a – 4 | ⇔ (a +
4)2 – 2| a + 4 | = 0 ⇔
|а+ 4 | =0,
|а+
4 |- 2= 0
Отсюда
получаем три значения параметра:
a = –6, a =
–4 и a = –2.
Пусть a = –6. Подставив a =
–6 в исходное уравнение, получим:
х2 + 4 = | x –
2 | + | x + 2 |.
Правая часть этого уравнения после
раскрытия на промежутках модулей имеет вид:
-2х,
если х˂ 2,
|х-2|+|х+2|
= 4, если -2≤ х ≤ 2,
2х, если х≥ 2
Уравнения x2
+ 4 = –2x и x2 + 4 = 2x не имеют корней, а
уравнение x2 + 4 = 4 имеет единственный корень x
= 0, удовлетворяющий условию –2 ≤ x < 2.
Пусть a = –2. Подставив это значение параметра
в исходное уравнение, получим:
х2
+ 4 = | x + 2 | + | x – 2 |.
Как только что было получено, это
уравнение имеет единственный корень x = 0.
Пусть a = –4. Подставив это
значение параметра в исходное уравнение, получим:
х2 = 2| x |
⇔ |х|=0
|х| =2 ⇔ x = 0, x = –2, x = 2.
Значение
a = –4 не соответствует условию задачи.
Ответ:
–6; –2.
Задание №2. Найдите все
значения a, при каждом из которых уравнение
4x – | 3x – | x + a | | = 9| x – 1 | имеет хотя бы один корень.
Решение:
Способ
I.
Запишем
уравнение в виде 9| x – 1 | – 4x + | 3x – | x + a
| | = 0.
Функция f(x) = 9| x –
1 | – 4x + | 3x – | x + a | | непрерывна и
1) неограниченно
возрастает при x ≥ 1, так как при любом раскрытии модулей имеем
f(x)
= 9x – 9 – 4x 3x x a = kx + m,
где k ≥ 9 – 4 – 4 = 1 > 0;
2) убывает при x
≤ 1, так как при любом раскрытии модулей имеем
f(x)
= –9x + 9 – 4x 3x x a = kx + m,
где k ≤ –9 – 4 + 4 = –9 < 0.
Следовательно,
наименьшее значение функция f принимает при x = 1, и уравнение f(x)
= 0 будет иметь корень тогда и только тогда, когда f(1) ≤ 0.
Решим это неравенство:
| 3 – | 1 + a | | ≤ 4, –4
≤ 3 – | 1 + a | ≤ 4,
| 1 + a |
≤ 7, –7 ≤ 1 + a ≤ 7, –8 ≤ a ≤ 6.
Способ II.
Запишем уравнение следующим образом: | 3x
– | x + a | | = 4x – 9| x – 1 |.
Раскрывая
модули в выражении, стоящем в правой части уравнения, получим:
g (x)= 4х-9|х-1|
= -5х+9, если х≥ 1
13х – 9, если х˂1
Для существования решения уравнения должно
выполняться условие
g(x) ≥ 0˂=˃
.
На отрезке исходное уравнение равносильно
совокупности двух уравнений:
3х- |х+а |= 4х-
9| х-1|
3х- |х+а |=- 4х+ 9|х- 1|,
| х+а|=-х+ 9|х-
1|
|х+а |= 7х- 9|х- 1|.
Раскрывая модули в правых частях уравнений
совокупности, получим замкнутую ломаную, звенья которой — отрезки прямых,
имеющих уравнения y = –2x + 9 (AD), y = 8x –
9 (CD), y = 16x – 9 (BA) и y = –10x +
9 (CB)
При каждом фиксированном
значении параметра a график функции yа(x)
= | x + a | получается параллельным переносом графика функции
y = | x | вдоль оси Ox на –a
единиц.
Имеется два
критических положения графика функции yа(x) = | x +
a |. В обоих случаях он проходит через точку A(1; 7). Из условия yа(1)
= 7 получаем уравнение | 1 + a | = 7. Отсюда a1 = –8 и
a2 = 6.
Соответственно,
исходное уравнение будет иметь решение при –6 ≤ –a ≤
8 или –8 ≤ a ≤ 6. При других значениях параметра a график
функции
уа(x) = | x
+ a | не будет иметь общих точек с ломаной AВСD.
Ответ: –8 ≤ a ≤
6.
Задание №3. Найдите
все значения а, при каждом из которых функция f(x)=х2-3|х-а2|-5х
имеет более двух точек экстремума.
Решение:
При х ≥ а2 f(x)=х2-8х+3а2,
поэтому график функции есть част параболы с ветвями, направленными вверх, и
осью симметрии х=4.
При х ≤ а2
f(x)=х2-2х-3а2,
поэтому график функции есть част параболы с ветвями, направленными
вверх, и осью симметрии х=1.
Все возможные виды графика функции f(x)
показаны на рисунках.
Обе параболы проходят через точку (а2; f(а2)).
Функция у= f(x) имеет более двух точек
экстремума, а именно три, в единственном слечае: 1˂а2˂4,
откуда 1˂|а|˂2.
Ответ: -2˂а˂-1;
1˂а˂2.
Дидактические материалы для проведения занятия по теме
«Модуль в заданиях ЕГЭ типа №13».
Задание №1. Решите уравнение:
|
cos x | = sin x .
Решение. Из данного
уравнения получаем равносильную систему
cos x =
sin x
tg х=
cos x = sin x
˂=˃ tg х=
sin х ≥0
sin х ≥0
х =
+2
п, п
Z
˂=˃
х =- +2
п, п
Z
sin х ≥0
Так
как функции tgx и sin x имеют общий наименьший положительный
период
2 , то отбор корней
проведем на тригонометрическом круге.
Ответ: х = +2
k,
+2
п; k, п
Z.
Задание №2. Решите уравнение:
|
cos x | =
cos x
+
2sin x
.
Решение:
Рассмотрим две
области на числовой прямой, на которых cos x ≥ 0 и cos x ˂ 0.
1) Пусть cos x ≥ 0 , тогда данное уравнение
принимает вид:
cos x = cos x
+
2sin
x ˂=˃
sin
x =
0
˂=˃
x
=π n, nZ.
Условию cos x ≥ 0 удовлетворяют только значения x
=
2πn,
nZ.
2) Для условия cos x ˂ 0 исходное уравнение
перепишем в таком виде и решим его:
— cos x = cos x
+
2sin
x
— 2 cos x = 2sin x
sin x + cos x
=
0
tgx +1 =0 ˂=˃
tgx =-
1
˂=˃ х=+
k; k
Z.
Условию
cos x ˂
0
удовлетворяют только значения х=+
k; k
Z.
.
Ответ: 2π n, nZ;
+
k; k
Z.
Задание №3. Найти все решения уравнения 2 cos 2 x —|1+2 1
на отрезке [0;4].
Решение:
1) Перепишем уравнение в виде |1+2=2 cos 2 x-1
2) Раскрывая знак модуля, получаем совокупность:
1+2
≥0
1+2
=2
cos 2 x-1
1+2˂0
—1-2=2
cos 2 x-1
3) Решим
каждую систему совокупности отдельно:
1+2
≥0
1+2˂0
1+2=2 cos 2 x-1 или —1-2
=2 cos 2 x-1
а) Решим первую полученную систему в
совокупности. С помощью формулы cos
2 x=1- 2
получим:
1+2
≥0
≥
2
+
=0
˂=˃
˂=˃ х=π n,
nZ
=
х=(-1)k+
k; k
Z.
Точка +
=
≈3,55
б) Решим вторую
полученную систему:
1+2
˂0
˂
—1-2=2 cos 2 x-1 ˂=˃
2—
-1=0
Данная система
решения не имеет.
Промежутку [0;4]
принадлежат корни: 0; ;
.
Ответ: 0; ;
.
Задания для самостоятельной работы:
а)
2sin2x=
||
б)
|х+3|
cos х=х+3
Скачано с www.znanio.ru
ЕГЭ по математике профильного уровня — один из самых сложных экзаменов. Планируете сдавать его, но не знаете, с чего начать? Этот экзамен не покажется вам таким трудным, если вы узнаете про него побольше и грамотно подготовитесь. В этой статье обсудим, что нужно знать про ЕГЭ по математике 2023, из каких разделов он состоит и как к нему подготовиться.
Какие темы важно знать для ЕГЭ по математике 2023?
В математике, как и в любом предмете, есть опорные темы. Если вы их выучите, будет легче справиться с экзаменом.
Формулы тригонометрии
Очень важно знать формулы тригонометрии и уметь применять их. Хорошая новость: в справочных материалах можно найти несколько тригонометрических формул.
Но формул гораздо больше. Я советую не зубрить их, а научиться выводить: приходить к формулам шаг за шагом, опираясь на тождества. Кстати, мы учим выводить формулы на курсах подготовки к ЕГЭ: это полезно, чтобы оказаться на экзамене во всеоружии и ничего не перепутать.
Квадратные уравнения
Эти уравнения мы учимся решать еще в 7 классе. Они встречаются в ЕГЭ по математике постоянно: и как самостоятельные задания, и внутри более сложных уравнений или неравенств. Квадратные уравнения могут встретиться в математических моделях № 9 и № 15, в задачах на геометрию и стереометрию, в задании № 17 с параметром.
Самое главное — хорошо знать универсальные методы решения. Первый — через формулу дискриминанта, второй — через теорему Виета, которая может сэкономить время на экзамене.
Треугольники
Эта замечательная тема, которую проходят в 7 классе — основа основ всей геометрии. Она нужна и для решения стереометрии, и для простейших планиметрических задач. Еще треугольники необходимы, чтобы освоить огромное количество теорем. Выучите все, что с ними связано! Особое внимание обратите на прямоугольные треугольники, которые встречаются чаще остальных — тогда геометрические задачи сразу станут проще.
Проценты
Самая нелюбимая тема моих учеников после тригонометрии, которую необходимо хорошо знать. Проценты нужны для реальной математики — это № 9 (с кратким ответом) и № 15 (с развернутым ответом). Понимание этой темы может принести вам 3 первичных балла.
План успешной подготовки к ЕГЭ по математике 2023
Если вы хотите получить больше 80 баллов на ЕГЭ, нужно идеально решать часть с кратким ответом, а также справляться с большинством заданий с развернутым ответом.
Чтобы постепенно прорабатывать материал, воспользуйтесь кодификатором. В нем обратите внимание на таблицу 2, а именно на блоки:
- Алгебра
- Уравнения и неравенства
- Элементы комбинаторики, статистики и теории вероятностей
- Функции
- Начала математического анализа
- Геометрия
Ориентируйтесь на указанную последовательность, но геометрию изучайте параллельно с остальными блоками — на нее нужно больше времени.
Самое главное — ни в коем случае не ограничивайтесь теорией. Ее у вас не спросят на экзамене, а вот задания решать придется. Поэтому тренируйте практические навыки: актуальные задания вы сможете найти в открытом банке заданий на сайте ФИПИ или в нашем тренажере «Решутест».
Как решать часть с кратким ответом
Ни в коем случае не пренебрегайте частью с кратким ответом! Иначе будет обидно: например, вы наберете за экономическую задачу № 15 полные 2 балла, но потеряете их в двух заданиях первой части. Это актуально для всех ЕГЭ: подробнее о том, как идеально справляться с первой частью экзамена, читайте здесь.
Еще одно заблуждение: «часть с кратким ответом простая, к ней можно не готовиться». Даже в первой части иногда встречаются такие задания, которые ученики даже не решают, потому что не готовились к ним.
Как я уже говорила, часть с кратким ответом содержит 11 заданий. Начинать подготовку необходимо именно с заданий базового уровня сложности, потому что это та основа, на которую потом накладывается более сложная теория.
Что касается задач повышенного уровня сложности, то среди каждого номера есть лайфхаки, например, в этой статье я уже рассказывала про № 11, в котором нужно работать с производной.
Задания с развернутым ответом: немного статистики
Многие думают, что эта часть ЕГЭ по математике очень сложная. Поэтому ребята, которые не рассчитывают на высокие баллы, даже не приступают к ней. И очень зря! С помощью этих заданий можно заработать дополнительные баллы и побороться за высокое место в рейтинге.
Сейчас будет немного статистики. В среднем около 35% учеников получают полные 2 балла за решение № 12, а вот неравенство № 14 дается хуже, только около 12% с ним справляются на полный балл. Геометрия даётся ещё хуже: стереометрию № 13 полностью решают 2% выпускников, планиметрию (№ 16) менее 5%. А вот с экономической задачей (№ 15) справляются около 20%, а это целых 2 балла! Что касается № 17 и 18, то они даются ещё хуже, но на то они и самые сложные, хотя 1 балл за № 18 по статистике получают около 25% сдающих — там нужно просто привести пример.
Особенности уровней ЕГЭ по математике
В 2015 году ЕГЭ по математике разделили на базовый и профильный уровни. Это упростило жизнь выпускникам, которые не планируют поступать на специальности, связанные с математикой. Если ЕГЭ по математике нужен только для получения аттестата, можно сдать его облегченную версию, оставив время и силы для профильных экзаменов.
Базовый уровень ЕГЭ по математике
Как устроен базовый ЕГЭ по математике? Экзамен идет 180 минут, он состоит из 21 задания, за каждое из которых можно получить 1 балл. Этот экзамен единственный, который переводится не в 100-бальную систему, а в оценки.
В ЕГЭ по математике базового уровня 6 тематических блоков:
Также обратите внимание, что базовый ЕГЭ по математике не поменялся с точки зрения наполнения, изменился лишь порядок заданий. Вот что пишут ФИПИ:
Подробнее про базовый ЕГЭ по математике, включая разбор всех заданий, читайте здесь, а мы перейдём к профильному.
Профильный уровень ЕГЭ по математике
Данный экзамен, как и остальные ЕГЭ, переводится в 100-бальную систему:
Экзамен состоит из двух частей: Часть 1 с кратким ответом, а Часть 2 — с развернутым. Длится он 235 минут. Всего есть 18 заданий, которые разделены на 3 блока: алгебра, геометрия и реальная математика. Максимальное количество первичных баллов — 31.
База, профиль — неважно, к какому именно уровню вы готовитесь. В любом случае надо не только правильно решить каждое задание, но и оформить его так, чтобы проверяющие ни к чему не придрались. Нарисовать и описать график, расписать решение уравнения или задачи… И это не все: нужно еще и внести ответы в бланк без ошибок. И все это — за ограниченный период времени! Так можно перенервничать и запороть даже самую простую задачку. А на ЕГЭ — каждый балл на счету.
Поэтому на своих занятиях я сразу показываю своим ученикам, как правильно оформлять каждое задание в ЕГЭ по математике. Мы разбираем все критерии и учимся правильно отвечать на вопросы. А еще я всегда помогаю ученикам закрыть пробелы в знаниях и объясняю сложные темы столько раз, сколько нужно. И куда же без лайфхаков? Всегда рассказываю лучший способ решения типичных заданий. Так что мои ученики приходят на экзамены подготовленными и не нервничают, когда видят задачу. Хотите также? Приходите ко мне на курсы подготовки к ЕГЭ по математике — научу!
Структура ЕГЭ по математике 2023
Часть 1:
- Приносит 11 баллов, то есть 35% всего экзамена
- 11 заданий с кратким ответом
Часть 2:
- Приносит 20 баллов, то есть 65% всего экзамена
- 7 заданий с развернутым ответом
Внимание! Вся нумерация заданий в статье соответствует ЕГЭ 2023 года.
В заданиях с кратким ответом нужно лишь записать верное число в бланк. Заданий с развернутым ответом 7, в них нужно подробно расписать решение, которое должно соответствовать критериям оценивания.
ЕГЭ — стандартизированный экзамен, поэтому каждое задание всегда соответствует определенной теме.
Обратите внимание, что по сравнению с 2022 годом, в части 1 изменился только порядок заданий. Сами сотрудники ФИПИ говорят следующее:
Задания с кратким ответом принесут вам до 11 первичных баллов (64 вторичных). Если не понимаете, что это за баллы и откуда они берутся, почитайте эту статью. Самая популярная цель на ЕГЭ по математике — набрать 80 баллов, для этого раньше было необходимо 19 первичных баллов. Ранее многие ученики пользовались рабочей стратегией — решить всю часть с кратким ответом, а также № 12, 14 и 15. Если хорошо разбирались в геометрии, выбирали № 13 и 16 — или использовали их как запасные задания. Сейчас стратегия должна быть другая, так как № 13 (стереометрия) стал стоить дороже — 3 балла вместо 2, а № 15 (экономическая задача) — подешевел с 3 баллов до 2. Изменилась также шкала перевода баллов, поэтому подумайте, какими заданиями вы сможете набрать необходимое количество первичных баллов.
Разделы ЕГЭ по математике
- Алгебра и начала анализа — 8 заданий, 13 первичных баллов
- Геометрия — 4 задания, 8 первичных баллов
- Реальная математика — 6 заданий, 10 первичных баллов
Какие задания входят в ЕГЭ по математике?
Здесь вам на помощь приходят документы с официального сайта ФИПИ: кодификатор, демоверсия и спецификация.
- Кодификатор — это краткий перечень всех блоков и тем, которые включены в экзамен.
Сейчас кодификатор общий для обоих уровней экзамена, как базового, так и профильного. Он снова представляет собой единый документ, так что не запутаетесь.
- Демоверсия — типовой вариант ЕГЭ. Он показывает уровень экзамена и ориентировочную сложность заданий.
- Спецификация — это документ, описывающий структуру экзамена и разбалловку.
Что в итоге
Теперь вы знаете больше про ЕГЭ по математике 2023. Вы познакомились со структурой и поняли, на что стоит обращать внимание при подготовке. А еще узнали, что первую часть обязательно решать на максимум, а вторая не такая страшная, как кажется. Но наверняка у вас еще осталась куча вопросов: по оформлению и конкретному решению каких-то заданий точно.
Обо всем этом я подробно рассказываю своим ученикам во время подготовки к ЕГЭ по математике. Мы изучаем все непонятные темы, а потом прорешиваем много однотипных заданий — так легче запоминается формат. Еще мы всегда проводим пробные экзамены, чтобы выявить слабые места. Я анализирую ошибки каждого ученика и индивидуально разбираю их с ними. Благодаря этому мои выпускники гарантированно сдают ЕГЭ на 80+. Если вы хотите оказаться среди них — записывайтесь на курсы!
Система подготовки обучающихся к ЕГЭ по математике
Ильяшева Зайра Жумадельевна, учитель математики БОУ г. Омска
«Средняя общеобразовательная школа №53».
Существует множество вариантов подготовки учащихся к итоговой аттестации. Но, идеального варианта подготовки не существует. Хочу поделиться опытом своей работы по подготовке обучающихся 11кл к с сдаче итоговой аттестации.
Основные трудности при подготовке к ЕГЭ
1) Нетипичность формулировок заданий в вариантах ЕГЭ. В учебниках используются стандартные формулировки. Слабых обучающихся незнакомые формулировки заданий ставят в тупик, хотя после пояснений они легко с ними справляются. 2) Непредсказуемость содержания заданий. 3) Насыщенность программы по математике новым материалом в 11 классе, который учителя вынуждены преподавать до марта, значит, подготовка к ЕГЭ в большом объеме идет во внеурочное время, что ведет к перегрузке обучающихся. 4) Демонстрационные материалы, предлагаемые для тренировки обучающихся, имеют большие расхождения с реальными вариантами ЕГЭ
Непредсказуемость содержания заданий ЕГЭ;
Нетипичность и многообразие формулировок заданий в вариантах ЕГЭ;
Невозможность проведения системного анализа результатов ЕГЭ;
Сокращение часов математики в старшей школе;
Нехватка времени для специализированной подготовки к ЕГЭ
Организация и планирование работы по подготовке учащихся к ЕГЭ по предмету;
Отсутствие специальной методики, педагогической системы подготовки учащихся к ЕГЭ;
Необходимость готовить к сдаче ЕГЭ всех учащихся класса в обязательном порядке;
Большая наполняемость классов
Цели и задачи:
Подготовить всех учащихся к успешной сдаче ЕГЭ с хорошим качеством
Для этого необходимо:
-Учителю обладать необходимыми компетенциями (самому уметь решать задачи ЕГЭ)
-Совершенствовать структуру и содержание учебного материала в ходе подготовки к ЕГЭ
-Систематизировать повторение программного материала
-Отработать тестовые технологии в ходе работы с контрольно-измерительными материалами через личностно-ориентированный подход.
При подготовке обучающихся к ЕГЭ выделяю следующие направления деятельности:
1) Методическая подготовка учителя к ЕГЭ. Знакомлюсь с нормативными документами по проведению ЕГЭ, посещаю семинары по подготовке к ЕГЭ. Повышаю свой уровень профессиональной грамотности (развиваю свои способности при решении заданий части С) через самообразование.
2) Создание банка тестовых заданий. В банк входят: тесты по основным темам курса; тренировочные тесты; итоговые тесты; тесты экзаменов прошлых лет; тесты пробных экзаменов.
Работа в тестовых технологиях должна занять определенное место не только в системе контроля образовательных достижений, но и вообще в системе уроков уже в основной школе (5-9 классах). Технологичность тестовых заданий позволяет обращаться к ним часто и без существенного ущерба для других форм и методов работы. В связи с этим учитель должен накопить определенную базу тестовых заданий по всем темам школьного курса
Методы работы с тестами
Необходимо
внедрять в учебный процесс разноуровневые тематические тесты;
обратить внимание на формулировки вопросов;
Укажите промежуток, которому принадлежит корень уравнения…
Выберите наибольшее целое число из промежутка…
Укажите наименьшее натуральное решение неравенства…
Найдите число целых решений неравенства…
Найдите среднее арифметическое натуральных решений системы неравенств…
Все тренировочные тесты стараюсь проводить с ограничением времени, чтобы учащиеся могли контролировать себя – за какое время сколько заданий они успевают решить.
3) Организация вводного, текущего и итогового повторения. Провожу вводное повторение, текущее (по горизонтали); итоговое (по вертикали) и повторение, ориентированное на индивидуальный уровень подготовки обучающихся.
Ключевым моментом по подготовке к ЕГЭ считаю ведение
«Тетрадей по теории», для записи формул, теорем, блок-схем, алгоритмов решения типовых заданий и др. которые ведутся учащимися с 5 класса. Таким образом, у ребят имеется полный комплект материалов по основным темам школьной программы. Такой приём позволяет иметь всю информацию в одном месте и вместе с тем даёт возможность быстро находить нужный раздел
В целях эффективного использования времени на экзамене, учу школьников приемам быстрого и рационального счета. Например, добиваться применения формулы корней квадратного уравнения с четным вторым коэффициентом, разложением на множители подкоренного выражения при извлечении квадратного корня, вычислении значения дробного выражения вида
Для достижения правильности и беглости устных вычислений, преобразований, решения задач в течение всех лет обучения в среднем и старшем звене на каждом уроке стараюсь отводить 5-7 минут для проведения упражнений в устных вычислениях, предусмотренных программой каждого класса.
Повторение темы «Текстовые задачи»
-задачи на проценты
-задачи на прогрессии
-задачи на смеси и сплавы
-задачи на совместную работу
-задачи на движение.
4) Диагностика и анализ качества знаний обучающихся при подготовке к ЕГЭ: — входное диагностирование учащихся 11 класса за курс 10 класса, — тематическое тестирование по основным разделам курса, — контрольные зачеты по алгебре и началам анализа в конце 11 класса, — пробные ЕГЭ.
Основная цель подобных работ – оперативное получение информации о качестве усвоения определенных тем, анализ типичных ошибок и организация индивидуальной работы с учащимися по устранению пробелов в знаниях. Ребята выполняют работы над ошибками каждой проверочной работы: результаты оперативно доводятся до сведения родителей, что, в свою очередь, благоприятно сказывается на дальнейшем процессе обучения.
|
ФИ |
№ 1 |
№ 2 |
№ 3 |
№ 4 |
№ 5 |
№ 6 |
№ 7 |
№ 8 |
№ 9 |
№ 10 |
№ 11 |
№ 1 2 |
|
Иванова |
5) Организация самостоятельной работы обучающихся при подготовке к ЕГЭ. помимо работы с учителем учащиеся должны и самостоятельно получать знания, поэтому рекомендую учащимся сайты Интернета, где собран теоретический материал, а также сайты, где ученики могут самостоятельно проверить уровень своей подготовки, работы в режиме онлайн .
1. сайт Федерального института педагогических измерений (ФИПИ). Можно скачать ДЕМО-версии ЕГЭ по всем предметам, в том числе и по математике. Есть Открытый банк заданий ЕГЭ по предметам;
2. официальный информационный портал ЕГЭ. Общие сведения о ЕГЭ (расписание, бланки, советы, демоверсии, консультации и т.д.), материалы для выпускников 11-х классов и поступающих в ВУЗы и ССУЗы;
3. официальный сайт Рособрнадзора;
4. «ЕГЭ-портал. Мы знаем о ЕГЭ все» http://4ege.ru/novosti-ege/1532-shkala-perevoda-ballov-ege.html ;
5. открытый банк заданий по математике ЕГЭ;
6. сайт Ларина А.А. «Математика. Репетитор». Есть генератор вариантов ЕГЭ;
7. Д. Гущин «Решу ЕГЭ». Базы заданий для портала «РЕШУ ЕГЭ» составлены на основе следующих источников: задания открытых банков и официальных сборников для подготовки к ЕГЭ; демонстрационные версии ЕГЭ и экзаменационные задания, разработанные ФИПИ; диагностические работы, подготовленные МИОО; тренировочные работы, проводимые органами управления образованием в различных регионах Российской Федерации. Все используемые в системе задания снабжены ответами и подробными решениями;
8. ЕГЭ IОГЭ. Информационный образовательный портал. Документы, материалы, пособия, пробники к ЕГЭ и ОГЭ. http://egeigia.ru /;
9. учебные (справочные) пособия для подготовки к ЕГЭ (книги, сборники тестов в форматах djvu/zip и pdf/zip) http://www.alleng.ru/edu/math3.htm .
Особенно часто использую в работе сайт Александра Ларина. Обучающиеся решают различные варианты, проверяю, данные вношу в таблицу, и в течение года я вижу динамику каждого обучающегося. Задания, с которыми ребята не смогли разобраться самостоятельно, обсуждаем на консультациях или уроках.
Очень важны уроки итогового повторения в конце 11 класса. Они дифференцированно ориентированы. Без ИКТ на этих уроках на обойтись: слайды с устными заданиями, с тестовыми заданиями ( uztest.ru ), с заданиями из 2 части, с показами готового решения и оформления для проверки, видеоуроки ( http://egetrener.ru / )
6) Психологическая подготовка обучающихся к ЕГЭ. Для всех учащихся 11 класса во втором полугодии провожу занятия «Как готовиться к экзаменам», «Как справиться с тревогой». ИЛИ оформляю информационный стенд в кабинете.
На занятиях обсуждаю вопросы: как оборудовать рабочее место для подготовки к экзаменам, составить план занятий, разработать индивидуальный режим дня, с чего начать занятие, учитывать особенности запоминания, использовать методы релаксации и активизации, приемы снижения экзаменационной тревожности, как организовать день перед экзаменом, настроить свои мысли на успех, как вести себя на экзамене, использовать полезные ссылки на Интернет-ресурсы по подготовке к ЕГЭ. Одним из существенных аспектов психолого-педагогического сопровождения выпускника, на мой взгляд, является ознакомление родителей со способами правильного общения с ним, оказания ему психологической поддержки, создания в семье благоприятного психологического климата. Работа с родителями нацелена на повышение осведомленности родителей и формирование реалистичной картины, экзамена, снижение родительской тревоги. На родительских собраниях были даны рекомендации по организации режима дня старшеклассников, поддержке и помощи детям в период до, во время и даже после экзаменов,
Что поможет подготовке?
Неоднократная репетиция ситуации экзамена, формирование адекватной оценки, позитивный настрой на экзамен;
Тренинг по совершенствованию вычислительных навыков;
Организация зачётов по вопросам функциональной грамотности, типологии выражений, функций, уравнений и неравенств по методам решения, по вопросам тождественных преобразований выражений и равносильности уравнений;
Регулярное проведение уроков обобщения;
Своевременная систематизация материала на этапах повторения;
С помощью сайта Ларина и http://uztest.ru/ организую контроль знаний учащихся. Здесь имеется более 13000 задач по всем разделам школьной математики. Также использую сайт учителя Савченко Е.М. (пи), Горкуновой Ольги. Программа сайта http://uztest.ru/ автоматически формирует индивидуальные задания для каждого ученика, согласно заданным учителем условиям, не нужно тратить время на проверку заданий – результаты выполнения работ учащихся видны на компьютере. На сайте Александра Ларина сейчас в генераторе ЕГЭ уже появились ответы.
Широко использую в своей работе Интернет — порталы ЕГЭ http://www.egeru.ru/, http://uztest.ru/, где пробное тестирование учащихся проводится в онлайн-режиме по заданиям, аналогичным тем, которые будут у выпускников на ЕГЭ, с последующим оцениванием их ответов.
Большую часть материала по видам заданий учащиеся смогли почерпнуть из Открытого банка заданий ЕГЭ по математике (http://mathege.ru).Здесь есть каталог по заданиям, по содержанию, по умениям. На страницах этого сайта можно не только взять ту или иную информацию по интересующей теме, но и выполнить тренировочные и диагностические работы в режиме on-line. Предложенная система позволяет каждому учащемуся выполнять задания в необходимом для него количестве и в доступном для него темпе, независимо от объёма работы и скорости её выполнения остальными.
Используя сайты http://shpargalkaege.ru , делаю подборку заданий первой части, представляю задания, используя презентацию или распечатку в виде текстового документа.
7) Как помочь ученику успешно сдать экзамены в условиях нехватки времени и большого объёма информации/
Цель тест-классов
«Тестовая подготовка школьников к итоговой аттестации» с использованием авторских
программ ведущих преподавателей омских вузов.
Цель элективного курса: оказание индивидуальной и систематической помощи выпускнику при систематизации, обобщении и повторении курса алгебры и подготовке к экзаменам.
Задачи курса:
1) подготовить учащихся к экзаменам;
2) дать ученику возможность проанализировать и раскрыть свои способности;
Во-первых, все такие задачи решаются по единому алгоритму, о котором мы вам расскажем. Во-вторых, многие из них однотипны — это задачи на движение или на работу. Главное — знать к ним подход.
Внимание! Чтобы научиться решать текстовые задачи, вам понадобится всего три-четыре часа самостоятельной работы, то есть два-три занятия. Всё, что нужно, — это здравый смысл плюс умение решать квадратное уравнение. И даже формулу для дискриминанта мы вам напомним, если вдруг забыли.
А ведь большинство задач №11 решается по вполне четким алгоритмам с ис- пользованием ясных и понятных формул Задания №11. Текстовые задачи www.alexlarin.net 2 и схем. По опыту авторов, научить решать большинство задач №11, содержащихся в открытом банке, можно практически любого выпускника. Безусловно, при этом определяющими факторами являются желание и стремление ученика, а также математическая и методическая грамотность преподавателя, его умение четко и ясно изложить на первых порах именно алгоритмы решения. Без первых удачных опытов у ученика не пройдет страх перед текстовыми задачами, а для этих опытов, на наш взгляд, нужны именно четкие алгоритмы.
Хочется отметить, что ЕГЭ не должен быть «головной болью» только учителей математики. В этом процессе важно задействовать всех педагогов и все предметные методические объединения. Независимо от того, вынесен тот или иной предмет на единый государственный экзамен или нет. В противном случае проблемы ЕГЭ останутся проблемами отдельных учителей, что сделает невозможным решение перспективных задач, поставленных перед школой. К примеру, существенную помощь в подготовке к ЕГЭ по математике могут оказать учителя химии, отработав методы и способы решения задач на смеси, сплавы. Учителя физики могут помочь не столько в решении задач №10, сколько в пояснении физического смысла задачи. Сложно подготовить обучающихся к ЕГЭ, это большой труд. Но не нужно этого бояться. Если вы хорошо знаете, объясняете, любите свой предмет и своих учеников, вы обязательно сможете подготовить их к ЕГЭ по математике. А каждый обучающийся должен помнить слова известного швейцарского математика Джорджа Полиа: «Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их».





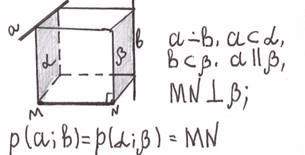
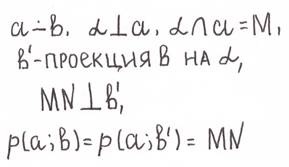
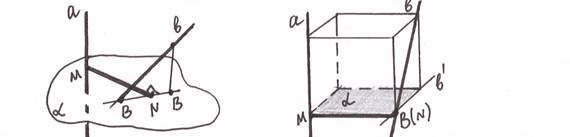
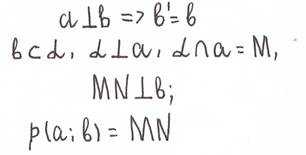

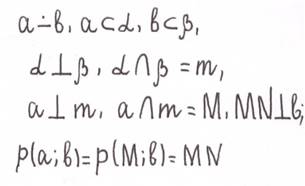
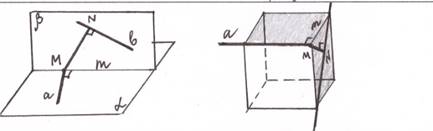
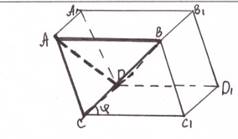
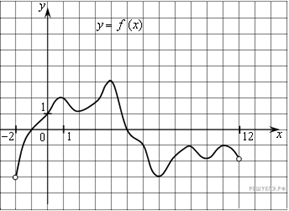

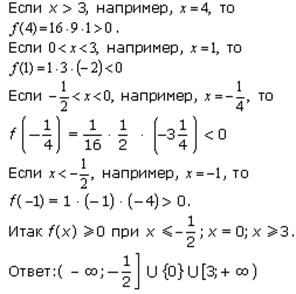
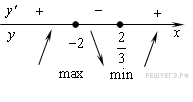
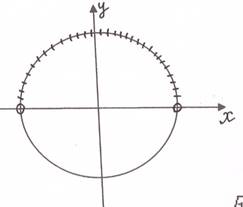
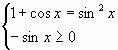
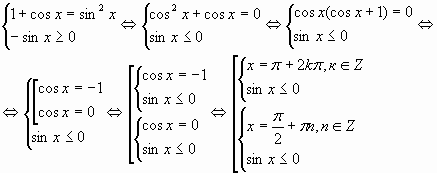
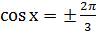
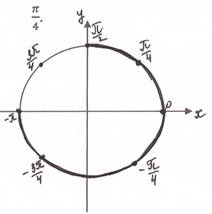
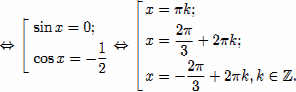
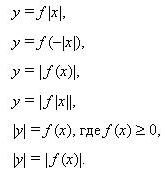
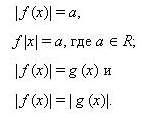
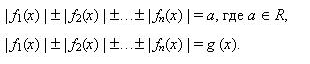
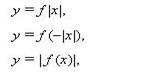
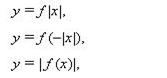
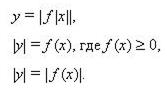
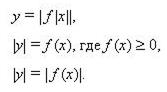
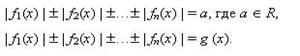
![[ |f(x)| = g(x)Leftrightarrow begin{cases} g(x)geqslant 0 \ left[begin{array}{l}f(x) = g(x) \ f(x)=-g(x)end{array}right. end{cases} ]](https://fs.znanio.ru/8c0997/89/0d/aaef2ae2e60a184b71e086b73e2f134054.png)