Решение задач
*** КАНАЛ ЮТЬЮБ ***
Выберите номер задания ЕГЭ с разбором примеров:
Структура заданий ЕГЭ по информатике
С 2021 года структура заданий и начисления баллов:
- Длительность ЕГЭ по информатике составляет 3 часа 55 минут или 235 минут.
- Задания выполняются с помощью компьютера. На протяжении всего экзамена будут доступны текстовый редактор, редактор электронных таблиц и системы программирования.
- На ЕГЭ допустимо использование следующих языков программирования: С++, Java, C#, Pascal, Python, Школьный алгоритмический язык.
- На экзамене будет разрешено использование программы Microsoft Windows «Калькулятор», а также графического редактора Microsoft Paint.
- При проведении ЕГЭ по информатике выдача КИМ на бумажных носителях не планируется.
- Кроме того, учащемуся будет предоставлен бумажный черновик для решения заданий «на бумаге». Но ответ необходимо внести в систему на компьютере.
- Задания ЕГЭ по информатике делятся на два типа: с использованием заготовленных на компьютере файлов (для выполнения которых требуется использование специализированного программного обеспечения) и без использования таковых.
- По уровню сложности: Базовый – 10 заданий (с № 1 по № 10), Повышенный – 13 (с № 11 по № 23), Высокий – 4 (с № 24 по № 27).
- Максимальный первичный балл за работу – 30.
- Общее время выполнения работы – 235 мин
Инструкция для участника КЕГЭ по использованию ПО для сдачи экзамена по информатике и ИКТ в компьютерной форме
Дата проведения (ГИА) ЕГЭ по информатике в 2023 году (ФИПИ)
Досрочный период:
Основной период:
Резерв:
Дополнительный период:
Шкала перевода баллов ЕГЭ по информатике
Таблица перевода первичных баллов в тестовые баллы для проведения ЕГЭ:
(* таблица является ориентировочной (проект), данные уточняются, шкалы для 2023 года пока нет)
| Первич балл |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тестов балл |
7 | 14 | 20 | 28 | 35 | 40 | 44 | 46 | 49 | 51 | 54 | 56 | 59 | 61 | 64 | 66 | 69 | 71 |
| Первич балл |
19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Тестов балл |
74 | 77 | 80 | 82 | 85 | 87 | 90 | 92 | 95 | 97 | 100 |
Минимальное количество баллов в 2021 г. — 43 балла
1 балл начисляется за выполнение заданий 1-24
2 балла начисляется за выполнение заданий 25-27
Тренировочные варианты (КИМы)
Научно-практическая конференция
«Шаг в будущее»
Тема доклада «Методы решения заданий ЕГЭ по информатике»
Выполнил ученик 11 класса МБОУ СОШ с.Хондергей
Монгуш Ай-Херел
Руководитель: Ховалыг Ш.Г., учитель информатики
Февраль 2019г.
Тема: «Методы решения задач ЕГЭ по информатике»
Проблема: Как успешно сдать ЕГЭ?
По окончанию школы каждый ученик должен сдать ЕГЭ. Немалые несдавшие ЕГЭ учащиеся не получают аттестаты. А для успешной сдачи ЕГЭ нужна тщательная подготовка. Поэтому вопрос «Как успешно сдать ЕГЭ?» остается актуальным для всех выпускников. Поэтому я выбрал тему «Методы решения задач ЕГЭ по информатике».
Цель: изучить методы решения заданий единого государственного экзамена по информатике
Задачи:
- Собрать различные задания из тренировочных вариантов ЕГЭ;
- Решить задачи ЕГЭ;
- Выявить, сколькими разными способами можно решить данные задачи.
Гипотеза:
Если научиться решать задачи ЕГЭ по информатике с разными способами, то можно успешно сдать ЕГЭ по информатике.
Рассмотрим несколько заданий из ЕГЭ.
Задача 1.
Сколько единиц в двоичной записи восьмеричного числа 3458?
1 способ. Число из восьмеричной системы счисления перевести в десятичную. Из десятичной системы счисления перевести в двоичную.
3458 = 3*82 + 4*81 + 5*80= 192+32+5=229.
22910 = 111001012. Вычислить количество 1 в двоичной записи.
Ответ: 5.
2 способ. Таблица соответствия.
|
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
|
2 |
0 |
0 |
1 |
0 |
|
3 |
0 |
0 |
1 |
1 |
|
4 |
0 |
1 |
0 |
0 |
|
5 |
0 |
1 |
0 |
1 |
|
6 |
0 |
1 |
1 |
0 |
|
7 |
0 |
1 |
1 |
1 |
|
8 |
0 |
0 |
0 |
0 |
|
9 |
1 |
0 |
0 |
1 |
|
A |
1 |
0 |
1 |
0 |
|
B |
1 |
0 |
1 |
1 |
|
C |
1 |
1 |
0 |
0 |
|
D |
1 |
1 |
0 |
1 |
|
E |
1 |
1 |
1 |
0 |
|
F |
1 |
1 |
1 |
1 |
См слайд 8.
3 способ. С помощью таблицы степени 2.
|
I |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
2i |
1024 |
512 |
256 |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
См. слайд 9. 1 1 1 0 0 1 0 1
3458 = 22910
229 = 128+64+32+4+1.
Наибольшее число 128. Под таблицей отметим 1.
128 есть. Отметим 1.
64 есть – отметим 1.
32 есть – отметим 1.
4 есть. Отметим 1.
1 есть. Отметим 1.
В остальных случаях отметим 0.
Получилось двоичное число 11100101.
В двоичном числе количество единиц — 5. Ответ 5.
4 способ. С помощью позиции чисел.
Представим число с помощью степеней двойки
229 = 128+64+32+4+1 = 27 + 26 + 25 + 22 + 20. Наибольший степень эта 7. Отметим позиции числе от 7 до 0.
Позиции: 7 6 5 4 3 2 1 0. Отмети если 27 есть, то под числом 7
1 1 1 0 0 1 0 1 отметим 1. Если 26 есть,то под числом
6 отметим 1. А если 23 нет среди
слагаемых, поставим 0 и т. д.
Получилось двоичное число 11100101. Количество единиц 5.
Правильность выполнения задания можно проверить с помощью калькулятора.
Задача 5.
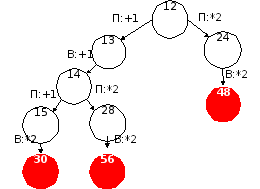
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный двоичный код, допускающий однозначное декодирование. Для букв А, Б, В и Г используются следующие кодовые слова: А — 10, Б — 00, В — 010, Г – 110. Укажите кратчайшее кодовое слово для буквы Д, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
1 способ: Посмотрим на таблицу. Нам понадобится восьмиричная СС. Между числами 010 и 110 лежит 3 числа. Среди них наименьшее 011.
2 способ графический. Построим дерево, у которого из корня и любой вершины выходят по две ветви. Сопоставим каждой левой ветки 0, а каждой правой 1.
Задача 10.
Рассмотрим 3 случая:
- Буква А встречается в слове ровно 1 раз.
- Буква А встречается в слове ровно 2 раза.
- Буква А встречается в слове не более двух раз.
1 случай. Саша составляет пятибуквенные слова, в которых есть только буквы А, Б, В, Г, Д, Е, причём в каждом слове буква А используется ровно 1 раз. Каждая из других допустимых букв может встречаться любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, необязательно осмысленная. Сколько существует таких слов, которые может написать Саша?
2 случай. Саша составляет четырехбуквенные слова, в которых есть только буквы Е, Д, А, Н и К, причём в каждом слове буква А используется ровно 2 раза. Каждая из других допустимых букв может встречаться любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, необязательно осмысленная. Сколько существует таких слов, которые может написать Саша?
3 случай. Саша составляет пятибуквенные слова, в которых есть только буквы А, Б, В, Г, причём в каждом слове буква А используется не более двух раз, и при этом может стоять только на первом или на последнем местах. Каждая из других допустимых букв может встречаться любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, необязательно осмысленная. Сколько существует таких слов, которые может написать Саша?
Задача 17.
Запрос «или» вычисляется по этой формуле.
Ш|Т = Ш + Т – Ш&Т. Обозначили через Ш – количество страниц запроса «Шахматы».
Через Т – количество страниц запроса «Теннис».
Из этой формулы выразим количество страниц запроса «Шахматы».
Есть два способа решения задания:
1 способ – выписать все нужные программы, построить дерево программ.
2 способ – подсчитать число программ, не выписывая их явно, а написав формулу, которая позволяет найти количество программ получения данного числа, если уже известно количество программ для получения меньших чисел (при таком решении удобно заполнять таблицу).
Из числа 3 нужно получить 23.
Есть две команды.
- Прибавить 1
- Умножь на 2.
Эти две команды записываем в обратными командами.
- Х-1 (не прибавляем, а наоборот вычитаем 1)
- х/2 (не умножаем, а делим на 2).
Получилось 2 новые команды.
Их записываем в таблицу.
На первом столбце таблицы записывали числа от 3 до 23. На 2 и 3 столбцах обратные команды. На последнем столбце количество программ.
1 строка. Проверяем первую команду. От трех вычитаем 1 получается 2. Число 2 не входит траекторию. Ничего не записываем. Проверяем вторую команду. 3 делим на 2. Единица получается, тоже не входит в траекторию. Ничего не записываем. Само число 3 это 1 программа.
2 строка. 4-1=3. Число 3 входит в траекторию. Поэтому 1 программа.
3 строка. 1 программа.
Таким образом, суммируются программы.
Вывод:
- Научился решать задачи ЕГЭ.
- Способы решения заданий ЕГЭ по информатике немного.
Литература:
- Информатика и ИКТ. Подготовка к ЕГЭ. Тренировочные варианты.
- Интернет-ресурсы.
- Видеоуроки.
МЕТОДИКА РЕШЕНИЯ ЗАДАЧ ЕГЭ ПО ИНФОРМАТИКЕ И ИКТ С ИСПОЛЬЗОВАНИЕМ ПОНЯТИЯ «ВЫИГРЫШНОЙ СТРАТЕГИИ»
Выступление на республиканском семинаре «Об особенностях преподавания информатики в общеобразовательных организациях Республики Крым в 2018/2019 учебном году» 23.08.2018
Сабитова Диляра Арифовна, методист отдела дистанционного образования
ГБОУ ДПО РК КРИППО
-
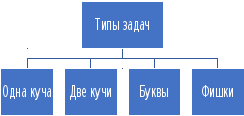
Понятие выигрышной стратегии. Типы задач
-
Разбор задания № 26 демонстрационной версии ЕГЭ-2018
-
Разбор проекта демонстрационной версии ЕГЭ-2018. Фишки
-
Разбор задачи основного периода ЕГЭ-2018. Две кучи
-
Разбор задачи №26 системы «Эксперт ЕГЭ». Буквы
-
Понятие выигрышной стратегии. Типы задач
Стратегия игрока определяет его действие в любой момент игры и для каждого возможного течения игры.
Игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
-
Разбор задания № 26 демонстрационной версии ЕГЭ-2018
Задача №26
Решение (таблица):
-
Вопрос 1а. Последним ходом может быть «+1» или «*2». Выиграть последним ходом «+1» можно, если S = 28. Ходом «*2» можно выиграть из любой позиции при S 14 (сюда входит и 28). Можно составить таблицу, в которой «В1» обозначает выигрыш за один ход:
|
S |
1 |
2 |
… |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
|
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
Поэтому ответ должен быть такой:
«1а. Петя может выиграть за один ход при любом S =15,…28. Он должен увеличить вдвое число камней, при этом в куче всегда получится не менее 30 камней.»
-
Вопрос 1б. Для ответа на этот вопрос нужно найти позицию, из которой все возможные ходы ведут к выигрышу за 1 ход, то есть к позиции, отмеченной в таблице как «В1». Например, это позиция при S = 14: ход «+1» ведёт в выигрышную позицию S = 15, а ход «*2» ведёт в выигрышную позицию S = 28. Поэтому позицию S = 14 отметим в таблице как «х1» (проигрыш за 1 ход):
|
S |
1 |
2 |
… |
13 |
|
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
|
|
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
Ответ на вопрос 1б должен быть такой:
«1б. При S = 14 Петя не может выиграть в один ход, потому что при его ходе «+1» число камней в куче становится равно 15 (меньше 29), а при ходе «*2» число камней в куче становится равно 28 (также меньше 29). Других возможных ходов у Пети нет. Из любой позиции после одного хода Пети (это может быть 15 или 28), Ваня может выиграть своим первых ходом, удвоив количество камней в куче.»
-
Вопрос 2. Пете, для того, чтобы гарантированно выиграть на втором ходу, нужно из начальной позиции перевести игру в проигрышную позицию, отмеченную знаком «х1». Пока мы нашли одну такую позицию: S = 14. Петя может перевести игру в эту позицию из позиций
S = 13 (ходом «+1») и S = 7 (ходом «*2»)

|
S |
1 |
… |
7 |
8 |
9 |
10 |
11 |
12 |
|
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
|
В2 |
В2 |
×1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
Поэтому ответ должен быть такой:
«2. Из позиций S = 7 и S = 13 Петя не может выиграть в один ход, но Петя может выиграть своим вторым ходом, независимо от того, как будет ходить Ваня. При S = 13 ходом «+1» Пете нужно перевести игру в позицию S = 14, которая является проигрышной (см. ответ на вопрос 1б). При S = 7 Петя переводит игру в ту же позицию ходом «*2».»
-
Вопрос 3. Нужно найти такую позицию, из которой оба возможных хода Пети ведут в позиции, отмеченные в таблице как «В1» (выигрыш в 1 ход) и «В2» (выигрыш в 2 хода). Например, это позиция S = 12, из которой можно «попасть» только в S = 13 («В2») и S = 24 («В1»). Отмечаем эту позицию как «х2» – проигрыш в два хода:
|
S |
1 |
… |
7 |
8 |
9 |
10 |
11 |
|
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
|
В2 |
|
В2 |
×1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
В1 |
Поэтому ответ должен быть такой:
«3. В позиции S = 12 у Вани есть выигрышная стратегия, которая позволяет ему выиграть первым или вторым ходом. Если Петя выбирает ход «+1», в куче становится 13 камней и Ваня выигрывает на 2-м ходу (см. ответ на вопрос 2). Если Петя выбирает ход «*2», Ваня выигрывает первым ходом, удвоив число камней в куче.»
-
Остается нарисовать дерево возможных вариантов игры из позиции S = 12. Для этого используем построенную таблицу:
Здесь красным цветом выделены позиции, в которых игра заканчивается.
На каждом шаге мы рассматриваем все возможные ходы Пети и только один лучший ход Вани. Например, в позиции S = 15 Ваня может сделать ход «+1» и получить 16 камней в куче, но тогда он проиграет (Петя следующим ходом удвоит число камней и получит 32 камня). Этот ход мы не рассматриваем, потому что мы хотим доказать, что у Вани есть выигрышная стратегия – ему достаточно хода «*2», после которого он выиграет. В то же время нужно рассмотреть все возможные ответы Пети, чтобы доказать, что у него нет шансов на выигрыш при правильной игре Вани. В этом суть теории игр – добиться лучшего результата в худшем случае, то есть при безошибочной игре соперника.
-
Разбор проекта демонстрационной версии ЕГЭ-2018. Фишки
Задача №26
Два игрока, Петя и Ваня играют в следующую игру. На столе в кучке лежат фишки. На лицевой стороне каждой фишки написано двузначное натуральное число, обе цифры которого находятся в диапазоне от 1 до 4. Никакие две фишки не повторяются. Игра состоит в том, что игроки поочередно берут из кучки по одной фишке и выкладывают в цепочку на стол лицевой стороной вверх таким образом, что каждая новая фишка ставится правее предыдущей и ближайшие цифры соседних фишек совпадают. Верхняя часть всех выложенных фишек направлена в одну сторону, то есть переворачивать фишки нельзя. Например, из фишки, на которой написано 23, нельзя сделать фишку, на которой написано 32. Первый ход делает Петя, выкладывая на стол любую фишку из кучки. Игра заканчивается, когда в кучке нет ни одной фишки, которую можно добавить в цепочку. Тот, кто добавил в цепочку последнюю фишку, выигрывает, а его противник проигрывает. Будем называть партией любую допустимую правилами последовательность ходов игроков, приводящую к завершению игры. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит указать, какую фишку он должен выставить в любой ситуации, которая ему может встретиться при различной игре противника.
Пример. Пусть на столе в кучке лежат фишки: 11, 12, 13, 21, 22, 23
Пусть первый ход Пети 12. Ваня может поставить 21, 22 или 23. Предположим, он ставит 21. Получим цепочку 12-21. Петя может поставить 11 или 13. Предположим, он ставит 11. Получим цепочку 12-21-11. Ваня может поставить только фишку со значением 13. Получим цепочку 12-21-11-13. Перед Петей в кучке остались только фишки 22 и 23, то есть нет фишек, которые он мог бы добавить в цепочку. Таким образом, партия закончена, Ваня выиграл.
Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}.
Задание 1.
а) Приведите пример самой короткой партии, возможной при данном наборе фишек. Если таких партий несколько, достаточно привести одну.
б) Пусть Петя первым ходом пошел 42. У кого из игроков есть выигрышная стратегия в этой ситуации? Укажите первый ход, который должен сделать выигрывающий игрок, играющий по этой стратегии. Приведите пример одной из партий, возможных при реализации выигрывающим игроком этой стратегии.
Задание 2
Пусть Петя первым ходом пошел 44. У кого из игроков есть выигрышная стратегия, позволяющая в этой ситуации выиграть своим четвертым ходом? Постройте в виде рисунка или таблицы дерево всех партий, возможных при реализации выигрывающим игроком этой стратегии. На рёбрах дерева указывайте ход, в узлах – цепочку фишек, получившуюся после этого хода.
Задание 3
Укажите хотя бы один способ убрать 2 фишки из исходного набора так, чтобы всегда выигрывал не тот игрок, который имеет выигрышную стратегию в задании 2. Приведите пример партии для набора из 6 оставшихся фишек.
Задание 1а.
-
партия заканчивается, когда цепочка закончилась на цифре X и не осталось ни одной фишки, которая бы начиналась с этой цифры;
-
меньше всего фишек заданного набора начинается с цифры 1 (только 12 и 14), поэтому самой короткой партией, вероятно, будет партия, которая заканчивается на цифре 1 (фишкой 21 или 41), при этом фишки 12 и 14 должны быть выставлены;
-
соединить эти фишки в цепочку можно с помощью фишек 21 или 41, таким образом, получается две возможных самых коротких партии:
12 – 21 – 14 – 41 и 14 – 41 – 12 – 21.
В ответе достаточно привести одну из них.
Задание 1б. (Идея решения – А. Сидоров).
-
заметим, что эта игра напоминает «одностороннее домино», в котором фишки можно выставлять только одной стороной и наращивать цепочку можно тоже только с одной стороны;
-
среди фишек есть две особые – 22 и 44 («дубли») они служат для того, чтобы передать ход сопернику; если выставить дубль, оказавшись в проигрышной позиции, то эта проигрышная позиция «переходит» к сопернику
-
пока построим дерево без учёта дублей, то есть для набора фишек
12, 14, 21, 24, 41 и 42
-
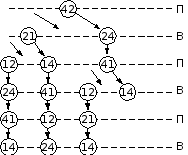
по условию Петя выставляет первым ходом фишку 42, дальнейшие варианты развития игры показаны на схеме:
-
итак, мы видим, что если никто из игроков не выставляет дублей, то выигрывает Ваня во всех случаях, причем все партии заканчиваются на цифре 4
-
если Ваня в ходе игры не выставит дубль, то в конце каждой ветки Петя может выставить дубль 44 и выиграть:
-
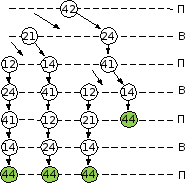
поэтому теперь посмотрим, где Ваня может изменить игру дублями; Ване нет смысла ставить дубль 44, потому что во всех вариантах партий он уже есть (с выигрышем для Пети), так что выставление дубля 44 просто перемещает его в середину цепочки, не изменяя её длину
-
у Вани в распоряжении есть еще дубль 22; на следующем рисунке выделены ходы, где Ваня может поставить этот дубль:
П
-
использование дубля 22 действительно изменяет игру, так как удлиняет цепочки на 1, при этом выигрывает Ваня:
а) Ваня может своим первым ходом выставить дубль 22, при этом он всегда выиграет
б) Ваня может первым ходом выставить фишку 21, при этом получив ход в позиции, когда текущая цепочка заканчивается на 2, он выставляет дубль 22 и выигрывает
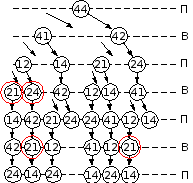
Задание 2.
-
построим дерево игры для случая, когда Петя в самом начале ходит фишкой 44, «забыв» пока про дубль 22:
-
по дереву видим, что при игре без дубля 22 выигрывает Петя своим третьим или четвёртым ходом
-
Ваня может изменить ход игры дублем 22 только в выделенных узлах, поэтому
-
если Ваня походит фишкой 41, Петя должен ответить ходом 14
-
если Ваня походит фишкой 42, Петя должен ответить ходом 21
-
при записи неполного дерева игры, доказывающего выигрыш Пети, нужно учесть, что по условию задачи нужно представить дерево с выигрышем именно в 4 хода, хотя Петя имеет стратегию выигрыша за 3 хода:
Задание 3.
-
в задании 2 выигрывает Петя, поэтому нужно убрать две фишки таким образом, чтобы всегда выигрывал Ваня
-
заметим, что нам нужно доказать, что Ваня выигрывает ВСЕГДА, при любом первом ходе Пети; это значит, что построение одного дерева (при конкретном первом ходе) ничего не доказывает
-
заметим, что последней цифрой цепочки для данного набора фишек всегда будет 1, 2 или 4, поэтому можно построить такой граф возможных переходов (например, ребро перехода 1 2 соответствует фишке 12, а петля у узла 2 – фишке 22):
по каждому ребру этого графа можно пройти только один раз (каждая фишка выставляется один раз)
-
по этому графу видно, что если убрать две петли, остается граф с одинаковой ситуацией для каждой из вершин: есть два контура, проходящие в разных направлениях через все узлы
-
итак, если убрать два дубля, то всегда будут выставлены 4 или все 6 фишек, поскольку 4 и 6 – чётные числа, то всегда выиграет Ваня, потому что он делает все ходы с чётными номерами; например, при первом ходе Пети 12 возможны партии:
-
– 21 – 14 – 41 или 12 – 24 – 41 – 14 – 42 – 21.
-
Разбор задачи основного периода ЕГЭ-2018. Две кучи
Задание №26 (2018 г, основной период)
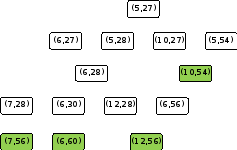
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 10 камней, а в другой 7 камней; такую позицию в игре будем обозначать (10, 7). Тогда за один ход можно получить любую из четырёх позиций: (11, 7), (20, 7), (10, 8), (10, 14). Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 63. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, при которой в кучах будет 63 камня или больше.
В начальный момент в первой куче было пять камней, во второй куче – S камней; 1 ≤ S ≤ 57.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т.е. не являющиеся выигрышными независимо от игры противника.
Выполните следующие задания.
Задание 1
а) Укажите все такие значения числа S, при которых Петя может выиграть за один ход.
б) Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
Задание 2
Укажите такое значение S, при котором у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Для указанного значения S опишите выигрышную стратегию Пети.
Задание 3
Укажите значение S, при котором одновременно выполняются два условия:
− у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
− у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Для указанного значения S опишите выигрышную стратегию Вани.
Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани (в виде рисунка или таблицы).
В узлах дерева указывайте позиции, на рёбрах рекомендуется указывать ходы. Дерево не должно содержать партии, невозможные при реализации выигрывающим игроком своей выигрышной стратегии. Например, полное дерево игры не является верным ответом на это задание.
Решение:
-
Задание 1. В первой куче – 5, во второй — 1…57.
Если во второй куче было S камней, то после первого хода Пети количество камней в двух кучах может стать равным
6+S (после добавления 1 камня в любую кучу)
10+S (после удвоения первой кучи)
5+2S (после удвоения второй кучи)
Выписываем условия выигрыша на первом ходу для всех трёх вариантов
6 + S 63 S 57
10 + S 63 S 53
5 + 2S 63 S 29
Отсюда следует, что при S 29 Петя выиграет первым же ходом, удвоив число камней во второй куче.
S=29,…57
-
S=29. Если Петя сделал неудачный ход, значит он имел выигрышную стратегию, при которой необходимо было увеличить вторую кучу вдвое. Пусть он при этом положил в первую или во вторую кучу 1 камень и привел Ваню к выигрышу. Значит у Вани была позиция (5, 30) или (6, 29). Ваня удваивает вторую кучу и выигрывает, получив позицию (5, 60) или (6, 58).
Задание 2.
S=28.
В позиции (5,28) своим первым ходом Петя должен добавить 1 камень в первую кучу, приведя противника к проигрышной ситуации (6, 28). Вторым ходом Петя удваивает количество камней во второй куче и выигрывает.
|
(5, 28) |
П1 |
В1 |
П2 |
|
(5+1=6, 28) |
(7, 28) |
(7, 56) |
|
|
(6, 30) |
(6, 60) |
||
|
(12, 28) |
(12, 56) |
||
|
(6, 56) |
(6, 112) |
Задание 3.
|
Начальная позиция (5, 27) |
П1 |
В1 |
П1 |
В2 |
|
(5+1=6, 27) |
(6, 27+1=28) |
(7, 28) |
(7, 56) |
|
|
(6, 30) |
(6, 60) |
|||
|
(12, 28) |
(12, 56) |
|||
|
(6, 56) |
(6, 112) |
|||
|
(5, 27+1=28) |
(5+1=6, 28) |
(7, 28) |
(7, 56) |
|
|
(6, 30) |
(6, 60) |
|||
|
(12, 28) |
(12, 56) |
|||
|
(6, 56) |
||||
|
(5*2=10,27) |
(10,27*2=54) |
|||
|
(5, 27*2=54) |
(5*2=10, 54) |
Построим дерево возможных партий. Важно, что для проигрывающего (Пети) нужно обязательно рассмотреть все возможные ходы (чтобы доказать, что его ничто не может спасти), а для выигрывающего достаточно указать на каждом шаге один выигрывающий ход:
Задача №26 (Буквы)
Два игрока, Петя и Ваня играют в следующую игру. Задан некоторый набор символьных цепочек («слов»), в котором ни одно слово не является началом другого. Игра начинается с пустой строки, в конец которой игроки по очереди дописывают буквы, по одной букве за ход так, чтобы полученная цепочка на каждом шаге была началом одного из заданных слов. Первый ход делает Петя. Выигрывает тот, кто первый составит слово из заданного набора.
Пример. Пусть заданы слова {МАК, МЫЛО, РАМА, РАК}. На первом ходу Петя может написать букву М или Р. Пусть он написал букву М. В ответ Ваня может написать А или Ы. В первом случае получается МА, и Петя, дописав букву К, получает слово МАК из заданного набора и выигрывает. Во втором случае получается МЫ, Петя вынужден дописать Л и Ваня выиграет вторым ходом, дописав О и получив слово МЫЛО.
Задание 1.
а) Определите, у кого из игроков есть выигрышная стратегия для набора слов {ВАРЕНЬЕ, КОРОВА}. Опишите эту стратегию. Определите, сколько различных партий может быть сыграно при этой стратегии и какое слово будет получено в каждом случае.
б) Определите, у кого из игроков есть выигрышная стратегия для набора слов {НУБНУБ…НУБ, PUMAPUMA…PUMA}. В первом слове 55 раз повторяется слово НУБ, а во втором – 32 раза повторяется слово PUMA. Опишите эту стратегию. Определите, сколько различных партий может быть сыграно при этой стратегии и какое слово будет получено в каждом случае.
Задание 2
В наборе слов, приведённом в задании 1а, поменяйте местами две буквы в любом слове так, чтобы выигрышная стратегия была у другого игрока. Опишите эту стратегию. Определите, сколько различных партий может быть сыграно при этой стратегии и какое слово будет получено в каждом случае.
Задание 3
Дан набор слов {МОРОКА, МОРС, МОРОЗ, ПЛАХА, ПЛАТЬЕ, ПЛОМБА}. У кого из игроков есть выигрышная стратегия? Приведите в виде рисунка или таблицы дерево всех партий, возможных при этой стратегии.
-
Сначала предположим, что в наборе одно слово. Если игроки дописывают каждый раз по одной букве то очевидно, что первый из них (Петя) допишет все нечётные буквы, а второй (Ваня) – все чётные. Таким образом, если в слове нечётное число букв, выиграет Петя, а если чётное – Ваня.
-
Если слов несколько, то стратегия Пети состоит в том, чтобы все время выбирать такое продолжение, при котором в итоге будет получено слово с нечётным количеством букв, а Ваня наоборот должен пытаться перескочить на слово с чётным количеством букв.
-
Задание 1а. В слове ВАРЕНЬЕ – 7 букв (нечётное количество, выиграет Петя), а в слове КОРОВА – 6 букв (чётное количество, выиграет Ваня). Петя ходит первый и может написать букву В. Поскольку слово КОРОВА начинается с другой буквы, Ваня будет вынужден «идти» по слову ВАРЕНЬЕ и проиграет. Этот вариант – единственный, то есть возможна только одна партия, при которой Петя следует своей стратегии, она заканчивается словом ВАРЕНЬЕ.
Задание 1а.
-
Для набора слов {ВАРЕНЬЕ, КОРОВА} выигрышная стратегия есть у Пети.
-
Выигрышная стратегия Пети состоит в том, чтобы написать первую букву В. Далее остается только одно допустимое слово – ВАРЕНЬЕ, и Петя выиграет, так как в этом слове 7 букв и он допишет последнюю букву, имеющую нечётный номер.
-
При выбранной стратегии возможна только одна партия.
-
В результате этой партии получится слово ВАРЕНЬЕ.
-
Задание 1б. В первом слове набора 3*55 = 165 букв, нечётное количество. Поэтому если игра «пойдёт» по первому слову, то выиграет Петя. Во втором слове 4*32 = 128 букв, чётное количество. Поэтому если игра пойдёт по второму слову, выиграет Ваня. Слова начинаются с разных букв, поэтому Петя может выбрать, по какому слову пойдёт игра. Если он напишет букву Н, он выиграет.
Задание 1б.
-
Для заданного набора слов выигрышная стратегия есть у Пети.
-
Выигрышная стратегия Пети состоит в том, чтобы написать первую букву Н. Далее остается только одно допустимое слово – НУБНУБ…НУБ, и Петя выиграет, так как в этом слове нечётное количество букв (165) и он допишет последнюю букву, имеющую нечётный номер.
-
При выбранной стратегии возможна только одна партия.
-
В результате этой партии получится слово НУБНУБ…НУБ.
-
Задание 2. В наборе слов {ВАРЕНЬЕ, КОРОВА} первое слово имеет нечётное количество букв, а второе – чётное. Чтобы Ваня мог выиграть, он должен получить возможность «перескочить» на второе слово. Для этого при любом ходе Пети у Вани должен остаться выбор. Это возможно только в том случае, когда оба слова начинаются с одной и той же буквы. Поскольку разрешается переставлять буквы только в одном слове, мы не можем сделать, чтобы оба слова начинались с буквы К – в первом слове её нет. Но можно сделать так, чтобы оба слова начинались с буквы В, переставив буквы К и В в слове КОРОВА. Получается набор {ВАРЕНЬЕ, ВОРОКА}, и Ваня выигрывает, своим первым ходом дописав букву О к букве В, которую (обязательно!) напишет Петя.
Задание 2.
-
Для того, чтобы Ваня мог выиграть, во втором слове нужно поменять местами буквы К и В.
-
Так как оба слова начинаются с буквы В, Петя обязательно напишет букву В. Выигрышная стратегия Вани состоит в том, чтобы своим ходом дописать букву О. После этого игра «идёт» по слову ВОРОКА, в нём чётное количество букв и выигрывает Ваня, который допишет последнюю букву.
-
При выбранной стратегии возможна только одна партия.
-
В результате этой партии будет получено слово ВОРОКА.
-
Задание 3. Расположим слова в столбики по начальным буквам, на каждом шаге вниз стараясь сохранить наибольшую общую часть (маркером выделена часть слова, которая совпадает с предыдущим словом в том же столбике):
МОРОКА + ПЛАХА
+ МОРОЗ ПЛАТЬЕ
МОРС ПЛОМБА
Знаком «плюс» отмечены слова, имеющие нечётное количество букв – это выигрышные варианты для Пети.
-
Если Петя первой напишет букву М, для выигрыша ему нужно перейти на слово МОРОЗ, но как только он составит слово МОР, Ваня тут же допишет С и выиграет, получив слово МОРС.
-
Если Петя напишет букву П, Ваня вынужден написать Л (это вторая буква всех оставшихся допустимых слов). Теперь Петя может написать А или О. В обоих случаях Ваня может перевести игру на слова с чётным количество букв (ПЛАТЬЕ, ПЛОМБА) и выиграть. Таким образом, при этом наборе слов выигрышную стратегию имеет Ваня.
Задание 3.
-
Для набора слов {МОРОКА, МОРС, МОРОЗ, ПЛАХА, ПЛАТЬЕ, ПЛОМБА} выигрышная стратегия есть у Вани.
-
Дерево всех возможных партий приводится на рисунке. Для Пети мы рассматриваем все возможные ходы, для Вани – только выигрышный вариант на каждом шаге. Буквами над схемой обозначены игроки (П – ход Пети, В – ход Вани).
Вместо рисунка можно использовать таблицу (зелёным цветом отмечен выигрыш Вани):
|
Начальная позиция |
П |
В |
П |
В |
П |
В |
|
– |
М |
МО |
МОР |
МОРС |
||
|
П |
ПЛ |
ПЛА |
ПЛАТ |
ПЛАТЬ |
ПЛАТЬЕ |
|
|
ПЛО |
ПЛОМ |
ПЛОМБ |
ПЛОМБА |
-
Разбор задачи №26 системы «Эксперт ЕГЭ». Буквы
Решение.
-
Сначала предположим, что в наборе одно слово. Если игроки дописывают каждый раз по одной букве то очевидно, что первый из них (Петя) допишет все нечётные буквы, а второй (Ваня) – все чётные. Таким образом, если в слове нечётное число букв, выиграет Петя, а если чётное – Ваня.
-
Если слов несколько, то стратегия Пети состоит в том, чтобы все время выбирать такое продолжение, при котором в итоге будет получено слово с нечётным количеством букв, а Ваня наоборот должен пытаться перескочить на слово с чётным количеством букв.
-
Задание 1а. В слове АБВГДАБВГДХ – 11 букв (нечётное количество, выиграет Петя), а в слове ДГВБАДГВБА – 10 букв (чётное количество, выиграет Ваня). Петя ходит первый и может написать букву А. Поскольку второе слово начинается с буквы Д, Ваня будет вынужден «идти» по первому слову и проиграет. Этот вариант – единственный, то есть возможна только одна партия, при которой Петя следует своей стратегии, она заканчивается словом АБВГДАБВГДХ.
Задание 1а.
-
Для набора слов { АБВГДАБВГДХ, ДГВБАДГВБА } выигрышная стратегия есть у Пети.
-
Выигрышная стратегия Пети состоит в том, чтобы написать первую букву А. Далее остается только одно допустимое слово – АБВГДАБВГДХ, и Петя выиграет, так как в этом слове 11 букв и он допишет последнюю букву, имеющую нечётный номер.
-
При выбранной стратегии возможна только одна партия.
-
В результате этой партии получится слово АБВГДАБВГДХ.
-
Задание 1б. В первом слове набора 3*33 = 99 букв, нечётное количество. Поэтому если игра «пойдёт» по первому слову, то выиграет Петя. Во втором слове 4*44 = 176 букв, чётное количество. Поэтому если игра пойдёт по второму слову, выиграет Ваня. Слова начинаются с разных букв, поэтому Петя может выбрать, по какому слову пойдёт игра. Если он напишет букву Т, он выиграет.
Задание 1б.
-
Для заданного набора слов выигрышная стратегия есть у Пети.
-
Выигрышная стратегия Пети состоит в том, чтобы написать первую букву Т. Далее остается только одно допустимое слово – ТРИТРИ … ТРИ, и Петя выиграет, так как в этом слове нечётное количество букв (99) и он допишет последнюю букву, имеющую нечётный номер.
-
При выбранной стратегии возможна только одна партия.
-
В результате этой партии получится слово ТРИТРИ … ТРИ.
-
Задание 2. В наборе слов { АБВГДАБВГДХ, ДГВБАДГВБА } первое слово имеет нечётное количество букв, а второе – чётное. Чтобы Ваня мог выиграть, он должен получить возможность «перескочить» на второе слово. Для этого при любом ходе Пети у Вани должен остаться выбор. Это возможно только в том случае, когда оба слова начинаются с одной и той же буквы. Поскольку переставить буквы нужно в коротком слове, мы должны сделать так, чтобы оба слова начинались с буквы А. Поменяем первую букву Д во втором слове с буквой А, находящейся на 5 месте. Получим слово АГВБДДГВБА с четным количеством букв. Петя вынужден будет написать А, а Ваня вслед за ним пишет вторую букву второго (короткого) слова – Г. В результате Ваня выиграет написав последнюю четную букву А. Получится слово — АГВБДДГВБА . Можно поменять первую букву Д с последней буквой А и тогда получим слово — АГВБАДГВБД. Это слово также приведет к выигрышу Вани.
Задание 2.
-
Для того, чтобы Ваня мог выиграть, во втором слове нужно поменять местами буквы Д и А.
-
Так как оба слова начинаются с буквы А, Петя обязательно напишет букву А. Выигрышная стратегия Вани состоит в том, чтобы своим ходом дописать букву Г. После этого игра «идёт» по слову АГВБДДГВБА, в нём чётное количество букв и выигрывает Ваня, который допишет последнюю букву.
-
При выбранной стратегии возможна только одна партия.
-
В результате этой партии будет получено слово АГВБДДГВБА.
-
Задание 3. Расположим слова в столбики по начальным буквам, на каждом шаге вниз стараясь сохранить наибольшую общую часть (маркером выделена часть слова, которая совпадает с предыдущим словом в том же столбике):
ДРАТВА + КРОНА
ДРОН КРОШКА
+ ДРОЗД + КРОКОДИЛИЩЕ
Знаком «плюс» отмечены слова, имеющие нечётное количество букв – это выигрышные варианты для Пети.
-
Если Петя первой напишет букву Д, для выигрыша ему нужно перейти на слово ДРОЗД , но как только он составит слово ДРО, Ваня тут же допишет Н и выиграет, получив слово ДРОН.
-
Если Петя напишет букву К, Ваня вынужден написать Р (это вторая буква всех оставшихся допустимых слов). Теперь Петя может написать только О. Ваня может написать Ш и перевести игру на слово с чётным количество букв (КРОШКА) и выиграть. Таким образом, при этом наборе слов выигрышную стратегию имеет Ваня.
Задание 3.
-
Для набора слов {ДРАТВА, ДРОН, ДРОЗД, КРОНА, КРОШКА, КРОКОДИЛИЩЕ } выигрышная стратегия есть у Вани.
-
Дерево всех возможных партий приводится на рисунке. Для Пети мы рассматриваем все возможные ходы, для Вани – только выигрышный вариант на каждом шаге. Буквами над схемой обозначены игроки (П – ход Пети, В – ход Вани).
Вместо рисунка можно использовать таблицу (зелёным цветом отмечен выигрыш Вани):
|
Начальная позиция |
П |
В |
П |
В |
П |
В |
|
– |
К |
КР |
КРО |
КРОШ |
КРОШК |
КРОШКА |
|
Д |
ДР |
ДРА |
ДРАТ |
ДРАТВ |
ДРАТВА |
|
|
ДРО |
ДРОН |
— |
Использованные источники:
-
Демонстрационный вариант ЕГЭ по информатике и ИКТ 2018г (проект). [Электронный ресурс. Режим доступа: http://fipi.ru/]
-
Демонстрационный вариант ЕГЭ по информатике и ИКТ 2018г. [Электронный ресурс. Режим доступа: http://fipi.ru/]
-
К. Ю. Поляков. Материалы для подготовки ЕГЭ. [Электронный ресурс. Режим доступа: http://kpolyakov.spb.ru]
-
Критерии оценивания заданий с развернутым ответом. [Электронный ресурс. Режим доступа: http://85.142.162.117/exp/]
13
Привет! Сегодня порешаем демонстрационный вариант ЕГЭ по информатике 2022.
В этой статье представлены задания с 1-ого по 5.
Источник задач: https://fipi.ru/ege/demoversii-specifikacii-kodifikatory#!/tab/151883967-5
Приятного прочтения!
Разбор демоверсии ЕГЭ по информатике 2022 (6-10 Задание)
Разбор демоверсии ЕГЭ по информатике 2022 (11-15 Задание)
Разбор демоверсии ЕГЭ по информатике 2022 (16-21 Задание)
Разбор демоверсии ЕГЭ по информатике 2022 (22-27 Задание)
Задание 1
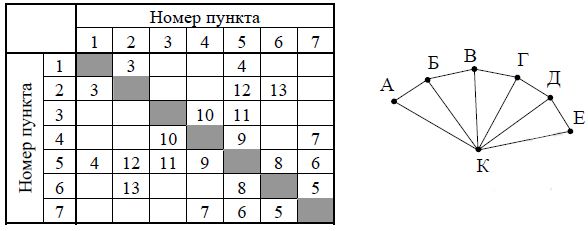
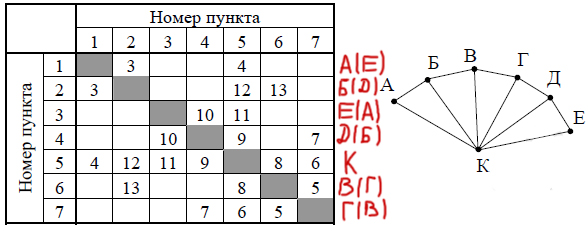
На рисунке схема дорог Н-ского района изображена в виде графа, в таблице
содержатся сведения о протяжённости каждой из этих дорог (в километрах).
Так как таблицу и схему рисовали независимо друг от друга, то нумерация
населённых пунктов в таблице никак не связана с буквенными
обозначениями на графе. Определите, какова сумма протяжённостей дорог
из пункта Б в пункт В и из пункта Г в пункт Д.
В ответе запишите целое число.
Решение:
В начале нужно понять, какой город под какой буквой находится в таблице.
Точка К — особая точка, т.е. она отличается от остальных, т.к. только она имеет 6 дорог. Поэтому её легко найти в таблице, она под номером 5.
Рисунок имеет симметричную структуру. Поэтому например точки A и E мы не сможем отличить друг от друга. Но найдём примерное их расположение.
Города A и E имеют по две дороги. Значит, им соответствуют номера 1 и 3.
Городам Б и Д соответствуют номера 2 и 4. Т.к. эти номера по таблице связаны с 1 и 3. Опять, какому номеру соответствует конкретная буква, мы не сможем узнать.
С номерами 2 и 4, должны быть связаны уже В и Г. Значит, городам В и Г соответствуют номера 6 и 7.
Получается, чтобы ответить на вопрос задачи, нужно суммировать расстояния между 2 и 6 И 4 и 7.
13+7=20
Ответ: 20
Смотреть 1 Задание на YouTube
Задание 2
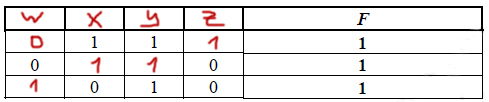
Миша заполнял таблицу истинности логической функции F
¬(y → (x ≡ w)) ∧ (z → x),
но успел заполнить лишь фрагмент из трёх различных её строк, даже
не указав, какому столбцу таблицы соответствует каждая из переменных
w, x, y, z.
Определите, какому столбцу таблицы соответствует каждая из переменных
w, x, y, z.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут
соответствующие им столбцы (сначала буква, соответствующая первому
столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы
в ответе пишите подряд, никаких разделителей между буквами ставить
не нужно.
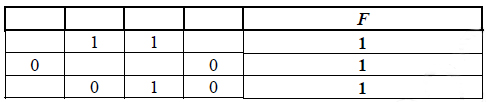
Пример. Функция F задана выражением ¬x / y, зависящим от двух
переменных, а фрагмент таблицы имеет следующий вид.
В этом случае первому столбцу соответствует переменная y, а второму
столбцу – переменная x. В ответе следует написать: yx.
Решение:
Напишем шаблон для решения 2 задания на языке программирования Python.
print('x', 'y', 'z', 'w') for x in range(0, 2): for y in range(0, 2): for w in range(0, 2): for z in range(0, 2): if not(not(y) or (x==w)) and (not(z) or x): print(x, y, z, w)
Здесь мы перебираем все варианты с помощью вложенных циклов. И если наша функция превращается в истину, то печатаем значения переменных.
Отрицание меняется на not, следование представляем по формуле A->B = ¬A or B.
Получается
x y z w
0 1 0 1
1 1 0 0
1 1 1 0
Видно, что третий столбец — это y.
Т.к. у нас нет столбца, который состоит только из одних нулей, то в четвёртом столбце в пустой ячейке будет 1.
Получилась строчка из трёх 1. Значит, в первом столбце в пустой ячейке вверху будет 0. Следовательно, первый столбец — w.
Последний столбец достаётся z, т.к. из оставшихся переменных только у неё два 0 и одна 1. Второй столбец, по принципу исключения, — это x.
Ответ: wxyz
Смотреть 2 Задание на YouTube
Задание 3
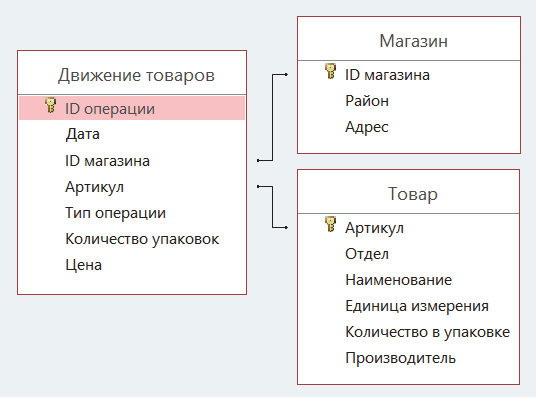
В файле приведён фрагмент базы данных «Продукты» о поставках товаров
в магазины районов города. База данных состоит из трёх таблиц.
Таблица «Движение товаров» содержит записи о поставках товаров в
магазины в течение первой декады июня 2021 г., а также информацию
о проданных товарах. Поле Тип операции содержит значение Поступление
или Продажа, а в соответствующее поле Количество упаковок, шт.
занесена информация о том, сколько упаковок товара поступило в магазин
или было продано в течение дня. Заголовок таблицы имеет следующий вид.
| ID операции |
Дата | ID магазина |
Артикул | Тип операции |
Количество упаковок, шт. |
Цена, руб./шт. |
Таблица «Товар» содержит информацию об основных характеристиках
каждого товара. Заголовок таблицы имеет следующий вид.
| Артикул | Отдел | Наименование | Ед. изм. |
Количество в упаковке |
Поставщик |
Таблица «Магазин» содержит информацию о местонахождении магазинов.
Заголовок таблицы имеет следующий вид.
На рисунке приведена схема указанной базы данных.
Используя информацию из приведённой базы данных, определите на
сколько увеличилось количество упаковок яиц диетических, имеющихся в
наличии в магазинах Заречного района, за период с 1 по 10 июня
включительно.
В ответе запишите только число.
Решение (через формулу):
Откроем файл Excel. Внизу у нас три вкладки (три таблицы).
Есть магазины, есть товары, есть операции, какие товары, куда перемещаются.
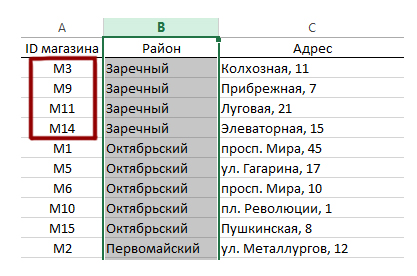
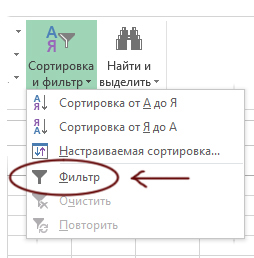
Прочитаем ещё раз внимательно вопрос задачи. Переходим на вкладку Магазин. Выделим столбец «Район» и отсортируем по данному столбцу таблицу (кнопка сортировки находится обычно в правом верхнем углу). Если появится вопрос об автоматическом расширении выделенного диапазона, отвечаем утвердительно.
Теперь удобно посмотреть ID магазинов Заречного Района. Всего получается 4 ID: M3, M9, M11, M14.
Переходим на вкладку Товар. Нас интересует яйцо диетическое. Ищем по поиску (Ctrl + F) и получаем Артикул данного товара. Это номер 15.
Данные мы собрали, теперь переходим на вкладку Движение товаров.
Сначала подсчитаем сколько поступило указанного товара в указанные торговые точки за период 1-10 июня. Убедимся, что первая строчка не подходит нам по условию и в ячейке H2 ставим значение 0. Это число олицетворяет количество поступивших товаров.
В ячейке H3 пропишем формулу:
=ЕСЛИ(И(ИЛИ(C3=«M3»;C3=«M9»;C3=«M11»; C3=«M14»); D3=15; F3=«Поступление»);H2+E3;H2)
Эту формулу мы распространяем на весь столбец H. Тогда она будет анализировать каждую строчку и подсчитывать количество поступившего товара, учитывая все обстоятельства задачи. В самой последней ячейке столбца H получается число 1420. Это и есть то количество нашего товара, которое поступило в указанные торговые точки. Про дату в этой задаче думать не нужно, т.к. вся таблица по операциям происходит в пределах 1-10 июня.
Аналогично, подсчитаем в столбце I, какое количество убыло. Тогда формула получается:
=ЕСЛИ(И(ИЛИ(C3=«M3»;C3=«M9»;C3=«M11»; C3=«M14»); D3=15; F3=«Продажа»);I2+E3;I2)
Получаем количество проданных товаров 454.
Подсчитаем на сколько же увеличилось товаров:
1420-454=966
Это и будет ответ.
Ответ: 966
Смотреть 3 Задание (решение через формулу) на YouTube
Решение (через фильтры)
В подобных задачах удобно воспользоваться фильтрами!
Выбираем вкладку Магазин и нажимаем кнопку Фильтр.
При этом должна быть выделена не пустая ячейка.
Кнопка Фильтр может находится и на главной панеле.
Теперь можно отфильтровать магазины Заречного района.
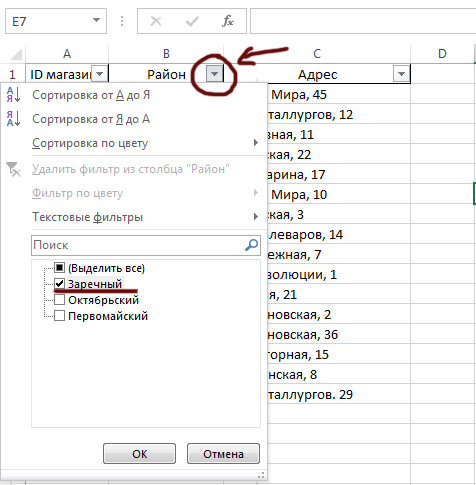
Нажмём «ОК», и у нас останутся только магазины Заречного района. Фиксируем их ID.
Переходим на вкладку Товар. Включаем фильтры. С помощью фильтров оставляем только яйцо диетическое и узнаём его Артикл.
Переходим на главную вкладку Движение товаров. Включаем фильтры. Фильтруем операции, которые подходят для наших магазинов и для нашего товара.
В начале найдём количество упаковок, которые поступили в магазины, поэтому в столбце Тип операции выбираем «Поступление«.
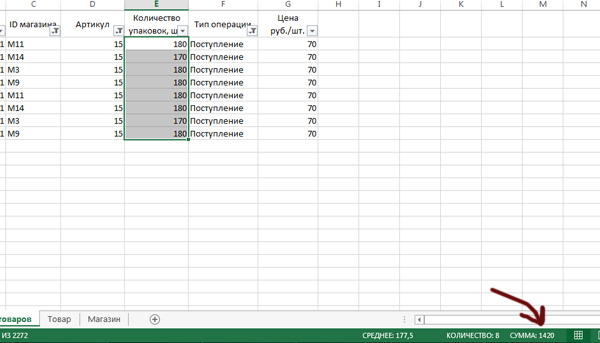
Выделяем ячейки столбца Количество упаковок для получившихся операций, и внизу смотрим сумму этих ячеек.
Здесь нельзя пользоваться стандартной функцией СУММ, потому что она суммируем ещё и скрытые ячейки. А так мы получаем сумму выделенных ячеек.
Получается количество поступивших упаковок равно 1420. Аналогично количество убывших получается 454.
1420-454=966
Ответ: 966
Смотреть 3 Задание (решение через фильтры) на YouTube
Задание 4
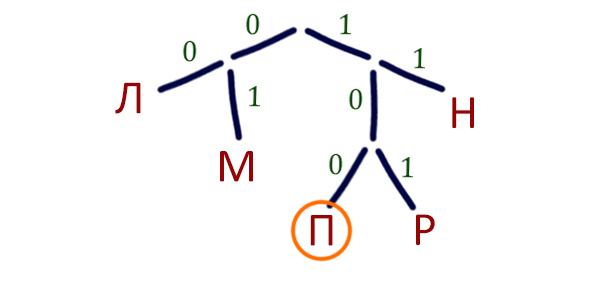
Для кодирования некоторой последовательности, состоящей из букв Л, М,
Н, П, Р, решили использовать неравномерный двоичный код,
удовлетворяющий условию, что никакое кодовое слово не является началом
другого кодового слова. Это условие обеспечивает возможность
однозначной расшифровки закодированных сообщений. Для букв Л, М, Н
использовали соответственно кодовые слова 00, 01, 11. Для двух оставшихся
букв П и Р кодовые слова неизвестны.
Укажите кратчайшее возможное кодовое слово для буквы П, при котором
код будет удовлетворять указанному условию. Если таких кодов несколько,
укажите код с наименьшим числовым значением.
Решение:
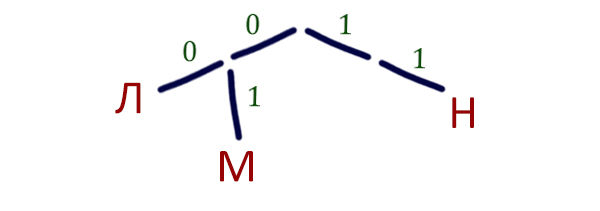
Т.к. никакое кодовое слово не является началом другого кодового слова, то, значит, выполняется условие Фано.
Следовательно, можно воспользоваться приёмом дерево Фано.
Разместим буквы для которых известны коды на дереве Фано.
При построении дерева Фано мы проращивает от корня две ветки 0 и 1. От каждой ветки тоже можно прорастить две ветки 0 и 1 и т.д. Если буква «села» на ветку, то она блокирует эту ветку, и больше нельзя проращивать новые ответвления от неё.
У нас остались две буквы П и Р, а прорастить можем только одну ветку (из 1 — прорастить 0). Мы проращиваем эту ветку и от неё проращиваем два ответвления, и теперь мы уже можем разместить оставшиеся буквы на дереве.
Для П выбираем код с меньшим числовым значением — 100, как написано в условии. Букве Р достаётся код — 101.
Ответ: 100
Смотреть 4 Задание на YouTube
Задание 5
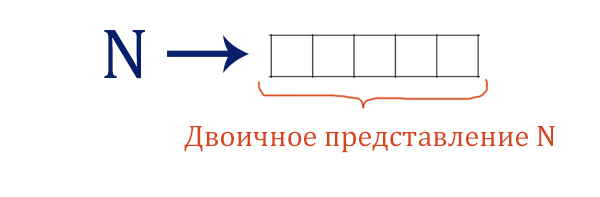
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему
новое число R следующим образом.
1. Строится двоичная запись числа N.
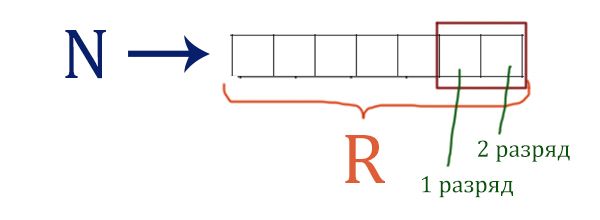
2. К этой записи дописываются справа ещё два разряда по следующему
правилу:
а) складываются все цифры двоичной записи числа N, и остаток от деления
суммы на 2 дописывается в конец числа (справа).
Например, запись 11100 преобразуется в запись 111001;
б) над этой записью производятся те же действия – справа дописывается
остаток от деления суммы её цифр на 2.
Полученная таким образом запись (в ней на два разряда больше, чем
в записи исходного числа N) является двоичной записью результирующего
числа R.
Укажите такое наименьшее число N, для которого результат работы
данного алгоритма больше числа 77. В ответе это число запишите
в десятичной системе счисления.
Решение:
На вход поступает натуральное (обычное, не дробное, положительное) число N.
Это число алгоритм переводит в двоичную систему.
Сказано, что дописываются два разряда справа к тому двоичному числу, которое получили в первом пункте.
Про первый дополнительный разряд написано в пункте a второго правила: «складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001».
Если сказать более просто, то автомат подсчитывает количество единиц у первоначального двоичного числа N, полученного в первом пункте. Если количество чётное, то автомат в первый дополнительный разряд должен поставить 0. Если количество нечётное, то автомат в первый дополнительный разряд должен поставить 1.
Про второй дополнительный разряд сказано в пункте б второго правила. Автомат сделает тоже самое, что и в предыдущем пункте, только теперь подсчёт единиц будет происходить не только в двоичной записи числа N, но и в первом дополнительном разряде.
В вопросе просят указать входящее наименьшее число N, чтобы автомат выдал число R больше 77.
Т.к. число R должно быть больше 77, то переведём число 78 (77 + 1) в двоичный вид, чтобы можно было оценить входящее число N.
Это можно сделать стандартным калькулятором windows, переключив его в режим «Программиста» (Вид->»Программист»).
Получилось число 1001110. Будем рассматривать (начиная с 1001110) числа на выполнение правил, которые заданы для алгоритма. Если все правила будут выполнены, значит, мы получили то число, по которому вычислим изначальное N. Нам нужно получить именно минимальное число, поэтому мы и начали с минимального возможного претендента для числа R (78).
Здесь нам сразу повезло, сразу число 78 удовлетворяет всем условиям. Нас просили написать именно число N, поэтому от числа 1001110 отбрасываем два разряда и переводим в десятичную систему.
Переводим в десятичную систему 10011 -> 19.
Ответ: 19
Смотреть 5 Задание на YouTube
Разбор демоверсии ЕГЭ по информатике 2022 (6-10 Задание)
Разбор демоверсии ЕГЭ по информатике 2022 (11-15 Задание)
Разбор демоверсии ЕГЭ по информатике 2022 (16-21 Задание)
Разбор демоверсии ЕГЭ по информатике 2022 (22-27 Задание)
Очень доступное объяснение. Жду разбор следующих заданий
Следующие задания уже разобраны из Демоверсии 2022. Можете посмотреть в разделе ЕГЭ.

 14
14 ×1
×1 13
13 12
12 ×2
×2