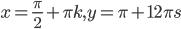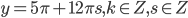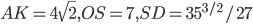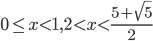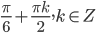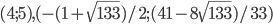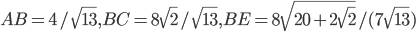Пример вступительного испытания по математике
№1. Решите уравнение
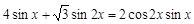
№2. Решите систему уравнений
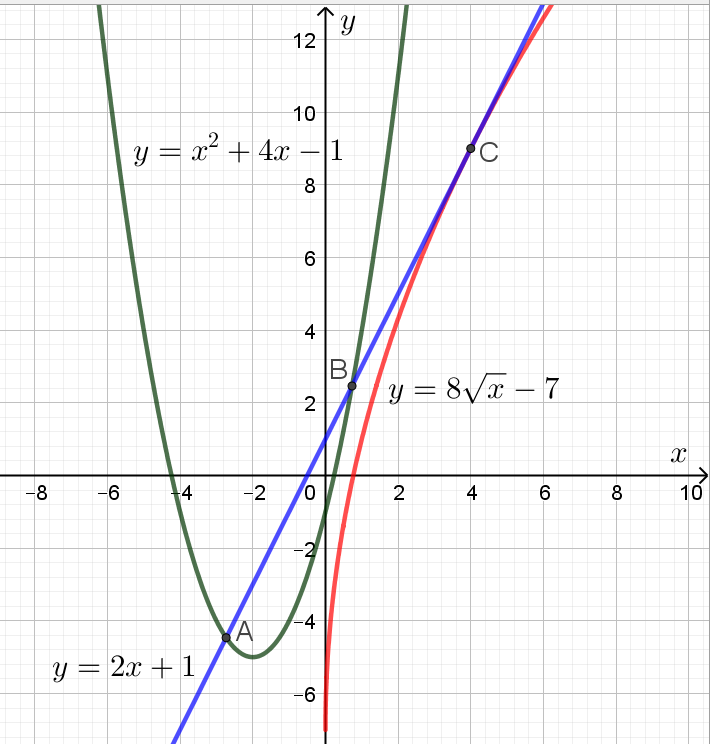
№3. Найдите уравнение прямой, проходящей через точку с координатами (1; 3), касающейся графика функции 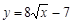
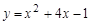
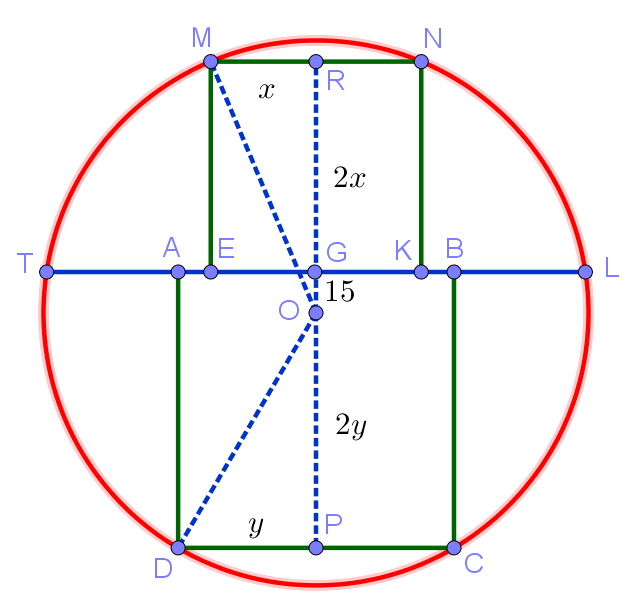
№4. Хорда окружности, удалённая от центра на расстояние 15, разбивает окружность на два сегмента, в каждый из которых вписан квадрат. Найдите разность сторон этих квадратов.
№5. Решите неравенство
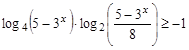
№6. В две бочки были налиты растворы соли, причём в первую бочку было налито 16 кг, а во вторую – 25 кг. Оба раствора разбавили водой так, что процентное содержание соли уменьшилось в k раз в первом бочке и в m раз во второй. О числах k и m известно, что km = k+m+3. Найдите наименьшее количество воды, которое могло быть долито в обе бочки вместе.
№7. Вершина прямого угла C прямоугольного треугольника ABC расположена на диаметре окружности, параллельном хорде AB. Найдите площадь треугольника ABC, если 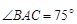
№8. Найдите все значения параметра a, для каждого из которых неравенство
выполняется для всех значений x.
Документы ЗФТШ Задания прошлых лет
Категория: Документы
Добавил: Сущенко А. А.
- 13 апреля 2022 г.
- 3 файла
- 0 комментариев
- 60495 просмотров
-
Вступительные 2019-20г
- 13.04.22
- 575 kB
- 4276 просмотров
- 4080 скачано
- Изменено 13.04.22
-
Вступительные 2020-21г
- 13.04.22
- 555 kB
- 2614 просмотров
- 3297 скачано
- Изменено 13.04.22
-
Вступительные 2021-22г
- 13.04.22
- 454 kB
- 11644 просмотра
- 9113 скачано
- Изменено 13.04.22
В данной статье разобран пример вступительного экзамена по математике в МФТИ (бакалавриат). Если вас интересует разбор вступительного экзамена по физике, вы можете найти его на этой странице. Все решения выполнены профессиональным репетитором по математике и физике, осуществляющим подготовку абитуриентов к вступительным экзаменам в МФТИ (ФизТех).
Разбор вступительного экзамена по математике в МФТИ
Используем формулу «синус двойного угла»:
Переносим слагаемые, находящиеся справа от знака равенства, в левую сторону, меняя при этом их знак на противоположный, и выносим за скобки:
Преобразуем теперь выражение, стоящее в скобках, используя формулу «косинус двойного угла»:
Произведение равно нулю, если хотя бы один из множителей равен нулю. То есть возможны два случая:
1) .
2)
Умножим обе части последнего уравнения на и введём замену
:
Примечание. Последнее уравнение является квадратным и решается по стандартному алгоритму с помощью дискриминанта.
Возвращаемся к исходной переменной. Получаем, что либо (это уравнение не имеет решений в действительных числах, так как
), либо
. Из последнего уравнения получаем
.
Ответ: .
Преобразуем выражение с суммой кубов:
В скобках заменим член на разность
. От этого равенство не нарушится. В результате получим:
Итак, исходную систему можно представить в следующем виде:
Теперь используем замену: и
. Тогда система принимает вид:
Теперь складываем почленно оба уравнения и приходим к следующему уравнению:
Корень этого уравнения угадывается автоматически: . Других корней не будет, так как справа стоит возрастающая функция, поскольку она является суммой возрастающих функций, поэтому нулевое значение она может принимать только при каком-то одном значении
.
Итак, , значит
. Возвращаясь к исходным переменным, получаем следующую систему:
В результате приходим к окончательному ответу: и
.
В общем виде уравнение прямой может быть записано следующим образом: . Известно, что эта прямая проходит через точку
, то есть имеет место равенство:
(1)
Кроме того, прямая касается графика функции . Значит уравнение
должно иметь ровно один корень. Введём замену . Тогда последнее условие эквивалентно тому, что дискриминант квадратного уравнения
(2)
равен нулю, и корень при этом неотрицателен. То есть получаем:
Таким образом с учётом уравнения (1) приходим к следующей системе:
Решая эту систему методом подстановки, получаем следующие результаты: ( и
) или (
и
). При
и
уравнение (2) имеет один неотрицательный корень
. При
и
уравнение (2) имеет один неотрицательный корень
.
То есть из двух прямых и
нужно выбрать такую, которая пересекает график функции
в двух различных точках.
- Решаем сперва уравнение:
Дискриминант последнего уравнения положителен. Значит, оно имеет два различных корня. Этот случай нам подходит.
- Решаем теперь уравнение:
Дискриминант этого уравнения равен нулю. Значит, решение в этом случае будет одно. Этот случай нам не подходит.
Ответ: .
Примечание. Для наглядности изобразим ситуацию на графике, хотя делать это необязательно, поскольку в задании этого не требуют:
4. Хорда окружности, удалённая от центра на расстояние 15, разбивает окружность на два сегмента, в каждый из которых вписан квадрат. Найдите разность сторон этих квадратов.
Пусть радиус окружности равен . Рассмотрим прямоугольные треугольники OMR и ODP. С учётом введённых на рисунке обозначений распишем теорему Пифагора для этих треугольников:
Вычтем почленно второе уравнение из первого:
Преобразуем полученное выражение, используя формулу «разность квадратов»:
Поделим обе части этого уравнения на и обозначит разность
за
. В результате приходим к следующему уравнению:
Искомая разность сторон квадратов в наших обозначениях будет равна .
Ответ: 24.
Введём замену: . Тогда неравенство принимает вид:
Теперь, используя стандартные свойства логарифмов, представим логарифмическое выражение слева от знака неравенства следующим образом:
Введём ещё одну замену: . Тогда после умножения обеих частей неравенства на положительное число
неравенство принимает вид:
Последовательно возвращаемся к исходной переменной :
Окончательно получаем следующий ответ:
Пусть в первую бочку долили кг воды, а во вторую —
кг. Пусть в первой бочке находится
кг, а во второй
кг соли.
Тогда изначально в первой бочке процентное содержание соли составляло:
а после доливания воды оно стало равно:
Аналогично, во второй бочке изначально процентное содержание соли составляло:
а после доливания воды оно стало равно:
Тогда справедливы равенства:
(3)
(4)
Из уравнения (3) выражаем , из уравнения (4) выражаем
, а из уравнения
выражаем
. Мы ищем минимальное значение суммы
. Проще всего найти его, используя неравенство Коши:
Итак, наименьшее количество воды, которое могло быть долито в обе бочки вместе равно 80 кг.
Этот случай реализуется при , когда неравенство Коши преобразуется в равенство. То есть при
. Подставляя это в выражение
, получаем после преобразований, что
. Отрицательный корень мы в расчёт не берём.
Ответ: 80 кг.
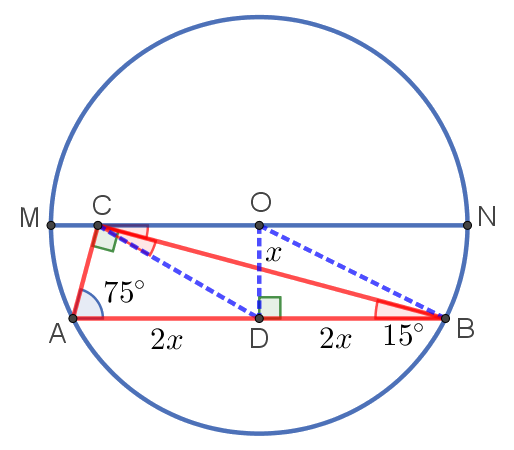
7. Вершина прямого угла C прямоугольного треугольника ABC расположена на диаметре окружности, параллельном хорде AB. Найдите площадь треугольника ABC, если ∠BAC = 75°, а радиус окружности равен 10.
Выполним следующие дополнительные построения:
- проведём высоту OD к хорде AB. Тогда D — середина AB, так как OD — высота и медиана, проведённая к основанию равнобедренного треугольника AOB;
- проведём отрезок CD. Он является медианой прямоугольного треугольника ACB, проведённой из вершины прямого угла. Значит, CD = AD = BD.
Переходим к решению:
- сумма углов в любом треугольнике равна 180°. Значит, ∠CBA = 15°;
- так как CD = BD, то треугольник CDB — равнобедренный и ∠CBD = ∠DCB = 15°;
- ∠CBD = ∠BCO = 15°, поскольку они являются накрест лежащими при параллельных прямых и секущей. Значит, ∠DСO = 30°;
- значит, в прямоугольном треугольнике COD против угла в 30° лежит катет OD, который равен половине гипотенузы CD. Пусть DO = x, а CD = AD = DB = 2x;
- из теоремы Пифагора для треугольника ODB получаем, что
, то есть
;
- тогда искомая площадь треугольника ABC равна половине произведения его высоты, проведённой к стороне AB, которая по длине равна x, на основание AB, которое по длине равно 4x. То есть искомая площадь равна
.
Ответ: 40.
выполняется для всех значений .
Преобразуем данное неравенство, раскрыв в нём скобки и использовав основное тригонометрическое тождество. В результате после всех преобразований получаем следующее неравенство:
Ведём замену , причём
. Тогда получим следующее неравенство:
Задача свелась к тому, чтобы найти все значения параметра , при котором последнее неравенство выполняется при всех
.
Для решения этой задачи представим последнее неравенство в виде:
Легко видеть, что при любых значениях
, так как дискриминант соответствующего квадратного уравнения отрицателен, и ветви соответствующей параболы направлены вверх. Поэтому мы можем разделить обе части последнего неравенства на положительное выражение
, при этом знак неравенства не поменяется:
(5)
Исследуем функцию на возрастание. Для этого определим при каких значениях
её производная положительна:
Так как , а
, то на промежутке
данная функция возрастает. Поэтому неравенство (5) будет выполняться при любом
при условии, что
, то есть
.
Ответ: .
Подготовка к вступительному экзамену по математике в МФТИ
Если вам требуется подготовка к вступительному экзамену по математике в МФТИ, обращайтесь к опытному профессиональному репетитору в Москве Сергею Валерьевичу. Возможны как очные, так и удаленный занятия через интернет с использованием интерактивной доски. Как показывает практика, в условиях ограниченности во времени именно занятия с репетитором обеспечивают наиболее эффективную подготовку к вступительным экзаменам. Подробную информацию о занятиях с репетитором вы можете найти на этой странице. Успехов вам в подготовке к экзаменам!
- — МЕНЮ —
- ЯГУБОВ.РФ
- ЕГЭ (ПРОФИЛЬ)
- ЕГЭ (БАЗА)
- ОГЭ (ГИА)
- ГЕНЕРАТОР
- ОЛИМПИАДЫ
- ЭКЗАМЕНЫ [МФТИ…]
- ЛИТ-РА
- ДВИ (МГУ)
- От Ягубова Р. Б.
- ЗАДАНИЯ
- ТЕМАТИКА
- РАСПИСАНИЕ
- ЗАНЯТИЯ
- ПРОГУЛЫ
- ПЛАТЕЖИ
- ФОРМУЛЫ
- ТЕТРАДЬ
- ЗАГАДКИ
- СОБЫТИЯ
- ИНВЕСТИЦИИ
- ГРУППА «ВК»
- МЫ В «YOUTUBE»
- ЯНДЕКС.КАРТЫ
- ПОИСК
- ОТЗЫВЫ
- — ВХОД —
Варианты вступительных экзаменов в МФТИ 2008 г. по математике
Вариант 1
- Решите неравенство
.
- Решите уравнение
.
- Найдите действительные решения системы уравнений
- Параллелограмм ABCD имеет площадь 4. Окружность с центром в точке О, расположенной на отрезке AD, касается отрезков AB, BC и прямой CD в точках M, N и K соответственно. Найти радиус этой окружности и стороны параллелограмма ABCD, если CK:BM=3:1.
- Найти все пары действительных чисел
, удовлетворяющие неравенству
.
- На основании ABCD четырехугольной пирамиды SABCD расположена точка O. Сфера с центром в точке О касается прямых SA, SB, SC, SD в точках A, B, K, L соответственно. Известно, что AB = KL =
, AL = 2, BK = 6, а отрезок SO составляет с плоскостью ABCD угол arccos
. Найти длины отрезков AK, OS и SD.
Вариант 5
- Решите неравенство
.
- Решите уравнение
.
- Решите систему уравнений
- В треугольнике ABC медиана BM равна 2, угол ABM равен
, угол CBM равен
. Найти стороны AB, BC и биссектрису BE треугольника ABC.
- Решите систему уравнений
- В основании пирамиды SABCD лежит параллелограмм ABCD. Сфера
радиуса
с центром O касается ребер AS, BS, AD, BC пирамиды SABCD соответственно в точках K, L, M, N, пересекает ребро AB в точках P и Q и касается грани CDS. Известно, что прямая SO перпендикулярна плоскости ABCD и пересекает ее в точке H, AB:PQ = 4:
, AS:LS=3:2. Найти угол SAB, угол SBH, высоту пирамиды и ее объем.
Ответы:
Вариант 1
или
Вариант 5
- (1;-1)
- arccos(4/9), arccos(5/9), h=2, V=64/21
вступительные экзамены в МФТИ
Задачи вступительных экзаменов по физике и математике в МФТИ в 1986-1988 годах
Экзамены — Экзамены по Физике
Задачи вступительных экзаменов по физике и математике в МФТИ в 1986-1988 годах
Задачи предлагались абитуриентам на письменных экзаменах по математике и физике.
Все задачи снабжены ответами.
Скачать и читать Задачи вступительных экзаменов по физике и математике в МФТИ в 1986-1988 годах
Билеты письменных вступительных экзаменов в МФТИ — Физика, математика — Ответы, решения — 2008
Экзамены — Экзамены по Физике
Билеты письменных вступительных экзаменов в МФТИ — Физика, математика — Ответы, решения — 2008
Очередная подборка экзаменационных билетов в Московский физико-технический институт. Все задачи снабжены ответами, часть — подробными решениями, некоторые — основными указаниями к решению.
Скачать и читать Билеты письменных вступительных экзаменов в МФТИ — Физика, математика — Ответы, решения — 2008
Билеты письменных вступительных экзаменов в МФТИ (2007) и олимпиады «Физтех-2007» — Методические разработки по физике и математике — Волкова И.А.
Экзамены — Экзамены по Физике
Билеты письменных вступительных экзаменов в МФТИ (2007) и олимпиады «Физтех-2007» — Методические разработки по физике и математике — Волкова И.А.
Приведены задачи, предлагавшиеся на олимпиаде «Физтех-2007» и вступительных экзаменах в Московский физико-технический институт(государственный университет) в 2007 году. Все задачи снабжены ответами, часть — подробными решениями, некоторые — основными указаниями к решению. На выполнение каждой работы давалось 4,5 часа.
Скачать и читать Билеты письменных вступительных экзаменов в МФТИ (2007) и олимпиады «Физтех-2007» — Методические разработки по физике и математике — Волкова И.А.
Билеты письменных вступительных экзаменов в МФТИ — Физика, математика — Ответы, решения — 2006
Экзамены — Экзамены по Физике
Билеты письменных вступительных экзаменов в МФТИ — Физика, математика — Ответы, решения — 2006
Предлагаем очередную подборку экзаменационных билетов по физике и математике с ответами и решениями для абитуриентов МФТИ и других технических ВУЗов, а также для преподавателей школ с углубленным изучением физики и математики.
Скачать и читать Билеты письменных вступительных экзаменов в МФТИ — Физика, математика — Ответы, решения — 2006
Билеты письменных вступительных экзаменов в МФТИ — Физика, математика — Ответы и решения — 2005
Экзамены — Экзамены по Физике
Билеты письменных вступительных экзаменов в МФТИ — Физика, математика — Ответы и решения — 2005
Вашему вниманию предлагаются экзаменационные билеты с ответами и решениями по физике и математике.
Скачать и читать Билеты письменных вступительных экзаменов в МФТИ — Физика, математика — Ответы и решения — 2005

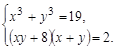
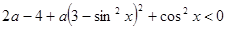
![Rendered by QuickLaTeX.com [ 4t^2-2sqrt{3}t-6=0Leftrightarrowleft[ begin{array}{l} t_1 = -frac{sqrt{3}}{2} \ t_2=sqrt{3}. end{array} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-8e85e67c476157c1f85c10a768fe9a26_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} x^3+y^3=19 \ (xy+8)(x+y)=2. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-e7bc49f8e253669ff9ba49d9426f85af_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} (x+y)((x+y)^2-3xy)=19 \ (xy+8)(x+y)=2. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-178655bc3fda7ef894fc3bbd7840314d_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} a(a^2-3b)=19 \ a(b+8)=2 end{cases}Leftrightarrow begin{cases} a^3-3ab = 19 \ 3ab+24a=6. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-5c997b7d3fe4081ba0adee4f624d29fa_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} x+y = 1 \ xy=-6. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-4a755b8f09270e84f7dc7d2a2b347511_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} k+b = 3 \ 16-7k-kb=0. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-f6bc14d85bd685587ec8be4ccf4a0b59_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} x^2 = R^2-(2x+15)^2 \ y^2 = R^2 - (2y-15)^2. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-4d914f9a98f6f9b06171fc2db0fd713e_l3.png)
![Rendered by QuickLaTeX.com [ =40sqrt{left(frac{m+3}{m-1}-1right)(m-1)}= ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-f3a93b14138c23455fa41a3e86698c39_l3.png)
![Rendered by QuickLaTeX.com [ y'=-frac{t^2+6t-29}{(t^2-6t+11)^2}>0Leftrightarrow ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-8059bcd31ba16c4f55ea4f68984b4b4a_l3.png)
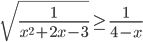
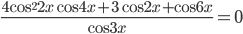
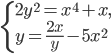
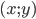
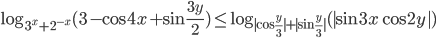
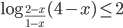
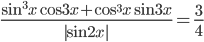
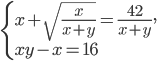
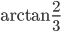
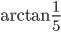
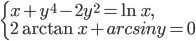
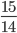
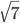
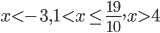
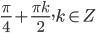
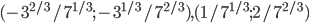
![R=sqrt[4]{3},AB=2/sqrt[4]{3},AD=4/sqrt[4]{3}](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_7115f99dd4e1ef69aaa4de6b780ebda9.gif)