Мировая экономика сга экзамен

   
   
Детали файла
Имя файла: 0037.Экз.04;ЭЭ.01;1
Размер: 37 Kb
Дата публикации: 2013-03-10 03:30:59
Описание:
Экономическая теория: Мировая экономика — Зачет

Внимание:

Эти ответы устарели! Самые свежие ответы ищите в разделе: КОМБАТ — ответы на тесты СГА

Попробуйте этот файл если не можете найти актуальные ответы, вполне вероятно что все подойдет.
Для скачивания этого файла Вы должны ввести код указаный на картинке справа в поле под этой картинкой —>
ВНИМАНИЕ:
Нажимая на кнопку «Скачать бесплатно» Вы подтверждаете свое полное и безоговорочное согласие с «Правилами сервиса»
Источник

Поиск ответов на вопросы онлайн-тестов и экзаменов из СГА и Roweb

В нашей базе знаний более 10 миллионов ответов. Мы позаботились об удобстве поиска: выполнять поиск ответов удобно как с персонального компьютера, так и с любого мобильного устройства.
В наличии есть ответы к различным системам онлайн обучения и тестирования:

  • Ответы к ГОСам в форме тестов
  • Ответы Ровеб или системе roweb.online
  • Ответы к тестам и экзаменам СГА
  • Ответы к ГОСам Комбат
  • Ответы к тестам Современной Гуманитарной Академии

Также имеются ответы к следующим дисциплинам и направлениям:

  • Ответы к тестам для менеджеров
  • Ответы к тестам для юристов
  • Ответы к тестам для экономистов
  • Ответы к тестам для психологов
  • Ответы к тестам по информатике
  • Ответы к тестам по математике
  • Ответы к тестам по русскому языку
  • Ответы к тестам по политологии
  • Ответы к тестам по повышению квалификации
  • И много другое …

Мы постоянно обновляем нашу базу ответов. С нами сдача экзаменов в СГА и Ровеб становится проще! Для автоматической сдачи тестов и экзаменов можно воспользоваться программой EasySGA.

Источник

Вопросы к экзамену по дисциплине «мировая экономика»

1. Мировая экономика (мэ) и международные экономические отношения (мэо): основные понятия и формы. Этапы становления и развития (в том числе традиционное, индустриальное, постиндустриальное общество).

МЭ —
совокупность национальных экономик
связанных между собой системой МЭО.

МЭ –
совокупность национальных экономик,
связанных друг с другой системой МРТ и
экономическими и политическими
отношениями (МЭО).

Субъектом МЭ
– национальные хозяйства/ государства;
ТНК/ТНБ; физические лица; МЭОРГ;
интеграционные объединения стран.

Объектом МЭ
– выступает экономика мира на базе
национальных экономик в исторической
и логической динамике.

Предмет МЭ
– является изучение комплекса связей
и взаимосвязей образующих МЭ.

МЭО
– это комплекс различных видов
экономических отношений между субъектами
мировой экономики, основанных на МРТ;
системы связей между национальными
экономиками отдельных стран.

Объекты МЭО
– товары, услуги, сотрудничество и т.д.

Предмет МЭО
– это система связей, совокупность
системообразующих связей.

Формы МЭО:

  • Международная
    специализация производства и
    научно-технических работ

  • Обмен
    результатами НТП

  • Международная
    производственная кооперация

  • Международная
    торговля

  • МВФиКДО

  • Миграция
    рабочих

  • Движение
    капитала

  • Деятельность
    МЭОРГ

Этапы становления
и развития:

  1. Римская
    Империя стлала первой формой МЭпредставляя из себя всемирную
    военно-политическую и экономическую
    систему

  2. XV-XVIвв.
    – в данный период происходит переход
    к новому этапу развития МЭО, в связи с
    великими географическими открытиями.
    В этот период торговля стала играть
    свою истинную роль, происходит
    формировании е мирового капиталистического
    рынка и мировой колониальной системы.
    Революция цен, мануфактура.

  3. XVII-первая
    половинаXIXв. Происходит
    развитие мирового капиталистического
    рынка. Развитие МРТ: промышленный
    переворот, буржуазная революция, переход
    от мануфактурной, фабричной системы
    производства.

  4. Середина
    XIX-XXвв. Промышленная революция, становление
    массового производства, усиление
    взаимозависимости экономик всех стран,
    появление новых видов МРТ, развитие
    НТП, интернационализация, интеграция,
    транснационализация.

Под
этапы:

    1. 1919-30гг-
      первая мировая война, социалистические
      революции, мировой экономический
      кризис.

    2. 1930-50гг
      – вторая мировая война, создание
      мировой социалистической системы.

    3. 1950-60гг
      – распад мировой колониальной системы

    4. 1990гг-
      настоящее время — распад мировой
      социалистической системы, развитее
      глобализации, усиление деятельности
      ТНК и ТНБ.

  1. Современный
    этап. Характеризуется НТП,
    интернационализацией, транснационализацией,
    глобализацией.

2. Причины развития экономических связей между странами. Международное разделение труда: содержание, формы, виды, цели и роль в мировой экономике.

Причина
возникновения и развития международных
экономических отношений — это различия
в наделенности стран факторами
производства (экономическими ресурсами).
С одной стороны, это ведет к международному
разделению труда. С другой стороны,
разная наделенность стран факторами
производства ведет к перемещению самих
этих факторов между странами.

МРТ – это форма МЭО, основа
функционирования МЭ и МЭО, представляет
собой специализацию страны на определенных
видах деятельности в целях последующей
ее реализации на мировом рынке(МР).

Факторы МРТ– труд, земля, капитал,
предпринимательский капитал или
технологии.

Основой МРТ— выступает специфика
обеспеченности различных стран факторами
производства и стремление к наиболее
эффективному их использованию.

Основная цель МРТ– увеличение
экономической эффективности производства,
той или иной продукции, т.е. получение
экономических выгод.

Виды МРТ:

МРТ:

-Общее
или межотраслевое МРТ

-Частное
или внутриотраслевое МРТ:

-предметное

-подетальное
(уход дальше, глубже в отрасль – авто
–стекло там-то)

-кооперационное
(специализация на определенных
технологических процессах — деталь
проходит обработку в нескольких странах)

Основные отрасли : с/х, промышленное
хозяйство и сфера услуг.

Формы
МРТ:

  • Международная
    специализация    – это форма МРТ;
    ориентация национальной экономики на
    производстве определенной продукции
    с целью ее последующей реализации на
    мировом рынке. (шире).

  • Международная
    кооперация    — это так же форма МРТ, но
    она представляет собой обмен между
    странами продуктами труда, произведенными
    с наибольшей экономической эффективностью.

Соседние файлы в предмете Мировая экономика

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Поделитесь с друзьями

Поиск тестов

Яндекс.Метрика

Источник

b>LU – разложение матрицы A представляет ее в виде
   -> произведения нижней треугольной матрицы на верхнюю треугольную матрицу
   произведения верхней треугольной матрицы на диагональную матрицу
   суммы двух треугольных матриц
   произведения симметричной матрицы на диагональную матрицу

Верны ли утверждения?

В виде, удобном для итераций, записаны системы линейных уравнений

А) ;

B) .

   -> A – нет, B – да
   A – да, B – нет
   A – да, B – да
   A – нет, B – нет

Верны ли утверждения?

В виде, удобном для итераций, записаны системы линейных уравнений

А) ;

B) ;

   -> A – да, B – да
   A – да, B – нет
   A – нет, B – нет
   A – нет, B – да

Верны ли утверждения?

В виде, удобном для итераций, записаны системы линейных уравнений:

А) ;

B) .

   -> A – нет, B – нет
   A – да, B – нет
   A – да, B – да
   A – нет, B – да

Верны ли утверждения?

В методе Гаусса решения систем линейных уравнений используются следующие виды матриц:

А) верхняя треугольная

В) симметричная

   -> A – да, B – нет
   A – да, B – да
   A – нет, B – нет
   A – нет, B – да

Верны ли утверждения?

Возможны следующие виды матриц:

А) единичная

B) нулевая

   -> A – да, B – да
   A – да, B – нет
   A – нет, B – нет
   A – нет, B – да

Верны ли утверждения?

Возможны следующие виды матриц:

А) единичная

В) прямоугольная

   -> A – да, B – да
   A – да, B – нет
   A – нет, B – нет
   A – нет, B – да

Верны ли утверждения?

Возможны следующие виды матриц:

А) продольная

В) прямоугольная

   -> A – нет, B – да
   A – да, B – нет
   A – да, B – да
   A – нет, B – нет

Верны ли утверждения?

Возможны следующие виды матриц:

А) трехдиагональная

В) ленточная

   -> A – да, B – да
   A – да, B – нет
   A – нет, B – нет
   A – нет, B – да

Верны ли утверждения?

Возможны следующие виды погрешностей:

А) абсолютная

В) округления

   -> A – да, B – да
   A – да, B – нет
   A – нет, B – да
   A – нет, B – нет

Верны ли утверждения?

Возможны следующие виды погрешностей:

A) чередующиеся

В) относительные

   -> A – нет, B – да
   A – да, B – нет
   A – да, B – да
   A – нет, B – нет

Верны ли утверждения?

Возможны следующие типы матриц:

А) ленточная

В) нижняя треугольная

   -> A – да, B – да
   A – да, B – нет
   A – нет, B – нет
   A – нет, B – да

Верны ли утверждения?

Даны линейные системы 1) 2) 3) 4). Свойством диагонального преобладания обладают системы

А) только 3

В) 2 и 4

   -> A – нет, B – нет
   A – да, B – нет
   A – да, B – да
   A – нет, B – да

Верны ли утверждения?

Даны линейные системы 1) 2) 3) 4). Свойством диагонального преобладания обладают системы

А) 1 и 2

В) 1 и 4

   -> A – да, B – нет
   A – да, B – да
   A – нет, B – нет
   A – нет, B – да

Верны ли утверждения?

Для систем линейных уравнений справедливы следующие утверждения:

A) для плохо обусловленных систем малые ошибки в правых частях и коэффициентах приводят к большим погрешностям в решении системы

B) метод Гаусса является прямым методом

   -> A – да, B – да
   A – да, B – нет
   A – нет, B – нет
   A – нет, B – да

Верны ли утверждения?

Для систем линейных уравнений справедливы следующие утверждения:

A) итерационный метод Зейделя сходится всегда

B) метод простой итерации сходится всегда

   -> A – нет, B – нет
   A – да, B – нет
   A – да, B – да
   A – нет, B – да

Верны ли утверждения?

Для систем линейных уравнений справедливы следующие утверждения:

А) метод разложения является итерационным методом

B) метод Гаусса является прямым методом

   -> A – нет, B – да
   A – да, B – нет
   A – нет, B – нет
   A – да, B – да

Верны ли утверждения?

Для систем линейных уравнений справедливы следующие утверждения:

A) для хорошо обусловленных систем малые ошибки в задании правых частей и коэффициентов системы приводят к малым ошибкам в решении

B) метод Гаусса является итерационным методом

   -> A – да, B – нет
   A – да, B – да
   A – нет, B – нет
   A – нет, B – да

Верны ли утверждения?

Для систем линейных уравнений справедливы следующие утверждения:

А) метод итераций Зейделя сходится всегда

B) метод простой итерации сходится, если все коэффициенты матрицы системы меньше единицы

   -> A – нет, B – нет
   A – да, B – нет
   A – нет, B – да
   A – да, B – да

Верны ли утверждения?

Для систем линейных уравнений справедливы следующие утверждения:

А) метод итераций Зейделя сходится, если матрица системы обладает свойством диагонального преобладания

B) метод простой итерации сходится, если все коэффициенты матрицы положительны

   -> A – да, B – нет
   A – нет, B – нет
   A – нет, B – да
   A – да, B – да

Верны ли утверждения?

Заданы системы линейных уравнений 1) 2) 3) . Свойством диагонального преобладания обладают матрицы систем:

А) 1 и 3

B) только 2

   -> A – да, B – нет
   A – да, B – да
   A – нет, B – нет
   A – нет, B – да

Верны ли утверждения?

Заданы системы линейных уравнений 1) 2) 3) . Свойством диагонального преобладания обладают матрицы систем

А) 1

B) 2 и 3

   -> A – да, B – нет
   A – да, B – да
   A – нет, B – нет
   A – нет, B – да

Верны ли утверждения?

Заданы системы линейных уравнений 1) 2) 3) . Свойством диагонального преобладания обладают матрицы систем

А) 1 и 2

B) 3

   -> A – нет, B – да
   A – да, B – нет
   A – да, B – да
   A – нет, B – нет

Верны ли утверждения?

Значительная потеря точности при выполнении арифметических операций на ЭВМ происходит:

А) при умножении близких чисел

B) при сложении близких чисел

   -> A – нет, B – нет
   A – да, B – нет
   A – да, B – да
   A – да, B – нет

Верны ли утверждения?

Значительная потеря точности при выполнении арифметических операций на ЭВМ происходит

А) при вычитании близких чисел

В) при сложении близких чисел

   -> A – да, B – нет
   A – да, B – да
   A – нет, B – нет
   A – нет, B – да

Верны ли утверждения?

Метод Зейделя для системы линейных уравнений

А) сходится при любом начальном приближении

В) приведет к зацикливанию

   -> A – да, B – нет
   A – да, B – да
   A – нет, B – нет
   A – нет, B – да

Верны ли утверждения?

При математическом моделировании на компьютере для возникающих погрешностей справедливы следующие утверждения:

А) Погрешность математической модели является неустранимой

В) Погрешность численного метода является регулируемой

   -> A – да, B – да
   A – да, B – нет
   A – нет, B – нет
   A – нет, B – да

Верны ли утверждения?

Существуют следующие методы решения систем линейных уравнений:

A) прямые

B) итерационные

   -> A – да, B – да
   A – да, B – нет
   A – нет, B – нет
   A – нет, B – да

Верны ли утверждения?

Существуют следующие методы решения систем линейных уравнений:

А) метод Гаусса

В) итерационный метод Зейделя

   -> A – да, B – да
   A – да, B – нет
   A – нет, B – нет
   A – нет, B – да

Верны ли утверждения?

Существуют следующие методы решения систем линейных уравнений

А) ортогональные

B) прямые

   -> A – нет, B – да
   A – да, B – нет
   A – да, B – да
   A – нет, B – нет
Aбсолютные погрешности величин x и y равны Δ(x) = 0,1 и Δ(y) = 0,4. Абсолютная погрешность разности Δ(x — y) равна
   -> 0,5
   0,3
   0,04
   0,1
Aбсолютные погрешности величин x и y равны Δ(x) = 0,1 и Δ(y) = 0,4. Абсолютная погрешность суммы Δ(x + y) равна
   -> 0,5
   0,3
   0,04
   0,2
Абсолютные погрешности величин x и y равны ∆x = 0,4 и ∆y =0,3. Абсолютная погрешность разности ∆(x – y) равна
   -> 0,7
   0,1
   0,12
   1,3333333
Алгоритм называется неустойчивым, если
   -> малые изменения исходных данных и погрешности округления приводят к значительному изменению окончательных результатов
   большие изменения в исходных данных не изменяют окончательный результат
   малые изменения исходных данных не изменяют окончательный результат
   большие изменения в исходных данных приводят к малому изменению результата
Выбор начального приближения на сходимость метода Зейделя при решении систем линейных уравнений
   -> не влияет
   влияет, если матрица не симметричная
   влияет, если матрица не является верхней треугольной
   не влияет, если матрица является ленточной
Дана система , задано начальное приближение (1; 1). Один шаг метода Зейделя дает первое приближение
   -> (0,6; 1,06)
   (0,1; 1,06)
   (0,6; 1)
   (0,6; 1,1)
Дана система . Первое приближение для метода простой итерации с начальным приближением (0,1; 0,2) равно
   -> (0,13; 0,14)
   (0,14; 0,13)
   (0,9; 0,9)
   (0,5; 0,4)
Дана система линейных уравнений . Для сходящегося метода Зейделя ее надо записать в виде
   -> 
   
   
   
Дана система уравнений . Для сходимости итерационного метода ее надо записать в виде
   -> 
   
   
   
Даны линейные системы 1) 2) 3) 4) . Свойством диагонального преобладания обладают системы
   -> 1 и 2
   1, 3 и 4
   1 и 4
   3 и 4
Для величин x = 1 и y = 2 известны абсолютные погрешности ∆(x) = 0,001 и ∆(y) = 0,005. Абсолютная погрешность произведения ∆(x∙y) равна
   -> 0,007
   0,011
   0,006
   0,000005
Для величин x = 10 и y = 20 известны относительные погрешности δ(x)=0,005 и δ(y) = 0,003. Относительная погрешность произведения δ(x ∙ y) равна
   -> 0,008
   0,002
   0,000015
   0,011
Для величин x = 2 и y = 1 известны относительные погрешности δ(x) = 0,001 и δ(y) = 0,002. Относительная погрешность разности δ(x – y) равна
   -> 0,004
   0,003
   0,0002
   0,001
Для величин x = 2 и y = 5 известны относительные погрешности δ(x)=0,005 и δ(y) = 0,002. Относительная погрешность частного δ(x ∕ y) равна
   -> 0,007
   0,003
   0,0025
   0,00001
Для величин x = 2 и y = 8 известны относительные погрешности δ(x)=0,01 и δ(y) = 0,02. Относительная погрешность суммы δ(x + y) равна
   -> 0,018
   0,016
   0,03
   0,003
Для величин x = 2, y = 1, z = 2 заданы их относительные погрешности δ(x)=0,005; δ(y) = 0,001; δ(z) =0,002. Относительная погрешность произведения δ(x ∙ y ∙z) равна
   -> 0,008
   0,0000002
   0,0001
   0,0002
Для величин x = 5 и y = 1 известны абсолютные погрешности ∆(x) = 0,001 и ∆(y) = 0,0005. Абсолютная погрешность частного ∆(x/y) равна
   -> 0,0035
   0,0005
   0,0015
   0,000005
Для величин x и y заданы абсолютные погрешности Δ(x) = 0,01 и Δ(y) =1,5. Тогда абсолютная погрешность разности Δ(x−y) равна
   -> 1,51
   1,49
   −1,49
   −1,51
Для величин x и z заданы их абсолютные погрешности ∆(x) = 0,05; ∆(z) = 0,02 . Тогда абсолютная погрешность величины ∆(x− z) будет равна
   -> 0,07
   0,01
   0,03
   0,0099
Для величин x и z заданы их абсолютные погрешности ∆(x) = 0,02; ∆(z) = 0,07 . Тогда абсолютная погрешность величины ∆(x− z) будет равна
   -> 0,09
   -0,05
   0,05
   0,01
Для величин x, y и z заданы их абсолютные погрешности ∆(x) = 0,008; ∆(y) = 0,004 ; ∆(z) = 0,001. Тогда абсолютная погрешность величины ∆(x+y− z) будет равна
   -> 0,013
   0,011
   0,008
   0,001
Для линейной системы уравнений известно LU – разложение матрицы A = LU. Тогда количество систем уравнений с треугольными матрицами, к которым сводится решение исходной системы уравнений, равно
   -> двум
   трем
   единице
   четырем
Для линейной системы уравнений вычисления по итерационной формуле называют методом
   -> Зейделя
   простой итерации
   Гаусса
   Ньютона
Для линейной системы уравнений вычисления по итерационной формуле называют методом
   -> простой итерации
   Зейделя
   релаксации
   Ньютона
Для матрицы A = метод Зейделя x(k+1) = Ax(k) будет
   -> расходящимся
   сходящимся
   сходящимся при начальном векторе
   сходящимся при начальном векторе
Для матрицы LU – разложение имеет вид
   -> L = U =
   L = U =
   L = U =
   L = U =
Для обратного хода метода Гаусса подготовлены следующие системы уравнений 1) 2) 3)
   -> только 2
   1 и 2
   3
   2 и 3
Для системы линейных уравнений известны обратная матрица A-1 и вектор правых частей . A-1 = , = . Тогда вектор решения системы равен
   -> {0,5; 1}
   {1; 0,1}
   {1; 0,5}
   {1,5; 1,1}
Достаточные условия сходимости метода Зейделя для системы линейных уравнений с матрицей A заключаются в том, что
   -> ( i = 1, 2, . . . n; j = 1, 2, . . . n)
   aii ≠ 0 ( i = 1, 2, . . . n)
   ( 1 ≤ j ≤ n , j ≠ i , i = 1, 2, . . . n)
   ( i = 1, 2, . . . n; j = 1, 2, . . . n)
Единичной матрицей является матрица
   -> 
   
   
   
Задана линейная система . Первое приближение метода Зейделя при начальном значении дает результат
   -> {1,8; 0,74}
   {1,8; 1,1}
   {2; 0,74}
   {2; 0,68}
Задана линейная система . Первое приближение метода простой итерации при начальном значении дает результат
   -> {1,9; 0,9}
   {1,9; 2,7}
   {2; 1}
   {2; 2,7}
Задана линейная система . Первое приближение метода Зейделя при начальном значении дает результат
   -> {2; 0,9}
   {2; 1}
   {2; 1,1}
   {1; 2}
Задана линейная система . Первое приближение метода простой итерации при начальном значении дает результат
   -> {2,1; 0,9}
   {2,2; 1,1}
   {2; 1}
   {2,1; 1,1}
Задана линейная система . Начиная с начального значения x1(0) = x2(0) = x3(0) = 0, один шаг метода Зейделя {x1(1), x2(1), x3(1)} будет равен
   -> {0,75; 1,35; 0,445}
   {0,75; 1,2; 0,1}
   {0,75; 1,35; 0,05}
   {0,75; 1,2; 0,445}
Задана линейная система . Начиная с начального значения x1(0) = x2(0) = x3(0) = 0 один шаг метода простой итерации{x1(1), x2(1), x3(1)} будет равен
   -> {0,75; 1,2; 0,1}
   {0,75; 1,55; 4,85}
   {0,75; 1,55; 0,1}
   {0,75; 1,2; 0,5}
Задана линейная система . Начиная с начального значения x1(0) = x2(0) = x3(0) = 0, один шаг метода Зейделя {x1(1), x2(1), x3(1)} будет равен
   -> {0,5; 0,75; 0,3}
   {0,5; 0,5; 0,1}
   {0,5; 1,2; 0,1}
   {0,75; 1,2; 0,1}
Задана линейная система уравнений в матричном виде . Ее степень обусловленности равна
   -> 105
   0,01
   10
   104
Задана линейная система уравнений с симметричной матрицей . Ее степень обусловленности равна
   -> 10
   1000
   -10
   5
Задана система линейных уравнений . Для заданного начального приближения x1(0) = 0; x2(0) = 1 первый шаг метода Зейделя дает следующие значения первого приближения {x1(1), x2(1)}
   -> {2,5; 0,95}
   {2,5; 0,2}
   {1,5; 0,2}
   {1,5; 0,8}
Задана система линейных уравнений . Для заданного начального приближения x1(0) = 0; x2(0) = 1, первый шаг метода простой итерации дает следующие значения первого приближения {x1(1), x2(1)}
   -> {2,5; 0,2}
   {2,5; 0,95}
   {2,5; 0,9}
   {2,5; 0,5}
Задана система линейных уравнений . Один шаг метода Зейделя с начальным приближением {0; 1; 0} дает следующее первое приближение:
   -> {0,5; 2,05; 0,205}
   {0,5; 2; 0,1}
   {0,3; 2,05; 2}
   {0,5; 2; 0,0205}
Задана система линейных уравнений . Один шаг метода простой итерации с начальным приближением {0; 0; 0} дает следующее первое приближение
   -> {0; 2; 0}
   {0; 0; 0}
   {0,5; 2; 0,1}
   {0,5; 2; 0}
Заданы матрицы 1) , 2) , 3) . Условиям диагонального преобладания удовлетворяют матрицы
   -> Первая
   третья
   первая и вторая
   вторая и третья
Заданы матрицы 1) , 2) , 3) . Условиям диагонального преобладания удовлетворяют матрицы
   -> 2 и 3
   1
   только 3
   только 2
Заданы матрицы 1) , 2) , 3) . Условиям диагонального преобладания удовлетворяют матрицы
   -> 1
   1 и 3
   только 2
   2 и 3
Заданы системы линейных уравнений 1) 2) 3) . Свойством диагонального преобладания обладают матрицы систем
   -> 1 и 3
   2 и 3
   только 2
   только 3
Заданы системы линейных уравнений 1) 2) 3) . Свойством диагонального преобладания обладают матрицы систем
   -> 2
   1 и 2
   только 3
   2 и 3
Заданы системы линейных уравнений 1) 2) 3) . Свойством диагонального преобладания обладают матрицы систем
   -> 1 и 3
   только 3
   только 2
   только 1
Заданы системы линейных уравнений 1) 2) 3) . Свойством диагонального преобладания обладают матрицы систем
   -> 2 и 3
   только 2
   только 3
   1 и 2
Линейная система уравнений задана в виде . Тогда x1 и x2 равны
   -> {1; 1}
   {2; 1}
   {1; 2}
   {2; 0}
Матрица A = называется
   -> нижней треугольной
   верхней треугольной
   диагональной
   верхней симметричной
Матрица A= называется
   -> верхней треугольной
   трехдиагональной
   треугольной
   ленточной
Метод Гаусса заключается в сведении исходной матрицы системы к эквивалентному виду, где матрица преобразованной системы является
   -> верхней треугольной матрицей
   диагональной матрицей
   ленточной матрицей
   симметричной матрицей
Метод Зейделя для системы линейных уравнений
   -> сходится при любом начальном приближении
   расходится при любом начальном приближении
   сходится только при x1 = 0, x2 = 0
   приведет к зацикливанию
Метод итераций для линейной системы
   -> будет сходиться при любом начальном приближении
   будет расходиться
   приведет к зацикливанию
   будет сходиться только при специальном выборе начального приближения
Невязкой линейной системы уравнений называется величина
   -> 
   
   
   
Обобщенное решение переопределенных систем линейных уравнений (как совместных, так и несовместных) можно найти методом
   -> наименьших квадратов
   Ньютона
   Зейделя
   интерполяции
Параметр релаксации ω для метода верхней релаксации при решении системы линейных уравнений методом итераций лежит в пределах
   -> 1 < ω < 2
   0 < ω < 1
   −1 < ω < 0
   2 < ω < 3
Погрешность математической модели является
   -> неустранимой
   регулируемой
   возрастающей
   вычислительной
Прямой ход метода Гаусса сводит линейную систему уравнений к виду
   -> с верхней треугольной матрицей
   с трехдиагональной матрицей
   с диагональной матрицей
   с симметричной матрицей
Система линейных уравнений записана в виде, удобном для итераций, если она имеет вид
   -> 
   
   
   
Система линейных уравнений называется недоопределенной, если
   -> количество уравнений меньше количества неизвестных
   не все коэффициенты системы заданы
   не заданы правые части системы
   все коэффициенты системы являются иррациональными числами
Система линейных уравнений называется определенной, если
   -> количество уравнений равно количеству неизвестных
   коэффициенты системы являются целыми числами
   правые части заданы с высокой точеностью
   коэффициенты системы являются рациональными
Система линейных уравнений называется переопределенной, если
   -> количество уравнений системы меньше количества неизвестных
   коэффициенты системы заданы недостаточно точно
   правые части системы не заданы
   часть уравнений системы является линейными, а часть – нелинейными
Степень обусловленности линейной системы уравнений равна
   -> 100
   0,01
   50
   10
Сходимость итерационного метода решения систем линейных уравнений зависит от
   -> вида матрицы системы
   начального приближения системы
   величины правых частей системы
   количества нулей в матрице
Число 0,0037 в ЭВМ для режима с плавающей точкой в нормализованном виде имеет следующее представление
   -> 
   
   
   37
Число 125,7 в ЭВМ для режима с плавающей точкой в нормализованном виде имеет следующее представление
   -> 0,1257∙103
   0,01257∙104
   125,7
   1,257∙102
Число 623 в ЭВМ для режима с плавающей точкой в нормализованном виде имеет следующее представление
   -> 0,623∙103
   6,23
   623
   62,3

Математическая статистика

Тема № 14 Генеральная
и выборочная совокупности

Вопросы для
самостоятельного изучения

1. Выборочный метод.

Пример 1.
Для выявления доли (удельного веса)
простаивающих станков было взято на
выборку 100 станков. Простаивающих
станков оказалось 20. с надежностью 0,99
оценить доверительный интервал, в
котором окажется доля
простаивающих станков во всей совокупности
станков.

Найдём долю
простаивающих станков в выборочной
совокупности

Определим предельную
ошибку выборки

Доверительные
интервалы доли простаивающих станков
во всей совокупности станков будут
,
подставляем

Чаще интервалы
для доли вычисляются в процентах, тогда

Т.е. с надёжностью
0,99 доля простаивающих станков во всей
совокупности будет заключена в пределах
доверительного интервала от 0,97% до 30,3%
всех станков.

Пример 2.
Имеются данные о производительности
труда 100 ткачих фабрики, на которой
работают 1000 ткачих.

Выработано
ткани, м

20-24

24-28

28-32

32-36

36-40

40-44

Число
ткачих

9

12

36

27

10

6

Определить: 1)
доверительный интервал, в котором с
надежностью 0,9973 заключена средняя
выработка одной ткачихи фабрики;

2) доверительный
интервал, в котором с надежность 0,9545
заключена доля ткачих, имеющих выработку
36 метров и более;

3) вероятность
того, что средняя выработка одной ткачихи
фабрики отличается от средней выработки
обследованных ткачих не более чем на
0,8 м по абсолютной величине.

Решение:
Вычислим характеристики выборочной
совокупности:

выборочную среднюю
—

выборочную дисперсию
—

Все необходимые
расчеты приведены в таблице:

Выработка
ткани, м

20-24

22

9

198

-9,4

88,36

795,24

24-28

26

12

312

-5,4

29,16

349,92

28-32

30

36

1080

-1,4

1,96

70,56

32-34

34

27

918

2,6

6,76

182,52

36-40

38

10

380

6,6

43,56

435,60

40-44

42

6

252

10,6

112,36

674,16

—

100

3140

—

—

2508

Из таблицы имеем:
м;м2

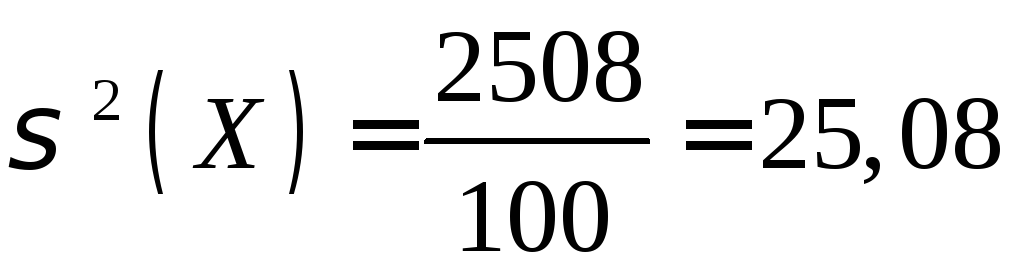
=5,008м,

1) При надёжности
,
коэффициент надежности(таблица 2).

Для повторного
отбора

=

Доверительный
интервал для генеральной средней

При
повторном отборе

м

Для
бесповторного отбора

м

С надёжностью
0,9973 можно утверждать, что средняя
выработка одной ткачихи фабрики
(генеральная средняя) будет изменяться
при повторном отборе от 29,898 м и до 32,902
м, а при бесповторном отборе от 29,975 м до
32,825 м.

2) Выборочная
дисперсия по доле

При
,
коэффициент надежности(таблица 2).

Предельные ошибки:

для повторного
отбора
==

для бесповторного
отбора

Доверительный
интервал для доли:

для повторного
отбора

или

для бесповторного
отбора

или

С надежностью
0,9545 можно утверждать, что доля ткачих
фабрики (генеральная доля), имеющих
выработку 36 метров и более будет
изменяться от 8,7% до 23,3% при повторном
отборе и от 9,04% до 22,96% для бесповторного
отбора.

3) Для определения
вероятности (надежности), что средняя
выработка одной ткачихи фабрики
отличается от средней выработки
обследованных ткачих не более чем на
0,8 м по абсолютной величине, используем
формулу теоремы Чебышева-Ляпунова

.

Значение
найдем
по формуле предельной ошибки выборки
для

бесповторного
отбора
.

Тогда имеем

По таблице №2
значение функции
находим

Окончательно
запишем

С вероятностью
0,9070 можно утверждать, что средняя
выработка одной ткачихи фабрики
отличается от средних обследованных
ткачих не более чем на 0,08 м.

Задания
для самостоятельной работы

1. В магазинах торга
выборочным методом был подсчитан средний
стаж работы 100 сотрудников. Оказалось,
что он равен в среднем 10 годам при среднем
квадратичном отклонении 3 года. Определить
надежность, с которой можно утверждать,
что отклонение полученной выборочной
средней от генеральной средней не
превысит 1 года

2.
Обследуется содержание белка в привезенной
на элеватор пшенице. В лабораторию взят
для исследования 1 кг (1000 гр) зерен. Доля
белка в этих зернах 0,17. С надежностью
0,9545 найти доверительный интервал, в
котором заключена доля белка во всей
пшенице.

3. Сколько рабочих
– сдельщиков можно включить в выборку
для определения средней выработки
одного рабочего, чтобы предельная ошибка
не превышала 2,5 ден. ед. с вероятностью
0,9973 при среднем квадратичном отклонении
15 д.е.

4. Был проведен
выборочный опрос 25 студентов о
распределении бюджета времени.
Обследование показало, что в среднем
ежедневные затраты времени на
самостоятельную работу составляют 4
часа при среднем квадратичном отклонении
0,5 часа. Определить с вероятностью 0,9973
среднюю и предельную ошибки, а также
доверительный интервал, в котором
заключена генеральная средняя.

5. Для выявления
удельного веса неработающих станков
отобрано 100 станков. Неработающих
оказалось 20. С надежностью 0,95 оценить
доверительный интервал, в котором
окажется доля неработающих станков во
всей совокупности.

6.
Сколько рабочих – сдельщиков можно
включить в выборку для определения
средней выборки одного рабочего –
сдельщика, чтобы предельная ошибка не
превышала 2,5 ден. ед., при среднем
квадратическом отклонении 15 ден. ед.,..а
надежность 0,9973

7. В магазинах
коопторга выборочным методом был
подсчитан средний стаж работы 100
продавцов. Оказалось, что он равен в
среднем 10 годам при среднем квадратическом
отклонении 3 года. С какой надежностью
можно утверждать, что отклонение
полученной выборочной средней от
генеральной средней не превысит одного
года.

8. Даны результаты
обследования 100 взрослых мужчин по
росту:

Рост,
см

164
— 166

166
— 168

168
— 170

170
— 172

172
— 174

174
— 176

Число
мужчин

2

8

14

45

26

5

Определить:

1)доверительный
интервал, в котором с надежностью 0,9973
заключен средний рост всех мужчин;

2)доверительный
интервал, в котором с надежностью 0,9545
заключена доля мужчин, имеющих рост
170см и более

9. Результаты
выборочного наблюдения за обработкой
рабочими одной детали даны в таблице:

Время
обработки, мин.

4.0
– 4.4

4.5
– 4.9

5.0
– 5.4

5.5
– 5.9

6.0
– 6.4

6.5-
6.9

Число
работающих

9

16

38

21

10

6

С вероятностью
0,9545 оценить:

1)среднее время
обработки одной детали рабочими всего
цеха, в котором работают 2000 рабочих;

2)долю рабочих
всего цеха, обрабатывающих детали менее
чем за 6 минут.

10. Даны результаты
выборочного (бесповторного) обследования
заработной платы 100 рабочих предприятия,
на котором занято 1000 рабочих:

Зарплата,
тыс.руб.

2,1
– 2,3

2,3
– 2,5

2,5
– 2,7

2,7
– 2,9

2,9
– 3,1

3,1
– 3,3

3,3
– 3,5

Число
рабочих

4

9

20

35

19

8

5

Определить:
1)доверительный интервал, в котором с
надежностью 0,9545 заключена средняя
заработная плата всех рабочих предприятия;

2)с вероятностью
0,9973 предельной доли
рабочих,
имеющих заработную плату менее 2,9 тыс.
руб.

11. В результате
обследования стажа работы сотрудников
предприятия получены следующие данные:

Стаж
работы, год

2-6

6-10

10-14

14-18

18-22

22-26

26-30

Число
работников

I

2

6

18

II

9

3

Определить: 1)
доверительный интервал, в котором с
надежностью 0,9973 заключен средний стаж
работы сотрудников всего предприятия,
на котором занято 1000 человек;

2)доверительный
интервал, в котором с надежностью 0,9545
заключена доля сотрудников предприятия,
имеющих стаж работы 10 лет и более.

Рекомендуемая
литература

1.
Гмурман В.Е. Теория вероятностей и
математическая статистика. Учебное
пособие. Издание десятое, стереотипное.
— М.: Высшая школа», 2004 г. – 480 с.

Тема № 15
Интервальные
оценки параметров распределения.
Непрерывное и дискретное распределения
признаков

Вопросы для
самостоятельного изучения

1. Точечные оценки
параметров распределения.

Контрольные
вопросы

  1. Дать определение
    точечной оценки
    неизвестного параметра θ.

  2. Каким свойствам
    должна удовлетворять точечная оценка?

Рекомендуемая
литература

1.
Гмурман В.Е. Теория вероятностей и
математическая статистика. Учебное
пособие. Издание десятое, стереотипное.
— М.: Высшая школа», 2004 г. – 480 с.

Тема № 16
Характеристики
вариационного ряда

Вопросы для
самостоятельного изучения

1. Вариационные
ряды.

2. Построение
интервального вариационного ряда.

3. Графическое
изображение вариационных рядов.

4. Средние величины.

5. Медиана и мода.

6. Показатели
вариации.

7. Свойства
эмпирической дисперсии.

8. Эмпирические
центральные и начальные моменты.

9. Эмпирические
асимметрия и эксцесс.

Контрольные
вопросы

1. Дать определение
накопленной
частости.

2. Дать
определение интервального
вариационного ряда.

3. Какие виды
графического изображения вариационных
рядов используются?

4. Для чего служит
гистограмма?

5. Дать определение
статистическим
характеристикам вариационного
ряда.

Рекомендуемая
литература

1.
Гмурман В.Е. Теория вероятностей и
математическая статистика. Учебное
пособие. Издание десятое, стереотипное.
— М.: Высшая школа», 2004 г. – 480 с.

Тема № 17
Доверительные
вероятности, доверительные интервалы

Вопросы для
самостоятельного изучения

1. Доверительные
вероятности, доверительные интервалы.

Контрольные
вопросы

1. Дать определение
доверительного интервала для параметра
θ.

2. Дать определение
доверительной вероятности.

Рекомендуемая
литература

1.
Гмурман В.Е. Теория вероятностей и
математическая статистика. Учебное
пособие. Издание десятое, стереотипное.
— М.: Высшая школа», 2004 г. – 480 с.

Тема № 18
Регрессионный
анализ, корреляционный анализ

Вопросы для
самостоятельного изучения

1. О связях
функциональных и статистических.

2. Определение
формы связи. Понятие регрессии.

3. Основные положения
корреляционного анализа.

4. Свойства
коэффициента корреляции.

5.
Поле корреляции. Вычисление оценок
параметров двумерной модели.

6. Проверка гипотезы
о значимости коэффициента корреляции.

7. Корреляционное
отношение.

8. Понятие о
многомерном корреляционном анализе.

9. Частный коэффициент
корреляции.

Множественный
коэффициент корреляции.

10. Ранговая
корреляция.

11. Основные положения
регрессионного анализа.

12. Линейная
регрессия.

13. Нелинейная
регрессия.

14. Оценка значимости
коэффициентов регрессии. Интервальная
оценка коэффициентов регрессии.

15. Интервальная
оценка для условного математического
ожидания.

16. Проверка
значимости уравнения регрессии.

17. Многомерный
регрессионный анализ.

18. Факторный анализ.

19. Факторное
отображение.

20. Определение
факторных нагрузок.

21. Метод главных
компонент.

Контрольные
вопросы

1. Какими методами
можно изучать статистические связи
между переменными?

2. Какова основная
задача корреляционного анализа?

3. Что является
оценкой коэффициента корреляции?

4. Как строят
корреляционную таблицу?

5. Что является
оценкой частного коэффициента корреляции
l-го
порядка?

6. Дать определение
множественного коэффициента детерминации.

7. Для чего служит
коэффициент
конкордации?

8. Какова основная
задача регрессионного анализа?

9. Дать определение
остаточной дисперсии.

10. Кто является
одним из основоположников факторного
анализа?

Рекомендуемая
литература

1.
Гмурман В.Е. Теория вероятностей и
математическая статистика. Учебное
пособие. Издание десятое, стереотипное.
— М.: Высшая школа», 2004 г. – 480 с.

36

Источник

Понравилась статья? Поделить с друзьями:
  • Мировая экономика презентация 11 класс обществознание егэ
  • Мировая экономика понятие егэ
  • Мировая экономика подготовка к экзамену
  • Мировая экономика план по обществознанию егэ 2022
  • Мировая экономика ниу вшэ экзамены