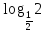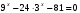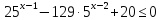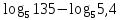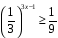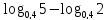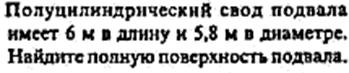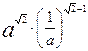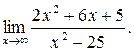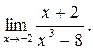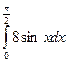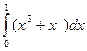Миссис экзамен по математике 1 семестр

Кафедра математики проводит обучение студентов всех специальностей и направлений подготовки НИТУ МИСИС по следующим дисциплинам:

  • Математика (модули)
    • Аналитическая геометрия и линейная алгебра (ИТКН, ИНМиН, ЭкоТех, ЭУПП, МГИ) (1 семестр);
    • Дифференциальное исчисление (ИТКН, ИНМиН) (1 семестр);
    • Дифференциальное исчисление функций одной переменной (ЭкоТех, ЭУПП, МГИ) (1 семестр);
    • Интегральное исчисление функций одной переменной и дифференциальное исчисление функций нескольких переменных (ЭкоТех, ЭУПП, МГИ) (2 семестр);
    • Интегральное исчисление (ИТКН) (2 семестр);
    • Интегральное исчисление и дифференциальные уравнения (ИНМиН) (2 семестр);
    • Дифференциальные уравнения (ИТКН) (3 семестр);
    • Ряды и дифференциальные уравнения (ЭкоТех, ЭУПП, МГИ) (3 семестр);
    • Ряды и теория функций комплексного переменного (ИТКН, ИНМиН) (3 семестр);
    • Теория вероятностей и математическая статистика (ИТКН, ЭкоТех, ЭУПП, МГИ) (4 семестр);
  • Методы математической физики (ИНМиН) (4 семестр);
  • Функциональный анализ (ИТКН) (5 семестр);
  • Математическая статистика и анализ данных (ИНМиН) (4 семестр);
  • Дополнительные главы математики (МГИ, магистратура 1 семестр).

Большинство курсов читаются с использованием мультимедийных средств. Все курсы ведутся с использованием системы смешанного обучения LMS Canvas.

Балльно-рейтинговая система кафедры математики

Положение о студенческой олимпиаде по математике НИТУ МИСИС

Регламент проведения студенческой олимпиады по математике (6,3 МБ)

Источник

Идет загрузка списка

    Идет загрузка списка

    Помогите рассортировать файлы. К какому предмету относится данный файл?

    Ненужные и мусорные файлы можно перемещать в предмет [НА УДАЛЕНИЕ].

    Помогите дать файлам осмысленные названия

    Примеры:
    lab1 => Лабораторная работа №1. Фотоэффект.
    Savelev_molekulyarnaya_fizika => Савельев. Молекулярная физика

    Источник

    II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант №1

    1. Вычислите значение выражения

    2. Решите уравнение

    3. Вычислите значение выражения

    4. Решите уравнение:

    5. Решите уравнение

    6. Вычислите +

    7. Найти угол между векторами

    8. В футбольной команде 11 человек. Необходимо выбрать капитана и его заместителя. Сколькими способами это можно сделать?

    9. . Решите уравнение

    1. Решите неравенство:

    II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант №2

    1. Вычислите значение выражения

    2. Решите уравнение

    3.Вычислите значение выражения: lg100-lg10+lg1

    4. Решить уравнение

    5.Решите уравнение

    6. Вычислить

    7. Даны координаты точек А(3;-2;1), В(5;1;-4),С(2;0;1),Д(5;-1;3). Найти угол между векторами АВ и СД.

    8. На соревнованиях по лёгкой атлетике наш техникум представляла команда из 10 спортсменов. Сколькими способами тренер может определить, кто из них побежит в эстафете на первом, втором, третьем и четвёртом этапах?

    9.Решить уравнение:5x+1+5x + 5x-1

    10. Решить неравенство:

    II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант №3

    1. Вычислите значение выражения: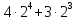

    2. Решите уравнение : =11.

    3.Вычислите значение выражения

    4.Решите уравнения:

    5. Вычислить:

    6. Решить уравнение:

    7.Найти скалярное произведение векторов:

    8. В теннисном турнире участвуют 10 спортсменов. Сколькими способами теннисисты могут завоевать золото, серебро и бронзу?

    9.Решить уравнение: 7x -7x-1 = 6

    10. Решить неравенство:

    II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант №4

    1. Вычислите значение выражения.

    2. Решите уравнение

    3. Вычислите значение выражения.

    4.Решите уравнение

    5. Вычислить:

    6. Решить уравнение: 0,5x+7*0,51-2x = 2

    7.Найти скалярное произведение векторов:

    8.  Сколькими способами из 15 учеников класса можно выбрать трёх для участия в праздничном концерте?

    9.Решить уравнение: 3x+2 +3x = 10

    10. Решить неравенство:

    II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 5

    1. Вычислите значение выражения. 2*53+3*52

    2. Решите уравнение = 7

    3. Вычислите значение выражения.

    4.Решите уравнение

    5. Вычислить:

    6. Решить уравнение:

    7. Вычислите длину вектора:

    8. Имеются помидоры, огурцы, лук. Сколько различных салатов можно приготовить, если в каждый салат должно входить 2 различных вида овощей?

    9.Решить уравнение: 4x – 2x+1 = 48

    10. Решить неравенство:

    II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 6

    1. Вычислите значение выражения. + log8+ log2

    2. Решите уравнение =4.

    3. Вычислите значение выражения.

    4.Решите уравнение

    5. Вычислить: log8+ log2

    6. Решить уравнение: 112Х+5=1

    7. Вычислите длину векторов:

    8.  Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными?.

    9.Решить уравнение: 32x – 2*32x-1 – 2*32x-2 = 1

    10. Решить неравенство:

    II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 7

    1. Вычислите значение выражения:

    2. Решите уравнение =0

    3. Вычислите значение выражения.

    4.Решите уравнение

    5 Найти , .

    6. Решить уравнение: 17Х+2=Х

    7. Вычислите длину вектора

    8. На 1 курсе 12 учащихся, имеющих по математике оценки «4-5». Сколькими способами можно сформировать команду из 4 человек для участия в математической олимпиаде?

    9.Решить уравнение:2x + 2x-3 = 18

    10. Решить неравенство:

    .

    II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 8

    1. Вычислите значение выражения:

    2.

    3. Вычислите значение выражения.

    4.Решите уравнение

    5. Вычислить:

    6. Решить уравнение: 11х-10=121

    7. Вычислите длину вектора

    8. Из города А в город В ведут две дороги, из города В в С – три дороги, из города С до пристани – две дороги. Туристы хотят проехать из города А через города В и С к пристани. Сколькими способами они могут выбрать маршрут?

    9.Решить уравнение: 3x +4*3x+1 = 13

    10. Решить неравенство:

    II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 9

    1. Вычислите значение выражения:

    2. Решите уравнение =0

    3. Вычислите значение выражения.

    4.Решите уравнение

    5. Вычислить:

    6. Решить уравнение: 11х-10=121

    7 Найти скалярное произведение а ( 4; — 7; — 3) в ( 3; -2; 1)

    8. Сколько двузначных чисел можно составить из чисел 1,2,3,4?

    9.Решить уравнение: 5x+1 +3*5x-1 -6*5x +10 = 0

    10. Решить неравенство:42x -5*4x + 4

    II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 10

    1. Вычислите значение выражения:

    2. Решить уравнение =

    3. Вычислите значение выражения.

    4.Решите уравнение

    5. Вычислить:

    6. Решить уравнение: 2х+1=64

    7 Найти угол между векторами, а = 6i + 4k в =2 i -12 k

    8. Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными?

    9.Решить уравнение: 2x+3— 2x+1 = 12

    10. Решить неравенство:2x+2x+2≤ 20

    II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 11

    1. Вычислите значение выражения:

    2. Решить уравнение = 5

    3. Вычислите значение выражения. —

    4.Решите уравнение

    5. Вычислить: 27log32

    6. Решить уравнение: 4х+1=8

    7 Найти скалярное произведение векторов а ( 4; — 7; — 3), в ( 3; -2; 1)

    8. Сколькими способами могут быть расставлены 5 участниц финального забега на 5-ти беговых дорожках?

    9.Решить уравнение: 2x+1 +2x-1 +2x =28

    10. Решить неравенство:

    II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 12

    1. Вычислите значение выражения: 27log32+

    2. Решить уравнение

    3. Вычислите значение выражения.

    4.Решите уравнение

    5. Вычислить: log8+ log2

    6. Решить уравнение: 4х+1=8

    7 Найти скалярное произведение векторов а ( 4; — 7; — 3), в ( 3; -2; 1)

    8. Сколькими способами из 7 человек можно выбрать комиссию, состоящую из 3 человек?

    9.Решить уравнение: 3x-1 -3x +3x+1 = 63

    10. Решить неравенство:

    II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 13

    1. Вычислите значение выражения:

    2. Решить уравнение 8

    3. Вычислите значение выражения. 27log32

    4.Решите уравнение

    5. Вычислить:

    6. Решить уравнение:

    7 Найти угол между векторами: а = 3i + 4k , в =5 i+ 12 k

    8. Восемь студентов обменялись рукопожатиями. Сколько было рукопожатий?

    9.Решить уравнение: 23x+2 -23x-2 = 30

    10. Решить неравенство: 16x 0,125

    II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 14

    1. Вычислите значение выражения:

    2. Решить уравнение

    3. Вычислите значение выражения.

    4.Решите уравнение

    5. Вычислить:

    6. Решить уравнение: 2х+1=64

    7 Найти угол между векторами: а = 2i + j + 2k в = 3i + 2j -2k

    8 Сколькими способами можно разложить 7 разных монет в три кармана?

    9.Решить уравнение: 2*4x =64

    10. Решить неравенство 2x -2x-415

    II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 15

    1. Вычислите значение выражения: при.

    2. Решить уравнение: 7

    3. Вычислите значение выражения.

    4.Решите уравнение

    5. Вычислить: log8+ log2

    6. Решить уравнение: 17х-16=1

    7 Найти угол между векторами: а = 2i + j + 2k в = 3i + 2j -2k

    8 Семь девушек водят хоровод. Сколькими различны ми способами они могут встать в круг?

    9.Решить уравнение: 64x -8x -56 = 0

    10. Решить неравенство: .

    II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 16

    1. Найдите значение выражения при.

    2. Решить уравнение: 7

    3. Вычислите значение выражения. log327-lg0,01+log0,6 0,36+log71.

    4.Решите уравнение

    5. Вычислить:

    6. Решить уравнение: 4x-1 =1

    7 Найти угол между векторами: а = 2i + j + 2k в = 3i + 2j -2k

    8 У мамы 2 яблока и 3 груши. Каждый день в течение 5 дней подряд она выдает по одному фрукту. Сколькими способами это может быть сделано?

    9.Решить уравнение: 16x -17*4x +16=0

    10. Решить неравенство: 1002х+1

    II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 17

    1. Вычислите значение выражения:

    2. Решить уравнение

    3. Вычислите значение выражения. log8+ log2

    4.Решите уравнение

    5. Вычислить:

    6. Решить уравнение:

    7 Найти угол между векторами: а = 2i + j + 2k в = 3i + 2j -2k

    8 В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человека, при условии, что все они должны ехать в различных вагонах?

    10. Решить неравенство: .

    II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 18

    1. Вычислите значение выражения:

    2. Решить уравнение

    3. Вычислите значение выражения.

    4.Решите уравнение

    5. Вычислить:

    6. Решить уравнение:

    7 Найти угол между векторами: а = 4i + j -2k в = 3i + 4j -2k

    8 Для участия в команде тренер отбирает 5 мальчиков из 10. Сколькими

    способами он может сформировать команду, если 2 определенных мальчика

    должны войти в команду?

    9.Решить уравнение: 3x+9x-1 – 810 = 0

    10. Решить неравенство: 7x-2 49

    II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 19

    1. Вычислите значение выражения:

    2. Решить уравнение

    3. Вычислите значение выражения. log5250 – log52

    4.Решите уравнение

    5. Вычислить:

    6. Решить уравнение:

    7 Найти угол между векторами: а = -2i + 5j + 2k в = 7i + 6j -2k

    8 В шахматном турнире принимали участие 15 шахматистов, причем

    каждый из них сыграл только одну партию с каждым из остальных.

    Сколько всего партий было сыграно в этом турнире?

    9.Решить уравнение: 9x -3x – 6 = 0

    10. Решить неравенство: 3x-2 9

    II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 20

    1. Вычислите значение выражения: 60,5 3 0,5(0,25) 0,25 .

    2. Решить уравнение = 5.

    3. Вычислите значение выражения.

    4.Решите уравнение

    5. Вычислить

    6. Решить уравнение:

    7 Найти угол между векторами: а = 2i + j + 2k в = 3i + 2j -2k

    8 Сколькими способами можно расставить 8 ладей на шахматной доске так, чтобы они не били друг друга?

    9.Решить уравнение: 52x -5x – 600 = 0

    10. Решить неравенство log5 (4х+1) -1.

    Источник

    Пояснительная
    записка

    К проведению  экзамена по математике для каждого обучающегося  готовится
    текст с вариантом экзаменационной работы и критериями оценивания результатов ее
    выполнения, краткая  инструкция для обучающихся, а также листы для черновика и
    для чистового оформления  работы. Все листы   подписываются     обучающимися и после завершения работы
    сдаются экзаменационной комиссии.

    Вместе с текстом экзаменационной
    работы обучающимся выдаются справочные материалы, линейки.

    Перед началом выполнения письменной экзаменационной работы обучающиеся
    должны быть ознакомлены с ее структурой и критериями оценки. Критерии оценки
    должны оставаться открытыми для обучающихся в течение всего времени,
    отведенного на экзамен.

    Обучающимся поясняется, что основные требования к выполнению заданий
    состоят в том, чтобы:

    – из
    представленного решения был понятен ход рассуждений обучающегося;

    – ход решения был
    математически грамотным;

    – представленный
    ответ был правильным. При этом метод и форма описания  решения задачи могут 
    быть произвольными.

    Им поясняется также, что выполнение каждого из  заданий оценивается в
    баллах.

    За правильное выполнение любого задания из  обязательной части обучающийся
    получает три балл    а, за правильное выполнение
    любого задания из дополнительной  части –       4 балла,  как в примерном варианте, 
    приведенном в Приложении 36). Обращается внимание на то, что число
    баллов, которое обучающийся может получить за правильное выполнение того или
    иного задания проставлено в скобках около его номера. Если обучающийся приводит
    неверный ответ или  не приводит никакого ответа, он получает 0 баллов. Баллы,
    полученные за все выполненные задания, суммируются.

    Особое внимание обучающихся необходимо обратить на таблицу с критериями
    оценки, в которой указано, сколько баллов достаточно набрать, чтобы получить ту
    или иную положительную оценку.

    Обучающиеся должны
    знать, что  критерии оценки  останутся  открытыми для них в течение всего
    времени, отведенного на экзамен, и что они должны ориентироваться на них и
    учитывать их в ходе выполнения экзаменационной работы.

    Обучающимся поясняется, что:

    – начинать работу всем следует с
    выполнения заданий обязательной части;

    – для получения любой из 
    положительных оценок  3, 4 или 5 сначала  надо правильно выполнить определенное
    число заданий обязательной части (это число определяют   по таблице критериев
    оценки); 

    – при этом для получения
    удовлетворительной оценки не обязательно выполнять все задания обязательной
    части;

    – правильное выполнение определенной
    части заданий обязательной части, во-первых, гарантирует получение «3», а
    во-вторых дает основу для повышения оценки до «4» или «5» при правильном
    выполнении нескольких  заданий дополнительной части.

    При выполнении заданий дополнительной
    части обучающимся следует также проследить по таблице критериев оценки, сколько
    заданий достаточно правильно выполнить, чтобы получить оценку «4» или «5».
    Обучающимся предоставляется право выбрать, в первую очередь,  те задания, при
    выполнении которых он будет чувствовать себя более уверенным.

    Ниже приводится примерный текст
    краткой инструкции для обучающихся, который  остается у них на столах до
    завершения работы.

     Краткая инструкция для обучающихся

    (выдается каждому обучающемуся вместе с
    текстом

    экзаменационной работы)

    На выполнение письменной экзаменационной работы по математике дается 4
    астрономических часа (240 минут).

    Экзаменационная работа состоит из 2-х
    частей: обязательной и дополнительной.

    Обязательная часть содержат задания
    минимально обязательного уровня, а дополнительная часть  – более сложные
    задания.

    При выполнении большинства заданий
    обязательной части требуется представить  ход решения и указать полученный
    ответ, и только   в нескольких  заданиях достаточно представить  ответ.

    При выполнении любого  задания дополнительной
    части  описывается ход  решения и дается ответ. 

                Правильное выполнение
    заданий оценивается баллами.

    Правильное выполнение любого задания
    обязательной части оценивается 3 баллами, правильное выполнение каждого задания
    дополнительной части –  четырьмя баллами. Баллы указываются в скобках около
    номера задания.

    Если приводится неверный ответ или
    ответ отсутствует, ставится 0 баллов.

    Баллы, полученные за все выполненные
    задания, суммируются.

    Постарайтесь правильно выполнить как
    можно больше заданий и набрать как можно больше баллов.

    Перед
    началом работы внимательно изучите критерии оценивания и обратите внимание, что
    начинать работу следует с заданий обязательной части. И только после того, как
    Вы наберете необходимое количество баллов для удовлетворительной оценки, можете
    переходить к заданиям дополнительной части, чтобы повысить оценку до четырех
    или пяти.

    Желаем
    успехов!

    Вариант 1

    Задания

    для проведения письменного экзамена по
    математике

    Критерии оценки выполнения работы

    Оценка

    Число баллов,

    необходимое для получения оценки

    «3» (удовлетворительно)

    18–23

    «4» (хорошо)

    24–29

    (не менее одного задания из дополнительной части)

    «5» (отлично)

    30–45

    (не менее двух заданий из дополнительной части)

    Обязательная часть

    При выполнении заданий 1-15 запишите ход
    решения и полученный ответ.

    1.  
    (3 балла) Разность двух чисел относится к их
    произведению как 1:24, а сумма этих чисел в 5 раз больше их разности.  Найти
    эти числа.

    2.  
    По (3 балла)
    Выполните действия     над комплексными числами:

    a)    
    Z= (3 —  2i) (i +
    2)           б) Z= (4 – 2i ) : ( 2 + i )

    3.    
    (3 балла)
    На рисунке 1 изображен график     y=f'(x)— производной функции f(x), определенной на интервале (-10; 2). Найдите точку экстремума
    функции     f(x), принадлежащую отрезку

    [-6; -1 ].task-9/ps/task-9.58

    4. .   (3 балла)  На рисунке изображены график функции
    y=f(x)и касательная к нему в точке
    с абсциссой     x_0. Найдите значение
    производной функции     f(x)в
    точке     x_0.

    task-14/ps/task-14.118

    5.    (3 балла) На рисунке изображен график функции y=f(x), определенной на интервале (-12; 2). Найдите количество точек, в
    которых производная функции     f(x)равна 0

    task-2/ps/task-2.123 укажите их.

    6.     (3 балла)  Найдите область определения функции:

    7.     (3 балла) Найдите модуль комплексного числа и укажите сопряженное число,  если

    Z = —
    3    i + 4

       
    8. (3 балла) Исследовать функцию на
    монотонность.

     у =  

        9. (3 балла)  На рисунке
    изображен график  y=f'(x) — производной функции f(x),
    определенной на интервале (-2; 9).
    Найдите промежутки возрастания функции f(x). В ответе
    укажите сумму целых точек, входящих в эти промежутки.

    task-6/ps/task-6.137

    10. (3 балла)
    Определите, какой из ниже приведенных графиков соответствует четной функции и
    кратко поясните, почему.

                        х

    Используя график
    функции у =     f () (см. рис. ниже), определите и запишите
    ответ:

    11. (3 балла)
    наименьшее и наибольшее значения функции;

    12. (3 балла)
    промежутки возрастания и убывания функции;

    13.
    (3
    балла)

     балла) при
    каких значениях        f() < 0.

    task-6/ps/task-6.127

    Дополнительная часть

    При выполнении заданий 14-16 запишите ход решения и полученный ответ

    14. (4
    балла) Найдите промежутки убывания функции      f () = 23 – 32 – 36.

    15. (4
    балла)     Представьте
    в тригонометрической форме число:     Z=1 — i

    16. (4 балла) Решите систему
    уравнений:

    Вариант 2

    Задания

    для проведения письменного экзамена по
    математике

    Критерии оценки выполнения работы

    Оценка

    Число баллов,

    необходимое для получения оценки

    «3» (удовлетворительно)

    18–23

    «4» (хорошо)

    24–29

     (не менее одного задания из дополнительной части)

    «5» (отлично)

    30–45

       (не менее двух заданий
    из дополнительной части)

    Обязательная часть

    При выполнении заданий 1-13 запишите
    ход решения и полученный ответ.

    1.    
    (3 балла) Определите, сколько банок краски по 2 кг необходимо
    купить для покраски пола в спортивном зале площадью     8 х 20 м2, если на 1м2
    расходуется     250 граммов краски.

    2.    
    По (3 балла)
    Выполните действия     над комплексными числами:

     а) 
    z= ( 5 —  3i ) ( i + 2 )      
    б)     z= ( 3 – 2i ) : ( 1 + i )

        
    3.(3 балла) На рисунке
    изображен график     y=f'(x)— производной       функции f(x), определенной на интервале (-5; 8). Найдите точки экстремума
    функции     f(x), принадлежащую отрезку [-1; 7 ].

    task-9/ps/task-9.78

    4.    
    ( 3
    балла) На рисунке изображены график функции     y=f(x)и касательная к нему в точке
    с абсциссой     x_0. Найдите значение
    производной функции     f(x)в
    точке     x_0.

    task-14/ps/task-14.88

       5.(3 балла) На
    рисунке изображен график     y=f'(x) —
    производной функции     f(x),
    определенной на интервале     (-12; 3). Найдите
    промежутки убывания функции     f(x). В ответе
    укажите сумму целых точек, входящих в эти промежутки.

    task-6/ps/task-6.127

    6.    
    3 балла)  Найдите область
    определения функции:

    у=—1

    7.    
    (3 балла) Найдите модуль комплексного числа и укажите сопряженное число,  если

    z =  3 —  4i

       
    8. (3 балла) Исследовать функцию на
    монотонность.

    у =  

    9.
    (3 балла) На рисунке изображен график функции     y=f(x), определенной на интервале (-7; 5). Найдите количество точек, в
    которых производная функции     f(x)равна 0 и укажите их.

    task-2/ps/task-2.140

    10.(1
    балл) Вычислите значение производной функции в точке х =1, если

    у=  

    .

     Используя график функции у = f() (см. рис. ниже),
    определите и запишите ответ:

    11. (3 балла)
    наименьшее и наибольшее значения функции;

    12. (3 балла) промежутки
    возрастания  функции;

    13.
    (3 балл    а) при
    каких значениях        f() ≥ 0.

                task-6/ps/task-6.27

    Дополнительная
    часть

    При выполнении
    заданий 14-16 запишите ход решения и полученный ответ

    14. (4 балла)
    Найдите промежутки возрастания функции

     f () = 23 – 62 +18.

    15. (4 балла) Представьте
    в тригонометрической форме число:

    z =1 –
         i  и найдите
    его модуль

    16.
    (4 балла) Тело движется по закону: S(t) =2 Определите ускорение в момент времени     t =2с, и  в какой момент времени
    скорость будет равна 3.

    Вариант 3

    Задания

    для проведения письменного экзамена по
    математике

    Критерии оценки выполнения работы

    Оценка

    Число баллов,

    необходимое для получения оценки

    «3» (удовлетворительно)

    18-23

    «4» (хорошо)

    24-29

    (не менее одного задания из дополнительной части)

    «5» (отлично)

                                        
    30–45

    (не менее двух заданий из дополнительной части)

    Обязательная часть

    При выполнении заданий 1-13 запишите ход решения и полученный ответ.

    1.    
    (3 балла)  Вычислите
    определитель:    1   2  3

                                               
                         3   2  1

    3       
    1  2

    2 .(3 балла) Определите модуль и сопряженное
    число для комплексного числа      z = 4 — 3i

    3.    
    (3 балла) Вычислите значение производной функции в точке  х = 1

                                 у  = 

    4.(3 балла)

    На
    рисунке изображен график     y=f'(x)— производной функции f(x), определенной на интервале (-8; 5). Найдите точку экстремума
    функции     f(x), принадлежащую отрезку [-7; -1 ].

    task-9/ps/task-9.98

    5. (3балла)

    На рисунке изображены график функции y=f(x)и касательная к нему в точке
    с абсциссой     x_0. Найдите значение
    производной функции     f(x)в
    точке     x_0.

    task-14/ps/task-14.88

    6.(3 балла)

    . На рисунке изображен
    график y=f'(x) —
    производной функции f(x), определенной на интервале (-3; 8).
    Найдите промежутки возрастания функции f(x). В ответе
    укажите сумму целых точек, входящих в эти промежутки.

    task-6/ps/task-6.27

    7.(3 балла) Выполнить действия над комплексными
    числами:

    z=

    8.    
    (3,балла) 
    На рисунке изображен график функции     y=f(x), определенной на интервале (-7; 4). Найдите количество точек, в
    которых производная функции     f(x)равна 0 .

    task-2/ps/task-2.85

    9.     

    .
    (    3 балла) Определите, какой из ниже приведенных
    графиков соответствует четной функции, и кратко поясните, почему.

    Используя график
    функции у =     f() (см. рис. ), определите  и
    запишите ответ:

    task-6/ps/task-6.167

    10. (3 балла) точки
    экстремума
    функции;

    11. 31 балла)
    промежутки возрастания и убывания функции;

    12.
    (3 балл    а) при
    каких значениях      для функции изображенной на
    рисунке
    f() ≥0.

    13.(1
    балл) Для функции у = — cosx —     sinx  найти первообразную, график которой проходит
    через точку М (.

    Дополнительная
    часть

    При выполнении заданий 14-16 запишите ход решения и
    полученный ответ

    14. (3
    балла) Найдите промежутки убывания и точки экстремума функции     f() = 3 – 32 +4

    15. .(3
    балла) Тело движется по закону: S(t) =6    2–6+13, где S(t) измеряется в м, а время – в сек. Определите, в
    какой момент времени скорость будет равна 6 сек?

    16.(1 балл) Найдите для
    функции      y =   её
    производную в точке х = -1

     
    Вариант 4

    Задания

    для проведения письменного экзамена по
    математике

    Критерии оценки выполнения работы

    Оценка

    Число баллов,

    необходимое для получения оценки

    «3» (удовлетворительно)

    8–12

    «4» (хорошо)

    13–18

    (не менее одного задания из дополнительной части)

    «5» (отлично)

    19–30

    (не менее двух заданий из дополнительной части)

    Обязательная часть

    При выполнении заданий 1-8 запишите ход
    решения и полученный ответ.

    1.(3 балла) В
    коробке     3 белых, 5 красных и 12
    черных одинаковых по форме пуговиц. Какова вероятность того, что наугад взятая
    пуговица будет черной?

    2.(3 балла) Выполните действия над комплексными числами, представив результат  в
    алгебраической форме:                                            

     z=  

    3.Вычислите определитель:        1 2  5

                                                           
    0 1 1                                        

                                                         
    -2 0  2

    4.(3 балла)
    Вычислите значение производной функции          

                у= sinx+cosx.  если  х=

    5. (3 балла) На рисунке изображен график функции y=f(x), определенной на интервале (-4; 10). Найдите количество точек
    экстремума и укажите их.

    task-2/ps/task-2.138

    6. (3 балла ).На рисунке изображен график y=f'(x) —
    производной функции f(x), определенной на интервале (-1; 11).
    Найдите промежутки убывания функции f(x). В ответе
    укажите сумму целых точек, входящих в эти промежутки.

    task-6/ps/task-6.167

    7(3 балла)  На
    рисунке изображен график y=f'(x) — производной
    функции f(x), определенной на
    интервале (-3; 8). Найдите и
    укажите точки экстремума функции.

    task-6/ps/task-6.27

    8.(3 балла) Найдите аргумент и сопряженное число для
    комплексного числа

                       
         z = 5  — 3i

         
    9.     (1
    балл) Определите, какой из ниже приведенных графиков соответствует четной
    функции. Отметьте его знаком «+» и кратко поясните, почему.

       а)                             б)

                       х

    Используя график
    функции у =     f() (см. рис. ниже), определите и
    запишите ответ:

    10. (1 балл)
    наименьшее и наибольшее значения функции;

    11. (1 балл)
    промежутки возрастания и убывания функции;

    12.
    (1 балл) при каких значениях        f() ≥ 0.

    13.(3 балла)
    Тело движется по закону: S(t) =     2–2+3. Определите, в какой момент времени скорость будет равна
    3.и чему равно ускорение

     Дополнительная
    часть

    При выполнении заданий 14-16 запишите ход решения и
    полученный ответ

    14. (4
    балла) Найдите промежутки убывания функции     f() = 43 – 32 – 18х

    15.
    (4 балла)
    Вычислите значение производной в точке х=2, если

                у=  

    16.
    (4 балла)     Вычислите интеграл

    ПРИЛОЖЕНИЯ

    Приложение
    1.

    Примерный
    перечень элементов содержания

    для
    составления экзаменационных работ по математике

    в
    образовательных учреждениях СПО1

    Перечень элементов содержания составлен на основе
    Обязательного минимума содержания основных образовательных программ по
    математике и Требований к уровню подготовки выпускников средней (полной) школы     (Приказ
    Минобразования России  от 05.03.2004 г. № 1089 «Об утверждении федерального
    компонента государственных образовательных стандартов начального общего,
    основного общего и среднего (полного) общего образования»    .

    Перечень элементов содержания по всем разделам
    учебного курса математики включает в себя элементы содержания по программе
    среднего (полного) общего образования (базовый уровень) и необходимые элементы
    содержания за учебный курс математики основной общеобразовательной школы.

    Элементы содержания, проверяемые заданиями

    экзаменационной работы

    Алгебра

    Числа, корни и степени

    Целые числа

    Степень с натуральным показателем

    Дроби, проценты, рациональные числа

    Степень с целым показателем

    Корень степени n >1 и его свойства

    Степень с рациональным показателем и ее свойства

    Свойства степени с действительным показателем

    Основы тригонометрии

    Синус, косинус, тангенс, котангенс произвольного угла

    Радианная мера угла

    Синус, косинус, тангенс и котангенс числа

    Основные тригонометрические тождества

    Формулы приведения

    Синус, косинус и тангенс суммы и разности двух углов

    Синус и косинус двойного угла

    Логарифмы

    Логарифм числа

    Логарифм произведения, частного, степени

    Десятичный и натуральный логарифмы, число е

    Преобразования выражений

    Преобразования выражений, включающих арифметические операции

    Преобразования выражений, включающих операцию
    возведения в степень

    Преобразования выражений, включающих корни натуральной степени

    Преобразования тригонометрических выражений

    Преобразование выражений, включающих операцию
    логарифмирования

    Модуль (абсолютная величина) числа

    Уравнения и неравенства

    Уравнения

    Квадратные уравнения

    Рациональные уравнения

    Иррациональные уравнения

    Тригонометрические уравнения

    Показательные уравнения

    Логарифмические уравнения

    Равносильность уравнений, систем уравнений

    Простейшие системы уравнений с двумя неизвестными

    Основные приемы решения систем уравнений: подстановка, алгебраическое
    сложение, введение новых переменных

    Использование свойств и графиков функций при решении уравнений

    Изображение на координатной плоскости множества решений уравнений с
    двумя переменными и их систем

    Применение математических методов для решения содержательных задач из
    различных областей науки и практики. Интерпретация результата, учет реальных
    ограничений

    Неравенства

    Квадратные неравенства

    Рациональные неравенства

    Показательные неравенства

    Логарифмические неравенства

    Системы линейных неравенств

    Системы неравенств с одной переменной

    Равносильность неравенств, систем неравенств

    Использование свойств и графиков функций при решении неравенств

    Метод интервалов

    Изображение на координатной плоскости множества решений неравенств с
    двумя переменными и их систем

    Функции

    Определение и график функции

    Функция, область определения функции

    Множество значений функции

    График функции. Примеры функциональных зависимостей в реальных
    процессах и явлениях

    Обратная функция. График обратной функции

    Преобразования графиков: параллельный перенос, симметрия относительно
    осей координат

    Элементарное исследование функций

    Монотонность функций. Промежутки возрастания и убывания

    Четность и нечетность функций

    Периодичность функций

    Ограниченность функций

    Точки экстремума (локального максимума и минимума) функции

    Наибольшее и наименьшее значения функции

    Основные элементарные функции

    Линейная функция, ее график

    Функция, описывающая обратную пропорциональную зависимость, ее график

    Квадратичная функция, ее график

    Степенная функция с натуральным показателем, ее график

    Тригонометрические функции, их графики

    Показательная функция, ее график

    Логарифмическая функция, ее график

    Начала математического анализа

    Производная

    Понятие о производной функции, геометрический смысл производной

    Физический смысл производной, нахождение скорости и ускорения для
    процесса, заданного формулой или графиком

    Уравнение касательной к графику функции и вычисление производной  с
    помощью касательной проведенной в данной точке.

    Производные суммы, разности, произведения, частного

    Производные основных элементарных функций

    Вторая производная и ее физический смысл

    Исследование функций

    Применение производной к исследованию функций и построению графиков

    Примеры использования производной для нахождения наилучшего решения в
    прикладных, в том числе в технических, задачах. По графику функции и  по
    графику её производной исследовать на монотонность, на нахождение критических
    точек и точек экстремума, вогнутость и выпуклость – с помощью второй
    производной и асимптот функции. Полное построение графика функции.

    Первообразная и интеграл

    Первообразные элементарных функций

    Примеры применения интеграла в физике и геометрии при вычислении
    площадей  и объемов тел.

    Элементы
    комбинаторики, статистики и теории вероятностей

    Элементы комбинаторики

    Поочередный и одновременный выбор

    Формулы числа сочетаний и перестановок. Бином
    Ньютона

    Элементы статистики

    Табличное и графическое представление данных

    Числовые характеристики рядов данных

    Элементы теории вероятностей

    Вероятности событий

    Примеры использования вероятностей и статистики при
    решении прикладных задач

    Приложение
    2.

    Примерный
    перечень требований к уровню подготовки обучающихся

    для
    составления заданий экзаменационных работ по математике в образовательных
    учреждениях НПО/СПО2

    Перечень требований к уровню подготовки по математике
    обучающихся образовательных учреждений НПО/СПО составлен на основе
    Обязательного минимума содержания основных образовательных программ и
    Требований к уровню подготовки обучающихся в результате освоения учебной
    дисциплины «Математика» на базовом уровне (Об утверждении федерального
    компонента Государственных стандартов начального общего, основного общего и
    среднего (полного) общего образования. // Приказ Минобрнауки РФ от 05.03.2004 №
    1089).

    Перечень требований по всем разделам включает в себя
    требования к уровню подготовки обучающихся по математике, освоивших программу
    среднего (полного) общего образования (базовый уровень).

    Требования (умения и виды деятельности),
    проверяемые заданиями

    письменной экзаменационной работы

    Уметь выполнять вычисления и преобразования:

    – выполнять арифметические действия, сочетая устные и
    письменные приемы; находить значения корня натуральной степени, степени с
    рациональным показателем, логарифма;

    – вычислять значения числовых и буквенных выражений,
    осуществляя необходимые подстановки и преобразования;

    – проводить по известным формулам и правилам
    преобразования буквенных выражений, включающих степени, радикалы, логарифмы и
    тригонометрические функции.

    Уметь решать уравнения и неравенства:

    – решать рациональные, иррациональные, показательные,
    тригонометрические и логарифмические уравнения, их системы;

    – решать уравнения, простейшие системы уравнений,
    используя свойства функций и их графиков; использовать для приближенного
    решения уравнений и неравенств графический метод;

    – решать рациональные, показательные и логарифмические
    неравенства.

    Уметь выполнять действия с функциями:

    – определять значение функции по значению аргумента
    при различных способах задания функции; описывать по графику поведение и
    свойства функций, находить по графику функции наибольшие и наименьшие значения;
    строить графики изученных функций;

    – вычислять производные и первообразные элементарных
    функций;

    – исследовать в простейших случаях функции на
    монотонность, находить наибольшие и наименьшие значения функций.

    Уметь выполнять
    действия с геометрическими фигурами, координатами и векторами:

    – решать планиметрические задачи на
    нахождение геометрических величин (длин, углов, площадей);

    – решать простейшие
    стереометрические задачи на нахождение геометрических величин (длин, углов,
    площадей, объемов); использовать при решении стереометрических задач
    планиметрические факты и методы;

    – определять координаты точки.

    Уметь строить и
    исследовать простейшие математические модели:

    – моделировать реальные ситуации на
    языке алгебры, составлять уравнения и неравенства по условию задачи;
    исследовать построенные модели с использованием аппарата алгебры;

    – моделировать реальные ситуации на
    языке геометрии, исследовать построенные модели с использованием геометрических
    понятий и теорем, аппарата алгебры; решать практические задачи, связанные с
    нахождением геометрических величин;

    – проводить доказательные
    рассуждения при решении задач, оценивать логическую правильность рассуждений,
    распознавать логически некорректные рассуждения.

    Уметь использовать
    приобретенные знания и умения в практической деятельности и повседневной жизни:

    – анализировать реальные числовые
    данные; осуществлять практические расчеты по формулам, пользоваться оценкой и
    прикидкой при практических расчетах;

    – описывать с помощью функций
    различные реальные зависимости между величинами и интерпретировать их графики;
    извлекать информацию, представленную в таблицах, на диаграммах, графиках;

    – решать прикладные задачи, в том
    числе социально-экономического и физического характера, на наибольшие и
    наименьшие значения, на нахождение скорости и ускорения.

    Источник

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ОДОБРЕНО

    предметной
    (цикловой) комиссией

     общегуманитарных
    и

    общеобразовательных
    дисциплин.

    Протокол№4  
    от 8 апреля 2019 г.

    Председатель П(Ц)К

    _____________ 
    Гаджиева. С.З.

    УТВЕРЖДАЮ

    зам. директора по

    учебной работе

    __________   Квиралашвили Н.У

    8 апреля 2019 г.

    Дисциплина«Математика»

    Билет №1

    1.       
    Корни
    натуральной степени из числа и их свойства.

    2.       
    Перпендикуляр
    и наклонная.

    3.       
    Событие,
    вероятность события.

    4.           
    Примеры:

    1)
    Решить уравнения

    2)Найти
    предел

    5.                
     Задача:

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_363_39.png

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ОДОБРЕНО

    предметной
    (цикловой) комиссией

     общегуманитарных
    и

    общеобразовательных
    дисциплин.

    Протокол№4  
    от 8 апреля 2019 г.

    Председатель П(Ц)К

    _____________Гаджиева
    С.З.

    УТВЕРЖДАЮ

    заместитель  директора по

    учебной работе

    __________   Квиралашвили Н.У

    8 апреля 2019 г.

    Дисциплина«Математика»

    Билет
    №2

    1.    
    Степени
    с рациональными показателями, их свойства.

    2.    
    Параллелепипед.
    Куб.

    3.    
    Понятие
    о пределе последовательности.

    4.    
    Примеры:

    1)Упростите выражение

    cos2x-6+sin2x

    2) Найти производную

    5.     Задача:

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_363_38.png

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ОДОБРЕНО

    предметной
    (цикловой) комиссией

     общегуманитарных
    и

    общеобразовательных
    дисциплин.

    Протокол№4  
    от 8 апреля 2019 г.

    Председатель П(Ц)К

    _____________ 
    Гаджиева. С.З.

    УТВЕРЖДАЮ

    заместитель  директора по

    учебной работе

    __________   Квиралашвили Н.У

    8 апреля 2019 г.

    Дисциплина«Математика»

    Билет
    №3

    1.    
    Логарифми
    его свойства

    2.     Двугранный угол.

    3.     Понятие о
    производной функции, её геометрический смысл.

    4.     Примеры:

    1) Найти значение производной функции

    f1(x)
    при     x=0—1

    2) Найти предел

    5.    
    Задача:

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_363_42.pnghttp://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_363_42.png

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ОДОБРЕНО

    предметной
    (цикловой) комиссией

     общегуманитарных
    и

    общеобразовательных
    дисциплин.

    Протокол
    №4   от 8 апреля 2019 г.

    Председатель П(Ц)К

    _____________ 
    Гаджиева. С.З.

    УТВЕРЖДАЮ

    заместитель  директора по

    учебной работе

    __________   Квиралашвили Н.У

    8 апреля 2019 г.

    Дисциплина«Математика»

    Билет
    №4

    1.     Радианная
    мера угла

    2.     Раскрытие
    неопределенностей 0/0  и  ∞/∞.

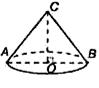
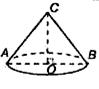
    3.     Цилиндр.

    4.     Примеры:

    1)Вычислите

                            

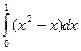
    2) Упростите выражение   

    cos4x—sin4x

    5.     Задача:

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_363_43.pnghttp://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_363_42.png

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ОДОБРЕНО

    предметной
    (цикловой) комиссией

     общегуманитарных
    и

    общеобразовательных
    дисциплин.

    Протокол
    №4   от 8 апреля 2019 г.

    Председатель П(Ц)К

    _____________ 
    Гаджиева. С.З..

    УТВЕРЖДАЮ

    заместитель  директора по

    учебной работе

    __________   Квиралашвили Н.У

    8 апреля 2019 г.

    Дисциплина«Математика»

    Билет
    №5

    1.       
    Основные
    тригонометрические тождества

    2.       
    Геометрические преобразования пространства:
    параллельный перенос

    3.       
    Понятие о производной функции

    4.       
    Примеры

    1)Необходимо
    выбрать в подарок 4 из 10 имеющихся  книг. Сколькими способами можно это
    сделать?

    2)
    Найти значение производной функции

    f1(x) при x=1

    5.    
    Задача:

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_362_23.png

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ОДОБРЕНО

    предметной
    (цикловой) комиссией

     общегуманитарных
    и

    общеобразовательных
    дисциплин.

    Протокол№4  
    от 8 апреля 2019 г.

    Председатель П(Ц)К

    _____________ 
    Гаджиева. С.З.

    УТВЕРЖДАЮ

    заместитель  директора по

    учебной работе

    __________   Квиралашвили Н.У

    8 апреля 2019 г.

    Дисциплина«Математика»

    Билет
    №6

    1.     Геометрический
    смысл производной функции

    2.     Геометрические
    преобразования пространства: симметрия относительно плоскости

    3.     Шар и сфера, их
    сечения.

    4.     Примеры:

    1)  
    Из 30 участников собрание надо
    выбрать председателя и секретаря. Сколькими способами это можно сделать?

    2)    Найти
    производную

    f(x)=xcosx

    5.    
    Задача:

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_349_1.png

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ОДОБРЕНО

    предметной
    (цикловой) комиссией

     общегуманитарных
    и

    общеобразовательных
    дисциплин.

    Протокол
    №4   от 8 апреля 2019 г.

    Председатель П(Ц)К

    _____________ 
    Гаджиева. С.З.

    УТВЕРЖДАЮ

    заместитель  директора по

    учебной работе

    __________   Квиралашвили Н.У

    8 апреля 2019 г.

    Дисциплина«Математика»

    Билет
    №7

    1.     Физический смысл
    производной функции

    2.    
    Арксинус, арккосинус, арктангенс
    числа

    3.    
    Формулы
    объема куба, прямоугольного параллелепипеда

    4.    
    Примеры:

    1)  Сколько шестизначных чисел (без повторения цифр) можно
    составить из цифр 0, 3, 5, 6, 7, 8?

    2)  Решите уравнения

    5.    
    Задача:

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_349_9.png

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ОДОБРЕНО

    предметной
    (цикловой) комиссией

     общегуманитарных
    и

    общеобразовательных
    дисциплин.

    Протокол
    №4   от 8 апреля 2019 г.

    Председатель П(Ц)К

    _____________ 
    Гаджиева. С.З.

    УТВЕРЖДАЮ

    заместитель  директора по

    учебной работе

    __________   Квиралашвили Н.У

    8 апреля 2019 г.

    Дисциплина«Математика»

    Билет
    №8

    1.    
    Функции.Область
    определения и множество значений; график функции.

    2.     Производные суммы,
    разности, произведения, частного.

    3.    
    Формулы
    объема цилиндра

    4.     Примеры:

    1)   
    Сколькими способами 8 человек
    могут встать в очередь в театральную кассу?

    2)  Вычислить:1)
    ;  2)

    5.     Задача:

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_334_1.png

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ОДОБРЕНО

    предметной
    (цикловой) комиссией

     общегуманитарных
    и

    общеобразовательных
    дисциплин.

    Протокол
    №4   от 8 апреля 2019 г.

    Председатель П(Ц)К

    _____________ 
    Гаджиева. С.З.

    УТВЕРЖДАЮ

    заместитель  директора по

    учебной работе

    __________   Квиралашвили Н.У

    8 апреля 2019 г.

    Дисциплина«Математика»

    Билет
    №9

    1.     Исследование
    функции по схеме.

    2.     Производные
    основных элементарных функций.

    3.     Формулы
    объема куба    .

    4.     Примеры:

    1)     
    Вычислить

               2)          3) 

    2)    Решить
    уравнения

    5.     Задача:

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_335_9.png

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ОДОБРЕНО

    предметной
    (цикловой) комиссией

     общегуманитарных
    и

    общеобразовательных
    дисциплин.

    Протокол
    №4   от 8 апреля 2019 г.

    Председатель П(Ц)К

    _____________ 
    Гаджиева. С.З.

    УТВЕРЖДАЮ

    заместитель  директора по

    учебной работе

    __________   Квиралашвили Н.У

    8 апреля 2019 г.

    Дисциплина«Математика»

    Билет
    №10

    1.     Действия над
    векторами в пространстве

    2.     Производные
    основных элементарных функций.

    3.     Параллелепипед.
    Куб.

    4.     Примеры:

    1)     
    Упростить:

    (sin2x+tx2xsin2x)ctgx

    2)   
    Найти
    значение выражения

                                   

    5.    
    Задача:

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_335_10.png

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ОДОБРЕНО

    предметной
    (цикловой) комиссией

     общегуманитарных
    и

    общеобразовательных
    дисциплин.

    Протокол
    №4   от 8 апреля 2019 г.

    Председатель П(Ц)К

    _____________ 
    Гаджиева. С.З.

    УТВЕРЖДАЮ

    заместитель  директора по

    учебной работе

    __________   Квиралашвили Н.У

    8 апреля 2019 г.

    Дисциплина«Математика»

    Билет
    №11

    1.     Перпендикуляр и
    наклонная.

    2.     Понятие о пределе последовательности.

    3.    
    Логарифми
    его свойства.

    4.    
    Примеры

    1)Вычислите

     5-4 *
    56;                3)   710 : 712;                  
    5)  (3-4)-1;

    2)Написать
    уравнение касательной к графику  функции в точке с абсциссой     x0

    5.    
    Задача:

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_336_19.pnghttp://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_336_19.png

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ОДОБРЕНО

    предметной
    (цикловой) комиссией

     общегуманитарных
    и

    общеобразовательных
    дисциплин.

    Протокол
    №4   от 8 апреля 2019 г.

    Председатель П(Ц)К

    _____________ 
    Гаджиева. С.З.

    УТВЕРЖДАЮ

    заместитель  директора по

    учебной работе

    __________   Квиралашвили Н.У

    8 апреля 2019 г.

    Дисциплина«Математика»

    Билет
    №12

    1.     Корни
    натуральной степени из числа и их свойства

    2.     Производные суммы,
    разности, произведения, частного.

    3.     Аксиомы
    стереометрии

    4.     Примеры:

    1)      Вычислите

      44 *4-3;            
    65-3 : 65-3;                (82)-2
    * 83

    2)    В группе 30 студентов. Необходимо выбрать старосту,
    заместителя старосты и профорга. Сколько существует способов это сделать?

    5. 
    Задача :

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_315_38.png

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ОДОБРЕНО

    предметной
    (цикловой) комиссией

     общегуманитарных
    и

    общеобразовательных
    дисциплин.

    Протокол
    №4   от 8 апреля 2019 г.

    Председатель П(Ц)К

    _____________ 
    Гаджиева. С.З.

    УТВЕРЖДАЮ

    заместитель  директора по

    учебной работе

    __________   Квиралашвили Н.У

    8 апреля 2019 г.

    Дисциплина«Математика»

    Билет
    №13

    1.     Пирамида.
    Правильная пирамида.

    2.     Показательная
    функция, свойства и график.

    3.    
    Арксинус, арккосинус, арктангенс
    числа

    4.    
    Примеры:

    1)   
    Вычислить:

      81* 3-4;                
    2)  9-6 * 95;                      3)   (3-1)5
    *272    ; 

    2)   
    Порядок выступления 7 участников конкурса
    определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?

    5.    
    Задача

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_315_37.png

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ОДОБРЕНО

    предметной
    (цикловой) комиссией

     общегуманитарных
    и

    общеобразовательных
    дисциплин.

    Протокол
    №4   от 8 апреля 2019 г.

    Председатель П(Ц)К

    _____________ 
    Гаджиева. С.З.

    УТВЕРЖДАЮ

    заместитель  директора по

    учебной работе

    __________   Квиралашвили Н.У

    8 апреля 2019 г.

    Дисциплина«Математика»

    Билет
    №14

    1.     Шар
    и сфера, их сечения

    2.     Основные
    понятия комбинаторики

    3.     Действия над
    векторами в пространстве

    4.     Примеры

    1)   
    Вычислить:

     60
    : 6-3   5)   9-2 :  3-6;                               6) 
    125-4 : 25-5

    2)     Вычислите

    5.    
    Задача:

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_316_42.pnghttp://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_316_42.png

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ОДОБРЕНО

    предметной
    (цикловой) комиссией

     общегуманитарных
    и

    общеобразовательных
    дисциплин.

    Протокол
    №4   от 8 апреля 2019 г.

    Председатель П(Ц)К

    _____________ 
    Гаджиева. С.З.

    УТВЕРЖДАЮ

    заместитель  директора по

    учебной работе

    __________   Квиралашвили Н.У

    8 апреля 2019 г.

    Дисциплина«Математика»

    Билет
    №1    5

    1.    
    Формулы
    объема цилиндра

    2.    
    Степени
    с рациональными показателями, их свойства.

    3.     Основные
    тригонометрические тождества

    4.     Примеры:

    1)   
    Решите уравнение    

    sin2x = cosx—
    cos2x

    2)    
    Найти производную

    f 1(x) при x=0 —1

    5.     Задача

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_337_35.pnghttp://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_337_35.png

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ОДОБРЕНО

    предметной
    (цикловой) комиссией

     общегуманитарных
    и

    общеобразовательных
    дисциплин.

    Протокол
    №4   от 8 апреля 2019 г.

    Председатель П(Ц)К

    _____________ 
    Гаджиева. С.З.

    УТВЕРЖДАЮ

    заместитель  директора по

    учебной работе

    __________   Квиралашвили Н.У

    8 апреля 2019 г.

    Дисциплина«Математика»

    Билет
    №1    6

    1.     Формулы
    объема цилиндра, конуса

    2.     Исследование
    функции по схеме.

    3.     Раскрытие
    неопределенностей 0/0 

    4.     Примеры:

    1)   
    Вычислите

    2)    В шахматном турнире участвуют 16 человек. Сколько
    партий должно быть сыграно в турнире, если между любыми двумя участниками
    должна быть сыграна одна партия?

    5.     Задача:

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_337_29.pnghttp://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_337_29.png

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ОДОБРЕНО

    предметной
    (цикловой) комиссией

     общегуманитарных
    и

    общеобразовательных
    дисциплин.

    Протокол
    №4   от 8 апреля 2019 г.

    Председатель П(Ц)К

    _____________ 
    Гаджиева. С.З.

    УТВЕРЖДАЮ

    заместитель  директора по

    учебной работе

    __________   Квиралашвили Н.У

    8 апреля 2019 г.

    Дисциплина«Математика»

    Билет
    №1    7

    1.     Формулы
    объема шара

    2.     Раскрытие
    неопределенностей ∞/∞.

    3.     Параллельный
    перенос

    4.     Примеры:

    1)    Решите
    графически 

    2) На борту самолёта 12 мест рядом с
    запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные
    места неудобны для пассажира высокого роста. Пассажир В. высокого роста.
    Найдите вероятность того, что на регистрации при случайном выбореместа пассажиру
    В. достанется удобное место, если всего в самолёте 300 мест

    5.    Задача:

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_287_4.pnghttp://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_287_4.png

    МИНИСТЕРСТВО
    ОБРАЗОВАНИЯ И НАУКИ РД

    ГБПОУ
    КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ОДОБРЕНО

    предметной
    (цикловой) комиссией

     общегуманитарных
    и

    общеобразовательных
    дисциплин

    протокол
    №4   от 8 апреля 2019 г.

    ______________ 
    Гаджиева. С.З.

    УТВЕРЖДАЮ

    зам.
    директора по учебной работе

    _______________  
    Квиралашвили Н.У

                        
    8 апреля 2019 г.

    Дисциплина«Математика»

    Билет
    №    18

    1.    
    Формулы
    объема куба, прямоугольного параллелепипеда

    2.     Радианная мера
    угла.

    3.    
    Логарифмическая
    функция, свойства и график

    4.    
    Примеры:

    1)   
    Вычислите

    2)    
     

    Из множества натуральных чисел от 10 до 19 наудачу
    выбирают        одно число. Какова вероятность того, что оно делится на 3?

    5.     Задача

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_288_7.png

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ОДОБРЕНО

    предметной
    (цикловой) комиссией

     общегуманитарных
    и

    общеобразовательных
    дисциплин.

    Протокол
    №4   от 8 апреля 2019 г.

    Председатель П(Ц)К

    _____________ 
    Гаджиева. С.З.

    УТВЕРЖДАЮ

    заместитель  директора по

    учебной работе

    __________   Квиралашвили Н.У

    8 апреля 2019 г.

    Дисциплина«Математика»

    Билет
    №1    9

    1.    
    Формулы
    объема призмы

    2.    
    Физический
    смысл производной

    3.    
    Событие,
    вероятность события

    4.    
    Примеры:

    1) Напишите
    первые пять членов последовательности.

    аn=2n+1/2n

    2)Решите
    уравнение

    5.    
    Задача:

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_288_10.png

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_288_10.png

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_288_10.png

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ОДОБРЕНО

    предметной
    (цикловой) комиссией

     общегуманитарных
    и

    общеобразовательных
    дисциплин.

    Протокол
    №4   от 8 апреля 2019 г.

    Председатель П(Ц)К

    _____________ 
    Гаджиева. С.З.

    УТВЕРЖДАЮ

    заместитель  директора по

    учебной работе

    __________   Квиралашвили Н.У

    8 апреля 2019 г.

    Дисциплина«Математика»

    Билет
    №    20

    1.    
    Формулы
    объема пирамиды, усеченной пирамиды 

    2.    
    Геометрический
    смысл производной

    3.     Степенная
    функция,  свойства и график.

    4.     Примеры:

    1)    Решить уравнения

    2)   В
    сборнике билетов по биологии всего 55 билетов, в 11 из них встречается вопрос
    по ботанике. Найдите вероятность того, что в случайно выбранном на экзамене
    билете     школьнику
    достанется    вопрос
    по ботанике.

    5.    Задача:

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_288_11.pnghttp://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_288_11.png

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ОДОБРЕНО

    предметной
    (цикловой) комиссией

     общегуманитарных
    и

    общеобразовательных
    дисциплин.

    Протокол
    №4   от 8 апреля 2019г.

    Председатель П(Ц)К

    _____________ 
    Гаджиева. С.З.

    УТВЕРЖДАЮ

    заместитель  директора по

    учебной работе

    __________   Квиралашвили Н.У

    8 апреля 2019г.

    Дисциплина«Математика»

    Билет
    №2    1

    1.     Площади
    поверхностей тел вращения.

    2.     Понятие о
    производной функции

    3.     Функции.Область
    определения и множество значений; график функции

    4.     Примеры:

    1)    Решите уравнения

    2)   В
    сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос
    по неравенствам. Найдите вероятность того, что в случайно выбранном на экзамене
    билете школьнику
    не достанется    вопроса по неравенствам.

    5.     Задача:

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_289_25.png

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_289_25.png

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ОДОБРЕНО

    предметной
    (цикловой) комиссией

     общегуманитарных
    и

    общеобразовательных
    дисциплин.

    Протокол
    №4   от 8 апреля 2019 г.

    Председатель П(Ц)К

    _____________ 
    Гаджиева. С.З.

    УТВЕРЖДАЮ

    заместитель  директора по

    учебной работе

    __________   Квиралашвили Н.У

    8 апреля 2019 г.

    Дисциплина«Математика»

    Билет
    №2    2

    1.    
    Векторы
    в пространстве.

    2.     Основные
    тригонометрические тождества.

    3.    
    Раскрытие
    неопределенностей 0/0.

    4.    
    Примеры:

    1)   
    Решить
    уравнение

    3(x-2)-5=4-(5x-1)

    2)   
    Исследуйте
    функцию и постройте график

    f(x)=3x-1

    5.    
    Задача:

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_289_25.pnghttp://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_289_25.png

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_289_25.png

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ОДОБРЕНО

    предметной
    (цикловой) комиссией

     общегуманитарных
    и

    общеобразовательных
    дисциплин.

    Протокол
    №4   от 8апреля 2019 г.

    Председатель П(Ц)К

    _____________ 
    Гаджиева. С.З.

    УТВЕРЖДАЮ

    заместитель  директора по

    учебной работе

    __________   Квиралашвили Н.У

    8 апреля 2019 г.

    Дисциплина«Математика»

    Билет
    №    23

    1.     Площади
    поверхностей тел вращения.

    2.     Логарифми его
    свойства

    3.     Радианная мера
    угла.

    4.     Примеры:

    1)  Решить уравнения

    .

    2)Исследуйте
    функцию и постройте график

    f(x)=x2+2

    5.    
    Задача:

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_289_25.pnghttp://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_289_25.png

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_289_25.png

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ОДОБРЕНО

    предметной
    (цикловой) комиссией

     общегуманитарных
    и

    общеобразовательных
    дисциплин.

    Протокол
    №4   от 8 апреля 2019 г.

    Председатель П(Ц)К

    _____________ 
    Гаджиева. С.З.

    УТВЕРЖДАЮ

    заместитель  директора по

    учебной работе

    __________   Квиралашвили Н.У

    8 апреля 2019 г.

    Дисциплина«Математика»

    Билет
    №2    4

    1.     Конус. Усеченный
    конус. 

    2.    
    Корни
    натуральной степени из числа и их свойства.      

    3.    
    Арксинус, арккосинус, арктангенс
    числа

    4.    
    Примеры:

    1)    Вычислите

                     

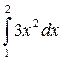
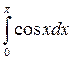
    2)   
    Первести из градусной меры в радианную

     450,600,360

    5.
    Задача

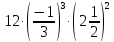
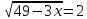
    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_289_25.pnghttp://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_289_25.png

    http://botanam.net/tasks/ru/geometriya/7_klass/pogorelov_a_v/zadanie_289_25.png

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин

    ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин

    ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин

    ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин

    ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин

    ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин

    ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин

    ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин

    ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин протокол №4 от 8 апреля 2019 г

    ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин протокол №4 от 8 апреля 2019 г

    ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин

    ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин

    ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин

    ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин

    ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин

    ОДОБРЕНО предметной (цикловой) комиссией общегуманитарных и общеобразовательных дисциплин

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

    Источник

    Понравилась статья? Поделить с друзьями:
  • Миссис экзамен математика
  • Миссис расписание экзаменов иткн
  • Миссис расписание экзаменов зимней сессии
  • Миссис предметы егэ
  • Миссис подготовка к егэ