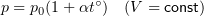Мкт физика формулы для егэ

Молекулярная физика Основные формулы

1. Основы молекулярно-кинетической теории. Газовые законы

1.1 Количество вещества

m — масса;

μ — молярная масса вещества;

N — число молекул;

N_A = 6,02·10²³ моль^-1 — число Авогадро

1.2 Основное уравнение молекулярно-кинетической теории идеального газа

p — давление идеального газа;

m — масса одной молекулы;

n = N/V — концентрация молекул;

V — объем газа;

N — число молекул;

— среднее значение квадрата скорости молекул.

1.3 Средняя квадратичная скорость молекул идеального газа

k = 1,38·10^-23 Дж/К — постоянная Больцмана;

R = kN_A = 8,31 Дж/(моль·К) — универсальная газовая постоянная;

T = t+273 — абсолютная температура;

t — температура по шкале Цельсия.

1.4 Средняя кинетическая энергия молекулы одноатомного газа

1.5 Давление идеального газа

n — концентрация молекул;

k — постоянная Больцмана;

T — абсолютная температура.

1.6 Закон Бойля-Мариотта

p — давление;

V — объем газа.

1.7 Закон Шарля

p₀ — давление газа при 0 °С;

α = 1/273 °C^-1 — температурный коэффициент давления.

1.8 Закон Гей-Люссака

V₀ — объем газа при 0 °С.

1.9 Уравнение Менделеева-Клапейрона

1.10 Объединенный закон газового состояния (уравнение Клапейрона)

1.11 Закон Дальтона

p_i — парциальное давление i-й компоненты смеси газов.

2. Основы термодинамики

2.1 Внутренняя энергия идеального одноатомного газа

ν — количество вещества;

R = 8,31 Дж/(моль·К) — универсальная газовая постоянная;

T — абсолютная температура.

2.2 Элементарная работа, совершаемая газом,

при изменении объема на бесконечно малую величину dV

p — давление газа.

При изменении объема от V₁ до V₂

2.3 Первый закон термодинамики

ΔQ — количество подведенной теплоты;

ΔA — работа, совершаемая веществом;

ΔU — изменение внутренней энергии вещества.

2.4 Теплоемкость идеального газа

ΔQ — количество переданной системе теплоты на участке процесса;

ΔT — изменение температуры на этом участке процесса.

Оглавление:

• Основные теоретические сведения
  • Основные положения МКТ
  • Основное уравнение МКТ идеального газа
  • Уравнение состояния идеального газа или уравнение Клапейрона-Менделеева
  • Газовые законы
  • Графическое изображение изопроцессов
  • Неизопроцессы
  • Изменение количества или массы вещества
  • Перегородки или поршни
  • Газовые законы и гидростатика
  • Тепловое расширение тел

Основные теоретические сведения

Основные положения МКТ

К оглавлению…

Молекулярно-кинетической теорией называют учение о строении и свойствах вещества на основе представления о существовании атомов и молекул как наименьших частиц химического вещества. В основе молекулярно-кинетической теории лежат три основных положения:

• Все вещества – жидкие, твердые и газообразные – образованы из мельчайших частиц – молекул, которые сами состоят из атомов («элементарных молекул»). Молекулы химического вещества могут быть простыми и сложными и состоять из одного или нескольких атомов. Молекулы и атомы представляют собой электрически нейтральные частицы. При определенных условиях молекулы и атомы могут приобретать дополнительный электрический заряд и превращаться в положительные или отрицательные ионы (соответственно: катионы и анионы).
• Атомы и молекулы находятся в непрерывном хаотическом движении и взаимодействии, скорость которого зависит от температуры, а характер – от агрегатного состояния вещества.
• Частицы взаимодействуют друг с другом силами, имеющими электрическую природу. Гравитационное взаимодействие между частицами пренебрежимо мало.

Атом – наименьшая химически неделимая частица элемента (атом железа, гелия, кислорода). Молекула – наименьшая частица вещества, сохраняющая его химические свойства. Молекула состоит из одного и более атомов (вода – Н₂О – 1 атом кислорода и 2 атома водорода). Ион – атом или молекула, у которых один или несколько электронов лишние (или электронов не хватает).

Молекулы имеют чрезвычайно малые размеры. Простые одноатомные молекулы имеют размер порядка 10^–10 м. Сложные многоатомные молекулы могут иметь размеры в сотни и тысячи раз больше. 

Беспорядочное хаотическое движение молекул называется тепловым движением. Кинетическая энергия теплового движения растет с возрастанием температуры. При низких температурах молекулы конденсируются в жидкое или твердое вещество. При повышении температуры средняя кинетическая энергия молекулы становится больше, молекулы разлетаются, и образуется газообразное вещество.

В твердых телах молекулы совершают беспорядочные колебания около фиксированных центров (положений равновесия). Эти центры могут быть расположены в пространстве нерегулярным образом (аморфные тела) или образовывать упорядоченные объемные структуры (кристаллические тела).

В жидкостях молекулы имеют значительно большую свободу для теплового движения. Они не привязаны к определенным центрам и могут перемещаться по всему объему жидкости. Этим объясняется текучесть жидкостей.

В газах расстояния между молекулами обычно значительно больше их размеров. Силы взаимодействия между молекулами на таких больших расстояниях малы, и каждая молекула движется вдоль прямой линии до очередного столкновения с другой молекулой или со стенкой сосуда. Среднее расстояние между молекулами воздуха при нормальных условиях порядка 10^–8 м, то есть в сотни раз превышает размер молекул. Слабое взаимодействие между молекулами объясняет способность газов расширяться и заполнять весь объем сосуда. В пределе, когда взаимодействие стремится к нулю, мы приходим к представлению об идеальном газе.

Идеальный газ – это газ, молекулы которого не взаимодействуют друг с другом, за исключением процессов упругого столкновения и считаются материальными точками.

В молекулярно-кинетической теории количество вещества принято считать пропорциональным числу частиц. Единица количества вещества называется молем (моль). Моль – это количество вещества, содержащее столько же частиц (молекул), сколько содержится атомов в 0,012 кг углерода ¹²C. Молекула углерода состоит из одного атома. Таким образом, в одном моле любого вещества содержится одно и то же число частиц (молекул). Это число называется постоянной Авогадро: N_А = 6,022·10²³ моль^–1.

Постоянная Авогадро – одна из важнейших постоянных в молекулярно-кинетической теории. Количество вещества определяется как отношение числа N частиц (молекул) вещества к постоянной Авогадро N_А, или как отношение массы к молярной массе:

Массу одного моля вещества принято называть молярной массой M. Молярная масса равна произведению массы m₀ одной молекулы данного вещества на постоянную Авогадро (то есть на количество частиц в одном моле). Молярная масса выражается в килограммах на моль (кг/моль). Для веществ, молекулы которых состоят из одного атома, часто используется термин атомная масса. В таблице Менделеева молярная масса указана в граммах на моль. Таким образом имеем еще одну формулу:

где: M – молярная масса, N_A – число Авогадро, m₀ – масса одной частицы вещества, N – число частиц вещества содержащихся в массе вещества m. Кроме этого понадобится понятие концентрации (количество частиц в единице объема):

Напомним также, что плотность, объем и масса тела связаны следующей формулой:

Если в задаче идет речь о смеси веществ, то говорят о средней молярной массе и средней плотности вещества. Как и при вычислении средней скорости неравномерного движения, эти величины определяются полными массами смеси:

Не забывайте, что полное количество вещества всегда равно сумме количеств веществ, входящих в смесь, а с объемом надо быть аккуратными. Объем смеси газов не равен сумме объемов газов, входящих в смесь. Так, в 1 кубометре воздуха содержится 1 кубометр кислорода, 1 кубометр азота, 1 кубометр углекислого газа и т.д. Для твердых тел и жидкостей (если иное не указано в условии) можно считать, что объем смеси равен сумме объемов ее частей.

Основное уравнение МКТ идеального газа

К оглавлению…

При своем движении молекулы газа непрерывно сталкиваются друг с другом. Из-за этого характеристики их движения меняются, поэтому, говоря об импульсах, скоростях, кинетических энергиях молекул, всегда имеют в виду средние значения этих величин.

Число столкновений молекул газа в нормальных условиях с другими молекулами измеряется миллионами раз в секунду. Если пренебречь размерами и взаимодействием молекул (как в модели идеального газа), то можно считать, что между последовательными столкновениями молекулы движутся равномерно и прямолинейно. Естественно, подлетая к стенке сосуда, в котором расположен газ, молекула испытывает столкновение и со стенкой. Все столкновения молекул друг с другом и со стенками сосуда считаются абсолютно упругими столкновениями шариков. При столкновении со стенкой импульс молекулы изменяется, значит на молекулу со стороны стенки действует сила (вспомните второй закон Ньютона). Но по третьему закону Ньютона с точно такой же силой, направленной в противоположную сторону, молекула действует на стенку, оказывая на нее давление. Совокупность всех ударов всех молекул о стенку сосуда и приводит к возникновению давления газа. Давление газа – это результат столкновений молекул со стенками сосуда. Если нет стенки или любого другого препятствия для молекул, то само понятие давления теряет смысл. Например, совершенно антинаучно говорить о давлении в центре комнаты, ведь там молекулы не давят на стенку. Почему же тогда, поместив туда барометр, мы с удивлением обнаружим, что он показывает какое-то давление? Правильно! Потому, что сам по себе барометр является той самой стенкой, на которую и давят молекулы.

Поскольку давление есть следствие ударов молекул о стенку сосуда, очевидно, что его величина должна зависеть от характеристик отдельно взятых молекул (от средних характеристик, конечно, Вы ведь помните про то, что скорости всех молекул различны). Эта зависимость выражается основным уравнением молекулярно-кинетической теории идеального газа:

где: p — давление газа, n — концентрация его молекул, m₀ — масса одной молекулы, v_кв — средняя квадратичная скорость (обратите внимание, что в самом уравнении стоит квадрат средней квадратичной скорости). Физический смысл этого уравнения состоит в том, что оно устанавливает связь между характеристиками всего газа целиком (давлением) и параметрами движения отдельных молекул, то есть связь между макро- и микромиром.

Следствия из основного уравнения МКТ

Как уже было отмечено в предыдущем параграфе, скорость теплового движения молекул определяется температурой вещества. Для идеального газа эта зависимость выражается простыми формулами для средней квадратичной скорости движения молекул газа:

где: k = 1,38∙10^–23 Дж/К – постоянная Больцмана, T – абсолютная температура. Сразу же оговоримся, что далее во всех задачах Вы должны, не задумываясь, переводить температуру в кельвины из градусов Цельсия (кроме задач на уравнение теплового баланса). Закон трех постоянных:

где: R = 8,31 Дж/(моль∙К) – универсальная газовая постоянная. Следующей важной формулой является формула для средней кинетической энергии поступательного движения молекул газа:

Оказывается, что средняя кинетическая энергия поступательного движения молекул зависит только от температуры, одинакова при данной температуре для всех молекул. Ну и наконец, самыми главными и часто применяемыми следствиями из основного уравнения МКТ являются следующие формулы:

Измерение температуры

Понятие температуры тесно связано с понятием теплового равновесия. Тела, находящиеся в контакте друг с другом, могут обмениваться энергией. Энергия, передаваемая одним телом другому при тепловом контакте, называется количеством теплоты.

Тепловое равновесие – это такое состояние системы тел, находящихся в тепловом контакте, при котором не происходит теплопередачи от одного тела к другому, и все макроскопические параметры тел остаются неизменными. Температура – это физический параметр, одинаковый для всех тел, находящихся в тепловом равновесии.

Для измерения температуры используются физические приборы – термометры, в которых о величине температуры судят по изменению какого-либо физического параметра. Для создания термометра необходимо выбрать термометрическое вещество (например, ртуть, спирт) и термометрическую величину, характеризующую свойство вещества (например, длина ртутного или спиртового столбика). В различных конструкциях термометров используются разнообразные физические свойства вещества (например, изменение линейных размеров твердых тел или изменение электрического сопротивления проводников при нагревании).

Термометры должны быть откалиброваны. Для этого их приводят в тепловой контакт с телами, температуры которых считаются заданными. Чаще всего используют простые природные системы, в которых температура остается неизменной, несмотря на теплообмен с окружающей средой – это смесь льда и воды и смесь воды и пара при кипении при нормальном атмосферном давлении. По температурной шкале Цельсия точке плавления льда приписывается температура 0°С, а точке кипения воды: 100°С. Изменение длины столба жидкости в капиллярах термометра на одну сотую длины между отметками 0°С и 100°С принимается равным 1°С.

Английский физик У.Кельвин (Томсон) в 1848 году предложил использовать точку нулевого давления газа для построения новой температурной шкалы (шкала Кельвина). В этой шкале единица измерения температуры такая же, как и в шкале Цельсия, но нулевая точка сдвинута:

При этом изменение температуры на 1ºС соответствует изменению температуры на 1 К. Изменения температуры по шкале Цельсия и Кельвина равны. В системе СИ принято единицу измерения температуры по шкале Кельвина называть кельвином и обозначать буквой К. Например, комнатная температура T_С = 20°С по шкале Кельвина равна T_К = 293 К. Температурная шкала Кельвина называется абсолютной шкалой температур. Она оказывается наиболее удобной при построении физических теорий.

Уравнение состояния идеального газа или уравнение Клапейрона-Менделеева

К оглавлению…

Уравнение состояние идеального газа является очередным следствие из основного уравнения МКТ и записывается в виде:

Данное уравнение устанавливает связь между основными параметрами состояния идеального газа: давлением, объемом, количеством вещества и температурой. Очень важно, что эти параметры взаимосвязаны, изменение любого из них неизбежно приведет к изменению еще хотя бы одного. Именно поэтому данное уравнение и называют уравнением состояния идеального газа. Оно было открыто сначала для одного моля газа Клапейроном, а впоследствии обобщено на случай большего количество молей Менделеевым.

Если температура газа равна T_н = 273 К (0°С), а давление p_н = 1 атм = 1·10⁵ Па, то говорят, что газ находится при нормальных условиях.

Газовые законы

К оглавлению…

Решение задач на расчет параметров газа значительно упрощается, если Вы знаете, какой закон и какую формулу применить. Итак, рассмотрим основные газовые законы.

1. Закон Авогадро. В одном моле любого вещества содержится одинаковое количество структурных элементов, равное числу Авогадро.

2. Закон Дальтона. Давление смеси газов равно сумме парциальных давлений газов, входящих в эту смесь:

Парциальным давлением газа называют то давление, которое он бы производил, если бы все остальные газ внезапно исчезли из смеси. Например, давление воздуха равно сумме парциальных давлений азота, кислорода, углекислого газа и прочих примесей. При этом каждый из газов в смеси занимает весь предоставленный ему объем, то есть объем каждого из газов равен объему смеси.

3. Закон Бойля-Мариотта. Если масса и температура газа остаются постоянными, то произведение давления газа на его объем не изменяется, следовательно:

Процесс, происходящий при постоянной температуре, называют изотермическим. Обратите внимание, что такая простая форма закона Бойля-Мариотта выполняется только при условии, что масса газа остается неизменной.

4. Закон Гей-Люссака. Сам закон Гей-Люссака не представляет особой ценности при подготовке к экзаменам, поэтому приведем лишь следствие из него. Если масса и давление газа остаются постоянными, то отношение объема газа к его абсолютной температуре не изменяется, следовательно:

Процесс, происходящий при постоянном давлении, называют изобарическим или изобарным. Обратите внимание, что такая простая форма закона Гей-Люссака выполняется только при условии, что масса газа остается неизменной. Не забывайте про перевод температуры из градусов Цельсия в кельвины.

5. Закон Шарля. Как и закон Гей-Люссака, закон Шарля в точной формулировке для нас не важен, поэтому приведем лишь следствие из него. Если масса и объем газа остаются постоянными, то отношение давления газа к его абсолютной температуре не изменяется, следовательно:

Процесс, происходящий при постоянном объеме, называют изохорическим или изохорным. Обратите внимание, что такая простая форма закона Шарля выполняется только при условии, что масса газа остается неизменной. Не забывайте про перевод температуры из градусов Цельсия в кельвины.

6. Универсальный газовый закон (Клапейрона). При постоянной массе газа отношение произведения его давления и объема к температуре не изменяется, следовательно:

Обратите внимание, что масса должна оставаться неизменной, и не забывайте про кельвины.

Итак, существует несколько газовых законов. Перечислим признаки того, что нужно применять один из них при решении задачи:

1. Закон Авогадро применяется во всех задачах где речь идет о количестве молекул.
2. Закон Дальтона применяется во всех задачах, в которых идет речь о смеси газов.
3. Закон Шарля применяют в задачах, когда объем газа остается неизменным. Обычно это или сказано явно, или в задаче присутствуют слова «газ в закрытом сосуде без поршня».
4. Закон Гей-Люссака применяют, если неизменным остается давление газа. Ищите в задачах слова «газ в сосуде, закрытом подвижным поршнем» или «газ в открытом сосуде». Иногда про сосуд ничего не сказано, но по условию понятно, что он сообщается с атмосферой. Тогда считается, что атмосферное давление всегда остается неизменным (если в условии не сказано иного).
5. Закон Бойля-Мариотта. Тут сложнее всего. Хорошо, если в задаче написано, что температура газа неизменна. Чуть хуже, если в условии присутствует слово «медленно». Например, газ медленно сжимают или медленно расширяют. Еще хуже, если сказано, что газ закрыт теплонепроводящим поршнем. Наконец, совсем плохо, если про температуру не сказано ничего, но из условия можно предположить, что она не изменяется. Обычно в этом случае ученики применяют закон Бойля-Мариотта от безысходности.
6. Универсальный газовый закон. Его используют, если масса газа постоянна (например, газ находится в закрытом сосуде), но по условию понятно, что все остальные параметры (давление, объем, температура) изменяются. Вообще, часто вместо универсального закона можно применять уравнение Клапейрона-Менделеева, вы получите правильный ответ, только в каждой формуле будете писать по две лишние буквы.

Графическое изображение изопроцессов

К оглавлению…

Во многих разделах физики зависимость величин друг от друга удобно изображать графически. Это упрощает понимание взаимосвязи параметров, происходящих в системе процессов. Такой подход очень часто применяется и в молекулярной физике. Основными параметрами, описывающими состояние идеального газа, являются давление, объем и температура. Графический метод решения задач и состоит в изображении взаимосвязи этих параметров в различных газовых координатах. Существует три основных типа газовых координат: (p; V), (p; T) и (V; T). Заметьте, что это только основные (наиболее часто встречающиеся типы координат). Фантазия составителей задач и тестов не ограничена, поэтому Вы можете встретить и любые другие координаты. Итак, изобразим основные газовые процессы в основных газовых координатах.

Изобарный процесс (p = const)

Изобарным процессом называют процесс, протекающий при неизменным давлении и массе газа. Как следует из уравнения состояния идеального газа, в этом случае объем изменяется прямо пропорционально температуре. Графики изобарического процесса в координатах р–V; V–Т и р–Т имеют следующий вид:

Обратите внимание на то, что продолжение графика в V–T координатах направлено точно в начало координат, однако этот график никогда не сможет начаться прямо из начала координат, так как при очень низких температурах газ превращается в жидкость и зависимость объема от температура меняется.

Изохорный процесс (V = const)

Изохорный процесс – это процесс нагревания или охлаждения газа при постоянном объеме и при условии, что количество вещества в сосуде остается неизменным. Как следует из уравнения состояния идеального газа, при этих условиях давление газа изменяется прямо пропорционально его абсолютной температуре. Графики изохорного процесса в координатах р–V; р–Т и V–Т имеют следующий вид:

Обратите внимание на то, что продолжение графика в p–T координатах направлено точно в начало координат, однако этот график никогда не сможет начаться прямо из начала координат, так как газ при очень низких температурах превращается в жидкость.

Изотермический процесс (T = const)

Изотермическим процессом называют процесс, протекающий при постоянной температуре. Из уравнения состояния идеального газа следует, что при постоянной температуре и неизменном количестве вещества в сосуде произведение давления газа на его объем должно оставаться постоянным. Графики изотермического процесса в координатах р–V; р–Т и V–Т имеют следующий вид:

Заметим, что при выполнении заданий на графики в молекулярной физике не требуется особой точности в откладывании координат по соответствующим осям (например, чтобы координаты p₁ и p₂ двух состояний газа в системе p(V) совпадали с координатами p₁ и p₂ этих состояний в системе p(T). Во–первых, это разные системы координат, в которых может быть выбран разный масштаб, а во–вторых, это лишняя математическая формальность, отвлекающая от главного – от анализа физической ситуации. Основное требование: чтобы качественный вид графиков был верным.

Неизопроцессы

К оглавлению…

В задачах этого типа изменяются все три основных параметра газа: давление, объем и температура. Постоянной остается только масса газа. Наиболее простой случай, если задача решается «в лоб» с помощью универсального газового закона. Чуть сложнее, если Вам надо отыскать уравнение процесса, описывающего изменение состояния газа, или проанализировать поведение параметров газа по данному уравнению. Тогда действовать надо так. Записать данное уравнение процесса и универсальный газовый закон (или уравнение Клапейрона-Менделеева, что Вам удобнее) и последовательно исключать ненужные величины из них.

Изменение количества или массы вещества

К оглавлению…

В сущности, ничего сложного в таких задачах нет. Надо только помнить, что газовые законы не выполняются, так как в формулировках любых из них записано «при постоянной массе». Поэтому действуем просто. Записываем уравнение Клапейрона-Менделеева для начального и конечного состояний газа и решаем задачу.

Перегородки или поршни

К оглавлению…

В задачах этого типа опять применяются газовые законы, при этом необходимо учесть следующие замечания:

• Во-первых, газ через перегородку не проходит, то есть масса газа в каждой части сосуда остается неизменной, и таким образом, для каждой части сосуда выполняются газовые законы.
• Во-вторых, если перегородка теплонепроводящая, то при нагревании или охлаждении газа в одной части сосуда температура газа во второй части останется неизменной.
• В-третьих, если перегородка подвижна, то давления по обе ее стороны равны в каждый конкретный момент времени (но это равное с обоих сторон давление может меняться со временем).
• А дальше пишем газовые законы для каждого газа по отдельности и решаем задачу.

Газовые законы и гидростатика

К оглавлению…

Специфика задач состоит в том, что в давлении надо будет учитывать «довески», связанные с давлением столба жидкости. Какие тут могут быть варианты:

• Сосуд с газом погружен под воду. Давление в сосуде будет равно: p = p_атм + ρgh, где: h – глубина погружения.
• Горизонтальная трубка закрыта от атмосферы столбиком ртути (или другой жидкости). Давление газа в трубке точно равно: p = p_атм атмосферному, так как горизонтальный столбик ртути не оказывает давления на газ.
• Вертикальная трубка с газом закрыта сверху столбиком ртути (или другой жидкости). Давление газа в трубке: p = p_атм + ρgh, где: h – высота столбика ртути.
• Вертикальная узкая трубка с газом повернута открытым концом вниз и заперта столбиком ртути (или другой жидкости). Давление газа в трубке: p = p_атм – ρgh, где: h – высота столбика ртути. Знак «–» ставится, так как ртуть не сжимает, а растягивает газ. Часто ученики спрашивают, почему ртуть не вытекает из трубки. Действительно, если бы трубка была широкой, ртуть бы стекла вниз по стенкам. А так, поскольку трубка очень узкая, поверхностное натяжение на дает ртути разорваться посередине и пропустить внутрь воздух, а давление газа внутри (меньшее, чем атмосферное) удерживает ртуть от вытекания.

Как только Вы сумели правильно записать давление газа в трубке, применяйте какой-либо из газовых законов (как правило, Бойля-Мариотта, так как большинство таких процессов изотермические, или универсальный газовый закон). Применяйте выбранный закон для газа (ни в коем случае не для жидкости) и решайте задачу.

Тепловое расширение тел

К оглавлению…

При повышении температуры возрастает интенсивность теплового движения частиц вещества. Это приводит к тому, что молекулы более «активно» отталкиваются друг от друга. Из-за этого большинство тел увеличивает свои размеры при нагревании. Не совершите типичную ошибку, сами атомы и молекулы не расширяются при нагревании. Увеличиваются лишь пустые промежутки между молекулами. Тепловое расширение газов описывается законом Гей-Люссака. Тепловое расширение жидкостей подчиняется следующему закону:

где: V₀ – объем жидкости при 0°С, V – при температуре t, γ – коэффициент объемного расширения жидкости. Обратите внимание, что все температуры в этой теме нужно брать в градусах Цельсия. Коэффициент объемного расширения зависит от рода жидкости (и от температуры, что не учитывается в большинстве задач). Обратите внимание, что численное значение коэффициента, выраженное в 1/°С или в 1/К, одинаково, так как нагреть тело на 1°С это то же самое, что нагреть его на 1 К (а не на 274 К).

Для расширения твердых тел применяются три формулы, описывающие изменение линейных размеров, площади и объема тела:

где: l₀, S₀, V₀ – соответственно длина, площадь поверхности и объем тела при 0°С, α – коэффициент линейного расширения тела. Коэффициент линейного расширения зависит от рода тела (и от температуры, что не учитывается в большинстве задач) и измеряется в 1/°С или в 1/К.

ФОРМУЛЫ физики для подготовки к ЕГЭ

МКТ и ТЕРМОДИНАМИКА

Основные формулы молекулярной физики

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

— масса вещества, — объём вещества, — плотность вещества (масса единицы объёма). Отсюда

— число частиц вещества (атомов или молекул).
— масса частицы вещества. Тогда

— концентрация вещества (число частиц в единице объёма), . Отсюда

Что получится, если умножить на ? Произведение массы частицы на число частиц в единице объёма даст массу единицы объёма, т. е. плотность. Формально:

Итак,

Массы и размеры частиц невообразимо малы по нашим обычным меркам. Например, масса атома водорода порядка г, размер атома порядка см. Из-за столь малых значений масс и размеров число частиц в макроскопическом теле огромно.

Оперировать столь грандиозными числами, как число частиц, неудобно. Поэтому для измерения количества вещества используют специальную единицу — моль.

Один моль — это количество вещества, в котором содержится столько же атомов или молекул, сколько атомов содержится в граммах углерода. А в граммах углерода содержится примерно атомов. Стало быть, в одном моле вещества содержится частиц. Это число называется постоянной Авогадро: моль.

Количество вещества обозначается . Это число молей данного вещества.

Что получится, если умножить на ? Число молей, умноженное на число частиц в моле, даст общее число частиц:

Масса одного моля вещества называется молярной массой этого вещества и обозначается ( = кг/моль). Ясно, что

Как найти молярную массу химического элемента? Оказывается, для этого достаточно заглянуть в таблицу Менделеева! Нужно просто взять атомную массу (число нуклонов) данного элемента — это будет его молярная масса, выраженная в г/моль. Например, для алюминия , поэтому молярная масса алюминия равна г/моль или кг/моль.

Почему так получается? Очень просто. Молярная масса углерода равна г/моль по определению. В то же время ядро атома углерода содержит нуклонов. Выходит, что каждый нуклон вносит в молярную массу г/моль. Поэтому молярная масса химического элемента с атомной массой оказывается равной г/моль.

Молярная масса вещества, молекула которого состоит из нескольких атомов, получается простым суммированием молярных масс. Так, молярная масса углекислого газа равна г/моль кг/моль.

Будьте внимательны с молярными массами некоторых газов! Так, молярная масса газообразного водорода равна г/моль, поскольку его молекула состоит из двух атомов . То же касается часто встречающихся в задачах азота и кислорода Вместе с тем, наиболее частый персонаж задач — гелий — является одноатомным газом и имеет молярную массу г/моль, предписанную таблицей Менделеева.

Ещё раз предостережение: при расчётах не забывайте переводить молярную массу в кг/моль! Если ваш ответ отличается от правильного на три порядка, то вы наверняка сделали именно эту, очень распространённую ошибку

Что получится, если умножить на ? Масса частицы, умноженная на число частиц в моле, даст массу моля, т. е. молярную массу: