Многоугольники формулы егэ - Помощь в подготовке к экзаменам и поступлению

Сумма углов многоугольника. Доказательство.

А теперь давай все-таки разберемся, откуда же взялась формула суммы углом многоугольника ( displaystyle 180^circ(n-2)).

Зачем?

Понимаешь, приемчик, который мы сейчас применим, часто оказывается полезным при решении разных задач.

Несмотря на то, что теорема о сумме углов многоугольника верна для всякого многоугольника, доказательство красивое и простое только для выпуклых многоугольников.

Итак, давай разделим многоугольник на треугольники.

Вот так: из одной точки проведем все диагонали, что можно. Сколько их будет? Считаем:

Всего вершин: ( displaystyle n)

Из вершины ( displaystyle B) можем провести диагонали во все вершины, кроме:

Самой вершины B
Вершины A
Вершины C

Значит всего диагоналей ( displaystyle (n-3)). А на сколько треугольников распался наш многоугольник?

Представь себе: на ( displaystyle n-2). Порисуй, посчитай – удостоверься, что треугольников оказывается ровно на один больше.

Итак, у нас ровно ( displaystyle n-2) треугольника. И сумма углов многоугольника просто равна сумме углов треугольников, на которые мы разбили многоугольник.

Чему равна сумма углов треугольника? Помнишь? Конечно ( displaystyle 180{}^circ ).

Ну вот, ( displaystyle n-2) треугольника, в каждом по ( displaystyle 180{}^circ ), значит:

Сумма углов многоугольника равна ( displaystyle 180{}^circ )( displaystyle (n-2))

Вот и доказали.

Что же из этого может оказаться полезным? Два момента:

Правильные многоугольники

Многоугольник называется правильным, если все его углы и все его стороны равны.

Так, например: квадрат – правильный четырехугольник, а вот прямоугольник – нет, хоть и все углы у него равные, и ромб – нет, хоть и все стороны равны. Нужно непременно, чтобы все углы и все стороны были равны.

Первый вопрос:

А можно ли найти величину одного (а значит и всех) угла правильного многоугольника?

И ответ: можно!

Давай посмотрим на примере.

Пусть есть, скажем, правильный восьмиугольник:

Сумма всех его углов равна ( displaystyle 180{}^circ left( 8-2 right)=1080{}^circ ).

А сколько всего углов? Восемь конечно, и они все одинаковые.

Значит любой угол, скажем ( displaystyle angle A) можно найти:

( displaystyle angle A=frac{1080{}^circ }{8}=135{}^circ ).

Что мы еще должны знать?

Любой правильный многоугольник можно вписать в окружность и вокруг любого правильного многоугольника можно описать окружность.

При этом центры этих окружностей совпадают.

Смотри, как это выглядит!

И более того, всегда можно посчитать соотношение между радиусом вписанной и описанной окружностей.

Давай опять на примере восьмиугольника.

Посмотри на ( displaystyle Delta OKG). В нем ( displaystyle OK=r,OG=R.)

Значит, ( displaystyle frac{r}{R}=sin angle x) – и это не только в восьмиугольнике!

Чему же равен в нашем случае ( displaystyle angle x)?

Ровно половине ( displaystyle angle G), представь себе!

Значит ( displaystyle angle x=frac{135{}^circ }{2}=67,5{}^circ ).

Смешно? Но так и есть! Поэтому для восьмиугольника ( displaystyle frac{r}{R}=sin 67,5{}^circ ).

Может возникнуть еще один вопрос: а можно ли посчитать углы «около» точки ( displaystyle O)?

И тот же ответ: конечно можно!

Опять рассмотрим наш восьмиугольник. Вот мы хотим найти ( displaystyle angle alpha) (то есть ( displaystyle angle HOG)).

Источник

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 451 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен 108°. Найдите число вершин многоугольника.

Угол между двумя соседними сторонами правильного многоугольника, равен 160°. Найдите число вершин многоугольника.

Угол между двумя соседними сторонами правильного многоугольника, равен 156°. Найдите число вершин многоугольника.

Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен 168°. Найдите число вершин многоугольника.

Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен 160°. Найдите число вершин многоугольника.

Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен 90°. Найдите число вершин многоугольника.

Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен 140°. Найдите число вершин многоугольника.

Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен 156°. Найдите число вершин многоугольника.

Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь.

Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.

Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?

Найдите радиус окружности, вписанной в правильный шестиугольник со стороной

Диагонали четырехугольника равны 6 и 2. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.

Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 39?

Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 28?

Найдите радиус окружности, вписанной в правильный шестиугольник со стороной

Около окружности, радиус которой равен 1, описан многоугольник, периметр которого равен 8. Найдите его площадь.

В треугольнике ABC угол A равен 43 градусам, углы B и C — острые, высоты BD и CE пересекаются в точке Найдите угол DOE. Ответ дайте в градусах.

Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 50. Найдите его площадь.

Всего: 451 1–20 | 21–40 | 41–60 | 61–80 …

Источник

6. Геометрия на плоскости (планиметрия). Часть II

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Использование различных формул площадей многоугольников

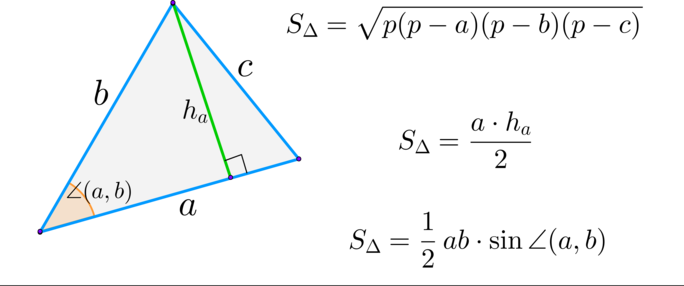
(blacktriangleright) Треугольник:

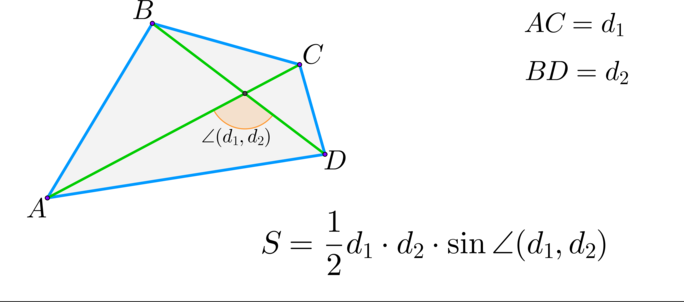
(blacktriangleright) Произвольный выпуклый четырехугольник:

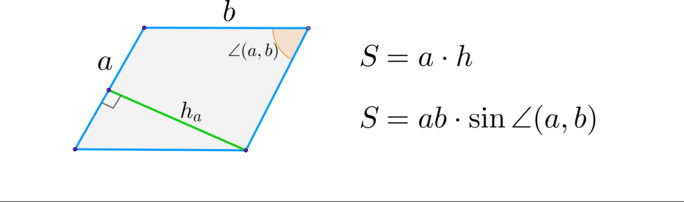
(blacktriangleright) Параллелограмм:

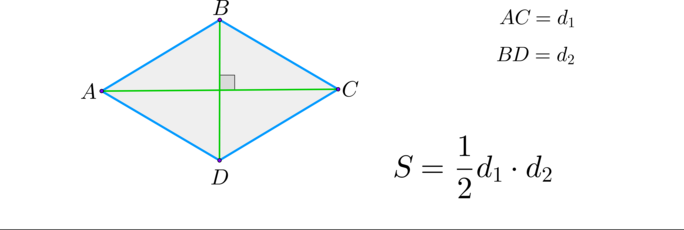
(blacktriangleright) Ромб:

(blacktriangleright) Прямоугольник:

(blacktriangleright) Квадрат:

(blacktriangleright) Трапеция:

Задание
1

#2269

Уровень задания: Легче ЕГЭ

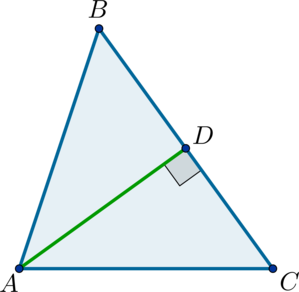
В треугольнике (ABC): (AD) – высота, (cos{angle DAC} = 0,7), (AC
= 6), (BC = 9). Найдите площадь треугольника (ABC).

Так как (AD) перпендикулярна (DC), то (sin{angle C} = cos{angle
DAC} = 0,7).

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними,
тогда площадь треугольника (ABC) равна (0,5cdot 6 cdot 9 cdot 0,7
= 18,9).

Ответ: 18,9

Задание
2

#2270

Уровень задания: Легче ЕГЭ

Периметр треугольника (ABC) равен (250), одна из его сторон равна (120), ещё одна сторона равна (17). Найдите его площадь.

Третья сторона треугольника равна (250 — 120 — 17 = 113).
По формуле Герона (S_{triangle ABC} = sqrt{p(p — AB)(p — BC)(p —
AC)}), где (p) – полупериметр треугольника (ABC).

Для данного треугольника

(S_{triangle ABC} = sqrt{125cdot (125 — 120)cdot (125 — 17)cdot (125 — 113)} = sqrt{125cdot 5 cdot 12 cdot 108} =)

(= 25sqrt{12cdot 108} = 100sqrt{3cdot 27} = 900.)

Ответ: 900

Задание
3

#2279

Уровень задания: Равен ЕГЭ

Найдите высоту треугольника, проведенную к стороне длиной (8), если высота, проведенная к стороне длиной (6), равна (4).

Т.к. площадь треугольника равна полупроизведению высоты и стороны, к которой эта высота проведена, то с одной стороны площадь равна [S=dfrac12cdot 6cdot 4,]

а с другой [S=dfrac12cdot 8cdot h,]

где (h) – высота, которую нужно найти. Таким образом, получаем следующее равенство:

[dfrac12cdot 6cdot 4=dfrac12cdot 8cdot h quad Leftrightarrow quad h=3.]

Ответ: 3

Задание
4

#2268

Уровень задания: Равен ЕГЭ

В треугольнике (ABC): (AC = 4), (AB = 6), (cos{angle BAC} =
dfrac{sqrt{15}}{4}). Найдите площадь треугольника (ABC).

Из основного тригонометрического тождества:
(sin^2angle BAC = 1 — dfrac{15}{16}), тогда (sinangle BAC = pm
0,25). Так как (angle BAC in (0^{circ}; 180^{circ})), то (sinangle BAC = 0,25).

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними,
тогда площадь треугольника (ABC) равна (0,5cdot 4 cdot 6 cdot
0,25 = 3).

Ответ: 3

Задание
5

#2280

Уровень задания: Равен ЕГЭ

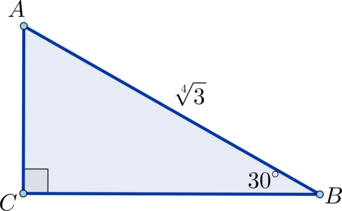
В прямоугольном треугольнике гипотенуза равна (sqrt[4]3), а один из углов равен (30^circ). Найдите площадь этого треугольника.

Т.к. катет, лежащий против угла в (30^circ), равен половине гипотенузы, то (AC=0,5cdot AB=0,5cdot sqrt[4]3).

Т.к. (angle A=90^circ -angle B=60^circ), то площадь равна [S=dfrac12cdot ACcdot ABcdot sin 60^circ=dfrac12cdot
0,5cdot sqrt[4]3cdot sqrt[4]3cdot
dfrac{sqrt3}2=dfrac38=0,375.]

Ответ: 0,375

Задание
6

#2274

Уровень задания: Равен ЕГЭ

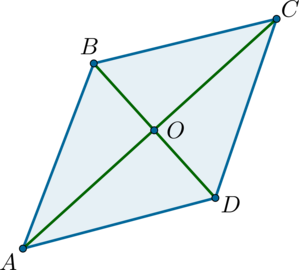
В ромбе (ABCD): (O) – точка пересечения диагоналей, (BD = , (mathrm{tg}, angle BDC = 3). Найдите площадь ромба (ABCD).

В ромбе диагонали пересекаются под прямым углом и точкой пересечения делятся пополам, тогда (OD = 4), (dfrac{CO}{OD} = mathrm{tg},
angle BDC = 3), откуда (CO = 12), следовательно, (AC = 24).

Площадь ромба равна половине произведения его диагоналей, тогда [S_{ABCD} = 0,5cdot 8cdot 24 = 96.]

Ответ: 96

Задание
7

#3326

Уровень задания: Равен ЕГЭ

Угол при вершине, противолежащей основанию равнобедренного треугольника, равен (150^circ). Найдите боковую сторону этого треугольника, если его площадь равна (100).

Пусть (a) – боковая сторона треугольника.
Площадь треугольника равна полупроизведению сторон на синус угла между ними, следовательно, [dfrac12cdot a^2cdot sin30^circ=S=100quadRightarrowquad
a^2=400quadRightarrowquad a=20]

Ответ: 20

Подготовка выпускников к сдаче аттестационного испытания по математике, как правило, начинается с повторения базовых определений и формул, в том числе и тех, которые позволяют произвести вычисление площадей плоских фигур в ЕГЭ. Данный раздел геометрии изучается в средней школе. Неудивительно, что с необходимостью повторения основных формул для правильного нахождения площади любого многоугольника сталкиваются многие выпускники. Умея выполнять расчеты с их применением, учащиеся смогут рассчитывать на получение конкурентных баллов по итогам сдачи аттестационного испытания.

Готовьтесь вместе с образовательным порталом «Школково»

Занимаясь перед сдачей экзамена, многие учащиеся сталкиваются с проблемой поиска определений и формул, которые позволяют выполнить вычисление площади правильного многоугольника в ЕГЭ. Школьный учебник далеко не всегда оказывается под рукой в нужный момент.

Вместе с образовательным порталом «Школково» подготовка к экзамену будет легкой и эффективной. Здесь представлен весь необходимый материал, подобранный и изложенный нашими специалистами в максимально понятной форме. Какая именно формула для нахождения площади многоугольника потребуется при работе с треугольником, четырехугольником, параллелограммом, ромбом, прямоугольником, квадратом, трапецией? Всю эту информацию вы найдете в разделе «Теоретическая справка». Ознакомившись с ней, выпускники смогут восполнить пробелы в знаниях.

Чтобы научиться быстро находить правильный ответ, необходимо также попрактиковаться в решении задач на нахождение площади фигур. Большая подборка упражнений представлена в разделе «Каталог». Для каждой задачи на нахождение площади фигур, например, вычисление площади параллелограмма, наши специалисты прописали подробный ход решения и указали правильный ответ. Перечень упражнений на сайте постоянно дополняется и обновляется.

Любое задание, например, на подобие площадей подобных треугольников, выпускники могут сохранить в разделе «Избранное». Это позволит в дальнейшем быстро найти интересующее упражнение, например, с целью обсуждения хода его решения с преподавателем.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Многоугольник, подготовка к ЕГЭ по математике

22.12.2017

Таблицы с теорией на тему: «Многоугольник» для подготовки к ЕГЭ по математике. В кратком содержании изложена вся необходимая теория для этой темы.

Смотреть в PDF:

Или прямо сейчас: cкачать в pdf файле.

Сохранить ссылку:

Комментарии (0)
Добавить комментарий

Добавить комментарий

Комментарии без регистрации. Несодержательные сообщения удаляются.

Имя (обязательное)

E-Mail

Подписаться на уведомления о новых комментариях

Отправить

Источник

Все формулы по геометрии. Площади фигур

Чтобы решать задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.

Начнем с квадрата.

Площадь квадрата равна квадрату его стороны.

Площадь прямоугольника равна произведению его длины и ширины.

Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне. Она также равна произведению его сторон на синус угла между ними.

Для площади треугольника есть целых 5 формул. И все они применяются в задачах ЕГЭ.

1) Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне: $S=displaystyle frac{1}{2}ah_a=displaystyle frac{1}{2}bh_b=displaystyle frac{1}{2}ch_c.$

2) Она также равна половине произведения его сторон на синус угла между ними:

$S=displaystyle frac{1}{2}ab{sin C=displaystyle frac{1}{2}ac{sin B= } }displaystyle frac{1}{2}bc{sin A }.$

3) По формуле Герона, где $p=displaystyle frac{1}{2}left(a+b+cright)$ полупериметр.

4) Также площадь треугольника равна произведению его полупериметра на радис вписанной окружности, S = pr.

5) Еще один способ. Площадь треугольника равна произведению его сторон, деленному на 4 радиуса описанной окружности, $S=displaystyle frac{abc}{4R}.$

Есть и другие формулы для площади треугольника. Но для решения заданий ЕГЭ, и первой, и второй части, достаточно этих пяти.

Площадь прямоугольного треугольника равна половине произведения его катетов. Она также равна половине произведения гипотенузы на высоту, проведенную к этой гипотенузе:

$S=displaystyle frac{1}{2}ab=displaystyle frac{1}{2}ch_{ }$

Площадь правильного треугольника равна квадрату его стороны, умноженному на sqrt{3} и деленному на 4:

Площадь трапеции равна произведению полусуммы оснований на высоту, $S=displaystyle frac{a+b}{2}cdot h.$

Также можно сказать, что площадь трапеции равна произведению ее средней линии на высоту,

Площадь произвольного четырехугольника равна половине произведения его диагоналей на синус угла между ними, $S=displaystyle frac{1}{2}ACcdot BDcdot {sin alpha }$

Площадь ромба равна произведению квадрата его стороны на синус угла ромба. Она также равна половине произведения диагоналей:

Площадь круга равна произведению числа и квадрата радиуса круга.

Ее также можно записать как произведение числа и квадрата диаметра круга, деленного на 4:

Вспомним важные свойства площадей фигур.

Равные фигуры имеют равные площади.
Иногда фигуры, имеющие равные площади, еще называют равновеликими.
Если фигура составлена из нескольких фигур, не имеющих общих внутренних точек, то ее площадь равна сумме площадей этих фигур.

Пример. Найдем площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1см times 1см.

Решение:

Найдем площадь фигуры на рисунке как сумму площадей нескольких фигур.

На рисунке это три треугольника и трапеция, указаны их площади. Тогда площадь фигуры равна 10 + 3,5 + 1,5 + 3 = 18.

Ответ: 18.

3. Отношение площадей подобных фигур равно квадрату коэффициента подобия.

Треугольники АВС и на рисунке называются подобными.

У треугольника все стороны в k раз длиннее, чем у треугольника АВС. Высота треугольника в k раз длиннее, чем высота треугольника АВС. Тогда площадь треугольника в k^2 раз больше, чем площадь треугольника АВС.

4. На рисунке показаны треугольники АВС и BCD, имеющие общую высоту. Отношение площадей этих треугольников равно отношению АС к CD:

$displaystyle frac{S_{ABC}}{S_{BCD}}=displaystyle frac{AC}{CD}$

5. Треугольники АВС и АЕС на рисунке имеют одинаковое основание и разные высоты.

Отношение площадей этих треугольников равно отношению их высот:

$displaystyle frac{S_{ABC}}{S_{AEC}}=displaystyle frac{BD}{EH}.$

6. Медиана треугольника делит его на два равновеликих, то есть равных по площади, треугольника.

На рисунке СМ — медиана треугольника АВС. Площади треугольников АСМ и ВСМ равны.

7. Три медианы треугольника делят его на шесть равных по площади треугольников.

На рисунке все 6 треугольников, из которых состоит треугольник АВС, имеют равные лощади.

Задачи ЕГЭ и ОГЭ по теме: Площади фигур.

Задача 1. Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен ${30}^circ.$

Решение:

Площадь треугольника равна половине произведения его сторон на синус угла между ними. Поэтому

$S=displaystyle frac{1}{2}cdot 8cdot 12cdot {sin 30{}^circ =displaystyle frac{1}{2}cdot 8cdot 12cdot displaystyle frac{1}{2}=24 }.$

Ответ: 24.

Задача 2. Площадь треугольника ABC равна 4, DE — средняя линия, параллельная стороне AB. Найдите площадь треугольника CDE.

Решение:

Так как DE и АВ параллельны, треугольники CDE и САВ подобны с коэффициентом подобия $displaystyle frac{1}{2}.$ Площади подобных фигур относятся как квадрат коэффициента подобия. Тогда

$S=displaystyle frac{1}{4}cdot 4=1.$

Ответ: 1.

Задача 3. У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?

Решение:

Выразим площадь двумя способами:
$S_{ABC}=displaystyle frac{1}{2}CHcdot AB=displaystyle frac{1}{2}AKcdot CB.$

Тогда $AK=displaystyle frac{CHcdot AB}{CB}=displaystyle frac{4cdot 9}{6}=6.$

Ответ: 6.

Задача 4. Площадь треугольника ABC равна 10, DE — средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED.

Решение:

Треугольник CDE подобен треугольнику CAB с коэффициентом $displaystyle frac{1}{2}.$ Площади подобных фигур относятся как квадрат коэффициента подобия, поэтому

$S_{CDE}=displaystyle frac{1}{4}cdot 10=2.5.$

Следовательно, .

Ответ: 7,5.

Задача 5. В параллелограмме ABCD AB = 3, AD = 21, ${sin A=displaystyle frac{6}{7}}$ . Найдите большую высоту параллелограмма.

Решение:

Большая высота — это DH, потому что проведена к меньшей стороне. Из треугольника АDН:

$DH=AD{sin A=21cdot displaystyle frac{6}{7}=3cdot 6=18 }.$

Ответ: 18.

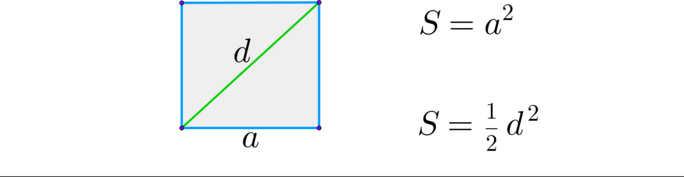
Задача 6. Найдите площадь квадрата, если его диагональ равна 1.

Решение:

Квадрат — это частный случай ромба. Площадь квадрата равна половине произведения его диагоналей. Поэтому она равна 0,5.

Ответ: 0,5.

Задача 7. Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1:2.

Решение:

Площадь прямоугольника равна произведению его длины на ширину. Периметр прямоугольника равен сумме длин всех сторон. Пусть одна из сторон прямоугольника равна a, тогда вторая равна 2a. Площадь прямоугольника равна тогда одна из сторон равна 3, а другая 6. Периметр P = 2 · 3 + 2 · 6 = 18.

Ответ: 18.

Задача 8. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.

Решение:

Площадь параллелограмма равна произведению его сторон на синус угла между ними. Площадь прямоугольника равна произведению длины на ширину. Пусть одна сторона параллелограмма и прямоугольника равна вторая равна а острый угол параллелограмма равен alpha . Тогда площадь параллелограмма равна а площадь прямоугольника равна

По условию площадь прямоугольника вдвое больше:

${S_2=2S_1} .$ Следовательно, $acdot b=2acdot bcdot {sin alpha Leftrightarrow {sin alpha }=0,5 }Leftrightarrow alpha =30{}^circ.$

Ответ: 30.

Задача 9. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.

Решение:

Площадь параллелограмма равна произведению его основания на высоту, проведенную к этому основанию. Пусть высоты равны соответственно a и b. Тогда S = 5 · a = 10 · b = 40. Поэтому a = 8, b = 4. Большая высота равна 8.

Ответ: 8.

Задача 10. Найдите площадь ромба, если его высота равна 2, а острый угол 30 ${}^circ.$

Решение:

Площадь ромба равна произведению квадрата его стороны на синус угла ромба. С другой стороны, площадь ромба равна произведению его основания на высоту, проведенную к этому основанию. Пусть сторона ромба равна

Получим уравнение:

$a^2=a{sin alpha }.$

Корень уравнения a = 4, поэтому

Ответ: 8.

Задача 11. Найдите площадь ромба, если его диагонали равны 4 и 12.

Решение:

Площадь ромба равна половине произведения его диагоналей. $S=displaystyle frac{1}{2}cdot 4cdot 12=24.$

Ответ: 24.

Задача 12. Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.

Решение:

Трапеция равнобедренная, значит,

$AH=displaystyle frac{AB-DC}{2}=6;$

$AD=displaystyle frac{P_{ABCD}-left(AB+DCright)}{2}=10.$

Тогда по теореме Пифагора из треугольника ADH:

$DH=sqrt{{AD}^2-{AH}^2}=8;$

$S=displaystyle frac{AB+CD}{2}cdot DH=20cdot 8=160.$

Ответ: 160.

Задача 13. Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 45 ${}^circ.$

Решение:

Проведем высоту CH. Треугольник CHB — прямоугольный, в нем

$angle B=45{}^circ ,$ значит, он также равнобедренный, CH = HB = 4.
$S_{ABCD}=displaystyle frac{AB+CD}{2}cdot CH=4cdot 4=16.$

Ответ: 16.

Задача 14. Высота трапеции равна 5, площадь равна 75. Найдите среднюю линию трапеции.

Решение:

Средняя линия трапеции равна полусумме оснований. Выразим её из формулы площади трапеции:
$S=displaystyle frac{a+b}{2}cdot hLeftrightarrow displaystyle frac{a+b}{2}cdot 5=75Leftrightarrow displaystyle frac{a+b}{2}=15.$

Ответ: 15.

Задача 15. Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ выразите в градусах.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту. Пусть высота равна h, тогда

$S=displaystyle frac{27+9}{2}cdot h=72.$

Из этого уравнения получим: h = 4.

Рассмотрим прямоугольный треугольник, гипотенузой которого является боковая сторона трапеции, равная 8, а катетом — высота трапеции. Длина катета равна половине гипотенузы, следовательно, он лежит напротив угла ${30}^circ.$

Ответ: 30.

Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Задача 16. Найдем площадь четырехугольника на рисунке.

Решение:

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным 5. Высоты этих треугольников равны 2 и 3. Тогда площадь четырёхугольника равна сумме площадей двух треугольников:

Ответ: 12,5.

В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Задача 17. Найдем площадь треугольника, изображенного на клетчатой бумаге.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной 5 и трёх прямоугольных треугольников. Видите их на рисунке? Получаем:

Ответ: 10,5.

Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.

Задача 18.

Найдите площадь сектора круга радиуса 1, длина дуги которого равна 2.

Решение:

На этом рисунке мы видим часть круга. Площадь всего круга равна так как R=1. Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как R = 1), а длина дуги данного сектора равна 2, следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть 360 градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

Ответ: 1.

Формула Пика

Покажем, как вычислять площадь фигуры, изображенной на координатной плоскости, с помощью формулы Пика.

Задача 19. Найдите площадь многоугольника АВСDE, изображенного на рисунке.

Первый способ:

Площадь многоугольника ABCDE равна сумме площадей треугольника BCD, трапеции BKDE и треугольника AKE.

Имеем:

$S_{vartriangle BCD}=displaystyle frac{1}{2}cdot 9cdot 2=9;$

$S_{BKDE}=displaystyle frac{1}{2}cdot (9+3)cdot 2=12;$

$S_{vartriangle AKE}=displaystyle frac{1}{2}cdot 3cdot 4=6;$

$S_{ABCDE}=9+12+6= 27.$

Второй способ — применить формулу Пика.

Назовем точку координатной плоскости целочисленной, если обе ее координаты — целые числа. На нашем рисунке это точки на пересечениях линий, разделяющих клетчатую бумагу на клетки.

Площадь многоугольника с целочисленными вершинами равна

Здесь В — количество целочисленных точек внутри многоугольника, Г — количество целочисленных точек на границе многоугольника.

Главное — аккуратно посчитать. На нашем рисунке

В = 24 (показаны зеленым),

Г = 8 (показаны красным),

S = 24 + $displaystyle frac{8}{2}$ — 1 = 27.

Ответ: 27.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Все формулы по геометрии. Площади фигур» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник