Множества егэ математика

Версия для печати и копирования в MS Word

Числовые множества

ЕГЭ по математике — экзамен чисто практический. Однако знания о том, какие бывают числа, необходимы при решении многих задач.

Первые числа, которыми люди начали пользоваться в доисторические ещё времена — это натуральные числа, то есть целые и положительные: 1, 2, 3, . . .

Натуральные числа — это числа, применяемые для счёта предметов. Натуральные числа можно использовать в качестве номеров.

Наименьшее натуральное число — единица¹. Числа 21, 249, 30988 являются натуральными. Все вместе они составляют множество натуральных чисел, обозначаемое буквой N:

N = {1, 2, 3, . . .}.

Что же такое множество? Это одно из первичных понятий математики, т. е. таких, которые лежат в основе логической системы и уже не определяются через другие понятия. Интуитивно мы понимаем, что множество — это набор или совокупность элементов, объединенных каким-либо общим признаком.

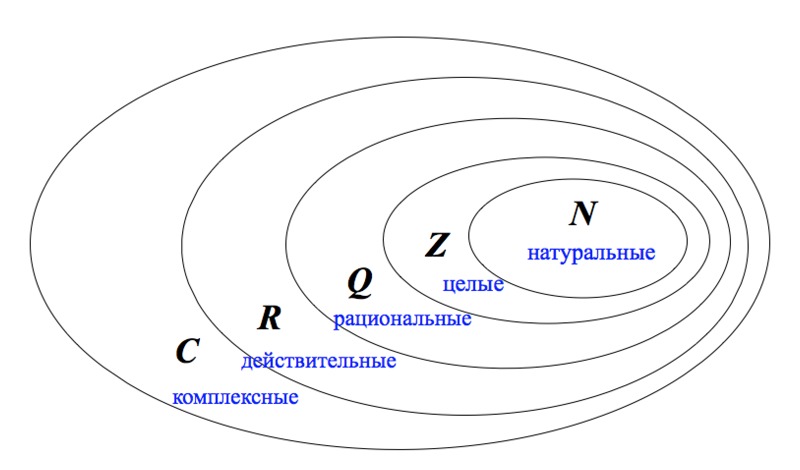
Множества обычно обозначаются заглавными буквами. Множество натуральных чисел мы можем условно изобразить вот так:

Но числа бывают не только натуральными. Индийцы изобрели число ноль и отрицательные числа. Теперь они для нас привычны, но когда-то европейцы — древние греки и римляне — долгое время обходились без нуля. Сейчас нам трудно это представить.

Натуральные числа, целые отрицательные числа и ноль вместе составляют множество целых чисел, которое обозначается Z :

Z = {0, ±1, ±2, ±3, . . .}.

Например, получая в тригонометрическом уравнении серию решений, мы пишем: n ∈ Z, и это означает, что n — целое число.

Очевидно, множество целых чисел включает в себя множество натуральных:

Кроме целых чисел, однако, имеются ещё и дроби.

Напомним, что дробь — это часть, доля, выражение вида (где p — целое, а q — натуральное). Например, — это «одна часть из трёх», 0,25 — это двадцать пять сотых. Десятичные дроби также можно записать в виде . Например, . А если вы вдруг забыли, как десятичную дробь перевести в обыкновенную, как складывать и умножать дроби или как их сокращать — срочно обращайтесь к нам за консультацией! Без этих простейших навыков готовиться к ЕГЭ будет крайне сложно.

Целые числа (положительные и отрицательные) также можно записать в виде . Например, в виде дроби со знаменателем 1:

Стало быть, целые числа — частный случай дробей.

Числа, которые можно записать в виде дроби , называются рациональными. Множество рациональных чисел обозначается Q. Ясно, что оно включает в себя множество целых чисел.

Хорошо, но любое ли число можно записать в виде дроби ? Иными словами, все ли числа являются рациональными?

Долгое время — в античности — считалось, что любое число можно записать в виде дроби с числителем и знаменателем. Дело в том, что для древних греков числа и их соотношения были почти священны. Пифагорейцы говорили: «Числа правят миром». Они верили, что все основные принципы мироздания можно выразить языком математики, что соотношения чисел выражают гармонию, закон и порядок природы, перед которым склоняют голову даже олимпийские боги. Греческое искусство, особенно архитектура, подчинялось правилам, канонам. Греки точно установили, какими должны быть пропорции в архитектуре — например, отношение диаметра колонны к её длине — чтобы здание было гармоничным. И все эти пропорции были отношениями целых чисел.

Однако в стройной и гармоничной системе божественных пропорций наметилась досадная брешь. Оказалось, что отношение диагонали квадрата к его стороне не выражается отношением целых чисел! Другими словами, если мы нарисуем квадрат со стороной 1, его диагональ не выражается никакой дробью вида .

По теореме Пифагора диагональ такого квадрата равна — то есть положительному числу, квадрат которого равен двум. Можно доказать, что это число не является рациональным. Но сами пифагорейцы не сразу смоги смириться с тем, что невозможно записать в виде — ведь это наносило удар всей их философской системе!

Открытие долго держалось в тайне, пока наконец ученик Пифагора Гиппас не разгласил его. За это Гиппас был изгнан из школы Пифагора и вскоре погиб во время кораблекрушения, в чём современники увидели несомненное возмездие богов. А числа, которые невозможно записать в виде , такие, как , назвали иррациональными, то есть не-разумными, неправильными.

Но иррациональные числа ничуть не хуже рациональных! Они отнюдь не ограничиваются выражениями вида или . К ним относятся также:

Ещё раз повторим, в чём разница между рациональными и иррациональными числами.

Рациональное число можно представить в виде дроби — например, , . А если мы просто поделим в столбик 7 на 11, мы обнаружим интересную закономерность:

7 : 11 = 0,636363636363…

Мы видим, что цифры повторяются, то есть дробь является периодической. Таким образом, любое рациональное число можно записать десятичной дробью — конечной или бесконечной периодической.

А вот в числе цифры не заканчиваются, и никакой периодичности их следования не наблюдается. Иррациональные числа — это бесконечные непериодические дроби.

Вместе оба множества — рациональных и иррациональных чисел — образуют множество действительных (или вещественных) чисел, которое обозначается R (от слова real).

Возникает вопрос: это всё? Все ли числа, какие только могут быть, содержатся в множестве действительных чисел? Или за его пределами ещё что-то есть?

Для успешной сдачи ЕГЭ других чисел не нужно. Да и, казалось бы, мы назвали все возможные числа. Но вот какой парадокс: положительные и отрицательные числа симметрично расположены на числовой прямой, верно? И при этом из положительных чисел можно извлечь квадратный корень, а из отрицательных — нельзя! Не существует действительного числа, которое при возведении в квадрат даёт −1.

Оказывается, однако, что существует числовое множество, содержащее в себе множество R и бесконечное множество других чисел, не являющихся действительными. В этом множестве находится мнимая единица i, для которой верно i² = −1. И называется оно множеством комплексных чисел.

Комплексные числа служат естественным языком описания многих физических явлений. Те из вас, кто выбрал инженерную специальность (в особенности связанную с распространением волн, электротехникой и радиофизикой), непременно встретятся с ними. В отличие от действительных («вещественных») чисел, применяемых для описания материального, плотного мира «вещей», комплексные числа оказываются удобным инструментом для построения математических моделей волн и колебаний всевозможной природы.

Ну а будущим физикам наверняка интересно будет узнать, что элементарные частицы живут и взаимодействуют по законам именно комплексных чисел. Наукой, описывающей комплексный микромир, является квантовая физика.

---

¹ В школьной математике ноль не является натуральным числом. Мы ведь не используем его для счёта предметов. Ну какой здравомыслящий человек скажет: «На столе стоит ноль чашек»?

07
Май 2013

Категория: Справочные материалы

Числовые множества

2013-05-07
2019-08-13

Автор: egeMax |

комментария 2

Задачи повышенной сложности

Числовые множества

1. Натуральные числа – числа, которые мы используем для счета предметов, счёт начинается с единицы, поэтому ноль не является натуральным числом. Множество натуральных чисел обозначается $N$.

2. Целые числа – это ноль и «плюс – минус натуральные числа». Множество целых чисел обозначается $Z$.

3. Рациональные числа – это всевозможные дроби ${m}/{n}$, где $m$ — целое число, а $n$ – натуральное число, т.е. $n≠0$. Множество рациональных чисел обозначается $Q$.

Делимость

Число $а$ делится на число $с≠0$, если найдется такое число $b$, что $a=c·b$.

Если число $а$ делится на $с$, то число с называется делителем числа $а$.

Если числа $а$ и $b$ делятся на $с$, то их сумма $а + b$ тоже делится на $с$.

Признаки делимости:

Признак делимости на $2$

Число делится на $2$ тогда и только тогда, когда его последняя цифра ноль или делится на $2$, то есть является чётной.

Признак делимости на $3$

Число делится на $3$ тогда и только тогда, когда сумма его цифр делится на 3.

Признак делимости на $4$

Число делится на $4$ тогда и только тогда, когда число из двух последних его цифр нули или делится на $4$.

Признак делимости на $5$

Число делится на $5$ тогда и только тогда, когда последняя цифра делится на $5$ (то есть равна $0$ или $5$).

Признак делимости на $6$

Число делится на $6$ тогда и только тогда, когда оно делится на $2$ и на $3$.

Признак делимости на $7$

Число делится на $7$ тогда и только тогда, когда результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на $7$ (например, $217$ делится на $7$, так как $21 — (2 · 7) = 7$ делится на $7$).

Признак делимости на $8$

Число делится на $8$ тогда и только тогда, когда три его последние цифры — нули или образуют число, которое делится на $8$.

Признак делимости на $9$

Число делится на $9$ тогда и только тогда, когда сумма его цифр делится на $9$.

Признак делимости на $10$

Число делится на $10$ тогда и только тогда, когда оно оканчивается на ноль.

Признак делимости на $11$

Число делится на $11$ тогда и только тогда, когда сумма цифр с чередующимися знаками делится на $11$ (то есть $182919$ делится на $11$, так как $1 — 8 + 2 — 9 + 1 — 9 = -22$ делится на $11$). Следствие факта, что все числа вида $10^n$ при делении на $11$ дают в остатке $(-1)^n$.

Признак делимости на $12$

Число делится на $12$ тогда и только тогда, когда оно делится на $3$ и на $4$.

Признак делимости на $13$

Число делится на $13$ тогда и только тогда, когда число его десятков, сложенное с учетверённым числом единиц, кратно $13$ (например, $949$ делится на $13$, так как $94 + (4 · 9) = 130$ делится на $13$).

Признак делимости на $14$

Число делится на $14$ тогда и только тогда, когда оно делится на $2$ и на $7$.

Признак делимости на $15$

Число делится на $15$ тогда и только тогда, когда оно делится на $3$ и на $5.$

Признак делимости на $17$

Число делится на $17$ тогда и только тогда, когда разность между числом его десятков и упятеренным числом единиц, кратно $17.$

Признак делимости на $19$

Число делится на $19$ тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, кратно $19$ (например, $646$ делится на $19$, так как $64 + (6 · 2) = 76$ делится на $19$).

Четность и нечетность чисел

1. Число называется четным, если оно делится нацело на $2$. Если $а$ четное число, то его вид можно записать $a=2n$.
2. Число называется нечетным, если оно не делится нацело на $2$. Если $а$ нечетное число, то его вид можно записать $a=2n+1$.
3. Сумма любого количества четных слагаемых четна.
4. Сумма четного количества нечетных слагаемых – четное число.
5. Сумма нечетного количества нечетных слагаемых – нечетное число.
6. Если в произведении все множители нечетные числа, то произведение – нечетное число.
7. Если в произведении попадется хотя бы одно четное число, то в результате умножения получится четное число.

Простые и взаимно простые числа

Простые числа – это целые числа, большие единицы, которые имеют только два положительных делителя, а именно самих себя и $1$.

Взаимно простые числа – это числа, которые не имеют общих делителей, кроме единицы. Например, числа $15$ и $4$ взаимно просты, так как их общий делитель равен $1$.

Свойства взаимно простых чисел.

Пусть $а$ и $b$ – взаимно простые числа, тогда для них справедливы следующие высказывания.

1. Если некоторое число делится на $а$ и $b$, то оно делится и на их произведение $аb$.
2. Если произведение $ас$ делится на $b$, то с делится на $b$.
3. Если целые числа $а$ и $b$ взаимно просты, то их сумма $(а + b)$ и произведение $(а·b)$ так же являются взаимно простыми числами.
4. Если целые числа $а$ и $b$ взаимно просты, то НОД (наименьший общий делитель) из суммы $(а + b)$ или разности ($а — b$) равен $1$ или $2$.
5. Любые два последовательных натуральных числа взаимно просты.
6. Если целые числа $а$ и $b$ взаимно просты, то НОД $(а + b$ или $a^2-ab+b^2)$ равен $1$ или $3$.

Числовые свойства степеней

1. Точный квадрат целого числа не может оканчиваться цифрами $2, 3, 7, 8,$ а также нечётным количеством нулей.
2. Квадрат натурального числа либо делится на $4$, либо при делении на $8$ даёт остаток $1$.
3. Квадрат натурального числа либо делится на $9$, либо при делении на $3$ даёт остаток $1$.
4. Разность квадратов двух целых чисел одинаковой четности делится на $4$.
5. При делении на $3$ куб целого числа и само число дают одинаковые остатки $(0,1,2)$.
6. При делении на $9$ куб целого числа дает в остатке $0,1$ или $8$.
7. При делении на $4$ куб целого числа дает в остатке $0,1$ или $3$.
8. Число $m^5$ оканчивается на ту же цифру, что и число $m$.

Среднее арифметическое чисел

Среднее арифметическое нескольких величин — это отношение суммы величин к их количеству.

Чтобы вычислить среднее арифметическое нескольких чисел, нужно взять сумму этих чисел и разделить все на количество слагаемых. Частное и будет средним арифметическим этих чисел.

Среднее геометрическое чисел

Чтобы найти среднее геометрическое чисел надо:

1. Перемножить все числа
2. Из полученного выражения в п.1 надо извлечь корень, степени, равной количеству элементов ряда.

Факториал

Факториал числа — это произведение натуральных чисел от $1$ до самого числа (включая данное число). Обозначается знаком (!).

$n!=1·2·3·….·n$

Факториал нуля равен единице $0!=1$

Последовательности

Последовательность чисел – это набор чисел, в котором каждому числу можно присвоить некоторый номер, причем каждому номеру соответствует единственное число данного набора. Номер числа – это всегда натуральное число, нумерация номеров начинается с единицы. Число с номером $n$ (то есть $n$ — ый член последовательности) обычно обозначается $a_n$.

Большинство последовательностей можно задать аналитическим способом.

Последовательность задана аналитически, если указана формула ее $n$ – го члена. Например, $a_n=4n+3$. В данной формуле указав конкретное число $n$, нетрудно найти член последовательности с соответствующим номером. Если номер $n=5$, то подставим $5$ в формулу последовательности, получим числовое выражение, вычислив которое получим член последовательности с соответствующим номером. $a_5=4·5+3=23$

Прогрессии

Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.

$а_1$ — первый член арифметической прогрессии

$d$ — разность между последующим и предыдущим членом прогрессии

$d=a_(n+1)-a_n$

$a_n$ — член арифметической прогрессии, стоящий на $n$-ом месте

$n$ — номер места для членов арифметической прогрессии

$S_n$ — сумма первых n членов арифметической прогрессии

Формула, для нахождения n-ого члена прогрессии:

$a_n=a_1+d(n-1)$

Формула суммы первых n членов арифметической прогрессии:

$S_n={(a_1+a_n)·n}/{2}$

Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.

$b_1$ — первый член геометрической прогрессии

$q$ — знаменатель геометрической прогрессии, показывает во сколько раз последующее число больше предыдущего.

$q={b_{n+1}}/{b_n}$

$b_n$ — $n$-ый член геометрической прогрессии

$S_n$ — сумма первых $n$ членов геометрической прогрессии

Формула, для нахождения $n$-ого члена прогрессии:

$b_n=b_1·q^{n-1}$

Формула суммы первых n членов арифметической прогрессии:

$S_n={b_1·(q^n-1)}/{q-1},q≠1$

Задача 19 на ЕГЭ по математике

Содержание

1 Необходимая теория 2

1.1 Числовые множества ………………………………………..………………..2

1.2 Делимость ……………………………………………………………………2

1.3 Чётность ………………………………………………………………………3

1.4 Деление с остатком …………………………………………………………..3

1.5 Каноническое разложение……………………………………………………4

1.6 Взаимно простые числа ………………………………………………………5

1.7 Последовательности …………………………………………………………5

1.8 Арифметическая прогрессия ………………………………………………..6

1.9 Геометрическая прогрессия ………………………………………………….7

1.10 Метод «оценка плюс пример» ……………………………………………..8

2 Задачи 10

3 Ответы 12

4 Решения 13

Известно, что на ЕГЭ по математике многие школьники не приступают к задаче 19 и даже не читают её (а зачем? — всё равно, мол, не решу). И очень напрасно!

Как правило, задача 19 состоит из двух или трёх пунктов, среди которых есть совсем несложные. За всю задачу даётся 4 первичных балла, по 1-2 балла за каждый пункт. Поэтому, сделав хотя бы часть задачи (скажем, просто предъявив нужный пример в одном из пунктов), можно получить себе в копилку дополнительные первичные баллы. А они дадут прирост итогового результата по стобалльной шкале!

Для решения задачи 19 необходим минимальный запас знаний. Это арифметика 6-го класса (всё, что связано с делимостью) и сведения по прогрессиям из алгебры 9-го класса. Больше ничего.

Почему же задача 19 считается (и, в общем-то, является) самой сложной на ЕГЭ по математике? Она нестандартна. Она требует так называемой математической культуры — умения грамотно строить рассуждения. А умение это у подавляющего большинства школьников отсутствует начисто — ведь в школе, к сожалению, до развития математической культуры дело обычно не доходит.

Учиться культурно рассуждать можно и обязательно нужно. Задача 19 предоставляет для этого отличную возможность. Получаться начнёт далеко не сразу, так что готовиться к 19 следует начинать задолго до ЕГЭ. Рецепт тут один: решать, решать и решать.

1 Необходимая теория

1.1 Числовые множества

В данном разделе мы определим числовые множества, необходимые для задачи 19. Введённую терминологию нужно твёрдо знать!

Натуральные числа — это числа 1, 2, 3, . . . Натуральные числа мы используем для счёта, а счёт начинается с единицы. Множество натуральных чисел обозначается N.

Целые числа — это числа 0, ±1, ±2, ±3, . . . Таким образом, целые числа — это нуль и «плюс-минус натуральные». Натуральные числа являются целыми положительными числами. Множество целых чисел обозначается Z.

Рациональные числа — это всевозможные дроби с целыми m и n (при этом, конечно, ; чтобы избежать данной оговорки, говорят также, что m — целое, а n — натуральное). Любое целое число является в то же время рациональным (например, ). Однако число не является целым. Множество рациональных чисел обозначается Q.

1.2 Делимость

Понятие делимости относится к целым числам (в частности, к натуральным). Начиная с этого момента все числа считаются целыми. Если в каком-то случае это окажется не так, мы сделаем специальную оговорку.

Целые числа мы обозначаем a, b, c, . . . , k, l, m, n, . . . , x, y, z, то есть используем все строчные буквы латинского алфавита.

Вы прекрасно знаете, что число 12 делится на 4, но не делится на 5. Каково формальное определение делимости? Вот оно.

Определение. Число a делится на , если найдётся число c такое, что .

Если a делится на b, то число b называется делителем числа a. Например, число 12 имеет шесть делителей: это 1, 2, 3, 4, 6 и 12.

Упражнение. Докажите, что если числа a и b делятся на c, то a + b делится на c.

Т.к. . Значит,

Сформулируем наиболее важные признаки делимости.

• a делится на 2 ⇔ последняя цифра числа a чётная;

• a делится на 3 ⇔ сумма цифр числа a делится на 3;

• a делится на 4 ⇔ последние две цифры числа а составляют число, которое делится на 4;

• a делится на 5 ⇔ последняя цифра числа a есть 0 или 5;

• a делится на 6 ⇔ число а делится и на 2, и на 3;

• a делится на 7 ⇔ результат вычитания удвоенной последней цифры из числа а без последней цифры делится 7 (напр., 343 делится на 7, т.к. делится на 7);

• a делится на 8 ⇔ последние три цифры числа а составляют число, которое делится на 8;

• a делится на 9 ⇔ сумма цифр числа a делится на 9;

• a делится на 10 ⇔ последняя цифра числа a равна 0;

• a делится на 11 ⇔ сумма цифр в записи числа а, стоящих на чётных местах равна сумме цифр, стоящих на нечётных местах, или отличается от неё на 11 (напр., 2673 делится на 11, т.к. 2+7=6+3; 1529 делится на 11, т.к. 1+2=3, 5+9=14, 14-3=11);

• a делится на 13 ⇔ число его десятков, сложенное с учетверённым числом единиц этого числа делится на 13 (напр., 533 делится на 13, т.к. делится на 13).

• a делится на 13 ⇔ если разность этого числа без его последней цифры и его последней цифры, умноженной на 5, делится на 17 (напр., 1564 делится на 17, т.к. делится на 17);

• a делится на 19 ⇔ если сумма этого числа без его последней цифры и его последней цифры, умноженной на 2, делится на 19 (напр., 1653 делится на 19, т.к. делится на 19).

1.3 Чётность

Соображения, связанные с чётностью или нечётностью, часто фигурируют в задачах 19. Поэтому необходимые факты имеет смысл отметить особо. Определение. Число называется чётным, если оно делится на 2. Число называется нечётным, если оно не делится на 2.

Вот все чётные числа: 0, ±2, ±4, ±6, . . . Если a чётно, то оно имеет вид . А вот все нечётные числа: ±1, ±3, ±5, . . . Ясно, что если a нечётно, то оно имеет вид .

Следующие утверждения весьма очевидны, и вы можете использовать их при решении задачи 19 (никто от вас не потребует их доказательства). Но вы можете доказать их в качестве упражнения.

• Сумма любого числа чётных слагаемых чётна.

• Сумма чётного числа нечётных слагаемых чётна. Сумма нечётного числа нечётных слагаемых нечётна.

• Пусть имеется произведение нескольких множителей. Если все множители нечётны, то произведение нечётно. Если хотя бы один множитель чётный, то произведение чётно.

1.4 Деление с остатком

Число 13 не делится на 5. Наибольшее число, которое делится на 5 и не превосходит 13, равно 10 = 5·2. Таким образом, 13 = 5·2+3, и мы скажем, что в результате деления 13 на 5 получается частное 2 и остаток 3. Оказывается, любое число a можно разделить с остатком на любое число . А именно, найдутся два числа q и r такие, что , и при этом будет выполнено неравенство |. Число q называется частным, а число r — остатком от деления a на b.

Если r = 0, то есть , то a делится на b.

Упражнение. Найдите частное и остаток от деления: а) 7 на 2; б) 15 на 4; в) 2012 на 5; г) 1001 на 13; д) 9 на 8; е) 8 на 9.

Остаток от деления любого нечётного числа на 2 равен единице. Вот почему всякое нечётное число может быть записано в виде 2n + 1. Остатки оказываются полезными во многих ситуациях. Допустим, в ходе решения задачи вам нужно доказать, что равенство не может выполняться ни при каких целых числах n и k. Рассуждаем следующим образом.

Число n при делении на 3 может давать остатки 0, 1 или 2. Иными словами, возможны три случая: или . Какие остатки при делении на 3 будут у числа ? Давайте посмотрим, что получается в каждом из трёх случаев.

(остаток 0); (остаток 1); (остаток 1). Таким образом, квадрат целого числа при делении на 3 не может давать остаток 2. Следовательно, равенство действительно невозможно ни при каких n и k.

Упражнение. Докажите, что число 100 . . . 004 (между 1 и 4 стоит любое число нулей) не является квадратом целого числа.

Упражнение. Докажите, что квадрат целого числа при делении на 4 может давать только два остатка: 0 и 1.

Упражнение. Докажите, что делится на 3.

1.5 Каноническое разложение

Всякое число делится на 1 и на само себя. Если натуральное число p не равно 1 и не имеет других натуральных делителей, кроме 1 и p, то такое число p называется простым.

Вот первые несколько простых чисел: 2, 3, 5, 7, 11, 13, 17, 19. Число 2 — единственное чётное простое число.

Число, не равное 1 и не являющееся простым, называется составным. Например, 15 — составное число (оно делится на 3). Число 1036 — тоже составное (оно чётное). Единица не является ни простым числом, ни составным.

Упражнение. Число является составным. Почему?

Оказывается, всякое число можно разложить на простые множители. Например:

.

Такое разложение единственно с точностью до порядка множителей и называется каноническим разложением. Утверждение о существовании и единственности канонического разложения носит название основной теоремы арифметики.

Каноническое разложение даёт полную картину делителей данного числа (и, в частности, позволяет найти их количество). Именно, пусть — каноническое разложение числа a. Тогда каноническое разложение любого делителя числа a состоит из простых множителей, входящих в набор показатели степени которых не превосходят соответственно чисел . Например, любой делитель числа имеет вид , где

Отвечаем на вопрос упражнения: является составным числом, т.к. при умножении нескольких раз числа 3 мы получим число, в конце которого стоит цифра 9, 7, 1 или 3. При вычитании из каждой из них единицы, всегда получаем чётное число, а, значит, всё число делится на 2, т.е. является составным.

Упражнение. Пусть p — простое число. Сколько делителей у числа: а) ; б) ;

в) ?

Упражнение. Пусть p и q — простые числа. Сколько делителей у числа: а) ; б); в) ?

Упражнение. Обобщив рассуждения пункта в) предыдущего упражнения, покажите, что количество делителей числа равно Найдите, сколько делителей имеет число 504.

Упражнение. Найдите канонические разложения чисел 540 и 252. С помощью полученных разложений найдите НОД (540, 252) — наибольший общий делитель этих чисел.

1.6 Взаимно простые числа

Числа называются взаимно простыми, если они не имеют общих делителей кроме 1. Иными словами, числа a и b взаимно простые, если НОД (a, b) = 1. Можно сказать и так: числа a и b взаимно простые тогда и только тогда, когда дробь несократима.

Например, числа 8 и 15 взаимно простые. Числа 9 и 15 не являются взаимно простыми — у них имеется общий делитель 3. Числа взаимно простые тогда и только тогда, когда их канонические разложения состоят из непересекающихся наборов простых чисел. Например, числа и являются взаимно простыми.

Свойства взаимно простых чисел. Пусть числа a и b взаимно просты. Тогда справедливы следующие утверждения.

1. Если некоторое число делится на a и b, то оно делится и на их произведение ab.

2. Если an делится на b, то n делится на b. (Вы легко поймёте, почему так получается, если представите себе «непересекающиеся» канонические разложения чисел a и b и вдобавок вспомните, что каноническое разложение делителя служит «частью» канонического разложения делимого числа).

Согласно утверждению 1, например, если некоторое число делится на 8 и на 15, то оно делится на 8 · 15 = 120. То, что числа взаимно простые, — важное условие. Так, 12 делится на 4 и на 6, но не делится на 4 · 6 = 24.

Упражнение. Какие цифры можно вставить вместо звёздочек в записи 35∗4∗, чтобы полученное пятизначное число делилось на 45?

Утверждение 2 обычно работает в ситуациях типа следующей. Пусть, например, 5n = 9m. Так как 5n делится на 9 и числа 5 и 9 взаимно простые, то n делится на 9. По той же самой причине m делится на 5.

1.7 Последовательности

Что такое последовательность? Представьте себе устройство, которое с некоторыми интервалами выдаёт одно число за другим. Например: 2, −3, 15, 28, −6, 0, 3, . . . Набор чисел на выходе этого устройства и будет последовательностью. Более строго, последовательность чисел, или числовая последовательность — это набор чисел, в котором каждому числу можно присвоить некоторый номер, причём каждому номеру отвечает единственное число данного набора. Номер — это натуральное число; нумерация начинается с единицы. Так, в приведённой выше последовательности первый номер имеет число 2 (это первый член последовательности), а номер пять — число −6 (это пятый член последовательности). Число с номером n (то есть n-й член последовательности) обозначается (или , , . . . ). Весьма удобно, когда n-й член последовательности можно задать некоторой формулой. Например, формула

задаёт последовательность: −1, 1, 3, 5, 7, . . . Формула задаёт последовательность: −1, 1, −1, 1, . . .

Упражнение. Придумайте формулу n-го члена для следующих последовательностей: а) 1, 3, 5, 7, . . . ; б) 5, 8, 11, 14, . . . ; в) 1, 4, 9, 16, . . . ; г) 1, −2, 3, −4, . . .

Все рассмотренные нами последовательности являются бесконечными, то есть содержащими бесконечное множество чисел. Но бывают и конечные последовательности. Собственно, любой конечный набор чисел является конечной последовательностью. Например, конечная последовательность 1, 2, 3, 4, 5 состоит из пяти чисел.

В задаче 19 нужны два специальных вида последовательностей: арифметическая и геометрическая прогрессии.

1.8 Арифметическая прогрессия

Арифметическая прогрессия — это последовательность, каждый член которой (начиная со второго) равен сумме предыдущего члена и некоторого фиксированного числа:

Фиксированное число d называется разностью арифметической прогрессии.

Например, последовательность 2, 5, 8, 11, . . . является арифметической прогрессией с первым членом 2 и разностью 3.

Нетрудно получить формулу n-го члена арифметической прогрессии. Пишем:

,

,

и становится ясно, что формула для имеет вид:

Упражнение. Сколько имеется трёхзначных чисел, делящихся на 13?

Нужно знать формулу суммы первых n членов арифметической прогрессии. Она имеет вид:

.

Полезная модификация этой формулы получается, если в неё подставить формулу n-го члена:

.

Свойство арифметической прогрессии. Если числа a, b, c образуют арифметическую прогрессию, то 2b = a + c.

Упражнение. Докажите это свойство.

1.9 Геометрическая прогрессия

Геометрическая прогрессия — это последовательность, каждый член которой (начиная со второго) равен произведению предыдущего члена и некоторого фиксированного числа:

Фиксированное число q называется знаменателем геометрической прогрессии.

Например, последовательность 2, 6, 18, 54, . . . является геометрической прогрессией с первым членом 2 и знаменателем 3. Получим формулу n-го члена геометрической прогрессии. Пишем:

и в результате имеем:

Для суммы первых n членов геометрической прогрессии нужно знать следующую формулу:

Свойство геометрической прогрессии. Пусть числа a, b, c образуют геометрическую прогрессию. Тогда .

Упражнение. Докажите это свойство.

Важное замечание: в конечной геометрической прогрессии, состоящей из целых чисел, знаменатель q может не быть целым числом! Вот пример: числа 4, 6, 9 образуют геометрическую прогрессию со знаменателем .

Упражнение. Между числами 27 и 64 вставьте два числа так, чтобы получилась геометрическая прогрессия.

Иметь дело с рациональным знаменателем не очень удобно. К счастью, это и не нужно. Дело в том, что для конечной геометрической прогрессии, состоящей из целых чисел, существует несколько иное представление, хорошо приспособленное именно для задач 19.

Представление конечной целочисленной геометрической прогрессии.

• Геометрическая прогрессия из трёх целых чисел имеет вид:

— целые).

• Геометрическая прогрессия из четырёх целых чисел имеет вид:

• Геометрическая прогрессия из пяти целых чисел имеет вид:

.

Вообще, пусть — целые числа, образующие геометрическую прогрессию. Тогда найдутся целые числа k, a, b такие, что

.

Доказательство. Докажем общий случай. Пусть знаменатель прогрессии

равен q. Очевидно, q — число рациональное (иначе прогрессия не была бы целочисленной). Запишем q в виде несократимой дроби: . Имеем:

.

Поскольку a и b взаимно простые и — целое, число должно делиться на . Иными словами, найдётся целое k такое, что . Далее. последовательно получаем:

,

что и требовалось.

1.10 Метод «оценка плюс пример»

«Оценка плюс пример» — это специальное математическое рассуждение, которое применяется в некоторых задачах при нахождении наибольших или наименьших значений.

Суть метода состоит в следующем. Предположим, что мы ищем наименьшее значение некоторой величины A. Действуем в два этапа.

1. Оценка. Показываем, что выполнено неравенство .

2. Пример. Предъявляем пример, когда достигается равенство .

Тем самым доказано, что наименьшее значение A равно α.

Мы проиллюстрируем данный метод на трёх задачах, расположенных по возрастанию сложности.

1. Найти наименьшее значение функции .

Решение. Выделим полный квадрат: Поскольку квадрат неотрицателен, получаем оценку: . Приводим пример, когда равенство достигается: . Следовательно, искомое наименьшее значение равно 2.

2. Натуральные числа от 1 до 10 разбили на две группы так, что произведение чисел в первой группе делится на произведение чисел во второй группе. Какое наименьшее значение может принимать частное от деления первого произведения на второе?

Решение. Число 7 должно быть в первой группе, поскольку оно простое и никакое другое число на него не делится. Следовательно, частное не меньше 7 (оценка). Приведём пример разбиения, при котором частное равно 7. Первая группа: 1, 2, 3, 4, 5, 6, 7; вторая группа: 8, 9, 10. В таком случае

.

Следовательно, наименьшее значение частного равно 7.

Хорошо, но откуда взялся пример? Возникает ощущение, что он с неба свалился. В общем-то, для читающего вашу работу так оно и должно быть. Запомните: при записи решения вы не обязаны объяснять, каким образом вы додумались до примера. Просто предъявляете пример, и всё! Угадали вы его, почувствовали или получили свой пример логическим путём — это абсолютно никого не касается. Мы, тем не менее, будем по возможности озвучивать те мысли, которые позволяют нужный пример сконструировать. Оформляться это будет следующим образом.

►В данном случае нам захотелось разбить числа 1, 2, 3, 4, 5, 6, 8, 9, 10 на две группы с равными произведениями. Для этого находим каноническое разложение произведения всех этих чисел: . Как видим, оно является квадратом числа . Остаётся лишь найти числа, произведение которых равно 720. Это, например, 8, 9, и 10.◄

3. Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 13 раз больше, либо в 13 раз меньше предыдущего. Сумма всех членов последовательности равна 6075.

а) Может ли последовательность состоять из двух членов?

б) Может ли последовательность состоять из трёх членов?

в) Какое наибольшее количество членов может быть в последовательности? Решение. а) Предположим, что в последовательности два члена. Тогда она имеет вид: a, 13a (или наоборот: 13a, a). Согласно условию получаем: 14a = 6075. Это невозможно, так как слева стоит чётное число, а справа — нечётное. Следовательно, последовательность не может состоять из двух членов.

б) Да, может. Пример: 405, 5265, 405.

►Данный пример строится легко. Ищем последовательность вида a, 13a, a. Получаем: 15a = 6075, откуда находим a = 405.◄

в) Прежде чем записывать решение, начнём с некоторых неформальных соображений.

►Ясно, что чисел в последовательности будет тем больше, чем меньше сами числа. Поэтому надо по максимуму использовать 1 и 13, чередуя их. Попробуем так и начать: 1, 13, 1, 13, . . . Последовательность состоит из идущих друг за другом пар (1, 13); сумма в каждой паре равна 14. Какое число будет последним? Очевидно, 13 в конце оказаться не может — тогда сумма всех членов последовательности будет делиться на 14, а 6075 — число нечётное. Остаётся проверить единицу. Делим 6075 на 14 с остатком и получаем: 6075 = 14 · 433 + 13. Значит, и единицы в конце быть не может. Наша попытка потерпела неудачу, но результат деления с остатком подсказывает, что нужно сделать. Изменим чередование: 13, 1, 13, 1, . . . Тогда после 433 пар (13, 1) мы сможем завершить последовательность числом 13. Таким образом, нам удалось обойтись только числами 1 и 13, и возникает ощущение, что это и есть наиболее длинная последовательность. Вот теперь переходим к записи решения.◄

Заметим, что в последовательности может оказаться 867 членов. Пример:

.

Действительно, 433 · (13 + 1) + 13 = 6075.

Покажем, что большего числа членов быть не может. Предположим обратное: наша последовательность , . . . содержит не менее 868 членов. Разобьём их последовательно на пары: . . . Сумма чисел в каждой паре как минимум 14, а самих пар не менее 434. Сумма всех членов получится тогда не менее 14 · 434 = 6076, что противоречит условию. Значит, в последовательности может быть самое большее 867 членов.

2 Задачи

Задача 1. Перед каждым из чисел 6, 7, . . . , 11 и 9, 10, . . . , 17 произвольным образом ставят знак плюс или минус, после чего к каждому из образовавшихся чисел первого набора прибавляют каждое из образовавшихся чисел второго набора, а затем все 54 полученных результата складывают. Какую наименьшую по модулю сумму и какую наибольшую сумму можно получить в итоге?

Задача 2. На доске написано более 42, но менее 54 целых чисел. Среднее арифметическое этих чисел равно −7, среднее арифметическое всех положительных из них равно 6, а среднее арифметическое всех отрицательных из них равно −12.

а) Сколько чисел написано на доске?

б) Каких чисел больше: положительных или отрицательных?

в) Какое наибольшее количество положительных чисел может быть среди них?

Задача 3. Набор состоит из 33 натуральных чисел, среди которых есть числа 3, 4 и 5. Среднее арифметическое любых 27 чисел этого набора меньше 2.

а) Может ли такой набор содержать ровно 13 единиц?

б) Может ли такой набор содержать менее 13 единиц?

в) Док-те, что в любом таком наборе есть несколько чисел, сумма которых равна 28.

Задача 4. Бесконечная арифметическая прогрессия, состоящая из различных натуральных чисел, первый член которой меньше 10, не содержит ни одного числа вида . Какое наименьшее значение может принимать сумма первых 10 членов этой прогрессии?

Задача 5. Можно ли привести пример пяти различных натуральных чисел, произведение которых равно 1512 и

а) пять;

б) четыре;

в) три

из них образуют геометрическую прогрессию?

Задача 6. Все члены геометрической прогрессии — различные натуральные числа, заключённые между числами 210 и 350.

а) Может ли такая прогрессия состоять из четырёх членов?

б) Может ли такая прогрессия состоять из пяти членов?

Задача 7. В возрастающей последовательности натуральных чисел каждые три последовательных члена образуют либо арифметическую, либо геометрическую прогрессию. Первый член последовательности равен 1, а последний 2046.

а) Может ли в последовательности быть три члена?

б) Может ли в последовательности быть четыре члена?

в) Может ли в последовательности быть меньше 2046 членов?

Задача 8. Дана последовательность натуральных чисел, причём каждый следующий член отличается от предыдущего либо на 10, либо в 7 раз. Сумма всех членов последовательности равна 163.

а) Какое наименьшее число членов может быть в этой последовательности?

б) Какое наибольшее число членов может быть в этой последовательности?

Задача 9. Каждое из чисел 1, −2, −3, 4, −5, 7, −8, 9, 10, −11 по одному записывают на 10 карточках. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел 1, −2, −3, 4, −5, 7, −8, 9, 10, −11. После этого числа на каждой карточке складывают, а полученные 10 сумм перемножают.

а) Может ли в результате получиться 0?

б) Может ли в результате получиться 1?

в) Какое наименьшее целое неотрицательное число может в результате получиться?

Задача 10. Каждый из группы учащихся сходил в кино или в театр, при этом возможно, что кто-то из них мог сходить и в кино, и в театр. Известно, что в театре мальчиков было не более от общего числа уч-ся группы, посетивших театр, а в кино мальчиков было не более от общего числа уч-ся группы, посетивших кино.

а) Могло ли быть в группе 10 мальчиков, если дополнительно известно, что всего в группе было 20 учащихся?

б) Какое наибольшее количество мальчиков могло быть в группе, если дополнительно известно, что всего в группе было 20 учащихся?

в) Какую наименьшую долю могли составлять девочки от общего числа учащихся в группе без дополнительного условия пунктов а) и б)?

Задача 11. Имеется 33 коробки массой 19 кг каждая и 27 коробок массой 49 кг каждая. Все эти коробки раскладываются по двум контейнерам. Пусть — модуль разности суммарных масс коробок в контейнерах. Найдите наименьшее значение :

а) если дополнительно требуется, что в контейнерах должно находиться одинаковое количество коробок;

б) без дополнительного условия пункта а).

Задача 12. Учитель в школе ставит отметки от 1 до 5. Средний балл ученика равен 4,625.

а) Какое наименьшее количество оценок может иметь ученик?

б) Если у ученика заменить оценки 3, 3, 5, 5 на две четвёрки, то на сколько максимально может увеличиться средний балл?

Задача 13. Натуральные числа от 1 до 12 разбивают на четыре группы, в каждой из которых есть по крайней мере два числа. Для каждой группы находят сумму чисел этой группы. Для каждой пары групп находят модуль разности полученных сумм и полученные 6 чисел складывают.

а) Может ли в результате получиться 0?

б) может ли в результате получиться 1?

в) Какое наименьшее возможное значение полученного результата?

Задача 14. По окружности расставляют 48 ненулевых целых чисел с общей суммой 20. При этом любые два стоящих рядом числа должны отличаться не более чем на 7 и среди любых четырёх, подряд идущих чисел, должно быть хотя бы одно положительное.

а) Среди таких 48 чисел найдите наибольшее возможное количество положительных.

б) Среди таких 48 чисел найдите наименьшее возможное количество положительных.

3 Ответы.

Задача 1

3 и 1161

Задача 2

а) 48; б) отрицательных; в) 12

Задача 3

а) да; б) нет

Задача 4

155

Задача 5

а) нет; б) нет; в) да

Задача 6

а) да; б) нет

Задача 7

а) нет; б) нет; в) да

Задача 8

а) 1; б) 39

Задача 9

а) нет; б) нет; в) 4

Задача 10

а) да; б) 10; в)

Задача 11

а) 30; б) 2

Задача 12

а) 8; б) на

Задача 13

а) нет; б) нет; в) 4

Задача 14

а) 45; б) 12

4 Решения.

Задача 1. В первом наборе 6 чисел; обозначим Во втором наборе 9 чисел; обозначим

Согласно условию строится следующая сумма:

Приводя подобные, получаем:

или ,

где и

1) Ясно, что сумма S получается наибольшей, когда все числа берутся с плюсом:

.

2) Заметим, что среди чисел ровно три нечётных. Следовательно, A нечётно. Поэтому и нечётно. Кроме того, S делится на 3. Наименьшее по модулю нечётное число, делящееся на 3, есть 3. Стало быть, (оценка). Приведём пример расстановки знаков, при которой в оценке достигается равенство:

Таким образом,

►Как мы додумались до этого примера? Вот некоторые наводящие соображения. Пишем: , то есть . Следовательно, нам нужно добиться, чтобы и отличались на единицу (поскольку знаки можно расставлять как угодно). Сумму можно сделать равной 5 (вычитая из 9 четыре единицы), а для можно получить значение 3 (складывая три единицы). Тогда , а это как раз то, что нам нужно.◄

Задача 2. Напомним, что среднее арифметическое нескольких чисел есть сумма этих чисел, делённая на их количество. Пусть на доске написано n чисел. Тогда их сумма: . Обозначим: p — количество положительных чисел, m — количество отрицательных чисел, z — количество нулей. Таким образом,

Пусть и — суммы положительных и отрицательных чисел соответственно. Имеем: и так как , то:

a) Правая часть данного равенства делится на 6. Поскольку 6 и 7 взаимно простые, число n делится на 6. Между числами 42 и 54 есть только одно такое число: n = 48.

б) Из равенства получаем после сокращения на 6:

.

Кроме того:

.

Сложим полученные равенства: . Т.к. 104 при делении на 3 даёт остаток 2, число z также даёт остаток 2: . Отсюда:или

Соответственно,

.

Составляем разность: так что — отрицательных чисел написано больше.

в) Из равенства видим, что .

Приведём пример с (тогда ). Пусть написано 12 чисел 6, 34 числа −12 и два нуля. Этот набор удовлетворяет условию задачи: среднее арифметическое положительных чисел равно, очевидно, 6; среднее арифметическое отрицательных чисел равно −12, а среднее арифметическое всех чисел:

Следовательно, наибольшее возможное количество положительных чисел равно 12.

Задача 3. Если среднее арифметическое любых 27 чисел набора меньше 2, то сумма любых 27 чисел набора меньше 27 · 2 = 54. Будучи натуральным числом, эта сумма не превосходит 53.

Обозначим S максимальную сумму 27 чисел данного набора. Итак, .

а) Да, может. Такой набор содержит 13 единиц, 17 двоек и 3, 4, 5. Для него, очевидно,

►Наводящее соображение очень простое. Если есть ровно 13 единиц и 3, 4, 5, то оставшиеся 17 вакансий заполняются как минимум двойками. Вот и возьмём набор с этими 17-ю двойками! Ясно, что максимальная сумма получится, если в качестве слагаемых взять 3, 4, 5 и все двойки, добрав остаток единицами.◄

б) Предположим, что набор содержит k единиц (). Остальные чисел набора (помимо 3, 4, 5) назовём вакантными. Вакантных чисел, стало быть, не менее 18, и каждое вакантное число не меньше 2.

Таким образом, наш набор содержит 3, 4, 5 и восемнадцать чисел, не меньших 2; остальные числа набора не меньше 1. Для максимальной суммы тогда получаем:

Данное неравенство показывает, что набор не может содержать менее 13 единиц.

в) Заметим сразу, что если набор содержит не менее 16 единиц, то Поэтому остаётся разобрать случаи, когда количество k единиц в наборе менее 16. Остальные чисел (помимо 3, 4, 5) продолжаем называть вакантными.

• . Легко видеть, что набор, предъявленный в пункте а), оказывается единственным набором с ровно 13 единицами. В самом деле, для любого другого такого набора сумма 17-ти вакантных чисел будет больше 17 · 2 = 34, и сумма станет больше 53. А для предъявленного набора имеем:

• или . Заметим, что среди вакантных чисел обязательно найдётся двойка. В самом деле, иначе все вакантные числа (которых, соответственно, 16 или 15) будут не меньше 3, и тогда их сумма окажется как минимум 15 · 3 = 45, что противоречит условию. Остаётся взять 14 единиц и эту двойку:

Доказательство закончено.

Задача 4. Числа вида будем называть запрещёнными. Вот начало последовательности запрещённых чисел: 1, 3, 6, 10, 15, . . .

Пусть a и d — первый член и разность арифметической прогрессии. Так как число 1 запрещённое, то . Так как члены прогрессии — различные натуральные числа, то .

Если , то прогрессия будет содержать запрещённое число — например, 10. Если , то прогрессия также будет содержать запрещённое число — например, 10 для чётного a и 15 для нечётного a. Стало быть, .

Сумма первых 10 членов прогрессии равна:

С учётом полученных неравенств имеем оценку:

Нижнее значение 155 нашей оценки реализуется для прогрессии с и (то есть для прогрессии 2, 5, 8, . . .). Остаётся показать, что эта прогрессия не содержит запрещённых чисел.

Под номером k в данной прогрессии идёт число . Нам нужно доказать, что равенство

невозможно ни при каких k и n. Перепишем это равенство в виде:

Число n при делении на 3 может давать остатки 0, 1 или 2. Рассмотрим отдельно каждый из этих случаев.

Всюду имеем противоречие: левая часть 6k делится на 3, а правая часть на 3 не делится (остаток 2 в первом и третьем случаях, остаток 1 во втором случае).

Таким образом, прогрессия 2, 5, 8, . . . действительно не содержит запрещённых чисел. Поскольку для неё , то 155 — наименьшее значение величины .

Задача 5. Найдём каноническое разложение числа 1512:

Пусть также 1512 = , где — различные натуральные числа.

а) Предположим, что все пять чисел образуют геометрическую прогрессию. Тогда согласно представлению конечной целочисленной геометрической прогрессии найдутся целые числа k, a, b такие, что:

Не теряя общности, можно считать, что прогрессия возрастающая. Тогда . Перемножая числа , получим:

Выходит, что 1512 делится на 10-ю степень некоторого натурального числа . Но это противоречит каноническому разложению числа 1512 (где нет простых множителей в десятой степени). Следовательно, числа не могут образовывать геометрическую прогрессию.

б) Предположим, что числа образуют возрастающую геометрическую прогрессию. Тогда:

Перемножаем числа :

Снова противоречие: 1512 не может делиться на шестую степень натурального числа .

Поэтому и в данном случае ответ отрицательный.

►Заметим, что из пункта б) следует пункт а). В самом деле, если среди сомножителей не найдётся четырёх членов геометрической прогрессии, то пяти членов не найдётся и подавно. Поэтому решение можно было бы начать сразу с пункта б). Мы привели отдельное решение для пункта а) из методических соображений.◄

в) Предъявляем соответствующий пример: 4 · 6 · 9 · 7 · 1 = 1512. Числа 4, 6, 9 образуют геометрическую прогрессию со знаменателем .

►Пример найден следующим образом. Предположим, что числа образуют геометрическую прогрессию:

Тогда . Глядя на каноническое разложение числа 1512, берём.◄

Задача 6.

а) Да, может: 216, 252, 294, 343. Это геометрическая прогрессия со знаменателем .

►Четыре числа, образующих геометрическую прогрессию, имеют вид:

Остаётся заметить, что , и положить .

Данный пример позволяет почувствовать также, что втиснуть в интервал от 210 до 350 пять чисел, образующих геометрическую прогрессию, уже вряд ли получится. Поэтому в пункте б) надо пытаться доказать, что это невозможно. ◄

б) Предположим, что прогрессия состоит из пяти членов:

Без ограничения общности считаем прогрессию возрастающей, так что . Поскольку все члены прогрессии находятся между числами 210 и 350, имеем:

Из неравенства (∗∗) следует, что b может принимать только значения 2, 3 или 4. Рассмотрим эти три случая по отдельности.

• . Тогда . Имеем:

Противоречие.

• . Тогда или . Имеем:

Противоречие.

• . Тогда . Имеем:

Снова противоречие.

Противоречия, полученные во всех трёх случаях, показывают, что прогрессия не может состоять из пяти членов.

Задача 7.

а) Предположим, что в последовательности три члена. Тогда она имеет вид:

Если эти числа образуют арифметическую прогрессию, то . Имеем противоречие: левая часть чётна, а правая нечётна.

Если эти числа образуют геометрическую прогрессию, то . Снова противоречие, ибо 2046 не является квадратом натурального числа

Поэтому три члена в последовательности быть не может.

б) Предположим, что в последовательности четыре члена: Логически возможны четыре случая.

1. Первые три числа образуют арифметическую прогрессию и вторые три числа образуют арифметическую прогрессию (то если все четыре числа образуют арифметическую прогрессию). Тогда имеем:

Выражаем b из первого равенства и подставляем во второе:

Противоречие: левая часть делится на 3, а правая не делится.

2. Первые три числа образуют арифметическую прогрессию, а вторые три числа образуют геометрическую прогрессию. Тогда:

После исключения b:

Слева стоит квадрат нечётного числа, который также является нечётным числом. Справа стоит чётное число. Противоречие.

3. Первые три числа образуют геометрическую прогрессию, вторые три числа образуют арифметическую прогрессию. Тогда:

Приходим к квадратному уравнению: . Его дискриминант 16369 не является квадратом натурального числа (). Значит, это уравнение не имеет натуральных корней.

4. Первые три числа образуют геометрическую прогрессию и вторые три числа образуют геометрическую прогрессию (то есть все четыре числа образуют геометрическую прогрессию). Тогда:

Отсюда , то есть . Это невозможно, поскольку 2046 не является кубом натурального числа

Итак, в каждом случае получаем противоречие. Следовательно, данная последовательность не может состоять из четырёх членов.

в) В последовательности может быть менее 2046 членов. Вот пример арифметической прогрессии из шести чисел: 1, 410, 819, 1228, 1637, 2046.

►Сконструируем арифметическую прогрессию с первым членом 1 и n-м членом 2046. Пусть разность этой прогрессии равна d. Имеем:

Полагаем, находим и выписываем прогрессию. ◄

Задача 8.

а) В последовательности не менее одного члена. Но последовательность, состоящая из одного числа 163, удовлетворяет условию задачи. Поэтому наименьшее возможное число членов последовательности равно 1.

б) Заметим прежде всего, что последовательность не может состоять только из чередующихся чисел 1 и 7. В самом деле, если такая последовательность содержит чётное число членов, то её сумма делится на 8. Если же число членов нечётно, то при делении суммы последовательности на 8 могут получиться только остатки 1 или 7 — в случаях (1, 7, . . . , 1, 7, 1) и (7, 1, . . . 7, 1, 7) соответственно. Однако число 163 при делении на 8 даёт остаток 3.

Стало быть, в последовательности имеется число b, отличное от 1 и 7. Ясно, что .

Покажем, что в последовательности не может быть более 39 чисел. Предположим обратное: пусть в последовательности имеется не менее 40 членов. Первые 40 чисел этой последовательности разобьём на пары: Имеются две возможности.

1. Число b не попадает ни в одну из этих первых 20 пар. Поскольку сумма чисел в каждой паре не менее 8, сумма всех членов последовательности будет не менее вопреки условию.

2. Число b попадает в одну из первых 20 пар. Сумма чисел в этой паре не менее сумма чисел во всех оставшихся 19 парах не менее . Тогда сумма последовательности оказывается не менее , а это снова противоречит условию.

Таким образом, последовательность содержит менее 40 членов. Предъявим пример последовательности, удовлетворяющей условию и состоящей из 39 членов. Она состоит из 19 пар (7, 1) и заканчивается числом 11:

Действительно, сумма такой последовательности равна .

Итак, наибольшее возможное число членов последовательности равно 39.

Задача 9. Присвоим каждой карточке номер от 1 до 10. Пусть — числа, данные в условии и записанные на карточках вначале (число записано на карточке с номером k). Аналогично, — числа того же набора, но записанные на карточках после их перемешивания.

Согласно условию рассматриваем число:

а) Предположим, что . Тогда в произведении (∗) найдётся нулевой множитель, то есть для некоторого k. Но это невозможно, так как в данном наборе ни для какого числа нет ему противоположного по знаку. Значит, 0 получиться не может.

б) Предположим, что c нечётно. Тогда в произведении (∗) каждый множитель должен быть нечётным, то есть нечётно для любого

Следовательно, для каждого k в паре одно число чётное, а другое нечётное. Поэтому в последовательности окажется 10 чётных и 10 нечётных чисел. Однако из условия вытекает, что указанная последовательность содержит 8 чётных чисел и 12 нечётных.

Возникшее противоречие показывает, что c обязано быть чётным. В частности, 1 получиться не может.

в) Далее считаем, что . Предположим, что . Тогда в произведении (∗) ровно один из множителей по модулю равен 2, а все остальные по модулю равны 1. Иными словами, для некоторого m и для всех остальных k.

Числа оба чётные или оба нечётные. В каждой из остальных девяти пар одно число чётное, а другое нечётное. Стало быть, в последовательности окажется или 11 чётных и 9 нечётных чисел (если чётны), или, наоборот, 9 чётных и 11 нечётных чисел (если нечётны). Но, как было указано выше, чётных и нечётных чисел в этой последовательности имеется 8 и 12 соответственно.

Значит, случай невозможен. Поскольку c чётно, имеем оценку: .

Приведём пример, в котором достигается равенство . Пусть сначала на карточках написаны числа в исходном порядке: 1, −2, −3, 4, −5, 7, −8, 9, 10, −11.

Затем на тех же карточках оказались числа: −2, 1, 4, −3, 7, −5, 9, −8, −11, 10.

Получаем:

Следовательно, наименьшее неотрицательное значение c равно 4.

Задача 10. Пусть m — число мальчиков, d — число девочек в группе. Пусть мальчиков сходили в театр, мальчиков сходили в кино, девочек сходили в театр, девочек сходили в кино.

Для случая похода в театр имеем:

Для случая посещения кино:

Сложим первое из полученных неравенств с удвоенным вторым:

Поскольку каждый мальчик сходил либо в театр, либо в кино, имеем . Кроме того, очевидно, Получаем:

то есть

a) Да, 10 мальчиков могло быть в группе из 20 учащихся. Например, в театр сходили 3 мальчика и все 10 девочек, в кино — остальные 7 мальчиков и 10 девочек. Нужные неравенства выполнены:

►Как построен пример? Прежде всего, значения не противоречат неравенству (∗), и это наводит на мысль, что пример тут возможен. Затем берём неравенства задействуем девочек по максимуму и находим подходящие . ◄

б) Предположим, что в группе из 20 учащихся имеется не менее 11 мальчиков: . Тогда . Имеем: , что противоречит неравенству (∗). Следовательно, , и с учётом пункта а) приходим к выводу, что наибольшее возможное количество мальчиков в группе равно 10.

в) Перепишем неравенство (∗) следующим образом:

Как видим, доля девочек не меньше . Приведём пример, когда равенство достигается. Пусть в группе 9 мальчиков и 8 девочек. В театр сходили 3 мальчика и 8 девочек, в кино сходили 6 мальчиков и 8 девочек. Нужные неравенства выполнены:

Следовательно, наименьшая возможная доля девочек равна .

Задача 11.

a) Всего имеется коробок. Значит, в каждом контейнере должно находиться по 30 коробок.

Пусть x — количество лёгких (по 19 кг) коробок в 1 контейнере. Тогда число тяжёлых (по 49 кг) коробок в 1 контейнере равно . Во 2 контейнере лёгких коробок получается , а тяжёлых коробок:

Суммарные массы коробок в первом и втором контейнерах равны соответственно:

Отсюда:

Числоявляется нечётным и принимает наименьшее возможное значение 1 при . Следовательно, наименьшее значение равно 30.

б) Пусть в первом контейнере находится x лёгких коробок и y тяжёлых коробок. Тогда во втором контейнере будет лёгких и тяжёлых коробок соответственно. Имеем:

При этом имеют место неравенства:

Величина равна:

Нам, таким образом, требуется найти минимальное значение при условии, что выполнены оба неравенства (1).

Заметим, что возможен прямой перебор всех значений

то есть последовательное рассмотрение всех вариантов. Вообще, исчерпывающий перебор конечного числа вариантов — это полноценное решение задачи! Но мы, естественно, таким путём не пойдём и поищем способ избежать прямого перебора.

Прежде всего проверим, не может ли равняться нулю. Для этого рассмотрим уравнение:

Будем использовать остатки от деления на 7. Перепишем уравнение (2) следующим образом:

Нетрудно проверить, что даёт остаток Значит, и слагаемое даёт остаток 2 (ведь остальные слагаемые в левой части делятся на 7). Какой остаток при этом даёт сам ? Перебор остатков от 0 до 6 показывает, что единственная возможность — это остаток 6, то есть

Подставляем (3) в (2):

и после сокращения на 7:

Благодаря этому сокращению уравнение (4) проще уравнения (2). Повторим всю эту процедуру — теперь уже применительно к уравнению (4). Начинаем так же:

Правая часть 123 даёт остаток . Значит, и даёт остаток 4. Тогда k может давать только остаток 5:

Подставляя (5) в (3), получим: . Таким образом, оказывается, что — вопреки первому неравенству (1).

Итак, уравнение (2) не имеет решений, удовлетворяющих (1). Поэтому .

►А какие решения есть? Доведём до конца решение уравнения (2) — полезно посмотреть, чем дело кончится. Подставим (5) в (4):

Отсюда видно, что единственная возможность — это . Остаётся найти x. Из (5) и (3) последовательно получаем:

Итак, уравнение (2) имеет единственное решение в натуральных числах. Это решение не удовлетворяет условию (1). ◄

Поскольку является чётным числом, имеем оценку: . Равенство достигается, например, в случае :

Следовательно, наименьшее значение равно 2.

►Как найден пример? Берём уравнение и решаем его тем же способом — через остатки от деления на 7. Упражняйтесь! ◄

Задача 12.

а) Пусть ученик имеет n оценок и — их сумма. Тогда:

Отсюда , так что n делится на 8. Поэтому .

Приведём пример с . Пусть ученик имеет семь пятёрок и двойку. Тогда его средний балл:

Итак, наименьшее возможное количество оценок ученика равно 8.

б) Пусть ученик имел оценки Обозначим

Заметим сразу, что

Посмотрим, какие ограничения на k накладывает тот факт, что средний балл равен 4,675. Сумма оценок ученика равна , количество оценок равно , так что

Отсюда легко получаем:

Правая часть должна делиться на 8. Число 20 при делении на 8 даёт остаток 4. Значит, при делении на 8 также должно давать остаток 4. Какой остаток даёт само k? Поскольку делится на 8, число при делении на 8 даёт остаток 4. Перебирая остатки от 0 до 7, легко видим, что и k даёт остаток 4:

Подставляем это в (2):

и после сокращения на 8 получим:

Теперь подставляем (3) и (4) в неравенство (1):

откуда , то есть . Вместе с (3) это даёт нам нужное неравенство на k:

Пусть теперь оценки ученика стали . Сумма оценок равна , количество оценок равно . Находим изменение среднего балла:

С учётом (2) имеем:

Максимальное значение ∆ достигается при минимально возможном значении k, равном 12:

Таким образом, максимальное увеличение среднего балла составляет .

Задача 13.

Пусть — суммы чисел в четырёх группах. Согласно условию нас интересует сумма:

Ясно, что — целое неотрицательное число.

Отметим сразу же, что

а) Предположим, что . Тогда все шесть слагаемых в (1) равны нулю, что немедленно даёт . Но это невозможно ввиду (2), поскольку 78 не делится на 4. Следовательно, 0 в результате получиться не может.

б) Предположим, что . Тогда одно слагаемое в (1) равно единице, а остальные пять слагаемых равны нулю.

Без ограничения общности можно считать, что . Но тогда из и получаем соответственно . Возникшее противоречие показывает, что 1 в результате получиться не может.

в) Заметим, что имеется самое большее три слагаемых в (1), которые не содержат фиксированную букву (например, букву не содержат слагаемые Поэтому, если взять любые четыре слагаемых в (1), то в них непременно будут фигурировать все четыре буквы .

Т.o., если четыре каких-то слагаемых в (1) равны нулю, то

Данное равенство, как было отмечено выше, невозможно. Следовательно, никакие четыре слагаемыe в (1) не могут равняться нулю.

Иными словами, как минимум три слагаемых в (1) должны быть отличны от нуля. Тем самым оказывается невозможным случай .

Предположим, что . Тогда три слагаемых в (1) равны единице, а остальные три — нулю. При этом нулю могут равняться лишь такие три слагаемых, которые не содержат некоторой буквы (в противном случае — когда в трёх нулевых слагаемых фигурируют все четыре буквы — остальные три слагаемых также обратятся в нуль).

Пусть, например, то есть . Тогда и

Получаем противоречие: слева стоит чётное число, а справа — нечётное. Значит, невозможно.

Приведём пример с . Группы возьмём такие: ( Здесь , . Подставляем в (1):

Тем самым доказано, что наименьшее возможное значение равно 4.

Задача 14. Пусть по кругу расставлены числа . Количество положительных чисел среди них обозначим p.

а) Поскольку сумма всех чисел равна 20, среди них есть как положительные, так и отрицательные. Поэтому .

Пусть . В этом случае сумма положительных чисел не менее 47. Но тогда единственное отрицательное число меньше или равно −27 и потому отличается от соседних чисел более чем на 7. Это противоречит условию. Значит, .

Пусть . Сумма положительных чисел не менее 46. Отрицательных чисел всего два, и их сумма меньше или равна −26. Значит, одно из отрицательных чисел меньше или равно −13. Это число отличается от соседнего положительного числа более чем на 7. Поэтому .

Приведём пример, когда . Положим

,

Легко видеть, что все условия задачи выполнены. Следовательно, наибольшее возможное значение p равно 45.

б) Из того, что среди любых четырёх, подряд идущих чисел, имеется хотя бы одно положительное, следует, что . В самом деле, разобьём наши 48 чисел на 12 четвёрок:

Если , то по крайней мере в одной четвёрке не будет положительного числа — вопреки условию.

Остаётся предъявить пример с . Пусть

а остальные 36 чисел равны −1. Легко проверить, что условия задачи выполнены.

Стало быть, наименьшее возможное значение p равно 12.

23

Это самая последняя и самая сложная задача в профильном ЕГЭ по математике, которая вполне претендует на олимпиадный уровень. Обычно такие задачи содержат в себе сразу несколько вопросов.

В целом задание 18 сводится к составлению и дальнейшему решению уравнения в целых числах (оно же — диофантово уравнение), иногда с привлечением комбинаторики. Но прежде чем приступать к решению таких уравнений, вам потребуется небольшая теоретическая подготовка и своего рода «разминка для мозгов».

§ 1.

Функции с целыми значениями — что за зверь?

§ 2.

Арифметическая прогрессия и делители чисел в уравнениях

§ 3.

Задача 19: арифметическая прогрессия из пробного ЕГЭ

§ 4.

Позиционная система счисления: свойства и следствия

§ 5.

Условия задач 19 и следствия из них