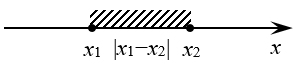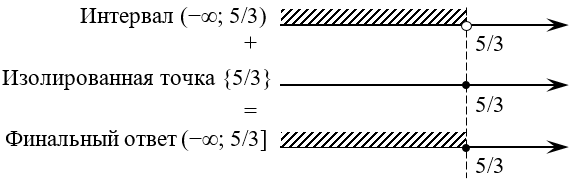Модуль на егэ профиль теория

Уравнения с модулем

Эта статья посвящена приёмам решения уравнений, содержащих переменную под знаком модуля.

Если на экзамене вам попадётся уравнение с модулем, его можно решить, вообще не зная никаких специальных методов и пользуясь только определением модуля. Правда, занять это может часа полтора драгоценного экзаменационного времени.

Поэтому мы и хотим рассказать вам о приёмах, упрощающих решение таких задач.

Прежде всего вспомним определение модуля.

Если число x неотрицательное, то модуль x равен самому числу x.

А для отрицательного числа x модуль равен противоположному ему положительному числу -x.

Рассмотрим различные типы уравнений с модулем.

Начнем с простых заданий.

к оглавлению ▴

Слева модуль, справа число

Это самый простой случай. Нам поможет геометрический смысл модуля.

Модуль числа — это расстояние от нуля до данного числа. Очевидно, расстояние не может быть отрицательным. Оно или положительно, или равно нулю. Например, . Другими словами, расстояние от точки -2 до нуля равно 2. Этим мы пользуемся при решении уравнений.

1. Решим уравнение:

Решение:

На числовой прямой есть ровно две точки, расстояние от которых до нуля равно двум. Это точки 2 и -2. Значит, у уравнения есть два решения: и .

Ответ: -2; 2.

2. Решите уравнение:

Решение:

Ответ:

3. Решите уравнение:

Решение:

Мы получили совокупность двух квадратных уравнений. А затем решили отдельно каждое из них.

Вот что мы делали, решая квадратные уравнения:

— применили теорему Виета и нашли корни.

корней нет.

Ответ:

4. Решим уравнение: 

Решение:

Задача похожа на предыдущую.

Есть только два числа, модули которых равны четырём. Это 4 и −4. Следовательно, уравнение равносильно совокупности двух простых:

или

Второе уравнение не имеет корней. Решения первого: x = 0 и x = 5.

Ответ: 0; 5.

к оглавлению ▴

Слева модуль, справа выражение, зависящее от переменной

Здесь приходится раскрывать модуль по определению. . . или соображать!

5.

Решение:

Уравнение распадается на два случая, в зависимости от знака выражения под модулем.

Другими словами, оно равносильно совокупности двух систем:

   

Решение первой системы: . У второй системы решений нет.

Ответ: 1.

6.

Решение:

Первый случай: x ≥ 3. Снимаем модуль:

Число , будучи отрицательным, не удовлетворяет условию x ≥ 3 и потому не является корнем исходного уравнения.

Выясним, удовлетворяет ли данному условию число . Для этого составим разность и определим её знак:

Значит, больше трёх и потому является корнем исходного уравнения.

Второй случай: x < 3. Снимаем модуль:

Число . больше, чем , и потому не удовлетворяет условию x < 3. Проверим :

Значит, . является корнем исходного уравнения.

Ответ:

7. Решите уравнение: = x.
Если уравнение имеет несколько корней, в ответе запишите меньший корень

Решение:

ОДЗ уравнения: x≠3. Так как в левой части уравнения — неотрицательная величина, должно также выполняться условие Возведем обе части уравнения в квадрат

= x

(разность квадратов),

Так как — это посторонний корень. Уравнение имеет два корня: или

Меньший корень: 1.

Ответ: 1.

8.

Решение:

Снимать модуль по определению? Страшно даже подумать об этом, ведь дискриминант — не полный квадрат.

Давайте воспользуемся следующим правилом:

Уравнение вида равносильно совокупности двух систем:

   

То же самое, но немного по-другому:

Иными словами, мы решаем два уравнения, A = B и A = −B, а потом отбираем корни, удовлетворяющие условию

Приступаем. Сначала решаем первое уравнение:

Затем решаем второе уравнение:

Теперь в каждом случае проверяем знак правой части:

Подходят только и .

Ответ:

Еще одно уравнение того же типа.

9. Решите уравнение: .

Это уравнение вида Вспомним, что оно равносильно системе:

Получим:

Решим отдельно каждое уравнение совокупности.

по теореме Виета.

Система примет вид:

Сравним и Для сравнения мы будем использовать вот такой символ:

.

Умножим обе части этого неравенства на 2: .

Прибавим 5 к обеим частям выражения: Обе части выражения неотрицательны, поэтому возведем их в квадрат и сравним квадраты. Очевидно, 17 9. Это значит, что и

Остальные корни, очевидно, меньше, чем -1.

Ответ: .

к оглавлению ▴

Квадратные уравнения с заменой

Замена переменной — универсальный способ решения всевозможных уравнений. И этот способ помогает нам решать квадратные уравнения, содержащие переменную под знаком модуля.

10. Решим уравнение:

Решение:

Поскольку , удобно сделать замену |x| = t. Получаем:

.

Ответ: ±1.

к оглавлению ▴

Модуль равен модулю

Речь идёт об уравнениях вида Это — подарок судьбы. Никаких раскрытий модуля по определению! Всё просто:

Как мы получили это равенство? Покажем на примере задачи.

11. Решите уравнение:

Решение:

Возведем обе части в квадрат, поскольку они неотрицательны.

Перенесем все в левую часть и воспользуемся формулой разности квадратов:

Ответ:

12. Решим уравнение: .

Решение:

Уравнение равносильно следующей совокупности:

Решим каждое из уравнений совокупности и запишем ответ.

1)

— корни первого квадратного уравнения.

2)

— корни второго квадратного уравнения.

В ответ запишем все 4 корня.

Ответ:

к оглавлению ▴

Два или несколько модулей

13. Решим уравнение:

Решение:

Не будем возиться с каждым модулем по отдельности и раскрывать его по определению — слишком много получится вариантов. Существует более рациональный способ — метод интервалов.

Выражения под модулями обращаются в нуль в точках x = 1, x = 2 и x = 3. Эти точки делят числовую прямую на четыре промежутка (интервала). Отметим на числовой прямой эти точки и расставим знаки для каждого из выражений под модулями на полученных интервалах. (Порядок следования знаков совпадает с порядком следования соответствующих модулей в уравнении).

Таким образом, нам нужно рассмотреть четыре случая — когда x находится в каждом из интервалов.

Случай 1: x ≥ 3. Все модули снимаются с «плюсом»:

Полученное значение x = 5 удовлетворяет условию x ≥ 3 и потому является корнем исходного уравнения.

Случай 2: 2 ≤ x ≤ 3. Последний модуль теперь снимается с «минусом»:

Полученное значение x также годится — оно принадлежит рассматриваемому промежутку.

Случай 3: 1 ≤ x ≤ 2. Второй и третий модули снимаются с «минусом»:

Мы получили верное числовое равенство при любом x из рассматриваемого промежутка [1; 2] служат решениями данного уравнения.

Случай 4: x ≤ 1 ≤ 1. Второй и третий модули снимаются «с минусом»:

Ничего нового. Мы и так знаем, что x = 1 является решением.

Ответ: [1; 2] ∪ {5}.

к оглавлению ▴

Модуль в модуле

14. Решим уравнение:

Решение:

Начинаем с раскрытия внутреннего модуля.

1) x ≤ 3. Получаем:

Выражение под модулем обращается в нуль при . Данная точка принадлежит рассматриваемому
промежутку. Поэтому приходится разбирать два подслучая.

1.1) Получаем в этом случае:

Это значение x не годится, так как не принадлежит рассматриваемому промежутку.

1.2) . Тогда:

Это значение x также не годится.

Итак, при x ≤ 3 решений нет. Переходим ко второму случаю.

2) x ≥ 3. Имеем:

Здесь нам повезло: выражение x + 2 положительно в рассматриваемом промежутке! Поэтому никаких подслучаев уже не будет: модуль снимается с «плюсом»:

Это значение x находится в рассматриваемом промежутке и потому является корнем исходного уравнения.

Ответ: 4.

Так решаются все задачи данного типа — раскрываем вложенные модули по очереди, начиная с внутреннего.

Часто в решении уравнений и неравенств с модулем используется график функции Он строится согласно определению модуля:

.

Для получаем участок графика y = x.

Для  получаем участок графика y = −x. Вот этот график:

15. Решите уравнение:

Решение:

Сделаем замену переменной:

Тогда

Получим:

Мы помним, что

Решим уравнение графически. В левой части — график функции

Построим этот график. Сначала изобразим графики функций (точка минимума (3; 0)) и (точка минимума ( -3; 0)). Можно сказать, что график функции сдвинут относительно графика на 3 единицы вправо, а график — на 3 единицы влево.

И построим график суммы функций и

В точке с абсциссой 3 значение одного из слагаемых равно 0, другое слагаемое равно 6, сумма равна 6.

В точке с абсциссой -3 аналогично.

При х = 0 оба слагаемых равны 3, сумма равна 6.

Легко доказать, что сумма двух линейных функций есть линейная функция.

Поэтому при — получим горизонтальный участок. При x 3 получим луч с угловым коэффициентом, равным 2, а при x — 3 — луч с угловым коэффициентом, равным — 2.

Решения нашего уравнения — все принадлежащие отрезку от до

значит,

Ответ:

Мы рассмотрели все основные типы уравнений с модулями.

Читайте также о том, как решать неравенства с модулем.

Как решать уравнения с модулем: основные правила

30 декабря 2016

Модуль — одна из тех вещей, о которых вроде-бы все слышали, но в действительности никто нормально не понимает. Поэтому сегодня будет большой урок, посвящённый решению уравнений с модулями.

Сразу скажу: урок будет несложный. И вообще модули — вообще тема относительно несложная. «Да конечно, несложная! У меня от неё мозг разрывается!» — скажут многие ученики, но все эти разрывы мозга происходят из-за того, что у большинства людей в голове не знания, а какая-то хрень. И цель этого урока — превратить хрень в знания.:)

Немного теории

Итак, поехали. Начнём с самого важного: что такое модуль? Напомню, что модуль числа — это просто то же самое число, но взятое без знака «минус». Т.е., например, $left| -5 right|=5$. Или $left| -129,5 right|=129,5$.

Вот так всё просто? Да, просто. А чему тогда равен модуль положительного числа? Тут ещё проще: модуль положительного числа равен самому этому числу: $left| 5 right|=5$; $left| 129,5 right|=129,5$ и т.д.

Получается любопытная вещь: разные числа могут иметь один тот же модуль. Например: $left| -5 right|=left| 5 right|=5$; $left| -129,5 right|=left| 129,5 right|=129,5$. Нетрудно заметить, что это за числа, у которых модули одинаковые: эти числа противоположны. Таким образом, отметим для себя, что модули противоположных чисел равны:

[left| -a right|=left| a right|]

Ещё один важный факт: модуль никогда не бывает отрицательным. Какое бы число мы ни взяли — хоть положительное, хоть отрицательное — его модуль всегда оказывается положительным (или в крайнем случае нулём). Именно поэтому модуль часто называют абсолютной величиной числа.

Кроме того, если объединить определение модуля для положительного и отрицательного числа, то получим глобальное определение модуля для всех чисел. А именно: модуль числа равен самому этому числу, если число положительное (или ноль), либо равен противоположному числу, если число отрицательное. Можно записать это в виде формулы:

[left| a right|=left{ begin{align}& a,quad age 0, \& -a,quad a lt 0. \end{align} right.]

Ещё есть модуль нуля, но он всегда равен нулю. Кроме того, ноль — единственное число, которое не имеет противоположного.

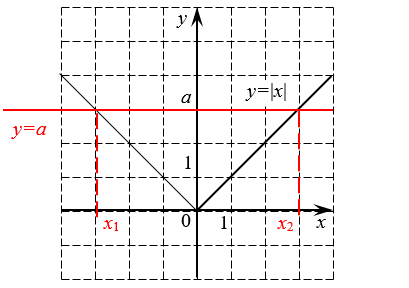
Таким образом, если рассмотреть функцию $y=left| x right|$ и попробовать нарисовать её график, то получится вот такая «галка»:

Из этой картинки сразу видно, что $left| -m right|=left| m right|$, а график модуля никогда не опускается ниже оси абсцисс. Но это ещё не всё: красной линией отмечена прямая $y=a$, которая при положительных $a$ даёт нам сразу два корня: ${{x}_{1}}$ и ${{x}_{2}}$, но об этом мы поговорим позже.:)

Помимо чисто алгебраического определения, есть геометрическое. Допустим, есть две точки на числовой прямой: ${{x}_{1}}$ и ${{x}_{2}}$. В этом случае выражение $left| {{x}_{1}}-{{x}_{2}} right|$ — это просто расстояние между указанными точками. Или, если угодно, длина отрезка, соединяющего эти точки:

Из этого определения также следует, что модуль всегда неотрицателен. Но хватит определений и теории — перейдём к настоящим уравнениям.:)

Основная формула

Ну хорошо, с определением разобрались. Но легче-то от этого не стало. Как решать уравнения, содержащие этот самый модуль?

Спокойствие, только спокойствие. Начнём с самых простых вещей. Рассмотрим что-нибудь типа такого:

[left| x right|=3]

Итак, модуль$x$ равен 3. Чему может быть равен $x$? Ну, судя по определению, нас вполне устроит $x=3$. Действительно:

[left| 3 right|=3]

А есть ли другие числа? Кэп как бы намекает, что есть. Например, $x=-3$ — для него тоже $left| -3 right|=3$, т.е. требуемое равенство выполняется.

Так может, если поискать, подумать, мы найдём ещё числа? А вот обломитесь: больше чисел нет. Уравнение $left| x right|=3$ имеет лишь два корня: $x=3$ и $x=-3$.

Теперь немного усложним задачу. Пусть вместо переменной $x$ под знаком модуля тусуется функция $fleft( x right)$, а справа вместо тройки поставим произвольное число $a$. Получим уравнение:

[left| fleft( x right) right|=a]

Ну и как такое решать? Напомню: $fleft( x right)$ — произвольная функция, $a$ — любое число. Т.е. вообще любое! Например:

[left| 2x+1 right|=5]

или:

[left| 10x-5 right|=-65]

Обратим внимание на второе уравнение. Про него сразу можно сказать: корней у него нет. Почему? Всё правильно: потому что в нём требуется, чтобы модуль был равен отрицательному числу, чего никогда не бывает, поскольку мы уже знаем, что модуль — число всегда положительное или в крайнем случае ноль.

А вот с первым уравнением всё веселее. Тут два варианта: либо под знаком модуля стоит положительное выражение, и тогда$left| 2x+1 right|=2x+1$, либо это выражение всё-таки отрицательное, и тогда $left| 2x+1 right|=-left( 2x+1 right)=-2x-1$. В первом случае наше уравнение перепишется так:

[left| 2x+1 right|=5Rightarrow 2x+1=5]

И внезапно получается, что подмодульное выражение $2x+1$ действительно положительно — оно равно числу 5. Т.е. мы можем спокойно решать это уравнение — полученный корень будет кусочком ответа:

[2x+1=5Rightarrow 2x=4Rightarrow x=2]

Особо недоверчивые могут попробовать подставить найденный корень в исходное уравнение и убедиться, что действительно под модулем будет положительное число.

Теперь разберём случай отрицательного подмодульного выражения:

[left{ begin{align}& left| 2x+1 right|=5 \& 2x+1 lt 0 \end{align} right.Rightarrow -2x-1=5Rightarrow 2x+1=-5]

Опа! Снова всё чётко: мы предположили, что $2x+1 lt 0$, и в результате получили, что $2x+1=-5$ — действительно, это выражение меньше нуля. Решаем полученное уравнение, при этом уже точно зная, что найденный корень нас устроит:

[2x+1=-5Rightarrow 2x=-6Rightarrow x=-3]

Итого мы вновь получили два ответа: $x=2$ и $x=3$. Да, объём вычислений оказался малость побольше, чем в совсем уж простом уравнении $left| x right|=3$, но принципиально ничего не изменилось. Так может, существует какой-то универсальный алгоритм?

Да, такой алгоритм существует. И сейчас мы его разберём.

Избавление от знака модуля

Пусть нам дано уравнение $left| fleft( x right) right|=a$, причём $age 0$ (иначе, как мы уже знаем, корней нет). Тогда можно избавиться от знака модуля по следующему правилу:

[left| fleft( x right) right|=aRightarrow fleft( x right)=pm a]

Таким образом, наше уравнение с модулем распадается на два, но уже без модуля. Вот и вся технология! Попробуем решить парочку уравнений. Начнём вот с такого

[left| 5x+4 right|=10Rightarrow 5x+4=pm 10]

Отдельно рассмотрим, когда справа стоит десятка с плюсом, и отдельно — когда с минусом. Имеем:

[begin{align}& 5x+4=10Rightarrow 5x=6Rightarrow x=frac{6}{5}=1,2; \& 5x+4=-10Rightarrow 5x=-14Rightarrow x=-frac{14}{5}=-2,8. \end{align}]

Вот и всё! Получили два корня: $x=1,2$ и $x=-2,8$. Всё решение заняло буквально две строчки.

Ок, не вопрос, давайте рассмотрим что-нибудь чуть посерьёзнее:

[left| 7-5x right|=13]

Опять раскрываем модуль с плюсом и минусом:

[begin{align}& 7-5x=13Rightarrow -5x=6Rightarrow x=-frac{6}{5}=-1,2; \& 7-5x=-13Rightarrow -5x=-20Rightarrow x=4. \end{align}]

Опять пара строчек — и ответ готов! Как я и говорил, в модулях нет ничего сложного. Нужно лишь запомнить несколько правил. Поэтому идём дальше и приступаем с действительно более сложным задачам.

Случай переменной правой части

А теперь рассмотрим вот такое уравнение:

[left| 3x-2 right|=2x]

Это уравнение принципиально отличается от всех предыдущих. Чем? А тем, что справа от знака равенства стоит выражение $2x$ — и мы не можем заранее знать, положительное оно или отрицательное.

Как быть в таком случае? Во-первых, надо раз и навсегда понять, что если правая часть уравнения окажется отрицательной, то уравнение не будет иметь корней — мы уже знаем, что модуль не может быть равен отрицательному числу.

А во-вторых, если права часть всё-таки положительна (или равна нулю), то можно действовать точно так же, как раньше: просто раскрыть модуль отдельно со знаком «плюс» и отдельно — со знаком «минус».

Таким образом, сформулируем правило для произвольных функций $fleft( x right)$ и $gleft( x right)$ :

[left| fleft( x right) right|=gleft( x right)Rightarrow left{ begin{align}& fleft( x right)=pm gleft( x right), \& gleft( x right)ge 0. \end{align} right.]

Применительно к нашему уравнению получим:

[left| 3x-2 right|=2xRightarrow left{ begin{align}& 3x-2=pm 2x, \& 2xge 0. \end{align} right.]

Ну, с требованием $2xge 0$ мы как-нибудь справимся. В конце концов, можно тупо подставить корни, которые мы получим из первого уравнения, и проверить: выполняется неравенство или нет.

Поэтому решим-ка само уравнение:

[begin{align}& 3x-2=2xRightarrow 3x-2x=2Rightarrow x=2; \& 3x-2=-2xRightarrow 5x=2Rightarrow x=frac{2}{5}. \end{align}]

Ну и какой их этих двух корней удовлетворяет требованию $2xge 0$? Да оба! Поэтому в ответ пойдут два числа: $x=2$ и $x={2}/{5};$. Вот и всё решение.:)

Подозреваю, что кто-то из учеников уже начал скучать? Что ж, рассмотрим ещё более сложное уравнение:

[left| {{x}^{3}}-3{{x}^{2}}+x right|=x-{{x}^{3}}]

Хоть оно и выглядит злобно, по факту это всё то же самое уравнение вида «модуль равен функции»:

[left| fleft( x right) right|=gleft( x right)]

И решается оно точно так же:

[left| {{x}^{3}}-3{{x}^{2}}+x right|=x-{{x}^{3}}Rightarrow left{ begin{align}& {{x}^{3}}-3{{x}^{2}}+x=pm left( x-{{x}^{3}} right), \& x-{{x}^{3}}ge 0. \end{align} right.]

С неравенством мы потом разберёмся — оно какое-то уж слишком злобное (на самом деле простое, но мы его решать не будем). Пока лучше займёмся полученными уравнениями. Рассмотрим первый случай — это когда модуль раскрывается со знаком «плюс»:

[{{x}^{3}}-3{{x}^{2}}+x=x-{{x}^{3}}]

Ну, тут и ежу понятно, что нужно всё собрать слева, привести подобные и посмотреть, что получится. А получится вот что:

[begin{align}& {{x}^{3}}-3{{x}^{2}}+x=x-{{x}^{3}}; \& 2{{x}^{3}}-3{{x}^{2}}=0; \end{align}]

Выносим общий множитель ${{x}^{2}}$ за скобку и получаем очень простое уравнение:

[{{x}^{2}}left( 2x-3 right)=0Rightarrow left[ begin{align}& {{x}^{2}}=0 \& 2x-3=0 \end{align} right.]

[{{x}_{1}}=0;quad {{x}_{2}}=frac{3}{2}=1,5.]

Тут мы воспользовались важным свойством произведения, ради которого мы и раскладывали исходный многочлен на множители: произведение равно нулю, когда хотя бы один из множителей равен нулю.

Теперь точно так же разберёмся со вторым уравнением, которое получается при раскрытии модуля со знаком «минус»:

[begin{align}& {{x}^{3}}-3{{x}^{2}}+x=-left( x-{{x}^{3}} right); \& {{x}^{3}}-3{{x}^{2}}+x=-x+{{x}^{3}}; \& -3{{x}^{2}}+2x=0; \& xleft( -3x+2 right)=0. \end{align}]

Опять то же самое: произведение равно нулю, когда равен нулю хотя бы один из множителей. Имеем:

[left[ begin{align}& x=0 \& -3x+2=0 \end{align} right.]

[{{x}_{1}}=0;quad {{x}_{2}}=frac{2}{3}.]

Ну вот мы получили три корня: $x=0$, $x=1,5$ и $x={2}/{3};$. Ну и что из этого набора пойдёт в окончательный ответ? Для этого вспомним, что у нас есть дополнительное ограничение в виде неравенства:

[x-{{x}^{3}}ge 0]

Как учесть это требование? Да просто подставим найденные корни и проверим: выполняется неравенство при этих $x$ или нет. Имеем:

[begin{align}& x=0Rightarrow x-{{x}^{3}}=0-0=0ge 0; \& x=1,5Rightarrow x-{{x}^{3}}=1,5-{{1,5}^{3}} lt 0; \& x=frac{2}{3}Rightarrow x-{{x}^{3}}=frac{2}{3}-frac{8}{27}=frac{10}{27}ge 0; \end{align}]

Таким образом, корень $x=1,5$ нас не устраивает. И в ответ пойдут лишь два корня:

[{{x}_{1}}=0;quad {{x}_{2}}=frac{2}{3}.]

Как видите, даже в этом случае ничего сложного не было — уравнения с модулями всегда решаются по алгоритму. Нужно лишь хорошо разбираться в многочленах и неравенствах. Поэтому переходим к более сложным задачам — там уже будет не один, а два модуля.

Уравнения с двумя модулями

До сих пор мы изучали лишь самые простые уравнения — там был один модуль и что-то ещё. Это «что-то ещё» мы отправляли в другую часть неравенства, подальше от модуля, чтобы в итоге всё свелось к уравнению вида $left| fleft( x right) right|=gleft( x right)$ или даже более простому $left| fleft( x right) right|=a$.

Но детский сад закончился — пора рассмотреть что-нибудь посерьёзнее. Начнём с уравнений вот такого типа:

[left| fleft( x right) right|=left| gleft( x right) right|]

Это уравнение вида «модуль равен модулю». Принципиально важным моментом является отсутствие других слагаемых и множителей: только один модуль слева, ещё один модуль справа — и ничего более.

Кто-нибудь сейчас подумает, что такие уравнения решаются сложнее, чем то, что мы изучали до сих пор. А вот и нет: эти уравнения решаются даже проще. Вот формула:

[left| fleft( x right) right|=left| gleft( x right) right|Rightarrow fleft( x right)=pm gleft( x right)]

Всё! Мы просто приравниваем подмодульные выражения, ставя перед одним из них знак «плюс-минус». А затем решаем полученные два уравнения — и корни готовы! Никаких дополнительных ограничений, никаких неравенств и т.д. Всё очень просто.

Давайте попробуем решать вот такую задачу:

[left| 2x+3 right|=left| 2x-7 right|]

Элементарно, Ватсон! Раскрываем модули:

[left| 2x+3 right|=left| 2x-7 right|Rightarrow 2x+3=pm left( 2x-7 right)]

Рассмотрим отдельно каждый случай:

[begin{align}& 2x+3=2x-7Rightarrow 3=-7Rightarrow emptyset ; \& 2x+3=-left( 2x-7 right)Rightarrow 2x+3=-2x+7. \end{align}]

В первом уравнении корней нет. Потому что когда это $3=-7$? При каких значениях $x$? «Какой ещё нафиг $x$? Ты обкурился? Там вообще нет $x$» — скажете вы. И будете правы. Мы получили равенство, не зависящее от переменной $x$, и при этом само равенство — неверное. Потому и нет корней.:)

Со вторым уравнением всё чуть интереснее, но тоже очень и очень просто:

[2x+3=-2x+7Rightarrow 4x=4Rightarrow x=1]

Как видим, всё решилось буквально в пару строчек — другого от линейного уравнения мы и не ожидали.:)

В итоге окончательный ответ: $x=1$.

Ну как? Сложно? Конечно, нет. Попробуем что-нибудь ещё:

[left| x-1 right|=left| {{x}^{2}}-3x+2 right|]

Опять у нас уравнение вида $left| fleft( x right) right|=left| gleft( x right) right|$. Поэтому сразу переписываем его, раскрывая знак модуля:

[{{x}^{2}}-3x+2=pm left( x-1 right)]

Возможно, кто-то сейчас спросит: «Эй, что за бред? Почему «плюс-минус» стоит у правого выражения, а не у левого?» Спокойно, сейчас всё объясню. Действительно, по-хорошему мы должны были переписать наше уравнение следующим образом:

[x-1=pm left( {{x}^{2}}-3x+2 right)]

Затем нужно раскрыть скобки, перенести все слагаемые в одну сторону от знака равенства (поскольку уравнение, очевидно, в обоих случаях будет квадратным), ну и дальше отыскать корни. Но согласитесь: когда «плюс-минус» стоит перед тремя слагаемыми (особенно когда одно из этих слагаемых — квадратное выражение), это как-то более сложно выглядит, нежели ситуация, когда «плюс-минус» стоит лишь перед двумя слагаемыми.

Но ведь ничто не мешает нам переписать исходное уравнение следующим образом:

[left| x-1 right|=left| {{x}^{2}}-3x+2 right|Rightarrow left| {{x}^{2}}-3x+2 right|=left| x-1 right|]

Что произошло? Да ничего особенного: просто поменяли левую и правую часть местами. Мелочь, которая в итоге немного упростит нам жизнь.:)

В общем, решаем это уравнение, рассматривая варианты с плюсом и с минусом:

[begin{align}& {{x}^{2}}-3x+2=x-1Rightarrow {{x}^{2}}-4x+3=0; \& {{x}^{2}}-3x+2=-left( x-1 right)Rightarrow {{x}^{2}}-2x+1=0. \end{align}]

Первое уравнение имеет корни $x=3$ и $x=1$. Второе вообще является точным квадратом:

[{{x}^{2}}-2x+1={{left( x-1 right)}^{2}}]

Поэтому у него единственный корень: $x=1$. Но этот корень мы уже получали ранее. Таким образом, в итоговый ответ пойдут лишь два числа:

[{{x}_{1}}=3;quad {{x}_{2}}=1.]

Миссия выполнена! Можно взять с полки и скушать пирожок. Там их 2, ваш средний.:)

Важное замечание. Наличие одинаковых корней при разных вариантах раскрытия модуля означает, что исходные многочлены раскладываются на множители, и среди этих множителей обязательно будет общий. Действительно:

[begin{align}& left| x-1 right|=left| {{x}^{2}}-3x+2 right|; \& left| x-1 right|=left| left( x-1 right)left( x-2 right) right|. \end{align}]

Одно из свойств модуля: $left| acdot b right|=left| a right|cdot left| b right|$ (т.е. модуль произведения равен произведению модулей), поэтому исходное уравнение можно переписать так:

[left| x-1 right|=left| x-1 right|cdot left| x-2 right|]

Как видим, у нас действительно возник общий множитель. Теперь, если собрать все модули с одной стороны, то можно вынести этот множитель за скобку:

[begin{align}& left| x-1 right|=left| x-1 right|cdot left| x-2 right|; \& left| x-1 right|-left| x-1 right|cdot left| x-2 right|=0; \& left| x-1 right|cdot left( 1-left| x-2 right| right)=0. \end{align}]

Ну а теперь вспоминаем, что произведение равно нулю, когда хотя бы один из множителей равен нулю:

[left[ begin{align}& left| x-1 right|=0, \& left| x-2 right|=1. \end{align} right.]

Таким образом, исходное уравнение с двумя модулями свелось к двум простейшим уравнениям, о которых мы говорили в самом начале урока. Такие уравнения решаются буквально в пару строчек.:)

Данное замечание, возможно, покажется излишне сложным и неприменимым на практике. Однако в реальности вам могут встретиться куда более сложные задачи, нежели те, что мы сегодня разбираем. В них модули могут комбинироваться с многочленами, арифметическими корнями, логарифмами и т.д. И в таких ситуациях возможность понизить общую степень уравнения путём вынесения чего-либо за скобку может оказаться очень и очень кстати.:)

Теперь хотелось бы разобрать ещё одно уравнение, которое на первый взгляд может показаться бредовым. На нём «залипают» многие ученики — даже те, которые считают, что хорошо разобрались в модулях.

Тем не менее, это уравнение решается даже проще, чем то, что мы рассматривали ранее. И если вы поймёте почему, то получите ещё один приём для быстрого решения уравнений с модулями.

Итак, уравнение:

[left| x-{{x}^{3}} right|+left| {{x}^{2}}+x-2 right|=0]

Нет, это не опечатка: между модулями именно плюс. И нам нужно найти, при каких $x$ сумма двух модулей равна нулю.:)

В чём вообще проблема? А проблема в том, что каждый модуль — число положительное, либо в крайнем случае ноль. А что будет, если сложить два положительных числа? Очевидно, снова положительное число:

[begin{align}& 5+7=12 gt 0; \& 0,004+0,0001=0,0041 gt 0; \& 5+0=5 gt 0. \end{align}]

Последняя строчка может натолкнуть на мысль: единственный случай, когда сумма модулей равна нулю — это если каждый модуль будет равен нулю:

[left| x-{{x}^{3}} right|+left| {{x}^{2}}+x-2 right|=0Rightarrow left{ begin{align}& left| x-{{x}^{3}} right|=0, \& left| {{x}^{2}}+x-2 right|=0. \end{align} right.]

А когда модуль равен нулю? Только в одном случае — когда подмодульное выражение равно нулю:

[x-{{x}^{3}}=0Rightarrow xleft( 1-{{x}^{2}} right)=0Rightarrow left[ begin{align}& x=0 \& x=pm 1 \end{align} right.]

[{{x}^{2}}+x-2=0Rightarrow left( x+2 right)left( x-1 right)=0Rightarrow left[ begin{align}& x=-2 \& x=1 \end{align} right.]

Таким образом, у нас есть три точки, в которых обнуляется первый модуль: 0, 1 и −1; а также две точки, в которых обнуляется второй модуль: −2 и 1. Однако нам нужно, чтобы оба модуля обнулялись одновременно, поэтому среди найденных чисел нужно выбрать те, которые входят в оба набора. Очевидно, такое число лишь одно: $x=1$ — это и будет окончательным ответом.

Метод расщепления

Что ж, мы уже рассмотрели кучу задач и изучили множество приёмов. Думаете, на этом всё? А вот и нет! Сейчас мы рассмотрим заключительный приём — и одновременно самый важный. Речь пойдёт о расщеплении уравнений с модулем. О чём вообще пойдёт речь? Давайте вернёмся немного назад и рассмотрим какое-нибудь простое уравнение. Например, это:

[left| 3x-5 right|=5-3x]

В принципе, мы уже знаем, как решать такое уравнение, потому что это стандартная конструкция вида $left| fleft( x right) right|=gleft( x right)$. Но попробуем взглянуть на это уравнение немного под другим углом. Точнее, рассмотрим выражение, стоящее под знаком модуля. Напомню, что модуль любого числа может быть равен самому числу, а может быть противоположен этому числу:

[left| a right|=left{ begin{align}& a,quad age 0, \& -a,quad a lt 0. \end{align} right.]

Собственно, в этой неоднозначности и состоит вся проблема: поскольку число под модулем меняется (оно зависит от переменной), нам неясно — положительное оно или отрицательное.

Но что если изначально потребовать, чтобы это число было положительным? Например, потребуем, чтобы $3x-5 gt 0$ — в этом случае мы гарантированно получим положительное число под знаком модуля, и от этого самого модуля можно полностью избавиться:

[3x-5 gt 0Rightarrow left| 3x-5 right|=3x-5]

Таким образом, наше уравнение превратится в линейное, которое легко решается:

[3x-5=5-3xRightarrow 6x=10Rightarrow x=frac{5}{3}]

Правда, все эти размышления имеют смысл только при условии $3x-5 gt 0$ — мы сами ввели это требование, дабы однозначно раскрыть модуль. Поэтому давайте подставим найденный $x=frac{5}{3}$ в это условие и проверим:

[x=frac{5}{3}Rightarrow 3x-5=3cdot frac{5}{3}-5=5-5=0]

Получается, что при указанном значении $x$ наше требование не выполняется, т.к. выражение оказалось равно нулю, а нам нужно, чтобы оно было строго больше нуля. Печалька.:(

Но ничего страшного! Ведь есть ещё вариант $3x-5 lt 0$. Более того: есть ещё и случай $3x-5=0$ — это тоже нужно рассмотреть, иначе решение будет неполным. Итак, рассмотрим случай $3x-5 lt 0$:

[3x-5 lt 0Rightarrow left| 3x-5 right|=5-3x]

Очевидно, что в модуль раскроется со знаком «минус». Но тогда возникает странная ситуация: и слева, и справа в исходном уравнении будет торчать одно и то же выражение:

[5-3x=5-3x]

Интересно, при каких таких $x$ выражение $5-3x$ будет равно выражению $5-3x$? От таких уравнений даже Капитан очевидность подавился бы слюной, но мы-то знаем: это уравнение является тождеством, т.е. оно верно при любых значениях переменной!

А это значит, что нас устроят любые $x$. Вместе с тем у нас есть ограничение:

[3x-5 lt 0Rightarrow 3x lt 5Rightarrow x lt frac{5}{3}]

Другими словами, ответом будет не какое-то отдельное число, а целый интервал:

[xin left( -infty ;frac{5}{3} right)]

Наконец, осталось рассмотреть ещё один случай: $3x-5=0$. Тут всё просто: под модулем будет ноль, а модуль нуля тоже равен нулю (это прямо следует из определения):

[3x-5=0Rightarrow left| 3x-5 right|=0]

Но тогда исходное уравнение $left| 3x-5 right|=5-3x$ перепишется следующим образом:

[0=3x-5Rightarrow 3x=5Rightarrow x=frac{5}{3}]

Этот корень мы уже получали выше, когда рассматривали случай $3x-5 gt 0$. Более того, это корень является решением уравнения $3x-5=0$ — это ограничение, которое мы сами же и ввели, чтобы обнулить модуль.:)

Таким образом, помимо интервала нас устроит ещё и число, лежащее на самом конце этого интервала:

Итого окончательный ответ: $xin left( -infty ;frac{5}{3} right]$. Не очень-то привычно видеть такую хрень в ответе к довольно простому (по сути — линейному) уравнению с модулем, правда? Что ж, привыкайте: в том и состоит сложность модуля, что ответы в таких уравнениях могут оказаться совершенно непредсказуемыми.

Куда важнее другое: мы только что разобрали универсальный алгоритм решения уравнения с модуляем! И состоит этот алгоритм из следующих шагов:

1. Приравнять каждый модуль, имеющийся в уравнении, к нулю. Получим несколько уравнений;
2. Решить все эти уравнения и отметить корни на числовой прямой. В результате прямая разобьётся на несколько интервалов, на каждом из которых все модули однозначно раскрываются;
3. Решить исходное уравнение для каждого интервала и объединить полученные ответы.

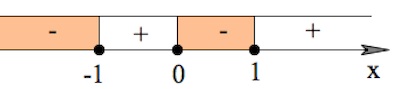
Вот и всё! Остаётся лишь один вопрос: куда девать сами корни, полученные на 1-м шаге? Допустим, у нас получилось два корня: $x=1$ и $x=5$. Они разобьют числовую прямую на 3 куска:

Ну и какие тут интервалы? Понятно, что их три:

1. Самый левый: $x lt 1$ — сама единица в интервал не входит;
2. Центральный: $1le x lt 5$ — вот тут единица в интервал входит, однако не входит пятёрка;
3. Самый правый: $xge 5$ — пятёрка входит только сюда!

Я думаю, вы уже поняли закономерность. Каждый интервал включает в себя левый конец и не включает правый.

На первый взгляд, такая запись может показаться неудобной, нелогичной и вообще какой-то бредовой. Но поверьте: после небольшой тренировки вы обнаружите, что именно такой подход наиболее надёжен и при этом не мешает однозначно раскрывать модули. Лучше уж использовать такую схему, чем каждый раз думать: отдавать левый/правый конец в текущий интервал или «перекидывать» его в следующий.

На этом урок заканчивается. Скачивайте задачи для самостоятельного решения, тренируйтесь, сравнивайте с ответами — и увидимся в следующем уроке, который будет посвящён неравенствам с модулями.:)

Смотрите также:

1. Простейшие уравнения с модулем
2. Уравнение с двумя модулями
3. Сложные выражения с дробями. Порядок действий
4. Сводный тест по задачам B15 (2 вариант)
5. Как решать биквадратное уравнение
6. B4: счетчики на электричество

Уравнения, содержащие переменную под знаком модуля ЕГЭ по математике

08.11.2013

Материал для подготовки к ЕГЭ по математике на тему: «Уравнения, содержащие переменную под знаком модуля».

Содержание темы:

10.  УРАВНЕНИЯ, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ
ПОД ЗНАКОМ МОДУЛЯ 
10.1.  Определение модуля числа 
10.2.  Раскрытие модуля 
10.3.  Методы решений уравнений 
Тест для проверки теоретических знаний 
Примеры 
Задачи для самостоятельного решения 
Контрольный тест 
 

Рекомендуем использовать этот материал при тщательной подготовке к сдаче ЕГЭ на высокий балл.

В теме содержатся теория и практические задания различного уровня сложности.

Смотреть в PDF:

Или прямо сейчас: Скачайте в pdf файле.

ЕГЭ Профиль №13. Уравнения с модулямиadmin2018-09-10T20:46:49+03:00

Используйте LaTeX для набора формулы

Уравнения с модулем

Эта статья посвящена приёмам решения различных уравнений и неравенств, содержащих
переменную под знаком модуля.

Если на экзамене вам попадётся уравнение или неравенство с модулем, его можно решить,
вообще не зная никаких специальных методов и пользуясь только определением модуля. Правда,
занять это может часа полтора драгоценного экзаменационного времени.

Поэтому мы и хотим рассказать вам о приёмах, упрощающих решение таких задач.

Прежде всего вспомним, что

Рассмотрим различные типы уравнений с модулем. (К неравенствам перейдём позже.)

Слева модуль, справа число

Это самый простой случай. Решим уравнение

Есть только два числа, модули которых равны четырём. Это 4 и −4. Следовательно, уравнение
равносильно совокупности двух простых:

Второе уравнение не имеет решений. Решения первого: x = 0 и x = 5.

Переменная как под модулем, так и вне модуля

Здесь приходится раскрывать модуль по определению. . . или соображать!

Уравнение распадается на два случая, в зависимости от знака выражения под модулем.
Другими словами, оно равносильно совокупности двух систем:

Решение первой системы: . У второй системы решений нет.
Ответ: 1.

Первый случай: x ≥ 3. Снимаем модуль:

Число , будучи отрицательным, не удовлетворяет условию x ≥ 3 и потому не является корнем исходного уравнения.

Выясним, удовлетворяет ли данному условию число . Для этого составим разность и определим её знак:

Значит, больше трёх и потому является корнем исходного уравнения

Стало быть, годятся лишь и .

Ответ:

Квадратные уравнения с заменой |x| = t

Поскольку , удобно сделать замену |x| = t. Получаем:

Модуль равен модулю

Речь идёт об уравнениях вида |A| = |B|. Это — подарок судьбы. Никаких раскрытий модуля по определению! Всё просто:

Например, рассмотрим уравнение: . Оно равносильно следующей совокупности:

Остаётся решить каждое из уравнений совокупности и записать ответ.

Два или несколько модулей

Не будем возиться с каждым модулем по отдельности и раскрывать его по определению — слишком много получится вариантов. Существует более рациональный способ — метод интервалов.

Выражения под модулями обращаются в нуль в точках x = 1, x = 2 и x = 3. Эти точки делят числовую прямую на четыре промежутка (интервала). Отметим на числовой прямой эти точки и расставим знаки для каждого из выражений под модулями на полученных интервалах. (Порядок следования знаков совпадает с порядком следования соответствующих модулей в уравнении.)

Таким образом, нам нужно рассмотреть четыре случая — когда x находится в каждом из интервалов.

Случай 1: x ≥ 3. Все модули снимаются «с плюсом»:

Полученное значение x = 5 удовлетворяет условию x ≥ 3 и потому является корнем исходного уравнения.

Случай 2: 2 ≤ x ≤ 3. Последний модуль теперь снимается «с минусом»:

Полученное значение x также годится — оно принадлежит рассматриваемому промежутку.

Случай 3: 1 ≤ x ≤ 2. Второй и третий модули снимаются «с минусом»:

Мы получили верное числовое равенство при любом x из рассматриваемого промежутка [1; 2] служат решениями данного уравнения.

Случай 4: x ≤ 1 ≤ 1. Второй и третий модули снимаются «с минусом»:

Ничего нового. Мы и так знаем, что x = 1 является решением.

Модуль в модуле

Начинаем с раскрытия внутреннего модуля.

1) x ≤ 3. Получаем:

Выражение под модулем обращается в нуль при . Данная точка принадлежит рассматриваемому
промежутку. Поэтому приходится разбирать два подслучая.

1.1) Получаем в этом случае:

Это значение x не годится, так как не принадлежит рассматриваемому промежутку.

1.2) . Тогда:

Это значение x также не годится.

Итак, при x ≤ 3 решений нет. Переходим ко второму случаю.

Здесь нам повезло: выражение x + 2 положительно в рассматриваемом промежутке! Поэтому никаких подслучаев уже не будет: модуль снимается «с плюсом»:

Это значение x находится в рассматриваемом промежутке и потому является корнем исходного уравнения.

Так решаются все задачи данного типа — раскрываем вложенные модули по очереди, начиная с внутреннего.

Читайте также о том, как решать неравенства с модулем.

Уравнения_с_модулями
материал для подготовки к егэ (гиа) по алгебре (10 класс) на тему

Элективный курс по математике для учащихся 10-11 классов

Скачать:

Вложение	Размер
20295_uravneniya_s_modulyami.rar	306.42 КБ

Предварительный просмотр:

Занятие 1. Алгебраические уравнения с модулем.

Чтобы решить уравнение, содержащее переменную под знаком модуля, следует освободиться от знака модуля, воспользовавшись его определением:

При решении таких уравнений обычно поступают следующим образом:

1. находят те значения переменной, при которых выражения, стоящие под знаком модуля, обращаются в нуль;
2. область допустимых значений переменной разбивается на промежутки, на каждом из которых выражения, стоящие под знаком модуля, сохраняют знак;
3. на каждом из найденных промежутков решается уравнение без знака модуля.

Совокупность решений на указанных промежутках составляет решение исходного уравнения.

Пример 1 . Решите уравнение: .

Найдем те значения переменной, при которых выражение, стоящее под знаком модуля, обращаются в нуль: х – 2 = 0, х = 2.

— +

Рассмотрим решение уравнения на промежутках: х (2; ).

1. Если х , то 2 – х = 5; — х = 3; х = — 3; — 3

2. Если : х (2; ), то х – 2 = 5; х = 7; 7 (2; ).

Пример 2 . Решите уравнение: = х + 2.

В левой части уравнения стоит неотрицательное число, следовательно

х + 2 0., т.е. х — 2. Раскроем модуль с учетом, что х — 2, получим:

х + 2 = х +2, решением уравнения является любое число х .

Пример 3. Решите уравнение: .

Найдем те значения переменной, при которых выражения, стоящие

под знаком модуля, обращаются в нуль: 2х + 1+ 0; х = — 0,5; х – 4 =0; х = 4.

— — + — + +

Рассмотрим решение уравнения на промежутках: х (4;+ ).

1. Если х , то -2х – 1 = — х + 4; -х = 5; х = — 5;

2. Если х , то 2х + 1 = — х +4; 3х = 3; х = 1.

3. Если х (4; + ), то 2х + 1 = х – 4; х = — 5;

Пример 4. Решите уравнение: 0,6 = х 2 + 0,27.

Найдем то значения переменной, при котором выражение, стоящее под знаком модуля, обращаются в нуль: х – 0,3 = 0; х = 0,3.

— +

0,3 х

0,6(0,3 – х) = х 2 + 0,27;

0,18 – 0,6х = х 2 + 0,27;

х 2 + 0,6х + 0,09 = 0;

2. Если х (0,3; + ), то

0,6(х — 0,3) = х 2 + 0,27;

0,6 х – 0,18 = х 2 + 0,27;

х 2 – 0,6х + 0,45 = 0;

D = 0,36 – 1,8 = — 1,44, т.к. D

Пример 5 . Решите уравнение: х 2 + 4 — 7х + 11 = 0.

Найдем то значения переменной, при котором выражение, стоящее под знаком модуля, обращаются в нуль: х – 3 = 0; х = 3.

— +

3 х

х 2 – 4(х – 3) – 7х + 11 = 0;

х 2 – 4х + 12 – 7х + 11 = 0;

х 2 – 11х + 23 = 0;

х 2 + 4х — 12 – 7х + 11 = 0;

1. = -2. Ответ: пустое множество;

2. = 5. Ответ: — 7; 3.

3. = 11. Ответ: — 4; 7.

4. = х. Ответ: пустое множество.

5. = 5 – 4х. Ответ: 1.

8. . Ответ: — 3,5; 3,5.

9. = + 2. Ответ: — 7; — 1.

.

По теме: методические разработки, презентации и конспекты

Методические рекомендации по теме: «Решение уравнений с модулем в курсе математики 7-8 класса»

Методические рекомендации по теме: «Решение уравнений с модулем в курсе математики 7-8 класса». В работе представлены способы решения уравнений с модулем. Даны карточки заданий: с применением классифи.

презентация уравнения с модулем

Данная презентация предназначена для использования на уроках алгеьбры и начал анализа в старшей школе при обобщении темы «Уравнения с модулем и способы их решения». Также презентацию можно использоват.

Решение дробно — рациональных уравнений с модулем.

Данная презентация разработана для подготовки учащихся 10 классса к КДР, может быть полезна для подготовки учащихся 11 класса к ЕГЭ.

Урок — семинар в 11 классе «Решение показательных и логарифмических уравнений с модулем»

Данный урок — семинар рекомендуется для работы в профильном классе, а также материал этого занятия можно использовать на факультативном занятии. Здесь предложен конспект урока, презентация, разадаточн.

Презентация к уроку»Графики уравнений с модулями»

Методическая разработка для повышения наглядности и качества усвоения материала по теме:»Графики уравнений с модулями».Основная цель-познакомить учащихся с основными приёмами построения графиков уравн.

Презентация «Уравнения с модулем»

Урок обобщения и систематизации знаний по теме: «Решение уравнений с модулем».

Решение уравнений, содержащих модуль.

Конспект урока для элективного занятия в 9 классе.

Уравнения с модулем

Что такое уравнение с модулем

Модуль числа — абсолютная величина, демонстрирующая удаленность точки от начала координат.

В том случае, когда число является отрицательным, его модуль соответствует числу, ему противоположному. Для неотрицательного числа модуль равен этому числу.

| x | = x , x ≥ 0 — x , x 0

Уравнения с модулем являются такими уравнениями, в составе которых имеется переменная, заключенная в знак модуля.

Самое простое уравнение с модулем |f(x)|=a является равносильным совокупности

Здесь a>0. При а отрицательном у такого уравнения отсутствует решение.

Уравнения с модулем могут быть предложены в качестве самостоятельного задания. Кроме того, подобные выражения нередко образуются в процессе решения других видов уравнений, к примеру, квадратных или иррациональных.

Разберем подробное решение квадратного уравнения:

Заметим, что справа имеется квадрат числа 4:

На первый взгляд, нужно избавиться от квадратов, чтобы получить линейное уравнение. С другой стороны, существует правило:

Вычисления следует продолжить с учетом записанной формулы. Тогда получим уравнение с модулем:

x 2 = 4 2 ⇔ x 2 = 4 2 ⇔ x = 4

Рассмотрим для тренировки пример, когда уравнения с модулем появляются при решении иррациональных уравнений. Например, дано уравнение:

2 x — 1 2 = 9 x 2 + 12 x + 4

Согласно стандартному алгоритму действий, в этом случае потребуется выполнить действия:

• перенос слагаемых;
• приведение подобных;
• решение квадратного уравнения, например, с помощью дискриминанта.

Второй вариант решения предусматривает использование формулы сокращенного умножения квадрат суммы:

9 x 2 + 12 x + 4 = 3 x + 2 2

Преобразуем сложное уравнение:

2 x — 1 2 = 3 x + 2 2

На первый взгляд, можно избавиться от квадратов и решить линейное уравнение. Однако:

В результате получим:

2 x — 1 2 = 3 x + 2 2 ⇔ 2 x — 1 = 3 x + 2 .

При решении уравнений, которые содержат модуль, необходимо помнить свойства модуля:

1. Модуль числа является неотрицательным числом: x ≥ 0 , x = 0 ⇔ x = 0 .
2. Противоположные числа равны друг другу по модулю: — x = x .
3. Произведение пары или более чисел по модулю равно произведению модулей этих чисел: x · y = x · y .
4. Частное пары чисел по модулю равно частному модулей этих чисел: x y = x y , y ≠ 0 .
5. Сумма чисел по модулю в любом случае меньше или равна сумме модулей данных чисел: x + y ≤ x + y .
6. Постоянный множитель, который больше нуля, допустимо вынести за знак модуля: c x = c · x при c > 0 .
7. Квадрат какого-то числа по модулю равен квадрату данного числа: x 2 = x 2 .

Пример 3

Руководствуясь перечисленными свойствами модуля, рассмотрим решение уравнения:

Заметим, что x равен x при x больше либо равно нулю. Значение –x возможно, когда x является отрицательным числом. Таким образом:

x = 7 ⇔ x = 7 , п р и x ≥ 0 — x = 7 , п р и x 0 ⇔ x = 7 x = — 7

Рассмотрим несколько иное уравнение:

В этом случае логика такая же, как в предыдущем примере:

x = — 7 ⇔ x = — 7 , при x ≥ 0 — x = — 7 , при x 0 ⇔ x = — 7 x ≥ 0 ⇒ р е ш е н и я н е т x = 7 x 0 ⇒ р е ш е н и я н е т

Способы решения уравнений с модулями для 10 и 11 классов

Существует три основных вида уравнений с модулем, которые предусматривают определенные подходы к решению:

1. Уравнения x = a . x = a ⇔ x = a , п р и x ≥ 0 — x = a , п р и x 0 ⇔ x = a x = — a .
2. Уравнения вида x = y . x = y ⇔ y ≥ 0 x = y x = — y

Примеры решения задач с объяснением

Уравнения, которые содержат модуль и имеют вид |x| = |a|, решают с помощью определения модуля.

Рассмотрим в качестве примера:

Определим x . Когда x ≥ 0 , значение равно х . Если x – х . Таким образом:

x = 5 ⇔ x = 5 при x ≥ 0 — x = 5 при x 0 ⇔ x = 5 x = — 5 .

Получим, что решением уравнения являются -5; 5.

Рассмотрим следующее задание, в рамках которого необходимо решить уравнение:

Воспользуемся стандартным алгоритмом:

x = — 3 ⇔ x = — 3 при x ≥ 0 — x = — 3 при x 0 ⇔ x = — 3 x ≥ 0 ⇒ решений нет x = 3 x 0 ⇒ решений нет

Согласно первому свойству модуля:

x ≥ 0 , то есть модуль в любом случае не является отрицательным числом.

Можно обобщить рассмотренные действия и записать правило для решения уравнений, которые имеют вид x = a . Данное правило можно использовать в работе:

x = a ⇒ a ≥ 0 x = a x = — a .

Используя данное правило, решим уравнение:

По сравнению с предыдущим примером, здесь под знаком модуля записано иное выражение. Однако суть решения от этого не меняется. Зная правило, выполним замену:

x — 5 = 3 ⇔ 3 ≥ 0 x — 5 = 3 x — 5 = — 3 ⇒ x = 8 x = 2

Решим следующее уравнение:

Воспользуемся правилом и получим:

3 x — 5 = 3 ⇔ 3 ≥ 0 3 x — 5 = 3 3 x — 5 = — 3 ⇒ x = 8 3 x = 2 3

Далее рассмотрим решение уравнений, которые записаны в виде | x | = | y | .

При раскрытии модулей, согласно определению, возникнет необходимость во множестве проверок. Например, потребуется определить, какое число является положительным, а какое будет отрицательным. Полученную в результате систему в дальнейшем необходимо упростить.

Второй вариант решения подразумевает изначально краткую запись вычислений. Вспомним, что по свойству модуля:

Применим это свойство к нашему примеру и исключим знаки модулей из уравнения:

x = y ⇔ x 2 = y 2 ⇔ x 2 = y 2 ⇔ x 2 — y 2 = 0 ⇔

⇔ x — y x + y = 0 ⇔ x = y x = — y .

Рассмотрим еще несколько примеров.

Воспользуемся рассмотренным правилом применения свойства модуля, получим:

x + 1 = 2 x — 1 ⇔ x + 1 = 2 x — 1 x + 1 = — 2 x — 1 ⇔ x = 2 x = 0 .

Решение выполняем по аналогии с предыдущими заданиями:

2 x — 9 = 3 — x ⇔ 2 x — 9 = 3 — x 2 x — 9 = x — 3 ⇔ 3 x = 12 x = 6 ⇔ x = 4 x = 6 .

Разберем на примере, как решать уравнения вида | x | = y .

Заметим, что справа записана переменная, которая может быть положительным или отрицательным числом. Исходя из того, что модуль не может быть отрицательным числом, убедимся в том, что эта переменная также не является отрицательным числом:

x = y ⇔ y ≥ 0 x = y x = — y

Воспользуемся стандартным алгоритмом:

x + 1 = 1 — 2 x ⇔ 1 — 2 x ≥ 0 x + 1 = 1 — 2 x x + 1 = 2 x — 1 ⇔ x ≤ 1 2 x = 0 x = 2 ⇔ x = 0 .

Заметим, что без проверки на положительность части уравнения, которая записана с правой стороны, существуют риски появления посторонних корней в решении. К примеру, проверим x=2 путем подстановки в начальное уравнение x + 1 = 1 — 2 x :

2 + 1 = 1 — 2 · 2 ⇔ 3 = — 3 не является верным.

При решении уравнений с модулем также применяют метод интервалов. Данный способ следует применять в тех случаях, когда уравнение содержит более двух модулей.

Рассмотрим пример такого выражения:

x + 3 — 2 x — 1 = 1

Первый модуль имеет вид:

Согласно определению модуля, при раскрытии знака выражение под ним сохраняется без изменений, если:

После раскрытия знака модуля получим противоположный знак, когда:

x + 3 = x + 3 , если x + 3 ≥ 0 — x — 3 , если x + 3 0 .

По аналогии выполним преобразования второго модуля:

2 x — 1 = 2 x — 1 , если 2 x — 1 ≥ 0 1 — 2 x , если 2 x — 1 0 .

Сложность заключается в том, что требуется проанализировать много вариантов, то есть по два варианта для каждого из модулей. Всего получится четыре уравнения. А в том случае, когда модулей три, потребуется рассмотреть восемь уравнений. Возникает необходимость в сокращении числа вариантов.

Заметим, что в нашем примере не предусмотрено одновременное выполнение всех условий:

Данные условия противоречивы относительно друг друга. В связи с этим, нецелесообразно раскрывать второй модуль со знаком плюс, когда первый модуль раскрыт со знаком минус. В результате получилось избавиться от одного уравнения.

Обобщая эту информацию, можно записать алгоритм действий. В первую очередь следует вычислить корни выражений, заключенных под знаком модуля. В результате получаются такие х , при которых выражения принимают нулевые значения:

x + 3 = 0 ⇒ x = — 3 2 x — 1 = 0 ⇒ x = 1 2

С помощью стандартного способа интервалов можно отметить на координатной прямой корни выражений, которые находятся под модулями, и расставить знаки. Далее для каждого из полученных интервалов нужно составить и решить уравнение.

В этом случае оба модуля раскрываются со знаком минус:

— x + 3 + 2 x — 1 = 1 ⇔ — x — 3 + 2 x — 1 = 1 ⇔ x = 5 > — 3 является сторонним корнем.

В данном выражении первый модуль раскроется со знаком плюс, а второй — со знаком минус:

x + 3 + 2 x — 1 = 1 ⇔ x + 3 + 2 x — 1 = 1 ⇔ x = — 1 3 полученный корень соответствует своему интервалу.

Теперь для обоих модулей будет записан знак плюс:

x + 3 — 2 x — 1 = 1 ⇔ x + 3 — 2 x + 1 = 1 ⇔ x = 3 данный корень также подходит для решения.

Выполним проверку корней. В первом случае корень посторонний:

x = 5 : 5 + 3 — 2 · 5 — 1 = 8 — 9 = — 1 ≠ 1

Второй корень является решением:

x = — 1 3 : — 1 3 + 3 — 2 · — 1 3 — 1 = 8 3 — 5 3 = 1 .

Третий корень также является решением:

x = 3 : 3 + 3 — 2 · 3 — 1 = 6 — 5 = 1 .

Таким образом, запишем ответ: — 1 3 ; 3 .

Существует ряд уравнений, в которых модуль расположен под знаком модуля. К примеру:

В этом случае следует раскрывать модули поочередно. Проанализируем два варианта решения.

Первое решение подразумевает вычисления для уравнения, которое имеет вид:

f x = a ⇔ f x = a f x = — a

Здесь f x является подмодульным выражением. Применительно к нашей задаче, это:

x — 5 = 3 ⇔ x — 5 = 3 x — 5 = — 3 ⇔ x = 8 x = 2

Получена пара простейших уравнений аналогичного вида, то есть:

x = 8 x = — 8 x = 2 x = — 2

Данные четыре числа являются решениями. Проверить это можно путем подстановки ответов в исходное уравнение.

Второй вариант решения является универсальным и позволяет справиться с нестандартными задачами.

Раскроем сначала внутренние модули:

Начальное уравнение будет записано, как пара уравнений:

x ≥ 0 x — 5 = 3 x 0 — x — 5 = 3

Задачи для самостоятельного решения

Найти корни уравнения:

Здесь нужно возвести в квадрат все части выражения, сохраняя знак плюса справа. Тогда получится система:

Найдем корни квадратного уравнения:

3 x 2 — 18 x + 24 = 0

В процессе потребуется сократить уравнение на 3:

D = ( — 6 ) 2 — 4 · 1 · 8 = 36 — 32 = 4

Заметим, что D>0. В таком случае у уравнения есть пара решений, которые можно определить так:

x 1 , 2 = — b ± D 2 a ⇒ x 1 , 2 = 6 ± 4 2 · 1 ⇒ x 1 , 2 = 6 ± 2 2 ⇒ x 1 = 4 , x 2 = 2

Заметим, что оба корня больше единицы. Это соответствует условию. В результате начальное уравнение обладает двумя решениями:

x 1 = 4 и x 2 = 2

Ответ: x 1 = 4 , x 2 = 2

Найти корни уравнения:

Здесь требуется возвести в квадрат обе части уравнения:

( 3 x — 1 ) 2 = ( x + 5 ) 2

9 x 2 — 6 x + 1 = x 2 + 10 x + 25

8 x 2 — 16 x — 24 = 0

Заметим, что получившееся равенство можно сократить на число 8:

Используя теорему Виета, определим корни уравнения. Предположим, что x 1 и x 2 являются в данном случае решениями, тогда:

x 1 + x 2 = 2 , а x 1 · x 2 = — 3 ⇒ x 1 = 3 и x 2 = — 1 . .

Ответ: x 1 = 3 , x 2 = — 1

Нужно решить уравнение:

| x + 1 | + | x — 5 | = 20

Воспользуемся методом интервалов. Определим х , при которых модули принимают нулевые значения:

x + 1 = 0 ⇒ x = — 1 ; x — 5 = 0 ⇒ x = 5

С помощью данных точек координатная прямая будет поделена на три интервала:

Далее необходимо решить уравнение в каждом случае:

Корень соответствует определенному ранее промежутку.

Этот промежуток не имеет корней.

Этот корень соответствует определенному ранее интервалу.

Ответ: x 1 = — 8 , x 2 = 12

3 x + 1 = 1 — 2 x ⇔ 3 x + 3 = 1 — 2 x 3 x + 3 = 2 x — 1 ⇔ 5 x = — 2 x = — 4 ⇔ x = — 2 5 x = — 4 .

Ответ: x = — 2 5 , x = — 4

Найти корни уравнения:

2 x — 9 = 3 — x ⇔ 3 — x ≥ 0 2 x — 9 = 3 — x 2 x — 9 = x — 3

x ≤ 3 3 x = 12 x = 6 ⇔ x ≤ 3 x = 4 x = 6 ⇔ x ∈ ∅ .

Найти корни уравнения:

— 2 x + 4 = 3 — 4 x ⇔ 2 x + 8 = 4 x — 3 ⇔ ;

4 x — 3 ≥ 0 2 x + 8 = 4 x — 3 2 x + 8 = 3 — 4 x ⇔ x ≥ 3 4 x = 11 2 x = — 5 6 ⇔ x = 11 2 .

Найти корни уравнения:

2 x 2 — 15 = x ⇔ x ≥ 0 2 x 2 — x — 15 = 0 1 2 x 2 + x — 15 = 0 2

Найдем корни квадратных уравнений:

Заметим, что они обладают идентичным дискриминантом:

D = 1 + 4 · 2 · 15 = 121 = 11 2 .

1 : x 1 , 2 = 1 ± 11 4 ⇔ x = 3 x = — 5 2

2 : x 1 , 2 = — 1 ± 11 4 ⇔ x = — 3 x = 5 2

Таким образом, начальное уравнение можно записать в виде системы:

2 x 2 — 15 = x ⇔ x ≥ 0 x = 3 x = — 5 2 x = — 3 x = 5 2 ⇔ x = 3 x = 5 2

Найти корни уравнения:

x + 2 — 3 x — 1 + 4 — x = 3

x + 2 — 3 x — 1 + 4 — x = 3 x + 2 = 0 ⇒ x = — 2 3 x — 1 = 0 ⇒ x = 1 3 4 — x = 0 ⇒ x = 4

— x + 2 + 3 x — 1 + 4 — x = 3

x = 2 > — 2 ⇒ — этот корень является посторонним.

x + 2 + 3 x — 1 + 4 — x = 3 ⇔

3 x = — 2 ⇔ x = — 2 3 ∈ — 2 ; 1 3 этот корень удовлетворяет условиям.

x + 2 — 3 x — 1 + 4 — x = 3 ⇔ — 3 x = — 4 ⇔ x = 4 3 ∈ 1 3 ; 4 этот корень удовлетворяет условиям.

x + 2 — 3 x — 1 — 4 — x = 3 ⇔ x = 4 ⇔ x = — 4 4 — корень посторонний

Ответ: — 2 3 ; 4 3 .

Найти корни уравнения:

3 x — 5 + 3 + 2 x = 2 x + 1

3 x — 5 + 3 + 2 x = 2 x + 1 ⇔ 3 x — 5 + 3 + 2 x — 2 x + 1 = 0 .

3 x — 5 = 0 ⇒ x = 5 3 3 + 2 x = 0 ⇒ x = — 3 2 x + 1 = 0 ⇒ x = — 1

— 3 x — 5 — 3 + 2 x + 2 x + 1 = 0 ⇔

— 3 x = — 4 ⇔ x = 4 3 > — 3 2 ⇒ — корень является посторонним

— 3 x — 5 + 3 + 2 x + 2 x + 1 = 0 ⇔

x = — 10 — 1 ⇒ — корень является посторонним

— 3 x — 5 + 3 + 2 x — 2 x + 1 = 0 ⇔

— 3 x = — 6 ⇔ x = 2 > 5 3 ⇒ — корень является посторонним

3 x — 5 + 3 + 2 x — 2 x + 1 = 0 ⇔

3 x = 4 ⇔ x = 4 3 5 3 ⇒ — корень является посторонним

В результате на рассмотренных интервалах графика координатной прямой отсутствуют корни. В таком случае уравнение не имеет решений.

Определение. Геометрический смысл

Модуль (или абсолютная величина)   числа   (обозначается как )— неотрицательное число, определение которого зависит от типа числа  

А именно:

Мы будем называть данное правило правилом раскрытия модуля.

Например, так как , попадаем в первую строку (ситуацию).

так как попадаем во вторую ситуацию.

С геометрической точки зрения,  – есть расстояние между числом   и началом координат.

Решением уравнения, например,  являются числа и , потому что расстояние от точки координатной прямой до нуля равно , и расстояние от точки   до нуля также равно 6.

|| с геометрической точки зрения означает расстояние между точками и .

Полезные примеры

1) Раскрыть модуль:

Так как больше, чем , то , а значит согласно правилу раскрытия модуля.

2) Раскрыть модуль:

Так как больше нуля при всех значениях , то согласно правилу раскрытия модуля.

3) Раскрыть модуль:

Так как , то , а значит, согласно правилу раскрытия модуля.

Решение уравнений

1) Решить уравнение .

Модуль – всегда неотрицательная величина, поэтому уравнение решений не имеет.

Ответ: { }

2) Решить уравнение: .

Модуль раскрывается таким образом в случае, когда  .

Ответ:

3) Решить уравнение:

Согласно геометрическому смыслу модуля левая и правая части равенства представляют из себя одно и то же.

Ответ:

4)  Решить уравнение:

Раскрываем модуль согласно правилу раскрытия модуля:

а)

Имеем: ,     

Откуда .

Поскольку мы находимся в ситуации , то подходит только корень .

б)

Имеем: ,    

Откуда или .

Поскольку мы находимся в ситуации , то ни один корень из найденных в пункте (б) нам не подходит.

Ответ: .

Коротко можно было бы решение оформить так:

5) Решить уравнение:

Раскрываем модуль согласно правилу раскрытия модуля:

a) Первый случай:

Что равносильно .

б) Второй случай:

Что равносильно

Ответ:

6) Решить уравнение:

Можно было бы действовать согласно правилу раскрытия модуля, но проще будет в данном случае рассуждать так:

Внутри модуля может «скрываться» как так и .

Поэтому или

или

Из первого уравнения или , а второе уравнение корней не имеет.

Ответ:

7) Решить уравнение:

Раскрываем модуль согласно правилу раскрытия модуля:

а) Первый случай:

Рассмотрим отдельно первую строку системы:

Рассмотрим уравнение из системы:

или

Разложим на множители левую часть уравнения способом группировки, предварительно разбив среднее слагаемое на два:

Откуда (трехчлен в скобках корней не имеет).

Данный корень удовлетворяет первой строке системы, он пойдет  в ответ.

б) Второй случай:

Решение неравенства системы:

Корень удовлетворяет решению неравенства системы.

Собираем решения.

Ответ:

Также, смотрите «Модуль. Простейшие неравенства с модулем» здесь.

Вы можете пройти тест  по теме «Модуль. Раскрытие модуля. Простешие уравнения с модулем»