Впереди ЕГЭ по математике! |
| Друзья, здравствуйте!
Кажется, что до ЕГЭ по математике целое лето и весь 11 класс. На самом деле, 11 месяцев. Из них 2 месяца летних. Остается всего 9 месяцев, в которые надо успеть все. Поэтому, давайте не будем терять время и начнем работу на поступление в вуз мечты заранее. Не отставайте! Самые умные десятиклассники уже готовятся к ЕГЭ! Не спеша, в комфортном режиме изучают темы профильной математики. |
Нельзя потерять лето
Лето – лучшее время, чтобы освоить геометрию, стереометрию, уравнения и неравенства, функции и графики, «экономическую» задачу и даже нестандартную задачу №19. Школа не отвлекает. Можно заниматься с удовольствием. Дома. В удобное для вас время.
Для тех, кто перешел в 11-й класс – наш Онлайн-курс «10 + 11» — два года по цене одного.
Почему сейчас для вас лучше всего подходит онлайн курс «10 + 11»?
Вы будете заниматься онлайн по авторской методике Анны Малковой. Прямо сейчас вы сможете повторить весь материал 10-го класса.
Вам будут доступны видеозаписи всех мастер-классов, проведенных в этом году для десятиклассников. А также вся теория, все домашние задания и их решения.
Ваши темы сейчас – это часть 1 ЕГЭ по математике, планиметрия и стереометрия, «экономические» и нестандартные задачи и решение вариантов ЕГЭ.
А в 11-м классе – продолжение. Подготовка на максимальные баллы в течение всего года. Освоим все задачи ЕГЭ, от части 1 до самых сложных.
Начинаем уже сейчас!
Онлайн-курс «10 + 11» по профильной математике. Ведет Анна Малкова.
Стоимость всего 4800 рублей. Два года занятий по цене одного!
Те, кто приходят в ЕГЭ-Студию на весенние интенсивы в 11-м классе, часто говорят: «Как жаль, что поздно о вас узнали. И вообще поздно начали заниматься». Не повторяйте чужих ошибок! Начинайте готовиться к ЕГЭ сейчас.
Записывайтесь на Онлайн-курс «10 + 11» по профильной математике.
Уверенный старт подготовки: 65 баллов за это лето
39 занятий по 2 часа + задачи для самостоятельного решения + ответы на ваши вопросы.
Ты пройдешь:
— Текстовые задачи ЕГЭ. Задачи на проценты. Движение и работа.
— Теория вероятностей.
— Геометрия.
— Алгебраические уравнения и системы уравнений.
— Тригонометрия. Преобразования тригонометрических выражений.
— Функции и графики.
— Производная.
— Алгебраические неравенства. Иррациональные неравенства. Неравенства с модулем.
— Геометрия и стереометрия.
— И даже «Экономические» задачи!
ЗАКАЗАТЬ
Что такое Онлайн-курс по математике.
Для учителей, репетиторов, абитуриентов и всех, кто сдает ЕГЭ на 65+ баллов. Поможет разобрать нужную тему с нуля или устранить недопонимания.
Курс разбит на темы, содержит видеоучебник и разбор всех типов задач, задания для самостоятельного решения с проверкой нашими преподавателями. Содержит 8 репетиционных ЕГЭ за год. Это полноценная, интерактивная система онлайн-обучения.
Ваша задача на лето выделить 5-10 часов в неделю и проходить все занятия подряд: читать теорию, самостоятельно решать предложенные задачи, смотреть видеоразбор, задавать вопросы, если что-то осталось непонятным.
Весь курс «10+11» сейчас: 15 600 руб 4 800 руб
ЗАКАЗАТЬ
Курс для преподавателей
Аналогично курсу «10+11 класс, 100 баллов»:
+ Бессрочный доступ.
+ Мастер-классы только для преподавателей.
Курс «10+11 класс, 100 баллов»
— 72 часа видеоучебника,
— 1-2 онлайн занятия в неделю,
— Домашние задания с проверкой,
— Доступ до 25 июня 2020 г.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Не забыть математику. План летней подготовки.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из Рубрики: Новости.
Публикация обновлена:
11.03.2023
Мы используем файлы cookie, чтобы персонализировать контент, адаптировать и оценивать результативность рекламы, а также обеспечить безопасность. Перейдя на сайт, вы соглашаетесь с использованием файлов cookie.
Вам стало плохо и неприятно от названия этой статьи — какая может быть подготовка в такую беззаботную пору, как лето? Но посудите сами: в это время года у нас есть огромное количество свободного времени. Выделяя буквально 30-40 минут пару раз в неделю, вы сделаете огромный вклад в вашу будущую подготовку. Прежде всего, вам будет легче готовиться в учебное время, ведь вы уже будете знакомы с основами экзамена. Встает другой вопрос — а как готовиться к ЕГЭ летом, ведь объем информации по подготовке очень большой. В этом вопросе могут помочь только эксперты экзамена — наши преподаватели.
В этой статье мы собрали для вас советы по подготовке к ЕГЭ летом по некоторым предметам от ведущих преподавателей учебного центра MAXIMUM Education. Читайте, вникайте, и прекрасной вам летней учебы! 🙂
Итак, как готовиться к ЕГЭ летом?
Математика
Рассказывает Татьяна Медведева:
Во-первых, вы должны хорошо отдохнуть, поэтому никаких зубрежек быть не должно, иначе вы перегорите и к началу 11 класса вам не будет хотеться ничего, кроме как окончания всего этого ада. Но с другой стороны, чтобы хорошо сдать профильную математику, нужно держать мозг в тонусе, в нем должна оставаться некая система, структура, поэтому полезно повторять какие-либо базовые вещи. Чаще всего именно на них ребята и «падают» потом на экзамене. Условно говоря, можно вспомнить то, что было в классе 8-9, базовую геометрию, какие-либо простейшие задачки. Можно просто взять задачник за 7-8 класс и прорешивать оттуда задания. Понятное дело, это не должна быть прям учеба учеба, но периодически простые задания делать нужно, потому что забываются как раз-таки базовые вещи.
Плюс, если на выходе из десятого класса вы понимаете, что у вас есть проблемы со структурой, вы учите теорию, но никогда не можете ее применить на практике, то вы можете заняться составлением неких «карт знаний», которые могут вам помочь. К примеру, в классе седьмом вы учили что такое треугольник и с чем его едят, но сейчас абсолютно не помните, как с ним работать, как применять теоремы и свойства, то вам имеет смысл нарисовать себе схему с треугольниками, сделать классификацию, на которой подписать все основные свойства и тут же подписать где эти свойства применяются, в каких простейших задачах используется. Но ни в коем случае не заниматься сверх нагрузкой, то есть не решать какие-либо сложные задачи, не проходить новые сложные темы. Если вы участвуете в олимпиадах, то да, интересные, нестандартные задачки можно порешать, чтобы мозг был в тонусе, но ни в коем случае не нагружать себя чем-то очень сложным.
Обществознание
Анна Гагарина:
1. Обществознание — это не предмет на потом. Это целых 5 отдельных наук! И да, они не легче физики. Начинай готовиться сейчас.
2. 3 часа 55 минут бывает мало, чтобы написать экзамен целиком. Тренируйте скорость письма, учитесь расставлять приоритеты.
3. Вторая часть может занимать до 8 листов. Почерк! Научитесь писать понятно, четко, структурно и быстро.
4. Учитесь писать планы сразу. По статистике все, кто откладывает тренировку на потом, просто не успевают в последствии понять, как писать ответ на это задание.
5. Знание критериев оценки — гарантия того, что вы сможете правильно оформить ответ. Многие теряют баллы именно из-за неверной записи ответов. Воспользуйтесь помощью экспертов.
6. По обществознанию нет универсально подходящего учебника или пособия. Не все, что пишут в учебнике нужно к экзамену. Не все, что есть в пособиях верно с точки зрения теории. Нужно внимательно относиться к выбору источника информации. Шанса подать апелляцию из-за того, что в вашем пособии был другой термин, не будет.
7. Обществознание — это стандартизированный экзамен, который проверяет не теорию, а умение применить эту теорию на практике. Почти все задания будут проверять именно понимание, поэтому просто заучить не получится. Совмещайте изучение теории с активной практической отработкой и решением заданий.
Английский язык
Валерия Козик:
Следует повторить грамматику, потому что потом будет не до нее — заведите привычку читать грамматические учебники и делать маленькие упражнения каждый день по 30 мин. Это было бы вообще топ 🙂
Как зубрить грамматику не скучно и при этом с пользой для экзамена? Слушайте/смотрите видео BBC Learning English, выполняйте к ним задания на сайте — морально готовя себя к аудированию.
Читайте, так как большая проблема — нехватка слов.
Чем больше новой информации ученик поглотит за летний период (и привыкнет поглощать в целом), тем лучше для экзамена, поскольку в течение учебного года мы делаем упражнения «лишь бы сделать», а летом, когда нас ничего не напрягает, мы обычно подходим с интересом ко всему новому и значит зубрежка слов дается проще.
Литература
Тамара Коновалова:
Читайте! У вас впереди год, чтобы потом не прийти в последние месяцы в состоянии: о боже, у меня ещё «Война и мир», «Тихий дон», что же делать! Просто читайте книги, учите стихотворения (заведите отдельную тетрадку, куда будете записывать те, что нужны для экзамена). С терминами и форматом ЕГЭ можно будет разобраться и уже после сентября, а лето посвятите книгам из кодификатора ФИПИ.
Физика
Михаил Ямашев:
Скачайте материалы с ФИПИ, т.е. демонстрационные варианты, кодификаторы, спецификации. Работайте следующим образом: дело в том, что, как и любой экзамен, ЕГЭ можно сдать, расписав билеты, по сути, как и в университете, и как раз-таки то, что нужно писать в том или ином билете (в нашем случае — в задании), содержится в кодификаторе и спецификации.
Я своим ученикам предлагаю делать следующее:
- Составить лист подготовки, где будут сосредоточены все формулы для решения какого-либо задания. Например, задание номер один.
- Смотреть в спецификацию, в кодификатор, и узнать, что же там будет.
- Дальше составить лист подготовки, который содержит все объяснения, формулы, основные алгоритмы решения задач именно на задачу номер один.
И вот так собирается несколько листов со всеми заданиями из экзаменов.
Человек, который это всё сделает, запоминает эти все знания, которые изложены на листах подготовки. Это можно легко сделать с помощью различных тестовых заданий. При их решении обращайтесь к приготовленным материалам.
Как видите, готовиться к ЕГЭ летом вполне возможно. Главное — правильно расставить приоритеты и распределить нагрузку. Дополнительный заряд мотивации вы найдете на летних курсах MAXIMUM Education! Наши преподаватели помогут закрыть пробелы в знаниях и освоить новые темы следующего учебного года. Это отличный шанс начать готовиться к ЕГЭ, пока остальные бездельничают, и обеспечить себе более спокойную подготовку. Записывайтесь сейчас и получите скидку 5% по промокоду MAXIMUMLETO5.
Подготовка к ЕГЭ по математике
Из каких частей состоит ЕГЭ по математике в 2023 году
Математика — один из двух обязательных предметов на ЕГЭ. Но, в отличие от русского языка, эта дисциплина предлагает 2 уровня сложности: профильный и базовый. Какий именно вариант выбрать, зависит от вашей цели. Если вуз, в который вы хотите поступить, требует профильного уровня, нужно сдавать его. Обычно это касается технических специальностей.
Для получения аттестата выпускникам школ хватит и базового. Но финальное решение за вами. Если вы хотите сдать профильный вариант, просто чтобы проверить свои знания и уровень подготовки, — дерзайте!
Структура базового уровня ЕГЭ по математике
Базовый уровень проверяет основные знания школьника по математике. Такой экзамен не делится на части: в него входит только 21 задание с кратким ответом. Ответом может быть целое число, десятичная дробь или ряд цифр. По уровням сложности задания экзамена тоже не делятся — все задачи в нем базового уровня. Чтобы выполнить такую работу, ученику дают 180 минут.
Структура профильного уровня ЕГЭ по математике
Варианты профильного уровня проверяют основные и углубленные знания школьника. В 2023 году ЕГЭ состоит из 2 частей:
-
1-я часть: 11 задач с кратким ответом;
-
2-я часть: 7 задач с развернутым ответом.
В первой части ответом может быть целое число, десятичная дробь или ряд цифр. Во второй части — полное обоснованное решение и ответ. Чтобы выполнить задания экзамена, школьнику дают 235 минут.
Задачи ЕГЭ по математике профильного варианта делятся на категории по уровням сложности. В таблице ниже можно увидеть, как именно.
| Базовый | 6 |
| Повышенный | 10 |
| Высокий | 2 |
| Всего | 18 |
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Демоурок по подготовке к экзаменам
Составим ваш личный путь к высоким баллам — учтем сроки, уровень знаний и цель.
Как сдать ЕГЭ по математике: разбор сложных задач
Экзамен по математике не зря считают одним из самых трудных. Даже в заданиях базового варианта можно легко ошибиться по невнимательности. Что уж говорить о действительно сложных задачах с полным решением, где много «подводных камней»? Чтобы вы знали, как подготовиться к ЕГЭ по профильной математике, мы разобрали несколько из них.
Задание 16
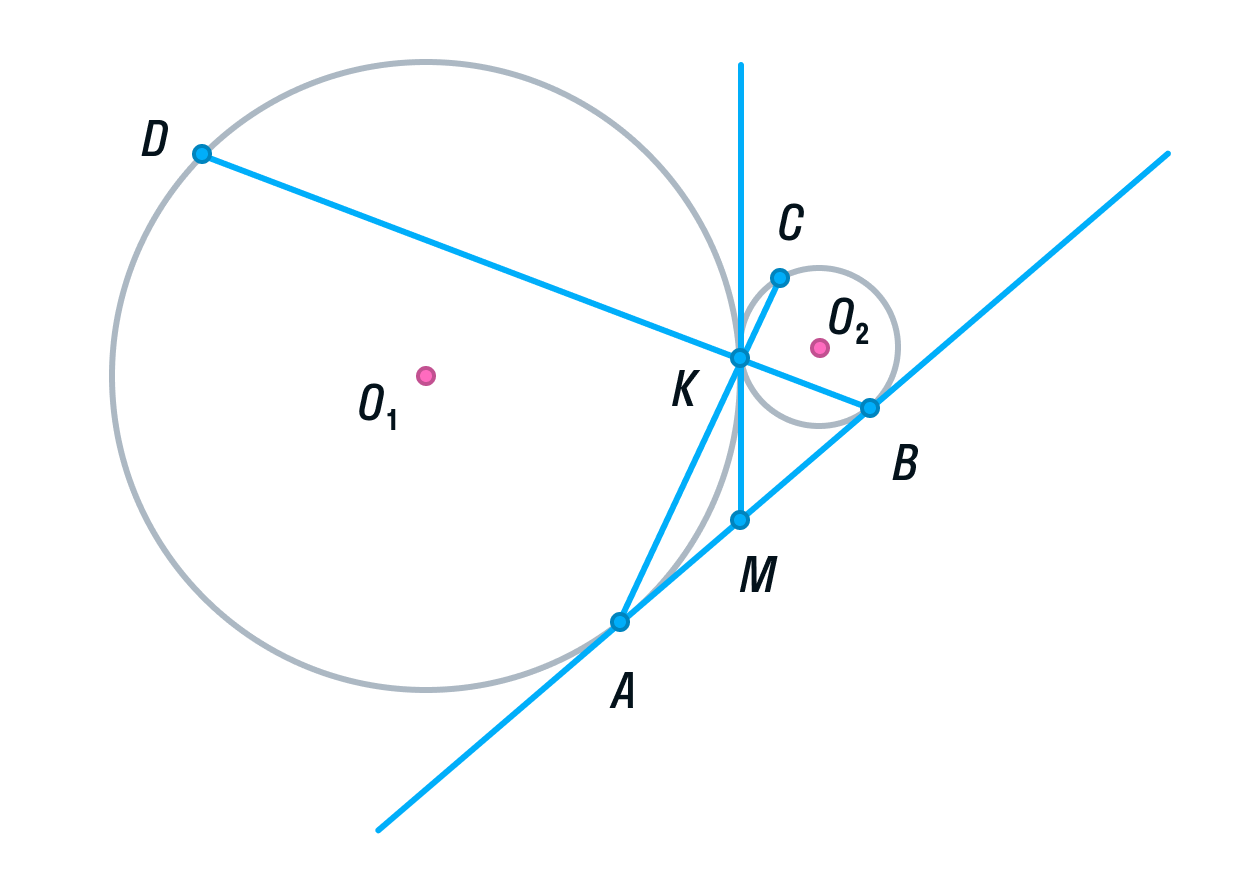
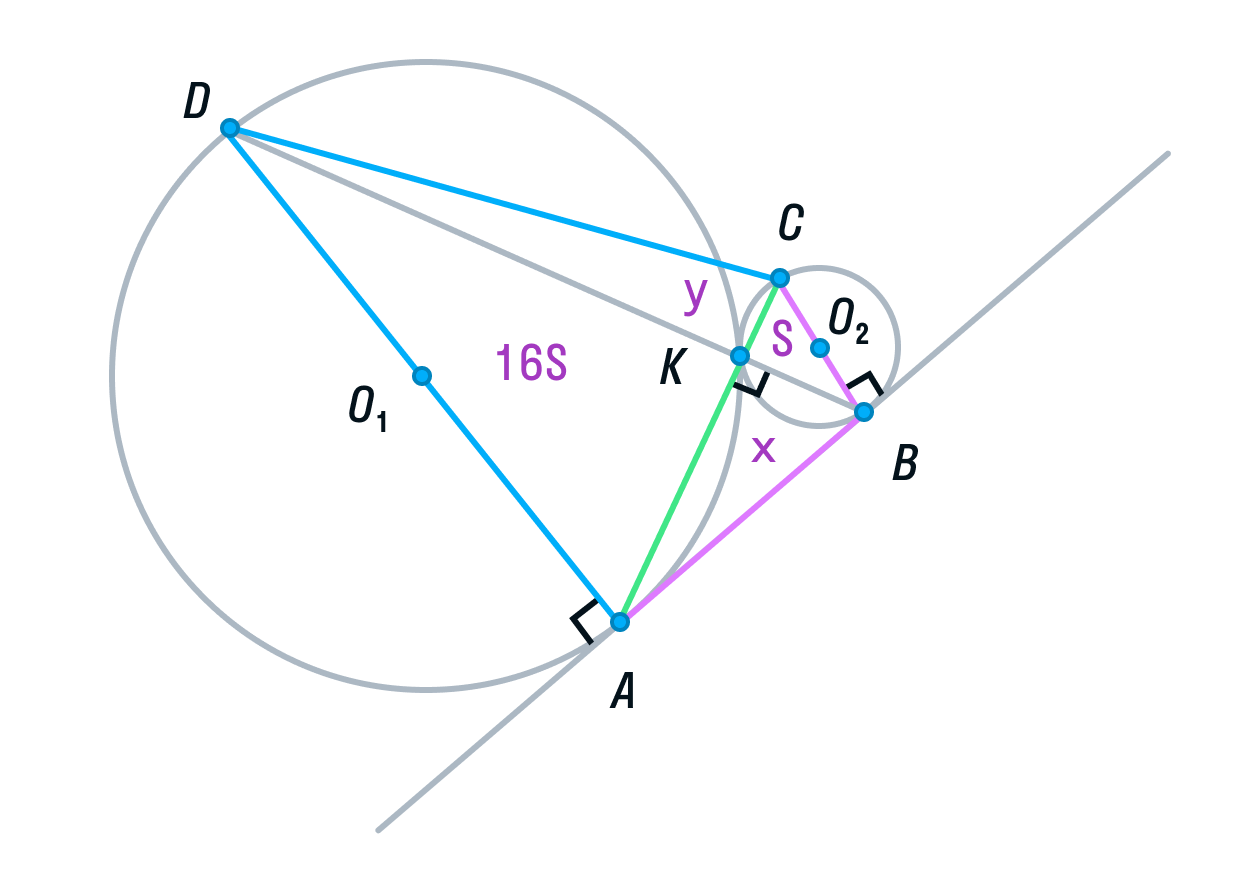
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Совет
Для этого задания советуем повторить темы:
-
Касательные к окружности и их свойства.
-
Свойства вписанных углов.
-
Взаимное расположение окружностей.
-
Свойства прямоугольного треугольника.
-
Признаки и свойства параллельных прямых.
-
Подобные треугольники, площади подобных фигур.
-
Свойство площадей (в частности: отношение площадей треугольников с одинаковой стороной).
-
Трапеция, её свойства. Площадь трапеции.
-
Теорема Пифагора.
Проследите, чтобы они были в вашем плане подготовки к профилю ЕГЭ по математике.
Решение
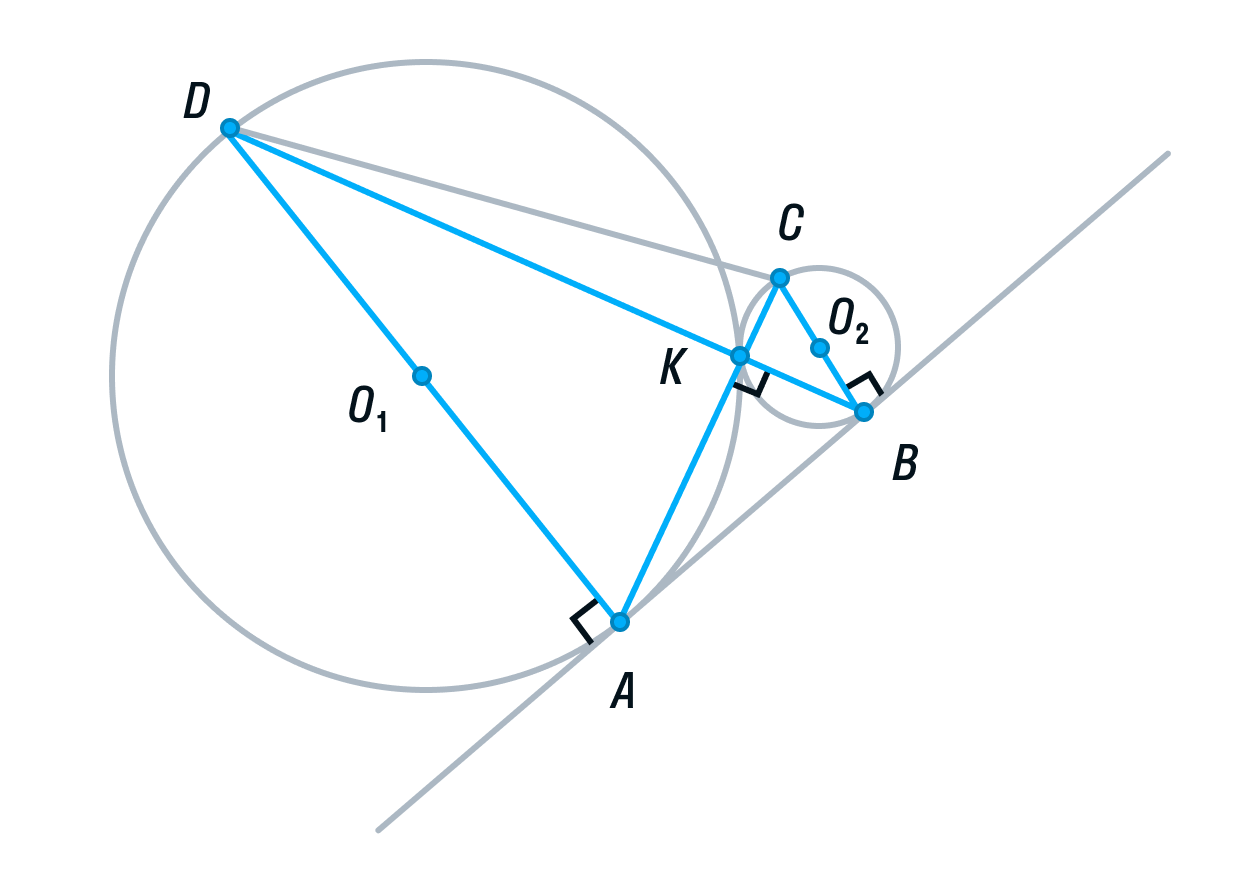
а) Выполним построение.
-
Окружности с центрами О1 и О2 соответственно касаются друг друга в одной точке К.
-
Прямая АВ касается обеих окружностей в точках А и В соответственно.
-
Прямые АК и ВК пересекают окружности в точках С и D соответственно
-
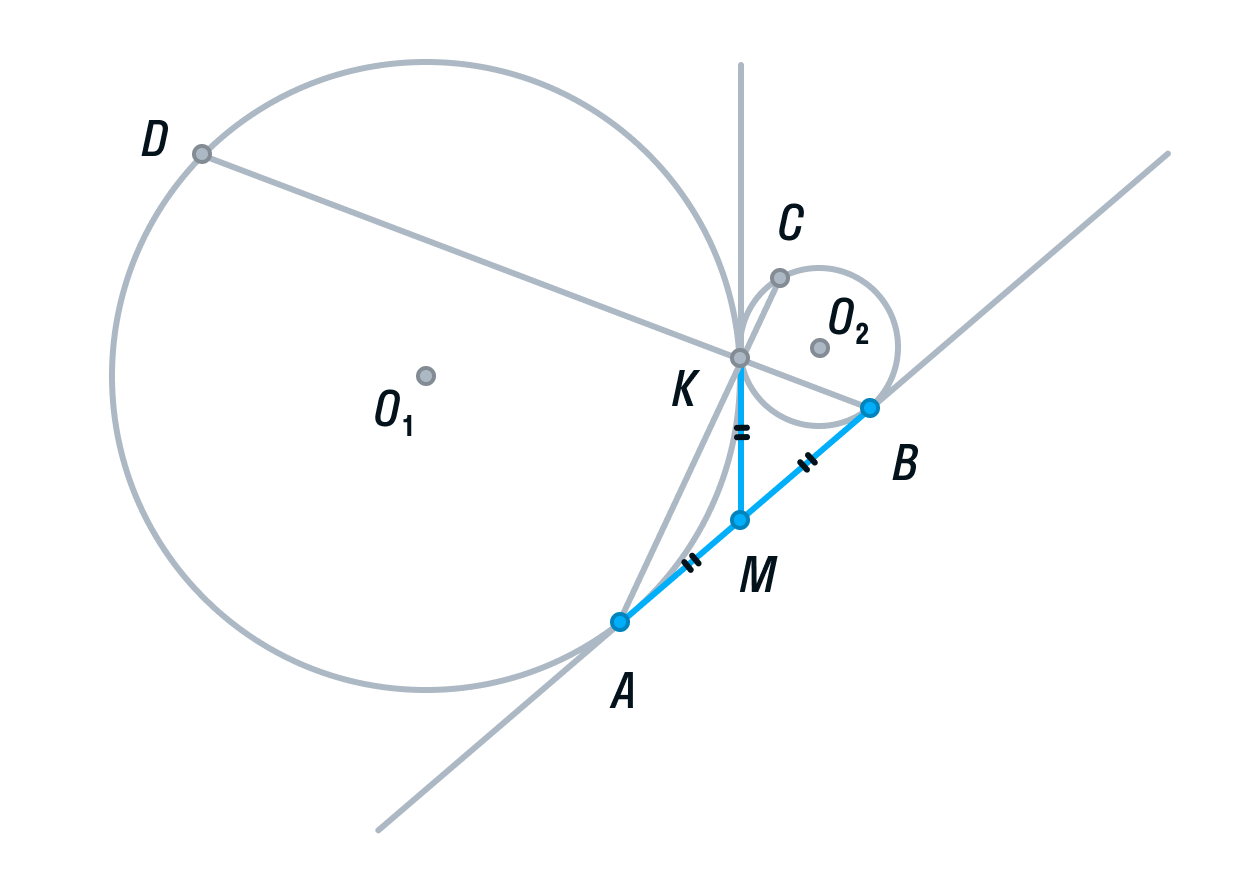
Пусть общая касательная окружностей в точке К, пересекает прямую АВ в точке М.
Тогда по свойству касательных, проведенных из одной точки, AM = KM и KM = BM.
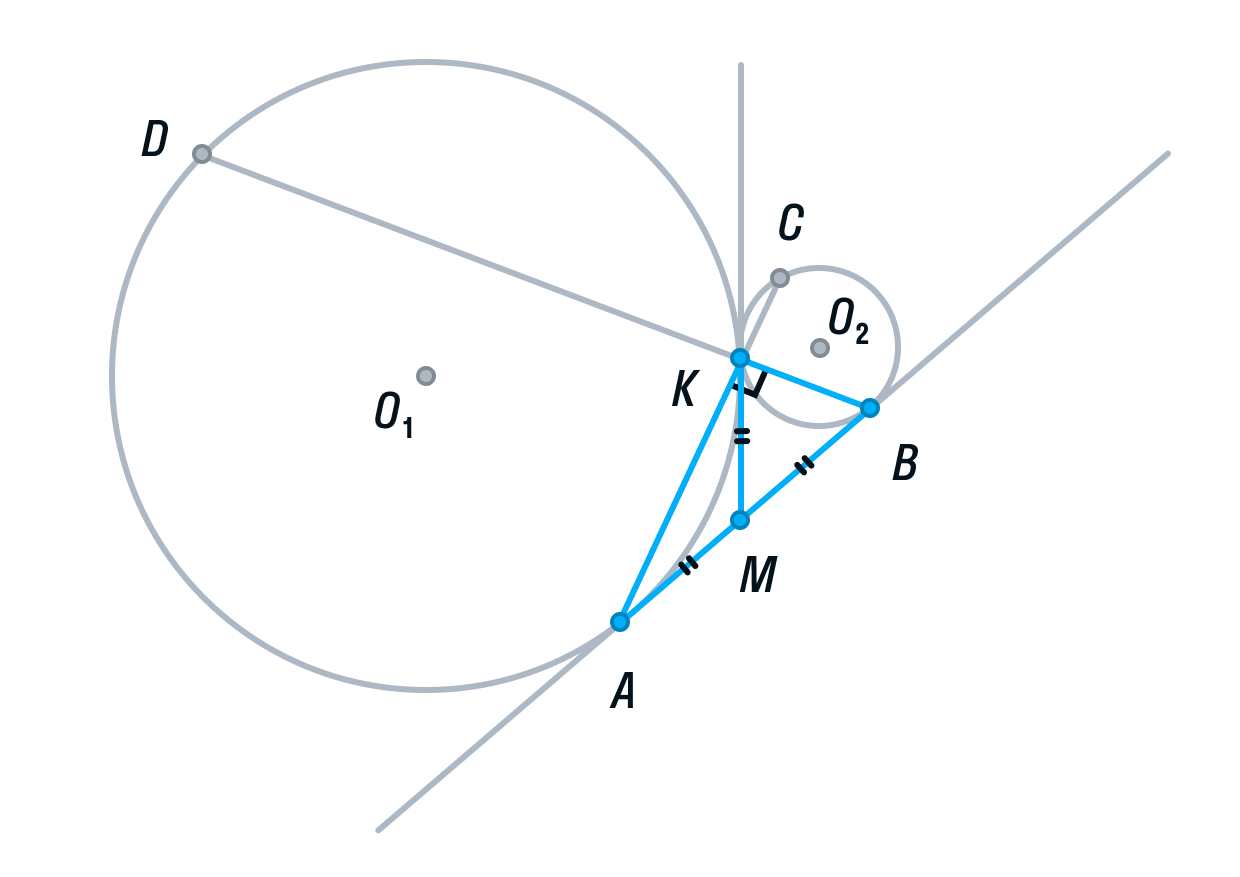
-
Рассмотрим треугольник АВК. Его медиана АМ равна половине стороны, которую она разбивает. Следовательно, делаем вывод, что треугольник АВК прямоугольный, а угол К = 90°.
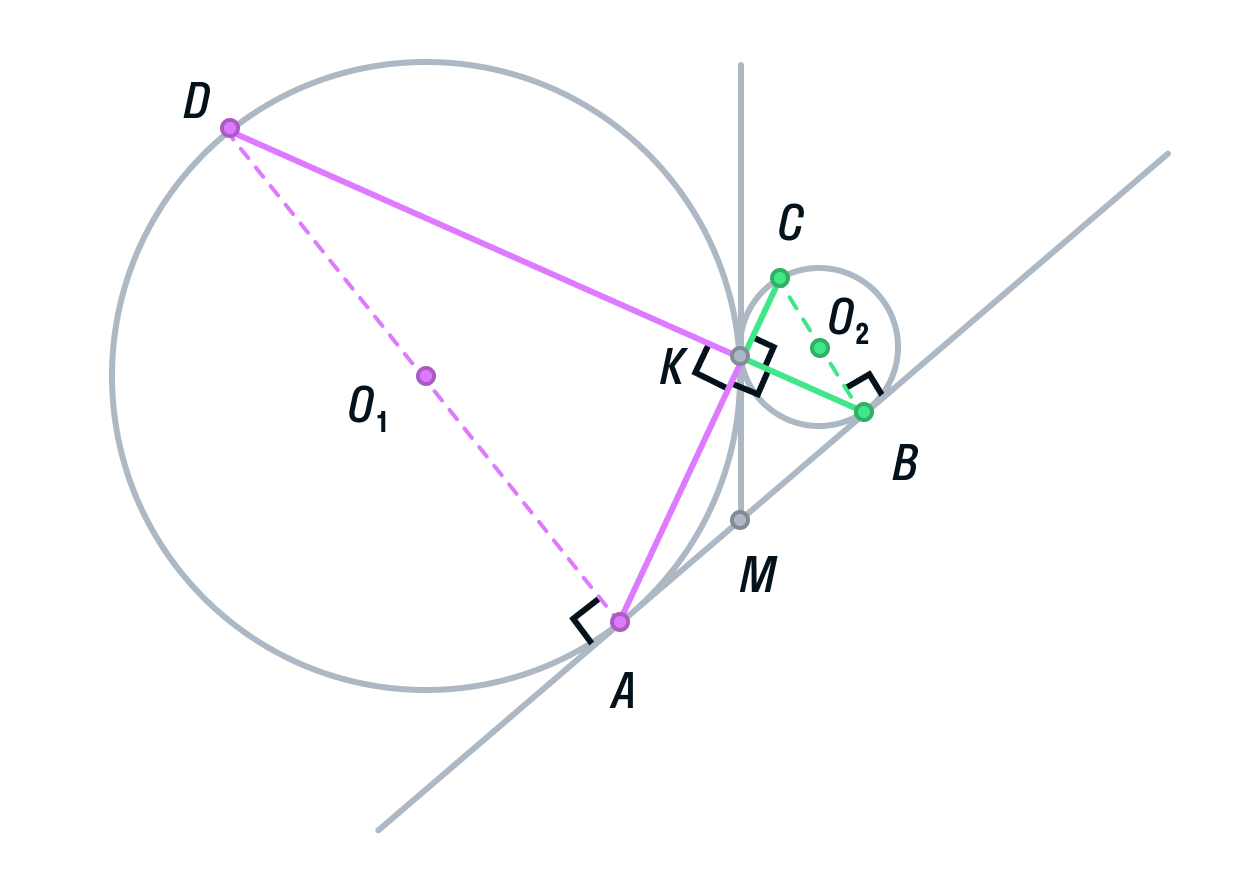
-
Вписанный угол AKD является смежным углом АКВ, а значит, он тоже 90° как прямой. Следовательно, угол AKD опирается на диаметр AD. Значит, AD ⊥ AB, так как радиус, а в данном случае диаметр, перпендикулярен касательной в точке касания.
-
Аналогично рассмотрев угол ВКС, получим, что BC⊥ AB.
-
Прямые AD и ВС перпендикулярны третьей прямой АВ, следовательно, прямые AD и BC параллельны. Ч. т. д.
б) Пусть радиус первой окружности равен 4, а радиус второй окружности равен 1. Тогда АD = 8, ВС = 2.
-
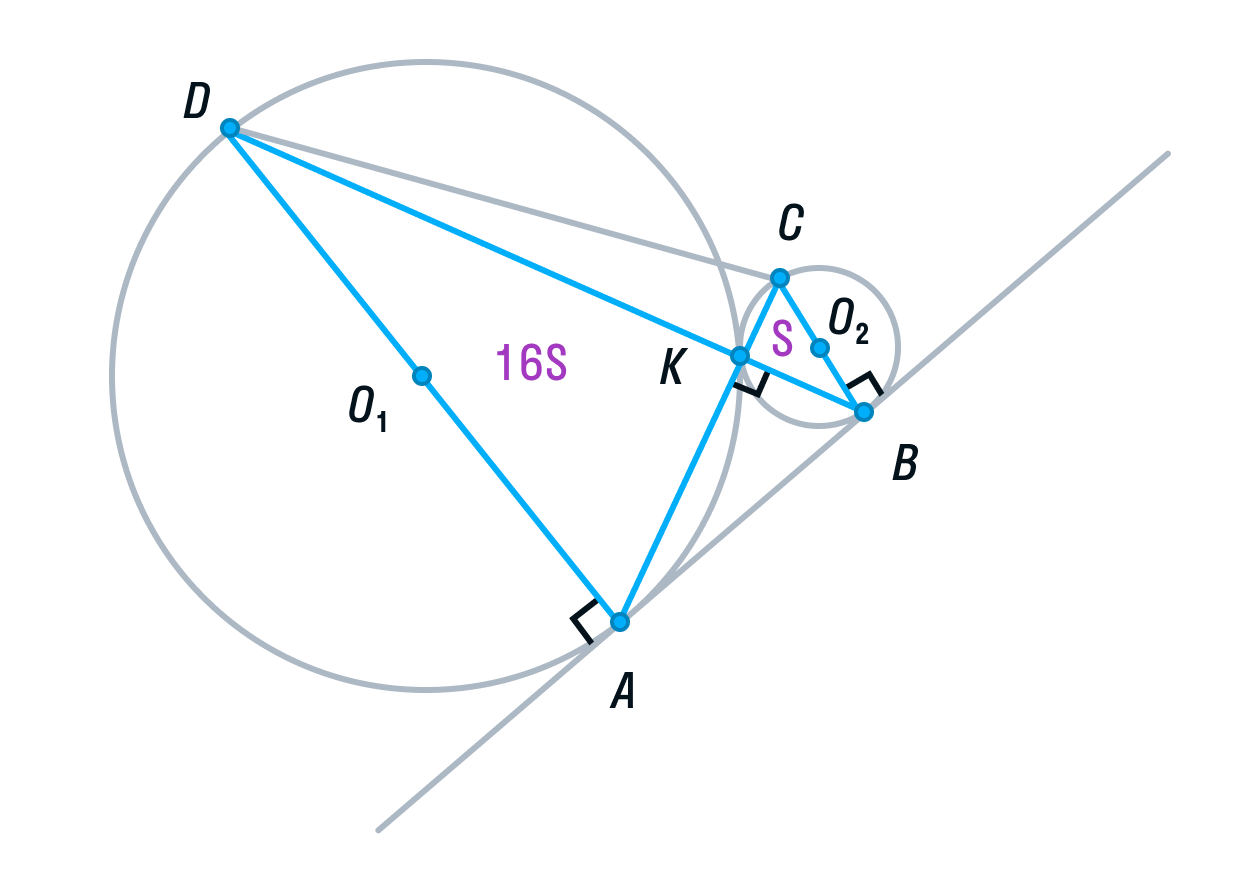
Рассмотрим треугольники ADK и СВК. Они подобны, т. к. имеют два равных угла (К – вертикальный, С и А — накрест лежащие). Из подобия треугольников следует, что их площади относятся как коэффициент подобия в квадрате:
-
Обозначим площадь треугольника СВК за S, тогда площадь треугольника ADK будет равна 16S.
-
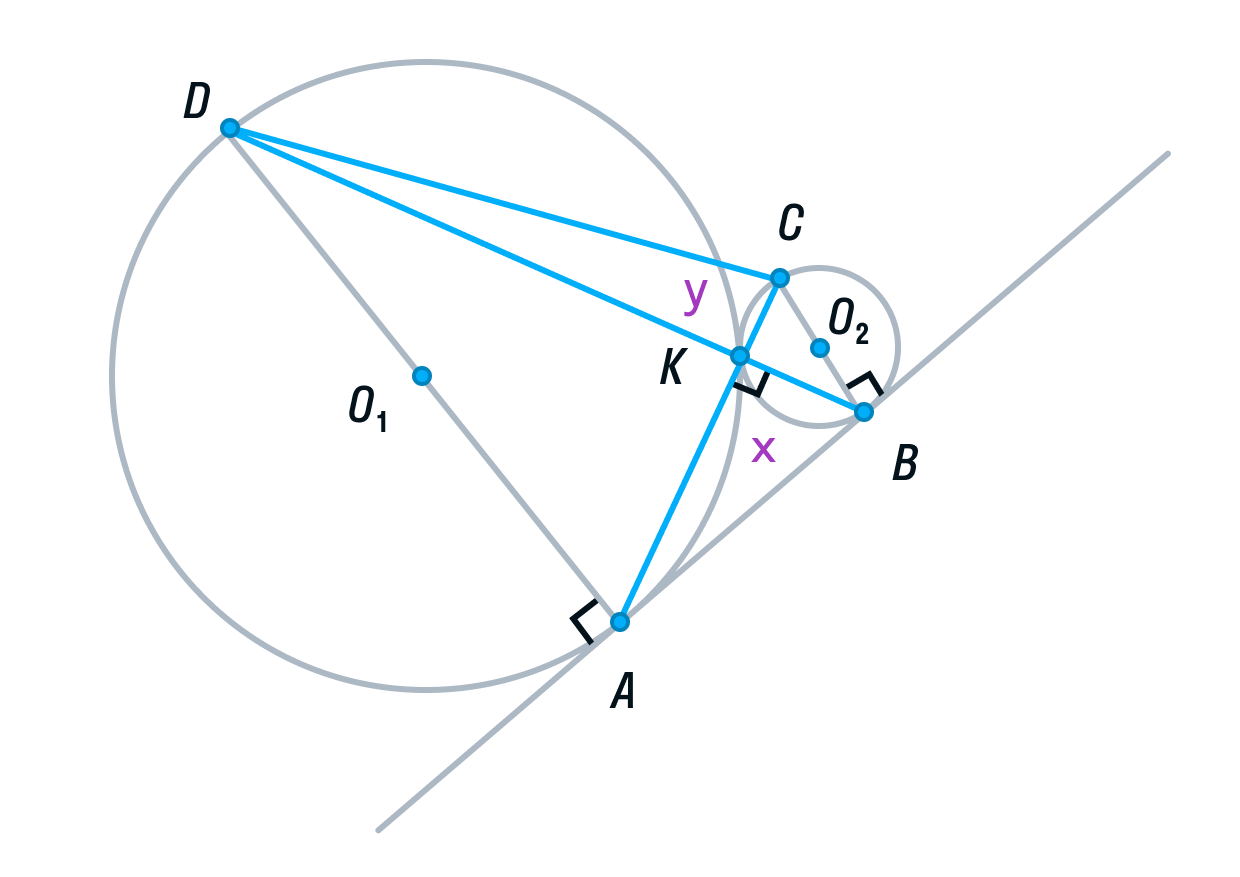
Пусть площади треугольников АВК и CDK будут равны х и у соответственно.
-
Вспомним свойство, связывающее высоты треугольников с общим основанием и получим следующие равенства: DB — общая сторона треугольников ADB и СDB, следовательно:
(равно 4 из подобия треугольников ADK и СВК, см. выше),
-
Аналогично, AC — общая сторона треугольников ADС и ABC, следовательно,
(равно 4 из подобия треугольников ADK и СВК, см. выше),
-
Решим полученную систему уравнений:
-
Из первого уравнения
подставим во второе и найдем y.
следовательно,
подставим во второе и найдем y.
-
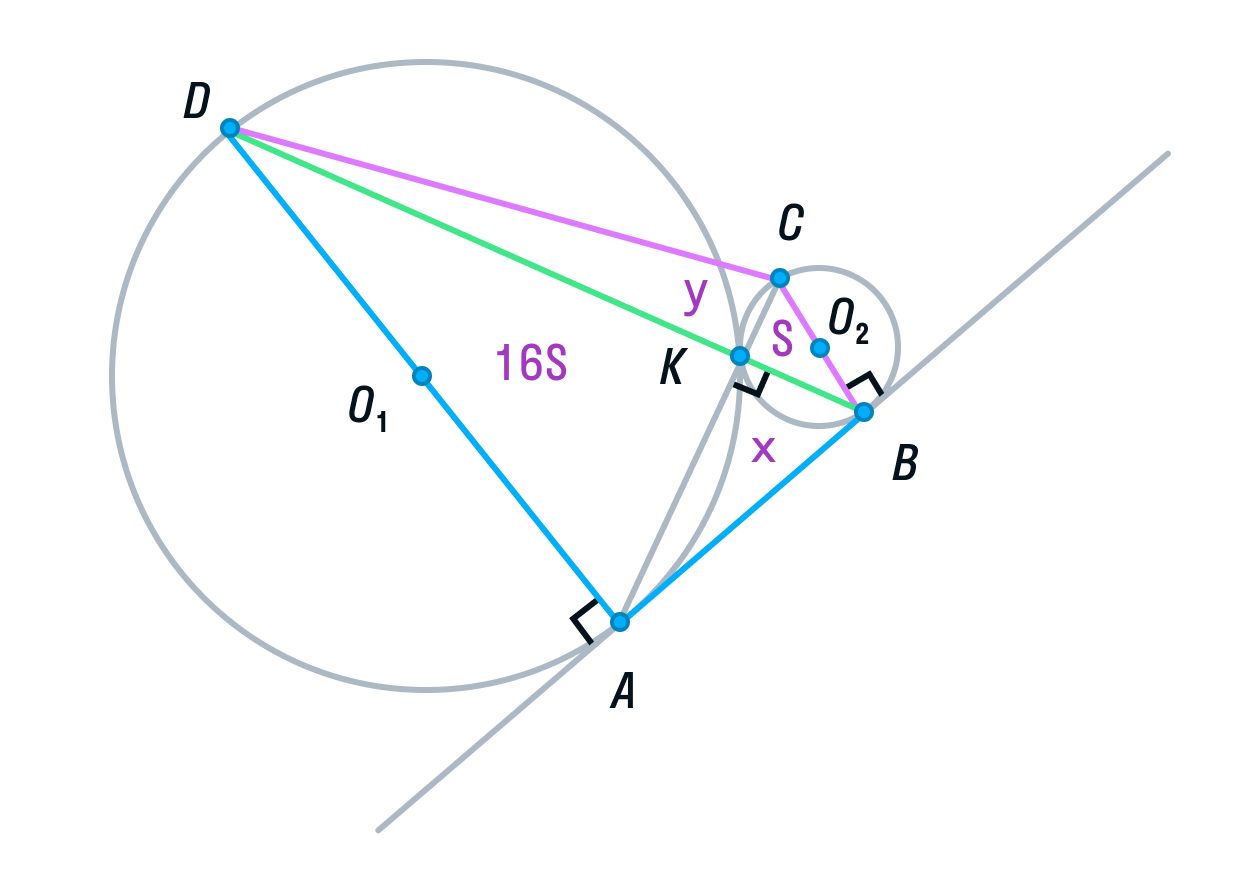
Площадь ABCD равна 16S + 4S + 4S + S = 25S.
-
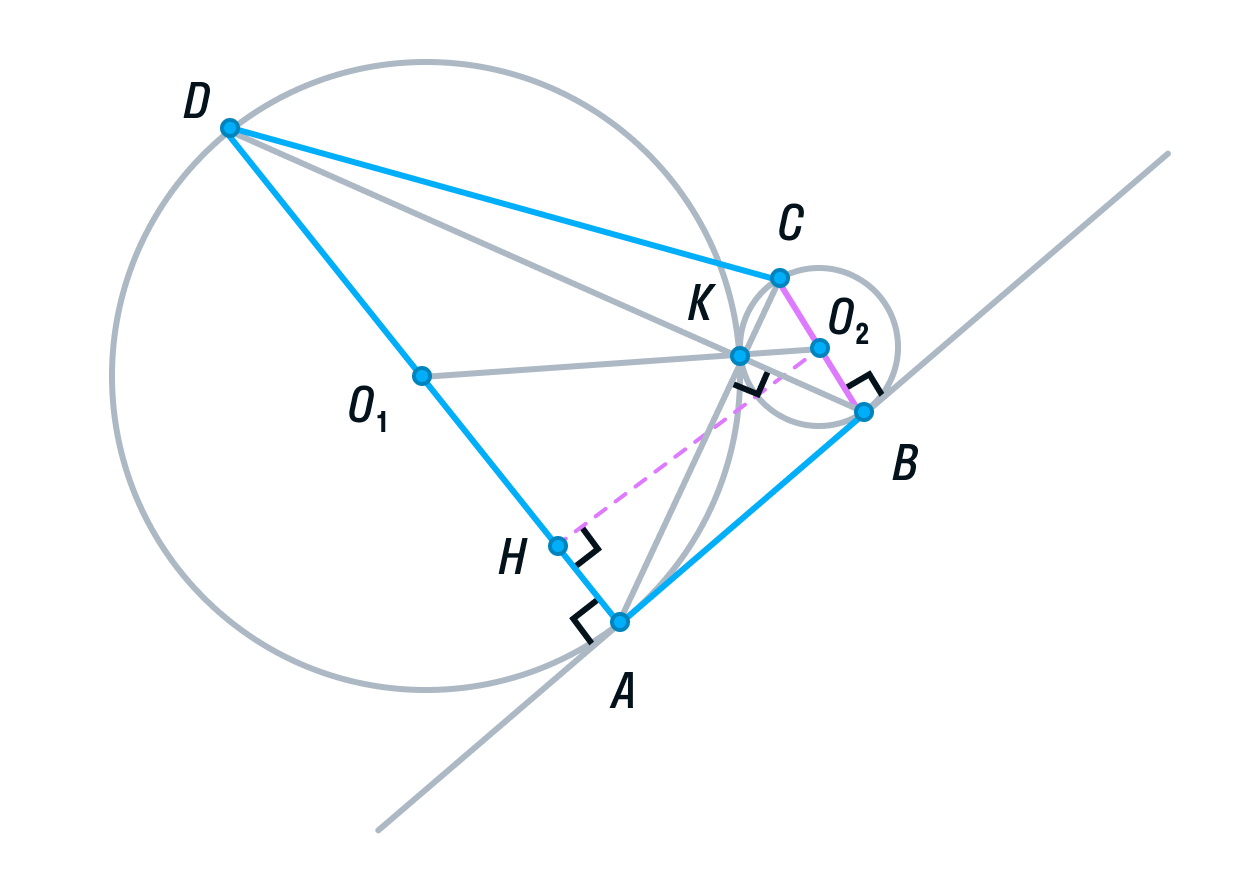
Заметим, что ABCD — прямоугольная трапеция (AD||BC, AB — перпендикулярна основаниям). Для вычисления ее площади нужно полусумму оснований умножить на высоту.
-
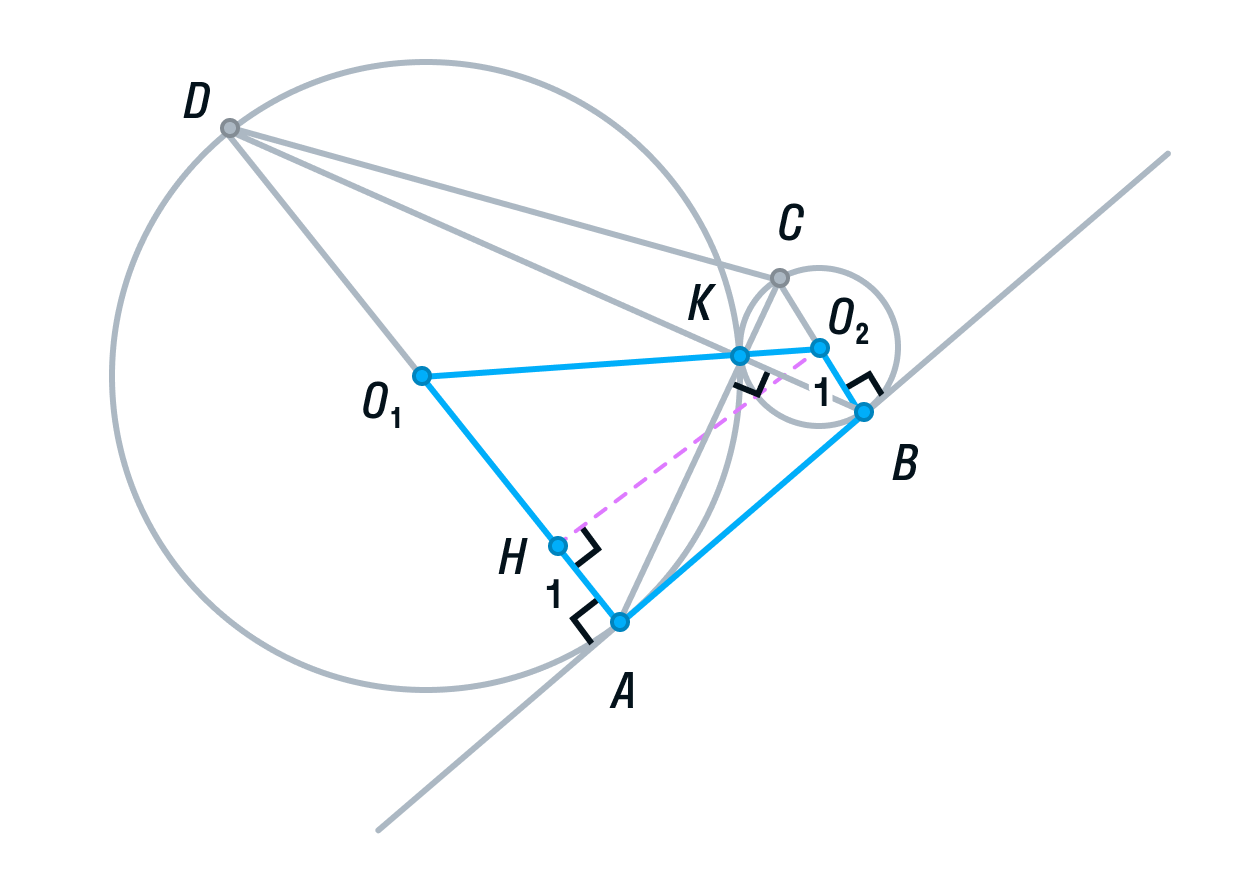
Для того, чтобы найти высоту, рассмотрим меньшую трапецию AO1O2B.
Ее основания равны 1 и 4, так как О2В и О1А — радиусы. O1O2 = 5, так как О2К и О1К — радиусы. О2H — высота трапеции AO1O2B.
-
По теореме Пифагора найдём О2H:
-
Вычислим площадь трапеции ABCD:
-
С другой стороны мы нашли
Отсюда S = 0,8.
-
Площадь треугольника АКВ = 4S, следовательно,
Ответ: 3,2.
Задание 18
В школах № 1 и № 2 учащиеся писали тест. В каждой школе тест писали по крайней мере 2 учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешел из школы № 1 в школу № 2, а средние баллы за тест были пересчитаны в обеих школах.
а) Мог ли средний балл в школе № 1 уменьшиться в 10 раз?
б) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе № 2 равняться 7?
в) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего балла в школе № 2.
Совет
Чтобы справиться с этой задачей, нужно повторить темы:
-
Понятие натурального и целого числа.
-
Среднее арифметическое.
-
Делимость чисел.
-
Процент. Нахождение процента от числа, уменьшение числа на заданный процент.
-
Составление и решение линейных уравнений.
Добавьте их в ваш план подготовки к ЕГЭ по математике, если собираетесь сдавать профиль.
Решение:
а)
-
Допустим, что в школе № 1 писали тест 2 учащихся, один из них набрал 1 балл, а второй набрал Х баллов и перешёл в другую школу. Тогда средний балл в школе был равен (1 + Х) : 2 = 10, а стал равен 1, т. е. уменьшился в 10 раз.
-
Решим уравнение и получим Х = 19 — натуральное число. Следовательно, наше предположение верно.
-
Или мы можем предположить другой вариант: что один учащийся набрал 2 балла. Тогда средний балл изначально равняется 20, а после ухода второго станет 2, т. е. изменится в 10 раз.
-
Решим уравнение (2 + Х) : 2 = 20, отсюда Х = 38 — натуральное число, что тоже удовлетворяет условию задачи.
Ответ: средний балл в школе № 1 мог уменьшиться в 10 раз.
б)
-
Пусть в школе № 2 писали тест m учащихся, n — сумма баллов m учащихся, средний балл равнялся B, а перешедший в неё учащийся набрал u баллов.
-
Умножим обе части полученного уравнения на 10, получим:
-
По условию B = 7, тогда получим, что 10u кратно 10, а
не делится на 10, так как ни один из множителей не делится на 10. Это противоречие.
Ответ: Первоначальный средний балл в школе № 2 не мог равняться 7.
в)
-
Пусть в школе № 1 средний балл равнялся A, общее количество баллов — p, количество писавших работу — (9 – m).
(из пункта б).
Следовательно,
-
Попробуем найти средний балл в школе № 2 методом подбора. Пусть:
В = 1, тогда:
кратно 10, а
не делится на 10.
В = 2, тогда:
пусть u = 1, тогда m = 4:
— не является целым числом.
u = 2 не может быть, т. к. m ≥ 1
В = 3, тогда:
кратно 10, а
не делится на 10.
В = 4, тогда:
Чтобы m было натуральным числом u должно быть четным, u = 2, тогда m = 4, что невозможно (доказали при В = 2).
u = 4, тогда m меньше 0, что невозможно т. к. m ≥ 1.
В = 5, тогда:
пусть u = 1, тогда m = 7, что невозможно (доказали в пункте б);
пусть u = 2, тогда m = 5:
— не является целым числом;
пусть u = 3, тогда m = 3:
-
Этот случай реализуется, например, в школе № 2 при m = 3, B = 5. Предположим, что каждый ученик набрал по 5 баллов. Тогда в школе № 1 писали 9 – m = 9 – 3 = 6 учащихся, 3 из них набрали по 1 баллу, а 3 – по 3 балла, тогда средний балл:
-
Переход из школы № 1 в школу № 2 совершил ученик с 3 баллами, тогда
средний балл в школе № 1 стал равен:что на 10% меньше от первоначального значения.
-
Тогда средний балл в школе № 2 стал равен:
что на 10% меньше от первоначального значения.
Ответ: наименьшее значение первоначального среднего балла в школе № 2 равно 5.
Ответ: а) да; б) нет; в) 5.
Как выставляют баллы за ЕГЭ по математике
С базовым уровнем сложности все просто: за каждый правильный ответ вашего варианта вы получаете по 1 первичному баллу. То же самое касается и первой части профиля: задания 1–11 тоже оценивают в 1 балл.
Как вы помните, во 2-й части профильного варианта нужны и решение, и ответ. Здесь задания оценивают по нескольким критериям. Они сложнее, но и баллов за них можно получить больше. Давайте же разберемся, как выставляют баллы во второй части профиля. Это поможет вам подготовиться к заданиям ЕГЭ по математике как самостоятельно, так и с учителем.
| Задание № 12 | Баллы |
|---|---|
| В обоих пунктах есть обоснованные ответы | 2 |
| Есть обоснованный ответ только в пункте а или есть неверный ответ из-за ошибки в вычислениях, но шаги в решениях обоих пунктов верные |
1 |
| Все остальные случаи | 0 |
| Максимальный балл | 2 |
| Задание № 13 | Баллы |
|---|---|
| Верно доказан пункт а, в пункте б есть обоснованный ответ | 3 |
| Есть только обоснованный ответ в пункте б или верно доказан пункт а, в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ |
2 |
| Есть только верное доказательство пункта а, или в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ, или есть обоснованный ответ в пункте в, который получен с помощью пункта а, но сам пункт а не выполнен |
1 |
| Все остальные случаи. | 0 |
| Максимальный балл | 3 |
| Задание № 14 | Баллы |
|---|---|
| Есть обоснованный ответ | 2 |
| Ответ обоснован, но он отличается от верного исключением точек –12 и/или 0 или шаги решения верные, но из-за ошибки в вычислениях получен неверный ответ |
1 |
| Все остальные случаи | 0 |
| Максимальный балл | 2 |
| Задание № 15 | Баллы |
|---|---|
| Есть обоснованный ответ | 2 |
| Ученик верно построил математическую модель | 1 |
| Все остальные случаи | 0 |
| Максимальный балл | 2 |
| Задание № 16 | Баллы |
|---|---|
| Верно доказан пункт а, в пункте б есть обоснованный ответ | 3 |
| Есть только обоснованный ответ в пункте б иЛИ Верно доказан пункт а, в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ |
2 |
| Есть только верное доказательство пункта а, или в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ, или есть обоснованный ответ в пункте в, который получен с помощью пункта а, но сам пункт а не выполнен |
1 |
| Все остальные случаи | 0 |
| Максимальный балл | 3 |
| Задание № 17 | Баллы |
|---|---|
| Есть обоснованный ответ | 4 |
| Рассуждения и значения параметра верные, но в ответе есть 1–2 неверных значения или решение недостаточно обосновано | 3 |
| Есть верное рассуждение и хотя бы одно правильное значение | 2 |
| Задача сведена к исследованию взаимного расположения 3 окружностей или двух квадратных уравнений с параметром | 1 |
| Все остальные случаи | 0 |
| Максимальный балл | 4 |
| Задание № 18 | Баллы |
|---|---|
| Есть обоснованный ответ в пунктах а, б, в | 4 |
| Есть обоснованный ответ в пункте в и есть обоснованный ответ в пунктах а или б | 3 |
| Есть обоснованный ответ в пунктах а и б или есть обоснованный ответ в пункте в. |
2 |
| Есть обоснованный ответ в пунктах а или б | 1 |
| Все остальные случаи | 0 |
| Максимальный балл | 4 |
Узнать больше о структуре экзамена, вариантах и критериях, по которым оценивают работы, можно на официальном сайте ФИПИ, в разделе «Демоверсии, спецификации, кодификаторы». Там же вы найдете методические указания для подготовки.
Сколько баллов нужно набрать, чтобы получить 3, 4 и 5
Теперь, когда мы разобрали критерии, можно посчитать, сколько баллов нужно набрать на конкретную оценку. В этом нам помогут таблицы ниже. Заодно разберемся, как первичные баллы переводятся в тестовые — финальные.
| Шкала перевода баллов в базовой математике | |
|---|---|
| Первичные баллы | Оценка |
| <7 | 2 |
| 7–11 | 3 |
| 12–16 | 4 |
| 17–21 | 5 |
| Максимальный балл | 4 |
Обратите внимание: с 2008 года официально баллы ЕГЭ не переводят в привычные нам оценки по пятибальной системе. Но если вам хочется это сделать, можно примерно оценить работу по таблице ниже.
| Шкала перевода баллов в профильной математике (неофициальная) | ||
|---|---|---|
| Первичные баллы | Тестовые баллы | Оценка |
| <5 | <27 | 2 |
| 5–8 | 27–49 | 3 |
| 8–20 | 50–67 | 4 |
| 21–31 | 68–100 | 5 |
6 советов от эксперта, как готовиться к ЕГЭ по математике
Мы занимаемся подготовкой учеников к экзамену каждый год и понимаем, насколько это важно и волнительно. Вам предстоит ответственная работа, от которой многое зависит. Чтобы облегчить ее, мы собрали несколько советов, которые помогут вам как можно лучше подготовиться к ЕГЭ по математике:
-
Осознанно выберите уровень сложности и поставьте цель в баллах.
-
Составьте план подготовки к ЕГЭ по математике: больше времени уделяйте темам, которые у вас «западают». Чтобы выявить их, ученики Skysmart проходят тест на бесплатном уроке.
-
Узнайте все о ЕГЭ: сколько времени длится экзамен, из каких частей состоит, по каким темам будут задания, сколько вариантов, какие дадут справочные материалы и т. д.
-
Составьте сбалансированное расписание для подготовки и следите, чтобы в нем было достаточно времени для отдыха.
-
Много практикуйтесь: решайте варианты из Открытого банка заданий ЕГЭ и сдавайте тестовые экзамены.
-
Систематически консультируйтесь и занимайтесь с наставником, который часто имеет дело с подготовкой к ЕГЭ — преподавателем в школе или репетитором.
Все пункты в этом списке важны для тех, кто хочет набрать 80–100 баллов, но последний — особенно. Преподаватель расскажет о том, что представляет из себя ЕГЭ, и тогда на реальном экзамене не будет неприятных сюрпризов.
На курсах подготовки к ЕГЭ по математике в Skysmart учителя помогают школьникам разобраться в КИМах и прорешать каждый тип задач. Ученики заранее знакомятся с частыми ошибками, что помогает избегать их в работе и сохранять баллы. А еще мы учим готовиться морально, чтобы не допустить ошибок из-за паники и невнимательности. Начните подготовку к ЕГЭ по математике с нуля вместе со Skysmart: первый урок — бесплатно!