На вступительном экзамене по математике были предложены три задачи по алгебре планиметрии - Помощь в подготовке к экзаменам и поступлению

Проиллюстрируем
теперь применение операций над
множествами для решения задач о
нахождении числа элементов множеств,
заданных несколькими условиями. Ниже
мы будем рассматривать только конечные
множества.

Пример:
В классе 30 учащихся, 16 из них занимаются
музыкой, 17 увлекаются теннисом, а 10
занимаются и музыкой, и теннисом. Есть
ли в классе ученики, равнодушные и к
музыке, и к теннису, и если есть, то
сколько их?

Решение:
Если сложить число учащихся, интересующихся
музыкой, с числом учащихся, занимающихся
теннисом, т. е. 16+17=33, то учащиеся,
интересующиеся и музыкой, и теннисом,
окажутся учтенными дважды. Поэтому,
чтобы определить число учащихся,
интересующихся музыкой или теннисом,
нужно из суммы 16+17 вычесть число учащихся,
учтенных дважды, т. е. тех, кто интересуется
и музыкой, и теннисом. По условию их 10.
Таким образом, число интересующихся
теннисом или музыкой равно: 16+17—10=23
ученика. А так как в классе всего 30
учащихся, то 30—23 ==7 учащихся равнодушны
и к музыке, и к теннису.

Задача
решена по следующему алгоритму: пусть
имеется два конечных множества А и В.
Тогда:

п(АВ)
= п(А) + п(В )- п(АВ)
(1)

В
нашем случае А — множество учащихся,
интересующихся музыкой, и n(A)
= 16, В—множество
учащихся, интересующихся теннисом, и
n(B) = 17, n(AB)
=10, и тогда по полученной формуле
n(AUВ)=16+17-10=23.

Усложним
задачу: пусть к тем, кто интересуется в
классе музыкой — множеству А, и к
тем, кто увлекается теннисом — множеству
В,
добавляются еще и те, кто интересуется
театром— множество С. Сколько учеников
увлекается или музыкой, или теннисом,
или театром, т. е. чему равно число
n{ABC)?

Если
множества А, В
и С пересекаются лишь попарно, т.
е.
АВС=,
то подсчет можно вести, как и прежде:
сначала сложить п(А)+п(В)+п(С),
а затем вычесть число тех элементов,
которые подсчитаны дважды, т. е. вычесть
число n{AB}+n(AC)+n(BC).
Если же множество АВС,,
то его элементы оказались неучтенными:
сначала их трижды учли, когда складывали
п(А}+п
(В)+п(С),
а затем трижды отнимали их, вычитая
n{AB}+n(AC)+n(BC).
Таким образом,
число
п(А)+п(В)+п(С
)- (n{AB}+n(AC)+n(BC))

меньше
истинного результата ровно на число
элементов в пересечении множеств
АВС,
которое и следует добавить для получения
верного результата:

п(А)+п(В)+п(С
)- (n{AB}+n(AC)+n(BC))+п(АВС)
(2)

Аналогичная формула
может быть получена для любого числа
множеств.

В
формулах (1) и (2) подсчитывается, сколько
раз каждый элемент включается и
исключается, поэтому их называют
формулами
включений и исключений.

Рассмотрим
несколько примеров применения полученных
формул.

Пример1:
На вступительном экзамене по математике
были предложены три задачи: по алгебре,
планиметрии и стереометрии. Из 1000
абитуриентов задачу по алгебре решили
800, по планиметрии — 700, а по стереометрии
— 600 абитуриентов. При этом задачи по
алгебре и планиметрии решили 600
абитуриентов, по алгебре и стереометрии
— 500, по планиметрии и стереометрии
— 400. Все три задачи решили 300 абитуриентов.
Существуют ли абитуриенты, не решившие
ни одной задачи, и если да, то сколько
их?

Решение.
Пусть U
—
множество всех абитуриентов, А
—. множество
абитуриентов, решивших задачу по алгебре,
В
— множество
абитуриентов, решивших задачу по
планиметрии, С — множество абитуриентов,
решивших задачу по стереометрии. По
условию
n(U) =1000,
n(A) = 800, n(В)=700,
n(С)=600,
n(AB)=
600, n(AC)
= 500, n(BC)
= 400, n(ABC)
=300. В
множество ABC
включены все абитуриенты, решившие
хотя бы одну задачу. По формуле (2)
имеем:

n(А
U В
U С) == 800 + 700 + 600 — 600 — 500 — 400 + 300 =900.

Отсюда
следует, что не все поступающие решили
хотя бы одну задачу. Ни одной задачи не
решили

n(U)
— n(AUBUC)=1000
— 900==100 (абитуриентов).

Пример2:
Социологи опросили 45 учащихся девятых
классов, среди которых 25 юношей. При
этом выяснилось: 30 человек имеют за
полугодие оценки 4 и 5, из них 16 юношей,
спортом занимаются 28 учеников, среди
них 18 юношей, и 17 учеников, успевающих
только на хорошо и отлично, 15 юношей
учатся на хорошо и отлично и занимаются
спортом. Первый математик
класса взглянул на результаты и заявил,
что там есть ошибки. Как это ему удалось
выяснить?

Решение:
Обозначим через А
множество юношей, В
—
множество успевающих на 4 и 5, С — множество
спортсменов. По условию задачи n(A)=25,
n(В)=30, n(С)=28, n(AB)=16,
n(AC)=18,
n(BC)=17,
n(ABC)=15.
Найдем общее число учащихся, которые
или являются юношами, или занимаются
спортом, или успевают на 4 и 5. По формуле
(2) получаем:

n
(A
UBUC)=25+30+28-
16- 18- 17+15=47. Этого быть не может, так как
обследовалось всего 45 учеников!
Следовательно, в данных сведениях есть
ошибки.

А
6

12
В

8
С

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

На экзамене по математике были предложены

	26.10.2013, 17:16
На экзамене по математике были предложены три задачи: одна по алгебре, одна по геометрии, одна по тригонометрии. Из 1000 абитуриентов задачу по алгебре решили 800, по геометрии — 700, по тригонометрии — 600. При этом задачи по алгебре и геометрии решили 600 абитуриентов, по алгебре и тригонометрии — 500, по геометрии и тригонометрии — 400. А 300 абитуриентов решили все задачи. Сколько абитуриентов не решили ни одной задачи?
1 2 3 4 5 Категория: Задачи по комбинаторике \|
Просмотров: 961 \| Загрузок: 0 \| Рейтинг: 0.0/0

Добавлять комментарии могут только зарегистрированные пользователи.

[

Регистрация

Вход

]

Источник

Слайд 1

Дискретная математика
Введение

Описание слайда:

Дискретная математика
Введение

Слайд 2

Описание слайда:

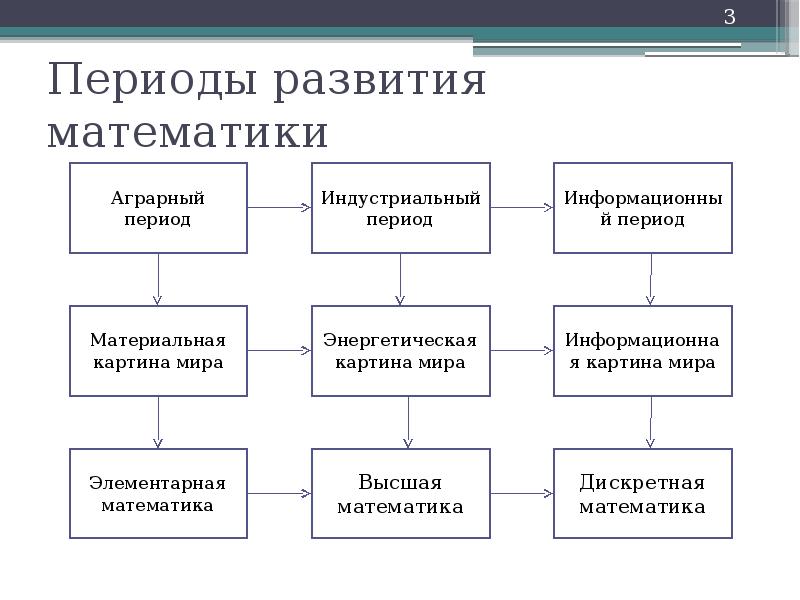
Периоды развития математики
В истории цивилизации можно выделить три крупных периода:
сельскохозяйственный, или аграрный — до XVII в.;
индустриальный — с XVII по XX в.;
информационный — с XX в.
Эти периоды определялись научно-техническими революциями и, следовательно, характером тех систем и явлений природы, которые вовлекались в сферу главных производственных интересов и потребностей людей. В каждый период создавались новые технологии производства, новая картина реального мира, новые системы знаний (науки) и, в частности, новая математика.

Слайд 3

Описание слайда:

Периоды развития математики

Слайд 4

Описание слайда:

Новый период развития математики
Дискретной математикой называют совокупность математических дисциплин, изучающих свойства абстрактных дискретных объектов.
Фундаментом дискретной математики являются:
Теория множеств;
Математическая логика;
Теория графов;
Теория кодирования;
Теория автоматов.

Слайд 5

Описание слайда:

Новый период развития математики
Стимулы развития дискретной математики:
растущий поток информации и проблемы ее передачи, обработки и хранения привели к возникновению и развитию теории кодирования;
различные экономические задачи, задачи электротехники стимулировали создание и развитие теории графов;
связь релейно-контактных схем с формулами алгебры логики и их использование для описания функционирования автоматов дали начало развитию и применению математической логики и теории автоматов.

Слайд 6

Обозначения
Кванторы:
Квантор общности:  - «любой», «всякий», «каждый»;
Квантор существования:  - «существует», «найдется», «можно найти»;
 «тогда и только тогда», «необходимо и достаточно»;
 «следует», «выполняется»;
: или  «такой, что»
Пример:

Описание слайда:

Обозначения
Кванторы:
Квантор общности:  — «любой», «всякий», «каждый»;
Квантор существования:  — «существует», «найдется», «можно найти»;
 «тогда и только тогда», «необходимо и достаточно»;
 «следует», «выполняется»;
: или  «такой, что»
Пример:

Слайд 7

Дискретная математика
Теория множеств

Описание слайда:

Дискретная математика
Теория множеств

Слайд 8

Основные понятия
«Под многообразием, или множеством, я понимаю вообще всякое многое, которое можно мыслить как единое, то есть всякую совокупность определённых элементов, которая может быть связана в одно целое с помощью некоторого закона…»
Георг Кантор

Описание слайда:

Слайд 9

Основные понятия
Понятие множества является одним из наиболее общих и наиболее важных математических понятий. Оно было введено в математику немецким ученым Георгом Кантором.
Множество, элементы множества – первичные базисные неопределяемые понятия, на которых строится теория множеств.
Объекты, составляющие множество, называются элементами множества.

Описание слайда:

Слайд 10

Пустое множество
Примеры множеств:
Множество решений уравнения;
Множество студентов в группе;
Множество предметов мебели в кабинете;
Множество натуральных чисел.

Описание слайда:

Слайд 11

Универсальное множество
Множество U, содержащее все возможные элементы, обладающие некоторым признаком, называется универсальным (универсумом).

Описание слайда:

Слайд 12

Основные понятия
Множества обозначают большими буквами латинского алфавита. Элементы множества – строчными буквами.

Описание слайда:

Слайд 13

Диаграммы Эйлера-Венна
Множества удобно изображать с помощью кругов Эйлера (диаграмм Венна).

Описание слайда:

Диаграммы Эйлера-Венна
Множества удобно изображать с помощью кругов Эйлера (диаграмм Венна).

Слайд 14

Равные множества
Определение равенства множеств 1.
Два множества называются равными (А=В) в том и только в том случае, когда они состоят из одних и тех же элементов.
Примеры:
Множества решений уравнений 4х-8=16 и х/15=2/5 равны, так как их решением является одно и то же число 6.
Равны множества букв, из которых составлены слова «навес» и «весна».

Описание слайда:

Слайд 15

Подмножество
Множество A называют подмножеством множества B (обозначается A  B ), если всякий элемент множества A является элементом множества B:

Описание слайда:

Слайд 16

Слайд 17

Слайд 18

Конечные и бесконечные
Множество, состоящее из конечного числа элементов называется конечным множеством.
Бесконечное множество- непустое множество, не являющееся конечным.
Мощностью конечного множества называется число его элементов. Обозначение: А , В .
  = 0

Описание слайда:

Слайд 19

Способы задания множеств
Множества могут быть заданы
списком;
порождающей процедурой;
описанием характеристических свойств элементов;
графическим представлением.

Описание слайда:

Слайд 20

Описание слайда:

Способы задания множеств

Слайд 21

Способы задания множеств
Задание множеств порождающей процедурой, которая описывает способ получения элементов множества из уже полученных элементов либо других объектов.
Например:
a)
(1)1 N; (2) если nN, то n+1N.
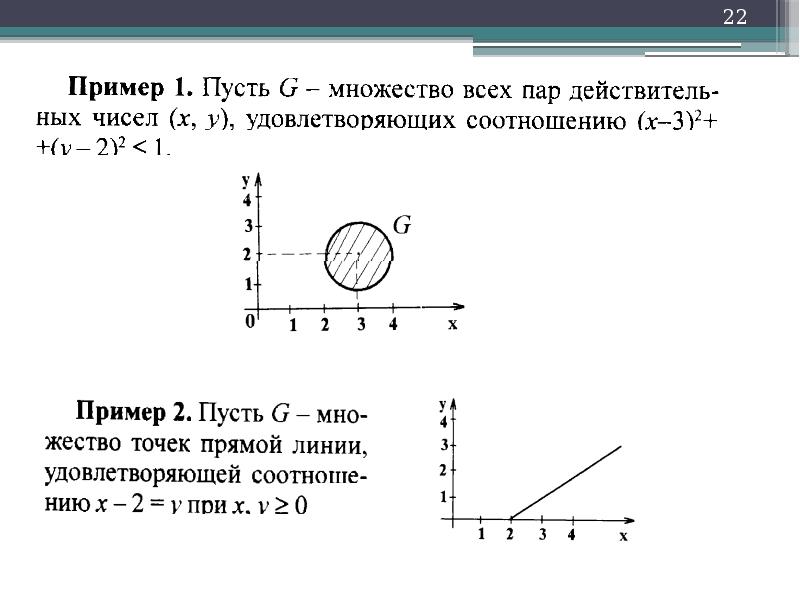
Графическое задание множеств с помощью диаграмм Эйлера-Венна.
Например,

Описание слайда:

Слайд 22

Слайд 23

Способы задания множеств
Задание множеств порождающей процедурой, которая описывает способ получения элементов множества из уже полученных элементов либо других объектов.
Например:
a) 2 M2n; б) если mM2n , то 2mM2n.
а) 1 N; б) если nN, то n+1N.
Графическое задание множеств с помощью диаграмм Эйлера-Венна.
Например,

Описание слайда:

Способы задания множеств
Задание множеств порождающей процедурой, которая описывает способ получения элементов множества из уже полученных элементов либо других объектов.
Например:
a) 2 M2n; б) если mM2n , то 2mM2n.
а) 1 N; б) если nN, то n+1N.
Графическое задание множеств с помощью диаграмм Эйлера-Венна.
Например,

Слайд 24

Способы задания множеств
Задайте списком множество:
1) букв в слове «алгебра»;
2) четных однозначных натуральных чисел;
3) нечетных однозначных натуральных чисел;
4) однозначных простых чисел.
Запишите множество описанием характеристических свойств :
а) натуральных делителей числа 12;
б) натуральных делителей числа 30;
в) целых делителей числа 6;
г) простых делителей числа 12.

Описание слайда:

Слайд 25

Описание слайда:

Способы задания множеств
По какому характеристическому свойству записаны такие множества:
{понедельник, вторник, среда, четверг, пятница, суббота, воскресенье};
{январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь, декабрь};
{до, ре, ми, фа, соль, ля, си};
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.
А — множество четных натуральных чисел, расположенных между числами 25 и 35. Задайте это множество списком, характеристическим свойством, порождающей процедурой.

Слайд 26

Описание слайда:

Операции над множествами

Слайд 27

Операции над множествами
Пересечением множеств A и В называется множество (АВ), состоящее из тех и только тех элементов, которые принадлежат множествам А и В одновременно.

Описание слайда:

Слайд 28

Описание слайда:

Операции над множествами

Слайд 29

Операции над множествами
Разностью множеств B и A (BA) называется множество всех элементов множества B, которые не содержатся в A.

Описание слайда:

Слайд 30

Описание слайда:

Операции над множествами

Слайд 31

Описание слайда:

Операции над множествами

Слайд 32

Слайд 33

Описание слайда:

Операции над множествами
Кортежем длины n (n-кой) называется упорядоченная последовательность из n элементов. Элемент, занимающий первое место, называется первой компонентой n-ки, элемент, занимающий второе место, называется второй компонентой n-ки и т.д. Обозначение: (а1, а2, … аn) или а1, а2, … аn.
Кортеж длины 2 называют двойкой или парой.
Прямым произведением двух множеств А и В называется множество всевозможных пар (a,b), таких, что: a А, bВ. Символическая запись:
АВ = {(a,b): aА, bВ}

Слайд 34

Операции над множествами
Известно, что M = {1;2;5}, N = {1;4;5;7;9}, K = {4;7;9}. Найдите:
1) пересечение M и N;
2) пересечение M и K;
3) пересечение N и K;
4) объединение M и K;
10) дополнение M, N, K до универсума, если U –все цифры.
11) Прямое произведение K и N, N и K;
12) Симметрическую разность M и K, M и N, K и N

Описание слайда:

Слайд 35

Операции над множествами
т

Описание слайда:

Операции над множествами
т

Слайд 36

Операции над множествами
Найти булеан множества М={a,b,c}.
(М)={, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}}.
Найти булеан множества М={1,3,5,7}

Описание слайда:

Слайд 37

Домашнее задание
Дано: U={1, 2, 3, 4, 5, 6, 7}, A={1, 2, 3, 4, 5},
В={2, 4, 6}, С={1,3,7}.
Найти: а) АС; б) В(СА); в) АВ;
г) (СВ)(АВ); д) (АВ)С.
Выписать булеан множества А, если А – множество нечетных однозначных чисел.

Описание слайда:

Слайд 38

Описание слайда:

Свойства операций над множествами
Пусть U — универсальное множество; A, B,C— его подмножества. Тогда имеют место следующие тождественные равенства:

Слайд 39

Описание слайда:

Свойства операций над множествами

Слайд 40

Описание слайда:

Доказательства

Слайд 41

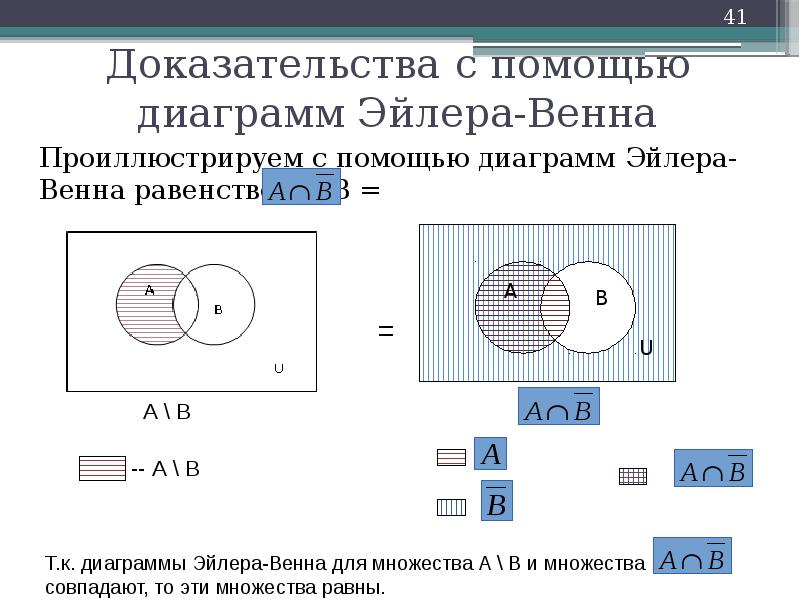
Описание слайда:

Проиллюстрируем с помощью диаграмм Эйлера-Венна равенство А В =
Проиллюстрируем с помощью диаграмм Эйлера-Венна равенство А В =

Слайд 42

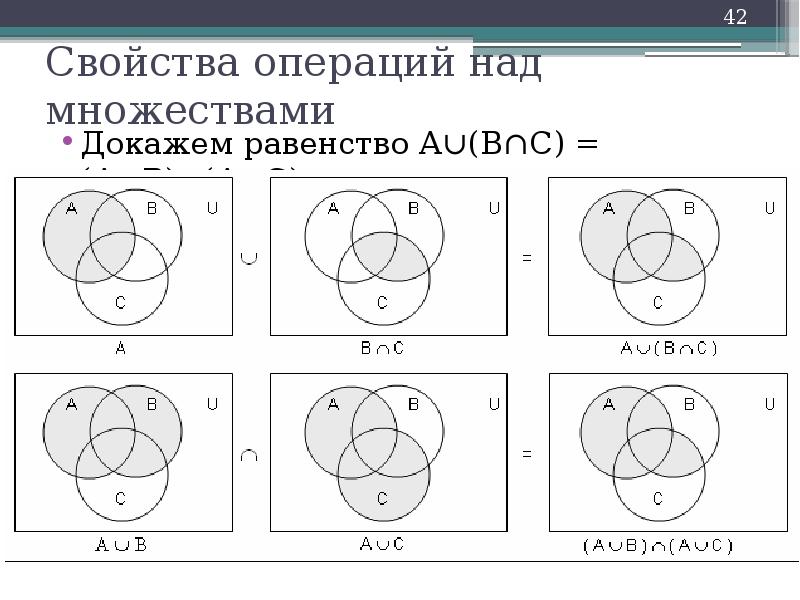
Описание слайда:

Докажем равенство А∪(В∩С) = (А∪В)∩(А∪С).
Докажем равенство А∪(В∩С) = (А∪В)∩(А∪С).

Слайд 43

Описание слайда:

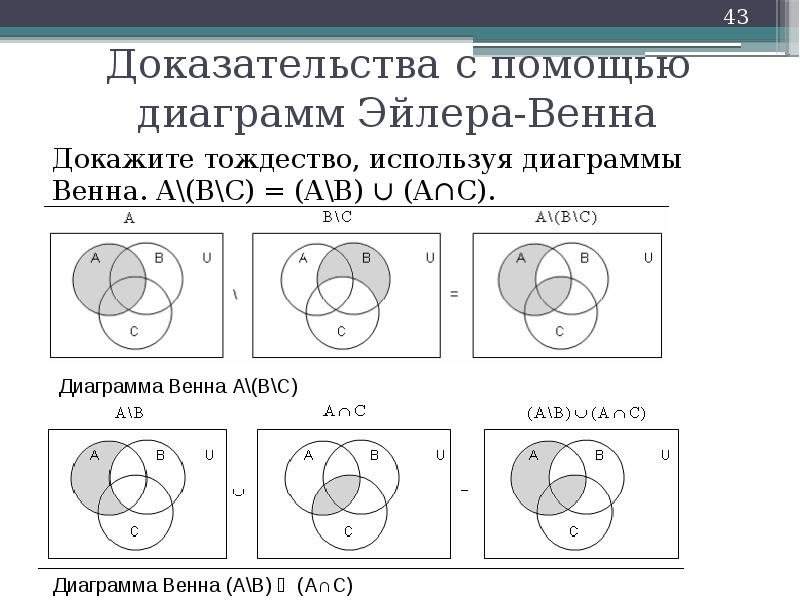
Доказательства с помощью диаграмм Эйлера-Венна
Докажите тождество, используя диаграммы Венна. А(ВС) = (АВ) ∪ (А∩С).

Слайд 44

Доказать, что:
Доказать, что:
A(BC)=(AB)(AC),
A(BC)=(AB)(AC),
A(AB)=AB,
AB=A(AB),
A(BC)=(AB)(AC)=(AB)C,
(AB)C=(AC)(BC),
AB=A(BA),
(AB)(A )=A,
(AB)(A )=A,
( B)A=AB,
(AB)C=(AC)(BC),
A(BC)=(AB)(AC),
A(BC)=(AB)C.

Описание слайда:

Слайд 45

Слайд 46

Описание слайда:

Доказательства (аналитически)
Справедливость законов алгебры множеств доказывается на основе определения равенства: Х = Y, если
1) Х  Y:  x  X  x  Y;
2) Y  Х:  y  Y  y  X.
Сформулированный принцип называют интуитивным принципом объемности

Слайд 47

Доказательства
Используя отношения принадлежности, доказать тождество
(A  B) C = (A C)  (B C).

Описание слайда:

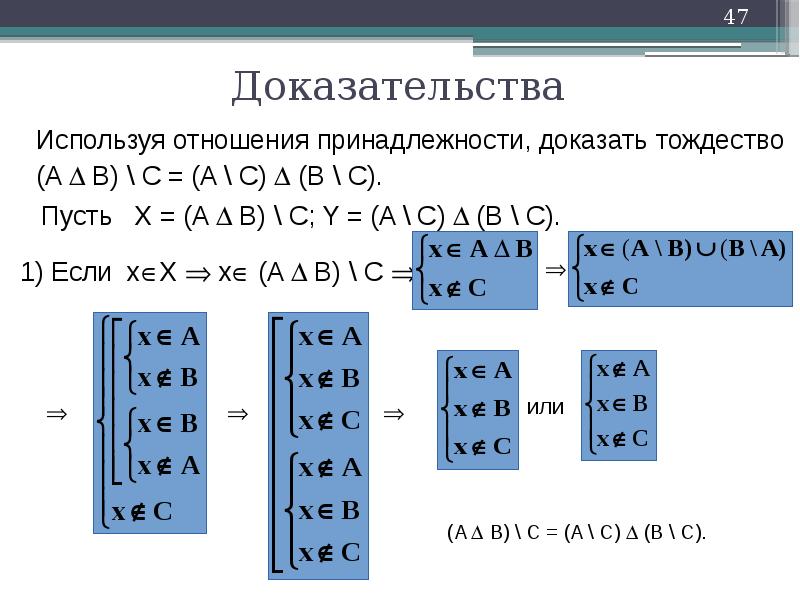
Доказательства
Используя отношения принадлежности, доказать тождество
(A  B) C = (A C)  (B C).

Слайд 48

Доказательства
2) Если y  Y  y  (A C)  (B C) 

Описание слайда:

Доказательства
2) Если y  Y  y  (A C)  (B C) 

Слайд 49

Описание слайда:

Доказательства

Слайд 50

1) Если
1) Если

Описание слайда:

1) Если
1) Если

Слайд 51

Описание слайда:

Докажем включение в обратную сторону:
Докажем включение в обратную сторону:

Слайд 52

Операции над множествами
Тест

Описание слайда:

Операции над множествами
Тест

Слайд 53

Вставьте слово или фразу
Пересечением множеств A и В называется множество, состоящее из тех и только тех элементов, которые_________
принадлежат множествам А и В одновременно;
принадлежат хотя бы одному из множеств A или B;
которые принадлежат множеству А, но не содержатся в B;
принадлежат одному из множеств: либо А, либо В, но не являются общими элементами.

Описание слайда:

Слайд 54

Вставьте слово или фразу
Разностью множеств B и A называется множество всех элементов множества B, которые_______________________
принадлежат множествам А и В одновременно;
принадлежат хотя бы одному из множеств A или B;
не принадлежат множеству А, но принадлежат универсальному множеству;
которые принадлежат множеству В, но не содержатся в А.

Описание слайда:

Слайд 55

Вставьте слово или фразу
Объединением множеств A и B называется множество, состоящее из всех тех элементов, которые_________________
принадлежат множествам А и В одновременно;
принадлежат хотя бы одному из множеств A или B;
не принадлежат множеству А, но принадлежат универсальному множеству;
которые принадлежат множеству А, но не содержатся в В.

Описание слайда:

Слайд 56

Вставьте слово или фразу
Симметрической разностью множеств А и В называется множество, содержащее те и только те элементы, которые____
принадлежат множествам А и В одновременно;
принадлежат хотя бы одному из множеств A или B;
которые не содержатся в B;
принадлежат одному из множеств: либо А, либо В, но не являются общими элементами;

Описание слайда:

Слайд 57

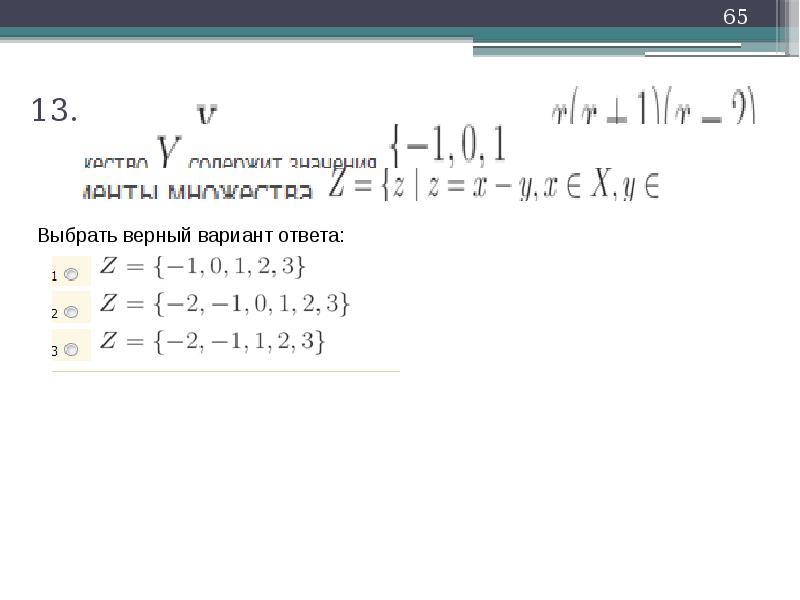
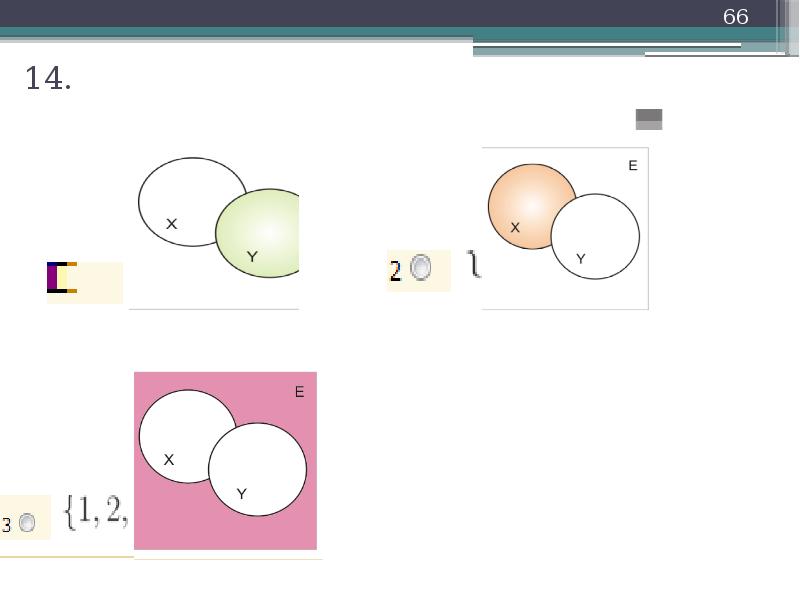
5.Установите соответствие
Объединение
Пересечение
Разность В/А
Симметрическая разность
Разность А/В
Дополнение

Описание слайда:

Слайд 58

Описание слайда:

6.Выбрать верное утверждение

Слайд 59

Слайд 60

Слайд 61

Слайд 62

10.

Слайд 63

11.

Слайд 64

Слайд 65

Слайд 66

Слайд 67

Описание слайда:

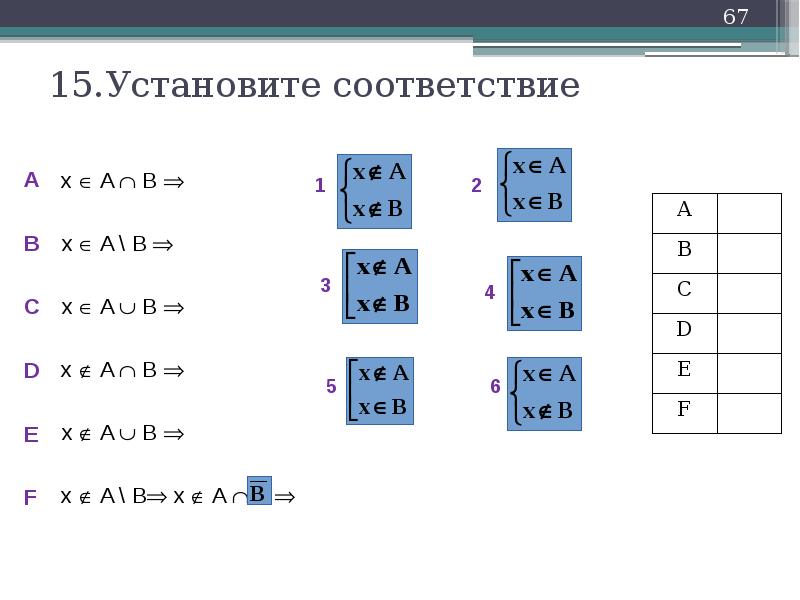
15.Установите соответствие

Слайд 68

Слайд 69

Слайд 70

Операции над множествами
Решение задач

Описание слайда:

Операции над множествами
Решение задач

Слайд 71

Описание слайда:

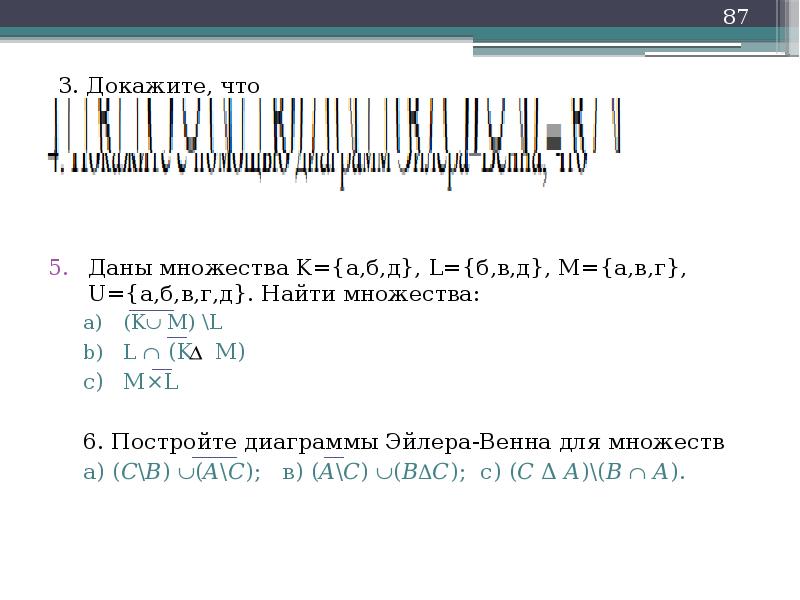
Даны множества K={а,б,д}, L={б,в,д}, M={а,в,г}, U={а,б,в,г,д}. Найти множества:
Даны множества K={а,б,д}, L={б,в,д}, M={а,в,г}, U={а,б,в,г,д}. Найти множества:
(KM) L
L(K M)
M×L

Слайд 72

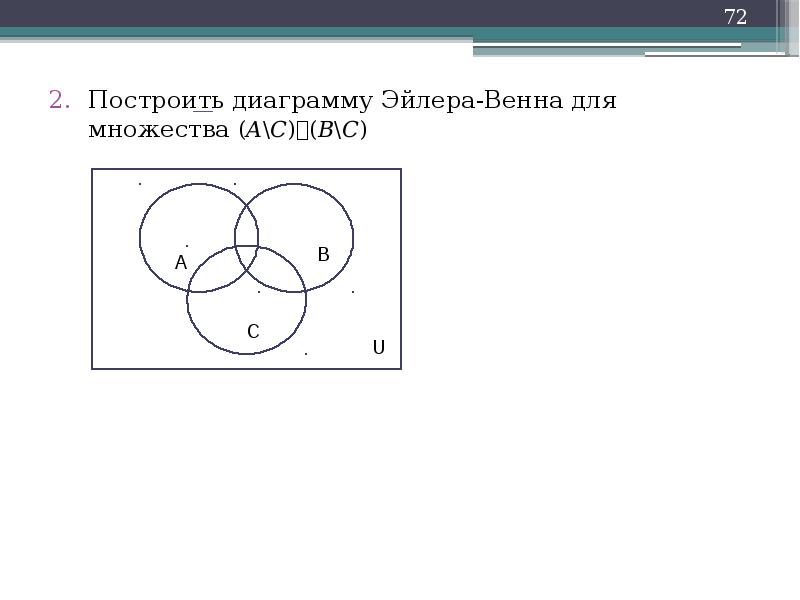
Описание слайда:

Построить диаграмму Эйлера-Венна для множества (AC)(BC)
Построить диаграмму Эйлера-Венна для множества (AC)(BC)

Слайд 73

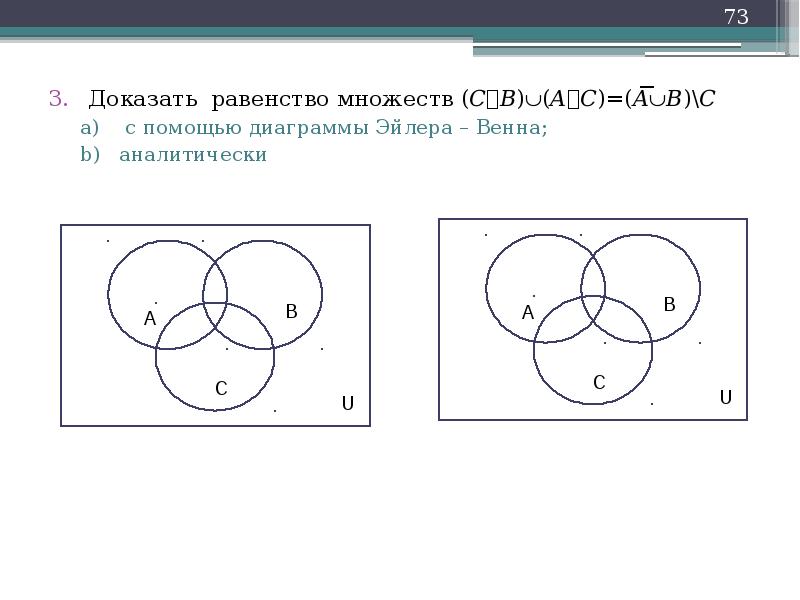
Описание слайда:

Доказать равенство множеств (СB)(AC)=(AB)C
Доказать равенство множеств (СB)(AC)=(AB)C
с помощью диаграммы Эйлера – Венна;
аналитически

Слайд 74

Описание слайда:

Доказать равенство множеств (СB)(AC)=(AB)C
Доказать равенство множеств (СB)(AC)=(AB)C
б) аналитически

Слайд 75

Слайд 76

Описание слайда:

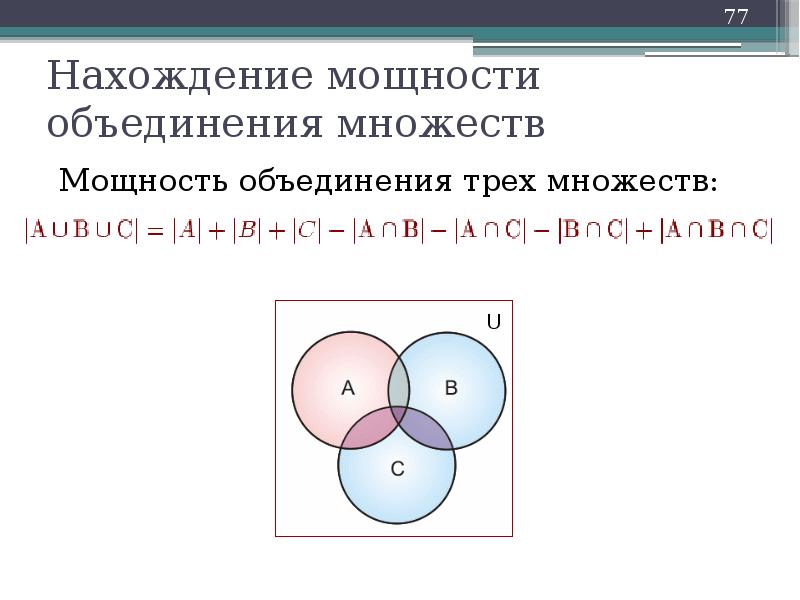
Нахождение мощности объединения множеств
Мощность объединения двух множеств равна сумме мощностей этих множеств баз мощности их пересечения:

Слайд 77

Описание слайда:

Нахождение мощности объединения множеств
Мощность объединения трех множеств:

Слайд 78

Описание слайда:

Нахождение мощности объединения множеств
Пример. На потоке из 100 студентов 28 человек изучают английский язык, 30 человек — немецкий язык, 42 человека — французский язык. Причем 8 человек изучают два языка — английский и немецкий, 10 человек изучает английский и французский языки, 5 человек — немецкий и французский языки. 3 человека изучают все 3 языка. Сколько студентов не изучает ни один из перечисленных языков?

Слайд 79

Описание слайда:

H- мн-во студентов, изучающих нем. язык , H=30;
H- мн-во студентов, изучающих нем. язык , H=30;
Ф- мн-во студентов, изучающих фр. язык, Ф=42.
Соответственно множества студентов, изучающих по 2 или 3 ин. языка:

Слайд 80

Описание слайда:

Задача. На вступительном экзамене по математике были предложены три задачи: по алгебре, планиметрии и стереометрии. Из 1000 абитуриентов задачу по алгебре решили 800, по планиметрии — 700, а по стереометрии — 600 абитуриентов. При этом задачи по алгебре и планиметрии решили 600 абитуриентов, по алгебре и стереометрии — 500, по планиметрии и стереометрии — 400. Все три задачи решили 300 абитуриентов. Существуют ли абитуриенты, не решившие ни одной задачи, и если да, то сколько их?
Задача. На вступительном экзамене по математике были предложены три задачи: по алгебре, планиметрии и стереометрии. Из 1000 абитуриентов задачу по алгебре решили 800, по планиметрии — 700, а по стереометрии — 600 абитуриентов. При этом задачи по алгебре и планиметрии решили 600 абитуриентов, по алгебре и стереометрии — 500, по планиметрии и стереометрии — 400. Все три задачи решили 300 абитуриентов. Существуют ли абитуриенты, не решившие ни одной задачи, и если да, то сколько их?

Слайд 81

Описание слайда:

Задача. В студенческой группе 25 человек. Во время летних каникул 9 из них выезжали в турпоездки за границу, 12 – путешествовали по России, 15 – отдыхали в Сочи, 6 – путешествовали за границей и по России,
Задача. В студенческой группе 25 человек. Во время летних каникул 9 из них выезжали в турпоездки за границу, 12 – путешествовали по России, 15 – отдыхали в Сочи, 6 – путешествовали за границей и по России,
7 – были и за границей и в Сочи, 8 – и путешествовали по России и были в Сочи и 3 – участвовали во всех трех поездках. Сколько студентов никуда не выезжало?

Слайд 82

Описание слайда:

Задача. Из 220 школьников 163 умеют играть в хоккей, 175 – в футбол, 24 не умеют играть в эти игры. Сколько школьников одновременно умеет играть в хоккей и футбол?
Задача. Из 220 школьников 163 умеют играть в хоккей, 175 – в футбол, 24 не умеют играть в эти игры. Сколько школьников одновременно умеет играть в хоккей и футбол?

Слайд 83

Описание слайда:

Задача. По итогам экзаменов из 37 студентов отличную оценку по математике имели 15 студентов, по физике – 16, по химии – 19, по математике и физике – 7, по математике и химии – 9, по физике и химии – 6, по всем трем предметам – 4. Сколько студентов получили хотя бы по одной отличной оценке?
Задача. По итогам экзаменов из 37 студентов отличную оценку по математике имели 15 студентов, по физике – 16, по химии – 19, по математике и физике – 7, по математике и химии – 9, по физике и химии – 6, по всем трем предметам – 4. Сколько студентов получили хотя бы по одной отличной оценке?

Слайд 84

Описание слайда:

Задача. Староста курса представил следующий отчет о физкультурной работе: Всего – 45 студентов. Футбольная секция – 25 человек, баскетбольная секция – 30 человек, шахматная секция – 28 человек, футбольная и баскетбольная – 16, футбольная и шахматная – 18, баскетбольная и шахматная – 17. В трех секциях одновременно занимаются 15 человек. Объясните, почему отчет не был принят?
Задача. Староста курса представил следующий отчет о физкультурной работе: Всего – 45 студентов. Футбольная секция – 25 человек, баскетбольная секция – 30 человек, шахматная секция – 28 человек, футбольная и баскетбольная – 16, футбольная и шахматная – 18, баскетбольная и шахматная – 17. В трех секциях одновременно занимаются 15 человек. Объясните, почему отчет не был принят?

Слайд 85

Описание слайда:

Домашняя работа
В течение 30 дней сентября было 12 дождливых, 8 ветреных, 4 холодных, 5 дождливых и ветреных, 3 дождливых и холодных, 2 ветреных и холодных, а один день был и дождливый, и ветреный, и холодный. В течение скольких дней в сентябре была хорошая погода?
В классе 35 учащихся. Из них 20 посещают математический кружок, 11 – физический, 10 учеников не посещают ни одного из этих кружков. Сколько учеников посещают и математический, и физический кружок? Сколько учащихся посещают только математический кружок?

Слайд 86

Описание слайда:

Подготовка к контрольной работе
Подготовка к контрольной работе

Слайд 87

3. Докажите, что
3. Докажите, что

Описание слайда:

3. Докажите, что
3. Докажите, что

Слайд 88

Контрольная работа
Продолжительность 45 минут
Критерии оценки:
На «3»- 2 и 3 задания
На «4» - 1, 2, 3, 4а)
На «5» - все! (и правильно)

Описание слайда:

Контрольная работа
Продолжительность 45 минут
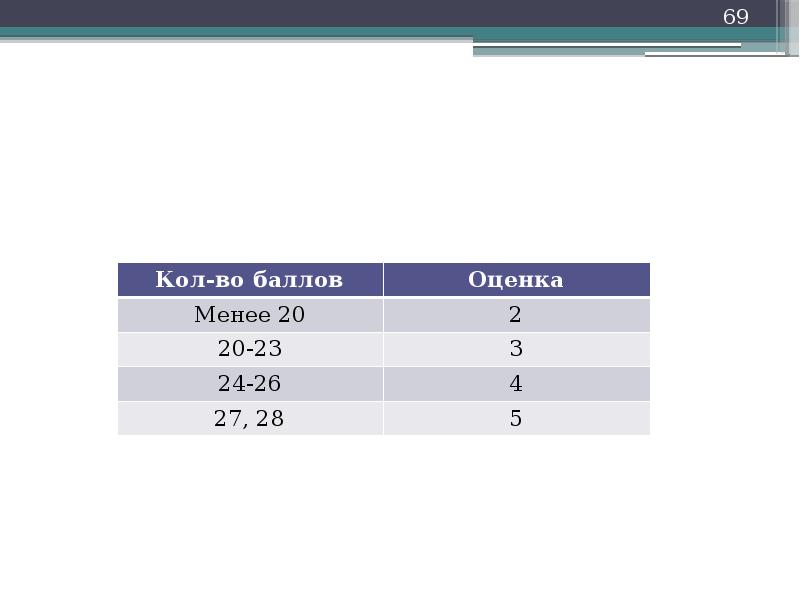
Критерии оценки:
На «3»- 2 и 3 задания
На «4» — 1, 2, 3, 4а)
На «5» — все! (и правильно)

Источник

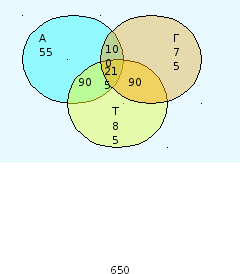
Решение: А – задачи по алгебре, Г – задачи по геометрии, Т – задачи по тригонометрии. По условию: АГ = 100, АТ – 90, Т – 85, Г = 75.

Нам надо найти количество студентов решивших одну задачу, т.е. m (А)+ m (Т) + m (Г), где неизвестно лишь m (А) – количество студентов решивших только алгебру. Из условия геометрию решили 480, следовательно, m (АТГ) = 480 m (Г) – m (АГ) – m (ГТ) = 480-75-100-90 = 215 – количество человек, которые решили все три задачи. Из условия тригонометрию решили 420, следовательно: m (А) = 400 – m (АГ) – m (АТГ) – m (АТ) = 400 – 100 – 215 – 30 = 55 – количество абитуриентов решили только алгебру.

Проверка: итак m (А) + m (Т) + m (Г) = 55 + 85 + 75 = 215 – количество человек, которые решили только 1 задачу. Так как всего 650 студентов, то должно выполниться равенство: 215 + 100 + 30 + 90 + 215 = 650 – верно!

Ответ: 215 человек, которые решили только 1 задачу.

Использование кругов Эйлера

Источник