Надо ли доказывать теорему менелая на егэ - Помощь в подготовке к экзаменам и поступлению

Анна Малкова

Эти две полезные теоремы – теорема Менелая и теорема Чевы — чаще применяются при решении олимпиадных задач, чем на ЕГЭ по математике. Однако в 2020 году в ряде вариантов ЕГЭ обнаружилась задача по планиметрии (№16), которую на первый взгляд невозможно решить без теоремы Менелая или теоремы Чевы. Но на самом деле, конечно, возможно. Например, в Санкт-Петербурге попались такие задачи.

Разберемся, что это за теоремы и как применяются. И действительно ли на ЕГЭ дали задачи на применение теорем, выходящих за рамки школьной программы. И можно ли эти задачи решить по-другому?

Теорема Менелая:

Пусть прямая пересекает произвольный треугольник ABC, причем C_1 – точка ее пересечения со стороной AB, A_1 – точка ее пересечения со стороной BC, и B_1 – точка ее пересечения с продолжением стороны AC.

Тогда выполняется равенство:

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_1}{A_1C} cdot frac{CB_1}{B_1A} = 1.$

Как это запомнить? Сначала рисуем треугольник ABC. Затем прямую, пересекающую две его стороны и продолжение третьей. На этой прямой лежат точки и B_1, причем на стороне должна лежать точка C_1, на стороне – точка A_1 и на продолжении – точка B_1.

Затем записываем равенство так, как будто «обходим» весь треугольник ABC, от точки к точкам и и затем возвращаемся в точку Но по дороге нам встречаются точки и B_1 – их тоже включаем в формулу.

Один из учащихся нашей ЕГЭ-Студии предложил такое мнемоническое правило: пусть точки A, B и – это города, а точки и B_1 – заправки, где можно пополнить запас бензина. Тогда правило звучит так: «Едем из города в город, заезжаем на заправку!»Возможно, вы придумаете свое правило : -)

В некоторых задачах полезна обратная теорема Менелая.

Теорема (Менелая, обратная). Пусть дан треугольник Предположим, что точка лежит на стороне точка лежит на стороне а точка лежит на продолжении стороны причём про эти точки известно, что

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_1}{A_1C} cdot frac{CB_1}{B_1A} = 1.$

Тогда эти точки лежат на одной прямой.

Как правило, не так-то просто бывает доказать, что три точки лежат на одной прямой. Обычно мы используем для доказательства такого факта косвенные методы. Например, если для точек A, , B и выполняется равенство: – то это означает, что точка лежит на отрезке AC. Или, если нам удается доказать, что угол ABC – развернутый, это и будет означать, что точки A, , B и лежат на одной прямой. Обратная теорема Менелая дает еще один способ доказательства того, что три точки – в данном случае и C_1 – лежат на одной прямой.

Теорема Чевы

Пусть точки и C_1 лежат соответственно на сторонах и треугольника ABC, причем отрезки и CC_1 пересекаются в одной точке. В этом случае выполняется равенство:

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_1}{A_1C} cdot frac{CB_1}{B_1A} = 1.$

Обратная теорема Чевы:

Теорема (Чевы, обратная). Пусть точки лежат соответственно на сторонах и треугольника причём

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_1}{A_1C} cdot frac{CB_1}{B_1A} = 1.$

Тогда отрезки и пересекаются в одной точке.

Как применяются теоремы Менелая и Чевы?

Вот задача Профильного ЕГЭ по математике 2020 года (№16), Санкт-Петербургский вариант.

На сторонах и треугольника отмечены точки и соответственно, причём Отрезки и пересекаются в точке

а) Докажите, что — параллелограмм.
б) Найдите если отрезки и перпендикулярны,

Докажем пункт (а) с помощью теоремы Менелая:

Пусть

По теореме Чевы,

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_2}{A_2C} cdot frac{CB_1}{B_1A} = 1.$

$displaystyle frac{8}{3} cdot frac{BA_2}{A_2C} cdot frac{3}{1} = 1$

$displaystyle frac{BA_2}{A_2C} = frac{1}{8},$ тогда

$displaystyle BA_2 = frac{1}{9}BC$

$displaystyle A_2A_1 = left ( frac{1}{3} - frac{1}{9} right ) BC = frac{2}{9}BC,$

$displaystyle A_1C = frac{2}{3}BC,$ тогда $displaystyle A_2A_1 = frac{1}{3}A_1C$

$displaystyle A_1C : A_2C = B_1C : AC = frac{3}{4},$

Это значит, что по двум углам и то есть

Рассмотрим треугольник ABB_1.

Прямая C_1C пересекает две его стороны и продолжение третьей стороны AB_1.

По теореме Менелая,

$displaystyle frac{AC_1}{C_1B} cdot frac{BD}{DB_1} cdot frac{B_1C}{AC} = 1$

$displaystyle frac{8}{3} cdot frac{BD}{DB_1} = frac{3}{4} = 1;$

$displaystyle frac{BD}{DB_1} = frac{1}{2} = frac{BA_1}{A_1C};$

тогда $displaystyle frac{BD}{BB_1} = frac{BA_1}{BC} = frac{1}{3},$

по углу и двум сторонам, отсюда

Мы получили:

— параллелограмм по определению.

Мы доказали то, что требовалось в пункте (а).
Но что делать, если теоремы Менелая и Чевы вы не проходили в школе? Ничего страшного, докажем без теорем Менелая и Чевы. Их легко заменят подобные треугольники.

Обозначим

Докажем, что — параллелограмм.

Пусть — середина AC.

Тогда

Тогда по углу и двум пропорциональным сторонам,

Проведём

По теореме Фалеса BN = y.

Пусть

по двум углам;

$displaystyle frac{AP}{BD} = frac{AC_1}{BC_1} = frac{8}{3}.$

Пусть

по 2 углам, $displaystyle frac{AP}{B_1D} = frac{AC}{B_1C} = frac{4}{3},$
тогда $displaystyle B_1D = frac{3}{4}AP = 6k,$

$displaystyle frac{BD}{B_1D} = frac{1}{2}.$

Это значит, что по углу и двум сторонам и

При этом $displaystyle A_1D = frac{1}{3}B_1C = Z = AB_1.$

Получим, что в четырёхугольнике :

Значит, — параллелограмм.

Как видим, эти решения примерно одного уровня сложности.
А вот в пункте (б) нет необходимости применять теоремы Чевы и Менелая. Он легко решается с помощью обычной школьной геометрии.

б) Найдём , если

Поскольку получим, что — прямоугольный.

Мы доказали в пункте (а), что — трапеция, причём

По условию,

Тогда $displaystyle A_1D = frac{28}{4} = 7,$

$displaystyle B_1C = frac{28}{4} cdot 3 = 21,$

$displaystyle A_1C = frac{2}{3}BC = frac{2}{3} cdot 18 = 12.$

Пусть

Тогда A_1MCD — параллелограмм (по признаку паралелограмма)

по теореме Пифагора из

$displaystyle B_1A_1 = sqrt{21^2-12^2} = 3 sqrt{7^2 - 4^2} = 3 sqrt{33},$

$displaystyle cos angle A_1B_1C = cos angle A_1B_1M = frac{B_1A_1}{B_1C} = frac{sqrt{33}}{7}$

Найдём A_1M из по теореме косинусов.

$displaystyle A_1M^2 = 9 cdot 33 + 28^2 - frac{2 cdot 28 cdot 3 sqrt{33} cdot sqrt{33}}{7} = 28^2 - 15cdot 33 = 784 - 495 = 289;$

Ответ: 17.

Вот еще одна задача, которую можно решить как с помощью теоремы Чевы, так и без нее.

На сторонах прямоугольного треугольника с прямым углом построены во внешнюю сторону квадраты и Докажите, что:

а) прямые и отсекают от катетов треугольника равные отрезки
б) прямые и высота треугольника проведённая из вершины пересекаются в одной точке.

Пункт (а) доказывается легко.

а) Пусть ,
.

Докажем, что CE=CF .

Обозначим

по 2 углам,

$displaystyle frac{FC}{A_2C_1}=frac{BC}{BC_1}$ , так как

получим:

$displaystyle frac{FC}{b}=frac{a}{a+b}. ,$ (1)

по 2 углам,

$displaystyle frac{CE}{C_2B_2}=frac{AC}{AC_2}; , , frac{CE}{a}=frac{b}{a+b}. ,$ (2)

$displaystyle frac{FC cdot a}{CE cdot b} = frac{a}{b},$ отсюда FC=CE.

Решим пункт (б) с помощью теоремы Чевы:

Запишем, чему равны длины отрезков Для длин и воспользуемся тем, что в прямоугольном треугольнике каждый катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.

$displaystyle AH = frac{b^2}{sqrt{a^2 + b^2}}$

$displaystyle HB = frac{a^2}{sqrt{a^2 + b^2}}$

$displaystyle BE = a - frac{ab}{a+b}$

$displaystyle CE = frac{ab}{a+b}$

$displaystyle CF = frac{ab}{a+b}$

$displaystyle AF = b - frac{ab}{a+b}$

Проверим выполнение равенства

$displaystyle frac{AH}{HB} cdot frac{BE}{CE} cdot frac{CF}{AF} = 1.$

$displaystyle frac{frac{b^2}{sqrt{a^2+b^2}}}{frac{a^2}{sqrt{a^2+b^2}}} cdot frac{a - frac{ab}{a+b}}{frac{ab}{a+b}} cdot frac{frac{ab}{a+b}}{b - frac{ab}{a+b}} = 1.$

Равенство выполняется.
Согласно теореме Чевы, это значит, что и пересекаются в одной точке.
А вот как решается эта задача без теоремы Чевы, с помощью векторов:

Смотрите решение: https://ege-study.ru/zadacha-na-dokazatelstvo-planimetriya/

Математик Менелай Александрийский жил в I веке до нашей эры (Древний Рим).
Математик и инженер Джованни Чева – XVII век, Италия.

Как видим, теоремы Менелая и Чевы оказываются полезны в некоторых задачах. Очень хорошо, если вы знаете эти теоремы. Однако если они для вас непривычны, можно применить простой школьный прием – пары подобных треугольников.

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Теорема Менелая, теорема Чевы – нужны на ЕГЭ или нет?» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.03.2023

Источник

5 февраля 2018

В закладки

Обсудить

Жалоба

Какие геометрические факты можно использовать на ЕГЭ без доказательства?

Начнём с того, что для ЕГЭ не нужны сколько-нибудь редкие теоремы, особенно где-нибудь на шпаргалке.

Нужно уметь применять всем знакомые факты, видеть рисунок и решать больше задач. Но вопрос из заголовка задают очень часто, и ответить на него нужно. Естественно, все сотни признаков и свойств, что есть в вашем школьном учебнике можно использовать. Но как насчет более редких фактов: что можно применять без доказательства, а что нет? Точный ответ: любые факты из школьных учебников, рекомендованных минобром на 2017-2018 год.

Ну а вот заветный список того, что мне все-таки удалось обнаружить в соответствующих учебниках:

→ Теорема Менелая (Атанасян. Геометрия 7-9 классы)
→ Теорема Чевы (Атанасян. Геометрия 7-9 классы)
→ Теорема Птолемея (Мерзляк. Геометрия 8 класс)
→ Прямая Эйлера (Мерзляк. Геометрия 8 класс)
→ Теорема об окружности Эйлера (Бутузов. Геометрия 8 класс)
→ Формула медианы треугольника (Шарыгин. Геометрия 7-9 классы)
→ Формула биссектрисы треугольника (Шарыгин. Геометрия 7-9 классы)
→ Теорема о четырех замечательных точках трапеции (Шарыгин. Геометрия 7-9 классы)

Формулу радиуса вневписанной окружности используйте. Каноническое уравнение эллипса — да пожалуйста! Ключевые формулы метода координат для задачи №14, опять же, есть

Но если здесь есть коллеги по цеху, которые могут уточнить еще несколько популярных вопросов насчет непопулярной теории — черкните, буду признателен! Вот интересующие факты: формула Брахмагупты, теорема Стюарта, формула Эйлера для расстояния между центрами вписанной и описанной окружностями треугольника, понятие определителя квадратной матрицы.

Ну и еще раз в заключение. Вероятность того, что задача ЕГЭ не решается без экзотики, равна нулю (такие события называются невозможными). Вероятность того, что вам вообще попадется конфигурация, для которой актуальна, например, теорема о девяти точках окружности, приблизительно равна 0,015. Вероятность того, что школьник в целом знает что-то «запрещенное», приблизительно равна, не кидайтесь камнями, 0,000037.

Источник: vk.com/wildmathing

Источник

Подготовка к ЕГЭ с преподавателем

Теорема Пифагора

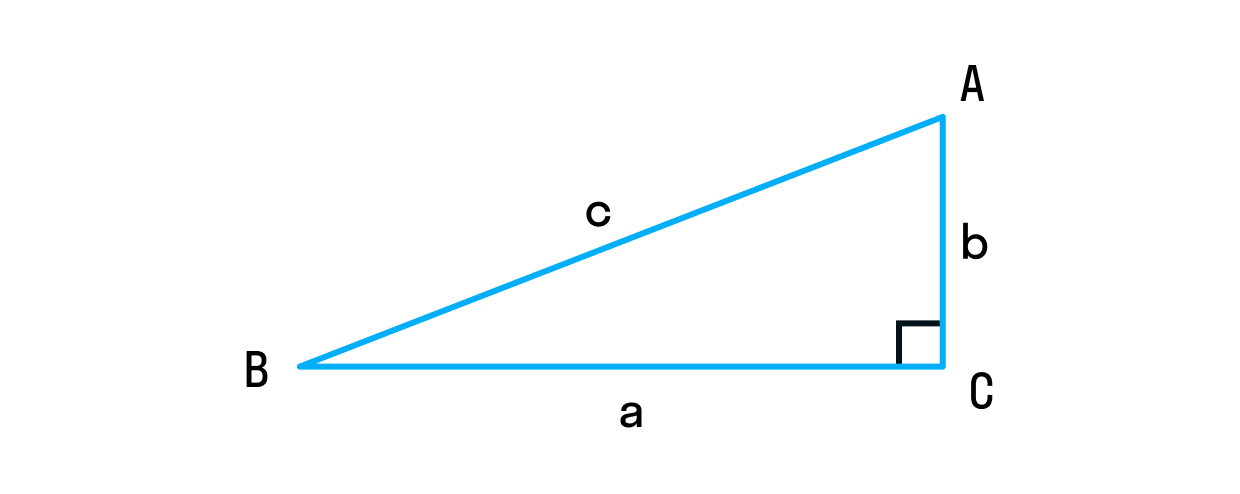
Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии. Она устанавливает соотношение между сторонами прямоугольного треугольника. И звучит так:

В прямоугольном треугольнике сумма квадратов длин катетов равна квадрату длины гипотенузы.

c² = a² + b².

Теорема Пифагора — это частный случай теоремы косинусов. Это объясняется тем, что косинус 90 градусов равен нулю.

Получай лайфхаки, статьи, видео и чек-листы по обучению на почту

Демоурок по подготовке к экзаменам

Составим ваш личный путь к высоким баллам — учтем сроки, уровень знаний и цель.

Теорема Фалеса

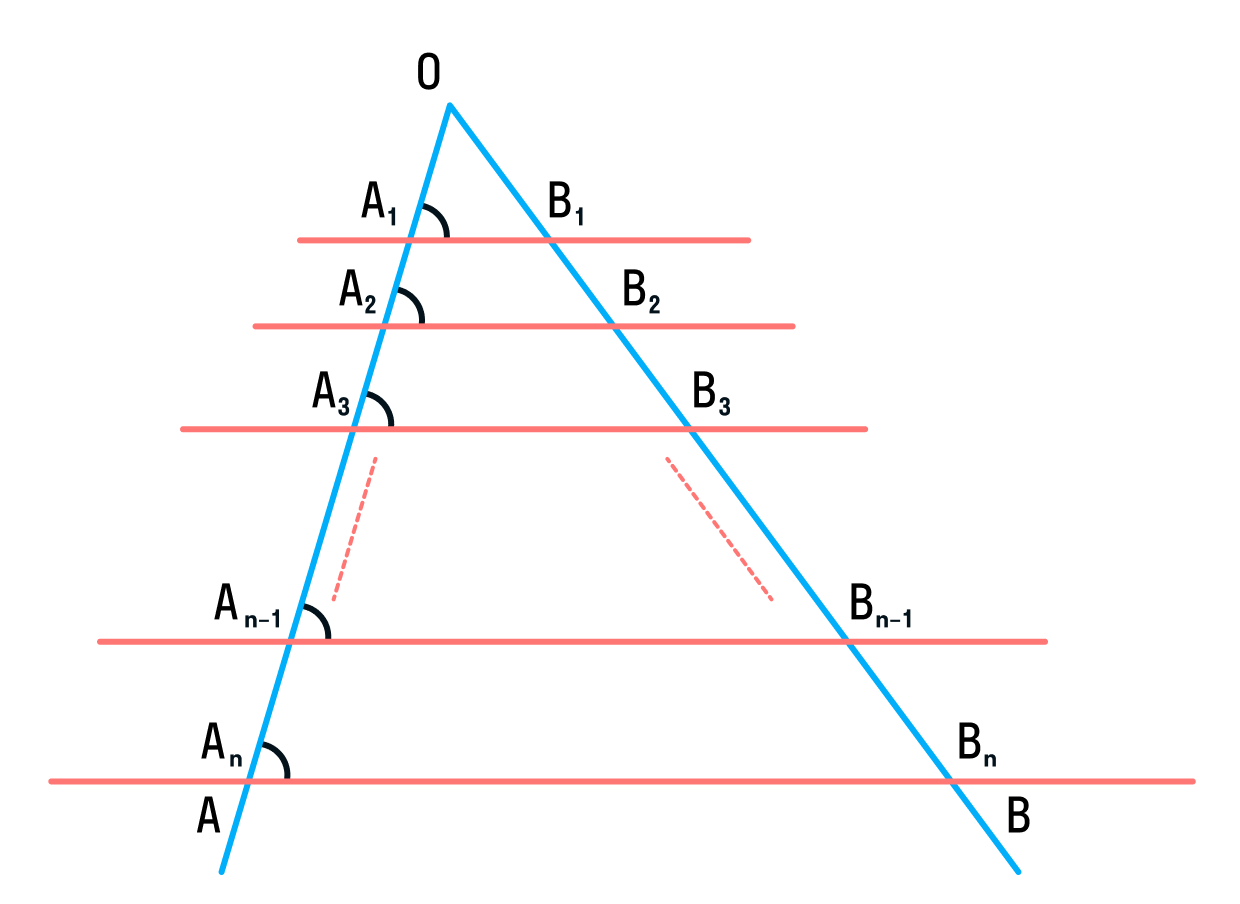
Теорема Фалеса — это свойство параллельных прямых, которые пересекают две секущие с общей точкой.

Вообще, есть две теоремы Фалеса — общая, на все случаи жизни, и частная — то, что нужно для решения задач на ЕГЭ по математике.

Через произвольные точки A₁, A₂, … A_n–1, A_n, лежащие на стороне AO угла AOB, проведены параллельные прямые, пересекающие сторону угла OB в точках B₁, B₂, … B_n–1, B_n, соответственно. Тогда справедливы равенства:

В ЕГЭ по математике теорема Фалеса встречается чаще всего в параллелограмме, у которого проведена диагональ, — будьте начеку.

Теорема косинусов

Теорема Пифагора — кайф, легко запомнить, часто встречается, применяем только тогда, когда у нас есть прямоугольный треугольник. Но на самом деле теорема Пифагора работает для любого треугольника, только называется она в этом случае теоремой косинусов.

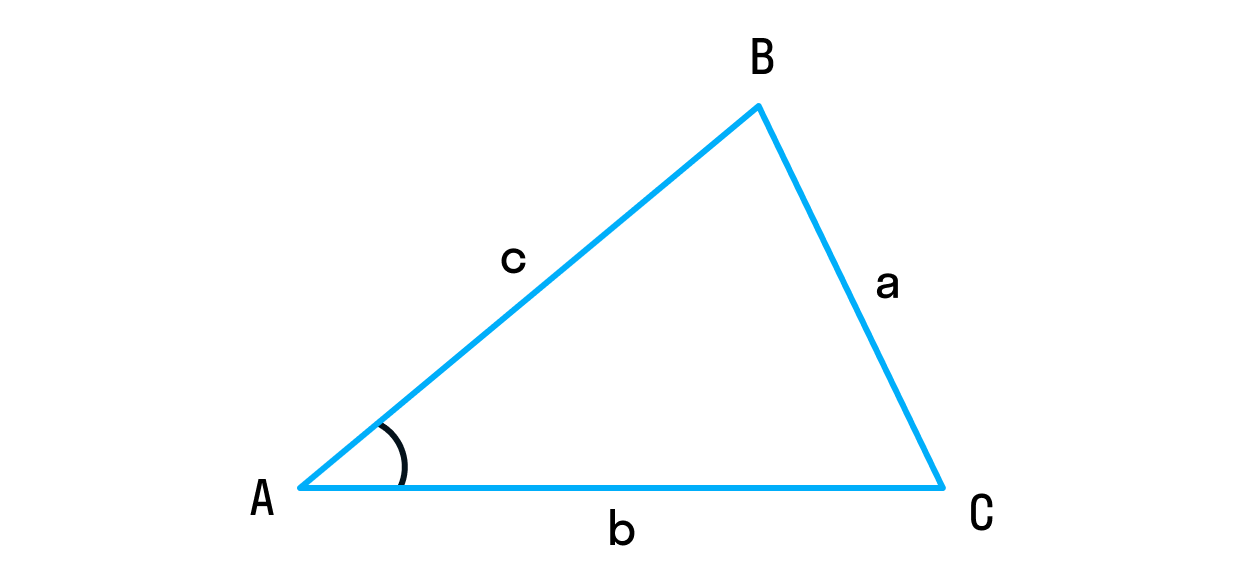
Квадрат длины стороны треугольника равен сумме квадратов длин других сторон минус удвоенное произведение длин этих сторон на косинус угла между ними.

a² = b² + c² – 2bc cos A

Собственно, по формуле сразу становится понятно, почему это соотношение называется теоремой косинусов. Ещё она крайне похожа на разность квадратов с учётом косинуса, поэтому запомнить её не очень сложно. И если вспомнить, что косинус 90 градусов — это 0, то мы увидим знакомую теорему Пифагора.

Теорема синусов

Казалось бы, синус — это что-то про тригонометрию, но на самом деле совсем не только. Планиметрия может с этим смело поспорить, и теорема синусов — явный аргумент в этом воображаемом споре. Если коротко, теорема синусов — это формула связи угла с противолежащей ему стороной в треугольнике.

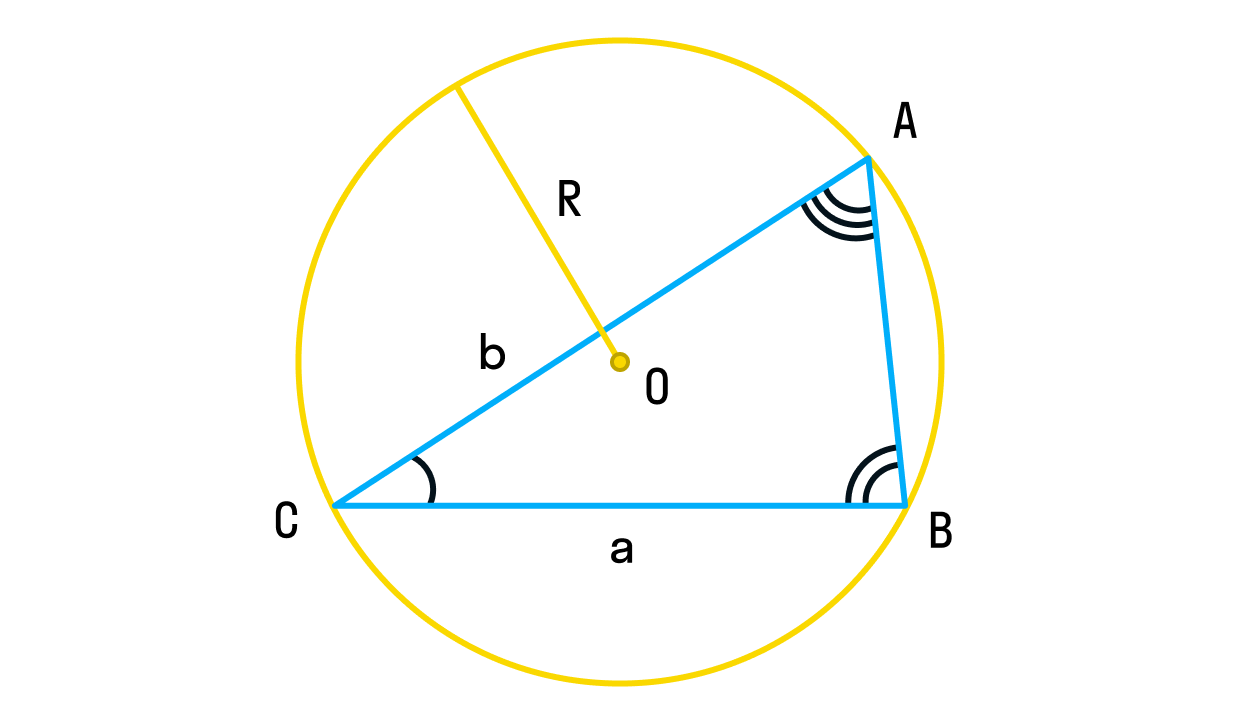
Для любого треугольника справедливы равенства:

где R — радиус описанной около треугольника окружности.

По теореме синусов, во-первых, можно быстро найти радиус описанной окружности по известной стороне и противолежащему ей углу. Во-вторых, если треугольник не прямоугольный, то в нём можно просто найти синус угла по известным стороне и радиусу описанной окружности. Ну и в конце концов, можно использовать отношение двух любых сторон и углов. Формула синусов в ЕГЭ по математике используется нечасто, но иметь её в своем арсенале полезно и обязательно.

Теорема Менелая

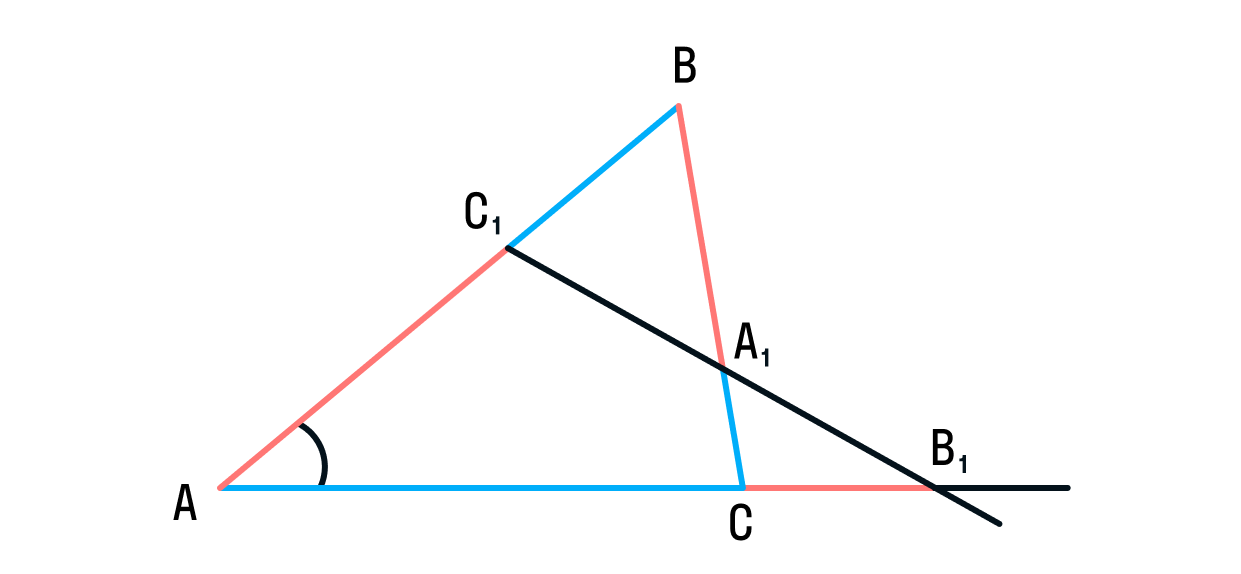
Её также называют теоремой о треугольнике и секущей, и звучит она так:

Если на сторонах AB и BC треугольника ABC взяты соответственно точки C₁ и A₁, а точка B₁ взята на продолжении стороны AC за точку C, то точки C₁, A₁ и B₁ лежат на одной прямой тогда и только тогда, когда выполнено равенство:

Теорема Менелая пригодится для решения 2-й части ЕГЭ по математике. Она поможет уменьшить огромную кучу исписанных листочков при решении и сохранить время на экзамене, ведь помогает решать в несколько действий.

Чтобы с лёгкостью запомнить все основные теоремы из геометрии для ЕГЭ по математике, скачайте и распечатайте удобную шпаргалку. Кроме теорем из этой статьи, там есть ещё две редкие — теоремы Чевы и Вариньона, а также задачи на доказательства.

Математика — обязательный для сдачи на ЕГЭ предмет, без которого не получишь аттестат. Это также один из самых сложных экзаменов для выпускников. Делимся типичными ошибками в ЕГЭ по математике, а также ресурсами, которые помогут отработать теорию на практике.

Источник

Теорема Менелая, теорема Чевы – нужны на ЕГЭ или нет?

Анна Малкова

Теорема Менелая:

Пусть прямая пересекает произвольный треугольник ABC, причем C_1 – точка ее пересечения со стороной ABC, A_1 – точка ее пересечения со стороной BC, и B_1 – точка ее пересечения с продолжением стороны AC.

Тогда выполняется равенство:

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_1}{A_1C} cdot frac{CB_1}{B_1A} = 1.$

В некоторых задачах полезна обратная теорема Менелая.

Теорема (Менелая, обратная). Пусть дан треугольник ABC. Предположим, что точка C_1 лежит на стороне AB, точка A_1 лежит на стороне BC, а точка B_1 лежит на продолжении стороны AC, причём про эти точки известно, что

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_1}{A_1C} cdot frac{CB_1}{B_1A} = 1.$

Тогда эти точки лежат на одной прямой.

Теорема Чевы

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_1}{A_1C} cdot frac{CB_1}{B_1A} = 1.$

Обратная теорема Чевы:

Теорема (Чевы, обратная). Пусть точки лежат соответственно на сторонах BC, AC и треугольника ABC, причём

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_1}{A_1C} cdot frac{CB_1}{B_1A} = 1.$

Тогда отрезки и CC_1 пересекаются в одной точке.

Как применяются теоремы Менелая и Чевы?

Вот задача Профильного ЕГЭ по математике 2020 года (№16), Санкт-Петербургский вариант.

На сторонах и треугольника ABC отмечены точки и B_1 соответственно, причём Отрезки BB_1 и CC1 пересекаются в точке

а) Докажите, что — параллелограмм.
б) Найдите CD, если отрезки и перпендикулярны,

Докажем пункт (а) с помощью теоремы Менелая:

Пусть

По теореме Чевы,

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_2}{A_2C} cdot frac{CB_1}{B_1A} = 1.$

$displaystyle frac{8}{3} cdot frac{BA_2}{A_2C} cdot frac{3}{1} = 1$

$displaystyle frac{BA_2}{A_2C} = frac{1}{8},$ тогда

$displaystyle BA_2 = frac{1}{9}BC$

$displaystyle A_2A_1 = left ( frac{1}{3} - frac{1}{9} right ) BC = frac{2}{9}BC,$

$displaystyle A_1C = frac{2}{3}BC,$ тогда $displaystyle A_2A_1 = frac{1}{3}A_1C$

$displaystyle A_1C : A_2C = B_1C : AC = frac{3}{4},$

Это значит, что по двум углам и то есть

Рассмотрим треугольник ABB_1.

Прямая C_1C пересекает две его стороны и продолжение третьей стороны AB_1.

По теореме Менелая,

$displaystyle frac{AC_1}{C_1B} cdot frac{BD}{DB_1} cdot frac{B_1C}{AC} = 1$

$displaystyle frac{8}{3} cdot frac{BD}{DB_1} = frac{3}{4} = 1;$

$displaystyle frac{BD}{DB_1} = frac{1}{2} = frac{BA_1}{A_1C};$

тогда $displaystyle frac{BD}{BB_1} = frac{BA_1}{BC} = frac{1}{3},$

по углу и двум сторонам, отсюда

Мы получили:

— параллелограмм по определению.

Обозначим

Докажем, что — параллелограмм.

Пусть — середина AC.

Тогда

Тогда по углу и двум пропорциональным сторонам,

Проведём

По теореме Фалеса BN = y.

Пусть

по двум углам;

$displaystyle frac{AP}{BD} = frac{AC_1}{BC_1} = frac{8}{3}.$

Пусть

по 2 углам, $displaystyle frac{AP}{B_1D} = frac{AC}{B_1C} = frac{4}{3},$
тогда $displaystyle B_1D = frac{3}{4}AP = 6k,$

$displaystyle frac{BD}{B_1D} = frac{1}{2}.$

Это значит, что по углу и двум сторонам и

При этом $displaystyle A_1D = frac{1}{3}B_1C = Z = AB_1.$

Получим, что в четырёхугольнике :

Значит, — параллелограмм.

б) Найдём , если

Поскольку получим, что — прямоугольный.

Мы доказали в пункте (а), что — трапеция, причём

По условию,

Тогда $displaystyle A_1D = frac{28}{4} = 7,$

$displaystyle B_1C = frac{28}{4} cdot 3 = 21,$

$displaystyle A_1C = frac{2}{3}BC = frac{2}{3} cdot 18 = 12.$

Пусть

Тогда A_1MCD — параллелограмм (по признаку паралелограмма)

по теореме Пифагора из

$displaystyle B_1A_1 = sqrt{21^2-12^2} = 3 sqrt{7^2 - 4^2} = 3 sqrt{33},$

$displaystyle cos angle A_1B_1C = cos angle A_1B_1M = frac{B_1A_1}{B_1C} = frac{sqrt{33}}{7}$

Найдём A_1M из по теореме косинусов.

Ответ: 17.

Вот еще одна задача, которую можно решить как с помощью теоремы Чевы, так и без нее.

На сторонах прямоугольного треугольника ABC с прямым углом построены во внешнюю сторону квадраты и Докажите, что:

а) прямые AB_2 и A_2B отсекают от катетов треугольника ABC равные отрезки
б) прямые и высота треугольника ABC, проведённая из вершины пересекаются в одной точке.

Пункт (а) доказывается легко.

а) Пусть ,
.

Докажем, что CE=CF .

Обозначим

по 2 углам,

$displaystyle frac{FC}{A_2C_1}=frac{BC}{BC_1}$ , так как

получим:

$displaystyle frac{FC}{b}=frac{a}{a+b}. ,$ (1)

по 2 углам,

$displaystyle frac{CE}{C_2B_2}=frac{AC}{AC_2}; , , frac{CE}{a}=frac{b}{a+b}. ,$ (2)

$displaystyle frac{FC cdot a}{CE cdot b} = frac{a}{b},$ отсюда FC=CE.

Решим пункт (б) с помощью теоремы Чевы:

$displaystyle AH = frac{b^2}{sqrt{a^2 + b^2}}$

$displaystyle HB = frac{a^2}{sqrt{a^2 + b^2}}$

$displaystyle BE = a - frac{ab}{a+b}$

$displaystyle CE = frac{ab}{a+b}$

$displaystyle CF = frac{ab}{a+b}$

$displaystyle AF = b - frac{ab}{a+b}$

Проверим выполнение равенства

$displaystyle frac{AH}{HB} cdot frac{BE}{CE} cdot frac{CF}{AF} = 1.$

Равенство выполняется.
Согласно теореме Чевы, это значит, что и пересекаются в одной точке.
А

Источник

Применение Теоремы Менелая в задаче 16

28 декабря 2015

Обратите внимание: у меня на сайте есть отдельный урок по теореме Менелая. Сегодня мы будем лишь применять её для решения конкретных задач из ЕГЭ.

Данная теорема в школьном курсе математики относится к категории тех знаний, которые дают далеко не во всех школах, но для успешной сдачи ЕГЭ знать её совершенно необходимо. Потому что эта теорема применяется для решения задачи 16 — сложной планиметрической задачи, состоящей из двух частей.

Сегодня мы рассмотрим, как работает теорема Менелая на примере одной довольно сложной задачи. Видео получилось довольно объёмным и отнюдь не самым простым, но очень полезным для тех, кто действительно хочет набрать много баллов на экзамене.:)

Смотрите также:

Пробный ЕГЭ 2016: задача 16 с доказательством и окружностями, для решения которой нужно знать пару теорем.:)
Угол между двумя прямыми
Тест к уроку «Округление с избытком и недостатком» (1 вариант)
Так сокращать дроби нельзя!
Задача B5: площадь сектора
Задача B4: тарифы на сотовую связь

Источник

Регистрация
Вход

Форум
Поиск
FAQ   alexlarin.net

Текущее время: 11 мар 2023, 17:03
Часовой пояс: UTC + 3 часа

Сообщения без ответов | Активные темы

Страница 1 из 2 [ Сообщений: 16 ] На страницу 1, 2 След.

Начать новую тему»>

Ответить

Можно ли пользоваться следующими теоремами на ЕГЭ?

Для печати

Предыдущая тема | Следующая тема

Можно ли пользоваться следующими теоремами на ЕГЭ?

Автор

Сообщение

Заголовок сообщения: Можно ли пользоваться следующими теоремами на ЕГЭ?

Добавлено: 23 фев 2015, 17:42

Центр пользователя

Зарегистрирован: 20 мар 2013, 13:26
Сообщений: 16

Можно ли пользоваться теоремой Вариньона, теоремой Менелая, формулой Стюарта, частными случаями формулой Стюарта без доказательства или же все это нужно доказывать на ЕГЭ?
Можно ли пользоваться формулой для длины отрезка, соединяющего середины диагоналей трапеции на ЕГЭ без доказательства?
Можно ли пользоваться формулами метода координат в пространстве через определители для определения углов и расстояний без доказательства?

uStas

Заголовок сообщения: Re: Можно ли пользоваться следующими теоремами на ЕГЭ?

Добавлено: 23 фев 2015, 17:46

Центр пользователя

Зарегистрирован: 14 июн 2010, 12:35
Сообщений: 6126
Откуда: Воронеж

Стесняюсь спросить, а без теоремы Вариньона никак?

Зачем придумывать страсти?

integral

Заголовок сообщения: Re: Можно ли пользоваться следующими теоремами на ЕГЭ?

Добавлено: 23 фев 2015, 17:56

Центр пользователя

Зарегистрирован: 20 мар 2013, 13:26
Сообщений: 16

uStas писал(а):

Стесняюсь спросить, а без теоремы Вариньона никак?

Зачем придумывать страсти?

Ясно дело, что ее можно попутно доказать «сполпинка», но ученики сильных физмат школ могут думать, что это по теореме, которую они изучали, потому ее можно использовать и не обосновывать подробно. Потому и спрашиваю. Нужно ведь знать — чем можно пользоваться без доказательства, а чем — нет? Можно тогда скатиться к тому, что нужно доказывать теорему о трех перпендикулярах. Ясно дело ,что если все доказать, то вопросов возникнуть не должно. Но если человек забыл доказательство теоремы и не знает — стоит ли его повторять перед ЕГЭ?

Еще попутно, можно ли сразу пользоваться тем, что медианы треугольника делят его на шесть равновеликих?

uStas

Заголовок сообщения: Re: Можно ли пользоваться следующими теоремами на ЕГЭ?

Добавлено: 23 фев 2015, 18:05

Центр пользователя

Зарегистрирован: 14 июн 2010, 12:35
Сообщений: 6126
Откуда: Воронеж

integral писал(а):

uStas писал(а):

Стесняюсь спросить, а без теоремы Вариньона никак?

Зачем придумывать страсти?

Еще попутно, можно ли сразу пользоваться тем, что медианы треугольника делят его на шесть равновеликих?

Да не берите Вы всё это в свою голову!

Пишите свои решения задачек с форума, народ оценит Ваши решения.

Были тут уже «герои», задававшие вопросы типа: «А если бы у бабушки были известные произведения Фаберже, кем бы она тогда была?»

integral

Заголовок сообщения: Re: Можно ли пользоваться следующими теоремами на ЕГЭ?

Добавлено: 23 фев 2015, 18:32

Центр пользователя

Зарегистрирован: 20 мар 2013, 13:26
Сообщений: 16

uStas писал(а):

integral писал(а):

uStas писал(а):

Стесняюсь спросить, а без теоремы Вариньона никак?

Зачем придумывать страсти?

Еще попутно, можно ли сразу пользоваться тем, что медианы треугольника делят его на шесть равновеликих?

Да не берите Вы всё это в свою голову!

Пишите свои решения задачек с форума, народ оценит Ваши решения.

Я не для себя интересуюсь, а для своих учеников (мне не нужно сдавать ЕГЭ), они такие вопросы задают.

uStas

Заголовок сообщения: Re: Можно ли пользоваться следующими теоремами на ЕГЭ?

Добавлено: 23 фев 2015, 18:43

Центр пользователя

Зарегистрирован: 14 июн 2010, 12:35
Сообщений: 6126
Откуда: Воронеж

Исчо раз, не берите в голову, задачки ЕГЭ решаются без участия Вариньона.

integral

Заголовок сообщения: Re: Можно ли пользоваться следующими теоремами на ЕГЭ?

Добавлено: 23 фев 2015, 19:12

Центр пользователя

Зарегистрирован: 20 мар 2013, 13:26
Сообщений: 16

uStas писал(а):

Исчо раз, не берите в голову, задачки ЕГЭ решаются без участия Вариньона.

Например, Вася Пупкин решает вот эту задачу

http://reshuege.ru/problem?id=505410

.
Вася Пупкин хорошо помнит теорему Вариньона, но напрочь забыл про ее доказательство. Спрашивается, если он в первом пункте напишет: По теореме Вариньона этот четырехугольник — параллелограмм, а в параллелограмме диагонали точкой пересечения делятся попалам. Чтд. Зачтут ли ему задачу? У меня уже так два ученика решили эту задачу, потому интересуюсь. А не просто фантазии, есть факты

uStas

Заголовок сообщения: Re: Можно ли пользоваться следующими теоремами на ЕГЭ?

Добавлено: 23 фев 2015, 19:20

Центр пользователя

Зарегистрирован: 14 июн 2010, 12:35
Сообщений: 6126
Откуда: Воронеж

Утомили Вы меня, Вы и Ваш Вася Пупкин.

Я не психиатр, ничем Вам помочь не смогу. :ymhug:

egetrener

Заголовок сообщения: Re: Можно ли пользоваться следующими теоремами на ЕГЭ?

Добавлено: 23 фев 2015, 19:21

Центр пользователя

Зарегистрирован: 17 авг 2010, 21:40
Сообщений: 2582

integral писал(а):

Вася Пупкин хорошо помнит теорему Вариньона, но напрочь забыл про ее доказательство.

Что значит — забыл? Забыл и не может доказать такую простую вещь?
И почему Вася претендует на то, чтобы ему засчитали задачу 18?

admin

Заголовок сообщения: Re: Можно ли пользоваться следующими теоремами на ЕГЭ?

Добавлено: 23 фев 2015, 19:57

Администратор

Центр пользователя

Зарегистрирован: 10 июн 2010, 15:00
Сообщений: 6119

Уважаемый integral, здесь важна исключительно официальная точка зрения организаторов ЕГЭ во главе с Гуру.
А она, если не ошибаюсь, такова: можно использовать без доказательства любые факты и теоремы, которые имеются в школьных учебниках.
Поскольку литературы рекомендованной, утвержденной и включенной во всякие чиновничьи списки, у нас — как грязи, то никто не скажет стопудово, может теорема Вариньона и содержится в какой-нибудь книженции, рекомендованной минобром. Где-то, когда-то, для кого-то и т.п.
И если на апелляции хлопнуть ей об стол, то после долгих словоизвержений, скорее всего все зачтут.
Но это все неважно.
Непосредственно по заданному вопросу — что говорить ученикам.
Я бы говорил — доказывать.

Показать сообщения за: Сортировать по:

Страница 1 из 2 [ Сообщений: 16 ] На страницу 1, 2 След.

Текущее время: 11 мар 2023, 17:03 | Часовой пояс: UTC + 3 часа

Удалить cookies форума | Наша команда | Вернуться наверх

Кто сейчас на форуме

Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 3

Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете добавлять вложения

Найти:

Перейти:

Источник

Выпускная работа

Тема: «Применение теорем Чевы и Менелая

при решении геометрических задач ЕГЭ»

Содержание

Теоретические факты:

Теорема Чевы
Теорема Менелая

Применение теорем Чевы и Менелая при подготовке к ЕГЭ

Теоретические факты

Решение задач с помощью теорем Чевы и Менелая более рационально, чем их решение другими способами, требующими дополнительных действий и построений, которые не всегда оказываются очевидными.

Теорема Чевы.

Если на сторонах AB, BC и CA треугольника ABC взяты соответственно точки C₁, A₁ и B₁ (рис.1), то отрезки AA₁, BB₁ и CC₁ пересекаются в одной точке тогда и только тогда, когда выполнено равенство

Теорема Менелая.

Если на сторонах ВС, АВ и продолжении стороны АС треугольника АВС за точку С отмечены соответственно точки А´, С´,В´, лежащие на одной прямой, то

Применение теорем Чевы и Менелая при подготовке к ЕГЭ

Хочу вам предложить два способа решения одной интересной задачи из ЕГЭ. Первый способ довольно длинный, но его нужно знать, поскольку прием, который в нем используется, применяется довольно часто при решении задач, в которых дано отношение отрезков.

Второй способ позволяет решить задачу в одно действие, но в нем используется Теорема Менелая.

Итак задача №1:

На сторонах AB и BC треугольника ABC взяты соответственно точки M и N так, что AM:MB=2:3, BN:NC=2:1. Отрезки AN и CM пересекаются в точке O. Найти отношение CO:OM.

Вот наш треугольник:

Проведем через точку В прямую параллельно отрезку AB, затем продолжим отрезок AN до пересечения с этой прямой и поставим там точку К:

Рассмотрим треугольники ANC и BNK. Эти треугольники подобны, так как AC||BK. Стороны треугольника BNK относятся к сторонам треугольника ANC как 2:1.

Пусть AC=x, BK=2x.

Теперь продолжим отрезок MC до пересечения с прямой BK. Поставим там точку L.

Мы получили подобные треугольники LMB и AMC, сходственные стороны которых относятся как 3:2. Так как AC=x, то LB=1,5x.

Пусть LM=3n, MC=2n. Тогда LC=5n.

Теперь рассмотрим подобные треугольники LOK и AOC.

, следовательно, . Пусть LO=3,5z, OC=z. Тогда LO+OC=LC=4,5z.

Получили, что 5n=4,5z. Тогда MC=2n=z. Отсюда MO=MC-CO=z-z=z

Отсюда CO:OM=z:z=5:4=1,25.

Ответ: 1,25

Применим теорему Менелая к нашей задаче. Рассмотрим треугольник MBC и прямую AN:

Запишем теорему Менелая для этого треугольника:

Ответ: 1,25

Задача №2.
Точки В´ и С´ лежат на сторонах соответственно АС и АВ ∆АВС, причем АВ´:В´С=АС´:С´В. Прямые ВВ´ и СС´ пересекаются в точке О.
а) Доказать, что прямая АО делит пополам сторону ВС.
б) Найти отношение площади четырехугольника АВ´ОС´ к площади ∆АВС, если АВ´:В´С=АС´:С´=1:2.

а)Доказать, что прямая АО делит пополам сторону ВС.

Докажем, что ВК=КС. Используем теорему Чевы.

т.к. , то ВК=КС

б) Найти отношение площади четырехугольника АВ´ОС´ к площади ∆АВС, если АВ´:В´С=АС´:С´В=1:2.

Т.к. АВ´:АС= 1:3, то

По теореме Менелая найдем

Для ∆АВВ´ и секущей СС´:

Значит

, значит =

Найдем .

Ответ:

Используемая литература

Учебник «Геометрия»10-11кл.: Л.С. Атанасян, В.Ф. Бутузов и др.-М.: Просвещение, 2011.
Атанасян Л.С., Бутузов В.Ф., Кадомцев С. Б., Шестаков С.А., Юдина И.И. Геометрия. Доп. главы к учебнику 8 кл.: Учеб. пособие для учащихся школ и классов с углубл. изуч. математики / Л.С. Атанасян, В.Ф. Бутузов, С.Б.Кадомцев и др.-М.: Вита-пресс, 2008.
Математика. ЕГЭ-2014. Типовые тестовые задания. 30 вариантов. Под ред. А.Л.Семенова, И.В.Ященко. 2013г.
Математика. ЕГЭ-2014. Под ред. А.Л.Семенова, И.В.Ященко. 2014г.
Математика. ЕГЭ-2014. Под ред. А.Л.Семенова, И.В.Ященко. 2015г.
Математика. Подготовка к ЕГЭ. Под ред.Ф.Ф.Лысенко. 2014г
Математика. Подготовка к ЕГЭ. Под ред.Ф.Ф.Лысенко. 2015г.
Математика. Подготовка к ЕГЭ. Под ред.Ф.Ф.Лысенко. 2016г.
Журнал математика в школе. М.: 2014
Пособие по геометрии. Часть І. Планиметрия, векторы. В помощь учащимся 10-11-х кл.О.В.Нагорнов, А.В.Баскаков и др.М.:НИЯУ МИФИ,2009.
Пособие по геометрии. Часть І. Планиметрия, векторы. В помощь учащимся 10-11-х кл.О.В.Нагорнов, А.В.Баскаков и др.М.:НИЯУ МИФИ,2009.
http://hijos.ru/2011/03/16/teorema-chevy/
http://www.resolventa.ru/demo/inform/demoinform.htm
http://fipi.ru/
http://alexlarin.net/

Источник

Какие геометрические факты можно использовать на ЕГЭ без доказательства?

Теорема Пифагора

Теорема Фалеса

Теорема косинусов

Теорема синусов

Теорема Менелая

Применение Теоремы Менелая в задаче 16

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://alexlarin.com/egetren4.png" />

Можно ли пользоваться следующими теоремами на ЕГЭ?

Можно ли пользоваться следующими теоремами на ЕГЭ?

Кто сейчас на форуме