Найдите абсциссу вершины параболы егэ

Сайты, меню, вход, новости

Как найти абсциссу вершины параболы егэ

Как найти абсциссу вершины параболы егэ

Уско­рен­ная под­го­тов­ка к ЕГЭ с ре­пе­ти­то­ра­ми Учи. До­ма. За­пи­сы­вай­тесь на бес­плат­ное за­ня­тие!

—>

Задание 9 № 564656

На рисунке изображён график функции вида где числа A, B и C — целые. Найдите абсциссу вершины параболы.

Из рисунка видно, что следовательно, Решая эту систему, находим Абсцисса вершины параболы

Задание 9 № 564656

—>

На рисунке изображён график функции вида где числа a, b и c целые.

Ege. sdamgia. ru

23.10.2019 19:16:13

2019-10-23 19:16:13

Источники:

Https://ege. sdamgia. ru/problem? id=564656

01Математика — Профиль — Парабола — Теория » /> » /> .keyword { color: red; } Как найти абсциссу вершины параболы егэ

Поверните устройство

Теория: 03 Парабола

По рисунку можно найти абсциссу точки (displaystyle B) Сделаем это.

Заметим, что графиком функции является парабола, а точка (displaystyle B ) с абсциссой (displaystyle color) – её вершина.

Абсцисса вершины параболы

Абсцисса (displaystyle x_0) вершины параболы (displaystyle y=colorax^2+colorbx+colorc) находится по формуле:

Заметим, что графиком функции является парабола, а точка displaystyle B с абсциссой displaystyle color её вершина.

M.01math. com

01.03.2019 20:41:58

2019-03-01 20:41:58

Источники:

Https://m.01math. com/maths/theory? subcategory_id=1429&task_id=45046

Найдите абсциссу вершины параболы: y — 2x^2 2x 3 » /> » /> .keyword { color: red; } Как найти абсциссу вершины параболы егэ

Найдите абсциссу вершины параболы: y — 2x^2 2x 3

Найдите абсциссу вершины параболы: y= — 2x^2+2x+3

Следовательно, значения коэффициентов в нашем примере: а = -2, b = 2, с = 3.

Координата x (абцисса) вершины параболы находится по формуле: x = ( — b) / (2 * а).

Подставим коэффициенты в формулу:

X = ( -2) / (2 * ( -2)) = ( -2) / ( -4) = 2/4 = 1/2 = 0,5.

Ответ: абцисса вершины параболы х (0,5).

Написать правильный и достоверный ответ; Отвечать подробно и ясно, чтобы ответ принес наибольшую пользу; Писать грамотно, поскольку ответы без грамматических, орфографических и пунктуационных ошибок лучше воспринимаются.

Списывать или копировать что-либо. Высоко ценятся ваши личные, уникальные ответы; Писать не по сути. «Я не знаю». «Думай сам». «Это же так просто» — подобные выражения не приносят пользы; Писать ответ ПРОПИСНЫМИ БУКВАМИ; Материться. Это невежливо и неэтично по отношению к другим пользователям.

Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.

Следовательно, значения коэффициентов в нашем примере а -2, b 2, с 3.

Vashurok. ru

18.01.2018 15:44:53

2018-01-18 15:44:53

Источники:

Https://vashurok. ru/questions/naydite-abstsissu-vershini-paraboli-y-2x-2-2x-3

• Решение

•   Видеорешение

Печать страницы

• Материалы для подготовки к ЕГЭ

•    

• Рубрики
  • 01 Геометрия (13)
  • 02 Стереометрия (9)
  • 03 Теория вероятностей ч.1 (1)
  • 04 Теория вероятностей ч.2 (1)
  • 05 Простейшие уравнения (5)
  • 06 Вычисления (5)
  • 07 Производная, ПО (4)
  • 08 «Прикладные» задачи (5)
  • 09 Текстовые задачи (7)
  • 10 Графики функций (7)
  • 11 Исследование функции (2)
  • 12 (С1) Уравнения (78)
  • 13 (С2) Стереометр. задачи (94)
  • 14 (С3) Неравенства (89)
  • 15 (С4) Практич. задачи (71)
  • 16 (С5) Планиметр. задачи (86)
  • 17 (С6) Параметры* (79)
  • 18 (С7) Числа, их свойства (38)
  • A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
  • A2 Читаем графики (нет в ЕГЭ-22) (1)
  • Видеоуроки (44)
  • ГИА (11)
    • II часть (11)
  • ЕГЭ (диагностич. работы) (70)
  • Иррациональные выражения, уравнения и неравенства (15)
  • Логарифмы (39)
  • МГУ (12)
  • Метод интервалов (4)
  • Метод рационализации (18)
  • Модуль (9)
  • Параметр (40)
  • Переменка (5)
  • Планиметрия (60)
  • Показательные выражения, уравнения и неравенства (8)
  • Разложение на множители (1)
  • Рациональные выражения, уравнения и неравенства (10)
  • Справочные материалы (92)
  • Стереометрия (52)
  • Т/P A. Ларина (443)
  • Текстовые задачи (12)
  • Теория чисел (2)
  • Тесты по темам (80)
  • Тригонометрические выражения, уравнения и неравенства (43)
  • Функции и графики (10)
• Дружественные сайты

  Сайт А. Ларина
  ЕгэТренер – О. Себедаш
  Математика?Легко!
  Егэ? Ок! – И. Фельдман
  

• Свежие записи
  • Тест «Гиперболы»
  • Тест. Графики функций. Комбинированные задачи
  • 10. Графики функций. Комбинированные задачи
  • Тест. Тригонометрические функции
  • 10. Тригонометрическая функция
  • Тест. Кусочно-линейная функция
  • 10. Кусочно-линейная функция
• Архивы Архивы

Предположим, вам попался график функции (y=ax^2+bx+c) и нужно по этому графику определить коэффициенты (a), (b) и (c). В этой статье я расскажу 3 простых способа сделать это.

1 способ – ищем коэффициенты на графике

Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью (y) – целые числа. Если это не так, советую использовать способ 2.

1. Коэффициент (a) можно найти с помощью следующих фактов:

   — Если (a>0), то ветви параболы направленных вверх, если (a<0), то ветви параболы направлены вниз.

   

   — Если (a>1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.

   

   — Аналогично с (a<-1), только график вытянут вниз.

   

   — Если (a∈(0;1)), то график сжат в (a) раз (по сравнению с «базовым» графиком с (a=1)). Вершина при этом остается на месте.

   

   — Аналогично (a∈(-1;0)), только ветви направлены вниз.

   

2. Парабола пересекает ось y в точке (c).

   

3. (b) напрямую по графику не видно, но его можно посчитать с помощью (x_в) — абсциссы (икса) вершины параболы:

   (x_в=-frac{b}{2a})
   (b=-x_вcdot 2a)
   

Пример (ЕГЭ):

Решение:
Во-первых, надо разобраться, где тут (f(x)), а где (g(x)). По коэффициенту (c) видно, что (f(x)) это функция, которая лежит ниже – именно она пересекает ось игрек в точке (4).

Значит нужно найти коэффициенты у параболы, которая лежит повыше.
Коэффициент (c) у неё равен (1).
Ветви параболы направлены вниз – значит (a<0). При этом форма этой параболы стандартная, базовая, значит (a=-1).

Найдем (b). (x_в=-2), (a=-1).

(x_в=-frac{b}{2a})
(-2=-frac{b}{-2})
(b=-4)

Получается (g(x)=-x^2-4x+1). Теперь найдем в каких точках функции пересекаются:

(-x^2-4x+1=-2x^2-2x+4)
(-x^2-4x+1+2x^2+2x-4=0)
(x^2-2x-3=0)
(D=4+4cdot 3=16=4^2)
(x_1=frac{2-4}{2}=-1);    (x_2=frac{2+4}{2}=3).

Ответ: (3).

2 способ – находим формулу по точкам

Это самый надежный способ, потому что его можно применить практически в любой ситуации, но и самый не интересный, потому что думать тут особо не надо, только уметь решать системы линейных уравнений. Алгоритм прост:

1. Ищем 3 точки с целыми координатами, принадлежащие параболе.
   Пример:

   

2. Выписываем координаты этих точек и подставляем в формулу квадратичной функции: (y=ax^2+bx+c). Получится система с тремя уравнениями.

   Пример: (A(-4;5)), (B(-5;5)), (C(-6;3)).

   (begin{cases}5=a(-4)^2+b(-4)+c\5=a(-5)^2+b(-5)+c\3=a(-6)^2+b(-6)+c end{cases})

3. Решаем систему.
   Пример:

   (begin{cases}5=16a-4b+c\5=25a-5b+c\3=36a-6b+c end{cases})

   Вычтем из второго уравнения первое:

   (0=9a-b)
   (b=9a)

   Подставим (9a) вместо (b):

   (begin{cases}5=16a-36a+c\5=25a-45a+c\3=36a-54a+c end{cases})
   (begin{cases}5=-20a+c\5=-20a+c\3=-18a+c end{cases})

   Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки (A) и (B) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:

   (2=-2a)
   (a=-1)

   Найдем (b):

   (b=-9)

   Подставим в первое уравнение (a):

   (5=20+c)
   (c=-15).

   Получается квадратичная функция:   (y=-x^2-9x-15).

Пример (ЕГЭ):

Решение:

Сразу заметим, что по графику можно сразу определить, что (c=4). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: (C(-1;8)), (D(1;2)) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи). 

Таким образом имеем систему:

(begin{cases}8=a(-1)^2+b(-1)+4\2=a+b+4 end{cases})

(begin{cases}8=a-b+4\2=a+b+4 end{cases})

(begin{cases}4=a-b\-2=a+b end{cases})

Сложим 2 уравнения:

(2=2a)
(a=1)

Подставим во второе уравнение:

(-2=1+b)
(b=-3)

Получается:

(g(x)=x^2-3x+4)

Теперь найдем точки пересечения двух функций:

(-3x+13=x^2-3x+4)
(x^2-9=0)
(x=±3)

Теперь можно найти ординату второй точки пересечения:

(f(-3)=-3cdot (-3)+13)
(f(-3)=9+13)
(f(-3)=22)

Ответ:   (22).

3 способ – используем преобразование графиков функций

Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.

Главный недостаток этого способа — вершина должна иметь целые координаты.

Сам способ базируется на следующих идеях:

1. График (y=-x^2) симметричен относительно оси (x) графику (y=x^2).

   

2. – Если (a>1) график (y=ax^2) получается растяжением графика (y=x^2) вдоль оси (y) в (a) раз.
   – Если (a∈(0;1)) график (y=ax^2) получается сжатием графика (y=x^2) вдоль оси (y) в (a) раз.

   

3. – График (y=a(x+d)^2) получается сдвигом графика (y=ax^2) влево на (d) единиц.
   — График (y=a(x-d)^2) получается сдвигом графика (y=ax^2) вправо на (d) единиц. 

   

4. График (y=a(x+d)^2+e) получается переносом графика (y=a(x+d)^2) на (e) единиц вверх.
   График (y=a(x+d)^2-e) получается переносом графика (y=a(x+d)^2) на (e) единиц вниз.

   

У вас наверно остался вопрос — как этим пользоваться? Предположим, мы видим такую параболу:

Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому (a=1). То есть она получена перемещениями графика базовой параболы (y=x^2).

А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на (4).

То есть наша функция выглядит так: (y=(x-5)^2-4).
После раскрытия скобок и приведения подобных получаем искомую формулу:

(y=x^2-10x+25-4)
(y=x^2-10x+21)

Готово.

Пример (ЕГЭ):

Чтобы найти (f(6)), надо сначала узнать формулу функции (f(x)). Найдем её:

1. Парабола растянута на (2) и ветви направлены вниз, поэтому (a=-2). Иными словами, первоначальной, перемещаемой функцией является функция (y=-2x^2).

   

2. Парабола смещена на 2 клеточки вправо, поэтому (y=-2(x-2)^2).

3. Парабола поднята на 4 клеточки вверх, поэтому (y=-2(x-2)^2+4).

4. Получается (y=-2(x^2-4x+4)+4=)(-2x^2+8x-8+4=-2x^2+8x-4).

5. (f(6)=-2cdot 6^2+8cdot 6-4=-72+48-4=-28)

Смотрите также:
Как найти k и b по графику линейной функции?

По условию парабола задана уравнением у = 2 — х^2, которое можно представить в виде у = -а х^2 + bх + с, что значит у = — х^2 + 0х + 2.

Коэффициенты квадратного многочлена при:

• члене в высшей степени х^2 равен а = -1;
• при х — b = 0;
• свободный член составляет с = 2.

Определение абсциссы вершины параболы

Формула для определения координаты х (абсциссы) параболы х = -b / 2а.

Подставив соответствующие коэффициенты а = -1 и b = 0 получается

х = -0 / (2 * (-1));

х = 0.

Вычисление ординаты вершины параболы

Подставив значение абсциссы х в уравнение параболы можно вычислить значение соответствующей ординаты:

у (0) = — 0^2 + 0 * 0 + 2;

у (0) = 2.

Таким образом, получена точка с координатами (0; 2), которая является вершиной заданной параболы у = 2 — х^2. Через эту точку проходит ось симметрии параболы. Точка (0; 2)  — самая высокая точка фигуры, так как a < 0 и ветви параболы опущены вниз. В область, где все значения функции у меньше 2 при различных значениях, принимаемых аргументом х.

Ответ: координаты вершины параболы х = 0 и у = 2.

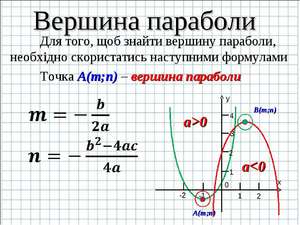
Как найти вершину параболы: три формулы

Парабола присутствует в мире математики, физики и других наук. По траектории параболы передвигаются искусственные спутники, которые стремятся покинуть пределы Солнечной системы, мяч при игре в волейбол тоже описывает её траекторию. Нужно уметь строить параболу. А чтобы это не составляло труда, надо знать, как найти вершину параболы.

Нахождение вершины параболы: способы, примеры, советы

График функции y = ax 2 + bx + c, где a — первый коэффициент, b — второй коэффициент, c — свободный член, называется параболой. Но обратите внимание на тот факт, что a ≠0.

У каждой точки параболы есть симметричная ей, кроме одной точки, и эта точка называется вершиной. Для того чтобы найти точку, которая является вершиной, нужно определиться, что такое точка на графике. Точка на графике – это определённая координата по оси абсцисс и по оси ординат. Она обозначается как (x; y). Давайте разбираться, как найти заветные числа.

Первый способ

Если вы хотите знать, как необходимо правильно вычислять координаты вершины, то нужно только выучить формулу x0 = -b/2a. Подставляя полученное число в функцию, получим y0.

Например, y =x 2 –8 x +15;

находим первый, второй коэффициенты и свободный член;

подставляем значения a и b в формулу;

вычисляем значения y;

Значит, вершина находится в точке (4;-1).

Ветви параболы симметричны относительно оси симметрии, которая идёт через вершину параболы. Зная корни уравнения, можно без особых трудностей посчитать абсциссу вершины параболы. Предположим, что k и n — корни квадратичного уравнения. Тогда точка x0 равноудалена от точек k и n, и её можно вычислить по формуле: x0 = (k + n)/2.

Рассмотрим на примере y =x 2 –6x+5

1) Приравниваем к нулю:

2) Находим дискриминант, используя формулу: D = b 2 –4 ac:

3) Находим корни уравнения по формуле (-b±√ D)/2a:

• 1 — первый корень;
• 5 — второй корень.

Второй способ

Дополнение до полного квадрата – отличный способ узнать, где располагается вершина. Используя этот способ, вы сможете вычислить точки x и y одновременно, без нужды подставлять x в начальный пример. Рассмотрим этот метод на примере функции: y=x 2 +8 x +10.

1. Сначала нужно приравнять выражение с переменной к 0. Потом перенести c в правую сторону с противоположным знаком, то есть у нас получается выражение x 2 + 8x = -10.

2. Теперь в левой части нужно сделать полный квадрат. Для этого посчитайте (b/2) 2 и увеличьте обе части уравнения результат. В этом случае нужно подставит 8 вместо b.

У нас получается 16. Теперь прибавьте это число к обеим частям уравнения:

3. Видно, что полученное выражение – полный квадрат. Его можно представить в форме: (x + 4) 2 = 6.

4. Используйте это выражение для поиска координат вершины параболы. Чтобы посчитать x, нужно приравнять его к 0. Получаем, x =-4. Координата y равна тому, что находится в правой части, то есть y =6. Вершина параболы этого уравнения (-4, 6).

Третий способ

Если вы знаете, что такое производная, то для вас есть другая формула. Несмотря на то, куда смотрят «рога» параболы, её вершина — точка экстремума. Для этого способа надо применить следующий алгоритм:

1. Нахождение первой производной по формуле f'(x) = (ax² + bx + c)’ = 2ax + b.

2. Приравнивание производной к 0. В итоге вы получите 0 = 2ax + b, отсюда можно найти то, что нас интересует.

Рассмотрим этот способ подробнее.

Дана функция y = 4x²+16x-17;

• Записываем производную и приравниваем к нулю.

f'(x) = (4x²+16x-17)’ = 8x+16 =0

Построение параболы

Самое трудное при построении – это верно найти точки функции. Для подробного построения нужно просчитать 5–7 точек (для школьного курса хватит этого). Для этого выбираем какое-либо значение x и подставляем его в данную функцию. Итогом подсчётов будет число точки по оси ординат. После этого ставим на координатную плоскость полученные нами точки. В итоге у нас получается парабола.

Рассмотрим подробнее вопрос о нахождении точек, которые нужно отметить. Для примера возьмём функцию y =-x 2 +11 x -24 с вершиной в точке (5,5;-6,25).

1) Строим таблицу

2) Заполняем таблицу

Так как парабола имеет осевую симметрию, то можно считать только значения справа или слева от вершины. Лучше считать те значения, которые ближе к 0, так удобнее. В нашем случае эти значения 4 и 5.

X	4	5	5,5	6	7
Y	-4	-6	-6,25	-6	-4

Советы

Правильно находите коэффициенты.

Пишите промежуточные вычисления на бумаге. Это не только облегчит нахождение вершины, но и поможет найти свои ошибки.

Делайте всё поэтапно. Следуйте алгоритму.

Обратите ваше внимание на то, что:

• Нужно проверять правильно ли ваше решение.
• Необходимо успокоиться. Решение любых задач по математике требует опыта. Просто нужно отработать данную тему, и тогда непременно у вас всё получится.

Видео

Это видео поможет вам научиться находить вершину параболы

Найдите абсциссу вершины параболы которая задается уравнением y 3×2 6x 5

Ответ:

а)координаты вершины параболы (0;6), нули функции: х₁=√6, х₂=-√6;

б) координаты вершины параболы (-10; 48), нули функции: х₁=-2, х₂=-8

Объяснение:

для вычисления координат вершины параболы можно воспользоваться формулами и :

чтобы найти нули функции, надо в уравнение графика подставить вместо у значение 0, иными словами, решить уравнение f(x)=0:

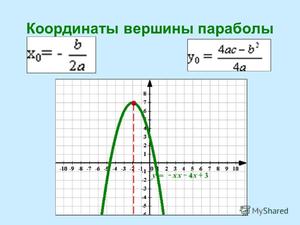
Координаты вершины параболы онлайн

Парабола — это функция, заданная уравнением:

Её график имеет следующий вид:

Причем, в зависимости от знака коэффициента , ветви параболы направлены вверх (если ) или вниз (если ).

В школьном курсе алгебры возникает задача нахождения координат вершины параболы. Их можно найти по формулам:

Вершина параболы, отмечена оранжевой точкой на приведённом выше графике.

Наш онлайн калькулятор позволяет найти координаты вершины параболы с описанием подробного хода решения на русском языке. Для работы калькулятора, необходимо ввести уравнение параболы и указать её переменную. Уравнение параболы можно вводить в различных форматах, а коэффициентами могут быть не только числа или дроби, но и параметры. Нажмите на кнопку «Примеры», расположенную на панели калькулятора, чтобы посмотреть различные форматы ввода.