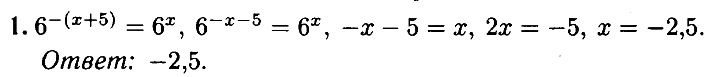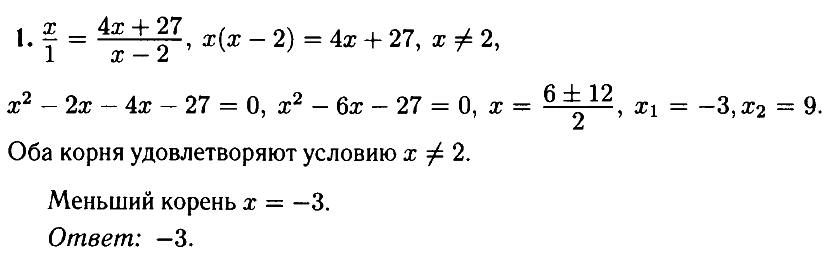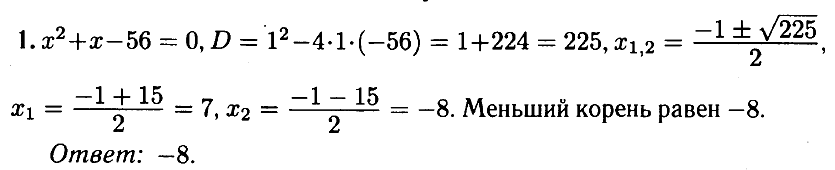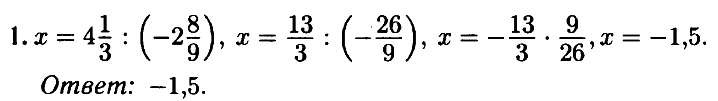Найдите корень уравнения егэ профиль

Тип 5 № 26653

Найдите корень уравнения левая круглая скобка дробь: числитель: 1, знаменатель: 2 конец дроби правая круглая скобка в степени левая круглая скобка 6 минус 2x правая круглая скобка =4.

Аналоги к заданию № 26653: 510382 510401 2857 13685 505143 505164 2859 2861 2863 2865 … Все

Источник: Пробный экзамен по математике Санкт-Петербург 2015. Вариант 1., ЕГЭ — 2017. Основная волна 02.06.2017. Вариант 301 (C часть)., ЕГЭ по математике 07.06.2021. Основная волна. Санкт-Петербург

Классификатор алгебры: Показательные уравнения

Кодификатор ФИПИ/Решу ЕГЭ: 1.4.2 Преобразования выражений, включающих операцию возведения в степень, 2.1.5 Показательные уравнения

Источник

В задании №5 варианта ЕГЭ вам встретятся всевозможные уравнения: квадратные и сводящиеся к квадратным, дробно-рациональные, иррациональные, степенные, показательные и логарифмические и даже тригонометрические. Видите, как много нужно знать, чтобы справиться с заданием! И еще ловушки и «подводные камни», которые ждут вас в самом неожиданном месте.

Вот список тем, которые стоит повторить:

Квадратные уравнения

Арифметический квадратный корень

Корни и степени

Показательная функция

Показательные уравнения

Логарифмическая функция

Логарифмические уравнения

Тригонометрический круг

Формулы приведения

Формулы тригонометрии

Простейшие тригонометрические уравнения 1

Уравнения, сводящиеся к квадратным

1. Решите уравнение frac{6}{13}x^2=19frac{1}{2}. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Кажется, что уравнение очень простое. Но иногда здесь ошибаются даже отличники. А вот шестиклассник бы не ошибся.

С левой частью уравнения все понятно. Дробь frac{6}{13} умножается на x^2. А в правой части — смешанное число 19frac{1}{2}. Его целая часть равна 19, а дробная часть равна frac{1}{2}. Запишем это число в виде неправильной дроби:

19frac{1}{2}= frac{19cdot 2+1}{2} = frac{39}{2}.

Получим:

frac{6}{13}x^2=frac{39}{2};

x^2=frac{39cdot 13}{2cdot 6}=frac{13cdot 3cdot 13}{2cdot 6}=frac{{13}^2}{4};

x=pm frac{13}{2};

x_1=-6,5 или x_2=6,5.

Выбираем меньший корень.

Ответ: -6,5.

2. Решите уравнение left ( x-6 right )^2=-24x.

Возведем в квадрат левую часть уравнения. Получим:

left ( x-6 right )^2=-24xLeftrightarrow x^2-12x+36=-24xLeftrightarrow

Leftrightarrow x^2+12x+36=0Leftrightarrow left ( x+6 right )^2=0Leftrightarrow x=-6.

Ответ: -6.

Дробно-рациональные уравнения

3. Найдите корень уравнения

Перенесем единицу в левую часть уравнения. Представим 1 как frac{4x-5}{4x-5} и приведем дроби к общему знаменателю:

frac{5x-3}{4x-5}-frac{4x-5}{4x-5}=0;

frac{x+2}{4x-5}=0;

x= - 2.

Ответ: -2.

Это довольно простой тип уравнений. Главное — внимательность.

Иррациональные уравнения

Так называются уравнения, содержащие знак корня — квадратного, кубического или n-ной степени.

4. Решите уравнение:

sqrt{frac{6}{4{x}-54} } =frac{1}{7}.

Выражение под корнем должно быть неотрицательно, а знаменатель дроби не равен нулю.

Значит, .

Возведём обе части уравнения в квадрат:

frac{6}{4{x}-{ 54}} =frac{1}{49}.

Решим пропорцию:

4{x}-{ 54}={ 6}cdot { 49};

4{x}=348;

{ x}={ 87}.

Условие  при этом выполняется.

Ответ: 87.

5. Решите уравнение sqrt{72-x}=x. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

А в этом уравнении есть ловушка. Решите его самостоятельно и после этого читайте дальше.

Выражение под корнем должно быть неотрицательно. И сам корень — величина неотрицательная. Значит, и правая часть должна быть больше или равна нуля. Следовательно, уравнение равносильно системе:

left{begin{matrix} 72-x=x^2\72-xgeq 0 hfill \xgeq 0 hfill end{matrix}right..

Решение таких уравнений лучше всего записывать в виде цепочки равносильных переходов:

sqrt{72-x}=x Leftrightarrow left{begin{matrix} 72-x=x^2\72-x geq 0 \x geq 0 end{matrix}right. Leftrightarrow

.

Мы получили, что x=8. Это единственный корень уравнения.

Типичная ошибка в решении этого уравнения такая. Учащиеся честно пишут ОДЗ, помня, что выражение под корнем должно быть неотрицательно:

72-xge 0.

Возводят обе части уравнения в квадрат. Получают квадратное уравнение: x^2+x-72=0. Находят его корни: x=8 или x=-9. Пишут в ответ: -9 (как меньший из корней). В итоге ноль баллов.

Теперь вы знаете, в чем дело. Конечно же, число -9 корнем этого уравнения быть не может.

Ответ: 8.

6. Решите уравнение sqrt{45+4x}=x. Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Запишем решение как цепочку равносильных переходов:

.

Ответ: 9.

Показательные уравнения

При решении показательных уравнений мы пользуемся свойством монотонности показательной функции.

7. Решите уравнение 5^{x-7}=frac{1}{125}.

Вспомним, что 125 = 5{}^{3}. Уравнение приобретает вид: 5{}^{x}{}^{-}{}^{7 }= 5{}^{-}{}^{3}. Функция y = 5^x монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

x - 7 = -3, откуда x = 4.

Ответ: 4.

8. Решите уравнение {left(frac{1}{49}right)}^{x-8}=7.

Представим {left(frac{1}{49}right)}^{ } как 7^{-2};

{left(7^{-2}right)}^{x-8}=7;

7^{-2x+16}=7.

Функция y = 7^x монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

-2x+16=1;

-2x=-15;

x=7,5.

Ответ: 7,5.

9. Решите уравнение left(frac{1}{9} right)^{{ x}-13} =3.

Представим {textstylefrac{1}{9}} в виде степени с основанием 3 и воспользуемся тем, что left({ a}^{{ m}} right)^{{ n}} ={ a}^{{ mn}}.

left(3^{-2} right)^{{ x}-{ 13}} =3;
3^{-2{ x}+{ 26}} =3^{1} ;

-2{ x}+{ 26}={ 1};

{ x}={ 12,5}.

Ответ: 12,5.

Логарифмические уравнения

Решая логарифмические уравнения, мы также пользуемся монотонностью логарифмической функции: каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, значит, равны и сами числа.

И конечно, помним про область допустимых значений логарифма:

Логарифмы определены только для положительных чисел.

Основание логарифма должно быть положительно и не равно единице.

10. Решите уравнение:

{{log}_5 left(4+xright)=2 }.

Область допустимых значений: . Значит, 

Представим 2 в правой части уравнения как {{log}_5 25 }, чтобы слева и справа в уравнении были логарифмы по основанию 5.

{{log}_5 left(4+xright)={{log}_5 25 } }.

Функция y = {{log}_5 x } монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом 

4+x=25;
x=21.

Ответ: 21.

11. Решите уравнение: {{log}_8 left(x^2+xright)={{log}_8 left(x^2-4right) } }.

Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:

.

Ответ: -4.

12. Решите уравнение: 2^{{{log}_4 left(4x+5right) }}=9.

Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:

{{log}_4 b }=frac{{{log}_2 b }}{{{log}_2 4 }}=frac{{{log}_2 b }}{2}.

Записываем решение как цепочку равносильных переходов.

.

Ответ: 19.

13. Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

{{log}_{x-5} 49=2 }.

В этом уравнении тоже есть ловушка. Мы помним, что основание логарифма должно быть положительно и не равно единице.

Получим систему:

small left{begin{matrix} left ( x-5 right )^2=49\x-50 \x-5 neq 1 end{matrix}right..

Первое уравнение мы получили просто из определения логарифма.

Квадратное уравнение имеет два корня: x=12 и x=-2.

Очевидно, корень x=-2 является посторонним, поскольку основание логарифма должно быть положительным. Значит, единственный корень уравнения: x=12.

Ответ: 12.

Тригонометрические уравнения (Часть 1 ЕГЭ по математике)

Тригонометрические уравнения? В первой части вариантов ЕГЭ? — Да. Причем это задание не проще, чем задача 13 из второй части варианта Профильного ЕГЭ.

14. Найдите корень уравнения: cos frac{pi (x+1)}{4}=frac{sqrt{2}}{2}. В ответе запишите наибольший отрицательный корень.

Типичная ошибка — решать это уравнение в уме. Мы не будем так делать! Несмотря на то, что это задание включено в первую части варианта ЕГЭ, оно является полноценным тригонометрическим уравнением, причем с отбором решений.

Сделаем замену frac{pi left(x+1right)}{4}=t. Получим: cos t=frac{sqrt{2}}{2}.

Получаем решения: t=pm frac{pi }{4}+2pi n, nin Z. Вернемся к переменной x.

frac{pi (x+1)}{4}=pm frac{pi }{4}+2pi n, nin Z. Поделим обе части уравнения на pi и умножим на 4.

x+1=pm 1+8n, nin Z;

left[ begin{array}{c}x=8n, nin Z \x=-2+8n end{array}right..

Первой серии принадлежат решения -8; 0; 8dots

Вторая серия включает решения -2; 6; 14dots

Наибольший отрицательный корень — тот из отрицательных, который ближе всех к нулю. Это x = -2.

Ответ: -2.

15. Решите уравнение: tg frac{pi left( x+1right)}{4}= -1. В ответе напишите наименьший положительный корень.

Решение:

Сделаем замену frac{pi left(x+1right)}{4}=t. Получим:tgt=-1. Решения этого уравнения:

t=-frac{pi }{4}+pi n, nin Z. Вернемся к переменной х:

frac{pi left(x+1right)}{4}=-frac{pi }{4}+pi n, n in Z. Умножим обе части уравнения на 4 и разделим на pi.

x+1=-1+4n;

x=-2+4n.

Выпишем несколько решений уравнения и выберем наименьший положительный корень:

x=-2 ;2; 6dots Наименьший положительный корень x = 2.

Ответ: 2.

Мы разобрали основные типы уравнений, встречающихся в задании №5 Профильного ЕГЭ по математике. Конечно, это не все, и видов уравнений в этой задаче существует намного больше. Именно поэтому мы рекомендуем начинать подготовку к ЕГЭ по математике не с задания 1, а с текстовых задач на проценты, движение и работу и основ теории вероятностей.
Успеха вам в подготовке к ЕГЭ!

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание №5. Простейшие уравнения. Профильный ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением. Выражение, стоящее слева от знака равенства, называется левой частью уравнения, а выражение, стоящее справа, — правой частью уравнения.

Линейные уравнения

Линейным называется такое уравнение, в котором неизвестное $x$ находится в числителе уравнения и без показателей. Например: $2х – 5 = 3$

Линейные уравнения сводятся к виду $ax = b$, которое получается при помощи раскрытия скобок, приведения подобных слагаемых, переноса слагаемых из одной части уравнения в другую, а также умножения или деления обеих частей уравнения на число, отличное от нуля.

$5 (5 + 3х) — 10х = 8$

Раскроем скобки.

$25 + 15х — 10х = 8$

Перенесем неизвестные слагаемые в левую часть уравнения, а известные в правую. При переносе из одной части в другую, у слагаемого меняется знак на противоположный.

$15х — 10х = 8 — 25$

Приведем подобные слагаемые.

$5х = -17$ — это конечный результат преобразований.

После преобразований к виду $ax = b$, где, a=0, корень уравнения находим по формуле $х = {b}/{a}$

$х=-{17}/{5}$

$х = — 3,4$

Ответ: $- 3,4$

Квадратные уравнения

Квадратное уравнение — уравнение вида $ax^2 + bx + c = 0$, где $a, b, c$ — некоторые числа a$≠0$, $x$ — неизвестное. Перед тем как решать уравнение, необходимо раскрыть скобки и собрать все слагаемые в левой части уравнения.

Числа $a, b, c$ называются коэффициентами квадратного уравнения.

  • $a$ — старший коэффициент;
  • $b$ — средний коэффициент;
  • $c$ — свободный член.

Если в квадратном уравнении коэффициенты $b$ и $c$ не равны нулю, то уравнение называется полным квадратным уравнением. Например, уравнение $2x^2 – 8x + 3 = 0$. Если один из коэффициентов $b$ или $c$ равен нулю или оба коэффициента равны нулю, то квадратное уравнение называется неполным. Например, $5x^2 – 2x = 0$.

Решение неполных квадратных уравнений

Неполное квадратное уравнение имеет вид $ax^2 + bx = 0$, если $a$≠0$; $c$=0$. В левой части этого уравнения есть общий множитель $x$.

1. Вынесем общий множитель $x$ за скобки.

Мы получим $x (ax + b) = 0$. Произведение равно нулю, если хотя бы один из множителей равен нулю. Поэтому получаем $x = 0$ или $ax + b =0$. Таким образом, данное уравнение эквивалентно двум уравнениям:

$x = 0; ax + b = 0$

2. Решаем получившиеся уравнения каждое отдельно.

Мы получим $x = 0$ и $x={-b}/{a}$. Следовательно, данное квадратное уравнение имеет два корня $x = 0$ и $x={-b}/{a}$

$4х^2 — 5х = 0$

Вынесем х как общий множитель за скобки:

$х (4х — 5) = 0$

Приравняем каждый множитель к нулю и найдем корни уравнения.

$x = 0$ или $4х — 5 = 0$

$х_1 = 0   х_2 = 1,25$

Ответ: $х_1 = 0; х_2 = 1,25$

Неполное квадратное уравнение вида $ax^2 + c = 0, a≠0, b=0$

Для решения данного неполного квадратного уравнения выразим $x^2$.

$ax^2 + c = 0$

$ax^2 = — c$

$x_2 = {-c}/{a}$

При решении последнего уравнения возможны два случая:

если ${-c}/{a}>0$, то получаем два корня: $x = ±v{{-c}/{a}}$

если ${-c}/{a}<0$, то уравнение во множестве действительных числе не имеет решений.

$x^2 — 16 = 0$

$x^2 = 16$

$x = ±4$

Ответ: $х_1 = 4, х_2 = — 4$

Решение полного квадратного уравнения

Решение с помощью дискриминанта

Дискриминантом квадратного уравнения D называется выражение

$b^2 — 4ac$.

При решении уравнения с помощью дискриминанта возможны три случая:

1. $D > 0$. Тогда корни уравнения равны:

$x_{1,2}={-b±√D}/{2a}$

2. $D = 0$. В данном случае решение даёт два двукратных корня:

$x_{1}=x_{2}={-b}/{2a}$

3. $D < 0$. В этом случае уравнение не имеет корней.

$3х^2 — 11 = -8х$

Соберем все слагаемые в левую часть уравнения и расставим в порядке убывания степеней

$3х^2 + 8х — 11 = 0$

$a = 3 ,b = 8, c = — 11$

$D = b^2- 4ac = 82- 4 · 3 · (-11) = 196 = 142$

$x_{1}={-b+√D}/{2a}={-8+14}/{6}=1$

$x_{2}={-b-√D}/{2a}={-8-14}/{6}=-3{2}/{3}$

Ответ: $x_1=1, x_2=-3{2}/{3}$

Устные способы

Если сумма коэффициентов равна нулю $(а + b + c = 0)$, то $х_1= 1, х_2={с}/{а}$

$4х^2+ 3х — 7 = 0$

$4 + 3 — 7 = 0$, следовательно $х_1= 1, х_2=-{7}/{4}$

Ответ: $х_1= 1, х_2 = -{7}/{4}$

Если старший коэффициент в сумме со свободным равен среднему коэффициенту $(a + c = b)$, то $х_1= — 1, х_2=-{с}/{а}$

$5х^2+ 7х + 2 = 0$

$5 + 2 = 7$, следовательно, $х_1= -1, х_2 =-{2}/{5}$

Ответ: $х_1= -1, х_2 = -{2}/{5}$

Кубические уравнения

Для решения простых кубических уравнений необходимо обе части представить в виде основания в третьей степени. Далее извлечь кубический корень и получить простое линейное уравнение.

$(x — 3)^3 = 27$

Представим обе части как основания в третьей степени

$(x — 3)^3 = $33

Извлечем кубический корень из обеих частей

$х — 3 = 3$

Соберем известные слагаемые в правой части

$x = 6$

Ответ: $х = 6$

Дробно рациональные уравнения

Рациональное уравнение, в котором левая или правая части являются дробными выражениями, называется дробным.

Чтобы решить дробное уравнение, необходимо:

  1. найти общий знаменатель дробей, входящих в уравнение;
  2. умножить обе части уравнения на общий знаменатель;
  3. решить получившееся целое уравнение;
  4. исключить из его корней те, которые обращают в ноль общий знаменатель.

$4x + 1 — {3}/{x} = 0$

1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)

$x≠0$

2. находим общий знаменатель дробей и умножаем на него обе части уравнения

$4x + 1 — {3}/{x}= 0¦· x$

$4x · x + 1 · x — {3·x}/{x} = 0$

3. решаем полученное уравнение

$4x^2 + x — 3 = 0$

Решим вторым устным способом, т.к. $а + с = b$

Тогда $х_1 = — 1, х_2 = {3}/{4}$

4. исключаем те корни, при которых общий знаменатель равен нулю В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.

Ответ: $х_1 = — 1, х_2 = {3}/{4}$

При решении уравнения с двумя дробями можно использовать основное свойство пропорции.

Основное свойство пропорции: Если ${a}/{b} = {c}/{d}$, то $a · d = b · c$

${3х-5}/{-2}={1}/{х}$

Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)

$x≠0$

Воспользуемся основным свойством пропорции

$х (3х — 5) = -2$

Раскроем скобки и соберем все слагаемые в левой части уравнения

$3х^2- 5х + 2 = 0$

Решим данное квадратное уравнение первым устным способом, т.к.

$a + b + c = 0$

$x_1 = 1, x_2 = {2}/{3}$

В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.

Ответ: $x_1 = 1, x_2 = {2}/{3}$

Рациональное уравнение – это уравнение вида $f(x)=g(x)$, где $f(x)$ и $g(x)$ — рациональные выражения.

Рациональные выражения — это целые и дробные выражения, соединённые между собой знаками арифметических действий: деления, умножения, сложения или вычитания, возведения в целую степень и знаками последовательности этих выражений.

Например,

${2}/{x}+5x=7$ – рациональное уравнение

$3x+√x=7$ — иррациональное уравнение (содержит корень)

Если хотя бы в одной части рационального уравнения содержится дробь, то уравнение называется дробно рациональным.

Чтобы решить дробно рациональное уравнение, необходимо:

  1. Найти значения переменной, при которых уравнение не имеет смысл (ОДЗ);
  2. Найти общий знаменатель дробей, входящих в уравнение;
  3. Умножить обе части уравнения на общий знаменатель;
  4. Решить получившееся целое уравнение;
  5. Исключить из его корней те, которые обращают в ноль общий знаменатель.

Решить уравнение: $4x+1-{3}/{x}=0$

Решение:

1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)

$x ≠ 0$

2. находим общий знаменатель дробей и умножаем на него обе части уравнения

$4x+1-{3}/{x}=0|·x$

$4x·x+1·x-{3·x}/{x}=0$

3. решаем полученное уравнение

$4x^2+x-3=0$

Решим вторым устным способом, т.к. $а+с=b$

Тогда, $x_1=-1, x_2=-{3}/{4}$

4. исключаем те корни, при которых общий знаменатель равен нулю

В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.

Ответ: $x_1=-1, x_2=-{3}/{4}$

При решении уравнения с двумя дробями, можно использовать основное свойство пропорции.

Основное свойство пропорции: Если ${a}/{b}={c}/{d}$ — пропорция, то $a·d=b·c$

Решить уравнение ${3x-5}/{-2}={1}/{x}$

Решение:

Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)

$x≠0$

Воспользуемся основным свойством пропорции

$х(3х-5)=-2$

Раскроем скобки и соберем все слагаемые в левой стороне

$3х^2-5х+2=0$

Решим данное квадратное уравнение первым устным способом, т.к. $a+b+c=0$

$x_1=1, x_2={2}/{3}$

В первом пункте получилось, что при x = 0 уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.

Ответ: $x_1=1, x_2={2}/{3}$

Уравнения, содержащие неизвестную под знаком корня, называются иррациональными.

Чтобы решить иррациональное уравнение, необходимо:

  1. Преобразовать заданное иррациональное уравнение к виду: $√{f(x)}=g(x)$ или $√{f(x)}=√{g(x)}$
  2. Обе части уравнение возвести в квадрат: $√{f(x)}^2=(g(x))^2$ или $√{f(x)}^2=√{g(x)}^2$
  3. Решить полученное рациональное уравнение.
  4. Сделать проверку корней, так как возведение в четную степень может привести к появлению посторонних корней. (Проверку можно сделать при помощи подстановки найденных корней в исходное уравнение.)

Решите уравнение $√{4х-3}=х$. Если уравнение имеет более одного корня, укажите наименьший из них.

Решение:

Обе части уравнение возведем в квадрат:

$√{4х-3}^2=х^2$

Получаем квадратное уравнение:

$4х-3=х^2$

Перенесем все слагаемые в левую часть уравнения:

${-х}^2+4х-3=0$

Решим данное квадратное уравнение устным способом, так как

$a+b+c=0$

$-1+4-3=0$, следовательно $х_1 = 1; х_2={с}/{а}={-3}/{-1}=3$

Проведем проверку корней, подставив их вместо икса в исходное уравнение

$√{4·1-3}=1$

$1=1$, получили в результате проверки верное равенство, следовательно $х_1=1$ подходит.

$√{4·(3)-3}=3$

$√9=3$

$3=3$, получили в результате проверки верное равенство, следовательно корень $х_2=3$ подходит

$х_1=1$ наименьший корень.

Ответ: $1$

Так как в иррациональных уравнениях иногда необходимо возводить в квадрат не только число, но и целое выражение, необходимо вспомнить формулы сокращенного умножения:

  1. Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе число плюс квадрат второго числа. $(a-b)^2=a^2-2ab+b^2$
  2. Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа. $(a+b)^2=a^2+2ab+b^2$

Решить уравнение: $х-6=√{8-х}$

Возведем обе части уравнения в квадрат

$(х-6)^2=8-х$

В левой части уравнения при возведении в квадрат получаем формулу сокращенного умножения квадрат разности. В правой части уравнения квадрат и корень компенсируют друг друга и в результате остается только подкоренное выражение

$х^2-2·6·х+6^2=8-х$

$х^2-12х+36=8-х$

Получили квадратное уравнение. Все слагаемые переносим в левую часть уравнения. При переносе слагаемых через знак равно их знаки меняются на противоположные.

$х^2-12х+36-8+х=0$

Приводим подобные слагаемые:

$х^2-11х+28=0$

Найдем корни уравнения через дискриминант:

$D=b^2-4ac=121-4·28=121-112=9=3^2$

$x_{1,2}={-b±√D}/{2a}={11±3}/{2}$

$x_1=7; x_2=4$

Проведем проверку корней, подставив их вместо икса в исходное уравнение

$x_1=7$

$7-6=√{8-7}$

$1=1$, получили верное равенство, следовательно, корень нам подходит.

$x_2=4$

$4-6=√{8-4}$

$-2=2$, получили неверное равенство, следовательно, данный корень посторонний.

Ответ: $7$

Показательными называют такие уравнения, в которых неизвестное содержится в показателе степени.

$a^x=b$

При решении показательных уравнений используются свойства степеней, вспомним некоторые из них:

1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.

$a^n⋅a^m=a^{n+m}$

2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели вычитаются

$a^n:a^m=a^{n-m}$

3. При возведении степени в степень основание остается прежним, а показатели перемножаются

$(a^n)^m=a^{n·m}$

4. При возведении в степень произведения в эту степень возводится каждый множитель

$(a·b)^n=a^n·b^n$

5. При возведении в степень дроби в эту степень возводиться числитель и знаменатель

$({a}/{b})^n={a^n}/{b^n}$

6. При возведении любого основания в нулевой показатель степени результат равен единице

$a^0=1$

7. Основание в любом отрицательном показателе степени можно представить в виде основания в таком же положительном показателе степени, изменив положение основания относительно черты дроби

$a^{-n}={1}/{a^n}$

${a^{-n}}/{b^{-k}}={b^k}/{a^n}$

8. Радикал (корень) можно представить в виде степени с дробным показателем

$√^n{a^k}=a^{{k}/{n}}$

Показательные уравнения часто сводятся к решению уравнения $a^x=a^m$, где, $а >0, a≠1, x$ — неизвестное. Для решения таких уравнений воспользуемся свойством степеней: степени с одинаковым основанием $(а >0, a≠1)$ равны только тогда, когда равны их показатели.

Решить уравнение $25·5^х=1$

Решение:

В левой части уравнения необходимо сделать одну степень с основанием $5$ и в правой части уравнения представить число $1$ в виде степени с основанием $5$

$5^2·5^х=5^0$

При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются

$5^{2+х}=5^0$

Далее проговариваем: степени с одинаковым основанием $(а >0, a≠1)$ равны только тогда, когда равны их показатели

$2+х=0$

$х=-2$

Ответ: $-2$

Решить уравнение $2^{3х+2}-2^{3х-2}=30$

Решение:

Чтобы решить данное уравнение, вынесем степень с наименьшим показателем как общий множитель

$2^{3x+2}-2^{3x-2}=30$

$2^{3x-2}({2^{3x+2}}/{2^{3x-2}}-{2^{3x-2}}/{2^{3x-2}})=30$

$2^{3x-2}(2^{3x+2-(3x-2)}-1)=30$

$2^{3x-2}(2^4-1)=30$

$2^{3x-2}·15=30$

Разделим обе части уравнения на $15$

$2^{3х-2}=2$

$2^{3х-2}=2^1$

$3х-2=1$

$3х=3$

$х=1$

Ответ: $1$

Источник

За это задание ты можешь получить 1 балл. На решение дается около 3 минут. Уровень сложности: базовый.
Средний процент выполнения: 93.6%
Ответом к заданию 5 по математике (профильной) может быть целое число или конечная десятичная дробь.

Разбор сложных заданий в тг-канале

Задачи для практики

Задача 1

Найдите корень уравнения $log_{x+5}{64} = 2$.

Решение

Найдем ОДЗ: ${tablex + 5 > 0; x + 5 ≠ 1;$ ${tablex > -5; x ≠ -4;$ $x ∈ (-5; -4) ∪ (-4; +∞)$.

По определению логарифма если $log_b a=c$, то $b^c=a$

$(x + 5)^2 = 64$,

$x + 5 = 8$ или $x + 5 = -8$,

$x = 3 $ или $x = -13 $

$x = -13$ — не входит в ОДЗ.

Ответ: 3

Задача 2

Найдите корень уравнения $log_{5}{(x^2+26x + 169)}-2 =log_{√5}{(5x-7)}$.

Решение

$log_{5}{(x^2+26x + 169)}-2 =log_{√5}{(5x-7)}$,

$log_{5}{(x+13)^2}-log_{5}{25} =log_{5^{1/2}}{(5x-7)}$,

$log_{5}{(x+13)^2/{25}} =2log_{5}{(5x-7)}$,

$log_{5}{(x+13)^2/{25}} =log_{5}{(5x-7)^2}$,

$(x+13)^2/{25} =(5x-7)^2$,

$(x+13)/{5} =(5x-7)$ или $(x+13)/{5} =-(5x-7)$,

Откуда: $x=2$ или $x=11/13 — $ второй корень не удовлетворяет ОДЗ,

Ответ: 2

Задача 3

Найдите корень уравнения $log_{3}{(4x-15)} =log_{3}{(x+3)}$.

Решение

$log_3 (4x — 15) = log_3 (x + 3)$,

$4x — 15 = x + 3$,

$3x = 18, x = 6$.

Проверка. При $x = 6$ получаем $log_3 (6 · 4 — 15) = log_3 (6 + 3)$ — верное равенство.

$x = 6$ — корень уравнения.

Ответ: 6

Задача 4

Найдите корень уравнения $625^{x+1}={1} / {5}$.

Решение

$(5^4)^{x+1} = 5^{-1}$, применим свойство $(a^b)^c=a^{bc}$

$5^{4x+4} = 5^{-1}$,

$4x + 4 = -1$,

$4x = -5$,

$x = -1.25$.

Ответ: -1.25

Задача 5

Найдите корень уравнения $9^{x-12}={1} / {3}$.

Решение

$(3^2)^{x-12}=3^{-1} $, применим свойство $(a^b)^c=a^{bc}$

$ 3^{2x-24} = 3^{-1} $,

$2x-24=-1 $,

$ 2x=23 $,

$ x=11{,}5$.

Ответ: 11.5

Задача 6

Найдите корень уравнения $(x-12)^3=-27$.

Решение

$(x-12)^3=-27$

$ (x-12)^3=(-3)^3 $,
$ x-12=-3 $,
$x=9$.

Ответ: 9

Задача 7

Найдите корень уравнения $log_{2}{(12+x)} =-2$.

Решение

По определению логарифма $12+x = 2^{-2}, 12+x = 0.25, x = 0.25-12, x = -11.75$.

Ответ: -11.75

Задача 8

Найдите корень уравнения $log_{3}{(4-x)} =5$.

Решение

По определению логарифма если $log_b a=c$, то $b^c=a$

$4-x = 3^5 $,

$ 4-x=243 $,

$x=-239$.

Ответ: -239

Задача 9

Решите уравнение $(x+7)^2 = x^2+7$. Если уравнение имеет более одного корня, в ответе запишите меньший из них.

Решение

Воспользуемся формулой квадрата суммы: $(a+b)^2=a^2+2ab+b^2$
$x^2 + 14x + 49 = x^2 + 7$,
$14x = -42$,
$x = -3$.

Ответ: -3

Задача 10

Решите уравнение $(5x+11)^2 = (5x-2)^2$. Если уравнение имеет более одного корня, в ответе запишите меньший из них.

Решение

Воспользуемся формулами сокращенного умножения:

$(a+b)^2=a^2+2ab+b^2$

$(a-b)^2=a^2-2ab+b^2$
Таким образом:

$25x^2+110x+121=25x^2-20x+4$,

$ 110x+20x=-117$,
$130x=-117$
$x=-117/130$
$x=-0.9$.

Ответ: -0.9

Задача 11

Найдите корень уравнения $√ {14-5x}=-x$. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Решение

Так как левая часть уравнения неотрицательна, то и правая тоже неотрицательна:

$-x ⩾ 0$, — домножим обе части на -1, в таком случае знак неравенства меняется

$ x ⩽ 0$.

Возведя обе части в квадрат, получим уравнение $14-5x=x^2$,

$x^2+5x-14=0$,

$ x_1=-7$,

$ x_2=2$ — не удовлетворяет условию $x⩽ 0$.

Пояснение: $(-x)^2=(-x)(-x)=x^2$

Ответ: -7

Задача 12

Найдите корень уравнения ${x+3} / {2x-11}={x+3} / {3x-7}$. Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Решение

Найдем ОДЗ: ${table2x-11 ≠ 0; 3x-7≠ 0;$ ${tablex ≠ 5.5; x ≠7/3;$

Удобно домножить обе стороны равенства на знаменатели, проще говоря «крест накрест»

$(x+3)(3x-7)=(2x-11)(x+3)$

${3x}^2-7x+9x-21={2x}^2+6x-11x-33$

$x^2+7x+12=0$

$x_1=-3, x_2=-4$ — оба корня удовлетворяют ОДЗ

Наибольший корень: $x=-3$

Ответ: -3

Задача 13

Найдите корень уравнения ${9-5x} / {x+3}=x$. Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Решение

При $x ≠ -3$ получим

$x(x + 3) = 9 — 5x$,

$x^2 + 3x + 5x — 9 = 0$,

$x^2 + 8x — 9 = 0$

По теореме Виета $х_1=1$, $х_2=-9$.

Больший корень $x_1=1$

Ответ: 1

Задача 14

Найдите корень уравнения $√ {{4x-21} / {117}}={1} / {3}$.

Решение

ОДЗ: ${4x — 21}/{117}⩾0, 4x-21⩾0, x⩾21/4, x⩾5.25$

$(√{{4x — 21}/{117}})^2 = ({1}/{3})^2$,

${4x — 21}/{117} = {1}/{9}$,

$9(4x — 21) = 117$,

$36x — 189 = 117$,

$36x = 306$,

$x = 8.5$ — удовлетворяет ОДЗ.

Ответ: 8.5

Задача 15

Решите уравнение $log_{{1} / {3}}(13 + x) = — 2$.

Решение

ОДЗ: $13+x>0, x>-13$

По определению логарифма если $log_b a=c$, то $b^c=a$

$(1/3)^(-2)=13+x$
$ 13+x=9$
$ x=-4$ — удовлетворяет ОДЗ

Ответ: -4

Задача 16

Решите уравнение $√^3{5+x}=2$.

Решение

Возведем обе части уравнения в третью степень:
$5+х=2^3$,
$5+х=8$,
$х=3$.

Ответ: 3

Задача 17

Решите уравнение ${x-9} / {3x-1}={x-9} / {x+33}$. Если уравнение имеет несколько корней, в ответ запишите меньший из них

Решение

Допустимые значения переменной: $3х-1≠0$, $х≠1/3$;

$х+33≠0$, $х≠-33$;

Домножим обе части уравнения на $(3х-1)(х+33)≠0 — $ говорят умножим «крест -накрест»

$(х-9)(х+33)=(х-9)(3х-1) — $ вынесем общий множитель

$(х-9)(х+33)-(х-9)(3х-1)=0$

$(х-9)(х+33-(3х-1))=0$

$(х-9)(х+33-3х+1)=0$

$(х-9)(-2х+34)=0$

$ х-9=0$, $х=9$ или

$-2х+34=0$, $х=17$;

$9<17$ — значит наименьший корень $x=9$

Ответ: 9

Рекомендуемые курсы подготовки

Источник
Skip to content

ЕГЭ Профиль №5. Показательные уравнения

ЕГЭ Профиль №5. Показательные уравненияadmin2022-11-29T21:46:56+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №5. Показательные уравнения

Задача 1. Найдите корень уравнения    ({8^{6 — x}} = 8.)

Ответ

ОТВЕТ: 5.

Решение

({8^{6 — x}} = 8,,,,,, Leftrightarrow ,,,,,,6 — x = 1,,,,, Leftrightarrow ,,,,,,x = 5.)

Ответ: 5.
Задача 2. Найдите корень уравнения     ({2^{x — 7}} = frac{1}{4}.)

Ответ

ОТВЕТ: 5.

Решение

({2^{x — 7}} = frac{1}{4},,,,,,, Leftrightarrow ,,,,,{2^{x — 7}} = {2^{ — 2}},,,,,, Leftrightarrow ,,,,,x — 7 =  — 2,,,,,, Leftrightarrow ,,,,,,x = 5.)

Ответ: 5.
Задача 3. Найдите корень уравнения    ({left( {frac{1}{4}} right)^{4x — 10}} = frac{1}{{16}}.)

Ответ

ОТВЕТ: 3.

Решение

({left( {frac{1}{4}} right)^{4x — 10}} = frac{1}{{16}},,,,,,, Leftrightarrow ,,,,,,{left( {frac{1}{4}} right)^{4x — 10}} = {left( {frac{1}{4}} right)^2},,,,,, Leftrightarrow ,,,,,,4x — 10 = 2,,,,,, Leftrightarrow ,,,,,x = 3.)

Ответ: 3.
Задача 4. Найдите корень уравнения    ({left( {frac{1}{2}} right)^{18 — 3x}} = 64.)

Ответ

ОТВЕТ: 8.

Решение

({left( {frac{1}{2}} right)^{18 — 3x}} = 64,,,,,, Leftrightarrow ,,,,,,{2^{ — 18 + 3x}} = {2^6},,,,,,, Leftrightarrow ,,,,,, — 18 + 3x = 6,,,,,, Leftrightarrow ,,,,,,x = 8.)

Ответ: 8.
Задача 5. Найдите корень уравнения    ({4^{x — 4}} = frac{1}{2}.)

Ответ

ОТВЕТ: 3,5.

Решение

({4^{x — 4}} = frac{1}{2},,,,,,, Leftrightarrow ,,,,,,,{2^{2x — 8}} = {2^{ — 1}},,,,,,, Leftrightarrow ,,,,,,,2x — 8 =  — 1,,,,,,, Leftrightarrow ,,,,,,x = 3,5.)

Ответ: 3,5.
Задача 6. Найдите корень уравнения    ({left( {frac{1}{{25}}} right)^{x — 1}} = 5.)

Ответ

ОТВЕТ: 0,5.

Решение

({left( {frac{1}{{25}}} right)^{x — 1}} = 5,,,,,, Leftrightarrow ,,,,,,,{5^{ — 2x + 2}} = {5^1},,,,,, Leftrightarrow ,,,,,, — 2x + 2 = 1,,,,,, Leftrightarrow ,,,,,,x = 0,5.)

Ответ: 0,5.
Задача 7. Найдите корень уравнения    ({7^{9 + x}} = 49.)

Ответ

ОТВЕТ: — 7.

Решение

({7^{9 + x}} = 49,,,,,, Leftrightarrow ,,,,,,{7^{9 + x}} = {7^2},,,,,, Leftrightarrow ,,,,,,9 + x = 2,,,,,, Leftrightarrow ,,,,,,x =  — 7.)

Ответ: – 7.
Задача 8. Найдите корень уравнения    ({left( {frac{1}{4}} right)^{2 + x}} = 64.)

Ответ

ОТВЕТ: — 5.

Решение

({left( {frac{1}{4}} right)^{2 + x}} = 64,,,,,,, Leftrightarrow ,,,,,,{4^{ — 2 — x}} = {4^3},,,,,, Leftrightarrow ,,,,,, — 2 — x = 3,,,,,, Leftrightarrow ,,,,,,x =  — 5.)

Ответ: – 5.
Задача 9. Найдите решение уравнения    ({left( {frac{1}{3}} right)^{x + 1}} = {81^x}.)

Ответ

ОТВЕТ: — 0,2.

Решение

({left( {frac{1}{3}} right)^{x + 1}} = {81^x},,,,,, Leftrightarrow ,,,,,,{3^{ — x — 1}} = {3^{4x}},,,,,, Leftrightarrow ,,,,,, — x — 1 = 4x,,,,,, Leftrightarrow ,,,,,,x =  — 0,2.)

Ответ: – 0,2.
Задача 10. Решите уравнение    ({9^{6 + x}} = {81^{2x}}.)

Ответ

ОТВЕТ: 2.

Решение

({9^{6 + x}} = {81^{2x}},,,,,, Leftrightarrow ,,,,,,{9^{6 + x}} = {9^{4x}},,,,,, Leftrightarrow ,,,,,,6 + x = 4x,,,,,,, Leftrightarrow ,,,,,,,x = 2.)

Ответ: 2.
Задача 11. Решите уравнение    ({2^{3 — 4x}} = 0,16 cdot {5^{3 — 4x}}.)

Ответ

ОТВЕТ: 0,25.

Решение

({2^{3 — 4x}} = 0,16 cdot {5^{3 — 4x}}left| {:,{5^{3 — 4x}},,,,, Leftrightarrow ,,,,,frac{{{2^{3 — 4x}}}}{{{5^{3 — 4x}}}} = frac{{16}}{{100}},,,,, Leftrightarrow ,,,,,,{{left( {frac{2}{5}} right)}^{3 — 4x}} = frac{4}{{25}},,,,,, Leftrightarrow } right.)

( Leftrightarrow ,,,,,{left( {frac{2}{5}} right)^{3 — 4x}} = {left( {frac{2}{5}} right)^2},,,,,, Leftrightarrow ,,,,,3 — 4x = 2,,,,,, Leftrightarrow ,,,,,,x = 0,25.)

Ответ: 0,25.
Задача 12. Решите уравнение    ({6^{3 — x}} = 0,6 cdot {10^{3 — x}}.)

Ответ

ОТВЕТ: 2.

Решение

({6^{3 — x}} = 0,6 cdot {10^{3 — x}}left| {:{{10}^{3 — x}},,,,, Leftrightarrow ,,,,,frac{{{6^{3 — x}}}}{{{{10}^{3 — x}}}} = frac{6}{{10}},,,,,, Leftrightarrow ,,,,,,{{left( {frac{6}{{10}}} right)}^{3 — x}} = frac{6}{{10}},,,,, Leftrightarrow ,,,,,3 — x = 1,,,,, Leftrightarrow ,,,,,x = 2.} right.)

Ответ: 2.

Источник

ЕГЭ по математике Профиль. Задание 1: Уметь решать уравнения. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».

ЕГЭ Профиль. Задание № 1.

АЛГОРИТМ ВЫПОЛНЕНИЯ

Задание № 1 рассчитано на умение решать простейшие уравнения. Такие уравнения содержат одну переменную и не требуют значительных алгебраических преобразований. Прежде чем приступить к решению, важно определить тип уравнения — линейное, квадратное, показательное, логарифмическое и т. д. Это позволит выбрать правильный метод решения. В ответе надо записать целое или дробное число. Если в результате получилась обыкновенная дробь, её нужно перевести в десятичную.

План выполнения:

  1. Внимательно прочитайте условие задания.
  2. Решите уравнение.
  3. Проверьте, все ли корни уравнения удовлетворяют области определения.
  4. Запишите полученное число в поле ответа КИМ и бланк ответов № 1.

Пример задания № 1. Найдите корень уравнения (х – 2)2 = (3 + х)2.

Решение:
ЕГЭ по математике Профиль. Задание 1

Ответ: –0,5.

АНАЛИЗ ТИПИЧНЫХ ОШИБОК

  • При решении уравнений определенного вида следует пользоваться формулами сокращённого умножения.
  • Часто учащиеся опускают чётную степень, что приводит к неправильному решению.
  • Учащиеся иногда неправильно возводят двучлен в квадрат, забывая удвоенное произведение.
  • Кубические уравнения всегда имеют действительные корни.
  • Иногда учащиеся неправильно извлекают кубический корень из числа.

Тренировочные задания с самопроверкой

№ 1.1. Найдите корень уравнения (1/6)x+5 = 6х.

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 1

№ 1.2. Найдите корень уравнения x = (4x + 27)/(x – 2). Если уравнение имеет более одного корня, в ответе запишите меньший из них.

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 1

№ 1.3. Решите уравнение х2 + х – 56 = 0. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 1

№ 1.4. Найдите корень уравнения log8(5x – 7) = log8(x + 11).

Открыть ОТВЕТ

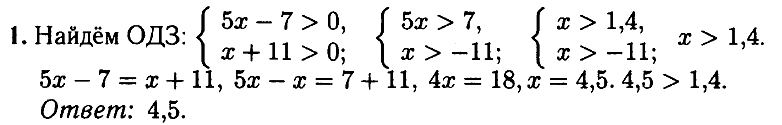
ЕГЭ по математике Профиль. Задание 1

№ 1.5. Найдите корень уравнения –2 8/9 • х = 4 1/3.

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 1

СПРАВОЧНЫЙ МАТЕРИАЛ

Равенство с одной или несколькими переменными называется уравнением. Значение переменной, при котором получается верное решение, называется корнем уравнения. Решить уравнение — значит найти все его корни или доказать, что уравнение не имеет корней.

При решении задания необходимо определить тип уравнения — линейное, квадратное, показательное, логарифмическое и т. д. Это позволит выбрать правильный метод решения.

1. Линейные уравнения

ЕГЭ по математике Профиль. Задание 1

2. Квадратные уравнения

ЕГЭ по математике Профиль. Задание 1

3. Рациональные уравнения

Задачи такого типа содержат уравнения, в знаменателе которых находится выражение, содержащее переменную.ЕГЭ по математике Профиль. Задание 1

4. Иррациональные уравнения

Задачи этого задания решаются методом возведения обеих частей уравнения в степень, соответствующую степени корня.ЕГЭ по математике Профиль. Задание 1

5. Показательные уравнения

Задание состоит из простейшего показательного уравнения. Ответом к заданию является целое или дробное число.ЕГЭ по математике Профиль. Задание 1

6. Логарифмические уравнения

Уравнения этого типа решаются по определению логарифма, а также с использованием свойств логарифма. Ответом является целое или дробное число. При решении логарифмических уравнений обязательно учитывается область определения логарифма.ЕГЭ по математике Профиль. Задание 1

Методы решения логарифмических уравнений:

ЕГЭ по математике Профиль. Задание 1

Вы смотрели: ЕГЭ по математике Профиль. Задание 1: Уметь решать уравнения. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».


Просмотров:
10 972

Источник

Найдите корень уравнения (displaystyle log_5 (x+7)=log_5 (5-x)-1).

Найдите корень уравнения (displaystyle log_3 (x+6)=log_3 (10-x)-1).

Найдите корень уравнения (displaystyle sqrt{2x-3}=x-3). Если уравнение имеет более одного корня, в ответ запишите наименьший из корней.

Найдите корень уравнения (displaystyle sqrt{11-5x}=1-x). Если уравнение имеет более одного корня, в ответ запишите наибольший из корней.

Найдите корень уравнения (displaystyle 0,2^{5+4x}=125).

Найдите корень уравнения (displaystyle 0,5^{4-5x}=64).

Найдите корень уравнения (displaystyle (x-11)^4=(x+3)^4).

Найдите корень уравнения (displaystyle (2x-11)^2=(2x-1)^2).

Найдите корень уравнения (displaystyle left( frac{1}{5} right)^{3x+5}=0,04).

Найдите корень уравнения (displaystyle left( frac{1}{4} right)^{x-2,5}=frac{1}{8}).


Источник

Понравилась статья? Поделить с друзьями:
  • Найдите корень уравнения егэ логарифмы
  • Найдите значения выражения дроби егэ
  • Наименование предмета егэ
  • Найдите значение производной функции егэ
  • Наименование мсу это для егэ