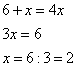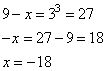Найдите корень уравнения решу егэ 5 задание - Помощь в подготовке к экзаменам и поступлению

Тип 5 № 26653

Найдите корень уравнения

Аналоги к заданию № 26653: 510382 510401 2857 13685 505143 505164 2859 2861 2863 2865 … Все

Источник: Пробный экзамен по математике Санкт-Петербург 2015. Вариант 1., ЕГЭ — 2017. Основная волна 02.06.2017. Вариант 301 (C часть)., ЕГЭ по математике 07.06.2021. Основная волна. Санкт-Петербург

Классификатор алгебры: Показательные уравнения

Кодификатор ФИПИ/Решу ЕГЭ: 1.4.2 Преобразования выражений, включающих операцию возведения в степень, 2.1.5 Показательные уравнения

Источник

Поиск

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 613 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Найдите корень уравнения

Найдите корень уравнения: Если уравнение имеет более одного корня, укажите меньший из них.

Найдите корень уравнения:

Если уравнение имеет более одного корня, в ответе укажите больший из них.

Найдите корень уравнения: В ответе запишите наибольший отрицательный корень.

Найдите корень уравнения

Всего: 613 1–20 | 21–40 | 41–60 | 61–80 …

Источник

Сегодня мы будем тренировать навык решения задания 5 ЕГЭ – найдите корень уравнения. Будем искать корень уравнения. Рассмотрим примеры решения такого рода заданий. Но для начала, давайте вспомним – что значит – найти корень уравнения?

Это значит найти такое, зашифрованное под х число, которое мы подставим вместо x и наше уравнение будет верным равенством.

Например, 3x=9 – это уравнение, а 3^.3=9 – это уже верное равенство. То есть в данном случае, мы вместо x подставили число 3 – получили верное выражение или равенство, это означает, что мы решили уравнение, то есть нашли данное число x=3, которое превращает уравнение в верное равенство.

Вот этим мы и займемся – будем находить корень уравнения.

Задание 1 – найдите корень уравнения 21-4x=32
Задание 2 – найдите корень уравнения 25-x = 1/16
Задание 3 – найдите корень уравнения
Задание 4 – найдите корень уравнения log3(15-х)=log32
Задание 5 – найдите корень уравнения log3(3-x)=3
Задание 6. Найдите корень уравнения log(x+3)=log2(3x-15).
Задание 7. Найдите корень уравнения log2(14-2x)=2log23

Задание 1 – найдите корень уравнения 2^1-4x=32

Это показательное уравнение. Оно решается следующим образом – нужно чтобы и слева, и справа от знака “равно” была степень с одинаковым основанием.

Слева у нас основание степени 2, а справа – степени нет вовсе. Но мы знаем, что 32 – это 2 в пятой степени. То есть, 32=2⁵

Таким образом, наше уравнение будет выглядеть так: 2^1-4х=2⁵

Слева и справа у нас основания степени одинаковы, значит, чтобы у нас было равенство, должны быть равны и показатели степени:

1-4х=5

Получаем обыкновенное уравнение. Решаем обычным способом – все неизвестные оставляем слева, а известные переносим вправо, получим:

-4х=5-1

-4х=4

х=-1.

Делаем проверку: 2^1-4(-1)=32

2⁵=32

32=32

Мы нашли корень уравнение. Ответ: х=-1.

Самостоятельно найдите корень уравнения в следующих заданиях:

а) 2^5-х=64

б) 2^1-3х=128

Задание 2 – найдите корень уравнения 2^5-x = 1/16

Уравнение решаем аналогично – путем приведения левой и правой частей уравнения к одному основанию степени. В нашем случае – к основанию степени 2.

Используем следующее свойство степени:

По этому свойству мы получим для правой части нашего уравнения:

Тогда наше уравнение запишется в виде:

Если равны основания степени, значит, равны и показатели степени:

5-х=-4

-х=-4-5

х=9

Ответ: х=9.

Сделаем проверку – подставим найденное значение х в исходное уравнение – если мы получим верное равенство, значит, мы решили уравнение правильно.

2^5-9=1/16

2^-4=1/16

1/16=1/16

Мы нашли корень уравнения правильно.

Задание 3 – найдите корень уравнения

Заметим, что справа у нас стоит 1/8, а 1/8 – это

Тогда наше уравнение запишется в виде:

Если основания степени равны, значит, равны и показатели степени, получим простое уравнение:

3х-12=3

3х=15

х=5

Ответ: х=5. Проверку сделайте самостоятельно.

Задание 4 – найдите корень уравнения log₃(15-х)=log₃2

Это уравнение решается также как и показательное. Нам нужно, чтобы основания логарифмов слева и справа от знака “равно” были одинаковыми. Сейчас они одинаковы, значит, приравниваем те выражения, которые стоят под знаком логарифмов:

15-х=2

-х=2-15

-х=-13

х=13

Ответ: х=13

Задание 5 – найдите корень уравнения log₃(3-x)=3

Число 3 – это log₃27. Чтобы было понятно внизу нижним индексом под знаком логарифма стоит число которое возводится в степень, в нашем случае 3, под знаком логарифма стоит число, которое получилось при возведении в степень – это 27, а сам логарифм – это показатель степени, в которую нужно возвести 3, чтобы получить 27.

Смотрите на картинке:

Таким образом, любое число можно записать в виде логарифма. В данном случае очень удобно записать число 3 в виде логарифма с основанием 3. Получим:

log₃(3-x)=log₃27

Основания логарифмов равны, значит, равны и числа, стоящие под знаком логарифма:

3-х=27

Получим,

-х=27-3

-х=24

х=-24

Сделаем проверку:

log₃(3-(-24))=log₃27

log₃(3+24)= log₃27

log₃27=log₃27

3=3

Ответ: x=-24.

Задание 6. Найдите корень уравнения log(x+3)=log₂(3x-15).

log₂(x+3)=log₂(3x-15)

Решение:

x+3=3x-15

x-3x=-3-15

-2x=-18

x=9

Проверка: log₂(9+3)=log₂(27-15)

log₂12=log₂12

Ответ: x=9.

Задание 7. Найдите корень уравнения log₂(14-2x)=2log₂3

log₂(14-2x)=2log₂3

log₂(14-2x)=log₂3²

14-2x=3²

14-2x=9

-2x=9-14

-2x=-5

x=2,5

Проверка: log₂(14-5)=2log₂3

log₂9=2log₂3

log₂3²=2log₂3

2log₂3=2log₂3

Ответ: x=2,5

Подготовьтесь к ЕГЭ и к ОГЭ -посмотрите предыдущие темы Найдите значение выражения и Как решать неравенства .

Источник

За это задание ты можешь получить 1 балл. На решение дается около 3 минут. Уровень сложности: базовый.
Средний процент выполнения: 93.6%
Ответом к заданию 5 по математике (профильной) может быть целое число или конечная десятичная дробь.

Разбор сложных заданий в тг-канале

Задачи для практики

Задача 1

Найдите корень уравнения $log_{x+5}{64} = 2$.

Решение

Найдем ОДЗ: ${tablex + 5 > 0; x + 5 ≠ 1;$ ${tablex > -5; x ≠ -4;$ $x ∈ (-5; -4) ∪ (-4; +∞)$.

По определению логарифма если $log_b a=c$, то $b^c=a$

$(x + 5)^2 = 64$,

$x + 5 = 8$ или $x + 5 = -8$,

$x = 3 $ или $x = -13 $

$x = -13$ — не входит в ОДЗ.

Ответ: 3

Задача 2

Найдите корень уравнения $log_{5}{(x^2+26x + 169)}-2 =log_{√5}{(5x-7)}$.

Решение

$log_{5}{(x^2+26x + 169)}-2 =log_{√5}{(5x-7)}$,

$log_{5}{(x+13)^2}-log_{5}{25} =log_{5^{1/2}}{(5x-7)}$,

$log_{5}{(x+13)^2/{25}} =2log_{5}{(5x-7)}$,

$log_{5}{(x+13)^2/{25}} =log_{5}{(5x-7)^2}$,

$(x+13)^2/{25} =(5x-7)^2$,

$(x+13)/{5} =(5x-7)$ или $(x+13)/{5} =-(5x-7)$,

Откуда: $x=2$ или $x=11/13 — $ второй корень не удовлетворяет ОДЗ,

Ответ: 2

Задача 3

Найдите корень уравнения $log_{3}{(4x-15)} =log_{3}{(x+3)}$.

Решение

$log_3 (4x — 15) = log_3 (x + 3)$,

$4x — 15 = x + 3$,

$3x = 18, x = 6$.

Проверка. При $x = 6$ получаем $log_3 (6 · 4 — 15) = log_3 (6 + 3)$ — верное равенство.

$x = 6$ — корень уравнения.

Ответ: 6

Задача 4

Найдите корень уравнения $625^{x+1}={1} / {5}$.

Решение

$(5^4)^{x+1} = 5^{-1}$, применим свойство $(a^b)^c=a^{bc}$

$5^{4x+4} = 5^{-1}$,

$4x + 4 = -1$,

$4x = -5$,

$x = -1.25$.

Ответ: -1.25

Задача 5

Найдите корень уравнения $9^{x-12}={1} / {3}$.

Решение

$(3^2)^{x-12}=3^{-1} $, применим свойство $(a^b)^c=a^{bc}$

$ 3^{2x-24} = 3^{-1} $,

$2x-24=-1 $,

$ 2x=23 $,

$ x=11{,}5$.

Ответ: 11.5

Задача 6

Найдите корень уравнения $(x-12)^3=-27$.

Решение

$(x-12)^3=-27$

$ (x-12)^3=(-3)^3 $,
$ x-12=-3 $,
$x=9$.

Ответ: 9

Задача 7

Найдите корень уравнения $log_{2}{(12+x)} =-2$.

Решение

По определению логарифма $12+x = 2^{-2}, 12+x = 0.25, x = 0.25-12, x = -11.75$.

Ответ: -11.75

Задача 8

Найдите корень уравнения $log_{3}{(4-x)} =5$.

Решение

По определению логарифма если $log_b a=c$, то $b^c=a$

$4-x = 3^5 $,

$ 4-x=243 $,

$x=-239$.

Ответ: -239

Задача 9

Решите уравнение $(x+7)^2 = x^2+7$. Если уравнение имеет более одного корня, в ответе запишите меньший из них.

Решение

Воспользуемся формулой квадрата суммы: $(a+b)^2=a^2+2ab+b^2$
$x^2 + 14x + 49 = x^2 + 7$,
$14x = -42$,
$x = -3$.

Ответ: -3

Задача 10

Решите уравнение $(5x+11)^2 = (5x-2)^2$. Если уравнение имеет более одного корня, в ответе запишите меньший из них.

Решение

Воспользуемся формулами сокращенного умножения:

$(a+b)^2=a^2+2ab+b^2$

$(a-b)^2=a^2-2ab+b^2$
Таким образом:

$25x^2+110x+121=25x^2-20x+4$,

$ 110x+20x=-117$,
$130x=-117$
$x=-117/130$
$x=-0.9$.

Ответ: -0.9

Задача 11

Найдите корень уравнения $√ {14-5x}=-x$. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Решение

Так как левая часть уравнения неотрицательна, то и правая тоже неотрицательна:

$-x ⩾ 0$, — домножим обе части на -1, в таком случае знак неравенства меняется

$ x ⩽ 0$.

Возведя обе части в квадрат, получим уравнение $14-5x=x^2$,

$x^2+5x-14=0$,

$ x_1=-7$,

$ x_2=2$ — не удовлетворяет условию $x⩽ 0$.

Пояснение: $(-x)^2=(-x)(-x)=x^2$

Ответ: -7

Задача 12

Найдите корень уравнения ${x+3} / {2x-11}={x+3} / {3x-7}$. Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Решение

Найдем ОДЗ: ${table2x-11 ≠ 0; 3x-7≠ 0;$ ${tablex ≠ 5.5; x ≠7/3;$

Удобно домножить обе стороны равенства на знаменатели, проще говоря «крест накрест»

$(x+3)(3x-7)=(2x-11)(x+3)$

${3x}^2-7x+9x-21={2x}^2+6x-11x-33$

$x^2+7x+12=0$

$x_1=-3, x_2=-4$ — оба корня удовлетворяют ОДЗ

Наибольший корень: $x=-3$

Ответ: -3

Задача 13

Найдите корень уравнения ${9-5x} / {x+3}=x$. Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Решение

При $x ≠ -3$ получим

$x(x + 3) = 9 — 5x$,

$x^2 + 3x + 5x — 9 = 0$,

$x^2 + 8x — 9 = 0$

По теореме Виета $х_1=1$, $х_2=-9$.

Больший корень $x_1=1$

Ответ: 1

Задача 14

Найдите корень уравнения $√ {{4x-21} / {117}}={1} / {3}$.

Решение

ОДЗ: ${4x — 21}/{117}⩾0, 4x-21⩾0, x⩾21/4, x⩾5.25$

$(√{{4x — 21}/{117}})^2 = ({1}/{3})^2$,

${4x — 21}/{117} = {1}/{9}$,

$9(4x — 21) = 117$,

$36x — 189 = 117$,

$36x = 306$,

$x = 8.5$ — удовлетворяет ОДЗ.

Ответ: 8.5

Задача 15

Решите уравнение $log_{{1} / {3}}(13 + x) = — 2$.

Решение

ОДЗ: $13+x>0, x>-13$

По определению логарифма если $log_b a=c$, то $b^c=a$

$(1/3)^(-2)=13+x$
$ 13+x=9$
$ x=-4$ — удовлетворяет ОДЗ

Ответ: -4

Задача 16

Решите уравнение $√^3{5+x}=2$.

Решение

Возведем обе части уравнения в третью степень:
$5+х=2^3$,
$5+х=8$,
$х=3$.

Ответ: 3

Задача 17

Решите уравнение ${x-9} / {3x-1}={x-9} / {x+33}$. Если уравнение имеет несколько корней, в ответ запишите меньший из них

Решение

Допустимые значения переменной: $3х-1≠0$, $х≠1/3$;

$х+33≠0$, $х≠-33$;

Домножим обе части уравнения на $(3х-1)(х+33)≠0 — $ говорят умножим «крест -накрест»

$(х-9)(х+33)=(х-9)(3х-1) — $ вынесем общий множитель

$(х-9)(х+33)-(х-9)(3х-1)=0$

$(х-9)(х+33-(3х-1))=0$

$(х-9)(х+33-3х+1)=0$

$(х-9)(-2х+34)=0$

$ х-9=0$, $х=9$ или

$-2х+34=0$, $х=17$;

$9<17$ — значит наименьший корень $x=9$

Ответ: 9

Простейшие уравнения

Задание №5 профильного уровня ЕГЭ по математике – решение простейшего уравнения, чаще всего степенного. Обычно, требуется сделать несколько операций и приравнять степени – после этого уравнение становится линейным и решается легко – как и любое линейное уравнение.

Разбор типовых вариантов заданий №5 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

[su_note note_color=”#defae6″]

Найдите корень уравнения 3^х-5=81

[/su_note]

Алгоритм решения задания:

Определяем вид уравнения.
Представляем правую часть в виде степени.
Отбрасываем основание и решаем уравнение.
Записываем ответ.

Решение:

1. Данное уравнение относится к показательным. Поэтому решаем его, приведя к виду: а^f(x)=a^g(x).

2. Представляем правую часть уравнения 81 в виде степени с основанием 3: 81=3⁴. Тогда уравнение примет вид: 3^х-5=3⁴.

3. Так как основания одинаковы, можно отбросить их. Получаем: х – 5=4.

Решаем полученное уравнение: х=4+5,

х=9.

Ответ: 9.

Второй вариант задания (из Ященко, №1)

[su_note note_color=”#defae6″]

Найдите корень уравнения

[/su_note]

Алгоритм решения задания:

Определяем вид уравнения.
Представляем правую часть в виде степени с основанием 9.
Отбрасываем основание и решаем уравнение.
Записываем ответ.

Решение:

1. Данное уравнение является показательным. Решаем его, приводя к виду: а^f(x)=a^g(x).

2. Число 81 справа представить в виде , откуда получаем в правой части .

Исходное уравнение принимает вид:

Так как у степеней в обеих частях уравнения равны, можно перейти к равенству степеней и решить уравнение:

Ответ: 2.

Третий вариант задания (из Ященко, №4)

[su_note note_color=”#defae6″]

Найдите корень уравнения

[/su_note]

Алгоритм решения задания:

Определяем вид уравнения.
Представляем правую часть в виде степени с основанием 9.
Отбрасываем основание и решаем уравнение.
Записываем ответ.

Решение:

1. Уравнение показательного вида, значит можно решить его приведя к виду: f(x)^a=g(x)^a

2. Число представляем в виде степени с основанием 8: , тогда исходное уравнение можем записать таким образом:

Поскольку степени равны, должны быть равны и их основания. Имеем:

Ответ: 5.

Четвертый вариант задания (из Ященко, №8)

[su_note note_color=”#defae6″]

Найдите корень уравнения

[/su_note]

Алгоритм решения задания:

Определяем вид уравнения.
Представляем правую часть в виде логарифма с основанием 7.
Отбрасываем логарифм и решаем уравнение.
Проверяем корни.
Записываем ответ.

Решение:

1. Уравнение логарифмическое, приводимое к виду: log_ag(x)=log_ag(x).

2. Преобразуем правую часть уравнения так, чтобы там стоял логарифм с основанием 7:

Отбрасываем знак логарифма, получим:

Проверяем полученный корень на принадлежность ОДЗ: 9 – (-18)=27>0, значит, корень принадлежит ОДЗ.

Ответ: -18.

Пятый вариант задания (из Ященко, №18)

[su_note note_color=”#defae6″]

Найдите корень уравнения

[/su_note]

Алгоритм решения задания:

Определяем вид уравнения.
Представляем правую часть в виде логарифма с основанием 7.
Отбрасываем логарифм и решаем уравнение.
Проверяем корни.
Записываем ответ.

Решение:

1. Уравнение логарифмическое, приводимое к виду: log_ag(x)=log_ag(x).

2. Преобразуем правую часть уравнения, чтобы там стоял логарифм с основанием 4. Для этого используем свойства логарифмов:

log₁₆25=log₄²25=1/2∙log₄25

Получаем уравнение:

2log₄(2 – x)=log₄25

Решаем полученное уравнение:

Или 2 – x = – 5

x=2+5=7

Проверим на принадлежность ОДЗ: 2 – (-3)=5>0, корень принадлежит ОДЗ.

2 – 7 = -5 < 0, корень не принадлежит ОДЗ.

Ответ: -3.

Даниил Романович | Просмотров: 9.4k

Источник

В задании №5 варианта ЕГЭ вам встретятся всевозможные уравнения: квадратные и сводящиеся к квадратным, дробно-рациональные, иррациональные, степенные, показательные и логарифмические и даже тригонометрические. Видите, как много нужно знать, чтобы справиться с заданием! И еще ловушки и «подводные камни», которые ждут вас в самом неожиданном месте.

Вот список тем, которые стоит повторить:

Квадратные уравнения

Арифметический квадратный корень

Корни и степени

Показательная функция

Показательные уравнения

Логарифмическая функция

Логарифмические уравнения

Тригонометрический круг

Формулы приведения

Формулы тригонометрии

Простейшие тригонометрические уравнения 1

Уравнения, сводящиеся к квадратным

1. Решите уравнение $frac{6}{13}x^2=19frac{1}{2}$ . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Кажется, что уравнение очень простое. Но иногда здесь ошибаются даже отличники. А вот шестиклассник бы не ошибся.

С левой частью уравнения все понятно. Дробь $frac{6}{13}$ умножается на x^2. А в правой части — смешанное число $19frac{1}{2}.$ Его целая часть равна 19, а дробная часть равна $frac{1}{2}.$ Запишем это число в виде неправильной дроби:

$19frac{1}{2}= frac{19cdot 2+1}{2} = frac{39}{2}.$

Получим:

$frac{6}{13}x^2=frac{39}{2};$

$x^2=frac{39cdot 13}{2cdot 6}=frac{13cdot 3cdot 13}{2cdot 6}=frac{{13}^2}{4};$

$x=pm frac{13}{2};$

или

Выбираем меньший корень.

Ответ: -6,5.

2. Решите уравнение

Возведем в квадрат левую часть уравнения. Получим:

Ответ: -6.

Дробно-рациональные уравнения

3. Найдите корень уравнения

Перенесем единицу в левую часть уравнения. Представим 1 как $frac{4x-5}{4x-5}$ и приведем дроби к общему знаменателю:

$frac{5x-3}{4x-5}-frac{4x-5}{4x-5}=0;$

$frac{x+2}{4x-5}=0;$

x= - 2.

Ответ: -2.

Это довольно простой тип уравнений. Главное — внимательность.

Иррациональные уравнения

Так называются уравнения, содержащие знак корня — квадратного, кубического или n-ной степени.

4. Решите уравнение:

$sqrt{frac{6}{4{x}-54} } =frac{1}{7}.$

Выражение под корнем должно быть неотрицательно, а знаменатель дроби не равен нулю.

Значит, .

Возведём обе части уравнения в квадрат:

$frac{6}{4{x}-{ 54}} =frac{1}{49}.$

Решим пропорцию:

Условие при этом выполняется.

Ответ: 87.

5. Решите уравнение Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

А в этом уравнении есть ловушка. Решите его самостоятельно и после этого читайте дальше.

Выражение под корнем должно быть неотрицательно. И сам корень — величина неотрицательная. Значит, и правая часть должна быть больше или равна нуля. Следовательно, уравнение равносильно системе:

$left{begin{matrix} 72-x=x^2\72-xgeq 0 hfill \xgeq 0 hfill end{matrix}right.$ .

Решение таких уравнений лучше всего записывать в виде цепочки равносильных переходов:

$sqrt{72-x}=x Leftrightarrow left{begin{matrix} 72-x=x^2\72-x geq 0 \x geq 0 end{matrix}right. Leftrightarrow$

Мы получили, что x=8 . Это единственный корень уравнения.

Типичная ошибка в решении этого уравнения такая. Учащиеся честно пишут ОДЗ, помня, что выражение под корнем должно быть неотрицательно:

Возводят обе части уравнения в квадрат. Получают квадратное уравнение: Находят его корни: x=8 или x=-9. Пишут в ответ: -9 (как меньший из корней). В итоге ноль баллов.

Теперь вы знаете, в чем дело. Конечно же, число -9 корнем этого уравнения быть не может.

Ответ: 8.

6. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Запишем решение как цепочку равносильных переходов:

Ответ: 9.

Показательные уравнения

При решении показательных уравнений мы пользуемся свойством монотонности показательной функции.

7. Решите уравнение $5^{x-7}=frac{1}{125}.$

Вспомним, что $125 = 5{}^{3}.$ Уравнение приобретает вид: $5{}^{x}{}^{-}{}^{7 }= 5{}^{-}{}^{3}.$ Функция y = 5^x монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

откуда x = 4.

Ответ: 4.

8. Решите уравнение ${left(frac{1}{49}right)}^{x-8}=7.$

Представим ${left(frac{1}{49}right)}^{ }$ как $7^{-2};$

${left(7^{-2}right)}^{x-8}=7;$

$7^{-2x+16}=7.$

Функция y = 7^x монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

x=7,5.

Ответ: 7,5.

9. Решите уравнение $left(frac{1}{9} right)^{{ x}-13} =3.$

Представим ${textstylefrac{1}{9}}$ в виде степени с основанием 3 и воспользуемся тем, что $left({ a}^{{ m}} right)^{{ n}} ={ a}^{{ mn}}.$

$left(3^{-2} right)^{{ x}-{ 13}} =3;$
$3^{-2{ x}+{ 26}} =3^{1} ;$

Ответ: 12,5.

Логарифмические уравнения

Решая логарифмические уравнения, мы также пользуемся монотонностью логарифмической функции: каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, значит, равны и сами числа.

И конечно, помним про область допустимых значений логарифма:

Логарифмы определены только для положительных чисел.

Основание логарифма должно быть положительно и не равно единице.

10. Решите уравнение:

${{log}_5 left(4+xright)=2 }.$

Область допустимых значений: . Значит,

Представим 2 в правой части уравнения как ${{log}_5 25 }$ , чтобы слева и справа в уравнении были логарифмы по основанию 5.

${{log}_5 left(4+xright)={{log}_5 25 } }.$

Функция $y = {{log}_5 x }$ монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом

4+x=25;
x=21.

Ответ: 21.

11. Решите уравнение: ${{log}_8 left(x^2+xright)={{log}_8 left(x^2-4right) } }.$

Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:

Ответ: -4.

12. Решите уравнение: $2^{{{log}_4 left(4x+5right) }}=9.$

Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:

${{log}_4 b }=frac{{{log}_2 b }}{{{log}_2 4 }}=frac{{{log}_2 b }}{2}.$

Записываем решение как цепочку равносильных переходов.

Ответ: 19.

13. Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

${{log}_{x-5} 49=2 }.$

В этом уравнении тоже есть ловушка. Мы помним, что основание логарифма должно быть положительно и не равно единице.

Получим систему:

$small left{begin{matrix} left ( x-5 right )^2=49\x-50 \x-5 neq 1 end{matrix}right..$

Первое уравнение мы получили просто из определения логарифма.

Квадратное уравнение имеет два корня: x=12 и x=-2.

Очевидно, корень x=-2 является посторонним, поскольку основание логарифма должно быть положительным. Значит, единственный корень уравнения: x=12.

Ответ: 12.

Тригонометрические уравнения (Часть 1 ЕГЭ по математике)

Тригонометрические уравнения? В первой части вариантов ЕГЭ? — Да. Причем это задание не проще, чем задача 13 из второй части варианта Профильного ЕГЭ.

14. Найдите корень уравнения: $cos frac{pi (x+1)}{4}=frac{sqrt{2}}{2}.$ В ответе запишите наибольший отрицательный корень.

Типичная ошибка — решать это уравнение в уме. Мы не будем так делать! Несмотря на то, что это задание включено в первую части варианта ЕГЭ, оно является полноценным тригонометрическим уравнением, причем с отбором решений.

Сделаем замену $frac{pi left(x+1right)}{4}=t.$ Получим: $cos t=frac{sqrt{2}}{2}.$

Получаем решения: $t=pm frac{pi }{4}+2pi n, nin Z.$ Вернемся к переменной x.

$frac{pi (x+1)}{4}=pm frac{pi }{4}+2pi n, nin Z.$ Поделим обе части уравнения на и умножим на 4.

$left[ begin{array}{c}x=8n, nin Z \x=-2+8n end{array}right..$

Первой серии принадлежат решения

Вторая серия включает решения

Наибольший отрицательный корень — тот из отрицательных, который ближе всех к нулю. Это x = -2.

Ответ: -2.

15. Решите уравнение: $tg frac{pi left( x+1right)}{4}= -1.$ В ответе напишите наименьший положительный корень.

Решение:

Сделаем замену $frac{pi left(x+1right)}{4}=t.$ Получим: tgt=-1. Решения этого уравнения:

$t=-frac{pi }{4}+pi n, nin Z.$ Вернемся к переменной х:

$frac{pi left(x+1right)}{4}=-frac{pi }{4}+pi n, n in Z.$ Умножим обе части уравнения на 4 и разделим на .

Выпишем несколько решений уравнения и выберем наименьший положительный корень:

Наименьший положительный корень x = 2.

Ответ: 2.

Мы разобрали основные типы уравнений, встречающихся в задании №5 Профильного ЕГЭ по математике. Конечно, это не все, и видов уравнений в этой задаче существует намного больше. Именно поэтому мы рекомендуем начинать подготовку к ЕГЭ по математике не с задания 1, а с текстовых задач на проценты, движение и работу и основ теории вероятностей.
Успеха вам в подготовке к ЕГЭ!

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание №5. Простейшие уравнения. Профильный ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Задача 1

Найдите корень уравнения $9^{log_{81}(5x-2)}=30$.

Задача 2

Найдите корень уравнения $log_2(9-2x)=log_2(6+x)+3$.

Задача 3

Найдите корень уравнения $({1} / {81})^{7+x}=243$.

Задача 4

Найдите корень уравнения $3{2} / {7}x =46$.

Задача 5

Найдите корень уравнения $2^{2x-7}=4{,}5⋅9^{2x-7}$.

Задача 6

Найдите корень уравнения $3^{2+x}=0{,}6⋅5^{2+x}$.

Задача 7

Найдите корень уравнения $log_{216}{6^{2x-11}}=3$.

Задача 8

Найдите корень уравнения $log_{81}{3^{4x+7}}=5$.

Задача 9

Найдите корень уравнения $tg{πx}/{4} = 1$. В ответе напишите наименьший положительный корень.

Задача 10

Найдите корень уравнения $7^{log_{49}{(6x-6)}}=6$.

Задача 11

Найдите корень уравнения $5^{log_{25}{(3x-3)}}=3$.

Задача 12

Найдите корень уравнения $log_{4}{(2x-1)} =log_{4}{(x+3)} — 1$.

Задача 13

Найдите корень уравнения $log_{x-4}{36} = 2$.

Задача 14

Найдите корень уравнения ${2} / {3} x +1{2} / {7} = {5} / {21} x $.

Задача 15

Найдите корень уравнения $(2x+7)^3=-64$.

Задача 16

Найдите корень уравнения $log_{2}{(2x+15)} =log_{2}{3} — 1$.

Задача 17

Найдите корень уравнения $log_{7}{(11-x)} =log_{7}{3} + 1$.

Задача 18

Найдите корень уравнения ${7} / {13}x^2=2{2} / {13}$. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Задача 19

Найдите корень уравнения $√ {-23x-120}=-x$. Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Задача 20

Найдите корень уравнения $√ {{36} / {2x-15}}=3$.

Задачи из курса стереометрии впервые появляются в ЕГЭ по математике в задании 5. Вам будут предложены вопросы по вычислению геометрических параметров шара, куба, параллельного параллелепипеда, призмы, пирамиды, цилиндра, конуса, составных многогранников, а также комбинаций нескольких фигур. Составители тестов также внесли в КИМ этого номера отдельно условия, касающиеся вычисления объемов геометрических тел и площади их сторон.

Пятые номера, касающиеся куба, одни из самых простых. Вам будет предложено найти объем фигуры, если известна сумма S всех его граней, и наоборот. Часть вопросов касается диагоналей, сторон. Такие же условия вам возможно дадут в заданиях с призмами, пирамидами. Другая часть может звучать так: «Во сколько раз увеличится V куба, если все ребра тела увеличить в три раза?».

Сложными называют школьники No 5 по математике о составных многогранниках и комбинациях тел. К примеру, вам может попасться вариант экзаменационного билета с поиском V параллельного параллелепипеда, который описан вокруг цилиндра, где d=1 м.

Варианты на тему «Шар» — это обычно поиск объема тела, площади его поверхности, радиуса или диаметра. Есть и мини-задачи такого типа: «Объем первой сферы в 27 раз больше, чем у второй. Сравните S поверхностей. Во сколько раз первая фигура больше второй по этому показателю?». В задачах о конусе вам нужно будет вычислять его V, площадь, образующую, высоту, диаметр или радиус основания.

Источник

Задание 1 – найдите корень уравнения 21-4x=32

Задание 2 – найдите корень уравнения 25-x = 1/16

Задание 4 – найдите корень уравнения log3(15-х)=log32

Задание 5 – найдите корень уравнения log3(3-x)=3

Задание 6. Найдите корень уравнения log(x+3)=log2(3x-15).

Задание 7. Найдите корень уравнения log2(14-2x)=2log23

Задачи для практики

Задача 1

Решение

Задача 2

Решение

Задача 3

Решение

Задача 4

Решение

Задача 5

Решение

Задача 6

Решение

Задача 7

Решение

Задача 8

Решение

Задача 9

Решение

Задача 10

Решение

Задача 11

Решение

Задача 12

Решение

Задача 13

Решение

Задача 14

Решение

Задача 15

Решение

Задача 16

Решение

Задача 17

Решение

Рекомендуемые курсы подготовки

Простейшие уравнения

Разбор типовых вариантов заданий №5 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

Алгоритм решения задания:

Решение:

Второй вариант задания (из Ященко, №1)

Алгоритм решения задания:

Решение:

Третий вариант задания (из Ященко, №4)

Алгоритм решения задания:

Решение:

Четвертый вариант задания (из Ященко, №8)

Алгоритм решения задания:

Решение:

Пятый вариант задания (из Ященко, №18)

Алгоритм решения задания:

Решение:

Задание 1 – найдите корень уравнения 2^1-4x=32

Задание 2 – найдите корень уравнения 2^5-x = 1/16

Задание 4 – найдите корень уравнения log₃(15-х)=log₃2

Задание 5 – найдите корень уравнения log₃(3-x)=3

Задание 6. Найдите корень уравнения log(x+3)=log₂(3x-15).

Задание 7. Найдите корень уравнения log₂(14-2x)=2log₂3