СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий.
Исследование тригонометрических функций
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 11 № 26692
Найдите наибольшее значение функции на отрезке
Аналоги к заданию № 26692: 3401 70043 517179 517217 561728 561769 3403 3405 3407 3409 … Все
Источник: Пробный экзамен Санкт-Петербург 2015. Вариант 2., Пробный экзамен по математике Санкт-Петербург 2015. Вариант 2.
Кодификатор ФИПИ/Решу ЕГЭ: 3.2.1 Монотонность функции. Промежутки возрастания и убывания, 3.2.5 Точки экстремума функции, 3.2.6 Наибольшее и наименьшее значения функции, 4.2.1 Применение производной к исследованию функций и построению графиков, Наименьшее (наибольшее) значение функции во внутренней точке отрезка
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
2
Тип 11 № 26693
Найдите наименьшее значение функции на отрезке
Аналоги к заданию № 26693: 70087 3417 3419 3421 3423 3425 3427 3429 3431 3433 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.2.1 Монотонность функции. Промежутки возрастания и убывания, 3.2.5 Точки экстремума функции, 3.2.6 Наибольшее и наименьшее значения функции, 4.2.1 Применение производной к исследованию функций и построению графиков, Наименьшее (наибольшее) значение функции во внутренней точке отрезка
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
3
Тип 11 № 26694
Найдите наименьшее значение функции на отрезке
Аналоги к заданию № 26694: 3437 70133 70137 509642 523374 523399 3439 3441 3443 3445 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.2.1 Монотонность функции. Промежутки возрастания и убывания, 3.2.5 Точки экстремума функции, 3.2.6 Наибольшее и наименьшее значения функции, 4.2.1 Применение производной к исследованию функций и построению графиков, Наименьшее (наибольшее) значение функции на границе отрезка
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
4
Тип 11 № 26695
Найдите наибольшее значение функции на отрезке
Аналоги к заданию № 26695: 3457 70187 509500 517158 3459 3461 3463 3465 3467 3469 … Все
Источник: Пробный экзамен по профильной математике Санкт-Петербург 05.04.2016. Вариант 2.
Кодификатор ФИПИ/Решу ЕГЭ: 3.2.1 Монотонность функции. Промежутки возрастания и убывания, 3.2.5 Точки экстремума функции, 3.2.6 Наибольшее и наименьшее значения функции, 4.2.1 Применение производной к исследованию функций и построению графиков, Наименьшее (наибольшее) значение функции на границе отрезка
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
5
Тип 11 № 26696
Найдите наименьшее значение функции на отрезке
Аналоги к заданию № 26696: 3475 70237 3477 3479 3481 3483 3485 3487 3489 3491 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.2.1 Монотонность функции. Промежутки возрастания и убывания, 3.2.5 Точки экстремума функции, 3.2.6 Наибольшее и наименьшее значения функции, 4.2.1 Применение производной к исследованию функций и построению графиков, Наименьшее (наибольшее) значение функции на границе отрезка
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Поиск
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 486 1–20 | 21–40 | 41–60 | 61–80 | 81–100 | 101–120 | 121–140 | 141–160 …
Добавить в вариант
Найдите наименьшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке [0; 6].
Найдите наименьшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Всего: 486 1–20 | 21–40 | 41–60 | 61–80 | 81–100 | 101–120 | 121–140 | 141–160 …
СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий.
Исследование показательных и логарифмических функций
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 11 № 26714
Найдите наименьшее значение функции на отрезке [−2,5; 0].
Аналоги к заданию № 26714: 3847 71037 3849 3851 3853 3855 3857 3859 3861 3863 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.2.1 Монотонность функции. Промежутки возрастания и убывания, 3.2.5 Точки экстремума функции, 3.2.6 Наибольшее и наименьшее значения функции, 4.2.1 Применение производной к исследованию функций и построению графиков, Наименьшее (наибольшее) значение функции во внутренней точке отрезка
Решение
·
·
Курс Д. Д. Гущина
·
1 комментарий · Сообщить об ошибке · Помощь
2
Тип 11 № 26715
Найдите наибольшее значение функции на отрезке [−4,5; 0].
Аналоги к заданию № 26715: 3865 71087 3867 3869 3871 3873 3875 3877 3879 3881 … Все
Источник: Пробный ЕГЭ по математике, Санкт-Петербург, 19.03.2019. Вариант 2
Кодификатор ФИПИ/Решу ЕГЭ: 3.2.1 Монотонность функции. Промежутки возрастания и убывания, 3.2.5 Точки экстремума функции, 3.2.6 Наибольшее и наименьшее значения функции, 4.2.1 Применение производной к исследованию функций и построению графиков, Наименьшее (наибольшее) значение функции во внутренней точке отрезка
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
3
Тип 11 № 26716
Найдите наименьшее значение функции на отрезке
Аналоги к заданию № 26716: 3885 71137 549375 3887 3889 3891 3893 3895 3897 3899 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.2.1 Монотонность функции. Промежутки возрастания и убывания, 3.2.5 Точки экстремума функции, 3.2.6 Наибольшее и наименьшее значения функции, 4.2.1 Применение производной к исследованию функций и построению графиков, Наименьшее (наибольшее) значение функции во внутренней точке отрезка
Решение
·
·
Курс Д. Д. Гущина
·
1 комментарий · Сообщить об ошибке · Помощь
4
Тип 11 № 26717
Найдите наибольшее значение функции на отрезке
Аналоги к заданию № 26717: 3905 71187 3907 3909 3911 3913 3915 3917 3919 3921 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.2.1 Монотонность функции. Промежутки возрастания и убывания, 3.2.5 Точки экстремума функции, 3.2.6 Наибольшее и наименьшее значения функции, 4.2.1 Применение производной к исследованию функций и построению графиков, Наименьшее (наибольшее) значение функции во внутренней точке отрезка
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
5
Тип 11 № 26718
Найдите наименьшее значение функции на отрезке
Аналоги к заданию № 26718: 3925 71217 513682 3927 3929 3931 3933 3935 3937 3939 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.2.1 Монотонность функции. Промежутки возрастания и убывания, 3.2.5 Точки экстремума функции, 3.2.6 Наибольшее и наименьшее значения функции, 4.2.1 Применение производной к исследованию функций и построению графиков, Наименьшее (наибольшее) значение функции во внутренней точке отрезка
Решение
·
·
Курс Д. Д. Гущина
·
1 комментарий · Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.
Вот какие типы задач могут встретиться в этом задании:
Нахождение точек максимума и минимума функций
Исследование сложных функций
Нахождение наибольших и наименьших значений функций на отрезке
Нахождение точек максимума и минимума функций
1. Найдите точку максимума функции
Найдем производную функции.
Приравняем производную к нулю. Получим:
Исследуем знаки производной.
В точке производная
меняет знак с «плюса» на «минус». Значит,
— точка максимума функции
Ответ: 17.
2. Найдите точку минимума функции
Найдем производную функции.
Приравняем производную к нулю.
Определим знаки производной.
В точке производная
меняет знак с «минуса» на «плюс». Значит,
— точка минимума функции
Ответ: 1.
Исследование сложных функций
3. Найдите точку максимума функции
Перед нами сложная функция Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.
Так как функция монотонно возрастает, точка максимума функции
будет при том же
, что и точка максимума функции
А ее найти легко.
при
. В точке
производная
меняет знак с «плюса» на «минус». Значит,
— точка максимума функции
.
Заметим, что точку максимума функции можно найти и без производной.
Графиком функции является парабола ветвями вниз, и наибольшее значение
достигается в вершине параболы, то есть при
Ответ: — 4.
4. Найдите абсциссу точки максимума функции
Напомним, что абсцисса — это координата по
Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.
Так как функция монотонно возрастает, точка максимума функции
является и точкой максимума функции
Это вершина квадратичной параболы
Нахождение наибольших и наименьших значений функций на отрезке
5. Найдите наибольшее значение функции на отрезке
Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.
Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.
Найдем знаки производной.
В точке производная равна нулю и меняет знак с «+» на «-«. Значит, x = — 2 — точка максимума функции
. Поскольку при
функция
убывает,
В этой задаче значение функции на концах отрезка искать не нужно.
Ответ: 12.
6. Найдите наименьшее значение функции на отрезке
Найдем производную функции и приравняем ее к нулю.
при
Найдем знаки производной.
Точка — точка минимума функции
. Точка
не лежит на отрезке
Поэтому
и
Значит, наименьшее значение функции на отрезке
достигается при
Найдем это значение.
Ответ: -11.
7. Найдите наименьшее значение функции на отрезке
Иногда перед тем, как взять производную, формулу функции полезно упростить.
Мы применили формулу для логарифма произведения. при
Если то
Если
, то
Значит, — точка минимума функции
. В этой точке и достигается наименьшее значение функции на отрезке
Ответ: 4.
8. Найдите наибольшее значение функции на отрезке
Найдем производную функции
Приравняем производную к нулю:
. Поскольку
если
Найдем знаки производной на отрезке
При знак производной меняется с «плюса» на «минус». Значит,
— точка максимума функции
Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при и
Мы нашли, что
Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.
Ответ: 4.
9. Найдите наименьшее значение функции на отрезке [0;2].
Снова сложная функция. Запишем полезные формулы:
Найдем производную функции
если
Тогда
При
знак производной меняется с «минуса» на «плюс». Значит,
— точка минимума функции
Ответ: -7.
10. Найдите наибольшее значение функции на отрезке
Как всегда, возьмем производную функции и приравняем ее к нулю.
По условию, . На этом отрезке условие
выполняется только для
Найдем знаки производной слева и справа от точки
В точке производная функции меняет знак с «плюса» на «минус». Значит, точка
— точка максимума функции
. Других точек экстремума на отрезке
функция не имеет, и наибольшее значение функции
на отрезке
достигается при
Ответ: 12.
11.Найдите наименьшее значение функции на отрезке
Найдем производную функции и приравняем ее к нулю. — нет решений.
Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.
Поскольку , получим, что
для всех
, и функция
монотонно возрастает при
Значит, наименьшее свое значение функция принимает в левом конце отрезка , то есть при
Ответ: 6
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 11 Профильного ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
1. Элементарные функции
2. Применение формул производной произведения и частного
| 2.1 | Найдите точку минимума функции y=(3-x)cdot e^{3-x}. | Смотреть видеоразбор |
| 2.2 | Найдите точку максимума функции y=(x^2-10x+10)cdot e^{5-x}. | Смотреть видеоразбор |
| 2.3 | Найдите наименьшее значение функции y=(x-1)e^x на отрезке [-1;1]. | Смотреть видеоразбор |
| 2.4 | Найдите наибольшее значение функции y=(10-x)sqrt{x+2} на отрезке [-1; 7]. | Смотреть видеоразбор |
| 2.5 | Найдите наименьшее значение функции y=2xsqrt{x}-9x+11 на отрезке [2; 9]. | Смотреть видеоразбор |
| 2.6 | Найдите наибольшее значение функции y=(x-2)^2(x-4)+5 на отрезке [1; 3]. | Смотреть видеоразбор |
| 2.7 | Найдите точку максимума функции y=(x+5)e^{5-x}. | Смотреть видеоразбор |
| 2.8 | Найдите точку минимума функции y=(10-x)e^{10-x}. | Смотреть видеоразбор |
| 2.9 | Найдите наименьшее значение функции y=x^2+frac{25+x^2-x^3}{x} на отрезке [1; 10]. | Смотреть видеоразбор |
3. Применение формулы производной сложной функции
4. Тригонометрические функции
| 4.1 | Найдите наибольшее значение функции y=8x-4tg;x-2pi+2 на отрезке [-frac{pi}{3}; frac{pi}{3}]. | Смотреть видеоразбор |
| 4.2 | Найдите наименьшее значение функции y=4sin{x}+3cos{x} на отрезке [0; 7]. | Смотреть видеоразбор |
| 4.3 | Найдите наибольшее значение функции y=2cos{x}-frac{18}{pi}x+4 на отрезке [-frac{2pi}{3}; 0]. | Смотреть видеоразбор |
| 4.4 | Найдите наименьшее значение функции y=5sin{x}+frac{24}{pi}x+6 на отрезке [-frac{5pi}{6}; 0]. | Смотреть видеоразбор |
| 4.5 | Найдите наибольшее значение функции y=3tg{x}-3x+5 на отрезке [-frac{pi}{4}; 0]. | Смотреть видеоразбор |
| 4.6 | Найдите наименьшее значение функции y=3cos{x}-frac{48}{pi}x+19 на отрезке [-frac{2pi}{3}; 0]. | Смотреть видеоразбор |
| 4.7 | Найдите наименьшее значение функции f(x)=sin{x}+sqrt{1+sin^2{x}}. | Смотреть видеоразбор |
| 4.8 | Найдите наибольшее значение функции y=33x-30sin{x}+29 на отрезке [-frac{pi}{2}; 0]. | Смотреть видеоразбор |
| 4.9 | Найдите точку максимума функции y=(2x-3)cos{x}-2sin{x}+5, принадлежащую промежутку (0; frac{pi}{2}). | Смотреть видеоразбор |
| 4.10 | Найдите точку максимума функции y=(2x-1)cos{x}-2sin{x}+5, на промежутке (0; frac{pi}{2}). | Смотреть видеоразбор |
| 4.11 | Найдите наибольшее значение функции y=2sin{x}-frac{36}{pi}x+9 на отрезке [-frac{5pi}{6}; 0]. | Смотреть видеоразбор |
| 4.12 | Найдите наибольшее значение функции y=7sqrt{2}cos{x}+7x-frac{7pi}{4}+4 на отрезке [0; frac{pi}{2}]. | Смотреть видеоразбор |
| 4.13 | Найдите наибольшее значение функции y=12cos{x}+6sqrt{3}x-2sqrt{3}pi+6 на отрезке [0; frac{pi}{2}]. | Смотреть видеоразбор |
| 4.14 | Найдите наибольшее значение функции y=12tg;x -12x+3pi-7 на отрезке [-frac{pi}{4}; frac{pi}{4}]. | Смотреть видеоразбор |
| 4.15 | Найдите наименьшее значение функции y=6cos{x}+frac{24x}{pi}+5 на промежутке [-frac{2pi}{3}; 0]. | Смотреть видеоразбор |
| 4.16 | Найдите наименьшее значение функции y=3+frac{5pi}{4}-5x-5sqrt{2}cos{x} на отрезке [0; frac{pi}{2}]. | Смотреть видеоразбор |
| 4.17 | Найдите наименьшее значение функции y=5cos{x}-6x+4 на отрезке [-frac{3pi}{2}; 0]. | Смотреть видеоразбор |
| 4.18 | Найдите наибольшее значение функции y=15x-3sin{x}+5 на отрезке [-frac{pi}{2}; 0]. | Смотреть видеоразбор |
| 4.19 | Найдите наименьшее значение функции y=9cos{x}+14x+7 на отрезке [0; frac{3pi}{2}]. | Смотреть видеоразбор |
| 4.20 | Найдите наименьшее значение функции y=7sin{x}-8x+9 на отрезке [-frac{3pi}{2}; 0]. | Смотреть видеоразбор |
| 4.21 | Найдите наименьшее значение функции y=6cos{x}+frac{24}{pi}x+5 на отрезке [-frac{2pi}{3}; 0]. | Смотреть видеоразбор |
| 4.22 | Найдите наибольшее значение функции y=10sin{x}-frac{36}{pi}x+7 на отрезке [-frac{5pi}{6}; 0]. | Смотреть видеоразбор |
5. Логарифмическая и показательная функции
| 5.1 | Найдите наименьшее значение функции y=3x-ln(x+3)^3 на отрезке [-2,5; 0]. | Смотреть видеоразбор |
| 5.2 | Найдите наименьшее значение функции y=9x-ln(9x)+3 на отрезке [frac{1}{18}; frac{5}{18}]. | Смотреть видеоразбор |
| 5.3 | Найдите наибольшее значение функции y=2x^2-13x+9cdot ln{x}+8 на отрезке [frac{13}{14}; frac{15}{14}]. | Смотреть видеоразбор |
| 5.4 | Найдите наименьшее значение функции y=5x-ln(x+5)^5 на отрезке [-4,5; 1]. | Смотреть видеоразбор |
| 5.5 | Найдите наименьшее значение функции y=7x-ln(x-2)^7 на отрезке [-1,5; 0]. | Смотреть видеоразбор |
| 5.6 | Найдите точку максимума функции y=ln(x+4)^2+2x+7. | Смотреть видеоразбор |
| 5.7 | Найдите наименьшее значение функции y=log_{sqrt{3}}(x-4sqrt{x-2}+5) на отрезке [5; 10]. | Смотреть видеоразбор |
| 5.8 | Найдите наименьшее значение функции y=4^x-2^{x+4}+100. | Смотреть видеоразбор |
6. Функции, в которых присутствует квадратичная в виде «вложенной»
| 6.1 | Найдите наименьшее значение функции y=2^{x^2+100x+2503} | Смотреть видеоразбор |
| 6.2 | Найдите наибольшее значение функции y=5^{-3x^2+18x-24}. | Смотреть видеоразбор |
| 6.3 | Найдите точку максимума функции y=-sqrt{x^2-8x+17}. | Смотреть видеоразбор |
| 6.4 | Найдите наибольшее значение функции y=3^{-7-6x-x^2}. | Смотреть видеоразбор |
| 6.5 | Найдите наибольшее значение функции y=log_5(4-2x-x^2)+3. | Смотреть видеоразбор |
| 6.6 | Найдите точку максимума функции y=sqrt{4-4x-x^2}. | Смотреть видеоразбор |
7. Задачи на первообразную (не входят в ЕГЭ этого года)
| 7.1 | Найдите первообразную F(x) для функции f(x)=frac{3x+2}{5}, если F(4)=5. В ответе укажите значение F(1). | Смотреть видеоразбор |
| 7.2 | Наименьшее значение первообразной F(x) для функции f(x)=x^2−2x−3 на отрезке [0;6] равно −9. Найдите наибольшее значение первообразной на этом отрезке. | Смотреть видеоразбор |
| 7.3 | Наименьшее значение первообразной F(x) для функции f(x)=x^2-2x-3 на отрезке [0; 6] равно −9. Найдите наибольшее значение первообразной на этом отрезке. | Смотреть видеоразбор |
| 7.4 | Найдите первообразную F(x) для функции f(x)=frac{3x+2}{5}, если F(4)=5. В ответе укажите значение F(1). | Смотреть видеоразбор |
| 7.5 | Один из двух нулей первообразной F(x) для функции f(x)=5x-1 равен -3. Найдите второй нуль. | Смотреть видеоразбор |
Задача 1. Найдите точку максимума функции
Решение: + показать
Задача 2. Найдите точку минимума функции
Решение: + показать
Задача 3. Найдите наименьшее значение функции на отрезке
.
Решение: + показать
Задача 4. Найдите наибольшее значение функции на отрезке
Решение: + показать
Задача 5. Найдите наибольшее значение функции на отрезке
Решение: + показать
Задача 6. Найдите наибольшее значение функции на отрезке
Решение: + показать
Задача 7. Найдите точку максимума функции
Решение: + показать
Задача 8. Найдите наибольшее значение функции на отрезке
Решение: + показать
Задача 9. Найдите точку минимума функции .
Решение: + показать
Задача 10. Найдите наименьшее значение функции на
Решение: + показать
Задача 11. Найдите точку максимума функции
Решение: + показать
Задача 12. Найдите точку минимума функции
Решение: + показать
Задача 13. Найдите точку максимума функции
Решение: + показать
Задача 14. Найдите наименьшее значение функции на отрезке
.
Решение: + показать
Задача 15. Найдите наибольшее значение функции на отрезке
Решение: + показать
Задача 16. Найдите наименьшее значение функции на отрезке
Решение: + показать
Задача 17. Найдите наименьшее значение функции на отрезке
Решение: + показать
Задача 18. Найдите наименьшее значение функции на отрезке
.
Решение: + показать
Задача 19. Найдите наибольшее значение функции на отрезке
Решение: + показать
Задача 20. Найдите наименьшее значение функции на отрезке
Решение: + показать
Задача 21. Найдите наибольшее значение функции на отрезке
.
Решение: + показать
Задача 22. Найдите наименьшее значение функции на отрезке
Решение: + показать
Задача 23. Найдите наименьшее значение функции на отрезке
Решение: + показать
Задача 24. Найдите точку минимума функции принадлежащую промежутку
.
Решение: + показать
* Замечание. Важно!
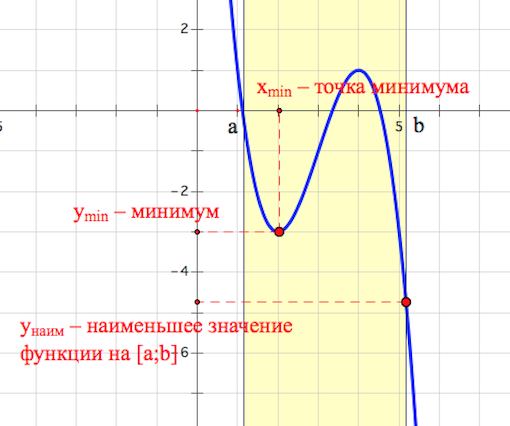
Не следует считать (могло сложиться такое мнение при разборе примеров выше), что наименьшее (наибольшее) значение функции на отрезке совпадает с минимумом (максимумом) на отрезке!
Например, на рисунке ниже наименьшее значение функции на отрезке достигается на конце отрезка
, а именно, в точке
.
То есть, вообще говоря, при нахождении наименьшего значения функции на отрезке следует выбрать наименьшую из величин:
1) (их может быть несколько) из рассматриваемого отрезка
2) ,
При нахождении наибольшего значения функции на отрезке следует выбрать большую из величин:
1) (их может быть несколько) из рассматриваемого отрезка
2) ,
Но, если, например, на рассматриваемом отрезке функция имеет только один экстремум – минимум и мы ищем наименьшее значение, то отпадает необходимость находить значения функции на концах отрезка.
Аналогично в случае с нахождением наибольшего значения функции на отрезке, на котором содержится только один экстремум – максимум.
В случае же, когда на отрезке рассматриваемом функция не имеет экстремумов, то для нахождения наибольшего/наименьшего значений требуется лишь сравнить эти самые значения функции на концах отрезка и взять наибольшее/наименьшее из них.
Вы можете пройти тест “Исследование функции при помощи производной”
За это задание ты можешь получить 1 балл. На решение дается около 10 минут. Уровень сложности: повышенный.
Средний процент выполнения: 60.8%
Ответом к заданию 11 по математике (профильной) может быть целое число или конечная десятичная дробь.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
Найдите наименьшее значение функции $y=-2ln(x+3)^5+10x$ на отрезке $[-2{,}5 ;-1]$.
Решение
Областью определения функции является интервал $(-3; +∞)$, на котором она дифференцируема. Отрезок $[-2.5; -1]$ принадлежит области определения.
Отметим, что по свойству логарифмов $ln(x + 3)^5 = 5 ln(x + 3)$, поэтому заданная функция имеет вид $y = -10 ln(x + 3) + 10x$.
1. Находим $y′$, пользуясь правилами дифференцирования и формулами производной степенной и логарифмической функций:
$y′ = {-10}/{x+3} + 10 = {-10 + 10x + 30}/{x + 3} = {10 x + 20}/{x + 3} = {10(x + 2)}/{x + 3}, y′ = {10(x + 2)}/{x + 3}$.
2. Заметим, что $y′ = 0$ при $x = -2$. Получаем единственную стационарную точку. $-2 ∈ [-2.5; -1]$.
3. Так как $x + 3 > 0$ в области определения, то $y′ < 0$ при $-2.5 < x < -2, y′ > 0$ при $-2 < x < -1$. Производная меняет знак с «минуса» на «плюс» при переходе через точку $x = -2$. Следовательно, эта точка является точкой минимума и в ней функция достигает наименьшего значения.
$y(-2) = -10 ln(-2 + 3) + 10 · (-2) = -20$, так как $ln 1 = 0$.
Ответ: -20
Задача 2
Найдите наибольшее значение функции $y=ln(x+7)^3-3x$ на отрезке $[-6{,}5 ;-4]$.
Решение
Областью определения функции является промежуток $(-7;+∞ )$, на котором она дифференцируема
Отрезок $[-6{,}5 ;-4]$ принадлежит области определения
Отметим, что по свойству логарифмов в области определения функции выполняется равенство $ln(x+7)^3=3ln(x+7)$, поэтому заданная функция может быть представлена в виде $y=3ln(x+7)-3x$
1. Находим $y^′ $, пользуясь правилами дифференцирования и формулами производной степенной и логарифмической функций: $y^′={3} / {x+7}-3={3-3x-21} / {x+7}={-3x-18} / {x+7}={-3(x+6)} / {x+7}$, $y^′={-3(x+6)} / {x+7}$
2. Заметим, что $y^′ =0$ при $x=-6$. Получаем единственную стационарную точку
3. Так как $x+7>0$ в области определения, то $y^′ >0$ при $x∈(-6,5;-6)$
$y^′ <0$ при $x∈(-6;-4)$. Производная меняет знак с «плюса» на «минус» при переходе через точку $x=-6$
Следовательно, эта точка является точкой максимума и в ней функция достигает наибольшего значения
$y(-6)=3ln(-6+7)-3⋅ (-6)=18$, так как $ln 1=0$.
Ответ: 18
Задача 3
Найдите наибольшее значение функции $y=ln(4-2x)+2x-7$ на отрезке $[0;1{,}7]$.
Решение
Областью определения этой функции будет интервал $(-∞; 2)$, в каждой точке которого функция дифференцируема, причём отрезок $[0; 1.7]$ целиком лежит в области определения.
1. Находим $y′$, пользуясь правилами дифференцирования, формулами производной сложной и логарифмической функций:
$y′ = {1}/{4 — 2x} · (4 — 2x)′ + (2x)′ — (7)’ = {-2}/{4-2x} + 2 = {2x — 3}/{x — 2}$.
$y′ = {2x — 3}/{x — 2}$.
2. Находим стационарные точки из условия $y′ = 0. {2x — 3}/{x — 2} = 0,$
$2x — 3 = 0,$
$x = {3}/{2}$.
Получили одну стационарную точку $x = {3}/{2}$, которая принадлежит промежутку $(0; 1.7)$.
3. Знак производной совпадает со знаком квадратного трёхчлена $(2x — 3)(x — 2) = 2x^2 — 7x + 6$. Его графиком является парабола, ветви которой направлены вверх, и корнями являются числа ${3}/{2}$ и $2$. Поэтому при $0 < x < {3}/{2}$ его знак «плюс», а при ${3}/{2} < x < 1.7$ знак «минус».
При переходе через точку $x = {3}/{2}$ производная меняет знак с «плюса» на «минус». Значит, $x = {3}/{2}$ является точкой максимума и в ней достигается наибольшее значение (так как других точек экстремума нет).
4. $y({3}/{2}) = ln (4 — 2 · {3}/{2}) + 2 · {3}/{2} — 7 = ln 1 + 3 — 7 = -4$.
Ответ: -4
Задача 4
Найдите точку максимума функции $y=-8√ x+12ln(x-4)-11$.
Решение
Областью определения этой функции является интервал $(4; +∞)$, на котором функция дифференцируема. Найдём стационарные точки на указанном интервале и выберем ту из них, в которой производная меняет знак с «плюса» на «минус».
1. Находим $y′$, пользуясь правилами дифференцирования и формулами производной степенной и логарифмической функций.
$y′ = {-8}/{2√x} + {12}/{x — 4} = {-8(x — 4) + 24√x}/{2√x(x — 4)} = {-4x + 16 + 12√x}/{√x(x — 4)}$.
2. Решаем уравнение $y′ = 0, -4x + 16 + 12√x = 0$.
Сделаем замену $√x = t$ $(t > 2)$. Получим уравнение $-4t^2 + 12t + 16 = 0; t^2 — 3t — 4 = 0$. По формуле корней квадратного уравнения получаем:
$t_{1,2} = {3± √{9 + 16}}/{2} = {3±2}/{5}$,
$t_1 = -1, t_2 = 4$.
$t = -1$ не удовлетворяет условию $t > 2$.
Уравнение $√x = 4$ имеет решение $x = 16$. Получили единственную стационарную точку $x = 16$, принадлежащую промежутку $(4; +∞)$.
При $x > 4$ знак производной совпадает со знаком функции $y_1 = -4x+16+12√x$. Для определения её знака на интервале $(4; +∞)$ достаточно найти её знак в двух точках, одна из которых меньше, чем $x = 16$, и другая, больше, чем $x = 16$.
$y_1 (9) = -4 · 9 + 16 + 12√9 = -36 + 16 + 36 > 0$, а $y_1 (25) = -4 · 25 + 16 + 12√25 = -100 + 16 + 60 < 0$.
3. Получаем, что производная меняет знак с «плюса» на «минус» при переходе через единственную экстремальную точку $x = 16$. Поэтому точка $x = 16$ будет точкой максимума.
Ответ: 16
Задача 5
Найдите точку максимума функции $y=2ln x-√ {x}-17$.
Решение
Областью определения этой функции является интервал $(0; +∞)$, в каждой точке которого она дифференцируема. Найдём стационарные точки в области определения и выберем ту из них, проходя через которую, производная меняет знак с «плюса» на «минус».
1. Находим $y′$, пользуясь правилами дифференцирования, формулами производных степенной и логарифмической функций:
$y′ = {2}/{x} — {1}/{2√x} = {4 -√x}/{2x}$.
2. Решаем уравнение $y′ = 0; 4 — √x = 0. √x = 4, x = 16$.
Получили одну стационарную точку.
3. Так как $x > 0$ и $√x > 0$ в области определения, то знак производной совпадает со знаком функции $y_1 = 4 — √x$. Она обращается в ноль в единственной точке $x = 16$.
Находим знак этой функции при $x < 16$ и $x > 16$. Для этого достаточно найти её значения хотя бы в одной точке каждого из указанных промежутков: $y_1 (1) = 4 — √1 = 3 > 0$, а $y_1 (25) = 4 — √{25} = -1 < 0$
Тем самым, производная меняет знак с «плюса» на «минус» при переходе через точку $x = 16$, которая и будет точкой максимума.
Ответ: 16
Задача 6
Найдите наибольшее значение функции $y=√ {-2log_{0{,}5} (5x+1)}$ на отрезке $[12{,}6;51]$.
Решение
Найдём без применения производной, какие значения принимает функция на отрезке $[12.6; 51]$ и выберем из них наибольшее.
1. Пусть $x$ – произвольное число из отрезка $[12.6; 51]$. Тогда $12.6 ≤ x ≤ 51$. Отсюда по свойствам неравенств получаем: $63 ≤ 5x ≤ 255, 64 ≤ 5x + 1 ≤ 256$.
2. Из предыдущего неравенства, по свойству логарифмов с основанием $0.5$, меньшим $1$, получаем $log_{0.5} 64 ≥ log_{0.5}(5x + 1) ≥ log_{0.5}256$. Но, $log_{0.5}64 = log_{{1}/{2}}64 = log_{{1}/{2}}2^6 = log_{{1}/{2}}(({1}/{2})^{-1})^6 = log_{{1}/{2}}({1}/{2})^{-6} = -6$.
Аналогично, $log_{0.5}256 = -8$. Поэтому $-8 ≤ log_{0.5}(5x + 1) ≤ -6, 6 ≤- log_{0.5}(5x + 1) ≤ 8, 12 ≤ -2 log_{0.5}(5x + 1) ≤ 16$.
Теперь, по свойству квадратного корня получаем, $√12 ≤ √{-2log_{0.5}(5x + 1)} ≤ √{16} = 4$.
Но $√{-2 log_{0.5}(5x + 1)} = y$, поэтому $√{12} ≤ y ≤ 4$.
3. Таким образом, функция определена на всём отрезке $[12.6; 51]$ наибольшим значением является $4$ и получается это значение при $x = 51$.
Ответ: 4
Задача 7
Найдите точку минимума функции $y=x^2-21x+6+55ln x$.
Решение
Областью определения функции является промежуток $(0; +∞)$, на котором она дифференцируема. Найдём стационарные точки и выберем ту из них, при переходе через которую, производная меняет знак с «минуса» на «плюс».
1. Находим $y′$, пользуясь правилами дифференцирования и формулами производной логарифмической и степенной функций.
$y′ = 2x − 21 + {55}/{x}, y′ = {2x^2-21x+55}/{x}$.
2. Решаем уравнение $y′ = 0; 2x^2 -21x +55 = 0. x_{1,2} = {21 ± √{441 — 440}}/{4} = {21 ± 1}/{4}. x_1 = 5, x_2 = 5.5$. Получаем две стационарные точки.
3. Знак производной совпадает со знаком квадратного трёхчлена $2x^2 -21x+55$. Графиком этого трёхчлена является парабола, ветви которой направлены вверх и корнями являются числа $x_1=5$ и $x_2=5.5$.
Поэтому при $x < 5$ производная имеет знак «плюс», знак «минус» при $5 < x < 5.5$, и знак «плюс» при $x > 5.5$.
| (0;5) | 5 | (5; 5.5) | 5.5 | (5.5;+∞) | |
| y′ | + | 0 | — | 0 | + |
| y | ↗ | ↘ | ↗ |
При переходе через точку $5.5$ производная меняет знак с «минуса» на «плюс». Поэтому эта точка и будет точкой минимума.
Ответ: 5.5
Задача 8
Найдите точку максимума функции $y=x^2-11x-17+15ln x$.
Решение
Областью определения функции является промежуток $(0; +∞)$, на котором она дифференцируема. Найдём стационарные точки и выберем ту из них, при переходе через которую, производная меняет знак с «плюса» на «минус».
1. Находим $y′$, пользуясь правилами дифференцирования и формулами производной логарифмической и степенной функций.
$y′ = 2x − 11 + {15}/{x} = {2x^2-11x+15}/{x}, y′ = {2x^2-11x+15}/{x}$.
2. Решаем уравнение $y′ = 0; 2x^2- 11x +15 = 0. x_{1,2} = {11 ± √{121 — 120}}/{4} = {11 ± 1}/{4}. x_1 = 2.5, x_2 = 3$. Получаем две стационарные точки.
3. Знак производной совпадает со знаком квадратного трёхчлена $2x^2 -11x+15$. Графиком этого трёхчлена является парабола, ветви которой направлены вверх и корнями являются числа $x_1=2.5$ и $x_2=3$.
Поэтому при $x < 2.5$ производная имеет знак «плюс», знак «минус» при $2.5 < x < 3$, и знак «плюс» при $x > 3$.
| (0;2.5) | 2.5 | (2.5; 3) | 3 | (3;+∞) | |
| y′ | + | 0 | — | 0 | + |
| y | ↗ | ↘ | ↗ |
При переходе через точку $2.5$ производная меняет знак с «плюса» на «минус». Поэтому эта точка и будет точкой максимума.
Ответ: 2.5
Задача 9
Найдите точку максимума функции $y=(5x^2-3x-3)e^{x+5}$.
Решение
Заметим, что заданная функция определена и дифференцируема при любом значении $x$. Найдём стационарные точки и выберем ту из них, при переходе через которую, производная меняет знак с «плюса» на «минус».
1. Находим $y′$, пользуясь правилами дифференцирования, формулой производной произведения двух функций, и производной степенной и показательной функции:
$y′ = (10x − 3)e^{x+5} + (5x^2 − 3x − 3)e^{x+5} = e^{x+5}(5x^2 + 7x − 6), y′ = e^{x+5}(5x^2 + 7x − 6)$.
2. Решаем уравнение $y′ = 0$. Так как $e^{x+5} > 0$, то $5x^2 + 7x − 6 = 0. x_{1,2} = {−7 ± √{49 + 120}}/{10} = {−7 ± 13}/{10}. x_1 = −2, x_2 = 0.6$. Получаем две стационарные точки.
3. Знак производной совпадает со знаком квадратного трёхчлена $5x^2 +7x-6$. Графиком этого трёхчлена является парабола, ветви которой направлены вверх и корнями являются числа $x_1=-2$ и $x_2=0.6$.
Поэтому при $x < −2$ производная имеет знак «плюс», знак «минус» при $−2 < x < 0.6$, и знак «плюс» при $x > 0.6$.
| (-∞;-2) | -2 | (-2; 0.6) | 0.6 | (0.6;+∞) | |
| y′ | + | 0 | — | 0 | + |
| y | ↗ | ↘ | ↗ |
При переходе через точку $x_1 = −2$ производная меняет знак с «плюса» на «минус». Поэтому эта точка и будет точкой максимума.
Ответ: -2
Задача 10
Найдите наименьшее значение функции $y=-4x-4cos x+5$ на отрезке $[- {π} ;0]$.
Решение
Заметим, что заданная функция непрерывна на отрезке $[-π; 0]$ и дифференцируема на интервале $(-π; 0)$. Наименьшее её значение на отрезке $[-π; 0]$ равно наименьшему из всех значений функции в стационарных точках интервала $(-π; 0)$ и концах отрезка $[-π; 0]$.
1. Находим $y′$, пользуясь правилами дифференцирования и формулами производных тригонометрических функций:
$y′ = -4 + 4 sin x = -4(1 — sin x), y′ = -4(1 — sin x)$.
2. Заметим, что $sin x < 0$ на интервале $(-π; 0)$. Поэтому $1 — sin x > 1$ и $-4(1 — sin x) < 0$. Следовательно, на нём $y′ < 0$ и функция $y=-4x — 4 cos x + 5$ убывает.
3. Наименьшее значение функции будет на правом конце промежутка, то есть в точке $x = 0$.
$y(0) = -4 · 0 — 4 cos 0 + 5 = -4 + 5 = 1$.
Ответ: 1
Задача 11
Найдите точку минимума функции $y=(12-5x)sin x-5cos x-10$, принадлежащую интервалу $({π} / {2};π)$.
Решение
Отметим, что функция дифференцируема на заданном интервале. Найдём стационарные точки на указанном интервале и выберем ту из них, в которой производная меняет знак с «минуса» на «плюс». 1. Находим $y^′$, пользуясь правилами дифференцирования, формулами производной произведения функций и производной линейной и тригонометрических функций. $y^′=(12-5x)^′⋅ sin x+(sin x)^′⋅(12-5x)+5sin x$, $y^′=-5sin x+cos x(12-5x)+5sin x=-cos x(5x-12)$, $y^′=-cos x(5x-12)$. 2. Решаем уравнение $y^′=0$. Так как $cos x<0$ на заданном интервале, то $5x-12=0$, $x=2{,}4$. ${π} / {2≈} 1{,} 57$, а $π ≈ 3{,} 14$, поэтому $2{,}4∈ ({π} / {2};π)$. Получили одну стационарную точку на заданном интервале. 3. $cos x<0$ на заданном интервале, поэтому знак производной совпадает со знаком функции $y_1=5x-12$. Эта функция является возрастающей, поэтому она имеет знак «минус» до точки $x=2{,}4$ и знак «плюс» после неё. Тем самым, точка $x=2{,}4$ будет точкой минимума.
Ответ: 2.4
Задача 12
Найдите точку минимума функции $y={x-8} / {x^2+225}$.
Решение
Заметим, что заданная функция определена и дифференцируема при любом значении $x$. Найдём стационарные точки и выберем ту из них, при переходе через которую, производная меняет знак с «минуса» на «плюс».
1. Находим $y′$, пользуясь формулой производной частного двух функций и правилом дифференцирования степенной функции:
$y′ = {(x-8)′·(x^2+225)-(x^2+225)′·(x-8)}/{(x^2+225)^2}$.
$y′ = {x^2+225-2x·(x-8)}/{(x^2+225)^2}={x^2+225-2x^2+16x}/{(x^2+225)^2}$.
$y′ = {-x^2+16x+225}/{(x^2+225)^2}$.
2. Решаем уравнение $y′ = 0, -x^2 + 16x+225 = 0, x^2-16x-225=0, x_{1,2} = 8±√{64+225}=8±√{289}=8±17, x_1=-9, x_2=25$. Получаем две стационарные точки.
3. Знак производной совпадает со знаком квадратного трёхчлена $-x^2 +16x+225$. Графиком этого трёхчлена является парабола, ветви которой направлены вниз и корнями являются числа $-9$ и $25$.
Поэтому на промежутке $(-∞;-9)$ производная меньше нуля, на промежутке $(-9; 25)$ она больше нуля и на промежутке $(25;+∞)$ меньше нуля.
| (-∞;-9) | -9 | (-9; 25) | 25 | (25;+∞) | |
| y′ | — | + | — | ||
| y | ↘ | 0 | ↗ | 0 | ↘ |
Тем самым производная меняет знак с «минуса» на «плюс» при переходе через точку $x = -9$, которая и будет точкой минимума.
Ответ: -9
Задача 13
Найдите точку максимума функции $y={x-5} / {x^2+144}$.
Решение
Заметим, что заданная функция определена и дифференцируема при любом значении $x$. Найдём стационарные точки и выберем ту из них, при переходе через которую, производная меняет знак с «плюса» на «минус».
1. Находим $y′$, пользуясь формулой производной частного двух функций и правилом дифференцирования степенной функции:
$y′ = {(x-5)′·(x^2+144)-(x^2+144)′·(x-5)}/{(x^2+144)^2}$.
$y′ = {x^2+144-2x·(x-5)}/{(x^2+144)^2}={x^2+144-2x^2+10x}/{(x^2+144)^2}$.
$y′ = {-x^2+10x+144}/{(x^2+144)^2}$.
2. Решаем уравнение $y′ = 0, -x^2 + 10x+144 = 0, x^2-10x-144=0, x_{1,2} = 5±√{25+144}=5±√{169}=5±13, x_1=-8, x_2=18$. Получаем две стационарные точки.
3. Знак производной совпадает со знаком квадратного трёхчлена $-x^2 +10x+144$. Графиком этого трёхчлена является парабола, ветви которой направлены вниз и корнями являются числа $-8$ и $18$.
Поэтому на промежутке $(-∞;-8)$ производная меньше нуля, на промежутке $(-8; 18)$ она больше нуля и на промежутке $(18;+∞)$ меньше нуля.
| (-∞;-8) | -8 | (-8; 18) | 18 | (18;+∞) | |
| y′ | — | + | — | ||
| y | ↘ | 0 | ↗ | 0 | ↘ |
Тем самым производная меняет знак с «плюса» на «минус» при переходе через точку $x = 18$, которая и будет точкой максимума.
Ответ: 18
Задача 14
Найдите наименьшее значение функции $y={4x^2+256} / {x}$ на отрезке $[16;98]$.
Решение
Областью определения функции является множество $(-∞;0)∪ (0;+∞)$, в каждой точке которого функция дифференцируема
Промежуток $[16;98]$ содержится в области определения функции
1. Находим $y^′$, представив заданную функцию в виде $y=4x+{256} / {x}$
По правилам дифференцирования и по формуле производной степенной функции получаем: $y^′=4-{256} / {x^2}={4x^2-256} / {x^2}={4(x^2-64)} / {x^2}$, $y^′={4(x^2-64)} / {x^2}$
2. Решаем уравнение $ y^′=0 $, $ x^2-64=0 $, $ x_1=-8 $, $ x_2=8 $
Получаем две стационарные точки на множестве $(-∞;0)∪ (0;+∞)$, но ни одна из них не попадает на промежуток $[16;98]$. Значит, на заданном отрезке стационарных точек нет
3. Так как $x^2>0$ в области определения, то знак производной совпадает со знаком квадратного трёхчлена $ x^2-64 $. Поэтому $ y^′ >0 $ при $ x>8$, а функция $y={4x^2+256} / {x}$ на отрезке $[16;98]$ возрастает
Наименьшее значение она принимает в точке $x=16$
$y(16)=4⋅ 16+{256} / {16}=64+16=80$.
Ответ: 80
Задача 15
Найдите точку минимума функции $y={25x^2+25} / {x}$.
Решение
Областью определения функции является множество $(-∞; 0) ∪ (0;+∞)$, в каждой точке которого функция дифференцируема. Найдём стационарные точки и выберем ту из них, при переходе через которую, производная меняет знак с «минуса» на «плюс».
1. Находим $y′$, представив заданную функцию в виде $y = 25x+{25}/{x}$. По правилам дифференцирования и формуле производной степенной функции получаем: $y′ = 25 — {25}/{x^2} = {25x^2 — 25}/{x^2} = {25(x^2 — 1)}/{x^2}$.
2. Решаем уравнение $y′ = 0, x^2 — 1 = 0, x_1 = -1, x_2 = 1$. Получаем две стационарные точки.
3. Так как $x^2 > 0$ в области определения, то знак производной совпадает со знаком квадратного трёхчлена $x^2 -1$, корнями которого являются числа $-1$ и $1$. Поэтому $y′ > 0$ при $x < -1, y′ < 0$ при $-1 < x < 0, y′ < 0$ при $0 < x < 1$ и $y′ > 0$ при $x > 1$.
| (-∞;-1) | -1 | (-1; 0) | 0 | (0; 1) | 1 | (0;+∞) | |
| y′ | + | 0 | — | Не сущ. | — | 0 | + |
| y | ↗ | ↘ | ↘ | ↗ |
При переходе через точку $x = 1$ производная меняет знак с «минуса» на «плюс». Поэтому эта точка и будет точкой минимума.
Ответ: 1
Задача 16
Найдите наименьшее значение функции $y=x^5-5x^3-270x$ на отрезке $[0 ;5]$.
Решение
Заметим, что заданная функция определена и дифференцируема при любом значении $x$.
1. Находим $y′$, пользуясь правилами дифференцирования и формулой производной степенной функции: $y′ = 5x^4 — 15x^2 — 270$.
2. Решаем уравнение $y′ = 0$. Сделаем подстановку $x^2 = t (t ≥ 0)$, получим уравнение $5t^2 — 15t — 270 = 0$ или $t^2 — 3t — 54 = 0$.
$t_1 = -6, t_2 = 9$.
$t_1 = -6$ не удовлетворяет условию $t ≥ 0$. Уравнение $x^2 = 9$ имеет два корня $x_1 = -3, x_2 = 3$. На промежуток (0; 5) попадает лишь одно число $x = 3$. Получаем единственную стационарную точку.
3. Найдем знак производной на двух промежутках (0; 3) и (3; 5), на которые точка $x = 3$ разбивает интервал (0; 5). Для этого найдем значения производной в точке $x = 1$ из первого интервала, и в точке $x = 4$ из другого интервала.
$y′(1) = 5·1^4 — 15·1^2 — 270 = 5 — 15 — 270 < 0$,
$y′(4) = 5·4^4 — 15·4^2 — 270 = 1280- 240 — 270 > 0$.
Производная меняет знак с «минуса» на «плюс» при переходе через точку $x = 3$. Следовательно, эта точка является точкой минимума и в ней функция достигает наименьшего значения.
$y(3) = 3^5 — 5·3^3 — 270·3 = 243-135-810 = -702$.
Ответ: -702
Задача 17
Найдите наибольшее значение функции $y=√ {240-8x-x^2}$ на отрезке $[-18;10]$.
Решение
Преобразуем подкоренное выражение: $240-8x-x^2 = -(x^2+8x-240) = -((x+4)^2-16-240) = 256-(x+4)^2$. Поэтому $y = √{256 — (x + 4)^2}$.
Так как $(x + 4)^2 ≥ 0$, то $y$ принимает наибольшее значение, если $(x + 4)^2 = 0$, то есть при $x = -4$. Точка $x = -4$ принадлежит заданному промежутку [-18; 10]. Это наибольшее значение равно $√{256} = 16$.
Ответ: 16
Задача 18
Найдите наименьшее значение функции $y=√ {x^2+2x+122}$ на отрезке $[-50;150]$.
Решение
Дискриминант квадратного трёхчлена, расположенного под знаком квадратного корня, меньше нуля ($D = 4 — 488$), значит трёхчлен корней не имеет. Ветви параболы, являющейся графиком этого трёхчлена направлены вверх, абсцисса вершины равна $-1$, а ордината $121$. Поэтому $x^2+2x+122 > 0$ при любых x и исходная функция определена при любом значении x из промежутка [-50; 150].
При $-50 ≤ x ≤ -1$ функция $y = x^2 + 2x + 122$ убывает, а значит убывает и функция $y = √{x^2 + 2x + 122}$.
При $-1 ≤ x ≤ 150$ функция $y = x^2 + 2x + 122$ возрастает, а значит возрастает и функция $y = √{x^2 + 2x + 122}$.
Из сказанного следует, что в точке $x = -1$ функция $y = √{x^2 + 2x + 122}$ принимает наименьшее значение на указанном отрезке.
$y(-1) = √{121} = 11$.
Ответ: 11
Задача 19
Найдите точку максимума функции $y=√ {77+4x-x^2}$.
Решение
Дискриминант квадратного трёхчлена $-x^2+4x+77$, расположенного под знаком квадратного корня, больше нуля ($D = 16+308 = 324$), значит этот квадратный трёхчлен имеет два корня.
$x_{1,2} = {-2±√{4 + 77}}/{-1} = {-2±9}/{-1}, x_1 = -7, x_2 = 11$.
Ветви параболы, являющейся его графиком, направлены вниз, поэтому при $x∈[-7; 11]$ он принимает неотрицательные значения. Исходная функция определена и непрерывна на отрезке при любом значении $x ∈ [-7; 11]$, и дифференцируема на интервале (-7; 11).
Найдём стационарные точки на интервале (-7; 11) и выберем ту из них, в которой производная меняет знак с плюса на минус.
1. Находим $y′$, пользуясь правилами дифференцирования и формулой производной сложной функции.
$y′ = {1}/{2√{77 + 4x — x^2}}·(77 + 4x — x^2)′ = {-2x + 4}/{2√{77 + 4x — x^2}} = {-(x — 2)}/{√{77 + 4x — x^2}}, y′ = {-(x — 2)}/{√{77 + 4x — x^2}}$,
2. Решаем уравнение $y′ = 0, x — 2 = 0, x = 2$. Получаем одну стационарную точку.
3. Так как $√{77 + 4x — x^2} > 0$ на интервале (-7; 11), то знак производной совпадает со знаком выражения $-x +2$. Тогда $y′ > 0$ при $-x +2 > 0, x < 2; y′ < 0$ при $-x + 2 < 0, x> 2$.
Следовательно, при переходе через точку $x = 2$ производная меняет знак с плюса на минус. Поэтому эта точка и будет точкой максимума.
Ответ: 2
Задача 20
Найдите точку минимума функции $y=√ {x^2-12x+40}$.
Решение
Дискриминант квадратного трёхчлена, расположенного под знаком квадратного корня, меньше нуля ($D=144-160$), значит, уравнение $x^2-12x+40=0$ корней не имеет. Ветви параболы, являющейся графиком этого трёхчлена, направлены вверх, поэтому все его значения больше нуля. Функция определена и дифференцируема при любом значении $x$. Найдём стационарные точки и выберем ту из них, в которой производная меняет знак с «минуса» на «плюс».
1. Находим $y^′$, пользуясь правилами дифференцирования и формулой производной сложной функции.
$y^′={1} / {2√ {x^2-12x+40}}⋅ (x^2-12x+40)^′={2x-12} / {2√ {x^2-12x+40}}=$
$={x-6} / {√ {x^2-12x+40}}$
$y^′={x-6} / {√ {x^2-12x+40}}$.
2. Решаем уравнение $y^′=0$, $x-6=0$, $x=6$. Получаем одну стационарную точку.
3. Так как $√ {x^2-12x+40}>0$, то знак производной совпадает со знаком выражения $x-6$. Тогда $y’>0$ при $x-6>0$, $x>6$; $y'<0$ при $x-6<0$, $x<6$.
Следовательно, при переходе через точку $x=6$ производная меняет знак с «минуса» на «плюс». Поэтому эта точка и будет точкой минимума.
Ответ: 6