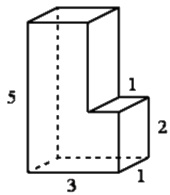
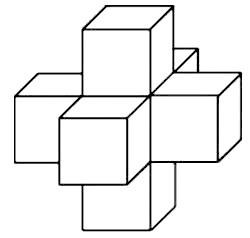
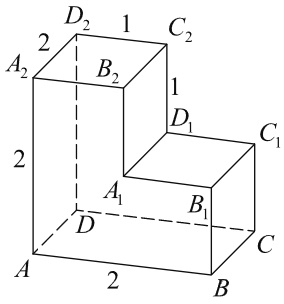
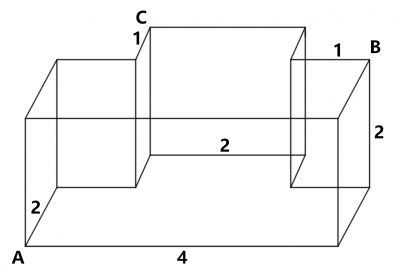
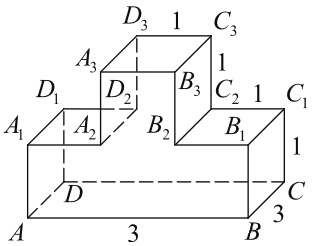
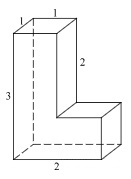
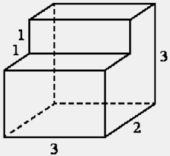
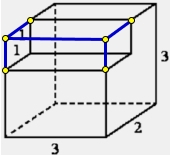
Найдите объём многогранника, изображённого на рисунке (все двугранные углы прямые).
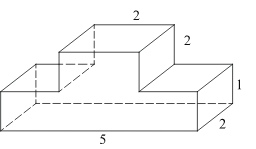
Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
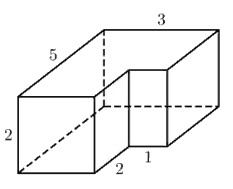
Деталь имеет форму изображённого на рисунке многогранника(все двугранные углы прямые). Числа на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Дайте объём в кубических сантиметрах.
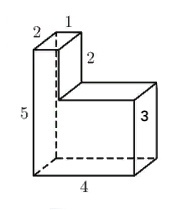
Найдите объём многогранника, изображённого на рисунке (все двугранные углы – прямые).
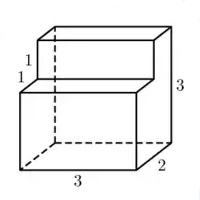
Найдите объём многогранника, изображённого на рисунке (все двугранные углы – прямые).
Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.
На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите тангенс угла B₂A₂C₂.
Найдите отношение квадратов длин отрезков AC и CB. Все двугранные углы многогранника прямые.
На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите квадрат расстояния между вершинами A и C₃.
Найдите площадь поверхности многогранника (все двугранные углы прямые).
Найдите объём многогранника, изображённого на рисунке (все двугранные углы прямые).
Источники: fipi, os.fipi.
Решение:
Найдём объём достроенного многогранника до параллелепипеда:
V1 = 3·2·3 = 18
Найдём объём кусочка многогранника параллелепипеда которым достроили:
V2 = 1·1·3 = 3
Найдём объём искомого многогранника:
V = V1 – V2 = 18 – 3 = 15
Ответ: 15.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 3
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
1. Нахождение объемов и площадей поверхности по готовым рисункам
| 1.1 | Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).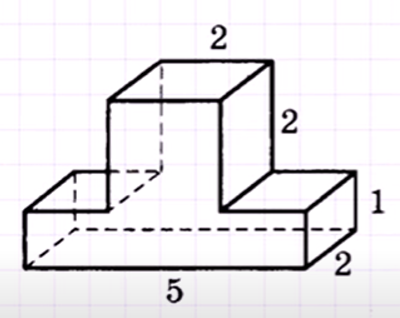 |
Смотреть видеоразбор |
| 1.2 | Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). |
Смотреть видеоразбор |
| 1.3 | Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). |
Смотреть видеоразбор |
| 1.4 | Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).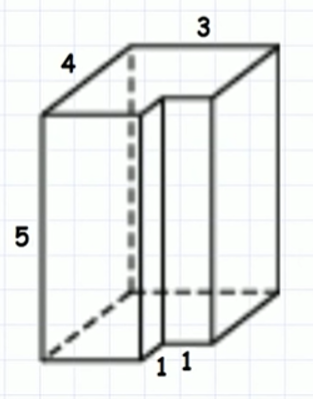 |
Смотреть видеоразбор |
| 1.5 | Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). |
Смотреть видеоразбор |
| 1.6 | Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).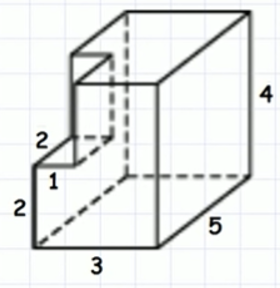 |
Смотреть видеоразбор |
2. Призма, пирамида
| 2.1 | В правильной четырехугольной пирамиде высота равна 3, боковое ребро равно 5. Найдите её объём |
Смотреть видеоразбор |
| 2.2 | В правильной шестиугольной пирамиде боковое ребро равно 17, а сторона основания равна 8. Найдите высоту пирамиды. |
Смотреть видеоразбор |
| 2.3 | Объем куба равен 126. Найдите объем четырехугольной пирамиды, основанием которой является грань, а вершиной — центр куба.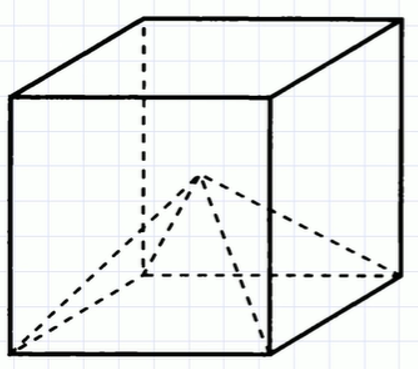 |
Смотреть видеоразбор |
| 2.4 | Найдите объем куба, если объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины, равен 21.
Другая формулировка условия: В кубе ABCDA_1B_1C_1D_1 точки E, F, E_1 и F_1 являются серединами ребер BC, DC, B_1C_1 и D_1C_1 соответственно. Объем призмы, отсекаемой от куба плоскостью EFF_1, равен 21. Найдите объем куба. |
Смотреть видеоразбор |
3. Цилиндр и конус
| 3.1 | Найдите площадь осевого сечения конуса, радиус основания которого равен 3, а образующая равна 5. |
Смотреть видеоразбор |
| 3.2 | В цилиндрический сосуд налили 600 кубических сантиметров воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,6 раза. Найдите объем детали. Ответ выразите в кубических сантиметрах. | Смотреть видеоразбор |
| 3.3 | Объём первого цилиндра равен 12. У второго цилиндра высота в три раза больше, а радиус основания в два раза меньше, чем у первого. Найдите объём второго цилиндра. |
Смотреть видеоразбор |
| 3.4 | Площадь боковой поверхности конуса равна 36pi, а площадь его осевого сечения рана 15sqrt{9}. Найдите косинус угла между образующей конуса и плоскостью его основания. |
Смотреть видеоразбор |
| 3.5 | Шар, объем которого равен pi, вписан в куб. Найдите объем куба |
Смотреть видеоразбор |
| 3.6 | Шар вписан в цилиндр объемом 42. Найдите объем шара. |
Смотреть видеоразбор |
| 3.7 | В сосуд в виде конуса налита жидкость до frac{1}{3} высоты. Объём налитой жидкости 16 мл. Сколько миллилитров жидкости нужно долить, чтобы наполнить сосуд доверху? |
Смотреть видеоразбор |
| 3.8 | Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности конуса равна 80. Найдите площадь боковой поверхности цилиндра. |
Смотреть видеоразбор |