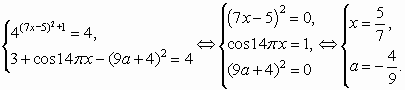Найдите область определения функции егэ

Исследование графика функции

На рисунке изображен график функции . Посмотрим, как исследовать функцию с помощью графика. Оказывается, глядя на график, можно узнать всё, что нас интересует, а именно:

• область определения функции;
• область значений функции;
• нули функции;
• промежутки возрастания и убывания;
• точки максимума и минимума;
• наибольшее и наименьшее значение функции на отрезке.

Уточним терминологию:

Абсцисса — это координата точки по горизонтали.
Ордината — координата по вертикали.
Ось абсцисс — горизонтальная ось, чаще всего называемая ось X.
Ось ординат — вертикальная ось, или ось Y.

Аргумент — независимая переменная, от которой зависят значения функции. Чаще всего обозначается x.
Другими словами, мы сами выбираем x, подставляем в формулу функции и получаем y.

Область определения функции — множество тех (и только тех) значений аргумента x, при которых функция существует.
Обозначается: D(f) или D(y).

На нашем рисунке область определения функции  — это отрезок . Именно на этом отрезке нарисован график функции. Только здесь данная функция существует.

Область значений функции — это множество значений, которые принимает переменная . На нашем рисунке это отрезок  — от самого нижнего до самого верхнего значения .

Нули функции — точки, где значение функции равно нулю, то есть . На нашем рисунке это точки и .

Значения функции положительны там, где . На нашем рисунке это промежутки и .
Значения функции отрицательны там, где . У нас это промежуток (или интервал) от до .

Важнейшие понятия — возрастание и убывание функции на некотором множестве . В качестве множества  можно взять отрезок , интервал , объединение промежутков или всю числовую прямую.

Функция возрастает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .

Иными словами, чем больше , тем больше , то есть график идет вправо и вверх.

Функция убывает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .

Для убывающей функции большему значению  соответствует меньшее значение . График идет вправо и вниз.

На нашем рисунке функция возрастает на промежутке и убывает на промежутках и .

Определим, что такое точки максимума и минимума функции.

Точка максимума — это внутренняя точка области определения, такая, что значение функции в ней больше, чем во всех достаточно близких к ней точках.
Другими словами, точка максимума — такая точка, значение функции в которой больше, чем в соседних. Это локальный «холмик» на графике.

На нашем рисунке  — точка максимума.

Точка минимума — внутренняя точка области определения, такая, что значение функции в ней меньше, чем во всех достаточно близких к ней точках.
То есть точка минимума — такая, что значение функции в ней меньше, чем в соседних. На графике это локальная «ямка».

На нашем рисунке  — точка минимума.

Точка  — граничная. Она не является внутренней точкой области определения и потому не подходит под определение точки максимума. Ведь у нее нет соседей слева. Точно так же и  на нашем графике не может быть точкой минимума.

Точки максимума и минимума вместе называются точками экстремума функции. В нашем случае это  и .

А что делать, если нужно найти, например, минимум функции на отрезке ? В данном случае ответ: . Потому что минимум функции — это ее значение в точке минимума.

Аналогично, максимум нашей функции равен . Он достигается в точке .

Можно сказать, что экстремумы функции равны  и .

Иногда в задачах требуется найти наибольшее и наименьшее значения функции на заданном отрезке. Они не обязательно совпадают с экстремумами.

В нашем случае наименьшее значение функции на отрезке равно  и совпадает с минимумом функции. А вот наибольшее ее значение на этом отрезке равно . Оно достигается в левом конце отрезка.

В любом случае наибольшее и наименьшее значения непрерывной функции на отрезке достигаются либо в точках экстремума, либо на концах отрезка.

• Курс

Цели: систематизировать, обобщать знания
учащихся, проверить уровень знаний по теме.

Развивать целеустремленность в достижении
поставленной задачи, честность в оценке своих
знаний и знаний товарищей, умения объяснять и
доступно рассказывать подготовленный материал.

Воспитывать познавательную активность,
культуру общения.

Цитата занятия: “Пока законы математики
остаются определенными, они не имеют ничего
общего с реальностью; как только у них появляется
нечто общее с реальностью, они перестают быть
определенными”.

Альберт Эйнштейн.

Ход занятия

1. Орг. момент. Проверить готовность учащихся
к занятию.

2. Теоретическая часть вопроса. Материал
подготовил и отвечал ученик.

Я хотел бы напомнить общие сведения о понятии
области определения функции.

– Рассмотрим числовое множество Х и
правило f, позволяющее поставить в
соответствие каждому элементу х на множестве
Х определенное число у, то говорят, что
задана функция у = f(x) с областью определения Х.
Пишут

у = f(x), х Х.

Областью определения функции, заданной
некоторым выражением, называется множество
значений аргумента, при которых можно выполнить
все действия в записи функции. Значения
аргумента, принадлежащие области определения
функции, называются допустимыми значениями.

Для области определения функции используют
обозначение D(y).

Если f(x) – алгебраическое выражение и
область определения функции у = f(x) совпадает
с областью определения этого выражения (такую
область определения называют естественной), то
вместо записи у = f(x), х Х используют более короткую
запись: у = f(x).

Для нахождения области определения функции
следует исключить те значения аргумента, при
которых указанные действия невозможно
выполнить. Невозможно, например, делить на нуль;
извлекать корень четной степени из
отрицательного числа; вычислять логарифм
отрицательного числа и нуля; вычислять логарифм
по отрицательному основанию и основанию, равному
нулю и единице; возводить нуль в степень нуля;
возводить отрицательное число в иррациональную
степень; вычислять arcsin x, arсcos x, если |x|>1.

3. Рассмотрение вопроса на примерах. Материал
подготовил и рассказывал ученик.

Я хотел бы рассмотреть некоторые важные
моменты при нахождении области определения:

1) знаменатель дробного выражения не должен
обращаться в нуль. Например: у = 1/х,
область определения состоит из всех х 0;

у = sin x/cos x, область определения
состоит из всех х, для которых cos x 0, т.е. из (n = 0, 1, 2, …):

2) выражение, находящееся под знаком корня
четной степени, должно быть неотрицательным.
Например: у = , область определения x-50, x5;

у = ,
область определения + 2х – 3 0, т.е. х -3 и х
1;

3) выражение, находящееся под знаком логарифма
должно быть положительным. Например: у = lg(2-х),
область определения 2-х >0, т.е. х < 2.

4) основание логарифма должно быть больше нуля и
не равным единице. Например: у = log_х+27,
область определения х + 2 > 0 и х + 2 1, т.е. х > -2 и х
– 1;

5) выражение, возводимое в иррациональную
степень, должно быть неотрицательным. Например: у
= ,
область определения х 0;

6) выражение стоящее под знаком функций arcsin и
arсcos, по абсолютной величине не должно быть
больше единицы. Например: у = arcsin(lg х),
область определения |lg x| 1 т.е. 0,1 х 10;

7) выражение, стоящее под знаком тангенса и
секанса, не должно равняться , где k = 0, 1, 2, 3, …;

8)выражение, находящееся под знаком котангенса
или косеканса, не должно равняться , где k =0, 1, 2, 3, …;

9)степенно-показательная функция считается
определенной, когда основание положительно.
Точки, в которых основание равно нулю, включаются
в область определения, если показатель в этих
точках отличен от нуля.

Этот вопрос я подготовил пользуясь пособием по
математике (авторы: М.Н.Горейко, А.Б. Антоневич)

4. Примеры нахождения D(y). Материал
подготовил и рассмотрел перед классом ученик.

Найти области определения функций:

1. у = (.

Решение. Так как sin x принимает и
иррациональные значения, то x + 0, т.е. х . Кроме того, х не
должен обращаться в , так как при х = и основание, и показатель
степени обращаются в нуль. Область определения
функции

у = (
есть х > .




2. у = .

Решение. Области определения этой функции
принадлежат те х, при которых определен и 0. Для этого
нужно, чтобы 1.
Но последнее неравенство справедливо лишь в
точках х = 0, 1, 2, … . Таким образом,
только в этих точках можно выполнить все
действия в записи функции и, значит, область
определения этой функции состоит только из целых
чисел.

3. у = log_{х – 1}(х² + х – 2).

Решение. Логарифм определен только для
положительных оснований, не равных единице.
Выражение, стоящее под знаком логарифма, должно
дыть положительным. Поэтому получаем систему:

х -1 > 0;

х² – х – 2 > 0;

х – 1 1.

Решая эту систему, находим область определения:

х > 1, х 2.

5. Метод Мажорант (метод оценки). Решение
уравнений.

Материал рассмотрен учителем вместе с
учениками.

Метод, который имел место быть во всех ЕГЭ по
математике. Отметим этот метод, как начальный
олимпиадный.

Основная идея метода мажорант состоит в
следующем:

Пусть мы имеем уравнение и существует такое число М,
что для любого х из области определения имеем . Тогда уравнение
равносильно
системе

Пример 1 Решите уравнение .

Решение. Оценим обе части уравнения.

При всех значениях х верны неравенства . Следовательно,
данное уравнение равносильно системе 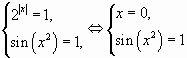. Полученная
система не имеет решений, так как не удовлетворяет второму
уравнению.

Ответ: нет решений.

Пример 2. Решить уравнение .

Решение. Оценим обе части уравнения.

Поскольку ,
равенство
выполняется тогда и только тогда, когда 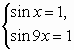. Решением
первого уравнения системы являются значения . При этих х
найдем .
Следовательно, решение системы.

Ответ: .

Пример 3 Решить уравнение .

Решение.

Пусть , тогда
уравнение примет вид . Поскольку и ,
неравенство выполняется тогда и только тогда,
когда .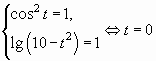
Обратная замена: х + 1 = 0 .

Ответ: – 1.

Пример 4. Найти все значения параметра а,
при каждом из которых уравнение имеет решения. Найдите эти
решения.

Решение.

Перепишем уравнение в виде . При всех значениях х
выражение
поэтому .

При всех значения х выражения и . Поэтому .

Следовательно, левая часть уравнения не меньше
4, а правая часть – не больше 4.

Получаем систему:

Ответ: при .

Разновидностью метода мажорант являются
задачи (“встреча на краю”) в которых множества
значений левой и правой частей уравнения или
неравенства имеют единственную общую точку,
являющуюся наибольшим значением для одной части
и наименьшим для другой. 

Прежде всего – привести заданные уравнения или
неравенства к более простому виду: путем
разложения на множители, избавлением от модулей,
логарифмов и т.д. Затем необходимо ещё раз
внимательно прочитать задание, попробовать
нарисовать графический образ функций входящих в
задачу.

Пример 1. Решить уравнение .

1 способ.

Решение: Заметим, что левая часть уравнения
не превосходит единицы, в то время как правая
часть не меньше единицы. Следовательно, исходное
уравнение имеет решение, только если обе его
части равны единицы. Это возможно только при .

Ответ: .

2 способ. Данное уравнение можно решить
графически. Для этого построим в одной системе
координат графики правой и левой частей
уравнения, т.е график функции и график функции . Из рисунка видно, что
исходное уравнение имеет решение, только при .

Пример 2. Решить уравнение .

Решение.

Так как при любом значении х: то данное уравнение
выполняется только в том случае, если
выполняется система 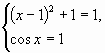. Первое уравнение системы имеет
единственный корень х = 1, но этот корень не
удовлетворяет второму уравнению. Поэтому
система решений не имеет.

Ответ: .

Пример 3. Решить уравнение .

Решение:

Так как , то
левая часть уравнения принимает значение от до 2. Для правой
части (в силу неравенства для суммы двух взаимно
обратных чисел) выполнено .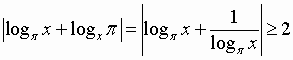

Поэтому уравнение имеет решения, если и только
если одновременно выполнены два условия 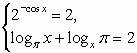. Решая эту
систему, получаем

Ответ:

Пример 4. Решить уравнение .

Решение.

Левая часть уравнения не больше 2, так как , значит . Равенство
возможно при условии .

Правая часть должна быть положительна, так как , а значит .

Кроме того, .

Тогда равенство обеих частей уравнения
возможно лишь при условии .

Отсюда находим, что .

Ответ: .

Пример 5. Решите уравнение .

Решение.

Для решения уравнения оценим его части: и . Поэтому равенство
возможно только при условии.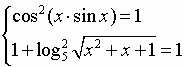

Сначала решим второе уравнение.

Получаем: , , , или . Корни этого уравнения и .

Проверим справедливость первого
равенства, подставив эти корни.

При
получаем:
(верное равенство).

Для
имеем: (неверное
равенство).

Итак, данное уравнение имеет
единственный корень .

Ответ: 0.

6. Подведем итоги занятия. Оценим выступление
учащихся.