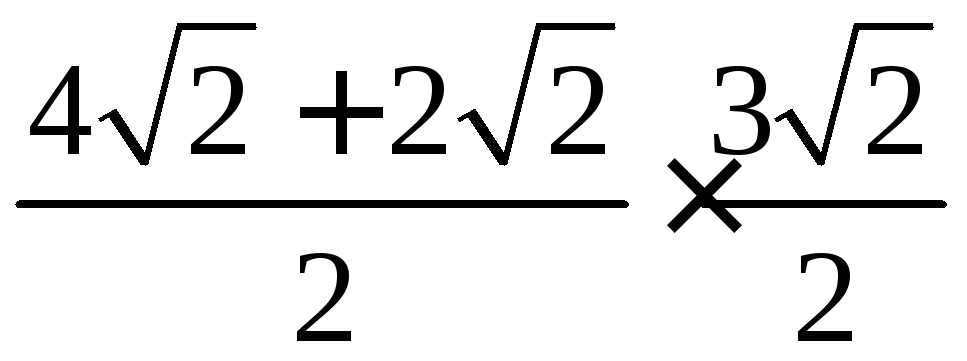Всего: 219 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
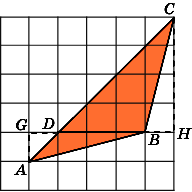
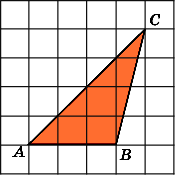
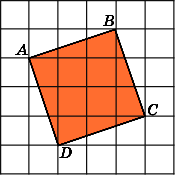
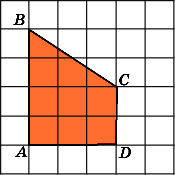
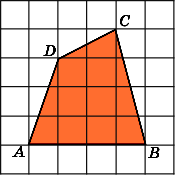
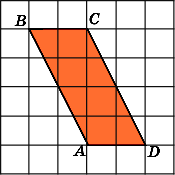
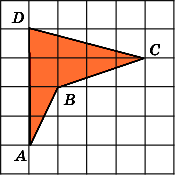
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
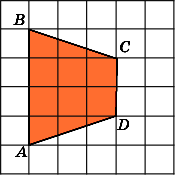
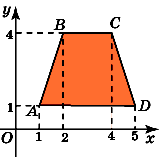
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
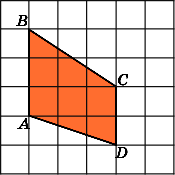
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
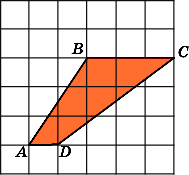
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Источник: ЕГЭ по математике. Основная волна 07.06.2021. Урал
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Источник: ЕГЭ по математике 07.06.2021. Основная волна. Подмосковье
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Источник: ЕГЭ по математике 07.06.2021. Основная волна. Санкт-Петербург
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Источник: ЕГЭ по математике 07.06.2021. Основная волна. Сибирь
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1см (см.рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь трапеции, изображённой на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Всего: 219 1–20 | 21–40 | 41–60 | 61–80 …
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
2
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
3
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
4
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
5
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Пройти тестирование по этим заданиям
Санкт-Петербургский
государственный
университет
аэрокосмического
приборостроения
Пятигорский
филиал
Методическое
пособие
г.
Пятигорск
2011
ВВЕДЕНИЕ
Данное
пособие предназначено для подготовки
к выполнению задания ЕГЭ по математике.
Его целями являются:
– показ
примерной тематики и уровня трудности
геометрических задач, включенных в
содержание ЕГЭ;
– проверка
качества знаний и умений учащихся по
геометрии, их готовность к сдаче ЕГЭ;
– развитие
представлений учащихся об основных
геометрических фигурах и их свойствах,
формирование навыков работы с рисунком;
– повышение
вычислительной культуры учащихся,
подготовка их к решению геометрических
задач с числовым ответом.
Пособие
содержит задачи на нахождение площадей
плоских фигур, нарисованных на клетчатой
бумаге или расположенных на координатной
плоскости. Наличие рисунков помогает
лучше понять условия задач, представить
соответствующую геометрическую
ситуацию, наметить план решения, при
необходимости провести дополнительные
построения и вычисления.
Для
решения предлагаемых задач требуются
знания формул площадей треугольников,
параллелограммов, трапеций, круга и
его частей, умения применять эти формулы
для нахождения площадей фигур, находить
площадь фигуры методом разбиения ее
на более простые фигуры.
Вначале
предлагается диагностическая работа
на нахождение площадей фигур различных
видов: треугольников, параллелограммов,
трапеций, выпуклых и невыпуклых
четырехугольников, круга и его частей,
фигур на координатной плоскости.
Для
тех, кто хочет проверить правильность
решения предложенных задач или убедиться
в верности полученного ответа, приводятся
решения задач, как правило, двумя
различными способами и даются ответы.
Затем,
для закрепления рассмотренных методов
решения задач, предлагаются тренировочные
работы на нахождение площадей для
каждого из перечисленных выше видов
фигур.
В
случае успешного решения этих задач
можно переходить к выполнению
заключительных самостоятельных работ.
В
конце пособия даны ответы ко всем
задачам.
По
аналогии с рассмотренными задачами
можно самим придумывать и решать задачи
на нахождение площадей фигур.
Отметим,
что лучшим способом подготовки к ЕГЭ
по геометрии являются систематические
занятия по учебнику геометрии. Данное
пособие не заменяет учебника. Оно может
быть использовано в качестве
дополнительного сборника задач при
изучении геометрии в 7-9 классах, а также
при организации обобщающего повторения
в 10-11 классах или при самостоятельных
занятиях по геометрии.
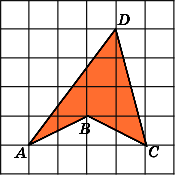
Примеры решения задач.
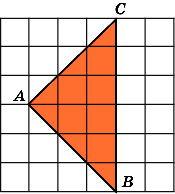
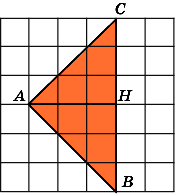
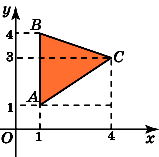
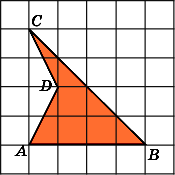
1.
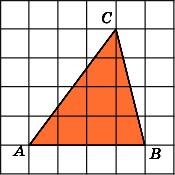
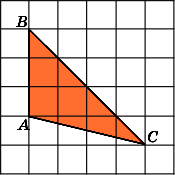
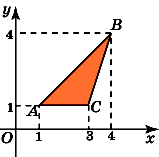
Найдите площадь треугольника ABC,
считая стороны квадратных клеток
равными 1.
Первое
решение.
Заметим, что данный треугольник ABC
является
прямоугольным (A
= 90о).
Воспользуемся тем, что диагональ
квадратной клетки со сторонами, равными
1, равна
.
Тогда катеты AB
и
AC
данного
треугольника будут равны
.
Так как площадь прямоугольного
треугольника равна половине произведения
его катетов, то площадь данного
треугольника будет равна
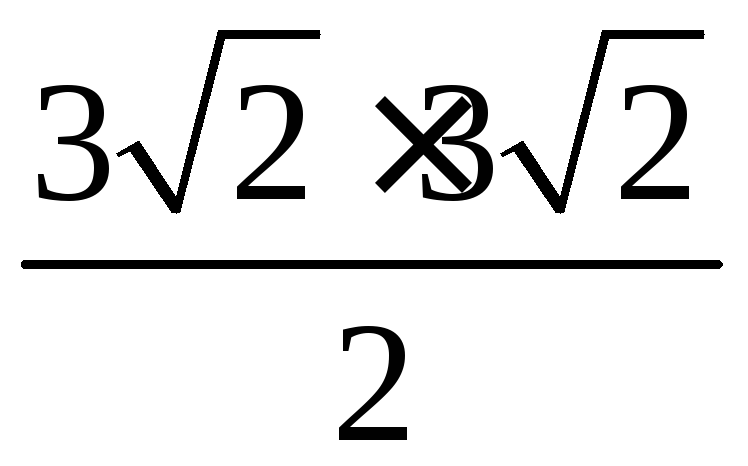
т.е. равна 9.
Второе
решение.
Проведем высоту AH.
Тогда BC
= 6,
AH
= 3
и, следовательно,
.
Ответ.
9.
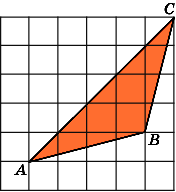
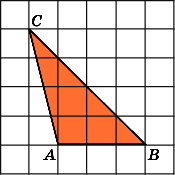
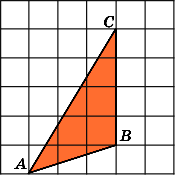
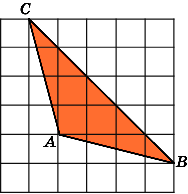
2.
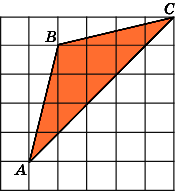
Найдите площадь треугольника ABC,
считая стороны квадратных клеток
равными 1.
Первое
решение.
Так как диагональ квадрата со стороной
1 равна
,
то сторона AC
треугольника
ABC
равна
,
высота BH,
проведенная к этой стороне, равна
.
Следовательно, площадь данного
треугольника равна
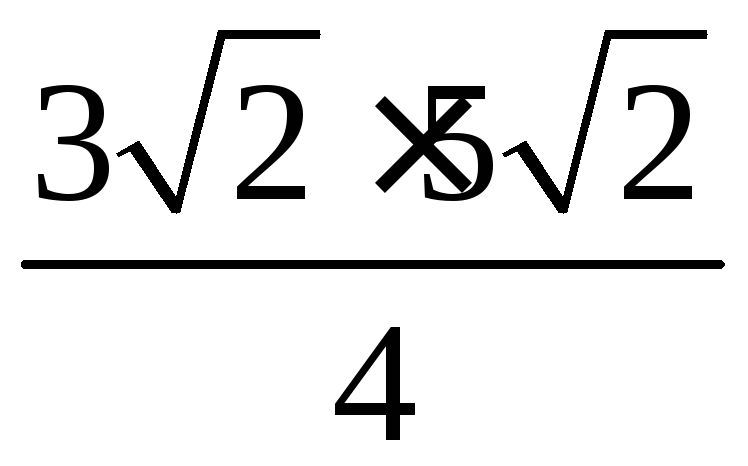
т.е. равна 7,5.
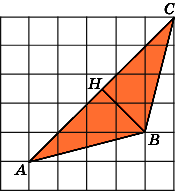
Второе
решение.
Разобьем данный треугольник ABC
на
два треугольника ABD
и
BDC.
Их общая сторона BD
равна
3, а высоты, к ней проведенные, равны
соответственно 1 и 4. Площадь треугольника
ABD
равна
1,5, а площадь треугольника BDC
равна
6. Площадь треугольника ABC
равна
сумме площадей этих треугольников и,
следовательно, равна 7,5.
Ответ.
7,5.
3.
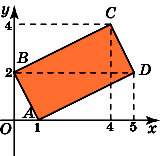
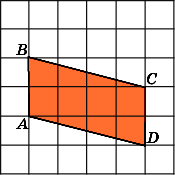
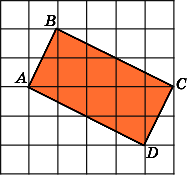
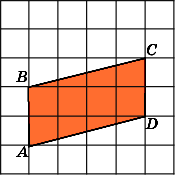
Найдите площадь прямоугольника ABCD,
считая стороны квадратных клеток
равными 1.
Первое
решение.
Найдем стороны данного прямоугольника.
Рассмотрим прямоугольный треугольник
ADE.
Катет
AE
равен
4, катет DE
равен
2. Следовательно, по теореме Пифагора
гипотенуза AD
равна
.
Аналогично, для прямоугольного
треугольника ABF
катет
AF
равен
1, катет BF
равен
2, Следовательно, по теореме Пифагора
гипотенуза AB
равна
.
Так как площадь прямоугольника равна
произведению его смежных сторон, то
площадь данного прямоугольника будет
равна
,
т.е. равна 10.
Второе
решение.
Разобьем данный прямоугольник ABCD
на
два треугольника ABD
и
BCD.
Сторона BD
у
них общая и равна 5. Высоты AE
и CF,
опущенные на эту сторону, равны 2. Так
как площадь треугольника равна половине
произведения стороны на высоту, опущенную
на эту сторону, то площадь каждого из
этих двух треугольников будет равна 5
и, следовательно, площадь прямоугольника
будет равна 10.
Ответ.
10.
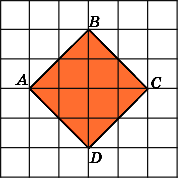
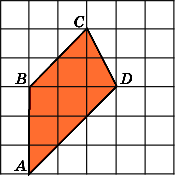
4.
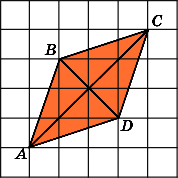
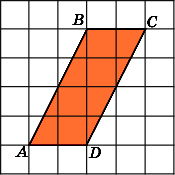
Найдите площадь ромба ABCD,
считая стороны квадратных клеток
равными 1.
4.
Первое
решение.
Напомним, что площадь ромба равна
половине произведения его диагоналей.
Воспользуемся тем, что диагональ
квадратной клетки со сторонами, равными
1, равна
.
Тогда диагонали AС
и
BD
данного
ромба будут равны соответственно
и
,
а его площадь будет равна
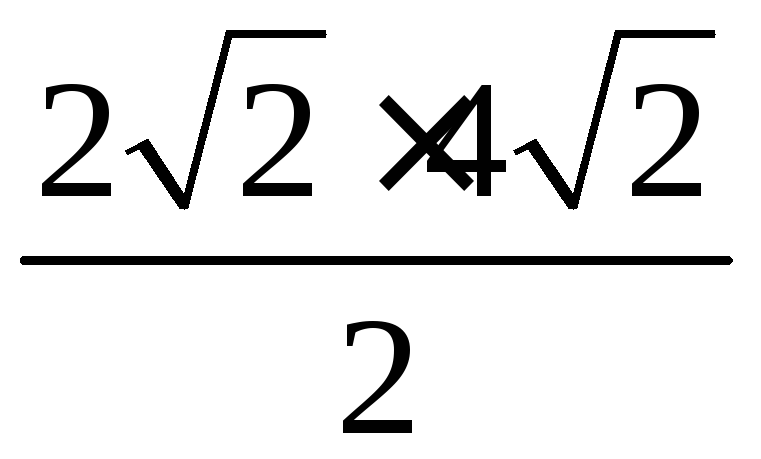
т.е. равна 8.
Второе
решение.
Достроим на сторонах ромба четыре
равных прямоугольных треугольника,
катеты которых равны 1 и 3. Площадь
каждого такого треугольника равна 1,5.
Ромб вместе с этими треугольниками
образует фигуру, состоящую из четырнадцати
единичных квадратов. Следовательно,
ее площадь равна 14. Вычитая из нее
площадь четырех треугольников, получим,
что площадь ромба равна 8.
Ответ.
8.
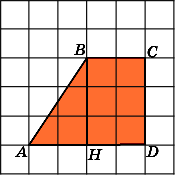
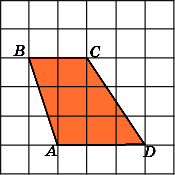
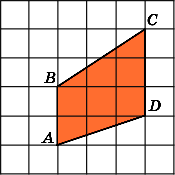
5.
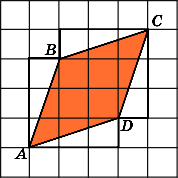
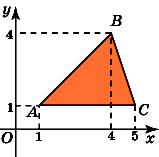
Найдите площадь трапеции ABCD,
считая стороны квадратных клеток
равными 1.
5.
Первое
решение.
Основания AD
и
BC
данной
трапеции равны соответственно 4 и 2.
Высотой является боковая сторона CD.
Она равна 3.
Так
как площадь трапеции равна произведению
полусуммы оснований на высоту, то
площадь данной трапеции будет равна
,
т.е. равна 9.
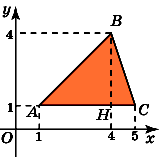
Второе
решение.
Из точки B
опустим
перпендикуляр BH
на
AD.
Он разобьет трапецию на прямоугольный
треугольник ABH
и
прямоугольник HBCD.
Катеты прямоугольного треугольника
равны 2 и 3, следовательно, его площадь
равна 3. Смежные стороны прямоугольника
равны 2 и 3, следовательно, его площадь
равна 6. Площадь трапеции равна сумме
площадей треугольника и прямоугольника
и, следовательно, равна 9.
Ответ.
9.
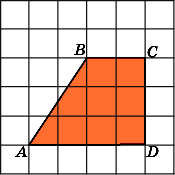
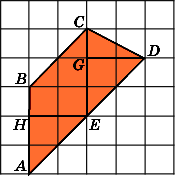
6. Найдите площадь трапеции abcd, считая стороны квадратных клеток равными 1.
6.
Первое
решение.
Основания AD
и
BC
трапеции
равны соответственно
и
.
Высота BH
трапеции
равна
.
Так как площадь трапеции равна
произведению полусуммы оснований на
высоту, то площадь данной трапеции
будет равна
и, следовательно, будет равна 9.
Второе
решение.
Разобьем трапецию на параллелограмм
ABCE
и
треугольник CDE.
Сторона AB
параллелограмма
ABCE
равна
3, высота EH,
к ней проведенная, равна 2, следовательно,
площадь этого параллелограмма равна
6. Сторона CE
треугольника
CDE
равна
3, высота DG,
к ней проведенная, равна 2, следовательно,
площадь этого треугольника равна 3.
Площадь трапеции равна сумме площадей
параллелограмма и треугольника и,
следовательно, равна 9.
Ответ.
9.
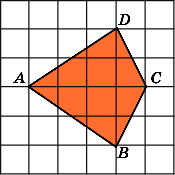
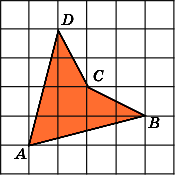
7.
Найдите площадь четырехугольника ABCD,
считая стороны квадратных клеток
равными 1.
Первое
решение.
Разобьем данный четырехугольник на
два треугольника ABC
и
ACD.
Сторона AC
у
них общая и равна 4. Высоты BH
и
DH
равны
2. Следовательно, площади этих треугольников
равны 4 и, значит, площадь четырехугольника
равна 8.
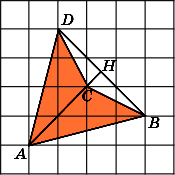
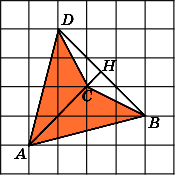
Второе
решение.
Разобьем данный четырехугольник на
два треугольника ABD
и
BCD.
Сторона BD
у
них общая и равна 4. Высоты AH
и
CH
равны
соответственно 3 и 1. Следовательно,
площади этих треугольников равны
соответственно 6 и 2. Значит, площадь
четырехугольника равна 8.
Ответ.
8.
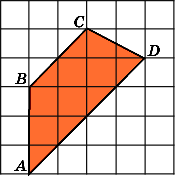
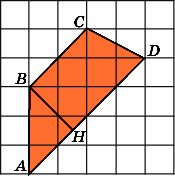
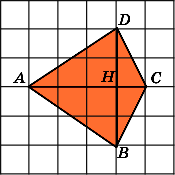
8.
Найдите площадь четырехугольника ABCD,
считая стороны квадратных клеток
равными 1.
Первое
решение.
Разобьем данный четырехугольник на
два треугольника ACB
и
ACD.
Сторона AC
у
них общая и равна
.
Высоты BH
и
DH
равны
.
Следовательно, площади этих треугольников
равны 3. Значит, площадь четырехугольника
равна 6.
Второе
решение.
Площадь данного четырехугольника равна
разности площадей треугольников ABD
и
CBD.
В треугольнике ABD
сторона
BD
равна
,
высота AH
равна
.
Следовательно, его площадь равна 7,5. В
треугольнике CBD
сторона
BD
равна
,
высота CH
равна
.
Следовательно, его площадь равна 1,5.
Таким образом, площадь данного
четырехугольника равна 6.
Ответ.
6.
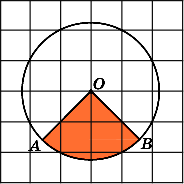
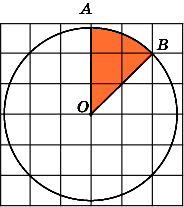
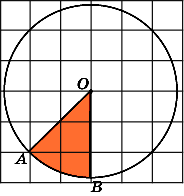
9.
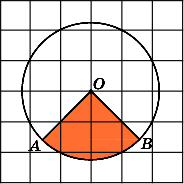
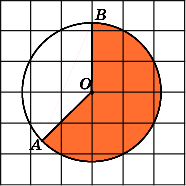
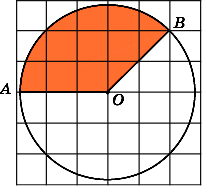
Найдите площадь S
сектора,
считая стороны квадратных клеток
равными 1. В ответе укажите
.
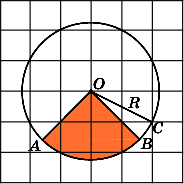
Первое
решение.
Напомним, что площадь S
кругового
сектора вычисляется по формуле
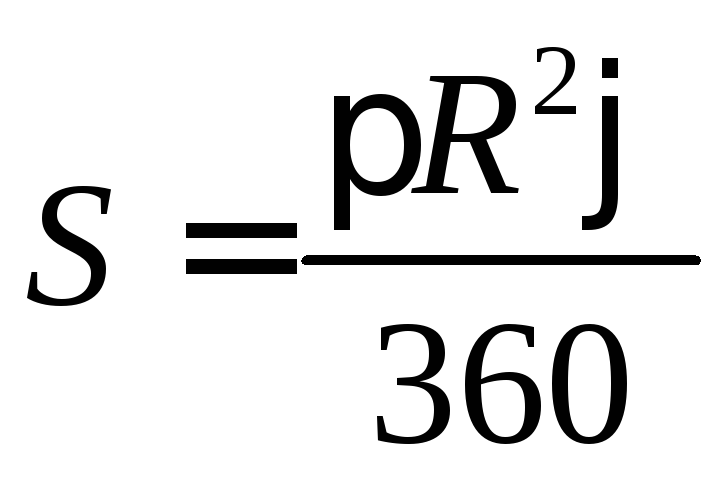
где R
–
радиус круга,
— градусная величина угла сектора. В
нашем случае
= 90о.
Радиус R
равен
.
Подставляя данные
значения
R
и
в формулу площади сектора, получим S
=
.
Откуда
.
Второе
решение.
Заметим, что данный сектор является
одной четвертой частью круга и,
следовательно, его площадь равна одной
четвертой площади круга. Площадь круга
равна
,
где R
–
радиус круга. В нашем случае R
=и,
следовательно, площадь S
сектора
равна
.
Откуда
.
Ответ.
1,25.
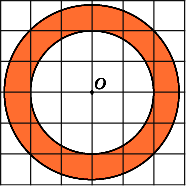
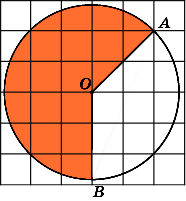
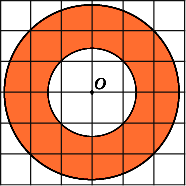
10.
Найдите площадь S
кольца,
считая стороны квадратных клеток
равными 1. В ответе укажите
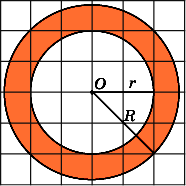
Площадь
кольца равна разности площадей внешнего
и внутреннего кругов. Радиус R
внешнего
круга равен
3,
радиус r
внутреннего
круга равен 2. Следовательно, площадь
S
кольца
равна
,
т.е. S
=
и,
следовательно,
Ответ.
5.
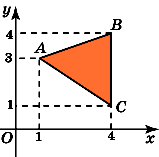
11.Найдите площадь треугольника, вершины
которого имеют координаты (1, 1), (4, 4), (5,
1).
Из
вершины B треугольникаABC опустим высотуBH. Она равна 3. СторонаAC равна 4.
Следовательно, площадь треугольника
равна 6.
Ответ.
6.
12.
Найдите площадь четырехугольника,
вершины которого имеют координаты
(1,
0), (0, 2), (4, 4), (5, 2).
Разобьем
четырехугольник ABCD
на
два треугольника ABD
и
BCD.
Высоты AG
и
CH
этих
треугольников, опущенные на сторону
BD,
равны
2,
сторона BD
равна
5. Следовательно, площади этих треугольников
равны 5 и, значит, площадь четырехугольника
ABCD
равна
10.
Ответ.
10.
Задания для тренировки.
1.
Площадь треугольника
1.
Найдите площадь треугольника ABC,
считая стороны квадратных клеток
равными 1.
2.
Найдите площадь треугольника ABC,
считая стороны квадратных клеток
равными 1.
3.
Найдите площадь треугольника ABC,
считая стороны квадратных клеток
равными 1.
4.
Найдите площадь треугольника ABC,
считая стороны квадратных клеток
равными 1.
5.
Найдите площадь треугольника ABC,
считая стороны квадратных клеток
равными 1.
6.
Найдите площадь треугольника ABC,
считая стороны квадратных клеток
равными 1.
7.
Найдите площадь треугольника ABC,
считая стороны квадратных клеток
равными 1.
8.
Найдите площадь треугольника ABC,
считая стороны квадратных клеток
равными 1.
2. Площадь
прямоугольника, квадрата, параллелограмма,
ромба
1.
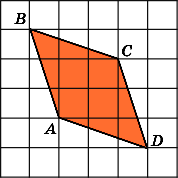
Найдите площадь параллелограмма ABCD,
считая стороны квадратных клеток
равными 1.
2.
Найдите площадь параллелограмма ABCD,
считая стороны квадратных клеток
равными 1.
3.
Найдите площадь квадрата ABCD,
считая стороны квадратных клеток
равными 1.
4.
Найдите площадь прямоугольника ABCD,
считая стороны квадратных клеток
равными 1.
5.
Найдите площадь квадрата ABCD,
считая стороны квадратных клеток
равными 1.
6.
Найдите площадь ромба ABCD,
считая стороны квадратных клеток
равными 1.
7.
Найдите площадь параллелограмма ABCD,
считая стороны квадратных клеток
равными 1.
8.
Найдите площадь параллелограмма ABCD,
считая стороны квадратных клеток
равными 1.
3.
Площадь трапеции
1.
Найдите площадь трапеции ABCD,
считая стороны квадратных клеток
равными 1.
2.
Найдите площадь трапеции ABCD,
считая стороны квадратных клеток
равными 1.
3.
Найдите площадь трапеции ABCD,
считая стороны квадратных клеток
равными 1.
4.
Найдите площадь трапеции ABCD,
считая стороны квадратных клеток
равными 1.
5.
Найдите площадь трапеции ABCD,
считая стороны квадратных клеток
равными 1.
6.
Найдите площадь трапеции ABCD,
считая стороны квадратных клеток
равными 1.
7.
Найдите площадь трапеции ABCD,
считая стороны квадратных клеток
равными 1.
8.
Найдите площадь трапеции ABCD,
считая стороны квадратных клеток
равными 1.
4.
Площадь выпуклых и невыпуклых
четырехугольников
1.
Найдите площадь четырехугольника ABCD,
считая стороны квадратных клеток
равными 1.
2.
Найдите площадь четырехугольника ABCD,
считая стороны квадратных клеток
равными 1.
3.
Найдите площадь четырехугольника ABCD,
считая стороны квадратных клеток
равными 1.
4.
Найдите площадь четырехугольника ABCD,
считая стороны квадратных клеток
равными 1.
5.
Найдите площадь четырехугольника ABCD,
считая стороны квадратных клеток
равными 1.
6.
Найдите площадь четырехугольника ABCD,
считая стороны квадратных клеток
равными 1.
7.
Найдите площадь четырехугольника ABCD,
считая стороны квадратных клеток
равными 1.
8.
Найдите площадь четырехугольника ABCD,
считая стороны квадратных клеток
равными 1.
5.
Площадь круга и его частей
1.
Найдите площадь S
сектора,
считая стороны квадратных клеток
равными 1. В ответе укажите
.
2.
Найдите площадь S
сектора,
считая стороны квадратных клеток
равными 1. В ответе укажите
.
3.
Найдите площадь S
сектора,
считая стороны квадратных клеток
равными 1. В ответе укажите
.
4.
Найдите площадь S
сектора,
считая стороны квадратных клеток
равными 1. В ответе укажите.
5.
Найдите площадь S
сектора,
считая стороны квадратных клеток
равными 1. В ответе укажите
.
6.
Найдите площадь S
сектора,
считая стороны квадратных клеток
равными 1. В ответе укажите
.
7.
Найдите площадь S
кольца,
считая стороны квадратных клеток
равными 1. В ответе укажите.
8.
Найдите площадь S
кольца,
считая стороны квадратных клеток
равными 1. В ответе укажите
.
6.
Площадь фигур на координатной плоскости
1.Найдите площадь треугольника, вершины
которого имеют координаты (1, 1), (4, 4), (3,
1).
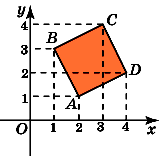
2.Найдите площадь квадрата, вершины
которого имеют координаты (2, 1), (1, 3), (3,
4), (4, 2).
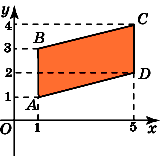
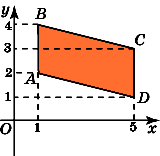
3.Найдите площадь параллелограмма,
вершины которого имеют координаты (1,
1), (1, 3), (5, 4), (5, 2).
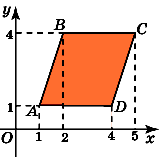
4.Найдите площадь параллелограмма,
вершины которого имеют координаты (1,
1), (2, 4), (5, 4), (4, 1).
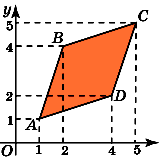
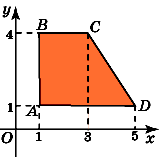
5.Найдите площадь трапеции, вершины
которой имеют координаты (1, 1), (2, 4), (4,
4), (5, 1).
6.Найдите площадь ромба, вершины которого
имеют координаты (1, 1), (2, 4), (5, 5), (4, 2).
7.Найдите площадь треугольника, вершины
которого имеют координаты (1, 3), (4, 4), (4,
1).
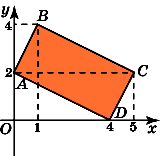
8.Найдите площадь прямоугольника, вершины
которого имеют координаты (0, 2), (1, 4), (5,
2), (4, 0).
Самостоятельная работа 1
1.Найдите площадь параллелограммаABCD,
считая стороны квадратных клеток
равными 1.
2.Найдите площадь треугольникаABC,
считая стороны квадратных клеток
равными 1.
3.Найдите площадь трапецииABCD,
считая стороны квадратных клеток
равными 1.
4.Найдите площадь четырехугольникаABCD,
считая стороны квадратных клеток
равными 1.
5.Найдите площадьS
сектора, считая стороны квадратных
клеток равными 1. В ответе укажите
.
6.
Найдите площадь треугольника, вершины
которого имеют координаты
(1,
1), (1, 4), (4, 3).
Самостоятельная работа 2
1.
Найдите площадь параллелограммаABCD, считая стороны
квадратных клеток равными 1.
2.
Найдите площадь треугольникаABC,
считая стороны квадратных клеток
равными 1.
3.
Найдите площадь трапецииABCD,
считая стороны квадратных клеток
равными 1.
4.Найдите площадь четырехугольникаABCD,
считая стороны квадратных клеток
равными 1.
5.Найдите площадьS
сектора, считая стороны квадратных
клеток равными 1. В ответе укажите
.
6.
Найдите площадь параллелограмма,
вершины которого имеют координаты (1,
2), (1, 4), (5, 3), (5, 1).
Самостоятельная работа 3
1.
Найдите площадь квадратаABCD,
считая стороны квадратных клеток
равными 1.
2.Найдите площадь треугольникаABC,
считая стороны квадратных клеток
равными 1.
3.Найдите площадь трапецииABCD,
считая стороны квадратных клеток
равными 1.
4.Найдите площадь четырехугольникаABCD,
считая стороны квадратных клеток
равными 1.
4.
Найдите площадьS
кольца, считая стороны квадратных
клеток равными 1. В ответе укажите
.
6.
Найдите площадь трапеции, вершины
которой имеют координаты
(1,
1), (1, 4), (3, 4), (5, 1).
ОТВЕТЫ
Задания
для тренировки.
1.
Площадь треугольника
1.
8.2.6.3.9.4. 6.5.7,5.6.8.7.6.8. 7,5.
2.
Площадь прямоугольника, квадрата,
параллелограмма, ромба
1.8.2.8.3.10.4. 10.5.8.6.8.7.8.8. 10.
3.
Площадь трапеции
1.92.7,5.3.9.4. 9.5.7,5.6.6.7.7,5.8. 9.
4.
Площадь выпуклых и невыпуклых
четырехугольников
1.12,5.2.12.3.10,5.4. 8.5.9.6.4.7.4.8. 6.
5.
Площадь круга и его частей
1.2.2.1.3.3.4. 5.5.3,125.6.3,75.7.6.8. 3.
6.
Площадь фигур на координатной плоскости
1.3.2.5.3.8.4. 9.5.9.6.8.7.4,5.8. 10.
Самостоятельные
работы
Самостоятельная
работа 1
1.
8. 2.6.3.7,5.4.8.5. 1.6.4,5.
Самостоятельная
работа 2
1.
8. 2.6.3.7,5.4.5,5.5. 3.6.
8.
Самостоятельная
работа 3
1.
10. 2.7,5.3.7,5.4.6.5. 4.6.
9.
3
46
4
45
5
44
6
43
7
42
8
41
9
40
10
39
11
38
12
37
13
36
14
35
15
34
16
33
17
32
18
31
19
30
20
29
21
28
22
27
23
26
24
25
Скачать материал

Скачать материал




- Сейчас обучается 266 человек из 64 регионов


- Сейчас обучается 412 человек из 63 регионов


Описание презентации по отдельным слайдам:
-
-
2 слайд
1. Найдите площадь ΔABC, считая стороны квадратных клеток равными 1
2
Ответ: 9
Решение Проведем высоту AH. Тогда BC = 6, AH = 3 и, следовательно, -
3 слайд
2. Найдите площадь ΔABC, считая стороны квадратных клеток равными 1
Ответ: 7,5
Решение Разобьем данный ΔABC на два треугольника ABD и BDC. Их общая сторона BD = 3, а высоты, к ней проведенные, равны соответственно 1 и 4. Площадь ΔABD равна 1,5, а площадь ΔBDC равна 6. Площадь ΔABC равна сумме площадей этих треугольников и, следовательно, равна 7,5
3 -
4 слайд
3. Найдите площадь прямоугольника ABCD, считая стороны квадратных клеток равными 1
Ответ: 10
Решение Разобьем данный прямоугольник ABCD на два треугольника ABD и BCD. Сторона BD у них общая и равна 5. Высоты AE и CF, опущенные на эту сторону, равны 2. Так как площадь треугольника равна половине произведения стороны на высоту, опущенную на эту сторону, то площадь каждого из этих двух треугольников будет равна 5 и, следовательно, площадь прямоугольника будет равна 10
4 -
5 слайд
4. Найдите площадь ромба ABCD, считая стороны квадратных клеток равными 1
Ответ: 8
Решение Достроим на сторонах ромба четыре равных прямоугольных треугольника, катеты которых равны 1 и 3. Площадь каждого такого треугольника равна 1,5. Ромб вместе с этими треугольниками образует фигуру, состоящую из четырнадцати единичных квадратов. Следовательно, ее площадь равна 14. Вычитая из нее площадь четырех треугольников, получим, что площадь ромба равна 8
5 -
6 слайд
5. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1
6
Ответ: 9Решение Основания AD и BC данной трапеции равны соответственно 4 и 2. Высотой является боковая сторона CD. Она равна 3. Так как площадь трапеции равна произведению полусуммы оснований на высоту, то площадь данной трапеции будет равна 9
-
7 слайд
6. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1
Ответ: 9
Решение Разобьем трапецию на параллелограмм ABCE и треугольник CDE. Сторона AB параллелограмма ABCE равна 3, высота EH, к ней проведенная, равна 2, следовательно, площадь этого параллелограмма равна 6. Сторона CE треугольника CDE равна 3, высота DG, к ней проведенная, равна 2, следовательно, площадь этого треугольника равна 3. Площадь трапеции равна сумме площадей параллелограмма и треугольника и, следовательно, равна 9.
7 -
8 слайд
7. Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1
Ответ: 8
Решение Разобьем данный четырехугольник на два треугольника ABC и ACD. Сторона AC у них общая и равна 4. Высоты BH и DH равны 2. Следовательно, площади этих треугольников равны 4 и, значит, площадь четырехуголь-ника равна 8
8 -
9 слайд
8. Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1
9
Ответ: 6
Решение Разобьем данный четырехугольник на два треугольника ACB и ACD. Сторона AC у них общая и равна . Высоты BH и DH равны . Следовательно, площади этих треугольников равны 3. Значит, площадь четырехугольника равна 6 -
10 слайд
10
9. Найдите площадь S сектора, считая стороны квадратных клеток равными 1. В ответе укажите
Ответ: 1,25
Решение
Если , , то ,
т. е. -
11 слайд
11
10. Найдите площадь S кольца, считая стороны квадратных клеток равными 1. В ответе укажите
Ответ: 4
Решение Площадь кольца равна разности площадей внешнего и внутреннего кругов.
Т.к и r = 2 ,
следовательно, ,
а -
12 слайд
11. Найдите площадь треугольника, вершины которого имеют координаты (1, 1), (4, 4), (5, 1)
Ответ: 6
Решение Из вершины B Δ ABC опустим высоту BH = 3. Сторона AC = 4. Следовательно, площадь треугольника равна 6
12 -
13 слайд
12. Найдите площадь четырехугольника, вершины которого имеют координаты (1, 0), (0, 2), (4, 4), (5, 2)
Ответ: 10
Решение Разобьем четырехугольник ABCD на два треугольника ABD и BCD. Высоты AG и CH этих треугольников, опущенные на сторону BD, равны 2, сторона BD равна 5. Следовательно, площади этих треугольников равны 5 и, значит, площадь четырехугольника ABCD равна 10
13
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 157 368 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 08.01.2017
- 4563
- 1
- 08.01.2017
- 479
- 0
- 08.01.2017
- 3956
- 41
- 08.01.2017
- 2100
- 2
- 08.01.2017
- 5734
- 5
- 08.01.2017
- 622
- 0
- 08.01.2017
- 645
- 1
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
Рассмотрим несколько задач.
| #1 | #2 | #3 | #4 | #5 |
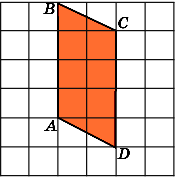
Задача #1
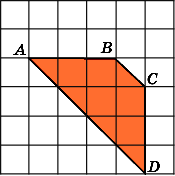
(Номер задачи на fipi.ru — B11571). На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Прежде чем приступать к решению задачи, вспомним теорию >>
Трапеция — четырёхугольник, две стороны которой параллелльны, а две другие нет. Параллельные стороны называются основаниями, а непаралельные — боковыми.
Площадь трапеции вычисляется по формуле:
где a и b — основания трапеции, h — высота трапеции.
Решение:
Посмотрим на рисунок. Из него видно, что основания трапеции равны соответственно: a = 2, b = 6. Из рисунка также находим высоту трапеции: h = 7.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь трапеции:
Ответ: площадь трапеции равна: 28 ед. кв.
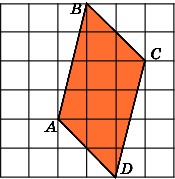
Задача #2
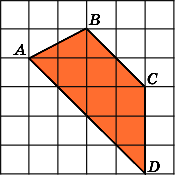
(Номер задачи на fipi.ru — E46263). На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Посмотрим на рисунок. Из него видно, что основания трапеции равны соответственно: a = 4, b = 8. Из рисунка также находим высоту трапеции: h = 6.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь трапеции:
Ответ: площадь трапеции равна: 36 ед. кв.
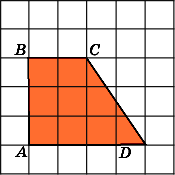
Задача #3
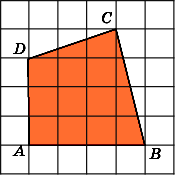
(Номер задачи на fipi.ru — 283DE4). На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Посмотрим на рисунок. Из него видно, что основания трапеции равны соответственно: a = 2, b = 6. Из рисунка также находим высоту трапеции: h = 3.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь трапеции:
Ответ: площадь трапеции равна: 12 ед. кв.
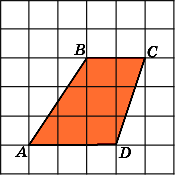
Задача #4
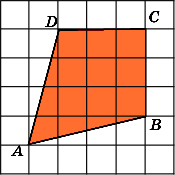
(Номер задачи на fipi.ru — 383C46). На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Посмотрим на рисунок. Из него видно, что основания трапеции равны соответственно: a = 3, b = 7. Из рисунка также находим высоту трапеции: h = 2.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь трапеции:
Ответ: площадь трапеции равна: 10 ед. кв.
Задача #5
(Номер задачи на fipi.ru — 2E7B84). На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Посмотрим на рисунок. Из него видно, что основания трапеции равны соответственно: a = 3, b = 7. Из рисунка также находим высоту трапеции: h = 6.
Таким образом, осталось подставить все найденный значения в формулу и найти площадь трапеции:
Ответ: площадь трапеции равна: 30 ед. кв.
Найдите площадь четырехугольника авсд считая стороны клеток равными 1
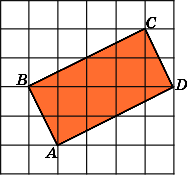
Найдите площадь прямоугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Это задание ещё не решено, приводим решение прототипа.
Найдите площадь прямоугольника ABCD, считая стороны квадратных клеток равными 1.
Площадь прямоугольника равна разности площади прямоугольника и четырех прямоугольных треугольников, гипотенузы которых являются сторонами исходного прямоугольника. Поэтому
см 2 .
Для вычисления площади фигуры можно сложить площади треугольников BCD и BAD, имеющих общую сторону BD, длина которой равна 5, и равные проведенные к ней высоты длины 2.
«решение заданий В-5» егэ
«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»
Сертификат и скидка на обучение каждому участнику
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
1. Найдите площадь ΔABC, считая стороны квадратных клеток равными 1 *
2. Найдите площадь ΔABC, считая стороны квадратных клеток равными 1 *
3. Найдите площадь прямоугольника ABCD, считая стороны квадратных клеток равными 1 *
4. Найдите площадь ромба ABCD, считая стороны квадратных клеток равными 1 *
5. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1 *
6. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1 *
7. Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1 *
8. Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1 *
11. Найдите площадь треугольника, вершины которого имеют координаты (1, 1), (4, 4), (5, 1) *
12. Найдите площадь четырехугольника, вершины которого имеют координаты (1, 0), (0, 2), (4, 4), (5, 2) *
Курс профессиональной переподготовки
Библиотечно-библиографические и информационные знания в педагогическом процессе
- Сейчас обучается 354 человека из 65 регионов
Курс повышения квалификации
Охрана труда
- Сейчас обучается 97 человек из 45 регионов
Курс профессиональной переподготовки
Охрана труда
- Сейчас обучается 212 человек из 54 регионов
Ищем педагогов в команду «Инфоурок»
- Гончарова Ирина АлександровнаНаписать 3016 08.01.2017
Номер материала: ДБ-072593
- 08.01.2017 3011
- 08.01.2017 295
- 08.01.2017 2185
- 08.01.2017 1308
- 08.01.2017 3378
- 08.01.2017 351
- 08.01.2017 375
Не нашли то, что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В России разработают рекомендации по сопровождению студентов с ОВЗ
Время чтения: 2 минуты
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Госдуме предложили продлить каникулы для школьников до 16 января
Время чтения: 1 минута
Минпросвещения готовит рекомендации по построению «идеальной школы»
Время чтения: 1 минута
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Глава СПЧ предложил ввести подготовительные курсы перед обучением в школе для детей мигрантов
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Найдите площадь четырехугольника авсд считая стороны клеток равными 1
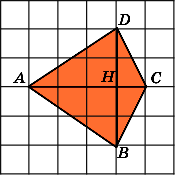
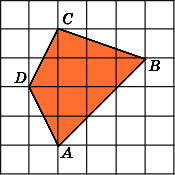
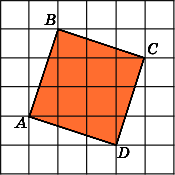
Задание 3. Найдите площадь четырёхугольника ABCD. Размер каждой клетки 1 см × 1 см. Ответ дайте в квадратных сантиметрах.
Разобьем фигуру на три прямоугольных треугольника и один квадрат как это показано на рисунке ниже.
Из рисунка видно, что площади треугольников ABF, BCE и CDH соответственно равны:
а площадь квадрата FECH равна

Таким образом, общая площадь фигуры, равна:

источники:
http://infourok.ru/reshenie-zadaniy-v-ege-1494639.html
http://self-edu.ru/math_egecat3.php?id=1_5
Обновлено: 10.10.2022
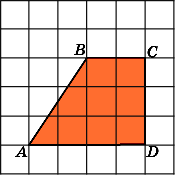
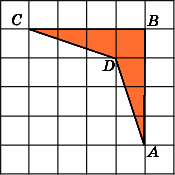
Задание
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
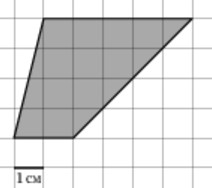
Решение
- Данный тип задач сводится к нахождению площади трапеции.
Площадь трапеции равна произведению полсуммы её оснований на высоту.
- Найдем площадь данной трапеции:
S = ( 5 + 2 ) / 2 * 4 = 14 см2
Ответ: 14