Найдите точку максимума функции y ln x 4 2 2x 7 решу егэ - Помощь в подготовке к экзаменам и поступлению

Найдите точку максимума функции y = ln(x + 4)²+ 2x + 7.

Решение:

y = ln(x + 4)²+ 2x + 7

ОДЗ: (x + 4)²> 0 – всегда больше 0(x + 4)² ≠ 0
х ≠ –4

Найдем производную функции:

y^{′}=(ln(x+4)^{2})^{′}+(2x)^{′}+7^{′}=frac{1}{(x+4)^{2}}cdot ((x+4)^{2})^{′}+2+0=frac{2cdot (x+4)}{(x+4)^{2}}+2=frac{2}{x+4}+2

Найдем нули производной:

frac{2}{x+4}+2=0\frac{2}{x+4}=-2\frac{2}{x+4}=frac{–2}{1}\2cdot 1=-2cdot (x+4)\2=-2x-8\2+8=-2x\x=frac{10}{–2}=-5

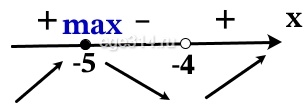
Определим знаки производной функции и изобразим поведение функции (учитывая ОДЗ):

Точка максимума: х = –5.

Ответ: –5.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.2 / 5. Количество оценок: 15

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

Решение №2

(ln a^2=2ln(a) )

(y=2ln(x+4)+2x+7)

1) (2ln(x+4)+2x+7, x>-4)

(frac{2}{x+4}+2, x>-4)

(frac{2(x+5)}{x+4}, x>-4)

2) (2ln(-x-4)+2x+7, x<-4)

(frac{2}{x+4}+2, x<-4)

(frac{2(x+5)}{x+4}, x<-4)

На луче (-4;+∞) y>0, а функция не линий экстремумов на луче (-∞;-4) y=0 в точке -5, которая является точкой максимума.

Ответ: х=-5

ЕГЭ-Центр «Пять с плюсом» основан в 2008 году. С основания и по настоящий момент Центр возглавляет Елизавета Владимировна Глазова, мать пятерых детей, профессиональный педагог и преподаватель русского языка и литературы.

Источник

Поиск

Всего: 32 1–20 | 21–32

Добавить в вариант

Найдите точку максимума функции

Источник: Демонстрационная версия ЕГЭ—2018 по математике. Профильный уровень., Демонстрационная версия ЕГЭ—2014 по математике., Демонстрационная версия ЕГЭ—2016 по математике. Профильный уровень., Демонстрационная версия ЕГЭ—2017 по математике. Профильный уровень.

Найдите точку максимума функции

Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 2., ЕГЭ по математике 07.06.2021. Основная волна. Санкт-Петербург

Найдите точку максимума функции

Источник: ЕГЭ по математике 05.06.2014. Основная волна. Запад. Вариант 1.

Найдите точку максимума функции

Источник: ЕГЭ по математике 05.06.2014. Основная волна. Запад. Вариант 1.

Найдите точку максимума функции

Источник: ЕГЭ по математике 05.06.2014. Основная волна. Восток. Вариант 1.

Найдите точку максимума функции

Источник: ЕГЭ — 2017. Основная волна 02.06.2017. Вариант 301 (C часть)., ЕГЭ по математике. Основная волна 07.06.2021. Урал

Найдите точку максимума функции

Источник: ЕГЭ по математике 05.06.2014. Основная волна. Восток. Вариант 1.

Найдите точку максимума функции

Источник: Досрочная волна ЕГЭ по математике 29.03.2019. Вариант 4

Найдите точку максимума функции

Найдите наибольшее значение функции на отрезке

Найдите наибольшее значение функции на отрезке [−4,5; 0].

Найдите наибольшее значение функции на отрезке

Всего: 32 1–20 | 21–32

Источник

Вы отправили работу на проверку эксперту. Укажите номер телефона на него придет СМС

Отправить

Незнайка → ЕГЭ → Математика → Профильная → Демонстрационный вариант → Задание 12

Задание № 5072

Найдите точку максимума функции [math]y=lnleft(x+4right)^2+2x+7[/math].

Показать ответ

Комментарий:

[math]y’=frac2{x+4}+2=frac{2(x+5)}{x+4}[/math]

[math]frac{2(x+5)}{x+4}=0[/math], при x=-5 — точка максимума.

Ответ: -5

Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.

2 259 229

Уже готовятся к ЕГЭ, ОГЭ и ВПР.
Присоединяйся!

Мы ничего не публикуем от вашего имени

Источник

Задача 1031 Найдите точку максимума функции…

Условие

Найдите точку максимума функции y=ln(x+4)^2+2x+7

математика 10-11 класс
26105

Решение

Находим производную
y’=2(x+5)/(x+4)
Приравниваем производную к нулю
x=-5
x=-4 — не может быть
Значит ответ -5

[b]Более подробное решение внизу. Опубликовал Гость.[/b]

Ответ: -5

Решение

★

исследуем функцию на максимум и минимум. Сначала преобразуем функцию y=2ln(x+4) +2x-7;
Производная y ‘(x)= 2/ (x+4) +2;
y ‘(x)=0; 2/(x+4) +2=0; 2/x+4 =-2; x+4=-1; x=-5.
Проверим значение производной слева и справа от критической точки и определим, что это за точка, максимум или минимум.
y ‘(-6)=2/-2 +2=1>0;
y ‘(-4,5)=2/-0,5 + 2=-4 +2=-2<0. Так как в точке х= -5 производная меняет знак с плюса на минус, то точка х=-5 — это точка максимума.

Написать комментарий

Источник

Kolychevyuriy

+10

Решено

5 лет назад

Математика

10 — 11 классы

Помогите найти точку максимума функции y=ln(x+4)^2+2x+7

Смотреть ответ

Ответ

0
(0 оценок)

artalex74
5 лет назад

Светило науки — 2019 ответов — 14682 помощи

D(y) = (-∞; -4)∪(-4; +∞)

+ — +
—-|——o——>
↗ -5 ↘ -4 ↗
х = -5 — точка максимума

(0 оценок)

Ответ

0
(0 оценок)

sedinalana
5 лет назад

Светило науки — 28486 ответов — 90605 раз оказано помощи

ОДЗ
(x+4)²≠0
x≠-4
x∈(-∞;-4) U (-4;∞)
y`=1/(x+4)²* 2(x+4)+2=2/(x+4)+2=(2+2x+8)/(x+4)=(2x+10)/(x+4)=0
2x+10=0
2x=-10
x=-5
+ _ +
———(-5)—————(-4)———————
max

(0 оценок)

Остались вопросы?

Задай вопрос

Найди нужный

Новые вопросы по предмету Математика

Запиши у вигляді правильного дробу або мішаного 1)4,13 2)13,2 3)8,07 4)4,013 5)0,004 6)0,052

знайти периметр трикутника дві сторони дорівнюють по чотири цілих сім десятих А третя сторона на одну цілу 30 кожного з них

4. Обчислити a. 3,14 0,24 +3,14 -0,76;Срочно даю 20 балів

Розв’яжіть рівняння ( х + 2,7 ) ( х — 5,4 ) = 0

пожалуйста помогите мне я много страдала пожалуйста даю 20 баллов пожалуйста

Источник

rineanerent357

Вопрос по математике:

Помогите найти точку максимума функции y=ln(x+4)^2+2x+7

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 2

pomounthithi755

D(y) = (-∞; -4)∪(-4; +∞)

+ — +
—-|——o——>
↗ -5 ↘ -4 ↗
х = -5 — точка максимума

gnoar955

ОДЗ
(x+4)²≠0
x≠-4
x∈(-∞;-4) U (-4;∞)
y`=1/(x+4)²* 2(x+4)+2=2/(x+4)+2=(2+2x+8)/(x+4)=(2x+10)/(x+4)=0
2x+10=0
2x=-10
x=-5
+ _ +
———(-5)—————(-4)———————
max

Знаете ответ? Поделитесь им!

Гость

Гость ?

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете
правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и
пунктуационных ошибок.

Этого делать не стоит:

Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее;
Использовать мат — это неуважительно по отношению к
пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Математика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи —
смело задавайте вопросы!

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

Источник