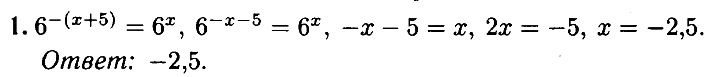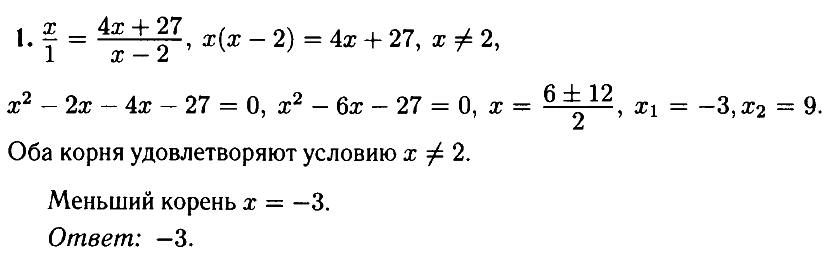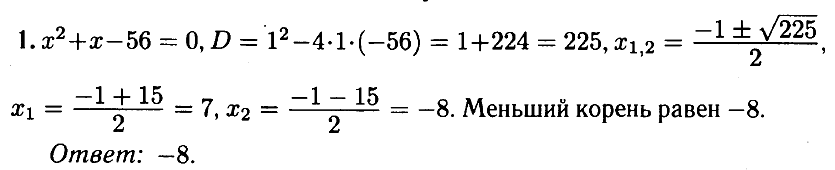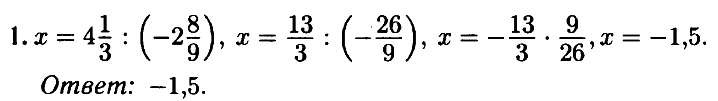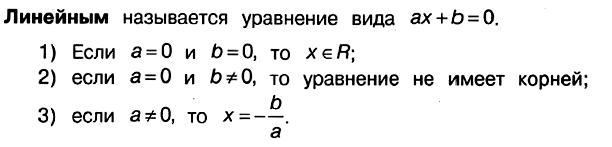Всё варианты 12 задания математика ЕГЭ Профиль 2022
Скачать задания в формате pdf.
Задания 12 ЕГЭ по математике профильного уровня 2022 год (уравнения)
1) (28.03.2022 досрочная волна) а) Решите уравнение ({4^{sin x}} + {4^{sin left( {pi + x} right)}} = frac{5}{2}.)
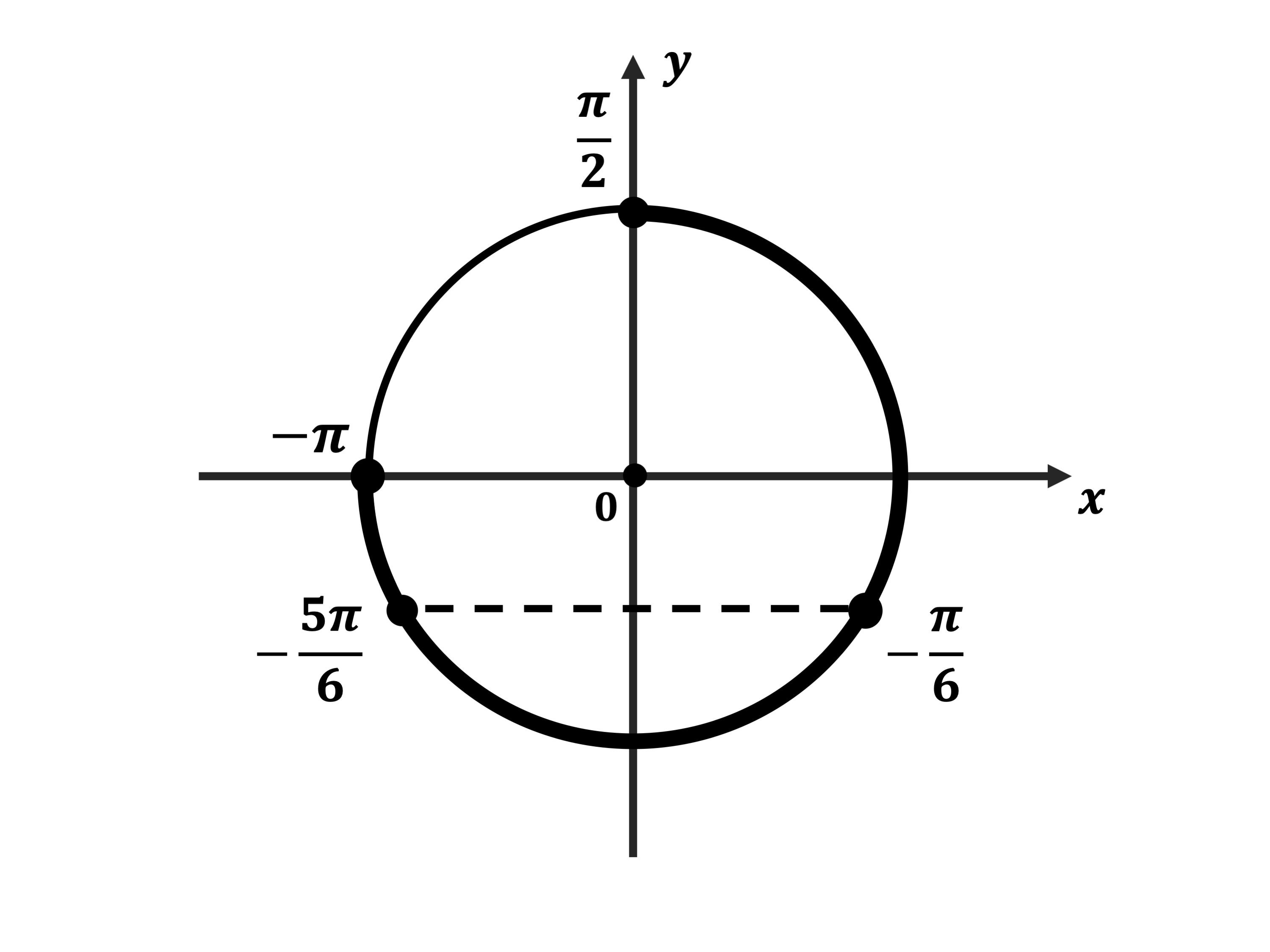
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{{{text{5}}pi }}{2};;4pi } right]).
ОТВЕТ: а) ( pm frac{pi }{6} + pi k;;;k in Z;) б) (frac{{17pi }}{6};,,,,,frac{{19pi }}{6};,,,,,frac{{{text{23}}pi }}{6}.)
2) (28.03.2022 досрочная волна) а) Решите уравнение ({81^{cos x}} — 12 cdot {9^{cos x}} + 27 = 0.)
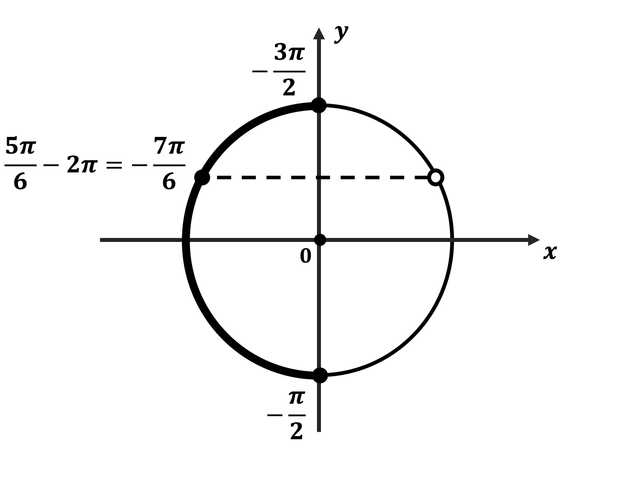
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ { — ,4pi ;,,, — frac{{{text{5}}pi }}{2}} right]).
ОТВЕТ: а) ( pm frac{pi }{3} + 2pi k;;;2pi k;;;k in Z;) б) ( — frac{{11pi }}{3};,,,, — 4pi .)
3) (28.03.2022 досрочная волна) а) Решите уравнение ({16^{sin x}} — 1,5 cdot {4^{sin x + 1}} + 8 = 0.)
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ { — ,5pi ;,,, — frac{{{text{7}}pi }}{2}} right]).
ОТВЕТ: а) (frac{pi }{6} + 2pi k;,,;frac{{{text{5}}pi }}{6} + 2pi k;;;frac{pi }{2} + 2pi k;;;k in Z;) б) ( — frac{{{text{23}}pi }}{6};,,,, — frac{{7pi }}{2}.)
4) (02.06.2022 основная волна) а) Решите уравнение (2{sin ^2}x — cos left( { — x} right) — 1 = 0.)
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ { — ,pi ;,,,frac{pi }{2}} right]).
ОТВЕТ: а) ( pm frac{pi }{3} + 2pi k;,,;pi + 2pi k;;;k in Z;) б) ( — pi ;,,, — frac{pi }{3};,,,,frac{pi }{3}.)
5) (06.2022 основная волна) а) Решите уравнение (2{cos ^2}x — 3sinleft( { — x} right) — 3 = 0.)
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{{{text{5}}pi }}{2};,,4pi } right]).
ОТВЕТ: а) (frac{pi }{6} + 2pi k;,,;frac{{{text{5}}pi }}{6} + 2pi k;;;frac{pi }{2} + 2pi k;;;k in Z;) б) (frac{{{text{17}}pi }}{6};,,,,frac{{{text{5}}pi }}{2}.)
6) (06.2022 основная волна) а) Решите уравнение (cos 2x + sinleft( { — x} right) — 1 = 0.)
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{pi }{2};,,2pi } right]).
ОТВЕТ: а) ( — frac{pi }{6} + 2pi k;,,; — frac{{{text{5}}pi }}{6} + 2pi k;;;pi k;;;k in Z;) б) (pi ;,,,,frac{{{text{7}}pi }}{6};,,,,frac{{{text{11}}pi }}{6};,,,2pi .)
7) (06.2022 основная волна) а) Решите уравнение (cos 2x + 3sinleft( { — x} right) — 2 = 0.)
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{{{text{3}}pi }}{2};,,3pi } right]).
ОТВЕТ: а) ( — frac{pi }{6} + 2pi k;,,; — frac{{{text{5}}pi }}{6} + 2pi k;;; — frac{pi }{{text{2}}}{text{ + 2}}pi k;;;k in Z;) б) (frac{{{text{3}}pi }}{2};,,,,frac{{{text{11}}pi }}{6}.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {{text{3}}pi ;,,frac{{{text{9}}pi }}{2}} right]).
ОТВЕТ: а) ( — frac{pi }{2} + 2pi k;,,;2pi k;;;;k in Z;) б) (frac{{{text{7}}pi }}{2};,,,4pi .)
9) (06.2022 основная волна) а) Решите уравнение (sin 2x + 2sin left( { — x} right) + cos left( { — x} right) — 1 = 0.)
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {{text{2}}pi ;,,frac{{{text{7}}pi }}{2}} right]).
ОТВЕТ: а) ( — frac{pi }{6} + 2pi k;,,; — frac{{{text{5}}pi }}{6} + 2pi k;;;2pi k;;;k in Z;) б) (frac{{{text{19}}pi }}{6};,,,2pi .)
10) (27.06.2022 резервная волна) а) Решите уравнение ({log _{11}}left( {2{{sin }^2}x + 7sqrt 3 sin x — 11} right) = 0.)
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{{{text{3}}pi }}{2};,,3pi } right]).
ОТВЕТ: а) (frac{pi }{3} + 2pi k;,,;frac{{{text{2}}pi }}{3} + 2pi k;;;k in Z;) б) (frac{{{text{7}}pi }}{3};,,,frac{{{text{8}}pi }}{3}.)
11) (27.06.2022 резервная волна) а) Решите уравнение ({log _9}left( {sqrt 2 sin x + sin 2x + 9} right) = 1.)
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ { — frac{{{text{7}}pi }}{2};,, — 2pi } right]).
ОТВЕТ: а) ( pm frac{{{text{3}}pi }}{4} + 2pi k;,,;;pi k;;;k in Z;) б) ( — frac{{{text{13}}pi }}{4};,, — 3pi ;,,, — frac{{{text{11}}pi }}{4};,, — 2pi .)
В задании №5 варианта ЕГЭ вам встретятся всевозможные уравнения: квадратные и сводящиеся к квадратным, дробно-рациональные, иррациональные, степенные, показательные и логарифмические и даже тригонометрические. Видите, как много нужно знать, чтобы справиться с заданием! И еще ловушки и «подводные камни», которые ждут вас в самом неожиданном месте.
Вот список тем, которые стоит повторить:
Квадратные уравнения
Арифметический квадратный корень
Корни и степени
Показательная функция
Показательные уравнения
Логарифмическая функция
Логарифмические уравнения
Тригонометрический круг
Формулы приведения
Формулы тригонометрии
Простейшие тригонометрические уравнения 1
Уравнения, сводящиеся к квадратным
1. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Кажется, что уравнение очень простое. Но иногда здесь ошибаются даже отличники. А вот шестиклассник бы не ошибся.
С левой частью уравнения все понятно. Дробь умножается на
А в правой части — смешанное число
Его целая часть равна 19, а дробная часть равна
Запишем это число в виде неправильной дроби:
Получим:
или
Выбираем меньший корень.
Ответ: -6,5.
2. Решите уравнение
Возведем в квадрат левую часть уравнения. Получим:
Ответ: -6.
Дробно-рациональные уравнения
3. Найдите корень уравнения
Перенесем единицу в левую часть уравнения. Представим 1 как и приведем дроби к общему знаменателю:
Ответ: -2.
Это довольно простой тип уравнений. Главное — внимательность.
Иррациональные уравнения
Так называются уравнения, содержащие знак корня — квадратного, кубического или n-ной степени.
4. Решите уравнение:
Выражение под корнем должно быть неотрицательно, а знаменатель дроби не равен нулю.
Значит, .
Возведём обе части уравнения в квадрат:
Решим пропорцию:
Условие при этом выполняется.
Ответ: 87.
5. Решите уравнение Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
А в этом уравнении есть ловушка. Решите его самостоятельно и после этого читайте дальше.
Выражение под корнем должно быть неотрицательно. И сам корень — величина неотрицательная. Значит, и правая часть должна быть больше или равна нуля. Следовательно, уравнение равносильно системе:
.
Решение таких уравнений лучше всего записывать в виде цепочки равносильных переходов:

Мы получили, что . Это единственный корень уравнения.
Типичная ошибка в решении этого уравнения такая. Учащиеся честно пишут ОДЗ, помня, что выражение под корнем должно быть неотрицательно:
Возводят обе части уравнения в квадрат. Получают квадратное уравнение: Находят его корни:
или
Пишут в ответ: -9 (как меньший из корней). В итоге ноль баллов.
Теперь вы знаете, в чем дело. Конечно же, число -9 корнем этого уравнения быть не может.
Ответ: 8.
6. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите больший из корней.
Запишем решение как цепочку равносильных переходов:

Ответ: 9.
Показательные уравнения
При решении показательных уравнений мы пользуемся свойством монотонности показательной функции.
7. Решите уравнение
Вспомним, что Уравнение приобретает вид:
Функция
монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.
откуда
Ответ: 4.
8. Решите уравнение
Представим как
Функция монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.
Ответ: 7,5.
9. Решите уравнение
Представим в виде степени с основанием 3 и воспользуемся тем, что
Ответ: 12,5.
Логарифмические уравнения
Решая логарифмические уравнения, мы также пользуемся монотонностью логарифмической функции: каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, значит, равны и сами числа.
И конечно, помним про область допустимых значений логарифма:
Логарифмы определены только для положительных чисел.
Основание логарифма должно быть положительно и не равно единице.
10. Решите уравнение:
Область допустимых значений: . Значит,
Представим 2 в правой части уравнения как , чтобы слева и справа в уравнении были логарифмы по основанию 5.
Функция монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом
Ответ: 21.
11. Решите уравнение:
Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:

Ответ: -4.
12. Решите уравнение:
Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:
Записываем решение как цепочку равносильных переходов.
.
Ответ: 19.
13. Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
В этом уравнении тоже есть ловушка. Мы помним, что основание логарифма должно быть положительно и не равно единице.
Получим систему:
Первое уравнение мы получили просто из определения логарифма.
Квадратное уравнение имеет два корня: и
Очевидно, корень является посторонним, поскольку основание логарифма должно быть положительным. Значит, единственный корень уравнения:
Ответ: 12.
Тригонометрические уравнения (Часть 1 ЕГЭ по математике)
Тригонометрические уравнения? В первой части вариантов ЕГЭ? — Да. Причем это задание не проще, чем задача 13 из второй части варианта Профильного ЕГЭ.
14. Найдите корень уравнения: В ответе запишите наибольший отрицательный корень.
Типичная ошибка — решать это уравнение в уме. Мы не будем так делать! Несмотря на то, что это задание включено в первую части варианта ЕГЭ, оно является полноценным тригонометрическим уравнением, причем с отбором решений.
Сделаем замену Получим:
Получаем решения: Вернемся к переменной x.
Поделим обе части уравнения на
и умножим на 4.
Первой серии принадлежат решения
Вторая серия включает решения
Наибольший отрицательный корень — тот из отрицательных, который ближе всех к нулю. Это
Ответ: -2.
15. Решите уравнение: В ответе напишите наименьший положительный корень.
Решение:
Сделаем замену Получим:
Решения этого уравнения:
Вернемся к переменной х:
Умножим обе части уравнения на 4 и разделим на
.
Выпишем несколько решений уравнения и выберем наименьший положительный корень:
Наименьший положительный корень
Ответ: 2.
Мы разобрали основные типы уравнений, встречающихся в задании №5 Профильного ЕГЭ по математике. Конечно, это не все, и видов уравнений в этой задаче существует намного больше. Именно поэтому мы рекомендуем начинать подготовку к ЕГЭ по математике не с задания 1, а с текстовых задач на проценты, движение и работу и основ теории вероятностей.
Успеха вам в подготовке к ЕГЭ!
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание №5. Простейшие уравнения. Профильный ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
Новые задания №1 ЕГЭ 2022 по математике профильного уровня — простейшие уравнения.
Для успешного результата необходимо уметь решать рациональные, иррациональные, показательные, тригонометрические и логарифмические уравнения, их системы.
Задание №1 ЕГЭ 2022 математика профильный уровень Прототипы
| Источник: math100.ru | → Рациональные уравнения
→ Иррациональные уравнения → Показательные уравнения → Логарифмические уравнения → Тригонометрические уравнения |
| time4math.ru | → скачать задания |
| vk.com/ekaterina_chekmareva | → задания |
При отработке данного задания будут полезны книги:
Купить ЕГЭ 2022 Математика. 100 баллов. Профильный уровень. Решение уравнений и неравенств
Купить Математика: уравнения и неравенства. Подготовка к ЕГЭ: профильный уровень
Купить Показательные и логарифмические уравнения. ЕГЭ. Математика
Купить Методы решения тригонометрических уравнений. ЕГЭ. Математика
Связанные страницы:
Тренировочные варианты ЕГЭ 2022 по математике профильного уровня
Решение 17 задания ЕГЭ по профильной математике
Тренировочные варианты ЕГЭ 2022 по математике базового уровня
Купить сборники типовых вариантов ЕГЭ по математике
Задание 9 профильного ЕГЭ по математике. Практика
Прототипы задания №1 профильного ЕГЭ 2022 по математике
Новые задания №1 ЕГЭ 2022 по математике профильного уровня — простейшие уравнения.
Для успешного результата необходимо уметь решать рациональные, иррациональные, показательные, тригонометрические и логарифмические уравнения, их системы.
Задание №1 ЕГЭ 2022 математика профильный уровень Прототипы
| Источник: math100.ru | → Рациональные уравнения
→ Тригонометрические уравнения |
| time4math.ru | → скачать задания |
| vk.com/ekaterina_chekmareva | → задания |
При отработке данного задания будут полезны книги:
Задание 1. Простейшие уравнения. ЕГЭ 2022 по математике профильного уровня
Задачи для практики
Задача 1
Найдите корень уравнения $log_ <64>= 2$.
Решение
По определению логарифма если $log_b a=c$, то $b^c=a$
$x + 5 = 8$ или $x + 5 = -8$,
$x = 3 $ или $x = -13 $
$x = -13$ — не входит в ОДЗ.
Задача 2
Решение
Откуда: $x=2$ или $x=11/13 — $ второй корень не удовлетворяет ОДЗ,
Задача 3
Найдите корень уравнения $log_<3> <(4x-15)>=log_<3><(x+3)>$.
Решение
$log_3 (4x — 15) = log_3 (x + 3)$,
Проверка. При $x = 6$ получаем $log_3 (6 · 4 — 15) = log_3 (6 + 3)$ — верное равенство.
$x = 6$ — корень уравнения.
Задача 4
Найдите корень уравнения $625^= <1>/ <5>$.
Решение
Задача 5
Найдите корень уравнения $9^= <1>/ <3>$.
Решение
Задача 6
Найдите корень уравнения $(x-12)^3=-27$.
Решение
Задача 7
Найдите корень уравнения $log_<2> <(12+x)>=-2$.
Решение
По определению логарифма $12+x = 2^<-2>, 12+x = 0.25, x = 0.25-12, x = -11.75$.
Задача 8
Найдите корень уравнения $log_<3> <(4-x)>=5$.
Решение
По определению логарифма если $log_b a=c$, то $b^c=a$
Задача 9
Решите уравнение $(x+7)^2 = x^2+7$. Если уравнение имеет более одного корня, в ответе запишите меньший из них.
Решение
Задача 10
Решите уравнение $(5x+11)^2 = (5x-2)^2$. Если уравнение имеет более одного корня, в ответе запишите меньший из них.
Решение
Воспользуемся формулами сокращенного умножения:
$(a+b)^2=a^2+2ab+b^2$
$(a-b)^2=a^2-2ab+b^2$
Таким образом:
$25x^2+110x+121=25x^2-20x+4$,
$ 110x+20x=-117$,
$130x=-117$
$x=-117/130$
$x=-0.9$.
Задача 11
Найдите корень уравнения $√ <14-5x>=-x$. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Решение
Так как левая часть уравнения неотрицательна, то и правая тоже неотрицательна:
$-x ⩾ 0$, — домножим обе части на -1, в таком случае знак неравенства меняется
Возведя обе части в квадрат, получим уравнение $14-5x=x^2$,
$ x_2=2$ — не удовлетворяет условию $x⩽ 0$.
Задача 12
Найдите корень уравнения $ / <2x-11>= / <3x-7>$. Если уравнение имеет более одного корня, в ответе запишите больший из корней.
Решение
Удобно домножить обе стороны равенства на знаменатели, проще говоря «крест накрест»
$x_1=-3, x_2=-4$ — оба корня удовлетворяют ОДЗ
Наибольший корень: $x=-3$
Задача 13
Найдите корень уравнения $ <9-5x>/ =x$. Если уравнение имеет более одного корня, в ответе запишите больший из корней.
Задание №1. Простейшие уравнения. Профильный ЕГЭ по математике
В задании №1 варианта ЕГЭ вам встретятся всевозможные уравнения: квадратные и сводящиеся к квадратным, дробно-рациональные, иррациональные, степенные, показательные и логарифмические и даже тригонометрические. Видите, как много нужно знать, чтобы справиться с заданием! И еще ловушки и «подводные камни», которые ждут вас в самом неожиданном месте.
Вот список тем, которые стоит повторить:
Уравнения, сводящиеся к квадратным
1. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Кажется, что уравнение очень простое. Но иногда здесь ошибаются даже отличники. А вот шестиклассник бы не ошибся.
С левой частью уравнения все понятно. Дробь умножается на А в правой части — смешанное число Его целая часть равна 19, а дробная часть равна Запишем это число в виде неправильной дроби:
Выбираем меньший корень.
Ответ: — 6,5.
2. Решите уравнение
Возведем в квадрат левую часть уравнения. Получим:
Дробно-рациональные уравнения
3. Найдите корень уравнения
Перенесем единицу в левую часть уравнения. Представим 1 как и приведем дроби к общему знаменателю:
Это довольно простой тип уравнений. Главное — внимательность.
Иррациональные уравнения
Так называются уравнения, содержащие знак корня — квадратного, кубического или n-ной степени.
4. Решите уравнение:
Выражение под корнем должно быть неотрицательно, а знаменатель дроби не равен нулю.
Значит, 
Возведём обе части уравнения в квадрат:
Условие 
5. Решите уравнение Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
А в этом уравнении есть ловушка. Решите его самостоятельно и после этого читайте дальше.
Выражение под корнем должно быть неотрицательно. И сам корень — величина неотрицательная. Значит, и правая часть должна быть больше или равна нуля. Следовательно, уравнение равносильно системе:
Решение таких уравнений лучше всего записывать в виде цепочки равносильных переходов:
Мы получили, что . Это единственный корень уравнения.
Типичная ошибка в решении этого уравнения такая. Учащиеся честно пишут ОДЗ, помня, что выражение под корнем должно быть неотрицательно:
Возводят обе части уравнения в квадрат. Получают квадратное уравнение: Находят его корни: или Пишут в ответ: -9 (как меньший из корней). В итоге ноль баллов.
Теперь вы знаете, в чем дело. Конечно же, число -9 корнем этого уравнения быть не может.
6. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите больший из корней.
Запишем решение как цепочку равносильных переходов.
Показательные уравнения
При решении показательных уравнений мы пользуемся свойством монотонности показательной функции.
7. Решите уравнение
Вспомним, что Уравнение приобретает вид: Функция монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.
8. Решите уравнение
Функция монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.
9. Решите уравнение
Представим в виде степени с основанием 3 и воспользуемся тем, что
Логарифмические уравнения
Решая логарифмические уравнения, мы также пользуемся монотонностью логарифмической функции: каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, значит, равны и сами числа.
И конечно, помним про область допустимых значений логарифма:
Логарифмы определены только для положительных чисел;
Основание логарифма должно быть положительно и не равно единице.
10. Решите уравнение:
Область допустимых значений: 
Представим 2 в правой части уравнения как — чтобы слева и справа в уравнении были логарифмы по основанию 5.
Функция монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом
11. Решите уравнение:
Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:
12. Решите уравнение:
Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:
Записываем решение как цепочку равносильных переходов.
13. Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
В этом уравнении тоже есть ловушка. Мы помним, что основание логарифма должно быть положительно и не равно единице.
Первое уравнение мы получили просто из определения логарифма.
Квадратное уравнение имеет два корня: и
Очевидно, корень является посторонним, поскольку основание логарифма должно быть положительным. Значит, единственный корень уравнения:
Тригонометрические уравнения (Часть 1 ЕГЭ по математике)
Тригонометрические уравнения? В первой части вариантов ЕГЭ? — Да. Причем это задание не проще, чем задача 13 из второй части варианта Профильного ЕГЭ.
14. Найдите корень уравнения: В ответе запишите наибольший отрицательный корень.
Типичная ошибка — решать это уравнение в уме. Мы не будем так делать! Несмотря на то, что это задание включено в первую части варианта ЕГЭ, оно является полноценным тригонометрическим уравнением, причем с отбором решений.
Сделаем замену Получим:
Получаем решения: Вернемся к переменной x.
Поделим обе части уравнения на и умножим на 4.
Первой серии принадлежат решения
Вторая серия включает решения
Наибольший отрицательный корень — тот из отрицательных, который ближе всех к нулю. Это
15. Решите уравнение В ответе напишите наименьший положительный корень.
Сделаем замену Получим: Решения этого уравнения:
Вернемся к переменной х:
Умножим обе части уравнения на 4 и разделим на
Выпишем несколько решений уравнения и выберем наименьший положительный корень:
Наименьший положительный корень
Мы разобрали основные типы уравнений, встречающихся в задании №1 Профильного ЕГЭ по математике. Конечно, это не все, и видов уравнений в этой задаче существует намного больше. Именно поэтому мы рекомендуем начинать подготовку к ЕГЭ по математике не с задания 1, а с текстовых задач на проценты, движение и работу и основ теории вероятностей.
Успеха вам в подготовке к ЕГЭ!
источники:
http://egeturbo.ru/ege/math/tasks/1
http://ege-study.ru/ru/ege/materialy/matematika/zadanie-1-prostejshie-uravneniya/
ЕГЭ по математике Профиль. Задание 1: Уметь решать уравнения. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.
Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».
ЕГЭ Профиль. Задание № 1.
АЛГОРИТМ ВЫПОЛНЕНИЯ
Задание № 1 рассчитано на умение решать простейшие уравнения. Такие уравнения содержат одну переменную и не требуют значительных алгебраических преобразований. Прежде чем приступить к решению, важно определить тип уравнения — линейное, квадратное, показательное, логарифмическое и т. д. Это позволит выбрать правильный метод решения. В ответе надо записать целое или дробное число. Если в результате получилась обыкновенная дробь, её нужно перевести в десятичную.
План выполнения:
- Внимательно прочитайте условие задания.
- Решите уравнение.
- Проверьте, все ли корни уравнения удовлетворяют области определения.
- Запишите полученное число в поле ответа КИМ и бланк ответов № 1.
Пример задания № 1. Найдите корень уравнения (х – 2)2 = (3 + х)2.
Решение:
Ответ: –0,5.
АНАЛИЗ ТИПИЧНЫХ ОШИБОК
- При решении уравнений определенного вида следует пользоваться формулами сокращённого умножения.
- Часто учащиеся опускают чётную степень, что приводит к неправильному решению.
- Учащиеся иногда неправильно возводят двучлен в квадрат, забывая удвоенное произведение.
- Кубические уравнения всегда имеют действительные корни.
- Иногда учащиеся неправильно извлекают кубический корень из числа.
Тренировочные задания с самопроверкой
№ 1.1. Найдите корень уравнения (1/6)x+5 = 6х.
Открыть ОТВЕТ
№ 1.2. Найдите корень уравнения x = (4x + 27)/(x – 2). Если уравнение имеет более одного корня, в ответе запишите меньший из них.
Открыть ОТВЕТ
№ 1.3. Решите уравнение х2 + х – 56 = 0. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Открыть ОТВЕТ
№ 1.4. Найдите корень уравнения log8(5x – 7) = log8(x + 11).
Открыть ОТВЕТ
№ 1.5. Найдите корень уравнения –2 8/9 • х = 4 1/3.
Открыть ОТВЕТ
СПРАВОЧНЫЙ МАТЕРИАЛ
Равенство с одной или несколькими переменными называется уравнением. Значение переменной, при котором получается верное решение, называется корнем уравнения. Решить уравнение — значит найти все его корни или доказать, что уравнение не имеет корней.
При решении задания необходимо определить тип уравнения — линейное, квадратное, показательное, логарифмическое и т. д. Это позволит выбрать правильный метод решения.
1. Линейные уравнения
2. Квадратные уравнения
3. Рациональные уравнения
Задачи такого типа содержат уравнения, в знаменателе которых находится выражение, содержащее переменную.
4. Иррациональные уравнения
Задачи этого задания решаются методом возведения обеих частей уравнения в степень, соответствующую степени корня.
5. Показательные уравнения
Задание состоит из простейшего показательного уравнения. Ответом к заданию является целое или дробное число.
6. Логарифмические уравнения
Уравнения этого типа решаются по определению логарифма, а также с использованием свойств логарифма. Ответом является целое или дробное число. При решении логарифмических уравнений обязательно учитывается область определения логарифма.
Методы решения логарифмических уравнений:
Вы смотрели: ЕГЭ по математике Профиль. Задание 1: Уметь решать уравнения. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.
Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».
Просмотров:
10 973
За это задание ты можешь получить 2 балла. На решение дается около 10 минут. Уровень сложности: повышенный.
Средний процент выполнения: 45.3%
Ответом к заданию 12 по математике (профильной) может быть развернутый ответ (полная запись решения с обоснованием выполненных действий).
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
а) Решите уравнение $11cos 2x=7sin (x-{π} / {2})-9$.
б) Укажите корни этого уравнения, принадлежащие отрезку $[-π;0]$.
Решение
а) $11cos 2x=7sin (x-{π} / {2})-9$,
$11(2cos^2 x-1)=-7cos x-9$,
$22cos^2 x -11+7cos x +9=0$,
$22cos^2 x+7cos x -2=0$.
Обозначим $cos x=t$, $|t|⩽1$.
Тогда уравнение примет вид: $22t^2+7t-2=0$.
Решим его. $22t^2+7t-2=0$,
$D=49+2⋅ 4⋅ 22=225$. $t_{1,2}={-7±15} / {44}$,
$t_1=-{1} / {2}$, $t_2={8} / {44}={2} / {11}$.
$1$. $cos x=-{1} / {2}$, $x=±(π-{π} / {3})+2π n$;
$x=± {2π} / {3}+2π n$, $n∈ Z$.
$2$. $cos x={2} / {11}$, $x=± arccos {2} / {11}+2π k$, $k∈ Z$.
б) Найдём корни этого уравнения, принадлежащие промежутку $[-π;0]$.
$x_1=-π+{π} / {3}=-{2π} / {3}$
$x_2=-arccos {2} / {11}$.
Ответ: а)$± {2π} / {3}+2πn, n∈ Z; ± arccos {2} / {11}+2π k, k∈ Z;б)-{2π}/{3}, -arccos{2}/{11}$
Задача 2
а) Решите уравнение $2 sin^2 x — 7 cos(x + {π}/{2})- 4 = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[-2π;-{π}/{2}]$.
Решение
а) Преобразуем уравнение, согласно формуле приведения:
$cos(x+{π}/{2})=-sinx,$
$2sin^2x + 7sinx -4 = 0$
Обозначим $sin x = t, −1 ≤ t ≤ 1$, получим
$2t^2 + 7t -4 = 0.$
$t_1 = {−7 − 9}/{2·2} = −4$ — не удовлетворяет условию $−1 ≤ t ≤ 1. $
$t_2 = {−7 + 9}/{2·2} = {1}/{2}$.
Вернёмся к исходной переменной:
$sinx ={1}/{2}$,
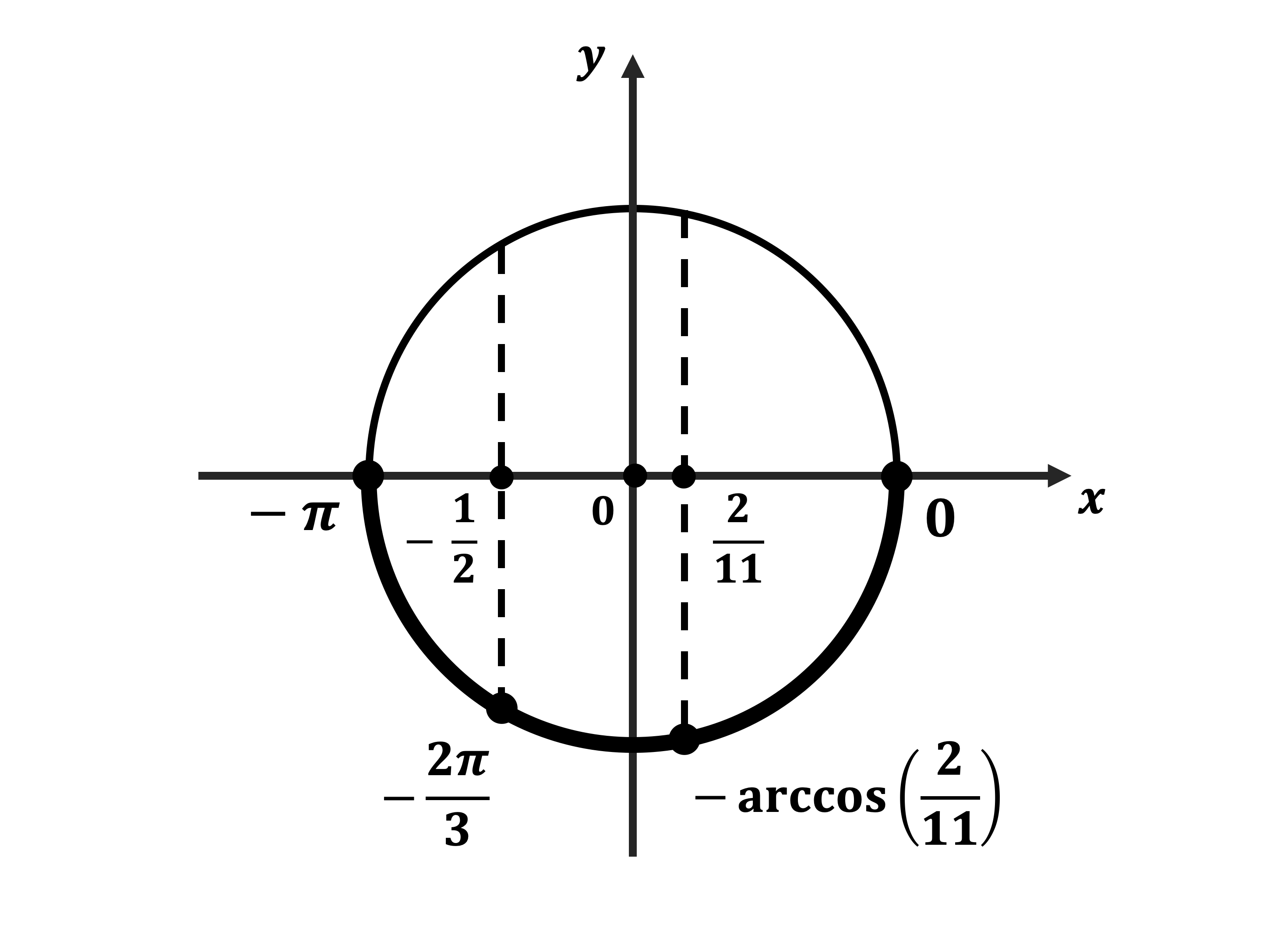
$x = {π}/{6} + 2πn, n ∈ Z$
$x = {5π}/{6} + 2πk, k ∈ Z$
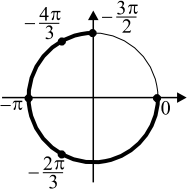
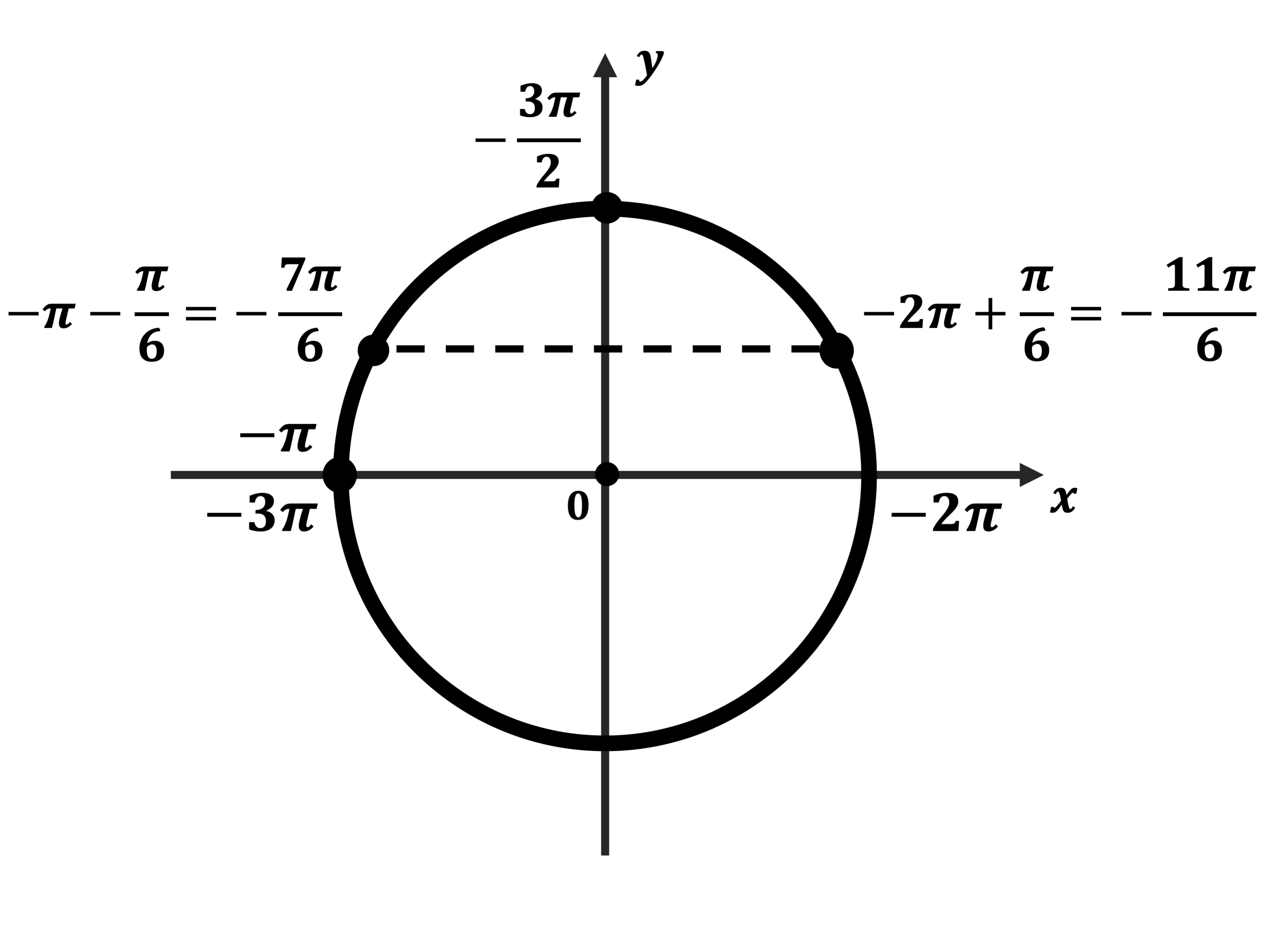
б) Корни, принадлежащие отрезку $[-2π; -{π}/{2}]$, найдём с помощью единичной окружности. Получим: ${π}/{6}-2π=-{11π}/{6}; {5π}/{6}-2π=-{7π}/{6}$.
Ответ: а) $ {π}/{6} + 2πn, n ∈ Z$; $ {5π}/{6} + 2πk, k ∈ Z$ б) $-{11π}/{6};-{7π}/{6}$
Задача 3
а) Решите уравнение $2 cos^2 x — 5 sin(x + {3π}/{2})+ 2 = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[{π}/{2};{3π}/{2}]$.
Решение
а) Преобразуем уравнение, согласно формуле приведения:
$sin(x+{3π}/{2})=-cosx,$
$2cos^2x + 5 cos x + 2 = 0$
Обозначим $cos x = t, −1 ≤ t ≤ 1$, получим $2t^2 + 5t + 2 = 0. t_1 = {−5 − 3}/{2·2} = −2$ — не удовлетворяет условию $−1 ≤ t ≤ 1. t_2 = {−5 + 3}/{2· 2} = −{1}/{2}$.
Вернёмся к исходной переменной: $cos x = − {1}/{2}$,
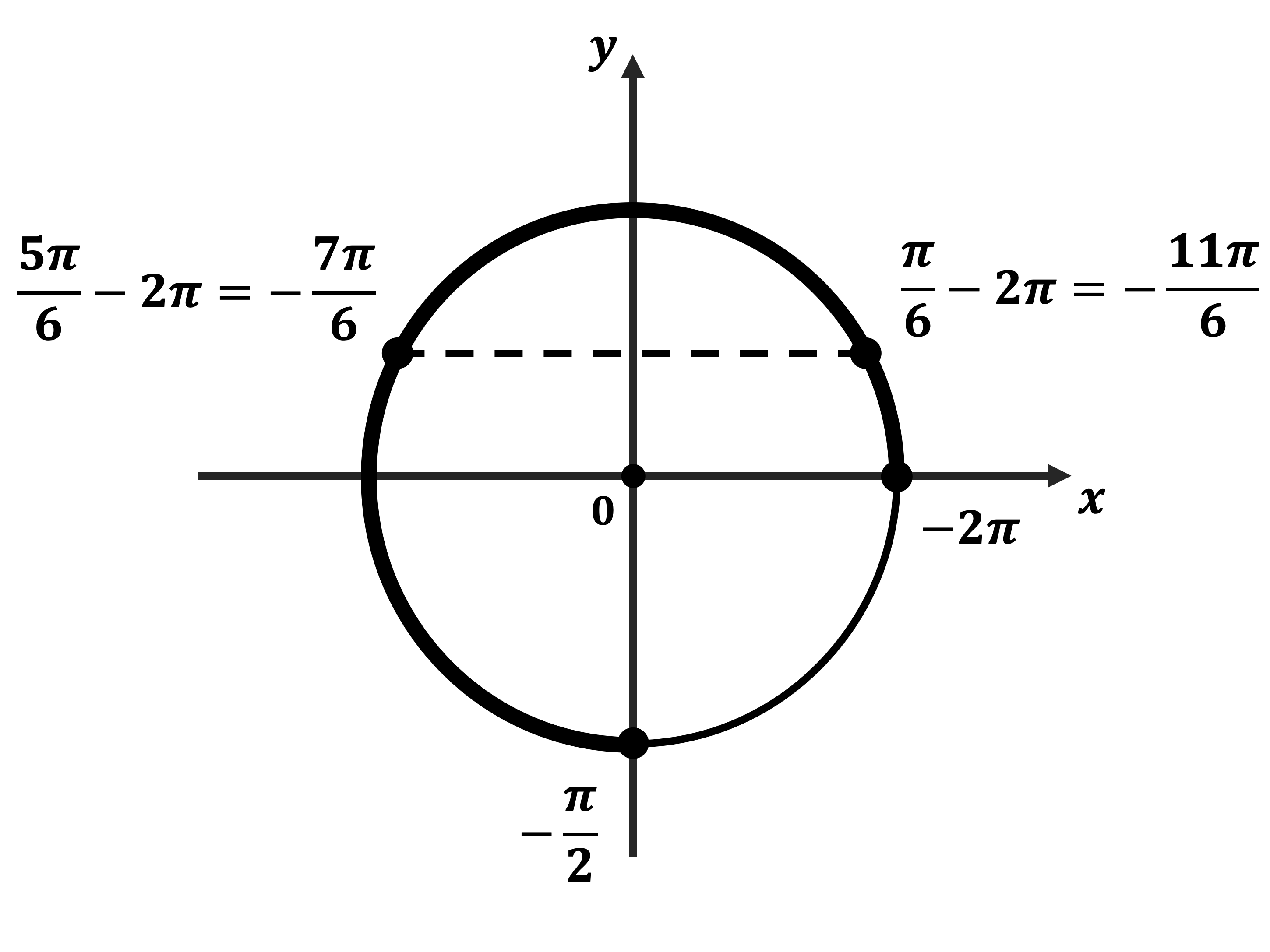
$x = ±(π − {π}/{3}) + 2πn, n ∈ Z , x = ±{2π}/{3} + 2πn, n ∈ Z.$
б) Корни, принадлежащие отрезку $[{π}/{2}; {3π}/{2}]$, найдём с помощью единичной окружности. Получим числа ${2π}/{3}; {4π}/{3}$.
Ответ: а)$±{2π}/{3}+2πn,n∈Z;$ б) ${2π}/{3};{4π}/{3}$
Задача 4
а) Решите уравнение $cos(x — {3π}/{2})= sin 2x$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[-{3π}/{2};0]$.
Решение
а) Преобразуем уравнение:
$−sin x = sin 2x,$
$sinx + 2 sin x cos x = 0,$
$sinx(1 + 2 cos x) = 0,$
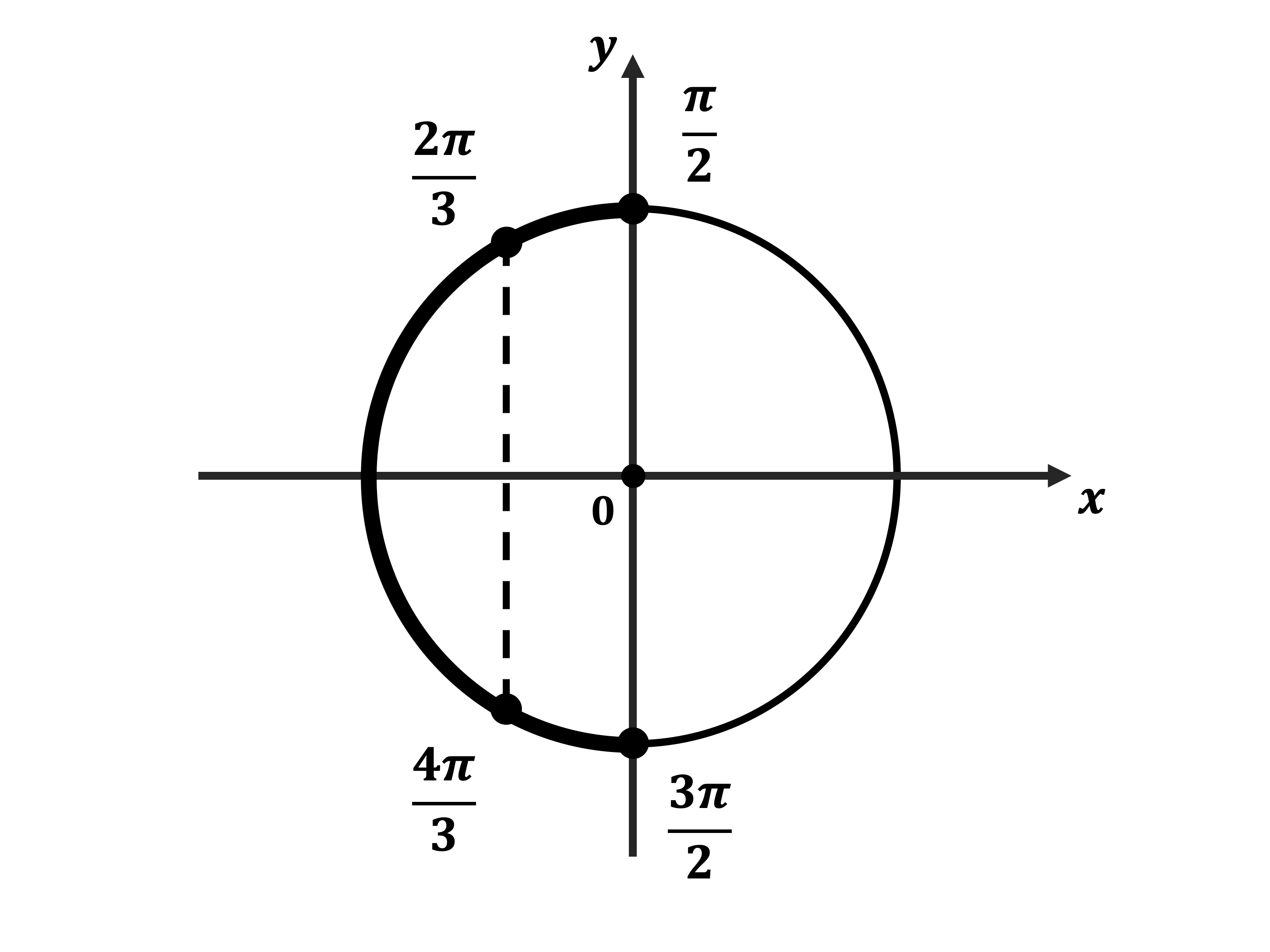
$sin x = 0;x = πn, n ∈ Z,$
$cosx = -{1}/{2}; x = ±{2π}/{3} + 2πk, k ∈ Z .,$
б) Корни, принадлежащие отрезку $[-{3π}/{2};0]$, найдём с помощью единичной окружности. Получим числа $−{4π}/{3}; −π; −{2π}/{3}; 0$.
Ответ: а) $x=±{2π}/{3}+2πk;x=πn,k,n∈Z$ б) $-{4π}/{3};-π;-{2π}/{3};0$.
Задача 5
а) Решите уравнение $sin({π}/{2}+ x)= sin (-2x)$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[0; π]$.
Решение
а) Преобразуем уравнение:
$cos x = − sin 2x,$
$cos x + 2 sin x cos x = 0,$
$cos x(1 + 2 sin x) = 0,$
$cos x = 0;$
$x = {π}/{2} + πn, n ∈ Z$
$sin x = −{1}/{2},$
$x = (−1)^{k+1}·{π}/{6} + πk, k ∈ Z$
б) Корни, принадлежащие отрезку $[0; π]$, найдём с помощью единичной окружности.
Указанному промежутку принадлежит единственное число ${π}/{2}$.
Ответ: а) ${π}/{2}+πn,n∈Z;(-1)^{k+1}{π}/{6}+πk,k∈Z$; б) ${π}/{2}$
Задача 6
а) Решите уравнение $sin x(2 sin x — 1) + √3 sin x + sin {4π}/{3}= 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[-{π}/{2};π]$.
Решение
а) Решим уравнение $sinx(2sinx-1) +√3sinx + sin{4π}/{3} = 0$.
Так как $sin{4π}/{3} = sin(π +{π}/{3}) = − sin{π}/{3} = −{√3}/{2}$, то уравнение примет вид $sin x(2 sin x-1) +√3 sin x-{√3}/{2} = 0$. Отсюда $2 sin x(sin x-{1}/{2})+ √3(sin x-{1}/{2}) = 0; (2sinx+√3)(sin x-{1}/{2}) = 0$.
Тогда $sin x = {1}/{2}; x = (−1)^n{π}/{6} + πn$ или $sin x = −{√3}/{2}; x = (−1)^{n+1}{π}/{3} + πn$, где $n ∈ Z.$
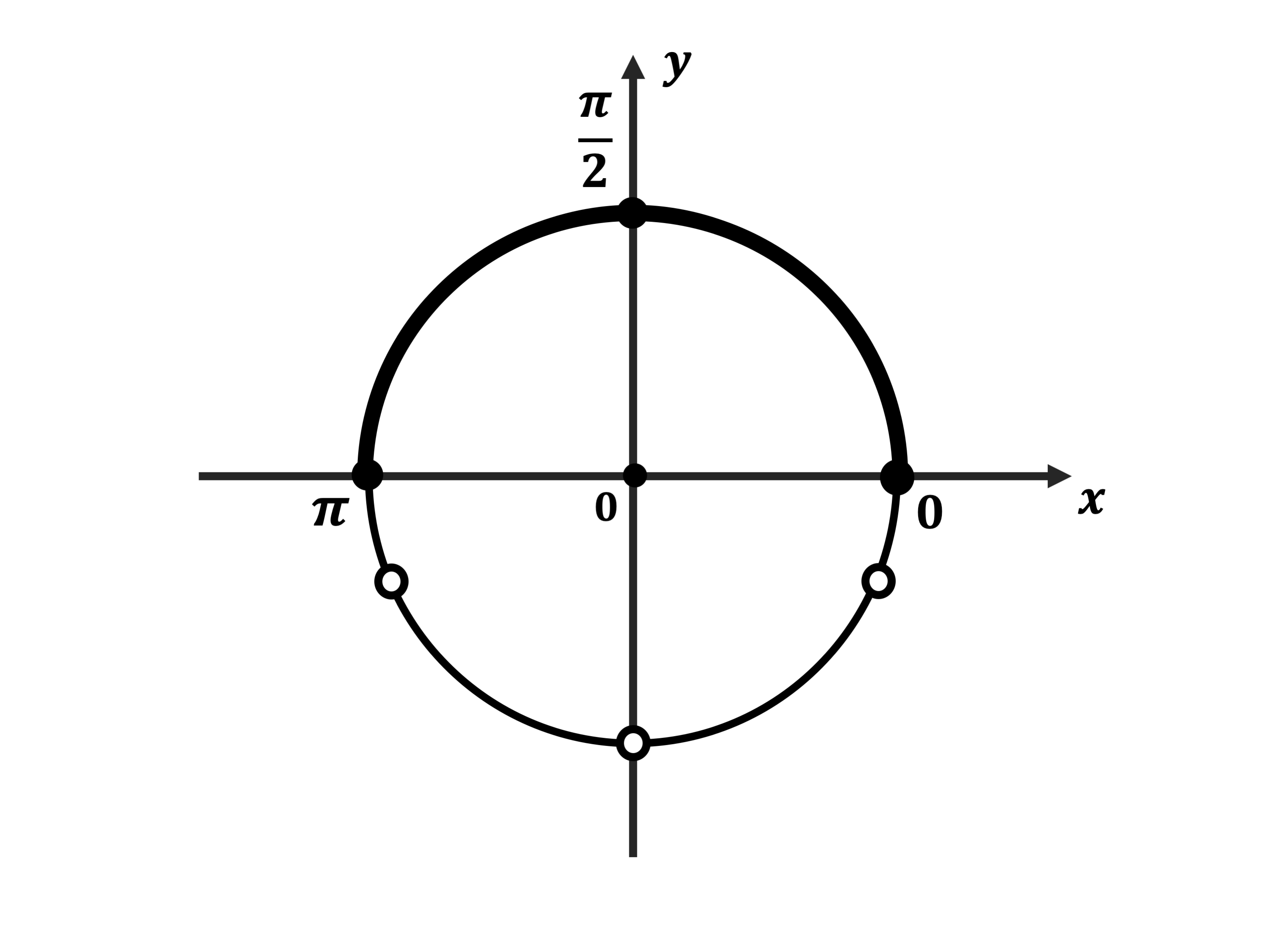
б) Корни, принадлежащие промежутку $[−{π}/{2}; π]$, найдём с помощью числовой окружности: $−{π}/{3}; {π}/{6}; {5π}/{6}$.
Ответ: а)$(-1)^{n}{π}/{6}+πn;(-1)^{n+1}{π}/{3}+πn,n∈Z$; б) $-{π}/{3};{π}/{6};{5π}/{6}$
Задача 7
а) Решите уравнение $4cos^{2}x = 3cos2x + 1$.
б) Найдите корни уравнения, принадлежащие отрезку $[-4π;-{5π}/{4})$.
Решение
a) $4cos^{2}x = 3cos2x+1$,
$4cos^{2}x = 3(2cos^{2}x-1)+1$,
$4cos^{2}x=6cos^{2}x-3+1$,
$cos^{2}x=1, [tablecosx=1; cosx=-1;$ $[tablex=2πn, n ∈ Z; x=π+2πk, k ∈ Z;$ $x=πk, k ∈ Z$
б) Корни, принадлежащие промежутку $[-4π;-{5π}/{4})$, найдем из неравенства $-4π ≤ πk < -{5π}/{4}; k=-4, -3, -2$
$x_1=-4π, x_2=-3π, x_3=-2π$.
Ответ: а)$πn,n∈Z$;б)$-4π;-3π;-π$
Задача 8
а) Решите уравнение $cos (2x) + 3 sin x — 2 = 0$.
б) Найдите корни уравнения, принадлежащие отрезку $[-3π;-π]$.
Решение
a) $cos(2x) + 3sinx-2=0$,
$1 — 2sin^{2}x + 3 sin x -2 = 0$,
$2 sin^{2}x — 3sin x +1 = 0$,
Пусть $sin x = y, |sinx| ≤ 1$, уравнение примет вид
$2y^2 — 3y + 1 = 0$,
$y_{1,2} = {3±√{9-8}}/{4} = {3±1}/{4};$
$ y_1=1, y_2={1}/{2}$.
$sin x = 1, x = {π}/{2}+2πn, n ∈ Z; sinx={1}/{2}, x=(-1)^{k}{π}/{6} + πk, k ∈ Z$.
б) Найдём корни уравнения на отрезке $[-3π;-π]$.
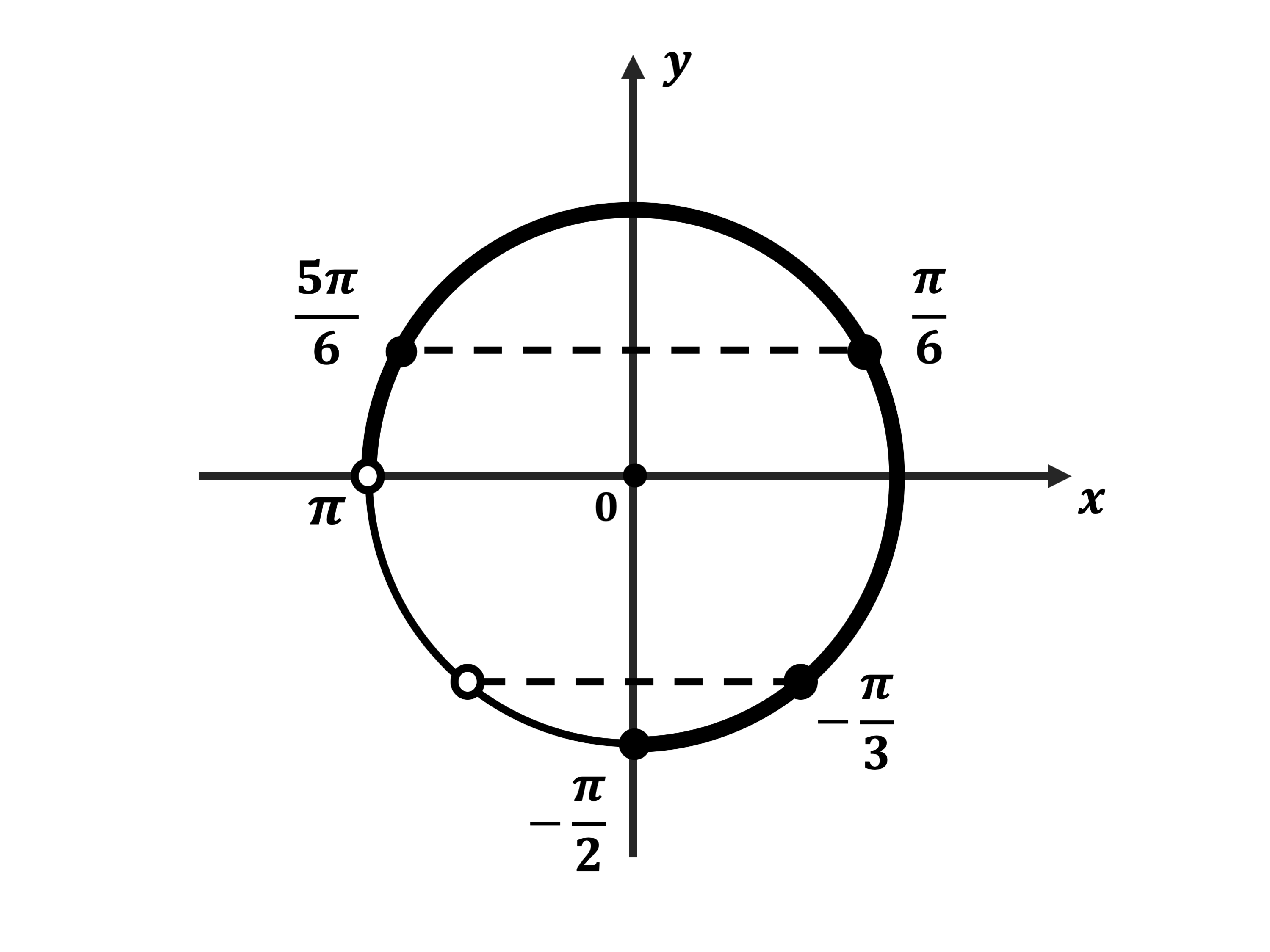
С помощью числовой окружности отберём корни уравнения, принадлежащие $[-3π;-π]$.
Это числа $-{11π}/{6}, -{3π}/{2}, -{7π}/{6}$.
Ответ: а)${π}/{2}+2πn,n∈Z;(-1)^{k}{π}/{6}+πk,k∈Z$;б)$-{11π}/{6};-{3π}/{2};-{7π}/{6}$
Задача 9
а) Решите уравнение $2 cos^2 x + 19 sin x + 8 = 0$.
б) Найдите корни уравнения, принадлежащие отрезку $[-π;{π}/{2}]$.
Решение
a) $2 cos^{2}x + 19sinx+8=0$,
$2(1 — sin^{2}x) + 19 sin x +8 = 0$,
$-2 sin^{2}x + 19 sin x +10 = 0$,
$2 sin^{2}x — 19 sin x -10 = 0$.
Пусть $sin x = y, |y| ≤ 1$, уравнение примет вид $2y^2 — 19y -10 = 0$, решим его: $y_{1,2} = {19±√{361 + 80}}/{4} = {19±21}/{4}$.
$y_1 = 10$ или $y_2 = -{1}/{2}$. $y_1=10$ не удовлетворяет условию $|y| ≤ 1$. $sin x = -{1}/{2}, x = (-1)^{n+1}{π}/{6} + πn, n ∈ Z$.
б) Найдём корни уравнения на отрезке $[-π;{π}/{2}]$.
Это числа $-{5π}/{6}$ и $-{π}/{6}$.
Ответ: а)$(-1)^{n+1}{π}/{6}+πn,n∈Z$; б) $-{5π}/{6},-{π}/{6}$
Задача 10
а) Решите уравнение $8sin x + 4 cos^2 x = 7$.
б) Найдите корни уравнения, принадлежащие отрезку $[-{3π}/{2};-{π}/{2}]$.
Решение
a) $8 sin x + 4 cos^{2} x = 7$,
$4(1 — sin^{2}x) + 8 sin x — 7 = 0$,
$-4 sin^{2}x + 8 sin x — 3 = 0$,
$4 sin^{2}x — 8 sin x + 3 = 0$.
Пусть $sin x = t, |t| ≤ 1$, уравнение примет вид $4t^2 — 8t + 3 = 0$, решим его: $t_{1,2} = {8±√{64 — 48}}/{8} = {8±√{16}}/{8} = {8±4}/{8} = 1±{1}/{2}$.
$t_1 = {1}/{2}$ или $t_2 = {3}/{2}$. $t_2$ не удовлетворяет условию $|t| ≤ 1$. $sin x = {1}/{2}, x = (-1)^{n}{π}/{6} + πn, n ∈ Z$.
б) Найдём корни уравнения на отрезке $[-{3π}/{2};-{π}/{2}]$.
Это число ${5π}/{6} — 2π = -{7π}/{6}$.
Ответ: а)$(-1)^{n}{π}/{6}+πn,n∈Z$;б)$-{7π}/{6}$
Задача 11
а) Решите уравнение ${sin 2x}/{sin({3π}/{2}+ x)}= 1$.
б) Укажите корни этого уравнения, принадлежащие промежутку $(3π;{9π}/{2})$.
Решение
а) ${{sin2x}/{sin({3π}/{2} + x)} = 1$.
Зная, что $sin2x = 2sinxcosx$ и $sin({3π}/{2}+ x)= −cosx$, получим: ${2sinxcosx}/{−cosx}= 1$, где $cosx≠0, x≠{π}/{2}+ πm, m ∈ Z$.
$−2sinx = 1, sinx =−{1}/{2}$.
$x=−{π}/{6}+2πn, n ∈ Z;$
$x=-{5π}/{6}+ 2πk, k ∈ Z$.
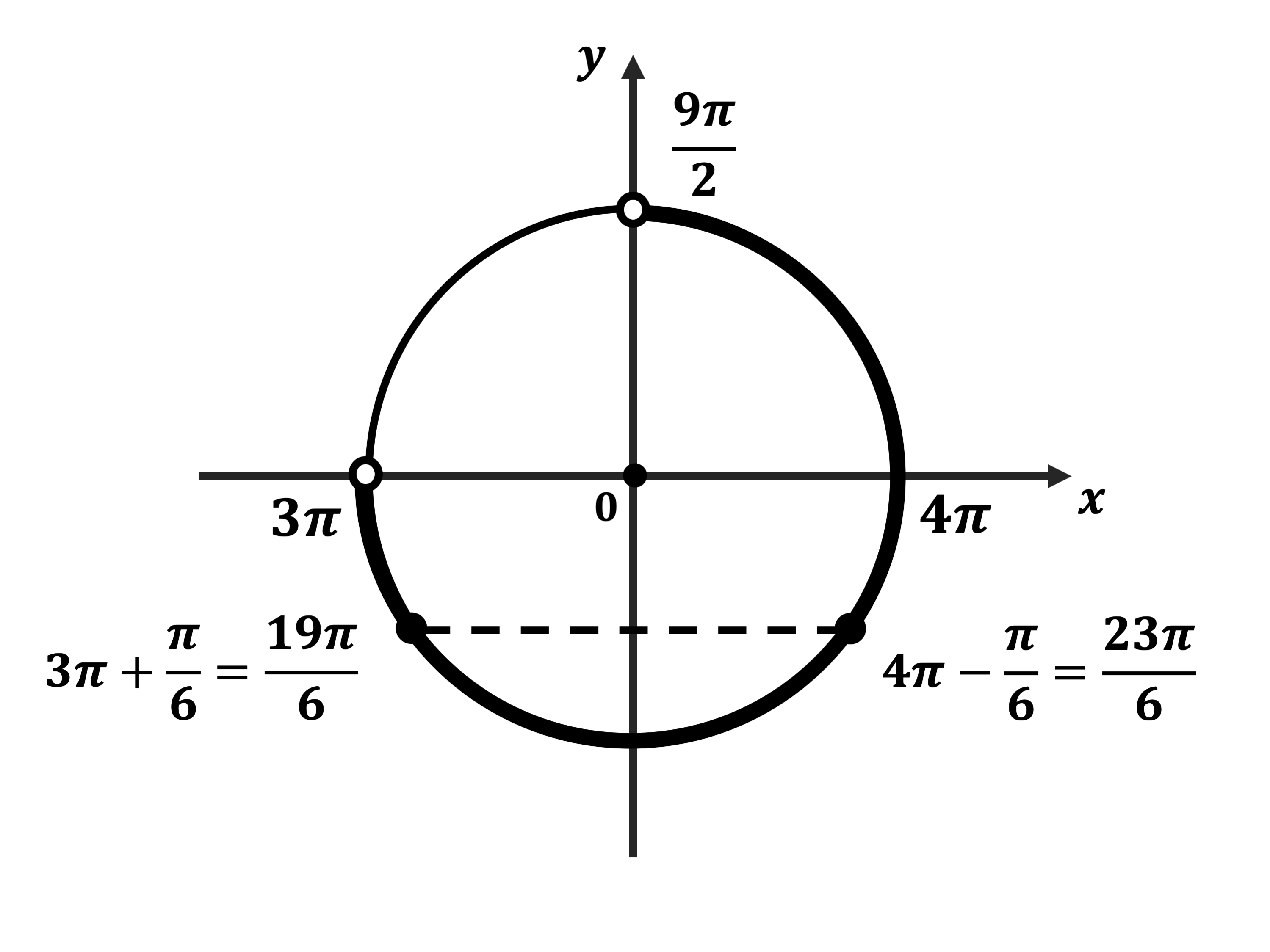
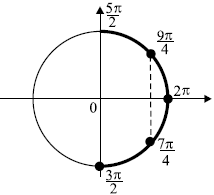
б) Отберём корни уравнения, принадлежащие промежутку $(3π; {9π}/{2})$,с помощью числовой окружности.
$x_1=3π+{π}/{6}={19π}/{6}$,
$x_2=4π−{π}/{6}={23π}/{6}$.
Ответ: а)$-{π}/{6}+2πn,-{5π}/{6}+2πk,n,k∈Z$;б)${19π}/{6};{23π}/{6}$
Задача 12
а) Решите уравнение ${sin 2x}/{sin(π — x)}= √2$.
б) Укажите корни этого уравнения, принадлежащие промежутку $[-{5π}/{2};-π)$.
Решение
а)${sin2x}/{sin(π — x)}=√2$.
а) Применим формулу синуса двойного аргумента $sin2x = 2sinxcosx$ и формулу приведения $sin(π — x) = sin x$.
Уравнение примет вид: ${2sinxcosx}/{sinx} = √2$.
Учитывая, что $sinx≠0, x≠πn, n∈Z$, получим:
$2cosx=√2$,
$cosx = {√2}/{2}$,
$x = ±{π}/{4} + 2πk, k∈Z$;
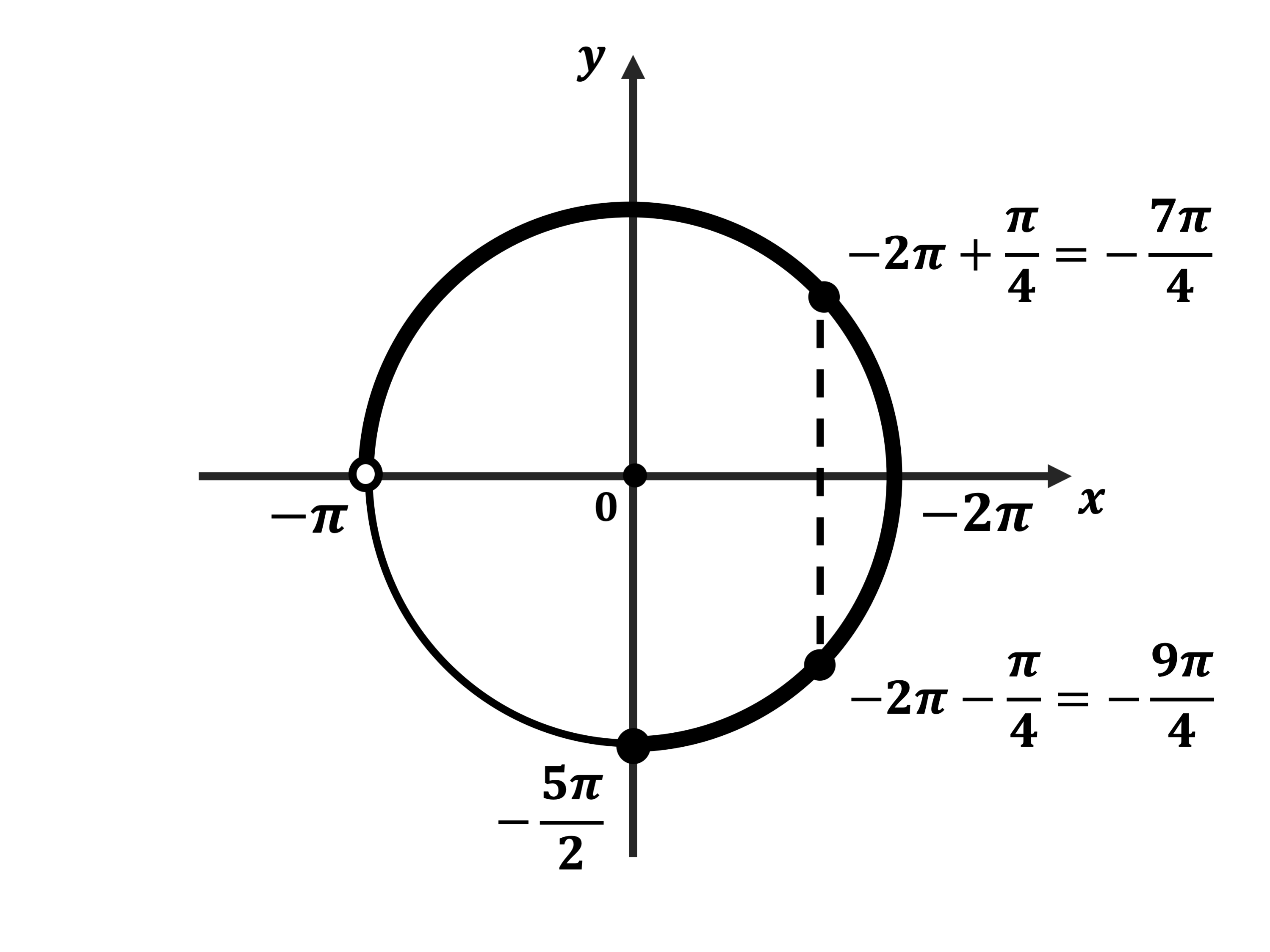
б) Отберём корни уравнения, принадлежащие промежутку $[-{5π}/{2};-π)$, с помощью окружности.
$x_1=-2π+{π}/{4}=-{7π}/{4}$
$x_2=-2π-{π}/{4}=-{9π}/{4}$
Ответ: а)$±{π}/{4}+2πk,k∈Z$;б)$-{9π}/{4};-{7π}/{4}$
Задача 13
а) Решите уравнение ${sin 2x}/{cos(π + x)}= -√2$.
б) Укажите корни этого уравнения, принадлежащие промежутку $(-2π;-{π}/{2})$.
Решение
а)${sin2x}/{cos(π + x)}=-√2$.
Зная, что $sin2x = 2sinxcosx, cos(π + x)=-cosx$, получим: ${2sinxcosx}/{-cosx}=-√2$.
Учитывая, что $cosx≠0, x≠{π}/{2} + πm, m∈Z$, имеем:
$2sinx=√2$,
$sinx = {√2}/{2}$,
$x = {π}/{4} + 2πn, n∈Z$;
$x = {3π}/{4} + 2πk, k∈Z$.
б) Отберём корни уравнения, принадлежащие промежутку $(-2π;-{π}/{2})$.
1. $x = {π}/{4} + 2πn, n∈Z$.
$-2π < {π}/{4} + 2πn < -{π}/{2},$
$-2 < {1}/{4} + 2n < -{1}/{2},$
$-2-{1}/{4} < 2n < -{1}/{2}-{1}/{4},$
$-{9}/{4} < 2n < -{3}/{4},$
$-{9}/{8} < n < -{3}/{8},$
$n = -1$.
При $n =-1$
$x = {π}/{4}-2π=-{7π}/{4}$.
2. $x = {3π}/{4} + 2πk, k∈Z$.
$-2π < {3π}/{4} + 2πk < -{π}/{2}$,
$-2 < {3}/{4} + 2k < -{1}/{2}$,
$-2-{3}/{4} < 2k < -{1}/{2}-{3}/{4}$,
$-{11}/{4} < 2k < -{5}/{4}$,
$-{11}/{8} < k < -{5}/{8}$,
$k = -1$.
При $k = -1$
$x = {3π}/{4}-2π = -{5π}/{4}$.
Ответ: а)${π}/{4}+2πn,{3π}/{4}+2πk,n,k∈Z$;б)$-{7π}/{4};-{5π}/{4}$
Задача 14
а) Решите уравнение $9·3^{2 cos x} — 10√3·3^{cos x} + 3 = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $[{3π}/{2};4π]$.
Решение
а) После замены $t = 3^{cosx}$ исходное уравнение примет вид $9t^2 — 10√3t + 3 = 0$. Корни этого уравнения $t = √3; t = {√3}/{9}$. Возвращаясь к переменной $x$, получим
$[table3^{cosx}=√3; 3^{cosx}={√3}/{9};$ $[table3^{cosx}=3^{{1}/{2}}; 3^{cosx}=3^{-{3}/{2}};$ $[tablecosx={1}/{2}; cosx=-{3}/{2};$
Второе уравнение совокупности не имеет корней. Решая первое уравнение, получим $x =±{π}/{3} + 2πn; n ∈ Z$.
б) Запишем решение уравнения в виде $x =-{π}/{3} + 2πn; n ∈ Z$ или $x ={π}/{3} + 2πk; k ∈ Z$ и выясним, для каких целых значений $n$ и $k$ справедливы неравенства ${3π}/{2}≤-{π}/{3}+2πn≤4π$ и ${3π}/{2}≤{π}/{3}+2πk≤4π$.
Получим ${11}/{12} ≤ n ≤ {26}/{12}$ и ${7}/{12} ≤ k ≤{22}/{12}$.
Откуда следует, что два целых значения $n = 1$ и $n = 2$ удовлетворяют неравенству ${11}/{12} ≤ n ≤ {26}/{12}; k = 1$ — единственное целое $k$, удовлетворяющее неравенству ${7}/{12} ≤ k ≤{22}/{12}$.
При $n = 1$ $x = -{π}/{3} + 2π·1 = {5π}/{3}$.
При $n = 2$ $x = -{π}/{3} + 2π·2 = {11π}/{3}$.
При $k = 1$ $x = {π}/{3} + 2π·1 = {7π}/{3}$. Итак, ${5π}/{3}; {7π}/{3}; {11π}/{3}$ — корни уравнения, принадлежащие промежутку $[{3π}/{2};4π]$.
Ответ: а)$x=±{π}/{3}+2πn,n∈Z$;б)${5π}/{3};{7π}/{3};{11π}/{3}$
Задача 15
а) Решите уравнение $log_2^2(2 sin x + 1) — 17 log_2(2 sin x + 1) + 16 = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $[{π}/{4};2π]$.
Решение
а) После замены $t = log_2(2 sin x+1)$ исходное уравнение примет вид $t^2-17t+16 = 0$. Корни этого уравнения $t = 1, t = 16$. Возвращаясь к переменной $x$, получим:
$[tablelog_2(2 sin x + 1) = 1; log_2(2 sin x + 1) = 16;$ $[table2 sin x + 1 = 2;; 2sin x + 1 = 2^{16};$
Второе уравнение совокупности не имеет корней. Решая первое уравнение, получим: $sin x = {1}/{2}; x = (-1)^n{π}/{6} + πn; n ∈ Z$.
б) Запишем решение уравнения в виде $x = {π}/{6} + 2πn; n ∈ Z$ или $x = {5π}/{6} + 2πk; k ∈ Z$ и выясним, для каких целых значений $n$ и $k$ справедливы неравенства ${π}/{4}≤{π}/{6}+2πn≤2π$ и ${π}/{4}≤{5π}/{6}+2πk≤2π$.
Получим: ${1}/{24}≤n≤{11}/{12}$ и $-{7}/{24}≤k≤{7}/{12}$, откуда следует, что нет целых значений $n$, удовлетворяющих неравенству ${1}/{24}≤n≤{11}/{12}; k = 0$ — единственное целое $k$, удовлетворяющее неравенству $-{7}/{24}≤k≤{7}/{12}$.
При $k = 0$ $x = {5π}/{6} + 2π·0 = {5π}/{6}$. Итак, ${5π}/{6}$ — корень уравнения, принадлежащий отрезку $[{π}/{4};2π]$.
Ответ: а)$(-1)^{n}{π}/{6}+πn,n∈Z$;б)${5π}/{6}$
Задача 16
а) Решите уравнение $6 log_2^2(2 cos x) — 9 log_2(2 cos x) + 3 = 0$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $[-{π}/{2};π]$.
Решение
а) Решим уравнение $6log_2^2(2 cos x)-9 log_2(2 cos x)+3 = 0$. Обозначим $log_2(2 cos x) = t$ и решим получившееся квадратное уравнение.
$6t^2 — 9t + 3 = 0, t = {9±3}/{12}; t_1 = {1}/{2}; t_2 = 1$.
$[tablelog_2(2 cos x) ={1}/{2}; log_2(2 cos x) = 1;$ $[table2 cos x = √2; 2 cos x = 2;$
$[tablecos x = {√2}/{2}; cos x= 1;$ $[tablex = ±{π}/{4}+ 2π n; n ∊ Z; x = 2πk; k ∊ Z;$
б) Корни, принадлежащие отрезку $[-{π}/{2};π]$, найдём с помощью числовой окружности:
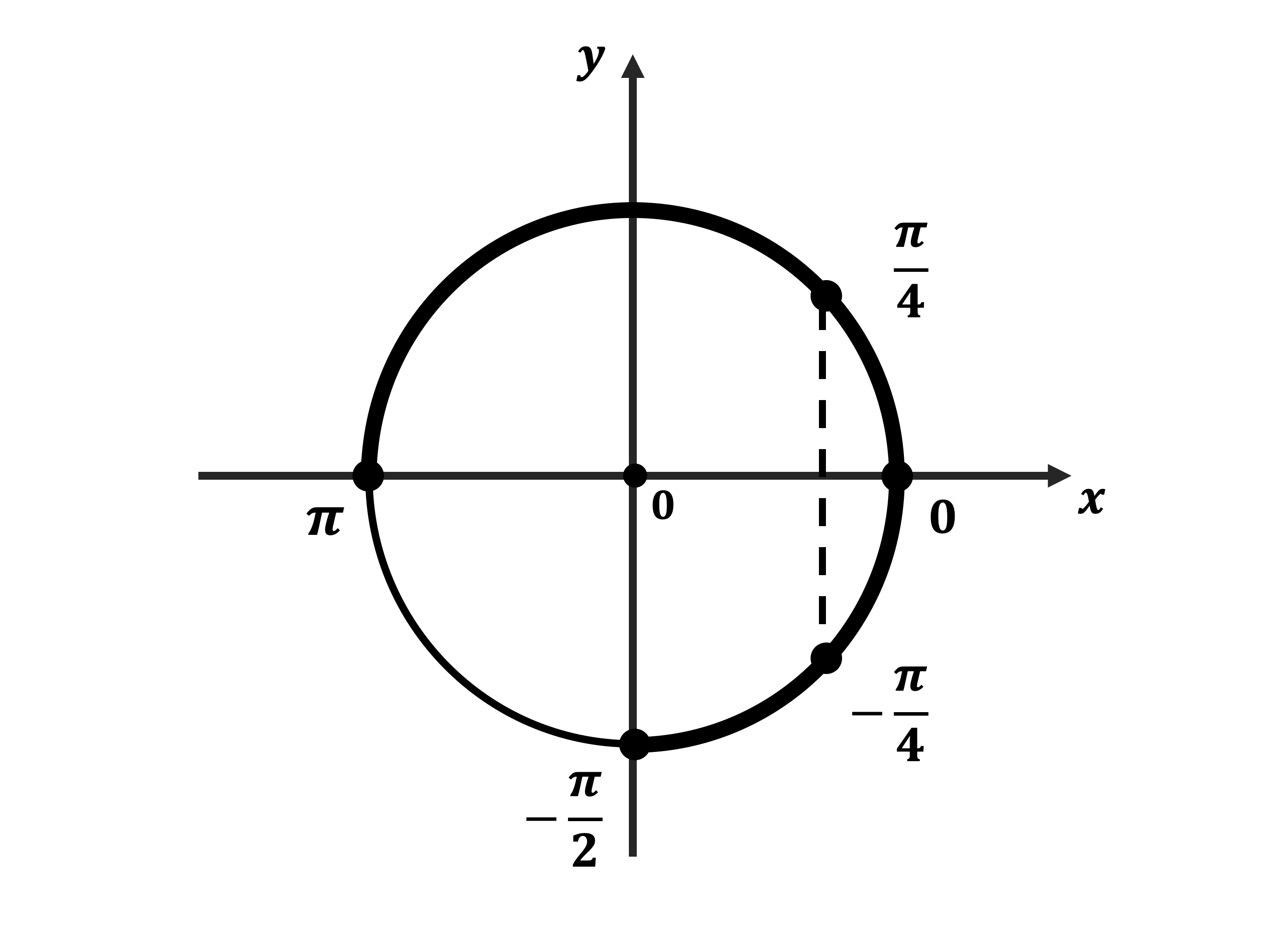
$x_1 = -{π}/{4}; x_2 = 0; x_3 ={π}/{4}$.
Ответ: а)$±{π}/{4}+2πn,n∈Z;2πk,k∈Z$;б)$-{π}/{4};0;{π}/{4}$
Задача 17
а) Решите уравнение $2log_2^2(2 sin x) — 3 log_2(2 sin x) + 1 = 0$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $[{3π}/{2}; 3π]$.
Решение
а) Решим уравнение $2log_2^2(2 sin x) — 3 log_2(2 sin x) + 1 = 0$. Обозначим $log_2(2 sin x) = t$ и решим получившееся уравнение. $2t^2 — 3t + 1 = 0, t = {3±1}/{4}; t_1 = 1; t_2 ={1}/{2}$
$[tablelog_2(2 sin x) = 1; log_2(2 sin x) ={1}/{2};$ $[table2 sin x = 2; 2 sin x=√2;$
$[tablesin x = 1; sin x = {√2}/{2};$ $[tablex={π}/{2}+2πn; x=(-1)^k{π}/{4}+πk;$ $n,k∈Z$
б) Корни, принадлежащие отрезку $[{3π}/{2}; 3π]$, найдём с помощью числовой окружности:
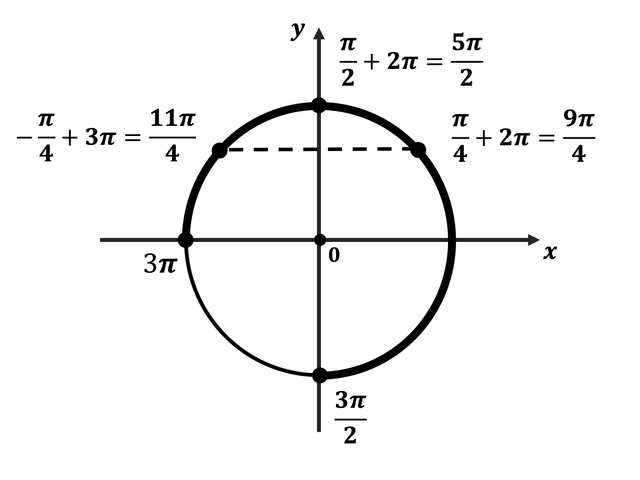
$x_1 = 2π + {π}/{4} = {9π}/{4}; x_2 = 2π + {π}/{2} ={5π}/{2}; x_3 = 3π -{π}/{4} = {11π}/{4}$.
Ответ: а)${π}/{2}+2πn,n∈Z;(-1)^k{π}/{4}+πk,k∈Z$;б)${9π}/{4};{5π}/{2};{11π}/{4}$
Задача 18
а) Решите уравнение $27^{x} — 5·9^{x} — 3^{x+4} + 405 = 0$.
б) Укажите все корни этого уравнения, принадлежащие отрезку $[log_{3}6; log_{3}10]$.
Решение
а) Преобразуем исходное уравнение и разложим на множители его левую часть.
$3^{3x} — 5·3^{2x} — 81·3^x + 405 = 0$,
$3^{2x}(3^x — 5) — 81(3^x — 5) = 0$,
$(3^{2x} — 81)(3^x — 5) = 0$.
Получаем: $3^{2x} -81 = 0$ или $3^x -5 = 0$. Значит, $3^{2x} = 81$, откуда $x = 2$ или $3^x = 5$, откуда $x = log_{3}5$.
б) Нам нужно выбрать те корни уравнения, которые принадлежат отрезку $[log_{3}6; log_{3}10]$. Заметим, что $2 = log_{3}9$. Тогда $log_{3}5 < log_{3}6 < 2 < log_{3}10$. Значит, указанному отрезку принадлежит корень $x = 2$.
Ответ: а)$2;log_{3}5$; б)$2$
Задача 19
а) Решите уравнение $3√{2}sin({π}/{2}+x)-2=2cos^{2}x$.
б) Укажите корни этого уравнения, принадлежащие отрезку $[{3π}/{2};{5π}/{2}]$.
Решение
а) Запишем исходное уравнение в виде $2 cos^2 x — 3√2 cos x + 2 = 0$.
Решая это уравнение как квадратное относительно $cos x$, получим $(cos x)_{1,2} ={3√2±√{18 — 16}}/{4}={3√2± √2}/{4}$.
Значит, $(cos x)_1 = {√2}/{2}$, откуда $x =π/4 + 2πn, n ∈ Z$ или $x =-π/4 + 2πn, n ∈ Z$.
Уравнение $(cosx)_2 = √2$ корней не имеет.
б) Отберём корни, принадлежащие отрезку $[{3π}/{2};{5π}/{2}]$ с помощью числовой окружности.
Получим числа
$2π -{π}/{4} ={7π}/{4}$;
$2π + {π}/{4} = {9π}/{4}$.
Ответ: а)$±{π}/{4}+2πn,n∈Z$;б)${7π}/{4},{9π}/{4}$
Задача 20
а) Решите уравнение $3√{3}cos({3π}/{2}+x)-3=2sin^{2}x$.
б) Укажите корни этого уравнения, принадлежащие отрезку $[2π; 3π]$.
Решение
а) Запишем исходное уравнение в виде $2sin^2 x — 3√3 sin x + 3 = 0$.
Решая это уравнение как квадратное относительно $sin x$, получим $(sin x)_{1,2} = {3√3±√{27-24}}/{4}= {3√3±√3}/{4}$.
Значит,$(sin x)_1 ={√3}/{2}$, откуда $x ={π}/{3} +2πn, n ∈ Z$ или $x ={2π}/{3}+2πm, m ∈ Z$.
Уравнение $(sin x)_2 = √3$ корней не имеет.
б) С помощью числовой окружности отберём корни, принадлежащие отрезку: $[2π; 3π]$
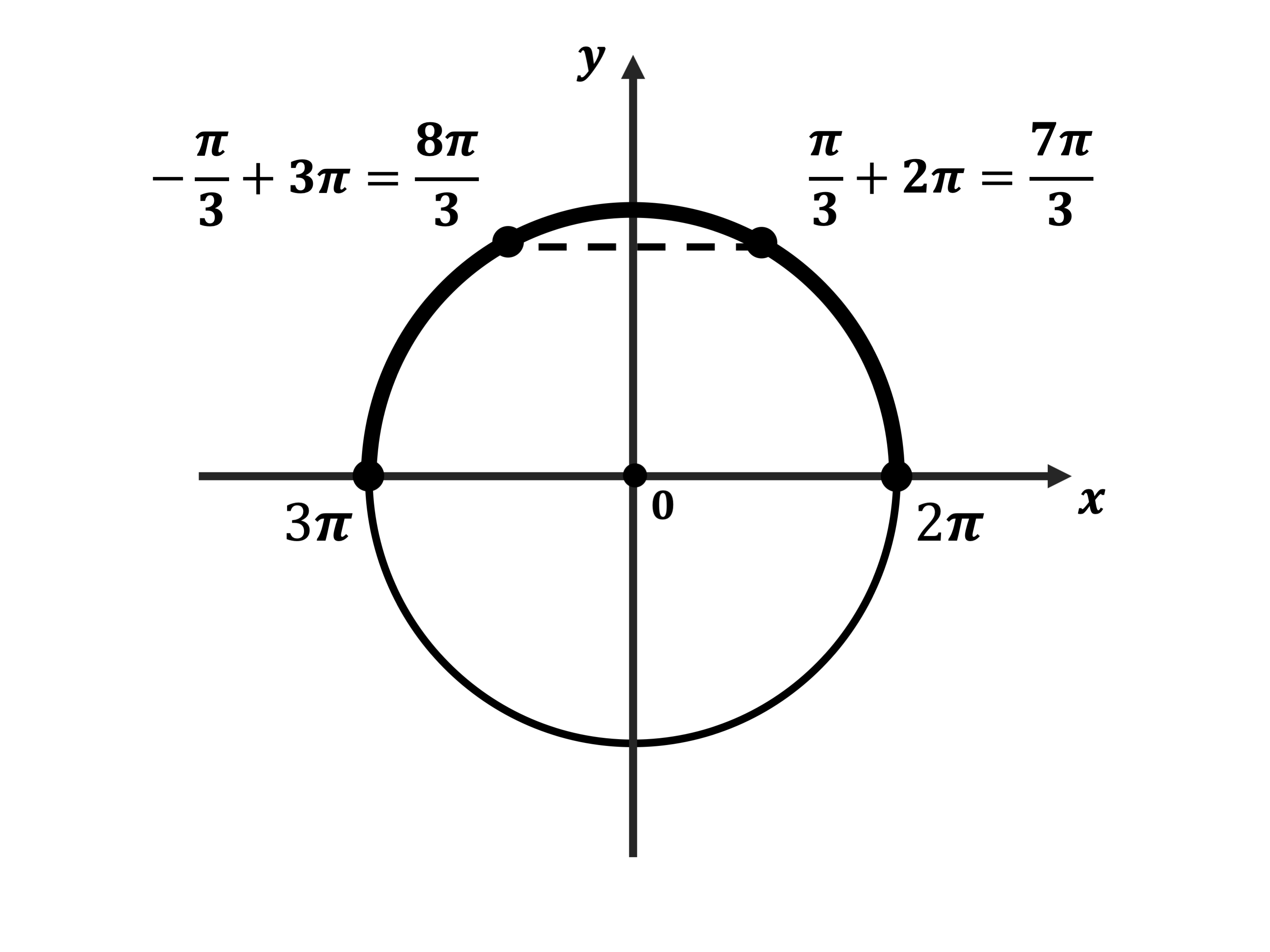
Получим числа:
$2π +{π}/{3}={7π}/{3}$;
$3π -{π}/{3}={8π}/{3}$.
Ответ: а)${π}/{3}+2πn,n∈Z;{2π}/{3}+2πm,m∈Z$;б)${7π}/{3},{8π}/{3}$
Рекомендуемые курсы подготовки
Время работы
Ежедневно 9.00 — 18:00
1. Найдите корень уравнения log3(7 + 2x) = log3(3 − 2x) + 2
2. Решить уравнение cos Pi*x/3= 0.5. В ответе напишите наименьший положительный корень.
3. Найдите корень уравнения log3(5 − 2𝑥) = 2 log3 5.
4. Найдите корень уравнения (1/4)13-5x=163x
5. Найдите корень уравнения √14 + 5𝑥 = 7
6. Решить уравнение: (11𝑥+13)/3 = 14𝑥/5
7. Решить уравнение 6/13х2 = 19 1/2. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
8. Решить уравнение (х-6)2=-24х
9. Решите уравнение √72 − 𝑥 = 𝑥. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
10.Найдите корень уравнения log7(9 − 𝑥) = 3 log7 3