Всего: 638 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Найдите наибольшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наибольшее значение функции на отрезке
Найдите наибольшее значение функции на отрезке
Найдите наибольшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наибольшее значение функции на отрезке [−4,5; 0].
Найдите наибольшее значение функции на отрезке
Найдите наибольшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наибольшее значение функции на отрезке
Найдите наибольшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наибольшее значение функции на отрезке
Найдите наибольшее значение функции на отрезке
Найдите наибольшее значение функции на отрезке
Всего: 638 1–20 | 21–40 | 41–60 | 61–80 …
Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.
Вот какие типы задач могут встретиться в этом задании:
Нахождение точек максимума и минимума функций
Исследование сложных функций
Нахождение наибольших и наименьших значений функций на отрезке
Нахождение точек максимума и минимума функций
1. Найдите точку максимума функции
Найдем производную функции.
Приравняем производную к нулю. Получим:
Исследуем знаки производной.
В точке производная
меняет знак с «плюса» на «минус». Значит,
— точка максимума функции
Ответ: 17.
2. Найдите точку минимума функции
Найдем производную функции.
Приравняем производную к нулю.
Определим знаки производной.
В точке производная
меняет знак с «минуса» на «плюс». Значит,
— точка минимума функции
Ответ: 1.
Исследование сложных функций
3. Найдите точку максимума функции
Перед нами сложная функция Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.
Так как функция монотонно возрастает, точка максимума функции
будет при том же
, что и точка максимума функции
А ее найти легко.
при
. В точке
производная
меняет знак с «плюса» на «минус». Значит,
— точка максимума функции
.
Заметим, что точку максимума функции можно найти и без производной.
Графиком функции является парабола ветвями вниз, и наибольшее значение
достигается в вершине параболы, то есть при
Ответ: — 4.
4. Найдите абсциссу точки максимума функции
Напомним, что абсцисса — это координата по
Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.
Так как функция монотонно возрастает, точка максимума функции
является и точкой максимума функции
Это вершина квадратичной параболы
Нахождение наибольших и наименьших значений функций на отрезке
5. Найдите наибольшее значение функции на отрезке
Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.
Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.
Найдем знаки производной.
В точке производная равна нулю и меняет знак с «+» на «-«. Значит, x = — 2 — точка максимума функции
. Поскольку при
функция
убывает,
В этой задаче значение функции на концах отрезка искать не нужно.
Ответ: 12.
6. Найдите наименьшее значение функции на отрезке
Найдем производную функции и приравняем ее к нулю.
при
Найдем знаки производной.
Точка — точка минимума функции
. Точка
не лежит на отрезке
Поэтому
и
Значит, наименьшее значение функции на отрезке
достигается при
Найдем это значение.
Ответ: -11.
7. Найдите наименьшее значение функции на отрезке
Иногда перед тем, как взять производную, формулу функции полезно упростить.
Мы применили формулу для логарифма произведения. при
Если то
Если
, то
Значит, — точка минимума функции
. В этой точке и достигается наименьшее значение функции на отрезке
Ответ: 4.
8. Найдите наибольшее значение функции на отрезке
Найдем производную функции
Приравняем производную к нулю:
. Поскольку
если
Найдем знаки производной на отрезке
При знак производной меняется с «плюса» на «минус». Значит,
— точка максимума функции
Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при и
Мы нашли, что
Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.
Ответ: 4.
9. Найдите наименьшее значение функции на отрезке [0;2].
Снова сложная функция. Запишем полезные формулы:
Найдем производную функции
если
Тогда
При
знак производной меняется с «минуса» на «плюс». Значит,
— точка минимума функции
Ответ: -7.
10. Найдите наибольшее значение функции на отрезке
Как всегда, возьмем производную функции и приравняем ее к нулю.
По условию, . На этом отрезке условие
выполняется только для
Найдем знаки производной слева и справа от точки
В точке производная функции меняет знак с «плюса» на «минус». Значит, точка
— точка максимума функции
. Других точек экстремума на отрезке
функция не имеет, и наибольшее значение функции
на отрезке
достигается при
Ответ: 12.
11.Найдите наименьшее значение функции на отрезке
Найдем производную функции и приравняем ее к нулю. — нет решений.
Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.
Поскольку , получим, что
для всех
, и функция
монотонно возрастает при
Значит, наименьшее свое значение функция принимает в левом конце отрезка , то есть при
Ответ: 6
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 11 Профильного ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
1. Элементарные функции
2. Применение формул производной произведения и частного
| 2.1 | Найдите точку минимума функции y=(3-x)cdot e^{3-x}. | Смотреть видеоразбор |
| 2.2 | Найдите точку максимума функции y=(x^2-10x+10)cdot e^{5-x}. | Смотреть видеоразбор |
| 2.3 | Найдите наименьшее значение функции y=(x-1)e^x на отрезке [-1;1]. | Смотреть видеоразбор |
| 2.4 | Найдите наибольшее значение функции y=(10-x)sqrt{x+2} на отрезке [-1; 7]. | Смотреть видеоразбор |
| 2.5 | Найдите наименьшее значение функции y=2xsqrt{x}-9x+11 на отрезке [2; 9]. | Смотреть видеоразбор |
| 2.6 | Найдите наибольшее значение функции y=(x-2)^2(x-4)+5 на отрезке [1; 3]. | Смотреть видеоразбор |
| 2.7 | Найдите точку максимума функции y=(x+5)e^{5-x}. | Смотреть видеоразбор |
| 2.8 | Найдите точку минимума функции y=(10-x)e^{10-x}. | Смотреть видеоразбор |
| 2.9 | Найдите наименьшее значение функции y=x^2+frac{25+x^2-x^3}{x} на отрезке [1; 10]. | Смотреть видеоразбор |
3. Применение формулы производной сложной функции
4. Тригонометрические функции
| 4.1 | Найдите наибольшее значение функции y=8x-4tg;x-2pi+2 на отрезке [-frac{pi}{3}; frac{pi}{3}]. | Смотреть видеоразбор |
| 4.2 | Найдите наименьшее значение функции y=4sin{x}+3cos{x} на отрезке [0; 7]. | Смотреть видеоразбор |
| 4.3 | Найдите наибольшее значение функции y=2cos{x}-frac{18}{pi}x+4 на отрезке [-frac{2pi}{3}; 0]. | Смотреть видеоразбор |
| 4.4 | Найдите наименьшее значение функции y=5sin{x}+frac{24}{pi}x+6 на отрезке [-frac{5pi}{6}; 0]. | Смотреть видеоразбор |
| 4.5 | Найдите наибольшее значение функции y=3tg{x}-3x+5 на отрезке [-frac{pi}{4}; 0]. | Смотреть видеоразбор |
| 4.6 | Найдите наименьшее значение функции y=3cos{x}-frac{48}{pi}x+19 на отрезке [-frac{2pi}{3}; 0]. | Смотреть видеоразбор |
| 4.7 | Найдите наименьшее значение функции f(x)=sin{x}+sqrt{1+sin^2{x}}. | Смотреть видеоразбор |
| 4.8 | Найдите наибольшее значение функции y=33x-30sin{x}+29 на отрезке [-frac{pi}{2}; 0]. | Смотреть видеоразбор |
| 4.9 | Найдите точку максимума функции y=(2x-3)cos{x}-2sin{x}+5, принадлежащую промежутку (0; frac{pi}{2}). | Смотреть видеоразбор |
| 4.10 | Найдите точку максимума функции y=(2x-1)cos{x}-2sin{x}+5, на промежутке (0; frac{pi}{2}). | Смотреть видеоразбор |
| 4.11 | Найдите наибольшее значение функции y=2sin{x}-frac{36}{pi}x+9 на отрезке [-frac{5pi}{6}; 0]. | Смотреть видеоразбор |
| 4.12 | Найдите наибольшее значение функции y=7sqrt{2}cos{x}+7x-frac{7pi}{4}+4 на отрезке [0; frac{pi}{2}]. | Смотреть видеоразбор |
| 4.13 | Найдите наибольшее значение функции y=12cos{x}+6sqrt{3}x-2sqrt{3}pi+6 на отрезке [0; frac{pi}{2}]. | Смотреть видеоразбор |
| 4.14 | Найдите наибольшее значение функции y=12tg;x -12x+3pi-7 на отрезке [-frac{pi}{4}; frac{pi}{4}]. | Смотреть видеоразбор |
| 4.15 | Найдите наименьшее значение функции y=6cos{x}+frac{24x}{pi}+5 на промежутке [-frac{2pi}{3}; 0]. | Смотреть видеоразбор |
| 4.16 | Найдите наименьшее значение функции y=3+frac{5pi}{4}-5x-5sqrt{2}cos{x} на отрезке [0; frac{pi}{2}]. | Смотреть видеоразбор |
| 4.17 | Найдите наименьшее значение функции y=5cos{x}-6x+4 на отрезке [-frac{3pi}{2}; 0]. | Смотреть видеоразбор |
| 4.18 | Найдите наибольшее значение функции y=15x-3sin{x}+5 на отрезке [-frac{pi}{2}; 0]. | Смотреть видеоразбор |
| 4.19 | Найдите наименьшее значение функции y=9cos{x}+14x+7 на отрезке [0; frac{3pi}{2}]. | Смотреть видеоразбор |
| 4.20 | Найдите наименьшее значение функции y=7sin{x}-8x+9 на отрезке [-frac{3pi}{2}; 0]. | Смотреть видеоразбор |
| 4.21 | Найдите наименьшее значение функции y=6cos{x}+frac{24}{pi}x+5 на отрезке [-frac{2pi}{3}; 0]. | Смотреть видеоразбор |
| 4.22 | Найдите наибольшее значение функции y=10sin{x}-frac{36}{pi}x+7 на отрезке [-frac{5pi}{6}; 0]. | Смотреть видеоразбор |
5. Логарифмическая и показательная функции
| 5.1 | Найдите наименьшее значение функции y=3x-ln(x+3)^3 на отрезке [-2,5; 0]. | Смотреть видеоразбор |
| 5.2 | Найдите наименьшее значение функции y=9x-ln(9x)+3 на отрезке [frac{1}{18}; frac{5}{18}]. | Смотреть видеоразбор |
| 5.3 | Найдите наибольшее значение функции y=2x^2-13x+9cdot ln{x}+8 на отрезке [frac{13}{14}; frac{15}{14}]. | Смотреть видеоразбор |
| 5.4 | Найдите наименьшее значение функции y=5x-ln(x+5)^5 на отрезке [-4,5; 1]. | Смотреть видеоразбор |
| 5.5 | Найдите наименьшее значение функции y=7x-ln(x-2)^7 на отрезке [-1,5; 0]. | Смотреть видеоразбор |
| 5.6 | Найдите точку максимума функции y=ln(x+4)^2+2x+7. | Смотреть видеоразбор |
| 5.7 | Найдите наименьшее значение функции y=log_{sqrt{3}}(x-4sqrt{x-2}+5) на отрезке [5; 10]. | Смотреть видеоразбор |
| 5.8 | Найдите наименьшее значение функции y=4^x-2^{x+4}+100. | Смотреть видеоразбор |
6. Функции, в которых присутствует квадратичная в виде «вложенной»
| 6.1 | Найдите наименьшее значение функции y=2^{x^2+100x+2503} | Смотреть видеоразбор |
| 6.2 | Найдите наибольшее значение функции y=5^{-3x^2+18x-24}. | Смотреть видеоразбор |
| 6.3 | Найдите точку максимума функции y=-sqrt{x^2-8x+17}. | Смотреть видеоразбор |
| 6.4 | Найдите наибольшее значение функции y=3^{-7-6x-x^2}. | Смотреть видеоразбор |
| 6.5 | Найдите наибольшее значение функции y=log_5(4-2x-x^2)+3. | Смотреть видеоразбор |
| 6.6 | Найдите точку максимума функции y=sqrt{4-4x-x^2}. | Смотреть видеоразбор |
7. Задачи на первообразную (не входят в ЕГЭ этого года)
| 7.1 | Найдите первообразную F(x) для функции f(x)=frac{3x+2}{5}, если F(4)=5. В ответе укажите значение F(1). | Смотреть видеоразбор |
| 7.2 | Наименьшее значение первообразной F(x) для функции f(x)=x^2−2x−3 на отрезке [0;6] равно −9. Найдите наибольшее значение первообразной на этом отрезке. | Смотреть видеоразбор |
| 7.3 | Наименьшее значение первообразной F(x) для функции f(x)=x^2-2x-3 на отрезке [0; 6] равно −9. Найдите наибольшее значение первообразной на этом отрезке. | Смотреть видеоразбор |
| 7.4 | Найдите первообразную F(x) для функции f(x)=frac{3x+2}{5}, если F(4)=5. В ответе укажите значение F(1). | Смотреть видеоразбор |
| 7.5 | Один из двух нулей первообразной F(x) для функции f(x)=5x-1 равен -3. Найдите второй нуль. | Смотреть видеоразбор |
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Найдем производную этой функции. Представим, что
$$sqrt[3]{(x+5)^{2}}=(x+5)^{frac{2}{3}}$$
$$ sqrt[3]{(x+5)^{5}}=(x+5)^{frac{5}{3}}$$
Тогда $$f_{‘}(x)=frac{2}{3}*(x+5)^{-frac{1}{3}}-frac{5}{3}*(x+5)^{frac{2}{3}}=0$$
$$0=frac{1}{3}*(2(x+5)^{-frac{1}{3}}-5*(x+5)^{frac{2}{3}})$$
$$0=2(x+5)^{-frac{1}{3}}-5*(x+5)^{frac{2}{3}}$$ Вынесем $$(x+5)^{-frac{1}{3}}$$ за скобки:
$$(x+5)^{-frac{1}{3}}(2-5*(x+5))=0$$
Получаем, что x = -4.6 и x = -5.
Если начертить координатную прямую и расставить на ней знаки производной, то увидим, что на промежутках (-∞;-5] и [-4.6;+∞) производная отрицательна, а на промежутке [-5;-4.6] — положительна. Значит x = -5 точка минимума
Задача 1. Найдите точку максимума функции
Решение: + показать
Задача 2. Найдите точку минимума функции
Решение: + показать
Задача 3. Найдите наименьшее значение функции на отрезке
.
Решение: + показать
Задача 4. Найдите наибольшее значение функции на отрезке
Решение: + показать
Задача 5. Найдите наибольшее значение функции на отрезке
Решение: + показать
Задача 6. Найдите наибольшее значение функции на отрезке
Решение: + показать
Задача 7. Найдите точку максимума функции
Решение: + показать
Задача 8. Найдите наибольшее значение функции на отрезке
Решение: + показать
Задача 9. Найдите точку минимума функции .
Решение: + показать
Задача 10. Найдите наименьшее значение функции на
Решение: + показать
Задача 11. Найдите точку максимума функции
Решение: + показать
Задача 12. Найдите точку минимума функции
Решение: + показать
Задача 13. Найдите точку максимума функции
Решение: + показать
Задача 14. Найдите наименьшее значение функции на отрезке
.
Решение: + показать
Задача 15. Найдите наибольшее значение функции на отрезке
Решение: + показать
Задача 16. Найдите наименьшее значение функции на отрезке
Решение: + показать
Задача 17. Найдите наименьшее значение функции на отрезке
Решение: + показать
Задача 18. Найдите наименьшее значение функции на отрезке
.
Решение: + показать
Задача 19. Найдите наибольшее значение функции на отрезке
Решение: + показать
Задача 20. Найдите наименьшее значение функции на отрезке
Решение: + показать
Задача 21. Найдите наибольшее значение функции на отрезке
.
Решение: + показать
Задача 22. Найдите наименьшее значение функции на отрезке
Решение: + показать
Задача 23. Найдите наименьшее значение функции на отрезке
Решение: + показать
Задача 24. Найдите точку минимума функции принадлежащую промежутку
.
Решение: + показать
* Замечание. Важно!
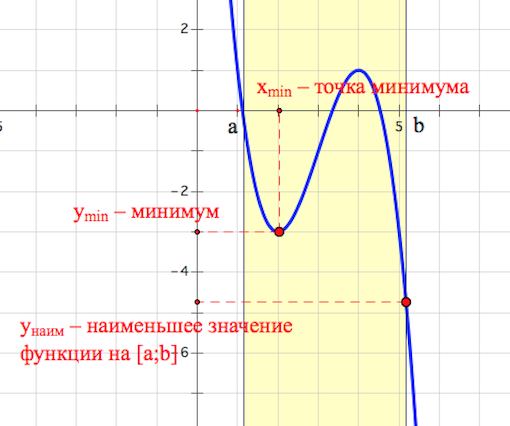
Не следует считать (могло сложиться такое мнение при разборе примеров выше), что наименьшее (наибольшее) значение функции на отрезке совпадает с минимумом (максимумом) на отрезке!
Например, на рисунке ниже наименьшее значение функции на отрезке достигается на конце отрезка
, а именно, в точке
.
То есть, вообще говоря, при нахождении наименьшего значения функции на отрезке следует выбрать наименьшую из величин:
1) (их может быть несколько) из рассматриваемого отрезка
2) ,
При нахождении наибольшего значения функции на отрезке следует выбрать большую из величин:
1) (их может быть несколько) из рассматриваемого отрезка
2) ,
Но, если, например, на рассматриваемом отрезке функция имеет только один экстремум – минимум и мы ищем наименьшее значение, то отпадает необходимость находить значения функции на концах отрезка.
Аналогично в случае с нахождением наибольшего значения функции на отрезке, на котором содержится только один экстремум – максимум.
В случае же, когда на отрезке рассматриваемом функция не имеет экстремумов, то для нахождения наибольшего/наименьшего значений требуется лишь сравнить эти самые значения функции на концах отрезка и взять наибольшее/наименьшее из них.
Вы можете пройти тест “Исследование функции при помощи производной”
Наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение ординаты на рассматриваемом интервале.
Чтобы найти наибольшее или наименьшее значение функции необходимо:
- Найти производную функции $f'(х)$
- Найти стационарные точки, решив уравнение $f'(х)=0$
- Проверить, какие стационарные точки входят в заданный отрезок.
- Вычислить значение функции на концах отрезка и в стационарных точках из п.3
- Выбрать из полученных результатов наибольшее или наименьшее значение.
Чтобы найти точки максимума или минимума необходимо:
- Найти производную функции $f'(х)$
- Найти стационарные точки, решив уравнение $f'(х)=0$
- Разложить производную функции на множители.
- Начертить координатную прямую, расставить на ней стационарные точки и определить знаки производной в полученных интервалах, пользуясь записью п.3.
- Найти точки максимума или минимума по правилу: если в точке производная меняет знак с плюса на минус, то это будет точка максимума (если с минуса на плюс, то это будет точка минимума). На практике удобно использовать изображение стрелок на промежутках: на промежутке, где производная положительна, стрелка рисуется вверх и наоборот.
Таблица производных некоторых элементарных функций:
| Функция | Производная |
| $c$ | $0$ |
| $x$ | $1$ |
| $x^n, n∈N$ | $nx^{n-1}, n∈N$ |
| ${1}/{x}$ | $-{1}/{x^2}$ |
| ${1}/x{^n}, n∈N$ | $-{n}/{x^{n+1}}, n∈N$ |
| $√^n{x}, n∈N$ | ${1}/{n√^n{x^{n-1}}, n∈N$ |
| $sinx$ | $cosx$ |
| $cosx$ | $-sinx$ |
| $tgx$ | ${1}/{cos^2x}$ |
| $ctgx$ | $-{1}/{sin^2x}$ |
| $cos^2x$ | $-sin2x$ |
| $sin^2x$ | $sin2x$ |
| $e^x$ | $e^x$ |
| $a^x$ | $a^xlna$ |
| $lnx$ | ${1}/{x}$ |
| $log_{a}x$ | ${1}/{xlna}$ |
Основные правила дифференцирования
1. Производная суммы и разности равна производной каждого слагаемого
$(f(x) ± g(x))′= f′(x)± g′(x)$
Пример:
Найти производную функции $f(x) = 3x^5 – cosx + {1}/{x}$
Производная суммы и разности равна производной каждого слагаемого
$f′(x)=(3x^5)′–(cosx)′+({1}/{x})’=15x^4+sinx-{1}/{x^2}$
2. Производная произведения.
$(f(x)∙g(x))′=f′(x)∙g(x)+f(x)∙g(x)′$
Пример:
Найти производную $f(x)=4x∙cosx$
$f′(x)=(4x)′∙cosx+4x∙(cosx)′=4∙cosx-4x∙sinx$
3. Производная частного
$({f(x)}/{g(x)})’={f^'(x)∙g(x)-f(x)∙g(x)’}/{g^2(x)}$
Пример:
Найти производную $f(x)={5x^5}/{e^x}$
$f'(x)={(5x^5)’∙e^x-5x^5∙(e^x)’}/{(e^x)^2}={25x^4∙e^x-5x^5∙e^x}/{(e^x)^2}$
4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции
$f(g(x))′=f′(g(x))∙g′(x)$
Пример:
$f(x)= cos(5x)$
$f′(x)=cos′(5x)∙(5x)′= — sin(5x)∙5= -5sin(5x)$
Пример:
Найдите точку минимума функции $y=2x-ln(x+11)+4$
Решение:
1. Найдем ОДЗ функции: $х+11>0; х>-11$
2. Найдем производную функции $y’=2-{1}/{x+11}={2x+22-1}/{x+11}={2x+21}/{x+11}$
3. Найдем стационарные точки, приравняв производную к нулю
${2x+21}/{x+11}=0$
Дробь равна нулю если числитель равен нулю, а знаменатель не равен нулю
$2x+21=0; x≠-11$
$2х=-21$
$х=-10,5$
4. Начертим координатную прямую, расставим на ней стационарные точки и определим знаки производной в полученных интервалах. Для этого подставим в производную любое число из крайней правой области, например, нуль.
$y'(0)={2∙0+21}/{0+11}={21}/{11}>0$
5. В точке минимума производная меняет знак с минуса на плюс, следовательно, точка $-10,5$ — это точка минимума.
Ответ: $-10,5$
Пример:
Найдите наибольшее значение функции $y=6x^5-90x^3-5$ на отрезке $[-5;1]$
Решение:
1. Найдем производную функции $y′=30x^4-270x^2$
2. Приравняем производную к нулю и найдем стационарные точки
$30x^4-270x^2=0$
Вынесем общий множитель $30x^2$ за скобки
$30x^2(x^2-9)=0$
$30x^2(х-3)(х+3)=0$
Приравняем каждый множитель к нулю
$x^2=0 ; х-3=0; х+3=0$
$х=0;х=3;х=-3$
3. Выберем стационарные точки, которые принадлежат заданному отрезку $[-5;1]$
Нам подходят стационарные точки $х=0$ и $х=-3$
4. Вычислим значение функции на концах отрезка и в стационарных точках из п.3
$y(-5)= 6∙(-5)^5-90∙(-5)^3-5=6∙(-3125)+90∙125-5= -18750+11250-5=-7505$
$y(-3)= 6∙(-3)^5-90∙(-3)^3-5=-1458+2430-5=967$
$y(0)= -5$
$y(1)= 6∙1^5-90∙1^3-5=6-90-5= -89$
Наибольшее значение равно $967$
Ответ: $967$
За это задание ты можешь получить 1 балл. На решение дается около 10 минут. Уровень сложности: повышенный.
Средний процент выполнения: 60.8%
Ответом к заданию 11 по математике (профильной) может быть целое число или конечная десятичная дробь.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
Найдите наименьшее значение функции $y=-2ln(x+3)^5+10x$ на отрезке $[-2{,}5 ;-1]$.
Решение
Областью определения функции является интервал $(-3; +∞)$, на котором она дифференцируема. Отрезок $[-2.5; -1]$ принадлежит области определения.
Отметим, что по свойству логарифмов $ln(x + 3)^5 = 5 ln(x + 3)$, поэтому заданная функция имеет вид $y = -10 ln(x + 3) + 10x$.
1. Находим $y′$, пользуясь правилами дифференцирования и формулами производной степенной и логарифмической функций:
$y′ = {-10}/{x+3} + 10 = {-10 + 10x + 30}/{x + 3} = {10 x + 20}/{x + 3} = {10(x + 2)}/{x + 3}, y′ = {10(x + 2)}/{x + 3}$.
2. Заметим, что $y′ = 0$ при $x = -2$. Получаем единственную стационарную точку. $-2 ∈ [-2.5; -1]$.
3. Так как $x + 3 > 0$ в области определения, то $y′ < 0$ при $-2.5 < x < -2, y′ > 0$ при $-2 < x < -1$. Производная меняет знак с «минуса» на «плюс» при переходе через точку $x = -2$. Следовательно, эта точка является точкой минимума и в ней функция достигает наименьшего значения.
$y(-2) = -10 ln(-2 + 3) + 10 · (-2) = -20$, так как $ln 1 = 0$.
Ответ: -20
Задача 2
Найдите наибольшее значение функции $y=ln(x+7)^3-3x$ на отрезке $[-6{,}5 ;-4]$.
Решение
Областью определения функции является промежуток $(-7;+∞ )$, на котором она дифференцируема
Отрезок $[-6{,}5 ;-4]$ принадлежит области определения
Отметим, что по свойству логарифмов в области определения функции выполняется равенство $ln(x+7)^3=3ln(x+7)$, поэтому заданная функция может быть представлена в виде $y=3ln(x+7)-3x$
1. Находим $y^′ $, пользуясь правилами дифференцирования и формулами производной степенной и логарифмической функций: $y^′={3} / {x+7}-3={3-3x-21} / {x+7}={-3x-18} / {x+7}={-3(x+6)} / {x+7}$, $y^′={-3(x+6)} / {x+7}$
2. Заметим, что $y^′ =0$ при $x=-6$. Получаем единственную стационарную точку
3. Так как $x+7>0$ в области определения, то $y^′ >0$ при $x∈(-6,5;-6)$
$y^′ <0$ при $x∈(-6;-4)$. Производная меняет знак с «плюса» на «минус» при переходе через точку $x=-6$
Следовательно, эта точка является точкой максимума и в ней функция достигает наибольшего значения
$y(-6)=3ln(-6+7)-3⋅ (-6)=18$, так как $ln 1=0$.
Ответ: 18
Задача 3
Найдите наибольшее значение функции $y=ln(4-2x)+2x-7$ на отрезке $[0;1{,}7]$.
Решение
Областью определения этой функции будет интервал $(-∞; 2)$, в каждой точке которого функция дифференцируема, причём отрезок $[0; 1.7]$ целиком лежит в области определения.
1. Находим $y′$, пользуясь правилами дифференцирования, формулами производной сложной и логарифмической функций:
$y′ = {1}/{4 — 2x} · (4 — 2x)′ + (2x)′ — (7)’ = {-2}/{4-2x} + 2 = {2x — 3}/{x — 2}$.
$y′ = {2x — 3}/{x — 2}$.
2. Находим стационарные точки из условия $y′ = 0. {2x — 3}/{x — 2} = 0,$
$2x — 3 = 0,$
$x = {3}/{2}$.
Получили одну стационарную точку $x = {3}/{2}$, которая принадлежит промежутку $(0; 1.7)$.
3. Знак производной совпадает со знаком квадратного трёхчлена $(2x — 3)(x — 2) = 2x^2 — 7x + 6$. Его графиком является парабола, ветви которой направлены вверх, и корнями являются числа ${3}/{2}$ и $2$. Поэтому при $0 < x < {3}/{2}$ его знак «плюс», а при ${3}/{2} < x < 1.7$ знак «минус».
При переходе через точку $x = {3}/{2}$ производная меняет знак с «плюса» на «минус». Значит, $x = {3}/{2}$ является точкой максимума и в ней достигается наибольшее значение (так как других точек экстремума нет).
4. $y({3}/{2}) = ln (4 — 2 · {3}/{2}) + 2 · {3}/{2} — 7 = ln 1 + 3 — 7 = -4$.
Ответ: -4
Задача 4
Найдите точку максимума функции $y=-8√ x+12ln(x-4)-11$.
Решение
Областью определения этой функции является интервал $(4; +∞)$, на котором функция дифференцируема. Найдём стационарные точки на указанном интервале и выберем ту из них, в которой производная меняет знак с «плюса» на «минус».
1. Находим $y′$, пользуясь правилами дифференцирования и формулами производной степенной и логарифмической функций.
$y′ = {-8}/{2√x} + {12}/{x — 4} = {-8(x — 4) + 24√x}/{2√x(x — 4)} = {-4x + 16 + 12√x}/{√x(x — 4)}$.
2. Решаем уравнение $y′ = 0, -4x + 16 + 12√x = 0$.
Сделаем замену $√x = t$ $(t > 2)$. Получим уравнение $-4t^2 + 12t + 16 = 0; t^2 — 3t — 4 = 0$. По формуле корней квадратного уравнения получаем:
$t_{1,2} = {3± √{9 + 16}}/{2} = {3±2}/{5}$,
$t_1 = -1, t_2 = 4$.
$t = -1$ не удовлетворяет условию $t > 2$.
Уравнение $√x = 4$ имеет решение $x = 16$. Получили единственную стационарную точку $x = 16$, принадлежащую промежутку $(4; +∞)$.
При $x > 4$ знак производной совпадает со знаком функции $y_1 = -4x+16+12√x$. Для определения её знака на интервале $(4; +∞)$ достаточно найти её знак в двух точках, одна из которых меньше, чем $x = 16$, и другая, больше, чем $x = 16$.
$y_1 (9) = -4 · 9 + 16 + 12√9 = -36 + 16 + 36 > 0$, а $y_1 (25) = -4 · 25 + 16 + 12√25 = -100 + 16 + 60 < 0$.
3. Получаем, что производная меняет знак с «плюса» на «минус» при переходе через единственную экстремальную точку $x = 16$. Поэтому точка $x = 16$ будет точкой максимума.
Ответ: 16
Задача 5
Найдите точку максимума функции $y=2ln x-√ {x}-17$.
Решение
Областью определения этой функции является интервал $(0; +∞)$, в каждой точке которого она дифференцируема. Найдём стационарные точки в области определения и выберем ту из них, проходя через которую, производная меняет знак с «плюса» на «минус».
1. Находим $y′$, пользуясь правилами дифференцирования, формулами производных степенной и логарифмической функций:
$y′ = {2}/{x} — {1}/{2√x} = {4 -√x}/{2x}$.
2. Решаем уравнение $y′ = 0; 4 — √x = 0. √x = 4, x = 16$.
Получили одну стационарную точку.
3. Так как $x > 0$ и $√x > 0$ в области определения, то знак производной совпадает со знаком функции $y_1 = 4 — √x$. Она обращается в ноль в единственной точке $x = 16$.
Находим знак этой функции при $x < 16$ и $x > 16$. Для этого достаточно найти её значения хотя бы в одной точке каждого из указанных промежутков: $y_1 (1) = 4 — √1 = 3 > 0$, а $y_1 (25) = 4 — √{25} = -1 < 0$
Тем самым, производная меняет знак с «плюса» на «минус» при переходе через точку $x = 16$, которая и будет точкой максимума.
Ответ: 16
Задача 6
Найдите наибольшее значение функции $y=√ {-2log_{0{,}5} (5x+1)}$ на отрезке $[12{,}6;51]$.
Решение
Найдём без применения производной, какие значения принимает функция на отрезке $[12.6; 51]$ и выберем из них наибольшее.
1. Пусть $x$ – произвольное число из отрезка $[12.6; 51]$. Тогда $12.6 ≤ x ≤ 51$. Отсюда по свойствам неравенств получаем: $63 ≤ 5x ≤ 255, 64 ≤ 5x + 1 ≤ 256$.
2. Из предыдущего неравенства, по свойству логарифмов с основанием $0.5$, меньшим $1$, получаем $log_{0.5} 64 ≥ log_{0.5}(5x + 1) ≥ log_{0.5}256$. Но, $log_{0.5}64 = log_{{1}/{2}}64 = log_{{1}/{2}}2^6 = log_{{1}/{2}}(({1}/{2})^{-1})^6 = log_{{1}/{2}}({1}/{2})^{-6} = -6$.
Аналогично, $log_{0.5}256 = -8$. Поэтому $-8 ≤ log_{0.5}(5x + 1) ≤ -6, 6 ≤- log_{0.5}(5x + 1) ≤ 8, 12 ≤ -2 log_{0.5}(5x + 1) ≤ 16$.
Теперь, по свойству квадратного корня получаем, $√12 ≤ √{-2log_{0.5}(5x + 1)} ≤ √{16} = 4$.
Но $√{-2 log_{0.5}(5x + 1)} = y$, поэтому $√{12} ≤ y ≤ 4$.
3. Таким образом, функция определена на всём отрезке $[12.6; 51]$ наибольшим значением является $4$ и получается это значение при $x = 51$.
Ответ: 4
Задача 7
Найдите точку минимума функции $y=x^2-21x+6+55ln x$.
Решение
Областью определения функции является промежуток $(0; +∞)$, на котором она дифференцируема. Найдём стационарные точки и выберем ту из них, при переходе через которую, производная меняет знак с «минуса» на «плюс».
1. Находим $y′$, пользуясь правилами дифференцирования и формулами производной логарифмической и степенной функций.
$y′ = 2x − 21 + {55}/{x}, y′ = {2x^2-21x+55}/{x}$.
2. Решаем уравнение $y′ = 0; 2x^2 -21x +55 = 0. x_{1,2} = {21 ± √{441 — 440}}/{4} = {21 ± 1}/{4}. x_1 = 5, x_2 = 5.5$. Получаем две стационарные точки.
3. Знак производной совпадает со знаком квадратного трёхчлена $2x^2 -21x+55$. Графиком этого трёхчлена является парабола, ветви которой направлены вверх и корнями являются числа $x_1=5$ и $x_2=5.5$.
Поэтому при $x < 5$ производная имеет знак «плюс», знак «минус» при $5 < x < 5.5$, и знак «плюс» при $x > 5.5$.
| (0;5) | 5 | (5; 5.5) | 5.5 | (5.5;+∞) | |
| y′ | + | 0 | — | 0 | + |
| y | ↗ | ↘ | ↗ |
При переходе через точку $5.5$ производная меняет знак с «минуса» на «плюс». Поэтому эта точка и будет точкой минимума.
Ответ: 5.5
Задача 8
Найдите точку максимума функции $y=x^2-11x-17+15ln x$.
Решение
Областью определения функции является промежуток $(0; +∞)$, на котором она дифференцируема. Найдём стационарные точки и выберем ту из них, при переходе через которую, производная меняет знак с «плюса» на «минус».
1. Находим $y′$, пользуясь правилами дифференцирования и формулами производной логарифмической и степенной функций.
$y′ = 2x − 11 + {15}/{x} = {2x^2-11x+15}/{x}, y′ = {2x^2-11x+15}/{x}$.
2. Решаем уравнение $y′ = 0; 2x^2- 11x +15 = 0. x_{1,2} = {11 ± √{121 — 120}}/{4} = {11 ± 1}/{4}. x_1 = 2.5, x_2 = 3$. Получаем две стационарные точки.
3. Знак производной совпадает со знаком квадратного трёхчлена $2x^2 -11x+15$. Графиком этого трёхчлена является парабола, ветви которой направлены вверх и корнями являются числа $x_1=2.5$ и $x_2=3$.
Поэтому при $x < 2.5$ производная имеет знак «плюс», знак «минус» при $2.5 < x < 3$, и знак «плюс» при $x > 3$.
| (0;2.5) | 2.5 | (2.5; 3) | 3 | (3;+∞) | |
| y′ | + | 0 | — | 0 | + |
| y | ↗ | ↘ | ↗ |
При переходе через точку $2.5$ производная меняет знак с «плюса» на «минус». Поэтому эта точка и будет точкой максимума.
Ответ: 2.5
Задача 9
Найдите точку максимума функции $y=(5x^2-3x-3)e^{x+5}$.
Решение
Заметим, что заданная функция определена и дифференцируема при любом значении $x$. Найдём стационарные точки и выберем ту из них, при переходе через которую, производная меняет знак с «плюса» на «минус».
1. Находим $y′$, пользуясь правилами дифференцирования, формулой производной произведения двух функций, и производной степенной и показательной функции:
$y′ = (10x − 3)e^{x+5} + (5x^2 − 3x − 3)e^{x+5} = e^{x+5}(5x^2 + 7x − 6), y′ = e^{x+5}(5x^2 + 7x − 6)$.
2. Решаем уравнение $y′ = 0$. Так как $e^{x+5} > 0$, то $5x^2 + 7x − 6 = 0. x_{1,2} = {−7 ± √{49 + 120}}/{10} = {−7 ± 13}/{10}. x_1 = −2, x_2 = 0.6$. Получаем две стационарные точки.
3. Знак производной совпадает со знаком квадратного трёхчлена $5x^2 +7x-6$. Графиком этого трёхчлена является парабола, ветви которой направлены вверх и корнями являются числа $x_1=-2$ и $x_2=0.6$.
Поэтому при $x < −2$ производная имеет знак «плюс», знак «минус» при $−2 < x < 0.6$, и знак «плюс» при $x > 0.6$.
| (-∞;-2) | -2 | (-2; 0.6) | 0.6 | (0.6;+∞) | |
| y′ | + | 0 | — | 0 | + |
| y | ↗ | ↘ | ↗ |
При переходе через точку $x_1 = −2$ производная меняет знак с «плюса» на «минус». Поэтому эта точка и будет точкой максимума.
Ответ: -2
Задача 10
Найдите наименьшее значение функции $y=-4x-4cos x+5$ на отрезке $[- {π} ;0]$.
Решение
Заметим, что заданная функция непрерывна на отрезке $[-π; 0]$ и дифференцируема на интервале $(-π; 0)$. Наименьшее её значение на отрезке $[-π; 0]$ равно наименьшему из всех значений функции в стационарных точках интервала $(-π; 0)$ и концах отрезка $[-π; 0]$.
1. Находим $y′$, пользуясь правилами дифференцирования и формулами производных тригонометрических функций:
$y′ = -4 + 4 sin x = -4(1 — sin x), y′ = -4(1 — sin x)$.
2. Заметим, что $sin x < 0$ на интервале $(-π; 0)$. Поэтому $1 — sin x > 1$ и $-4(1 — sin x) < 0$. Следовательно, на нём $y′ < 0$ и функция $y=-4x — 4 cos x + 5$ убывает.
3. Наименьшее значение функции будет на правом конце промежутка, то есть в точке $x = 0$.
$y(0) = -4 · 0 — 4 cos 0 + 5 = -4 + 5 = 1$.
Ответ: 1
Задача 11
Найдите точку минимума функции $y=(12-5x)sin x-5cos x-10$, принадлежащую интервалу $({π} / {2};π)$.
Решение
Отметим, что функция дифференцируема на заданном интервале. Найдём стационарные точки на указанном интервале и выберем ту из них, в которой производная меняет знак с «минуса» на «плюс». 1. Находим $y^′$, пользуясь правилами дифференцирования, формулами производной произведения функций и производной линейной и тригонометрических функций. $y^′=(12-5x)^′⋅ sin x+(sin x)^′⋅(12-5x)+5sin x$, $y^′=-5sin x+cos x(12-5x)+5sin x=-cos x(5x-12)$, $y^′=-cos x(5x-12)$. 2. Решаем уравнение $y^′=0$. Так как $cos x<0$ на заданном интервале, то $5x-12=0$, $x=2{,}4$. ${π} / {2≈} 1{,} 57$, а $π ≈ 3{,} 14$, поэтому $2{,}4∈ ({π} / {2};π)$. Получили одну стационарную точку на заданном интервале. 3. $cos x<0$ на заданном интервале, поэтому знак производной совпадает со знаком функции $y_1=5x-12$. Эта функция является возрастающей, поэтому она имеет знак «минус» до точки $x=2{,}4$ и знак «плюс» после неё. Тем самым, точка $x=2{,}4$ будет точкой минимума.
Ответ: 2.4
Задача 12
Найдите точку минимума функции $y={x-8} / {x^2+225}$.
Решение
Заметим, что заданная функция определена и дифференцируема при любом значении $x$. Найдём стационарные точки и выберем ту из них, при переходе через которую, производная меняет знак с «минуса» на «плюс».
1. Находим $y′$, пользуясь формулой производной частного двух функций и правилом дифференцирования степенной функции:
$y′ = {(x-8)′·(x^2+225)-(x^2+225)′·(x-8)}/{(x^2+225)^2}$.
$y′ = {x^2+225-2x·(x-8)}/{(x^2+225)^2}={x^2+225-2x^2+16x}/{(x^2+225)^2}$.
$y′ = {-x^2+16x+225}/{(x^2+225)^2}$.
2. Решаем уравнение $y′ = 0, -x^2 + 16x+225 = 0, x^2-16x-225=0, x_{1,2} = 8±√{64+225}=8±√{289}=8±17, x_1=-9, x_2=25$. Получаем две стационарные точки.
3. Знак производной совпадает со знаком квадратного трёхчлена $-x^2 +16x+225$. Графиком этого трёхчлена является парабола, ветви которой направлены вниз и корнями являются числа $-9$ и $25$.
Поэтому на промежутке $(-∞;-9)$ производная меньше нуля, на промежутке $(-9; 25)$ она больше нуля и на промежутке $(25;+∞)$ меньше нуля.
| (-∞;-9) | -9 | (-9; 25) | 25 | (25;+∞) | |
| y′ | — | + | — | ||
| y | ↘ | 0 | ↗ | 0 | ↘ |
Тем самым производная меняет знак с «минуса» на «плюс» при переходе через точку $x = -9$, которая и будет точкой минимума.
Ответ: -9
Задача 13
Найдите точку максимума функции $y={x-5} / {x^2+144}$.
Решение
Заметим, что заданная функция определена и дифференцируема при любом значении $x$. Найдём стационарные точки и выберем ту из них, при переходе через которую, производная меняет знак с «плюса» на «минус».
1. Находим $y′$, пользуясь формулой производной частного двух функций и правилом дифференцирования степенной функции:
$y′ = {(x-5)′·(x^2+144)-(x^2+144)′·(x-5)}/{(x^2+144)^2}$.
$y′ = {x^2+144-2x·(x-5)}/{(x^2+144)^2}={x^2+144-2x^2+10x}/{(x^2+144)^2}$.
$y′ = {-x^2+10x+144}/{(x^2+144)^2}$.
2. Решаем уравнение $y′ = 0, -x^2 + 10x+144 = 0, x^2-10x-144=0, x_{1,2} = 5±√{25+144}=5±√{169}=5±13, x_1=-8, x_2=18$. Получаем две стационарные точки.
3. Знак производной совпадает со знаком квадратного трёхчлена $-x^2 +10x+144$. Графиком этого трёхчлена является парабола, ветви которой направлены вниз и корнями являются числа $-8$ и $18$.
Поэтому на промежутке $(-∞;-8)$ производная меньше нуля, на промежутке $(-8; 18)$ она больше нуля и на промежутке $(18;+∞)$ меньше нуля.
| (-∞;-8) | -8 | (-8; 18) | 18 | (18;+∞) | |
| y′ | — | + | — | ||
| y | ↘ | 0 | ↗ | 0 | ↘ |
Тем самым производная меняет знак с «плюса» на «минус» при переходе через точку $x = 18$, которая и будет точкой максимума.
Ответ: 18
Задача 14
Найдите наименьшее значение функции $y={4x^2+256} / {x}$ на отрезке $[16;98]$.
Решение
Областью определения функции является множество $(-∞;0)∪ (0;+∞)$, в каждой точке которого функция дифференцируема
Промежуток $[16;98]$ содержится в области определения функции
1. Находим $y^′$, представив заданную функцию в виде $y=4x+{256} / {x}$
По правилам дифференцирования и по формуле производной степенной функции получаем: $y^′=4-{256} / {x^2}={4x^2-256} / {x^2}={4(x^2-64)} / {x^2}$, $y^′={4(x^2-64)} / {x^2}$
2. Решаем уравнение $ y^′=0 $, $ x^2-64=0 $, $ x_1=-8 $, $ x_2=8 $
Получаем две стационарные точки на множестве $(-∞;0)∪ (0;+∞)$, но ни одна из них не попадает на промежуток $[16;98]$. Значит, на заданном отрезке стационарных точек нет
3. Так как $x^2>0$ в области определения, то знак производной совпадает со знаком квадратного трёхчлена $ x^2-64 $. Поэтому $ y^′ >0 $ при $ x>8$, а функция $y={4x^2+256} / {x}$ на отрезке $[16;98]$ возрастает
Наименьшее значение она принимает в точке $x=16$
$y(16)=4⋅ 16+{256} / {16}=64+16=80$.
Ответ: 80
Задача 15
Найдите точку минимума функции $y={25x^2+25} / {x}$.
Решение
Областью определения функции является множество $(-∞; 0) ∪ (0;+∞)$, в каждой точке которого функция дифференцируема. Найдём стационарные точки и выберем ту из них, при переходе через которую, производная меняет знак с «минуса» на «плюс».
1. Находим $y′$, представив заданную функцию в виде $y = 25x+{25}/{x}$. По правилам дифференцирования и формуле производной степенной функции получаем: $y′ = 25 — {25}/{x^2} = {25x^2 — 25}/{x^2} = {25(x^2 — 1)}/{x^2}$.
2. Решаем уравнение $y′ = 0, x^2 — 1 = 0, x_1 = -1, x_2 = 1$. Получаем две стационарные точки.
3. Так как $x^2 > 0$ в области определения, то знак производной совпадает со знаком квадратного трёхчлена $x^2 -1$, корнями которого являются числа $-1$ и $1$. Поэтому $y′ > 0$ при $x < -1, y′ < 0$ при $-1 < x < 0, y′ < 0$ при $0 < x < 1$ и $y′ > 0$ при $x > 1$.
| (-∞;-1) | -1 | (-1; 0) | 0 | (0; 1) | 1 | (0;+∞) | |
| y′ | + | 0 | — | Не сущ. | — | 0 | + |
| y | ↗ | ↘ | ↘ | ↗ |
При переходе через точку $x = 1$ производная меняет знак с «минуса» на «плюс». Поэтому эта точка и будет точкой минимума.
Ответ: 1
Задача 16
Найдите наименьшее значение функции $y=x^5-5x^3-270x$ на отрезке $[0 ;5]$.
Решение
Заметим, что заданная функция определена и дифференцируема при любом значении $x$.
1. Находим $y′$, пользуясь правилами дифференцирования и формулой производной степенной функции: $y′ = 5x^4 — 15x^2 — 270$.
2. Решаем уравнение $y′ = 0$. Сделаем подстановку $x^2 = t (t ≥ 0)$, получим уравнение $5t^2 — 15t — 270 = 0$ или $t^2 — 3t — 54 = 0$.
$t_1 = -6, t_2 = 9$.
$t_1 = -6$ не удовлетворяет условию $t ≥ 0$. Уравнение $x^2 = 9$ имеет два корня $x_1 = -3, x_2 = 3$. На промежуток (0; 5) попадает лишь одно число $x = 3$. Получаем единственную стационарную точку.
3. Найдем знак производной на двух промежутках (0; 3) и (3; 5), на которые точка $x = 3$ разбивает интервал (0; 5). Для этого найдем значения производной в точке $x = 1$ из первого интервала, и в точке $x = 4$ из другого интервала.
$y′(1) = 5·1^4 — 15·1^2 — 270 = 5 — 15 — 270 < 0$,
$y′(4) = 5·4^4 — 15·4^2 — 270 = 1280- 240 — 270 > 0$.
Производная меняет знак с «минуса» на «плюс» при переходе через точку $x = 3$. Следовательно, эта точка является точкой минимума и в ней функция достигает наименьшего значения.
$y(3) = 3^5 — 5·3^3 — 270·3 = 243-135-810 = -702$.
Ответ: -702
Задача 17
Найдите наибольшее значение функции $y=√ {240-8x-x^2}$ на отрезке $[-18;10]$.
Решение
Преобразуем подкоренное выражение: $240-8x-x^2 = -(x^2+8x-240) = -((x+4)^2-16-240) = 256-(x+4)^2$. Поэтому $y = √{256 — (x + 4)^2}$.
Так как $(x + 4)^2 ≥ 0$, то $y$ принимает наибольшее значение, если $(x + 4)^2 = 0$, то есть при $x = -4$. Точка $x = -4$ принадлежит заданному промежутку [-18; 10]. Это наибольшее значение равно $√{256} = 16$.
Ответ: 16
Задача 18
Найдите наименьшее значение функции $y=√ {x^2+2x+122}$ на отрезке $[-50;150]$.
Решение
Дискриминант квадратного трёхчлена, расположенного под знаком квадратного корня, меньше нуля ($D = 4 — 488$), значит трёхчлен корней не имеет. Ветви параболы, являющейся графиком этого трёхчлена направлены вверх, абсцисса вершины равна $-1$, а ордината $121$. Поэтому $x^2+2x+122 > 0$ при любых x и исходная функция определена при любом значении x из промежутка [-50; 150].
При $-50 ≤ x ≤ -1$ функция $y = x^2 + 2x + 122$ убывает, а значит убывает и функция $y = √{x^2 + 2x + 122}$.
При $-1 ≤ x ≤ 150$ функция $y = x^2 + 2x + 122$ возрастает, а значит возрастает и функция $y = √{x^2 + 2x + 122}$.
Из сказанного следует, что в точке $x = -1$ функция $y = √{x^2 + 2x + 122}$ принимает наименьшее значение на указанном отрезке.
$y(-1) = √{121} = 11$.
Ответ: 11
Задача 19
Найдите точку максимума функции $y=√ {77+4x-x^2}$.
Решение
Дискриминант квадратного трёхчлена $-x^2+4x+77$, расположенного под знаком квадратного корня, больше нуля ($D = 16+308 = 324$), значит этот квадратный трёхчлен имеет два корня.
$x_{1,2} = {-2±√{4 + 77}}/{-1} = {-2±9}/{-1}, x_1 = -7, x_2 = 11$.
Ветви параболы, являющейся его графиком, направлены вниз, поэтому при $x∈[-7; 11]$ он принимает неотрицательные значения. Исходная функция определена и непрерывна на отрезке при любом значении $x ∈ [-7; 11]$, и дифференцируема на интервале (-7; 11).
Найдём стационарные точки на интервале (-7; 11) и выберем ту из них, в которой производная меняет знак с плюса на минус.
1. Находим $y′$, пользуясь правилами дифференцирования и формулой производной сложной функции.
$y′ = {1}/{2√{77 + 4x — x^2}}·(77 + 4x — x^2)′ = {-2x + 4}/{2√{77 + 4x — x^2}} = {-(x — 2)}/{√{77 + 4x — x^2}}, y′ = {-(x — 2)}/{√{77 + 4x — x^2}}$,
2. Решаем уравнение $y′ = 0, x — 2 = 0, x = 2$. Получаем одну стационарную точку.
3. Так как $√{77 + 4x — x^2} > 0$ на интервале (-7; 11), то знак производной совпадает со знаком выражения $-x +2$. Тогда $y′ > 0$ при $-x +2 > 0, x < 2; y′ < 0$ при $-x + 2 < 0, x> 2$.
Следовательно, при переходе через точку $x = 2$ производная меняет знак с плюса на минус. Поэтому эта точка и будет точкой максимума.
Ответ: 2
Задача 20
Найдите точку минимума функции $y=√ {x^2-12x+40}$.
Решение
Дискриминант квадратного трёхчлена, расположенного под знаком квадратного корня, меньше нуля ($D=144-160$), значит, уравнение $x^2-12x+40=0$ корней не имеет. Ветви параболы, являющейся графиком этого трёхчлена, направлены вверх, поэтому все его значения больше нуля. Функция определена и дифференцируема при любом значении $x$. Найдём стационарные точки и выберем ту из них, в которой производная меняет знак с «минуса» на «плюс».
1. Находим $y^′$, пользуясь правилами дифференцирования и формулой производной сложной функции.
$y^′={1} / {2√ {x^2-12x+40}}⋅ (x^2-12x+40)^′={2x-12} / {2√ {x^2-12x+40}}=$
$={x-6} / {√ {x^2-12x+40}}$
$y^′={x-6} / {√ {x^2-12x+40}}$.
2. Решаем уравнение $y^′=0$, $x-6=0$, $x=6$. Получаем одну стационарную точку.
3. Так как $√ {x^2-12x+40}>0$, то знак производной совпадает со знаком выражения $x-6$. Тогда $y’>0$ при $x-6>0$, $x>6$; $y'<0$ при $x-6<0$, $x<6$.
Следовательно, при переходе через точку $x=6$ производная меняет знак с «минуса» на «плюс». Поэтому эта точка и будет точкой минимума.
Ответ: 6