Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
2
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.
3
Прямоугольный параллелепипед описан около сферы радиуса 1. Найдите его площадь поверхности.
4
Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда.
5
Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.
Пройти тестирование по этим заданиям
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи по теме «Прямоугольный параллелепипед»
(blacktriangleright) Прямоугольный параллелепипед – это параллелепипед, все грани которого являются прямоугольниками.
Другими словами, это прямая призма, основания которой – прямоугольники.
(эти определения эквивалентны).
Тогда:
1) противоположные грани равны между собой;
2) боковые ребра перпендикулярны основаниям, то есть являются высотами;
3) как следствие, формула для объема принимает вид: ({Large{V=abc}}), где (a, b, c) – три различных боковых ребра.
(blacktriangleright) Диагональ прямоугольного параллелепипеда – это отрезок, соединяющий две противоположные (не лежащие в одной грани) вершины.
1) Все диагонали равны, пересекаются в одной точке и делятся ею пополам;
2) Диагональ (d) можно найти по формуле: ({Large{d^{,2}=a^2+b^2+c^2}}).
Задание
1
#2863
Уровень задания: Легче ЕГЭ
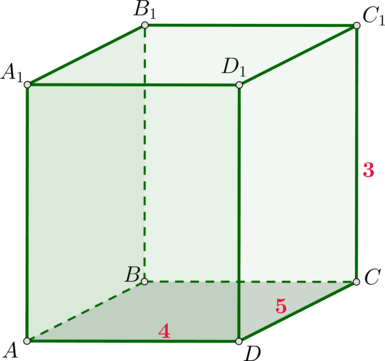
Дан прямоугольный параллелепипед, стороны основания которого равны (4) и (5), а боковое ребро равно (3). Найдите наибольшую площадь его грани.
Заметим, что все варианты для площадей его граней – это всевозможные попарные произведения чисел (3,4,5), то есть (3cdot
4), (4cdot 5) или (3cdot 5). Среди этих произведений наибольшим является (4cdot 5=20).
Ответ: 20
Задание
2
#2864
Уровень задания: Легче ЕГЭ
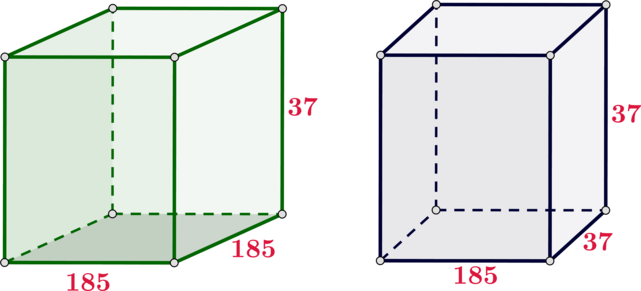
Даны два прямоугольных параллелепипеда: ребра одного равны (185), (185) и (37); а ребра другого равны (185, 37) и (37). Во сколько раз объем первого параллелепипеда больше объема второго параллелепипеда?
Отношение их объемов равно: [dfrac{V_1}{V_2}=dfrac{185cdot 185cdot 37}{185cdot 37cdot 37}=
dfrac{185}{37}=5.]
Ответ: 5
Задание
3
#2865
Уровень задания: Легче ЕГЭ
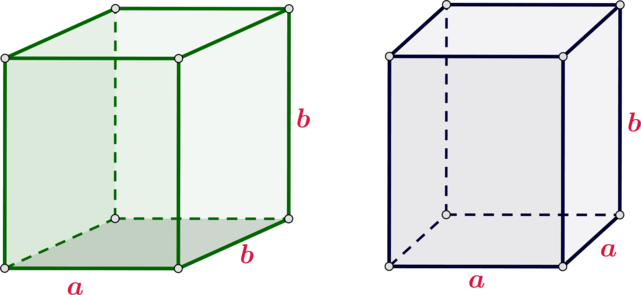
Даны два прямоугольных параллелепипеда: ребра одного равны (a, b) и (b), а ребра другого равны (a, a) и (b). На сколько площадь полной поверхности первого параллелепипеда больше, чем площадь поверхности второго параллелепипеда, если (a=1000, b=1001).
Площадь полной поверхности первого параллелепипеда [S_1=2(ab+b^2+ab)] Площадь полной поверхности второго параллелепипеда [S_2=2(ab+ab+a^2)] Следовательно, [S_1-S_2=2(b^2-a^2)=2(b-a)(b+a)=2(1001-1000)(1001+1000)=4002.]
Ответ: 4002
Задание
4
#3974
Уровень задания: Равен ЕГЭ
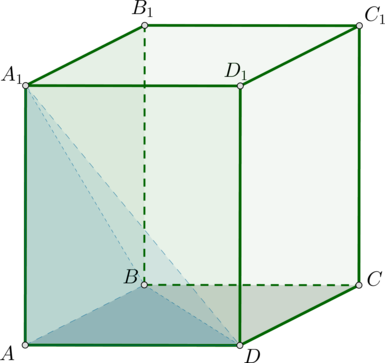
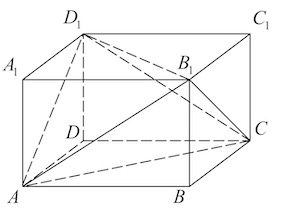
Дан прямоугольный параллелепипед (ABCDA_1B_1C_1D_1). Во сколько раз объем пирамиды (AA_1BD) меньше объема этого параллелепипеда?
Пусть (AB=x), (AD=y), (AA_1=z). Тогда объем параллелепипеда равен [V_{par}=S_{ABCD}cdot AA_1=xycdot z.] Так как (S_{ABD}=0,5S_{ABCD}) (потому что по определению прямоугольного параллелепипеда в основании лежит прямоугольник), то объем пирамиды [V_{pir}=dfrac13cdot S_{ABC}cdot AA_1=
dfrac13cdot dfrac12xycdot z=dfrac16xyz.] Следовательно, объем пирамиды в 6 раз меньше объема параллелепипеда.
Ответ:
6
Задание
5
#2867
Уровень задания: Равен ЕГЭ
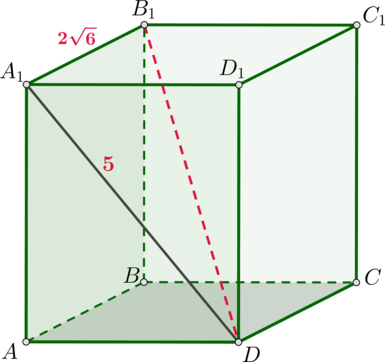
В прямоугольном параллелепипеде диагональ грани (AA_1D_1D) равна (5), а (AB=2sqrt6). Найдите диагональ параллелепипеда.
Так как параллелепипед прямоугольный, то все его грани – прямоугольники, а у прямоугольника обе диагонали равны. Следовательно, (A_1D=AD_1). Рассмотрим диагональ (A_1D) и диагональ параллелепипеда (B_1D). Треугольник (A_1B_1D) прямоугольный, так как ребро (A_1B_1) перпендикулярно грани (AA_1D_1D) (по определению прямоугольного параллелепипеда). Следовательно, гипотенуза [B_1D=sqrt{A_1B_1^2+A_1D^2}=sqrt{5^2+(2sqrt6)^2}=7.]
Ответ: 7
Задание
6
#2641
Уровень задания: Равен ЕГЭ
Дан прямоугольный параллелепипед с ребрами (2, 3) и (6). Найдите его диагональ.
Пусть (AB=2, AD=3 , AA_1=6).
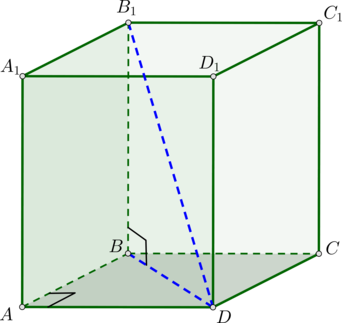
По теореме Пифагора из прямоугольного треугольника (ABD) ((angle
A=90^circ)) имеем: (BD^2=AB^2+AD^2).
Из прямоугольного треугольника (BB_1D) ((angle B=90^circ)) по теореме Пифагора (B_1D^2=BD^2+BB_1^2).
Подставляя (BD^2) из первого равенства во второе, получим:
[B_1D^2=AB^2+AD^2+BB_1^2=2^2+3^2+6^2=4+9+36=49 quad Leftrightarrow quad B_1D=7.]
Ответ: 7
Задание
7
#2689
Уровень задания: Равен ЕГЭ
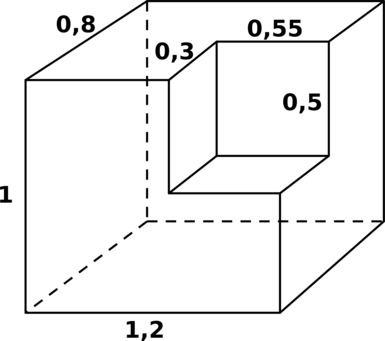
Найдите объём фигуры, получившейся после удаления маленького прямоугольного параллелепипеда из большого.
Объём оставшейся фигуры равен разности объёмов большого прямоугольного параллелепипеда (каким он был до удаления) и маленького (удалённого).
Таким образом, искомый объём равен [0,8cdot 1cdot 1,2 — 0,3cdot 0,5cdot 0,55 = 0,8775,.]
Ответ: 0,8775
Учащимся старших классов будет полезно научиться решать задачи ЕГЭ на нахождение объема и других неизвестных параметров прямоугольного параллелепипеда. Опыт предыдущих лет подтверждает тот факт, что подобные задания являются для многих выпускников достаточно сложными.
При этом понимать, как найти объем или площадь прямоугольного параллелепипеда, должны старшеклассники с любым уровнем подготовки. Только в этом случае они смогут рассчитывать на получение конкурентных баллов по итогам сдачи единого госэкзамена по математике.
Основные нюансы, которые стоит запомнить
- Параллелограммы, из которых состоит параллелепипед, являются его гранями, их стороны — ребрами. Вершины этих фигур считаются вершинами самого многогранника.
- Все диагонали прямоугольного параллелепипеда равны. Так как это прямой многогранник, то боковые грани представляют собой прямоугольники.
- Так как параллелепипед — это призма, в основании которой находится параллелограмм, эта фигура обладает всеми свойствами призмы.
- Боковые ребра прямоугольного параллелепипеда перпендикулярны основанию. Следовательно, они являются его высотами.
Готовьтесь к ЕГЭ вместе со «Школково»!
Чтобы занятия проходили легко и максимально эффективно, выбирайте наш математический портал. Здесь вы найдете весь необходимый материал, который потребуется на этапе подготовки к единому государственному экзамену.
Специалисты образовательного проекта «Школково» предлагают пойти от простого к сложному: сначала мы даем теорию, основные формулы и элементарные задачи с решением, а затем постепенно переходим к заданиям экспертного уровня. Вы можете потренироваться, например, с решением задач на тему “Призма”.
Нужную базовую информацию вы найдете в разделе «Теоретическая справка». Вы также можете сразу приступить к решению задач по теме «Прямоугольный параллелепипед» в онлайн-режиме. В разделе «Каталог» представлена большая подборка упражнений разной степени сложности. База заданий регулярно пополняется.
Проверьте, легко ли вы сможете найти объем прямоугольного параллелепипеда, прямо сейчас. Разберите любое задание. Если упражнение дается вам легко, переходите к более сложным задачам. А если возникли определенные сложности, рекомендуем вам планировать свой день таким образом, чтобы ваше расписание включало занятия с дистанционным порталом «Школково».

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Задача 1. В прямоугольном параллелепипеде известно, что
Найдите длину диагонали
Решение: + показать
Задача 2. Найдите угол прямоугольного параллелепипеда, для которого
. Ответ дайте в градусах.
Решение: + показать
Задача 3. В прямоугольном параллелепипеде известны длины рёбер
Найдите синус угла между прямыми
и
Решение: + показать
Задача 4. Площадь поверхности куба равна Найдите его диагональ.
Решение: + показать
Задача 5. Объем куба равен Найдите площадь его поверхности.
Решение: + показать
Задача 6. Диагональ куба равна . Найдите его объем.
Решение: + показать
Задача 6. Объем куба равна . Найдите его диагональ.
Решение: + показать
Задача 7. Во сколько раз увеличится объем куба, если его ребра увеличить в десять раз?
Решение: + показать
Задача 8. Если каждое ребро куба увеличить на , то его площадь поверхности увеличится на
Найдите ребро куба.
Решение: + показать
Задача 9. Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в раза?
Решение: + показать
Задача 10. Объем одного куба в раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
Решение: + показать
Задача 11. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны и
Площадь поверхности этого параллелепипеда равна
Найдите третье ребро, выходящее из той же вершины.
Решение: + показать
Задача 12. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны
и
Найдите ребро равновеликого ему куба.
Решение: + показать
Задача 13. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны и
Диагональ параллелепипеда равна
Найдите объем параллелепипеда.
Решение: + показать
Задача 14. Площадь грани прямоугольного параллелепипеда равна Ребро, перпендикулярное этой грани, равно
Найдите объем параллелепипеда.
Решение: + показать
Задача 15. В прямоугольном параллелепипеде известны длины рёбер:
Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки
и
Решение: + показать
Задача 16. Диагональ прямоугольного параллелепипеда равна и образует углы
,
и
с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.
Решение: + показать
Задача 17. В прямоугольном параллелепипеде ребро
, ребро
, ребро
. Точка
— середина ребра
Найдите площадь сечения, проходящего через точки
.
Решение: + показать
Задача 18. Одна из граней прямоугольного параллелепипеда — квадрат. Диагональ параллелепипеда равна и образует с плоскостью этой грани угол
°. Найдите объем параллелепипеда.
Решение: + показать
Задача 19. Найдите объем многогранника, вершинами которого являются точки прямоугольного параллелепипеда
у которого
Решение: + показать
Задача 20. Найдите объем параллелепипеда , если объем треугольной пирамиды
равен
Решение: + показать
Задача 21. Найдите объем многогранника, вершинами которого являются точки прямоугольного параллелепипеда
у которого
Решение: + показать
Задача 22. Найдите объем многогранника, вершинами которого являются точки прямоугольного параллелепипеда
у которого
Решение: + показать
Задача 23. Объем параллелепипеда равен
Найдите объем треугольной пирамиды
Решение: + показать
Задача 24. В кубе точка
— середина ребра
, точка
— середина ребра
, точка
— середина ребра
Найдите угол
. Ответ дайте в градусах.
Решение: + показать
Вы можете пройти тест
Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.
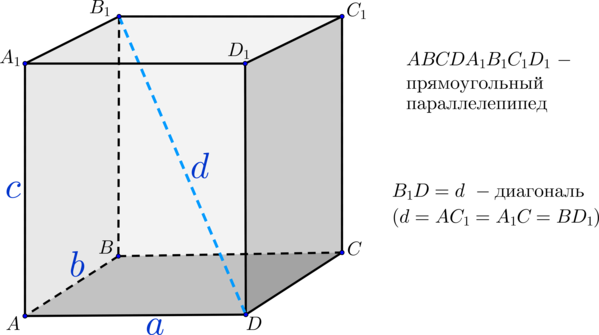
На рисунке изображен прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Его основаниями являются прямоугольники $ABCD$ и $A_1B_1C_1D_1$, а боковые ребра $AA_1, BB_1, CC_1$ и $DD_1$ перпендикулярны к основаниям.
Свойства прямоугольного параллелепипеда:
- В прямоугольном параллелепипеде $6$ граней и все они являются прямоугольниками.
- Противоположные грани попарно равны и параллельны.
- Все двугранные углы прямоугольного параллелепипеда – прямые.
- Диагонали прямоугольного параллелепипеда равны.
- Прямоугольный параллелепипед имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.
- Любая грань прямоугольного параллелепипеда может быть принята за основание.
- Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
- Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
$B_1D^2=AD^2+DC^2+C_1C^2$
Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.
Чтобы были понятны формулы, введем обозначения:
$а$ — длина;
$b$ — ширина;
$с$ — высота(она же боковое ребро);
$P_{осн}$ — периметр основания;
$S_{осн}$ — площадь основания;
$S_{бок}$ — площадь боковой поверхности;
$S_{п.п}$ — площадь полной поверхности;
$V$ — объем.
$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.
$S_{бок}=P_{осн}·c=2(a+b)·c$ – площадь боковой поверхности равна произведению периметра основания на боковое ребро.
$S_{п.п}=2(ab+bc+ac).$
Дополнительные сведения, которые пригодятся для решения задач:
Куб
$а$ — длина стороны.
$V=a^3;$
$S_{бок}=4а^2;$
$S_{п.п}=6а^2;$
$d=a√3$ – диагональ равна длине стороны, умноженной на $√3$.
Пирамида
Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) — треугольники, имеющие общую вершину.
Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.
Объем любой пирамиды равен трети произведения основания и высоты.
$V={1}/{3}S_{осн}·h$
В основании у произвольной пирамиды могут лежать различные многоугольники, рассмотрим площади некоторых из них.
В основании лежит треугольник.
Площадь треугольника.
- $S={a·h_a}/{2}$, где $h_a$ — высота, проведенная к стороне $а$.
- $S={a·b·sinα}/{2}$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
- Формула Герона $S=√{p(p-a)(p-b)(p-c)}$, где $р$ — это полупериметр $p={a+b+c}/{2}$.
- $S=p·r$, где $r$ — радиус вписанной окружности.
- $S={a·b·c}/{4R}$, где $R$ — радиус описанной окружности.
- Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ — катеты прямоугольного треугольника.
- Для равностороннего треугольника $S={a^2√3}/{4}$, где $а$ — длина стороны.
В основании лежит четырехугольник.
- Прямоугольник.
$S=a·b$, где $а$ и $b$ — смежные стороны. - Ромб.
$S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ — диагонали ромба.
$S=a^2·sinα$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами. - Трапеция.
$S={(a+b)·h}/{2}$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции. - Квадрат.
$S=a^2$, где $а$ — сторона квадрата.
Пример:
Найдите объём многогранника, вершинами которого являются точки $C, A_1, B_1, C_1, D_1$ параллелепипеда $ABCDA_1B_1C_1D_1$, у которого $AB=8, AD=12, AA_1=4$.
Решение:
Изобразим прямоугольный параллелепипед и на нем отметим вершины многогранника $C, A_1, B_1, C_1, D_1$, получим в итоге четырехугольную пирамиду. В основании пирамиды лежит прямоугольник, так основание пирамиды и прямоугольного параллелепипеда совпадают.
Объем пирамиды, в основании которой лежит прямоугольник
$V={S_{прямоугольника}·h}/{3}={a·b·h}/{3}$, где $a$ и $b$ — стороны прямоугольника.
Для нашего рисунка стороны прямоугольника – это $А_1В_1$ и $A_1D_1$.
В прямоугольном параллелепипеде противоположные ребра равны и параллельны, следовательно, $AB=А_1В_1=8; AD=A_1D_1=12$.
Высотой в пирамиде $CA_1B_1C_1D_1$ будет являться ребро $СС_1$, так как оно перпендикулярно основанию (из прямоугольного параллелепипеда).
$СС_1=АА_1=4$
$V={А_1В_1·A_1D_1·СС_1}/{3}={8·12·4}/{3}=128$
Ответ: $128$
Теорема Пифагора.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
Стереометрия на ЕГЭ. Приемы и секреты.
Вы уже знаете, что задачи по стереометрии в первой части ЕГЭ на самом деле простые. Правильный чертеж, элементарная логика, внимательность, плюс некоторые приемы, о которых мы рассказали в первой части статьи и еще расскажем — вот и всё, что вам нужно. Перейдем сразу к практике.

. Найдите объем треугольной пирамиды
.
Мы помним, что объем параллелепипеда равен . А объем пирамиды равен
. Иными словами, если у параллелепипеда и пирамиды одинаковые основания и одинаковые высоты, то объем пирамиды будет в три раза меньше, чем объем параллелепипеда. А у нашей пирамиды еще и площадь основания в два раза меньше. Значит, ее объем в шесть раз меньше объема параллелепипеда.
Ответ: .

. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
Об одном из способов решения этой задачи мы уже рассказали. Посчитайте, сколько нужно четырехугольных пирамидок, чтобы сложить из них такой кубик.
Есть и второй способ. Если бы пирамида и куб имели одинаковые высоты, объем пирамиды был бы в раза меньше объема куба (поскольку площади основания у них одинаковые). А у нашей пирамиды высота в два раза меньше, чем у куба. Значит, ее объем будет в
раз меньше, чем у куба.
Ответ: .
3. Радиусы трех шаров равны ,
и
. Найдите радиус шара, объем которого равен сумме их объемов.
На самом деле это задача по алгебре, причем элементарная. Объем шара равен . Осталось решить уравнение:
Как извлечь кубический корень из этого числа? Очень просто — разложите его на множители.
Ответ: .

, а объем равен
.
Мы говорили, что в основании правильной треугольной пирамиды лежит правильный треугольник. У него все углы равны и все стороны тоже равны. Площадь его проще всего найти по формуле
. Она равна
. Поскольку
, высота равна
.
5.
конуса, образующая которого равна
и наклонена к плоскости основания под углом
градусов. В ответе укажите
.
Если вы вдруг забыли, что такое образующая, — смотрите нашу таблицу с формулами. А что значит «наклонена к плоскости основания»? Вспомним, что угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость, то есть угол .
Из прямоугольного треугольника находим, что
. Объем конуса найдем по известной формуле и поделим на
.
Ответ: .
6. Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами , а боковые ребра равны
и наклонены к плоскости основания под углом
градусов.
Нарисуйте вид сверху, то есть правильный шестиугольник. У него все стороны равны, все углы тоже равны.
Как найти площадь правильного шестиугольника, если специальную формулу вы не знаете? Проще всего разбить его на одинаковых равносторонних треугольников. Формула площади равностороннего треугольника вам известна:
Итак, площадь основания равна . Осталось найти высоту.
Высота призмы — это отрезок, перпендикулярный ее основаниям. Из прямоугольного треугольника АСН находим:
Ответ: .
7. 
и образует углы
,
и
градусов с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.
Мы уже говорили, что угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.
Обозначим вершины параллелепипеда.
Проекцией диагонали на нижнее основание будет отрезок
. Пусть диагональ образует угол
градусов именно с плоскостью нижнего основания.
Рассмотрим прямоугольный треугольник . По теореме Пифагора,
. Итак, мы нашли высоту параллелепипеда.
Проекцией на переднюю грань будет отрезок
.
Из прямоугольного треугольника найдем
. Мы нашли ширину параллелепипеда. А его длина (то есть отрезок
) находится аналогично. Она тоже равна
. Объем параллелепипеда равен
.
Ответ: .
8.
Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно . Найдите объем пирамиды.
Если решать «в лоб», считая, что — основание, то у нас получится задача по стереометрии из второй части ЕГЭ. Но зачем такие сложности? Развернем пирамиду.
Объем пирамиды равен . В основании лежит равнобедренный прямоугольный треугольник, площадь которого равна
. Тогда объем пирамиды равен
.
Ответ: .
9.

, являющейся частью правильной шестиугольной пирамиды
, равен
. Найдите объем шестиугольной пирамиды.
У треугольной и шестиугольной пирамид, о которых говорится в условии, одинаковые высоты. Разные только площади основания. Нарисуем вид снизу.
Видим, что площадь основания треугольной пирамиды в раз меньше, чем у шестиугольной.
Ответ: .
Если в условии задачи по стереометрии дан рисунок — значит, повезло. Рисунок — это уже половина решения. А если его нет? Значит, рисуйте сами, как умеете. Отговорки «не умею» или «рисование у нас было только в детском саду» — не принимаются. Вам ведь не девочку на шаре надо изобразить, а намного более простые объекты 
10. 
является центром шара радиуса
. Найдите площадь части поверхности шара, лежащей внутри куба. В ответе запишите
.
Обратите внимание, что . Значит, сторона куба является диаметром шара. Осталось понять, какая часть шара лежит внутри куба.
Правильный ответ: .
11. Вершина куба
со стороной
является центром сферы, проходящей через точку
. Найдите площадь
части сферы, содержащейся внутри куба. В ответе запишите величину
.
Здесь главное — понять, какая часть шара лежит внутри куба. Порисуйте кубики и шарики. Пока есть возможность, возьмите яблоко (оно почти шарообразной формы), потренируйтесь. Жаль, что на ЕГЭ вам не выдадут килограмма яблок для отработки пространственного мышления.
Правильный ответ: .
Если вы его не получили, смотрите подсказку в конце статьи.
12. 
. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении
, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду.
Прежде всего, что значит «точка делит боковое ребро в отношении , считая от вершины»? Это значит, что она делит его на отрезки, длины которых
и
.
Плоскость делит пирамиду
на две. У пирамид
и
общее основание
. Ясно, что отношение их объемов равно отношению высот.
Проведем перпендикуляры и
к плоскости основания пирамиды.
— высота пирамиды
,
— высота пирамиды
. Очевидно, что отрезок
параллелен отрезку
, поскольку два перпендикуляра к одной плоскости параллельны друг другу. Через две параллельные прямые можно провести плоскость, причем только одну. Итак, точки
и
лежат в одной плоскости, то есть мы от стереометрической задачи перешли к плоской, планиметрической.
Треугольники и
подобны,
.
Значит, . Объем пирамиды
равен
объема пирамиды
.
Ответ: .
13.

. Найдите площадь сечения, проходящего через середины четырех его ребер.
Прежде всего, все ребра равны, значит, тетраэдр — правильный. В его основании лежит равносторонний треугольник, а вершина проецируется в центр этого треугольника.
Как вы думаете, какая фигура получится в сечении?
Заметим, что отрезок параллелен
поскольку является средней линией треугольника
. И отрезок
тоже параллелен
, потому что является средней линией треугольника
. Значит,
параллелен
. Аналогично
параллелен
. Мы помним, что средняя линия треугольника не только параллельна основанию — она равна половине основания. А у нашего тетраэдра все ребра равны. Значит,
— ромб, все стороны которого равны
. Уже хорошо.
Мы уже сказали, что у правильного тетраэдра вершина (точка ) проецируется в центр основания (точка
). В основании — правильный треугольник. Значит, точка
будет точкой пересечения биссектрис, медиан и высот этого треугольника, и тогда
перпендикулярен
.
Вспомним теорему о трех перпендикулярах. является проекцией
на плоскость основания, следовательно, отрезок
тоже перпендикулярен
. И тогда
— квадрат. Его площадь равна
.
А теперь — самые сложные задачи по стереометрии из первой части варианта ЕГЭ. Для их решения существуют секретные приемы. Конечно же, лучше знать их заранее, чем изобретать на экзамене.
14.

. Найдите объем многогранника, вершинами которого являются середины сторон данного тетраэдра.
Можно долго искать формулу объема октаэдра (а именно он там и находится, в серединке), а можно поступить умнее. Помните, как в задаче мы считали площадь неудобно расположенных фигур?
Здесь проще всего посчитать площадь квадрата со стороной , в который вписан данный треугольник. И вычесть из нее площади трех прямоугольных треугольников. Видите их на рисунке?
В нашей задаче про тетраэдр и многогранник можем поступить аналогично. Как получился этот многогранник в серединке? От исходного тетраэдра отрезали четыре маленьких тетраэдра, объем каждого из которых в раз меньше, чем объем большого (об этом мы уже говорили). Получаем:
.
Ответ: .
15.

. Найдите объем треугольной пирамиды
.
Обратите внимание, нарисован куб, а написано — параллелепипед. Мы знаем, что его объем равен , но не знаем, чему равны его длина, ширина и высота. Обозначим их
и
. Не так-то просто найти площадь основания и высоту пирамиды
. Так может, и не надо этого делать? Есть более удобный способ — тот же, что и в предыдущей задаче. Ведь пирамида
получается, если мы отрежем от параллелепипеда четыре пирамиды по углам —
,
,
и
. А объем каждой из них легко посчитать — мы делали это в первой задаче этой статьи. Например, объем пирамиды
равен
объема параллелепипеда. Объем четырех всех пирамид, которые отрезали, равен
объема параллелепипеда. Значит, объем пирамиды
равен
объема параллелепипеда.
Ответ: .
Поздравляем! Задачи по стереометрии из первой части ЕГЭ по математике освоены — от простых до самых сложных. Заходите чаще на наш сайт.
Подсказка к задаче :
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Стереометрия на ЕГЭ. Приемы и секреты.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.03.2023
ЕГЭ Профиль №5. Куб, прямоугольный параллелепипед
Скачать файл в формате pdf.
ЕГЭ Профиль №5. Куб, прямоугольный параллелепипед
| Задача 1. Площадь поверхности куба равна 18. Найдите его диагональ.
Ответ
ОТВЕТ: 3. |
| Задача 2. Объем куба равен 8. Найдите площадь его поверхности.
Ответ
ОТВЕТ: 24. |
| Задача 3. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
Ответ
ОТВЕТ: 4. |
| Задача 4. Во сколько раз увеличится объем куба, если его ребра увеличить в три раза?
Ответ
ОТВЕТ: 27. |
| Задача 5. Диагональ куба равна (sqrt {12} ). Найдите его объем.
Ответ
ОТВЕТ: 8. |
| Задача 6. Объем куба равен (24sqrt 3 ). Найдите его диагональ.
Ответ
ОТВЕТ: 6. |
| Задача 7. Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба.
Ответ
ОТВЕТ: 2. |
| Задача 8. Диагональ куба равна 1. Найдите площадь его поверхности.
Ответ
ОТВЕТ: 2. |
| Задача 9. Площадь поверхности куба равна 24. Найдите его объем.
Ответ
ОТВЕТ: 8. |
| Задача 10. Объем одного куба в 8 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
Ответ
ОТВЕТ: 4. |
| Задача 11. В кубе ABCDA1B1C1D1 точка K — середина ребра AA1, точка L — середина ребра A1B1, точка M — середина ребра A1D1. Найдите угол MLK. Ответ дайте в градусах.
Ответ
ОТВЕТ: 60. |
| Задача 12. В кубе ABCDA1B1C1D1 найдите угол между прямыми AD1 и B1D1. Ответ дайте в градусах.
Ответ
ОТВЕТ: 60. |
| Задача 13. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
Ответ
ОТВЕТ: 5. |
| Задача 14. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.
Ответ
ОТВЕТ: 3. |
| Задача 15. Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.
Ответ
ОТВЕТ: 24. |
| Задача 16. Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда.
Ответ
ОТВЕТ: 48. |
| Задача 17. Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.
Ответ
ОТВЕТ: 8. |
| Задача 18. Объем прямоугольного параллелепипеда равен 60. Площадь одной его грани равна 12. Найдите ребро параллелепипеда, перпендикулярное этой грани.
Ответ
ОТВЕТ: 5. |
| Задача 19. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
Ответ
ОТВЕТ: 4. |
| Задача 20. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба.
Ответ
ОТВЕТ: 6. |
| Задача 21. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.
Ответ
ОТВЕТ: 32. |
| Задача 22. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 3. Объем параллелепипеда равен 36. Найдите его диагональ.
Ответ
ОТВЕТ: 7. |
| Задача 23. Одна из граней прямоугольного параллелепипеда – квадрат. Диагональ параллелепипеда равна (sqrt 8 ) и образует с плоскостью этой грани угол 45o. Найдите объем параллелепипеда.
Ответ
ОТВЕТ: 4. |
| Задача 24. Диагональ прямоугольного параллелепипеда равна (sqrt 8 ) и образует углы 30o, 30o и 45o с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.
Ответ
ОТВЕТ: 4. |
| Задача 25. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите площадь поверхности параллелепипеда.
Ответ
ОТВЕТ: 64. |
| Задача 26. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Объем параллелепипеда равен 6. Найдите площадь его поверхности.
Ответ
ОТВЕТ: 22. |
| Задача 27. Объем параллелепипеда ABCDA1B1C1D1 равен 4,5.
Ответ
ОТВЕТ: 1,5. |
| Задача 28. Найдите объем многогранника, вершинами которого являются точки A, D, A1, B, C, B1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 3, AD = 4, AA1 = 5.
Ответ
ОТВЕТ: 30. |
| Задача 29. Найдите объем многогранника, вершинами которого являются точки A, B, C, D1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 4, AD = 3, AA1 = 4.
Ответ
ОТВЕТ: 8. |
| Задача 30. Найдите объем многогранника, вершинами которого являются точки A1, B, C, C1, B1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 4, AD = 3, AA1 = 4.
Ответ
ОТВЕТ: 16. |
| Задача 31. Найдите объем многогранника, вершинами которого являются точки A, B, C, B1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 3, AD = 3, AA1 = 4.
Ответ
ОТВЕТ: 6. |
| Задача 32. Найдите объем многогранника, вершинами которого являются точки A, B, B1, C1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 5, AD = 3, AA1 = 4.
Ответ
ОТВЕТ: 10. |
| Задача 33. Найдите угол ABD1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 3. Ответ дайте в градусах.
Ответ
ОТВЕТ: 45. |
| Задача 34. Найдите угол C1BC прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 4. Ответ дайте в градусах.
Ответ
ОТВЕТ: 45. |
| Задача 35. Найдите угол DBD1 прямоугольного параллелепипеда, для которого AB = 4, AD = 3, AA1 = 5. Ответ дайте в градусах.
Ответ
ОТВЕТ: 45. |
| Задача 36. В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AC1 = 13, C1D1 = 3, B1C1 = 12. Найдите длину ребра AA1.
Ответ
ОТВЕТ: 4. |
| Задача 37. В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BB1 = 11, C1D1 = 16, B1C1 = 8. Найдите длину диагонали DB1.
Ответ
ОТВЕТ: 21. |
| Задача 38. В прямоугольном параллелепипеде ABCDA1B1C1D1 ребро (AB = 2), ребро (AD = sqrt 5 ), ребро (A{A_1} = 2). Точка K — середина ребра BB1. Найдите площадь сечения, проходящего через точки A1, D1 и K.
Ответ
ОТВЕТ: 5. |
| Задача 39. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны ребра AB = 24, AD = 10, AA1 = 22. Найдите площадь сечения, проходящего через точки A, A1 и С.
Ответ
ОТВЕТ: 572. |
| Задача 40. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны ребра AB = 8, AD = 6, AA1 = 21. Найдите синус угла между прямыми CD и A1C1.
Ответ
ОТВЕТ: 0,6. |
| Задача 41. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны ребра (AB = 3,;;AD = 5,;;A{A_1} = 12). Найдите площадь сечения параллелепипеда, проходящего через точки A, B и С1.
Ответ
ОТВЕТ: 39. |