Найти площадь закрашенной фигуры егэ первообразная - Помощь в подготовке к экзаменам и поступлению

СДАМ ГИА:

РЕШУ ЕГЭ

Образовательный портал для подготовки к экзаменам

Математика профильного уровня

≡ Математика

Базовый уровень

Профильный уровень

Информатика

Русский язык

Английский язык

Немецкий язык

Французский язык

Испанский язык

Физика

Химия

Биология

География

Обществознание

Литература

История

Сайты, меню, вход, новости

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Об экзамене

Каталог заданий

Варианты

Ученику

Учителю

Школа

Эксперту

Справочник

Карточки

Теория

Сказать спасибо

Вопрос — ответ

Чужой компьютер

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

Играть в ЕГЭ-игрушку

Новости

10 марта

Как подготовиться к ЕГЭ и ОГЭ за 45 дней

6 марта

Изменения ВПР 2023

3 марта

Разместили утвержденное расписание ЕГЭ

27 января

Вариант экзамена блокадного Ленинграда

23 января

ДДОС-атака на Решу ЕГЭ. Шантаж.

6 января

Открываем новый сервис: «папки в избранном»

22 декабря

Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!

4 ноября

Материалы для подготовки к итоговому сочинению 2022–2023

31 октября

Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР

21 марта

Новый сервис: рисование

31 января

Внедрили тёмную тему!

НАШИ БОТЫ

Все новости

ЧУЖОЕ НЕ БРАТЬ!

Экзамер из Таганрога

10 апреля

Предприниматель Щеголихин скопировал сайт Решу ЕГЭ

Наша группа

Поиск

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 9 1–9

Добавить в вариант

Тип 7 № 323079

На рисунке изображён график функции y = f(x). Функция   — одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.

Аналоги к заданию № 323079: 323283 323373 323375 323379 323285 323287 323289 323291 323293 323295 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 4.3.1 Первообразные элементарных функций, 4.3.2 Примеры применения интеграла в физике и геометрии

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 7 № 323477

На рисунке изображён график некоторой функции Функция   — одна из первообразных функции  Найдите площадь закрашенной фигуры.

Аналоги к заданию № 323080: 323383 323475 323477 323385 323387 323389 323391 323393 323395 323397 … Все

Решение

Прототип задания

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 7 № 323080

На рисунке изображён график некоторой функции y = f(x). Функция   — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.

Аналоги к заданию № 323080: 323383 323475 323477 323385 323387 323389 323391 323393 323395 323397 … Все

Решение

Курс Д. Д. Гущина

3 комментария · Сообщить об ошибке · Помощь

Тип 7 № 323383

Аналоги к заданию № 323080: 323383 323475 323477 323385 323387 323389 323391 323393 323395 323397 … Все

Решение

Прототип задания

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 7 № 323475

Аналоги к заданию № 323080: 323383 323475 323477 323385 323387 323389 323391 323393 323395 323397 … Все

Решение

Прототип задания

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 7 № 323283

Аналоги к заданию № 323079: 323283 323373 323375 323379 323285 323287 323289 323291 323293 323295 … Все

Решение

Прототип задания

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 7 № 323373

Аналоги к заданию № 323079: 323283 323373 323375 323379 323285 323287 323289 323291 323293 323295 … Все

Решение

Прототип задания

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 7 № 323375

Аналоги к заданию № 323079: 323283 323373 323375 323379 323285 323287 323289 323291 323293 323295 … Все

Решение

Прототип задания

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 7 № 323379

На рисунке изображён график функции Функция   — одна из первообразных функции  Найдите площадь закрашенной фигуры.

Аналоги к заданию № 323079: 323283 323373 323375 323379 323285 323287 323289 323291 323293 323295 … Все

Решение

Прототип задания

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Всего: 9 1–9

О проекте · Редакция · Правовая информация · О рекламе

Источник

Лучшие репетиторы для сдачи ЕГЭ

Задания по теме «Первообразная функции»

Открытый банк заданий по теме первообразная функции. Задания B7 из ЕГЭ по математике (профильный уровень)

Геометрические фигуры на плоскости: вычисление величин с использованием углов

Геометрические фигуры в пространстве: нахождение длины, площади, объема

Задание №1164

Тип задания: 7
Тема:
Первообразная функции

Условие

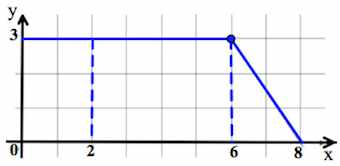
На рисунке изображён график функции y=f(x) (являющийся ломаной линией, составленной из трёх прямолинейных отрезков). Пользуясь рисунком, вычислите F(9)-F(5), где F(x) — одна из первообразных функции f(x).

Показать решение

Решение

По формуле Ньютона-Лейбница разность F(9)-F(5), где F(x) — одна из первообразных функции f(x), равна площади криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми y=0, x=9 и x=5. По графику определяем, что указанная криволинейная трапеция является трапецией с основаниями, равными 4 и 3 и высотой 3.

Её площадь равна frac{4+3}{2}cdot 3=10,5.

Ответ

10,5

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1158

Тип задания: 7
Тема:
Первообразная функции

Условие

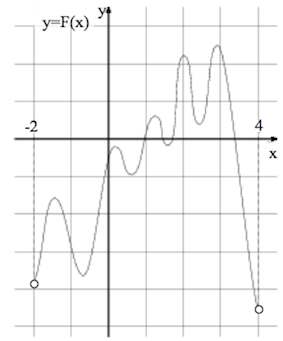
На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-5; 5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-3; 4].

Показать решение

Решение

Согласно определению первообразной выполняется равенство: F'(x)=f(x). Поэтому уравнение f(x)=0 можно записать в виде F'(x)=0. Так как на рисунке изображён график функции y=F(x), то надо найти те точки промежутка [-3; 4], в которых производная функции F(x) равна нулю. Из рисунка видно, что это будут абсциссы экстремальных точек (максимума или минимума) графика F(x). Их на указанном промежутке ровно 7 (четыре точки минимума и три точки максимума).

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1155

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображён график функции y=f(x) (являющийся ломаной линией, составленной из трёх прямолинейных отрезков). Пользуясь рисунком, вычислите F(5)-F(0), где F(x) — одна из первообразных функции f(x).

Показать решение

Решение

По формуле Ньютона-Лейбница разность F(5)-F(0), где F(x) — одна из первообразных функции f(x), равна площади криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми y=0, x=5 и x=0. По графику определяем, что указанная криволинейная трапеция является трапецией с основаниями, равными 5 и 3 и высотой 3.

Её площадь равна frac{5+3}{2}cdot 3=12.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1149

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-5; 4). Пользуясь рисунком, определите количество решений уравнения f (x)=0 на отрезке (-3; 3].

Показать решение

Решение

Из рисунка видно, что это будут абсциссы экстремальных точек (максимума или минимума) графика F(x). Их на указанном промежутке ровно 5 (две точки минимума и три точки максимума).

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1146

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображен график некоторой функции y=f(x). Функция F(x)=-x^3+4,5x^2-7 — одна из первообразных функции f(x).

Найдите площадь заштрихованной фигуры.

Показать решение

Решение

Заштрихованная фигура является криволинейной трапецией, ограниченной сверху графиком функции y=f(x), прямыми y=0, x=1 и x=3. По формуле Ньютона-Лейбница её площадь S равна разности F(3)-F(1), где F(x) — указанная в условии первообразная функции f(x). Поэтому S= F(3)-F(1)= -3^3 +(4,5)cdot 3^2 -7-(-1^3 +(4,5)cdot 1^2 -7)= 6,5-(-3,5)= 10.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №907

Тип задания: 7
Тема:
Первообразная функции

Условие

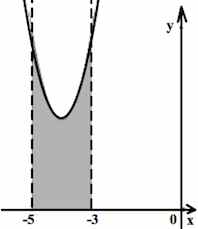
На рисунке изображён график некоторой функции y=f(x). Функция F(x)=x^3+6x^2+13x-5 — одна из первообразных функции f(x). Найдите площадь заштрихованной фигуры.

Показать решение

Решение

Заштрихованная фигура является криволинейной трапецией, ограниченной графиком функции y=f(x) и прямыми y=0, x=-4 и x=-1. По формуле Ньютона-Лейбница её площадь S равна разности F(-1)-F(-4), где F(x) — указанная в условии первообразная функции f(x).

Поэтому S= F(-1)-F(-4)= (-1)^3+6(-1)^2+13(-1)-5-((-4)^3+6(-4)^2+13(-4)-5)= -13-(-25)=12.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №307

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображен график некоторой функции y=f(x). Функция F(x)=x^3+18x^2+221x-frac12 — одна из первообразных функции f(x). Найдите площадь заштрихованной фигуры.

Показать решение

Решение

По формуле Ньютона-Лейбница S=F(-1)-F(-5).

F(-1)= (-1)^3+18cdot(-1)^2+221cdot(-1)-frac12= -204-frac12.

F(-5)= (-5)^3+18cdot(-5)^2+221cdot(-5)-frac12= -125+450-1105-frac12= -780-frac12.

F(-1)-F(-5)= -204-frac12-left (-780-frac12right)= 576.

Ответ

576

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №306

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображен график некоторой функции y=f(x).Пользуясь рисунком, вычислите F(9)-F(3), где F(x) — одна из первообразных функции f(x).

Показать решение

Решение

F(9)-F(3)=S, где S — площадь фигуры, ограниченной графиком функции y=f(x), прямыми y=0 и x=3,:x=9. Рассмотрим рисунок ниже.

Данная фигура — трапеция с основаниями 6 и 1 и высотой 2. Ее площадь равна frac{6+1}{2}cdot2=7.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №104

Тип задания: 7
Тема:
Первообразная функции

Условие

На координатной плоскости изображен график функции y=f(x). Одна из первообразных этой функции имеет вид: F(x)=-frac13x^3-frac52x^2-4x+2. Найдите площадь заштрихованной фигуры.

Показать решение

Решение

На рисунке видно, что заштрихованная фигура ограничена по оси абсцисс точками −4, −1, а по оси ординат графиком функции: f(x). Значит площадь фигуры мы можем найти с помощью разности значений первообразных в точках −4 и −1, по формуле определенного интеграла:

intlimits_{-4}^{-1}f(x)dx=F(-1)-F(-4)

Подставим значение первообразной из условия и получим площадь фигуры:

F(-1)-F(-4)=

=frac13-frac52+4+2-frac{64}{3}+frac{80}{2}-16-2=

=-frac{63}{3}+frac{75}{2}-12=-21+37,5-12=4,5

Ответ

4,5

Задание №103

Тип задания: 7
Тема:
Первообразная функции

Условие

Первообразная y=F(x) некоторой функции y=f(x) определена на интервале (−16; −2). Определите сколько решений имеет уравнение f(x) = 0 на отрезке [−10; −5].

Показать решение

Решение

Формула первообразной имеет следующий вид:

f(x) = F'(x)

По условию задачи нужно найти точки, в которых функция f(x) равна нулю. Принимая во внимание формулу первообразной, это значит, что, нужно найти точки, в которых F'(x) = 0, то есть те точки, в которых производная от первообразной равна нулю.

Мы знаем, что производная равна нулю в точках локального экстремума, т.е. функция имеет решения в тех точках, в которых возрастание F(x) сменяется убыванием и наоборот.

На отрезке [−10; −5] видно что это точки: −9; −7; −6. Значит уравнение f(x) = 0 имеет 3 решения.

Ответ

Лучшие репетиторы для сдачи ЕГЭ

Сложно со сдачей ЕГЭ?

Звоните, и подберем для вас репетитора: 78007750928

Источник

Решение:

Площадь под графиком функции f(x) на отрезке [a; b] равна разности первообразных:

S = F(b) — F(a)

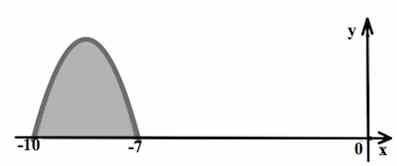
Нам необходимо найти площадь закрашенной фигуры на отрезке [-8; -6], то есть a = -8; b = -6. Значит S = F(-6) — F(-8).

Найдем F(-8):

F(-8) = (-8)³ + 21⋅(-8)² +151⋅(-8) — 1

F(-8) = — 512 + 21⋅64 — 151⋅8 — 1

F(-8) = — 512 + 1344 — 1208 — 1

F(-8) = — 513 + 136

F(-8) = -377

Найдем F(-6):

F(-6) = (-6)³ + 21⋅(-6)² +151⋅(-6) — 1

F(-6) = — 216 + 21⋅36 — 151⋅6 — 1

F(-6) = — 216 + 756 — 906 — 1

F(-6) = — 217 — 150

F(-6) = -367

Тогда площадь закрашенной фигуры равна:

S = F(-6) — F(-8) = -367 — (-377) = -367 + 377 = 10

Ответ: 10

Источник

10
Авг 2013

Категория: 07 Производная, ПО

07. Первообразная

2013-08-10
2022-09-11

Задача 1. На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите , где — одна из первообразных функции .

Решение: + показать

Задача 2. На рисунке изображён график некоторой функции . Функция — одна из первообразных функции . Найдите площадь закрашенной фигуры.

Решение: + показать

Задача 3. На рисунке изображён график некоторой функции . Функция $F(x)=-frac{4}{9}x^3-frac{34}{3}x^2-frac{280}{3}x-frac{18}{5}$ — одна из первообразных функции . Найдите площадь закрашенной фигуры.

Решение: + показать

Задача 4. На рисунке изображён график функции – одной из первообразных некоторой функции , определённой на интервале . Пользуясь рисунком, определите количество решений уравнения на отрезке .

Решение: + показать

Загляните –> + показать

Вы можете пройти тест «Первообразная»

Автор: egeMax |

комментариев 7

Источник

Результат поиска:

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

Результат поиска:

ЕГЭ Профиль №7. Первообразная

ЕГЭ Профиль №7. Первообразнаяadmin2023-03-09T22:51:12+03:00

Скачать файл в формате pdf.

Решение задач

Задача 1	Задача 2	Задача 3
Задача 4	Задача 5	Задача 6
Задача 7	Задача 8	Задача 9

Комментарии для сайта Cackle

Вставить формулу как

Блок

Строка

Дополнительные настройки

Цвет формулы

Цвет текста

#333333

ID формулы

Классы формулы

Используйте LaTeX для набора формулы

Предпросмотр

({})

Формула не набрана

Вставить

Источник

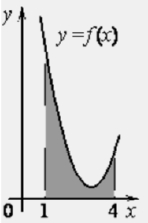
На рисунке изображён график некоторой функции 𝑦 = 𝑓(𝑥). Функция 𝐹(𝑥) = 𝑥³− 𝑥² + 14𝑥 − 10 − одна из первообразных функции 𝑓(𝑥). Найдите площадь закрашенной фигуры.