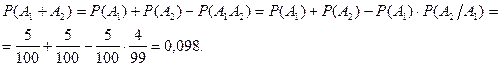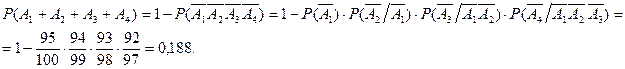Найти вероятность того что студент сдаст хотя бы один экзамен

Решение задач с формулировкой «хотя бы один»

Поговорим о задачах, в которых встречается фраза «хотя бы один». Наверняка вы встречали такие задачи в домашних и контрольных работах, а теперь узнаете, как их решать. Сначала я расскажу об общем правиле, а потом рассмотрим частный случай независимых событий и схемы Бернулли, выпишем формулы и примеры для каждого.

Общая методика и примеры

Общая методика для решения задач, в которых встречается фраза «хотя бы один» такая:

1. Выписать исходное событие $A$ = (Вероятность того, что … хотя бы …).
2. Сформулировать противоположное событие $bar{A}$.
3. Найти вероятность события $P(bar{A})$.
4. Найти искомую вероятность по формуле $P(A)=1-P(bar{A})$.

А теперь разберем ее на примерах. Вперед!

Пример 1. В ящике находится 25 стандартных и 6 бракованных однотипных деталей. Какова вероятность того, что среди трёх наудачу выбранных деталей окажется хотя бы одна бракованная?

Действуем прямо по пунктам.
1. Записываем событие, вероятность которого надо найти прямо из условия задачи:
$A$ =(Из 3 выбранных деталей хотя бы одна бракованная).

2. Тогда противоположное событие формулируется так $bar{A}$ = (Из 3 выбранных деталей ни одной бракованной) = (Все 3 выбранные детали будут стандартные).

3. Теперь нужно понять, как найти вероятность события $bar{A}$, для чего еще раз посмотрим на задачу: говорится об объектах двух видов (детали бракованные и нет), из которых вынимается некоторое число объектов и изучаются (бракованные или нет). Это задача решается с помощью классического определения вероятности (точнее, по формуле гипергеометрической вероятности, подробнее о ней читайте в статье).

Для первого примера запишем решение подробно, далее будем уже сокращать (а полные инструкции и калькуляторы вы найдете по ссылке выше).

Сначала найдем общее число исходов — это число способов выбрать любые 3 детали из партии в 25+6=31 деталей в ящике. Так как порядок выбора несущественнен, применяем формулу для числа сочетаний из 31 объектов по 3: $n=C_{31}^3$.

Теперь переходим к числу благоприятствующих событию исходов. Для этого нужно, чтобы все 3 выбранные детали были стандартные, их можно выбрать $m = C_{25}^3$ способами (так как стандартных деталей в ящике ровно 25).

Вероятность равна:

$$
P(bar{A})=frac{m}{n}=frac{C_{25}^3 }{C_{31}^3} = frac{23 cdot 24cdot 25}{29cdot 30cdot 31} =frac{2300}{4495}= 0.512.
$$

4. Тогда искомая вероятность:

$$
P(A)=1-P(bar{A})=1- 0.512 = 0.488.
$$

Ответ: 0.488.

Пример 2. Из колоды в 36 карт берут наудачу 6 карт. Найти вероятность того, что среди взятых карт будут: хотя бы две пики.

1. Записываем событие $A$ =(Из 6 выбранных карт будут хотя бы две пики).

2. Тогда противоположное событие формулируется так $bar{A}$ = (Из 6 выбранных карт будет менее 2 пик) = (Из 6 выбранных карт будет ровно 0 или 1 пиковые карты, остальные другой масти).

Замечание. Тут я остановлюсь и сделаю небольшое замечание. Хотя в 90% случаях методика «перейти к противоположному событию» работает на отлично, существуют случаи, когда проще найти вероятность исходного события. В данном случае, если искать напрямую вероятность события $A$ потребуется сложить 5 вероятностей, а для события $bar{A}$ — всего 2 вероятности. А вот если бы задача была такая «из 6 карт хотя бы 5 — пиковые», ситуация стала бы обратной и тут проще решать исходную задачу. Если опять попытаться дать инструкцию, скажу так. В задачах, где видите «хотя бы один», смело переходите к противоположному событию. Если же речь о «хотя бы 2, хотя бы 4 и т.п.», тут надо прикинуть, что легче считать.

3. Возвращаемся к нашей задаче и находим вероятность события $bar{A}$ с помощью классического определения вероятности.

Общее число исходов (способов выбрать любые 6 карт из 36) равно $n=C_{36}^6$ (калькулятор сочетаний тут).

Найдем число благоприятствующих событию исходов. $m_0 = C_{27}^6$ — число способов выбрать все 6 карт непиковой масти (их в колоде 36-9=27), $m_1 = C_{9}^1cdot C_{27}^5$ — число способов выбрать 1 карту пиковой масти (из 9) и еще 5 других мастей (из 27).

Тогда:

$$
P(bar{A})=frac{m_0+m_1}{n}=frac{C_{27}^6+C_{9}^1cdot C_{27}^5 }{C_{36}^6} =frac{85215}{162316}= 0.525.
$$

4. Тогда искомая вероятность:

$$
P(A)=1-P(bar{A})=1- 0.525 = 0.475.
$$

Ответ: 0.475.

Пример 3. В урне 2 белых, 3 черных и 5 красных шаров. Три шара вынимают наугад. Найти вероятность того, что среди вынутых шаров хотя бы два будут разного цвета.

1. Записываем событие $A$ =(Среди вынутых 3 шаров хотя бы два разного цвета). То есть, например, «2 красных шара и 1 белый», или «1 белый, 1 черный, 1 красный», или «2 черных, 1 красный» и так далее, вариантов многовато. Попробуем правило перехода к противоположному событию.

2. Тогда противоположное событие формулируется так $bar{A}$ = (Все три шара одного цвета) = (Выбраны 3 черных шара или 3 красных шара) — всего 2 варианта получилось, значит, этот способ решения упрощает вычисления. Кстати, все шары белого цвета не могут быть выбраны, так как их всего 2, а вынимается 3 шара.

3. Общее число исходов (способов выбрать любые 3 шара из 2+3+5=10 шаров) равно $n=C_{10}^3=120$.

Найдем число благоприятствующих событию исходов. $m = C_{3}^3+C_{5}^3=1+10=11$ — число способов выбрать или 3 черных шара (из 3), или 3 красных шара (из 5).

Тогда:

$$
P(bar{A})=frac{m}{n}=frac{11}{120}.
$$

4. Искомая вероятность:

$$
P(A)=1-P(bar{A})=1- frac{11}{120}=frac{109}{120} = 0.908.
$$

Ответ: 0.908.

Частный случай. Независимые события

Идем дальше, и приходим к классу задач, где рассматривается несколько независимых событий (стрелки попадают, лампочки перегорают, машины заводятся, рабочие болеют с разной вероятностью каждый и т.п.) и нужно «найти вероятность наступления хотя бы одного события». В вариациях это может звучать так «найти вероятность, что хотя бы один стрелок из трех попадет в цель», «найти вероятность того, что хотя бы один автобус из двух вовремя приедет на вокзал», «найти вероятность, что хотя бы один элемент в устройстве из четырех элементов откажет за год» и т.д.

Если в примерах выше речь шла о применении формулы классической вероятности, здесь мы приходим к алгебре событий, используем формулы сложения и умножения вероятностей (небольшая теория тут).

Итак, рассматриваются несколько независимых событий $A_1, A_2,…,A_n$, вероятности наступления каждого известны и равны $P(A_i)=p_i$ ($q_i=1-p_i$). Тогда вероятность того, что в результате эксперимента произойдет хотя бы одно из событий, вычисляется по формуле

$$
P=1-q_1cdot q_2 cdot …cdot q_n. quad(1)
$$

Строго говоря, эта формула тоже получается применением основной методики «перейти к противоположному событию». Ведь действительно, пусть $A$=(Наступит хотя бы одно событие из $A_1, A_2,…,A_n$), тогда $bar{A}$ = (Ни одно из событий не произойдет), что значит:

$$
P(bar{A})=P(bar{A_1} cdot bar{A_2} cdot … bar{A_n})=P(bar{A_1}) cdot P(bar{A_2}) cdot … P(bar{A_n})=\
=(1-P(A_1)) cdot (1-P(A_2)) cdot … (1-P(A_n))=\
=(1-p_1) cdot (1-p_2) cdot … (1-p_n)=q_1cdot q_2 cdot …cdot q_n,\
$$
откуда и получаем нашу формулу
$$
P(A)=1-P(bar{A})=1-q_1cdot q_2 cdot …cdot q_n.
$$

Пример 4. Узел содержит две независимо работающие детали. Вероятности отказа деталей соответственно равны 0,05 и 0,08. Найти вероятность отказа узла, если для этого достаточно, чтобы отказала хотя бы одна деталь.

Событие $A$ =(Узел отказал) = (Хотя бы одна из двух деталей отказала). Введем независимые события: $A_1$ = (Первая деталь отказала) и $A_2$ = (Вторая деталь отказала). По условию $p_1=P(A_1)=0,05$, $p_2=P(A_2)=0,08$, тогда $q_1=1-p_1=0,95$, $q_2=1-p_2=0,92$. Применим формулу (1) и получим:

$$
P(A)=1-q_1cdot q_2 = 1-0,95cdot 0,92=0,126.
$$

Ответ: 0,126.

Пример 5. Студент разыскивает нужную ему формулу в трех справочниках. Вероятность того, что формула содержится в первом справочнике, равна 0,8, во втором — 0,7, в третьем — 0,6. Найти вероятность того, что формула содержится хотя бы в одном справочнике.

Действуем аналогично. Рассмотрим основное событие
$A$ =(Формула содержится хотя бы в одном справочнике). Введем независимые события:
$A_1$ = (Формула есть в первом справочнике),
$A_2$ = (Формула есть во втором справочнике),
$A_3$ = (Формула есть в третьем справочнике).

По условию $p_1=P(A_1)=0,8$, $p_2=P(A_2)=0,7$, $p_3=P(A_3)=0,6$, тогда $q_1=1-p_1=0,2$, $q_2=1-p_2=0,3$, $q_3=1-p_3=0,4$. Применим формулу (1) и получим:

$$
P(A)=1-q_1cdot q_2cdot q_3 = 1-0,2cdot 0,3cdot 0,4=0,976.
$$

Ответ: 0,976.

Пример 6. Рабочий обслуживает 4 станка, работающих независимо друг от друга. Вероятность того, что в течение смены первый станок потребует внимания рабочего, равна 0,3, второй – 0,6, третий – 0,4 и четвёртый – 0,25. Найти вероятность того, что в течение смены хотя бы один станок не потребует внимания мастера.

Думаю, вы уже уловили принцип решения, вопрос только в количестве событий, но и оно не оказывает влияния на сложность решения (в отличие от общих задач на сложение и умножение вероятностей). Только будьте внимательны, вероятности указаны для «потребует внимания», а вот вопрос задачи «хотя бы один станок НЕ потребует внимания». Вводить события нужно такие же, как и основное (в данном случае, с НЕ), чтобы пользоваться общей формулой (1).

Получаем:
$A$ = (В течение смены хотя бы один станок НЕ потребует внимания мастера),
$A_i$ = ($i$-ый станок НЕ потребует внимания мастера), $i=1,2,3,4$,
$p_1 = 0,7$, $p_2 = 0,4$, $p_3 = 0,6$, $p_4 = 0,75$.

Искомая вероятность:

$$
P(A)=1-q_1cdot q_2cdot q_3 cdot q_4= 1-(1-0,7)cdot (1-0,4)cdot (1-0,6)cdot (1-0,75)=0,982.
$$

Ответ: 0,982. Почти наверняка мастер будет отдыхать всю смену;)

Частный случай. Повторные испытания

Думаете, дальше будет сложнее? Напротив, случаи все более частные, решения и формулы все более простые.

Итак, у нас есть $n$ независимых событий (или повторений некоторого опыта), причем вероятности наступления этих событий (или наступления события в каждом из опытов) теперь одинаковы и равны $p$. Тогда формула (1) упрощается к виду
:

$$
P=1-q_1cdot q_2 cdot …cdot q_n = 1-q^n.
$$

Фактически мы сужаемся к классу задач, который носит название «повторные независимые испытания» или «схема Бернулли», когда проводится $n$ опытов, вероятность наступления события в каждом из которых равна $p$. Нужно найти вероятность, что событие появится хотя бы раз из $n$ повторений:

$$
P=1-q^n. quad(2)
$$

Подробнее о схеме Бернулли можно прочитать в онлайн-учебнике, а также посмотреть статьи-калькуляторы о решении различных подтипов задач (о выстрелах, лотерейных билетах и т.п.). Ниже же будут разобраны задачи только с «хотя бы один».

Пример 7. Пусть вероятность того, что телевизор не потребует ремонта в течение гарантийного срока, равна 0,9. Найти вероятность того, что в течение гарантийного срока из 3 телевизоров хотя бы один не потребует ремонта.

Решения короче вы еще не видели.
Просто выписываем из условия: $n=3$, $p=0,9$, $q=1-p=0,1$.
Тогда вероятность того, что в течение гарантийного срока из 3 телевизоров хотя бы один не потребует ремонта, по формуле (2):

$$
P=1-0,1^3=1-0,001=0,999
$$

Ответ: 0,999.

Пример 8. Производится 5 независимых выстрелов по некоторой цели. Вероятность попадания при одном выстреле равна 0,8. Найти вероятность того, что будет хотя бы одно попадание.

Опять, начинаем с формализации задачи, выписывая известные величины. $n=5$ выстрелов, $p=0,8$ — вероятность попадания при одном выстреле, $q=1-p=0,2$.
И тогда вероятность того, что будет хотя бы одно попадание из пяти выстрелов равна:
$$
P=1-0,2^5=1-0,00032=0,99968
$$

Ответ: 0,99968.

Думаю, с применением формулы (2) все более чем ясно (не забудьте почитать и о других задачах, решаемых в рамках схемы Бернулли, ссылки были выше). А ниже я приведу чуть более сложную задачу. Такие задачи встречаются пореже, но и их способ решения надо усвоить. Поехали!

Пример 9. Производится n независимых опытов, в каждом из которых некоторое событие A появляется с вероятностью 0,7. Сколько нужно сделать опытов для того, чтобы с вероятностью 0,95 гарантировать хотя бы одно появление события A?

Имеем схему Бернулли, $n$ — количество опытов, $p=0,7$ — вероятность появления события А.

Тогда вероятность того, что произойдет хотя бы одно событие А в $n$ опытах, равна по формуле (2):
$$
P=1-q^n=1-(1-0,7)^n=1-0,3^n
$$
По условию эта вероятность должна быть не меньше 0,95, поэтому:

$$
1-0,3^n ge 0,95,\
0,3^n le 0,05,\
n ge log_{0,3} 0,05 = 2,49.
$$

Округляя, получаем что нужно провести не менее 3 опытов.

Ответ: минимально нужно сделать 3 опыта.

Полезные ссылки

• Калькуляторы на схему Бернулли
• Основные формулы комбинаторики
• Примеры решений задач по теории вероятностей
• Заказать свои задачи на вероятность

В решебнике вы найдете более 1000 задач со словами «хотя бы …»:

Соседние файлы в предмете Высшая математика

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Пример 1. Определить вероятность того, что выбранное наудачу изделие является первосортным, если известно, что 4 % всей продукции является браком, а 75 % небракованных изделий удовлетворяют требованиям первого сорта.

Решение. Пусть событие A={выбранное изделие небракованное}, событие B={небракованное изделие удовлетворяет требованиям первого сорта}, событие C={выбранное наудачу изделие первосортное}. Событие C предоставляет собой произведение событий A и B: C=AB. По условию , . Тогда по теореме умножения вероятностей (см. 2.1) искомая вероятность .

Пример 2. В первом ящике 2 белых и 10 красных шаров; во втором ящике 8 белых и 4 красных шара. Из каждого ящика вынули по шару. Какова вероятность, что оба шара белые?

Решение. В данном случае речь идет о совмещении событий A и B, где событие A={появление белого шара из первого ящика}, событие B={появление белого шара из второго ящика}. При этом A и B – независимые события. Имеем , . По теореме умножения для независимых событий (см. (6)) находим .

Пример 3. На 100 лотерейных билетов приходится 5 выигрышных. Какова вероятность выигрыша хотя бы по одному билету, если приобретено: а) 2 билета; б) 4 билета?

Решение. Пусть событие ={выигрыш по -му билету}, =1, 2, 3, 4. События — совместные, но зависимые.

А) По формулам (8) и (4) вероятность выигрыша хотя бы по одному из двух билетов

Б) по формулам (9) и (5) вероятность выигрыша хотя бы по одному из четырех билетов

Пример 4. Произведено три выстрела по цели из орудия. Вероятность попадания при первом выстреле равна 0,75, при втором – 0,8, при третьем – 0,9. Определить вероятность того, что будет: а) три попадания; б) хотя бы одно попадание.

Решение. А) Пусть событие A состоит в том, что будет три попадания в цель. Событие A представляет собой произведение трех событий: , где — попадание в цель при -м выстреле, . События — независимые. По теореме умножения для независимых событий (см. (7)) .

Б) Пусть событие B состоит в том, что будет хотя бы одно попадание в цель при трех выстрелах (т. е. не менее одного попадания в цель). Событие — сложное событие. События — совместные, а потому использовать аксиому сложения для вычисления вероятности события B нельзя. Представим событие B в виде суммы несовместных событий (вариантов):

.

По теореме умножения для независимых событий можно найти вероятность каждого варианта и все эти вероятности сложить в соответствии с аксиомой сложения. Однако такой путь решения задачи слишком сложен. Целесообразнее от события B перейти к противоположному событию ={нет ни одного попадания в цель при трех выстрелах}. Учитывая, что событие , по теореме умножения для независимых событий (см. (7)), найдем , откуда .

На этом примере проиллюстрирован принцип целесообразности применения противоположных событий в теории вероятностей.

Пример 5. Радист трижды вызывает корреспондента. Вероятность того, что будет принят первый вызов, равна 0,3, второй – 0,4, третий -0,5. По условиям приема события, состоящие в том, что данный вызов будет услышан, независимы. Найти вероятность того, что корреспондент вообще услышит вызов.

Решение. Пусть событие ={принят корреспондентом -й вызов}, =1, 2, 3. События совместные и независимые. По условию ; ; . Событие B={корреспондент вообще услышит вызов}: . Найдем вероятность события B. Для этого от события B перейдем к противоположному событию {корреспондент не услышит вызов}: , воспользовавшись формулой (9), найдем:

Пример 6. Вероятность того, что студент сдаст первый экзамен, равна 0,9; второй – 0,9, третий – 0,8. Найти вероятность того, что студентом будут сданы: а) только 2-й экзамен; б) только один экзамен; в) три экзамена; г) по крайней мере два экзамена; д) хотя бы один экзамен.

Решение. а) Обозначим события: = {студент сдаст -й экзамен}, 1,2,3; B = {студент сдаст только 2-й экзамен из трех}. Очевидно, что событие B представляет собой совместное наступление трех событий, состоящих в том, что студент сдаст 2-й экзамен и не сдаст 1-й и 3-й экзамены, т. е. . Учитывая, что события независимы, получим .

Б) Пусть событие C = {студент сдаст один экзамен из трех}. Очевидно, что событие C можно представить в виде суммы трех несовместных событий: .

По аксиоме сложения и теореме умножения для независимых событий .

В) Пусть событие E = {студент сдаст все три экзамена}, т. е. . Тогда по формуле (7) .

Г) Пусть событие F = {студент сдаст, по крайней мере, два экзамена} (т. е. хотя бы два экзамена или не менее двух экзаменов). Ясно, что событие F означает сдачу любых двух экзаменов из трех, либо всех трех экзаменов. Представим событие F в виде суммы несовместных событий: .

Тогда по аксиоме сложения и теореме умножения для независимых событий найдем .

Д) Пусть событие K – студент сдал хотя бы один экзамен (т. е. не менее одного экзамена). От прямого события K перейдем к противоположному событию и воспользуемся формулой (2.7). Тогда

Т. е. сдача хотя бы одного экзамена из трех является событием практически достоверным.

< Предыдущая		Следующая >