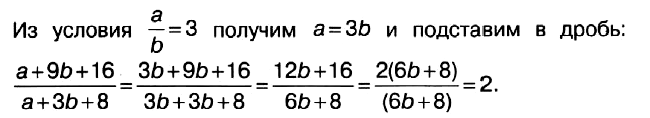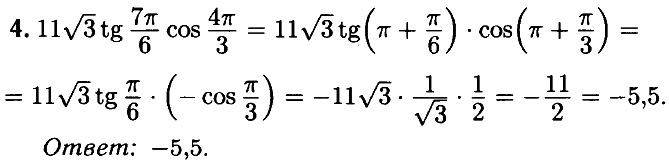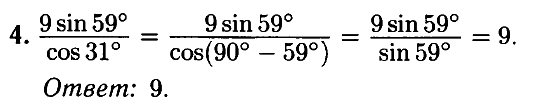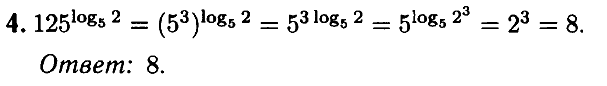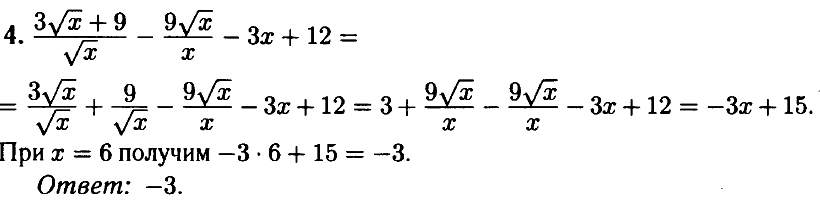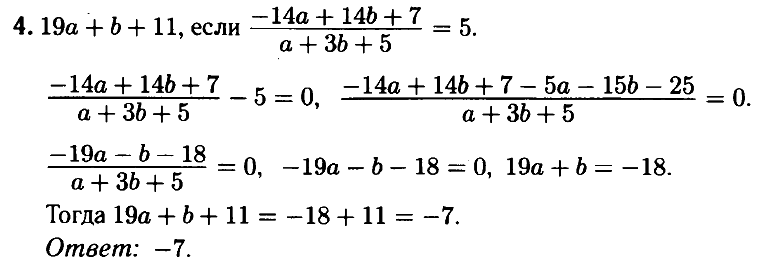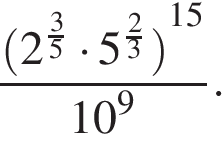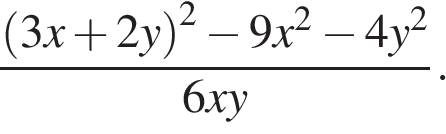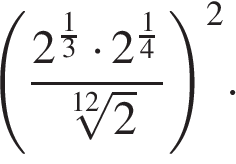Найти значение выражения егэ профиль математика

Есть в Профильном ЕГЭ по математике, и даже в первой его части, такие задачи, для решения которых нужно знать ВСЁ. То есть всю школьную программу алгебры, с 5 класса до 11. Или почти всю.

Например, задание №6 Профильного ЕГЭ по математике – вычисления и преобразования. Вам могут встретиться и совсем простые задачи (на сложение дробей), и задания, которые не решить без подготовки. Например, вычисление и преобразование иррациональных выражений, тригонометрических, логарифмических. Задачи на определение модуля и понятие функции. В общем, типов задач здесь множество, по всему курсу алгебры.

И помните, что в ответе в заданиях первой части Профильного ЕГЭ по математике у вас должны получаться целые числа или конечные десятичные дроби.

Дробно-рациональные выражения. Формулы сокращенного умножения

Темы для повторения: Формулы сокращенного умножения, Приемы быстрого счета

Если вам встретится такое задание на ЕГЭ – значит, повезло!

1. Найдите значение выражения frac{2,88cdot 44,5}{0,288cdot 4,45}.

Не спешите перемножать десятичные дроби. Посмотрите на задачу внимательно.

frac{2,88cdot 44,5}{0,288cdot 4,45}=frac{2,88cdot 44,5}{2,88cdot 0,445}=frac{44,5}{0,445}=100.

Первый множитель в знаменателе умножили на 10, а второй поделили на 10, просто передвинув запятую.

Ответ: 100.

2. Найдите значение выражения 7frac{9}{13}:frac{5}{13}.

7frac{9}{13}:frac{5}{13}=frac{100}{13}cdot frac{13}{5}=20.

Ответ: 20.

Корни и степени. Иррациональные выражения

Темы для повторения: Арифметический квадратный корень.

Арифметический квадратный корень из числа a — это такое неотрицательное число, квадрат которого равен a.

left ( sqrt{a} right )^{2}=a;;sqrt{a}geq 0;;ageq 0 .

3. Вычислите sqrt{12+4sqrt{5}}cdot sqrt{12-4sqrt{5}} .

sqrt{12+4sqrt{5}}cdot sqrt{12-4sqrt{5}}=sqrt{left ( 12+4sqrt{5} right )left ( 12-4sqrt{5} right )}=

=sqrt{144-80}=sqrt{64}=8.

Применили одну из формул сокращенного умножения.

Ответ: 8.

4. Вычислите:
left ( sqrt{28}-sqrt{12} right )cdot sqrt{10+sqrt{84}}.

Упростим множители:

sqrt{28}-sqrt{12}=sqrt{4cdot 7}-sqrt{3cdot 4}=2left ( sqrt{7}-sqrt{3} right );

sqrt{84}=sqrt{3cdot 7cdot 4}=2sqrt{3cdot 7};

left ( sqrt{28}-sqrt{12} right )cdot sqrt{10+sqrt{84}}=2left ( sqrt{7}-sqrt{3} right )cdot sqrt{10+2sqrt{3cdot 7}}=

=2left ( sqrt{7}-sqrt{3} right )cdot sqrt{left ( sqrt{7} right )^{2}+2sqrt{3}cdot sqrt{7}+left ( sqrt{3} right )^{2}}=

=2left ( sqrt{7}-sqrt{3} right )cdot sqrt{left ( sqrt{7}+sqrt{3}right )^{2}}=2left ( sqrt{7}-sqrt{3} right )left ( sqrt{7}+sqrt{3} right )=

=2cdot left ( 7-3 right )=8.

Ответ: 8.

Действия со степенями

Темы для повторения:
Вспомним правила действий со степенями.

a^{m}cdot a^{n}=a^{m+n}.

frac{a^{m}}{a^{n}}=a^{m-n}.

left ( a^{m} right )^{n}=left ( a^{n} right )^{m}=a^{mn}.

a^{n}b^{n}=left ( ab right )^{n}.

frac{a^{n}}{b^{n}}=left ( frac{a}{b} right )^{n}.

5. Найдите значение выражения: frac{a^{8,9}}{a^{4,9}} при a=4.

frac{a^{8,9}}{a^{4,9}}=a^{8,9-4,9}=a^{4}=4^{4}=256.

Применили формулу частного степеней frac{a^{m}}{a^{n}}=a^{m-n}.

Ответ: 256.

6. Вычислите left ( frac{2^{frac{1}{3}}cdot 2^{frac{1}{4}}}{sqrt[12]{2}} right )^{2}.

left ( frac{2^{frac{1}{3}}cdot 2^{frac{1}{4}}}{sqrt[12]{2}} right )^{2}=left ( frac{2^{frac{1}{3}}cdot 2^{frac{1}{4}}}{2^{frac{1}{12}}} right )^{2}=left ( 2^{frac{1}{3}+frac{1}{4}-frac{1}{12}} right )^{2}=left ( 2^{frac{4}{12}+frac{3}{12}-frac{1}{12}} right )^{2}=

=left (2^{frac{1}{2}} right )^{2}=2.

Ответ: 2.

7. Вычислите frac{5left ( m^{6} right )^{5}+13left ( m^{10} right )^{3}}{left ( 2m^{15} right )^{2}}, если m=3,7.

Спокойно, не пугаемся. И конечно, не спешим подставлять значение m=3,7. Сначала упростим выражение.

frac{5left ( m^{6} right )^{5}+13left ( m^{10} right )^{3}}{left ( 2m^{15} right )^{2}}=frac{5m^{30}+13m^{30}}{4m^{30}}=frac{18m^{30}}{4m^{30}}=4,5.

Ответ: 4,5.

8. Вычислите 0,75^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot 12^{frac{7}{8}}.

0,75^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot 12^{frac{7}{8}}=left ( frac{3}{4} right )^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot left ( 3cdot 4 right )^{frac{7}{8}}=frac{3^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot 3^{frac{7}{8}}cdot 4^{frac{7}{8}}}{4^{frac{1}{8}}}=3cdot 4=12.

Применили формулу для произведения степеней: a^{m}cdot a^{n}=a^{m+n}.

Ответ: 12.

9. Вычислите frac{sqrt[28]{3}cdot 3cdot sqrt[21]{3}}{sqrt[12]{3}}.

frac{sqrt[28]{3}cdot 3cdot sqrt[21]{3}}{sqrt[12]{3}}=frac{3^{frac{1}{28}}cdot 3cdot 3^{frac{1}{21}}}{3^{frac{1}{12}}}=3^{frac{1}{28}+1+frac{1}{21}-frac{1}{12}}=3^{frac{3}{84}+1+frac{4}{84}-frac{7}{84}}=3.

Записали корни в виде степеней (это удобно!) и применили формулу произведения степеней.

Ответ: 3.

Логарифмические выражения

Темы для повторения:
Логарифмы

Логарифм положительного числа b по основанию a — это показатель степени, в которую надо возвести a, чтобы получить b.

log _{a}b=cLeftrightarrow a^{c}=b.

При этом b> 0, a > 0, aneq 1.

Основные логарифмические формулы:

Основное логарифмическое тождество: boldsymbol{log _{a}a^{c}=c, ; a^{log _{a}b}=b}.

Логарифм произведения равен сумме логарифмов: boldsymbol{log _{a}left ( bc right )=log _{a}b+log _{a}c}.

Логарифм частного равен разности логарифмов: boldsymbol{log _{a}left ( frac{b}{c} right )=log _{a}b-log _{a}c}.

Формула для логарифма степени: boldsymbol{log _{a}b^{m}=mlog_{a}b}.

Формула перехода к новому основанию: boldsymbol{log _{a}b=frac{1}{log _{b}a},; log _{a}b=frac{log _{c}b}{log _{c}a}}.

10. Вычислите: log _{5}7cdot log _{7}25.

log _{5}7cdot log _{7}25=log _{5}7cdot log _{7}5^{2}=2log _{5}7cdot log _{7}5=2.

Снова формула перехода к другому основанию.

log _{a}b=frac{1}{log _{b}a}, поэтому
log _{a}bcdot log _{b};a=1.

11. Найдите log _{a}frac{a^{6}}{b^{4}}, если log _{a}b=-2.

log _{a}frac{a^{6}}{b^{4}}=log _{a}a^{6}-log _{a}b^{6}=6-4log _{a}b=6-4cdot left ( -2 right )=6+8=14.

12. Найдите значение выражения frac{log _{2}80}{3+log _{2}10}.

frac{log _{2}80}{3+log _{2}10}=frac{log _{2}left (8cdot 10 right )}{3+log _{2}10}=frac{log _{2}8+log _{2}10}{3+log _{2}10}=frac{3+log _{2}10}{3+log _{2}10}=1.

13. Найдите значение выражения frac{log _{9}sqrt[10]{8}}{log _{9}8}.

frac{log _{9}sqrt[10]{8}}{log _{9}8}=frac{log _{9}8^{frac{1}{10}}}{log _{9}8}=frac{1}{10}=0,1.

14. Найдите значение выражения left ( 1-log _{3}18 right )left ( log _{6}54 -1right ).

left ( 1-log _{3}18 right )left ( log _{6}54 -1right )=-left ( log _{3}18-log _{3}3 right )cdot left ( log _{6}54-log _{6}6 right )=-log _{3}6cdot log _{6}9=-2log _{3}6cdot log _{6}3=-2.

Тригонометрия. Формулы тригонометрии и формулы приведения

Темы для повторения:
Тригонометрический круг.
Формулы тригонометрии.
Формулы приведения.

15. Вычислите: 44sqrt{3}tgleft ( -480^{circ} right ).

44sqrt{3}tgleft ( -480^{circ} right )=44sqrt{3}cdot frac{sin left ( -480^{circ} right )}{cos left ( -480^{circ} right )}=-44sqrt{3}cdot frac{sin 480^{circ}}{cos 480^{circ}}=-44sqrt{3}cdot frac{sin 120^{circ}}{cos 120^{circ}}=-44sqrt{3}cdot frac{sqrt{3}}{2}:left ( -frac{1}{2} right )=132.

16. Найдите 3cos alpha, если sin alpha =-frac{2sqrt{2}}{3} и alpha in left ( frac{3pi }{2};;2pi right ).

cos ^{2}alpha =1-sin ^{2}alpha =1-left ( -frac{2sqrt{2}}{3} right )^{2}=1-frac{8}{9}=frac{1}{9}.

Т.к. alpha in left ( frac{3pi }{2};;2pi right ), то cos alpha =frac{1}{3}.
3cos alpha =3cdot frac{1}{3}=1.

17. Найдите tgalpha, если sin alpha =-frac{1}{sqrt{5}} и alpha in left ( 1,5pi ;;2pi right ).

cos ^{2}alpha =1-sin ^{2}alpha =1-left ( -frac{1}{sqrt{5}} right )^{2}=1-frac{1}{5}=frac{4}{5}.

Т.к. alpha in left ( 1,5pi ;;2pi right ), то
cos alpha =frac{2}{sqrt{5}}.

tgalpha =frac{sin alpha }{cos alpha }=-frac{1}{sqrt{5}}:frac{2}{sqrt{5}}=-2.

18. Найдите значение выражения: frac{13sin 152^{circ}}{cos 76^{circ}cdot cos 14^{circ}}.

frac{13sin 152^{circ}}{cos 76^{circ}cdot cos 14^{circ}}=frac{13cdot 2sin 76^{circ}cdot cos 76^{circ}}{cos 76^{circ}cdot cos 14^{circ}}=frac{26sin 76^{circ}}{cos 14^{circ}}=frac{26sin left ( 90^{circ}-14^{circ} right )}{cos 14^{circ}}=

=frac{26cos 14^{circ}}{cos 14^{circ}}=26.

Применили формулу приведения.

19. Упростите выражение: frac{3cos(pi - beta)+sin(frac{pi}{2}+beta)}{cos(beta+3pi)}.

frac{3cos left ( pi -beta right )+sin left ( frac{pi }{2}+beta right )}{cos left ( beta +3pi right )}=frac{-3cos beta +cos beta }{-cos beta }=frac{-2cos beta }{-cos beta }=2.

Применили формулу приведения.

20. Найдите 2cos 2alpha, если sin alpha =-0,7..

2cos 2alpha =2left ( 1-2sin ^{2}alpha right )=2-4sin ^{2}alpha =2-4cdot left ( -0,7 right )^{2}=0,04.

21. Вычислите frac{1-cos 2alpha +sin 2alpha }{1+cos 2alpha +sin 2alpha }, если tgalpha =0,3.

frac{1-cos 2alpha +sin 2alpha }{1+cos 2alpha +sin 2alpha }=frac{1-cos ^{2}alpha +sin ^{2}alpha +2sin alpha cos alpha }{1+cos ^{2}alpha -sin ^{2}alpha +2sin alpha cos alpha }=

=frac{2sin ^{2}alpha +2sin alpha cos alpha }{2cos ^{2}alpha +2sin alpha cos alpha }=frac{sin alpha left ( sin alpha +cos alpha right )}{cos alpha left ( cos alpha +sin alpha right )}=frac{sin alpha }{cos alpha }=tgalpha =0,3.

Алгебраические выражения, корни, степени и логарифмы. И еще тригонометрия. Это всё, что может встретиться в задании 6 Профильного ЕГЭ по математике?

Оказывается, и это не всё! Еще нужно знать, что такое модуль. И как найти sqrt{a^{2}}.

Другие типы заданий

Темы для повторения:
Модуль числа.
Что такое функция.

22. Найдите значение выражения
sqrt{left ( a-2 right )^{2}}+sqrt{left ( a-4 right )^{2}} при 2leq aleq 4.

Запомним: sqrt{a^{2}}=left | a right |.

sqrt{left ( a-2 right )^{2}}+sqrt{left ( a-4 right )^{2}}=left | a-2 right |+left | a-4 right |.

Если 2leq aleq 4, то a-2geq 0 и left | a-2 right |=a-2.

При этом a-4leq 0 и left | a-4 right |=4-a.

При 2leq aleq 4 получаем: left | a-2 right |+left | a-4 right |=a-2+4-a=2.

Ответ: 2.

23. Найдите значение выражения

x+sqrt{x^{2}-24x+144} при xleq 12.

При xleq 12 получим:

x+sqrt{x^{2}-24x+144}=x+sqrt{left ( x-12 right )^{2}}=x+left | x-12 right |=x+12-x=12.

Ответ: 12.

24. Найдите frac{gleft ( 5-x right )}{gleft ( 5+x right )}, если gleft ( x right )=sqrt[9]{xleft ( 10-x right )}, при left | x right |neq 5.

Что такое gleft ( x right )? Это функция, каждому числу ставящая в соответствие число sqrt[9]{xleft ( 10-x right )}. Например, gleft ( 0 right )=0;

gleft ( 1 right )=sqrt[9]{1cdot left ( 10-1 right )}=sqrt[9]{9}.

Тогда:

gleft ( 5-x right )=sqrt[9]{left ( 5-x right )left ( 10-5+x right )}=sqrt[9]{left ( 5-x right )left ( 5+x right )};

gleft ( 5+x right )=sqrt[9]{left ( 5+x right )left ( 10-5-x right )}=sqrt[9]{left ( 5+x right )left ( 5-x right )}.

Заметим, что gleft ( 5-x right )=gleft ( 5+x right ).

Значит, при left | x right |neq 5.
frac{gleft ( 5-x right )}{gleft ( 5+x right )}=1.

25. Найдите frac{pleft ( b right )}{pleft ( frac{1}{b} right )}, если pleft ( b right )=left ( b-frac{9}{b} right )left ( -9b+frac{1}{b} right ), при bneq 0.

pleft ( b right )=left ( b-frac{9}{b} right )left ( -9b+frac{1}{b} right ) — функция, каждому числу b ставящая в соответствии число
left ( b-frac{9}{b} right )left ( -9b+frac{1}{b} right ).

Тогда при bneq 0.

pleft ( frac{1}{b} right )=left ( frac{1}{b}-9b right )left ( -frac{9}{b} +bright )=left ( b-frac{9}{b} right )left (-9b +frac{1}{b} right )=pleft ( b right ), и значение выражения frac{pleft ( b right )}{pleft ( frac{1}{b} right )} равно 1.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 6 ЕГЭ по математике. Вычисления и преобразования» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Итак, давайте разберем, задание №9 в ЕГЭ по математике профильного уровня. Все эти задания требуют – найдите значение выражения. То есть, наша задача вычислить – найти значение выражения и записать в ответ число.

Задания ЕГЭ профильного уровня по математике

Какие бывают задания с требованием найти значение выражения. Эти задания бывают разными и относящимися к разным темам. Например, выражения в задании 9 ЕГЭ по математике профильного уровня бывают:

  • степенные
  • логарифмические
  • тригонометрические
  • числовые
  • иррациональные (с корнями)
  • с переменными заданными величинами

Давайте рассмотрим общий принцип и необходимые теоретические сведения для решения каждого типа выражения.

Степенные выражения

Для того, чтобы найти значение выражения со степенями, вам понадобятся формулы для вычисления степеней. Приведем самые распространенные из них, на которые обычно дается задание нахождения значения выражения со степенями. Вы должны четко понимать, что если число находится в какой то степени, то оно не свободное, оно в отношении степени. И нельзя сократить два числа в дроби, если у них одно основание и разные показатели степени. Или если разные основания и разные показатели степени.

Например, вот здесь frac{6^{5}}{2^{3}}  мы никак не можем получить 3^5. Потому что мы не имеем право делить 6 на 2, пока 6 находится в степени. И 2 находится в степени. Степень вообще всегда первое действие. То есть среди действий +, – ,  : , cdot  и степень, мы сначала будем возводить в степень. Именно это свойство степени проверяется, например, в этом задании:

Найдите значение выражения - 9 задание егэ

Найдите значение выражения frac {3^{6,5}}{9^{2,25}}. Мы не можем сократить 3 и 9, потому что они находятся в отношении степени. И нам нужно сначала возвести в степень. Только потом мы можем разделить числитель на знаменатель.

Итак, найдем значение этого выражения: frac {3^{6,5}}{9^{2,25}}=frac{3^{6,5}}{(3^2)^{2,25}}=frac{3^{6,5}}{3^{4,5}}=3^{6,5-4,5}=3^2=9.

Здесь мы использовали свойство степени при делении степеней с одинаковыми основаниями. Приведем все необходимые для решения данных заданий свойства степеней:

boxed {a^m cdot a^n=a^{m+n}}

boxed {frac{a^m}{a^n}=a^{m-n}}

boxed {(a^m)^n=a^{mn}}

boxed { (frac{a^m}{b^n})^k=frac{a^{mk}}{b^{nk}}}

boxed {(a^m cdot b^n)^k=a^{mk}cdot b^{nk}}

boxed {a^{-n}=frac{1}{a^n}}

Давайте рассмотрим еще несколько заданий.

Найдите значение выражения

Задание 1.

Найдите значение выражения (sqrt{3}-sqrt{13})(sqrt{3} + sqrt{13}).

Очевидно, что перед нами формула сокращенного умножения в развернутом виде: a^2-b^2=(a-b)(a+b). Применяя эту формулу к нашему выражению, увидим, что a=sqrt{3}, а b=sqrt{13}. Получим: a^2-b^2=(sqrt{3})^2-(sqrt{13})^2=3-13=-10.

Ответ: -10.

Задание 2.

Найдите значение выражения frac{(5sqrt{3})^2}{10}.

При возведении произведения в степень, в нее возводится каждый множитель, то есть получим: frac{5^2 cdot (sqrt{3})^2}{10}=frac{25cdot3}{10}=frac{75}{10}=7,5.

Ответ: 7,5.

Ничего сложного, если вы знаете формулы сокращенного умножения и свойства степеней.

А для того, чтобы найти значение выражения, в котором есть логарифмы, нужно знать свойства логарифмов.

Задание 3.

Найдите значение выражения frac{log_{3}4}{log_{3}2}+log_{2}0,5.

Здесь для нахождения значения выражения мы будем использовать следующие свойства логарифмов:

переход к новому основанию log_{a}b=frac{log_{c}b}{log_{c}a}.

сложение логарифмов с одинаковыми основаниями: log_{a}b+log_{a}c=log_{a}{bc}.

Итак, получим: frac{log_{3}4}{log_{3}2}+log_{2}0,5=log_{2}4+log_{2}0,5=log_{2}{4cdot 0,5}=log_{2}2=1

Ответ: 1.

Задание 4.

Найдите значение выражения frac{(2^{frac{4}{7}}cdot 3^{frac{2}{3}})^{21}}{6^{12}}.

Помните: при возведении в степень произведения, в нее возводится каждый множитель: (a^m cdot b^n)^k=a^{mk} cdot b^{nk}

Преобразуем выражение в числителе дроби:

frac{(2^{frac{4cdot 21}{7}}cdot 3^{frac{2cdot 21}{3}})}{6^{12}}=frac{2^{4cdot 3}cdot 3^{2cdot 7}}{6^{12}}

Разложим 6 на множители 2 и 3, получим:

frac{2^{4cdot 3}cdot 3^{2cdot 7}}{(2 cdot 3)^{12}}=frac{2^{4cdot 3}cdot 3^{2cdot 7}}{2^{12} cdot 3^{12}}=frac {2^{12}cdot 3^{14}}{2^{12} cdot 3^{12}}

Далее используем свойства степеней:

frac{a^m}{a^n}=a^{m-n}.

Сокращая числитель и знаменатель на 2^{12}, получим: frac {2^{12}cdot 3^{14}}{2^{12} cdot 3^{12}}=3^{14-12}=3^2=9.

Ответ: 9.

Задание 5

Найдите значение выражения: frac {81^{2,6}}{9^{3,7}}.

Решим данное выражение, учитывая, что 81=3^4, а 9=3^2. Получим: frac{(3^4)^{2,6}}{(3^2)^{3,7}}. При возведении степени в степень, показатели степени перемножаются, имеем: frac{(3^4)^{2,6}}{(3^2)^{3,7}}=frac{3^{4cdot 2,6}}{3^{2cdot 3,7}}=frac{3^{10,4}}{3^{7,4}}=3^{10,4-7,4}=3^3=27.

Ответ: 27.

Задание 6

Найдите значение выражения log_{8}144-log_{8}2,25.

Для того чтобы найти значение этого выражения надо применить  следующее свойство логарифмов: log_{a}b-log_{a}c=log_{a}{frac{b}{c}}.

Получим: log_{8}144-log_{8}2,25=log_{8}{frac{144}{2,25}}=log_{8}{64}=2.

Ответ: 2.

Задание 7

Найдите значение выражения log_{4}40-log_{4}2,5.

Действуем также, как и в предыдущем задании, используя свойство разности логарифмов:

log_{4}40-log_{4}2,5=log_{4}{frac{40}{2,5}}=log_{4}{16}=2.

Ответ: 2.

Задание 8

Найдите 28cos{2alpha}, если cos{alpha}=-0,7.

Для того, чтобы найти значение данного выражения нам понадобятся две тригонометрические формулы:

  1. Основное тригонометрическое тождество: cos^{2} {alpha}+sin^{2} {alpha}=1.
  2. Косинус двойного аргумента: cos{2alpha}=cos^{2} {alpha}-sin^{2} {alpha}.

Итак, по формуле (2) распишем наше выражение в следующем виде: 28cos{2alpha}=28(cos^{2} {alpha}-sin^{2} {alpha}) . Однако, нам известен только косинус, для того чтобы из синуса сделать косинус, используем основное тригонометрическое тождество: sin^{2} {alpha}=1-cos^{2} {alpha}.

Тогда наше выражение примет вид:

28cos{2alpha}=28(cos^{2} {alpha}-sin^{2} {alpha})=28(cos^{2} {alpha}-(1-cos^{2} {alpha}))=28(2cos^{2} {alpha}-1).

Подставляем значение косинуса, получим:

28(2cos^{2} {alpha}-1)=28(2(-0,7)^2-1)=28(2cdot 0,49 - 1)=28cdot (-0,02)=-0,56.

Ответ: -0,56.

Задание 9

Найдите значение выражения 3sqrt{2}cos ^2 {frac{13 pi}{8}}-3sqrt{2}sin ^2 {frac{13 pi}{8}}.

Решим. Вынесем 3sqrt{2} за скобки. Получим: 3sqrt{2}(cos ^2 {frac{13 pi}{8}}-sin ^2 {frac{13 pi}{8}}).

В скобках видим формулу косинуса двойного аргумента: cos{2alpha}=cos^{2} {alpha}-sin^{2} {alpha}. Применяя ее, имеем:

3sqrt{2}(cos ^2 {frac{13 pi}{8}}-sin ^2 {frac{13 pi}{8}})=3sqrt{2}cos {frac{2 cdot 13 pi}{8}}=3sqrt{2} cos {frac{13 pi}{4}}

Мы знаем, что cos {pi/4}=frac{sqrt{2}}{2}. Но мы не знаем, чему равен cos {frac{13pi}{4}}, давайте рассуждать в 13pi/4 это 3pi и еще frac{pi}{4}}.

То есть, cos {frac{13pi}{4}}=cos{(3pi+frac{pi}{4})}. Применяя формулы или правило приведения, получим: cos {frac{13pi}{4}}=cos{(3pi+frac{pi}{4})}=-cos{frac{pi}{4}}=-frac{sqrt{2}}{2}. Подставляя это значение в наше выражение 3sqrt{2} cos {frac{13 pi}{4}}, вычислим: 3sqrt{2} cos {frac{13 pi}{4}}=3sqrt{2} cdot(-frac{sqrt{2}}{2})=-3

Ответ: -3.

Источник

1. Алгебраические выражения

2. Выражения с корнями

2.1 Найдите значение выражения sqrt{9-4sqrt{5}}-sqrt{5} Смотреть видеоразбор
2.2 Найдите значение выражения frac{(2sqrt{7})^2}{14} Смотреть видеоразбор
2.3 Найдите значение выражения (sqrt{13}-sqrt{7})(sqrt{13}+sqrt{7}) Смотреть видеоразбор
2.4 Найдите значение выражения frac{sqrt{2,8} cdot sqrt{4,2}}{sqrt{0,24}} Смотреть видеоразбор
2.5 Найдите значение выражения (sqrt{3frac{6}{7}}-sqrt{1frac{5}{7}}):sqrt{frac{3}{28}} Смотреть видеоразбор
2.6 Найдите значение выражения frac{(sqrt{13}+sqrt{7})^2}{10+sqrt{91}} Смотреть видеоразбор

3. Логарифмические выражения

4. Выражения со степенями

4.1 Найдите значение выражения 5^{0,36} cdot 25^{0,32} Смотреть видеоразбор
4.2 Найдите значение выражения frac{3^{6,5}}{9^{2,25}} Смотреть видеоразбор
4.3 Найдите значение выражения 7^{frac{4}{9}} cdot 49^{frac{5}{18}} Смотреть видеоразбор
4.4 Найдите значение выражения frac{2^{3,5} cdot 3^{5,5}}{6^4,5} Смотреть видеоразбор
4.5 Найдите значение выражения 35^{-4,7} cdot 7^{5,7} : 5^{-3,7} Смотреть видеоразбор
4.6 Найдите значение выражения frac{sqrt[9]{7} cdot sqrt[18]{7}}{sqrt[6]{7}} Смотреть видеоразбор
4.7 Найдите значение выражения frac{sqrt[5]{10} cdot sqrt[5]{16}}{sqrt[5]{5}} Смотреть видеоразбор
4.8 Найдите значение выражения (frac{2^{frac{1}{3}} cdot 2^{frac{1}{4}}}{sqrt[12]{2}})^2 Смотреть видеоразбор
4.9 Найдите значение выражения frac{(2^{frac{3}{5}} cdot 2^{frac{2}{3}})^{15}}{10^9} Смотреть видеоразбор
4.10 Найдите значение выражения 0,8^{frac{1}{7}} cdot 5^{frac{2}{7}} cdot 20^{frac{6}{7}} Смотреть видеоразбор
4.11 Найдите значение выражения 5 cdot sqrt[3]{9} cdot sqrt[6]{9} Смотреть видеоразбор
4.12 Найдите значение выражения frac{sqrt[28]{3} cdot 3 cdot sqrt[21]{3}}{sqrt[12]{3}} Смотреть видеоразбор
4.13 Найдите значение выражения frac{sqrt[15]{5} cdot 5 cdot sqrt[10]{5}}{sqrt[6]{5}} Смотреть видеоразбор
4.14 Найдите значение выражения 0,75^{frac{1}{8}} cdot 4^{frac{1}{4}} cdot 12^{frac{7}{8}} Смотреть видеоразбор
4.15 Найдите значение выражения 7^{sqrt{5}-1} cdot 7^{2+sqrt{5}} : 7^{2sqrt{5}-1} Смотреть видеоразбор
4.16 Найдите значение выражения frac{1}{2^{log_{sin{frac{pi}{3}}}sqrt{2}}} Смотреть видеоразбор

5. Тригонометрические выражения

5.1 Найдите значение выражения sqrt{18}-sqrt{72}sin^2{frac{13pi}{8}} Смотреть видеоразбор
5.2 Найдите значение выражения sqrt{128} cdot cos^2{frac{11pi}{8}} — sqrt{32} Смотреть видеоразбор
5.3 Найдите sin{alpha}, если cos{alpha} = 0,6 и pi lt alpha lt 2pi. Смотреть видеоразбор
5.4 Найдите значение выражения frac{4sin{17^{circ}}cos{17^{circ}}}{cos{56^{circ}}} Смотреть видеоразбор
5.5 Найдите значение выражения sin{10^{circ}} cdot sin{50^{circ}} cdot sin{70^{circ}} Смотреть видеоразбор
5.6 Найдите значение выражения 5sqrt{3}-10sqrt{2}cos(-frac{pi}{12}) Смотреть видеоразбор
5.7 Найдите значение выражения sqrt{50}-sqrt{200}cos^2{frac{5pi}{8}} Смотреть видеоразбор

6. Нестандартные задачи (не входят в ЕГЭ)

6.1 Найдите значение выражения sqrt[3]{9+sqrt{80}}+sqrt[3]{9-sqrt{80}} Смотреть видеоразбор
6.2 Докажите равенство cos{36^{circ}} — cos{72^{circ}} = frac{1}{2} Смотреть видеоразбор
6.3 Найдите sin 10 + |sin 10| Смотреть видеоразбор
6.4 Вычислите 4^{sqrt{log_4{5}}} — 5^{sqrt{log_5{4}}} Смотреть видеоразбор
6.5 Вычислите frac{2sin{10^{circ}}+sin{50^{circ}}}{2sin{80^{circ}}-sqrt{3}sin{50^{circ}}} Смотреть видеоразбор
Источник

ЕГЭ по математике Профиль. Задание 4: Уметь выполнять вычисления и преобразования. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».

ЕГЭ Профиль. Задание № 4

АЛГОРИТМ ВЫПОЛНЕНИЯ

Задание № 4 проверяет умение производить вычисления и преобразования рациональных, иррациональных, степенных, логарифмических и тригонометрических выражений. Задание состоит из числового или алгебраического выражения, значение которого необходимо найти, применяя математические преобразования. Ответом является целое число или конечная десятичная дробь.

План выполнения:

  1. Внимательно прочитайте условие задачи.
  2. Выполните преобразования.
  3. Найдите числовое значение выражения.
  4. Запишите полученное число в поле ответа КИМ и бланк ответов № 1.

Вычисление значений рациональных выражений

Задачи этого типа заключаются в вычислении значений рациональных, то есть дробных выражений. При подготовке необходимо повторить правила действий с дробями, формулы сокращённого умножения.

ЕГЭ по математике Профиль. Задание 4

Задача № 4 (1). Найдите значение выражения
ЕГЭ по математике Профиль. Задание 4

Решение:
ЕГЭ по математике Профиль. Задание 4

Ответ: 1.

Задача № 4 (2). Найдите (a + 9b + 16)/(a + 3b + 8), если a/b = 3.

Решение:
ЕГЭ по математике Профиль. Задание 4

Ответ: 2.

Вычисление значений иррациональных выражений

Задачи этого типа заключаются в вычислении значений иррациональных (содержащих корни) выражений. При подготовке следует повторить правила вычисления корней, свойства корней.

ЕГЭ по математике Профиль. Задание 4

Задача № 4 (3). Найдите значение выражения (3√5 • 6√5) : √5.

Решение:
ЕГЭ по математике Профиль. Задание 4

Ответ: 1.

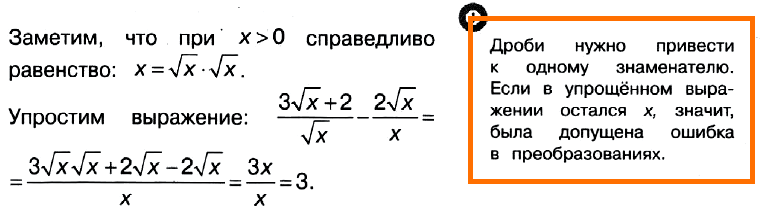
Задача № 4 (4). Найдите значение выражения (3√x + 2)/√x – 2√x/x при х > 0.

Решение:
ЕГЭ по математике Профиль. Задание 4

Ответ: 3.

Вычисление значений степенных выражений

Задачи этого типа заключаются в вычислении значений степенных выражений. При подготовке нужно повторить правила действий со степенями, правило возведения числа в степень.

ЕГЭ по математике Профиль. Задание 4

Задача № 4 (5). Найдите значение выражения 21,5 • 80,5.

Решение:
ЕГЭ по математике Профиль. Задание 4

Ответ: 8.

Задача № 4 (6). Найдите значение выражения (3 – 140,25)(3 + 140,25) : (9 + (70,5 – 21/2)2).

Решение:
ЕГЭ по математике Профиль. Задание 4

Ответ: 27.

Вычисление значений логарифмических выражений

Задачи этого типа заключаются в вычислении значений логарифмических выражений. При подготовке нужно повторить понятие логарифма, основные свойства логарифмов.

ЕГЭ по математике Профиль. Задание 4

Задача № 4 (7). Вычислите log1/2 4√2.

Решение:
ЕГЭ по математике Профиль. Задание 4

Ответ: –0,25.

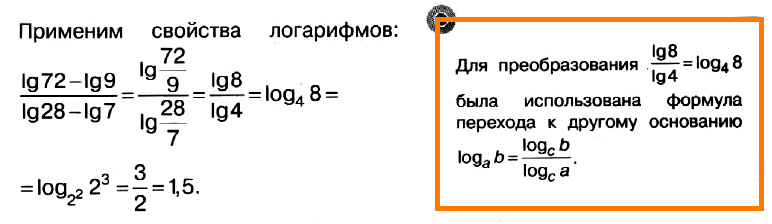
Задача № 4 (8). Найдите значение выражения (lg 72 – lg 9) : (lg 28 – lg 7).

Решение:
ЕГЭ по математике Профиль. Задание 4

Ответ: 1,5.

Вычисление значений тригонометрических выражений

Задачи этого типа заключаются в вычислении значений тригонометрических выражений. При подготовке необходимо повторить основное тригонометрическое тождество, знаки синуса, косинуса, тангенса, формулы приведения, формулы синуса и косинуса двойного аргумента, понятие периодичности тригонометрических функций и табличные значения тригонометрических функций основных углов.

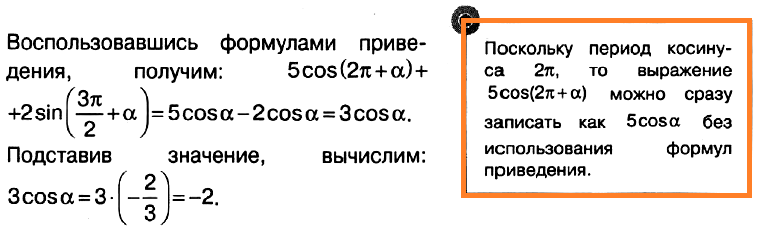
ЕГЭ по математике Профиль. Задание 4

Задача № 4 (9). Найдите значение выражения 5 cos (2π + α) + 2 sin (3π/2 + α), если cos α = –2/3.

Решение:
ЕГЭ по математике Профиль. Задание 4

Ответ: –2.

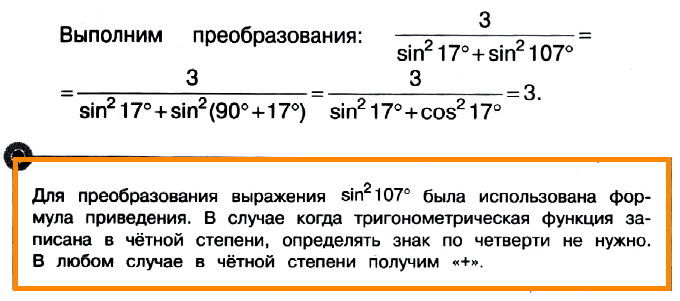
Задача № 4 (10). Найдите значение выражения 3/(sin2 17° + sin2 107°).

Решение:
ЕГЭ по математике Профиль. Задание 4

Ответ: 3.

Тренировочные задания с самопроверкой

№ 4.1. Найдите значение выражения 11√3 • tg (7π/6) • cos (4π/3).

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 4

№ 4.2. Найдите значение выражения (9 sin 59°) / (cos 31°).

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 4

№ 4.3. Найдите значение выражения ЕГЭ по математике Профиль. Задание 4

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 4

№ 4.4. Найдите значение выражения (3√x + 9)/√x – (9√x)/x – 3x + 12 при х = 6.

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 4

№ 4.5. Найдите значение выражения 19а + b + 11, если (–14a + 14b + 7) : (a + 3b + 5) = 5.

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 4

Вы смотрели: ЕГЭ по математике Профиль. Задание 4: Уметь выполнять вычисления и преобразования. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».


Просмотров:
14 784

Источник

В задании (6) ЕГЭ по профильной математике нужно преобразовать числовое, буквенное, степенное, иррациональное, логарифмическое или тригонометрическое выражение и найти его значение. За это задание можно получить (1) балл.

Пример:

найди значение выражения

−20tg53°⋅tg143°=−20tg53°⋅tg(90°+53°)=−20tg53°⋅ctg53°.

Алгоритм выполнения задания

    1. Определи тип выражения. 
       
    2. Выполни преобразования, соответствующие типу выражения.
       
    3. Если задано значение переменной, подставь это значение в упрощённое выражение. Вычисли его значение.
       
    4. Запиши ответ.

Как решить задание из примера?

    1. Дано тригонометрическое выражение. 
       

    2. Заметим, что

      143°=90°+53°

      . Используем формулу приведения

      tg(90+α)=−ctgα

       и преобразуем выражение:

      −20tg53°⋅tg143°=−20tg53°⋅tg(90°+53°)=−20tg53°⋅ctg53°.
       

    3. Воспользуемся формулой

      tgα⋅ctgα=1

      :

      −20tg53°⋅ctg53°=−20⋅1=−20.
       

    4. Запишем ответ (непосредственно в самом задании — без точки в конце).

      Ответ: (-20).

Обрати внимание!

В заданиях «Как на ЕГЭ» ответы записывай в виде целого числа или десятичной дроби без пробелов и точки в конце.

Если получилась обыкновенная дробь и её нельзя перевести в конечную десятичную дробь — ищи ошибку в решении!

Источник

Вариант 1 9. Вычисления и преобразования

1. Найдите значение выражения 

2. Найдите значение выражения 

3. Найдите , если 

4. Найдите , если 

5. Найдите значение выражения  при 

6. Найдите , если  при 

7. Найдите значение выражения 

8. Найдите значение выражения 

9. Найдите значение выражения 

10. Найдите значение выражения 

Вариант 2 9. Вычисления и преобразования

1. Найдите , если 

2. Найдите значение выражения 

3. Найдите значение выражения 

4. Найдите значение выражения 

5. Найдите значение выражения 

6. Найдите значение выражения 

7. Найдите значение выражения 

8. Найдите значение выражения 

9. Найдите значение выражения 

10. Найдите значение выражения 

Вариант 3 9. Вычисления и преобразования

1. Найдите значения выражения 

2. Найдите , если  и 

3. Найдите значение выражения  при 

4. Найдите значение выражения 

5. Найдите значение выражения  при 

6. Найдите значение выражения 

7. Найдите значение выражения 

8. Найдите значение выражения 

9. Найдите , если  При 

10. Найдите значение выражения 

Вариант 4 9. Вычисления и преобразования

1. Найдите значение выражения  при 

2. Найдите значение выражения 

3. Найдите значение выражения 

4. Найдите , если 

5. Найдите  если 

6. Найдите значение выражения 

7. Найдите значение выражения 

8. Найдите значение выражения 

9. Найдите значение выражения , если 

10. Найдите значение выражения 

Вариант 5 9. Вычисления и преобразования

1. Найдите значение выражения  при 

2. Найдите значение выражения  при 

3. Найдите значение выражения 

4. Найдите значение выражения , если 

5. Найдите , если  и 

6. Найдите , если  и 

7. Найдите , если 

8. Найдите , если 

9. Найдите , если 

10. Найдите , если 

Вариант 6 9. Вычисления и преобразования

1. Найдите значение выражения 

2. Найдите значение выражения 

3. Найдите значение выражения 

4. Найдите значение выражения 

5. Найдите значение выражения , если 

6. Найдите значение выражения 

7. Найдите значение выражения 

8. Найдите значение выражения 

9. Найдите значение выражения 

10. Найдите значение выражения 

Вариант 7 9. Вычисления и преобразования

1. Найдите значение выражения 

2. Найдите значение выражения 

3. Найдите значение выражения 

4. Найдите значение выражения 

5. Найдите значение выражения 

6. Найдите значение выражения 

7. Найдите значение выражения ( − ) 

8. Найдите значение выражения 

9. Найдите значение выражения 

10. Найдите значение выражения  если  и 

Вариант 8 9. Вычисления и преобразования

1. Найдите значение выражения 

2. Найдите значение выражения: 

3. Найдите значение выражения 

4. Найдите значение выражения 

5. Найдите значение выражения 

6. Найдите значение выражения 

7. Найдите значение выражения 

8. Найдите значение выражения 

9. Найдите значение выражения 

10. Найдите значение выражения 

Вариант 9 9. Вычисления и преобразования

1. Найдите , если 

2. Найдите значение выражения 

3. Найдите значение выражения 

4. Найдите значение выражения 

5. Найдите значение выражения  при 

6. Найдите значение выражения 

7. Найдите значение выражения 

8. Найдите значение выражения  при 

9. Найдите значение выражения  при 

10. Найдите значение выражения  при 

Вариант 10 9. Вычисления и преобразования

1. Найдите значение выражения:  при 

2. Найдите значение выражения  при 

3. Найдите значение выражения 

4. Найдите значение выражения 

5. Найдите значение выражения 

6. Найдите значение выражения 

7. Найдите значение выражения 

8. Найдите значение выражения 

9. Найдите значение выражения 

10. Найдите значение выражения 

9. Вычисления и преобразования

Вариант 1

  1. 1

  2. 5

  3. 2

  4. 14

  5. -0,5

  6. 0

  7. 6

  8. 2

  9. 23

  10. 1

Вариант 2

  1. 71

  2. 2

  3. -1,5

  4. -1,25

  5. 7

  6. 3

  7. 243

  8. 4

  9. 28

  10. -56

Вариант 3

  1. 11,5

  2. 1,12

  3. 0,5

  4. 0,5

  5. 1

  6. -40,5

  7. 24

  8. 14

  9. 1

  10. -47

Вариант 4

  1. 0,75

  2. 3

  3. 2

  4. 0

  5. 0,04

  6. -2

  7. -5

  8. 5

  9. -28

  10. 25

Вариант 5

  1. 4

  2. 2187

  3. 1

  4. -28

  5. 0,6

  6. -10

  7. -2,5

  8. 7

  9. -9

  10. 5

Вариант 6

  1. 25

  2. 12

  3. 49

  4. 2

  5. 12,8

  6. 7

  7. 12

  8. 1

  9. 59

  10. -19

Вариант 7

  1. -47

  2. -1,5

  3. 59

  4. -19

  5. 9,5

  6. 14,75

  7. 7

  8. 42

  9. 46

  10. -3

Вариант 8

  1. 7

  2. 425

  3. 9

  4. 3

  5. 0,5

  6. 12

  7. -0,5

  8. 4

  9. 0,5

  10. 121

Вариант 9

  1. -8

  2. 4

  3. 0,5

  4. 121

  5. 333

  6. 243

  7. 80,625

  8. 16

  9. -367

  10. 150

Вариант 10

  1. 7776

  2. 4

  3. 8

  4. 28

  5. 25

  6. -0,5

  7. 1,5

  8. 1

  9. -3

  10. -1
Источник

Задание 903

Найдите значение выражения $$log^{3}_{sqrt{3}}{{frac{1}{3}}^3}$$

Ответ: -216

Скрыть

Рассмотрим сам логарифм: $$ log_{sqrt{3}}{{frac{1}{3}}^3}=log_{3^{1/2}}{3^{-3}}=frac{1}{frac{1}{2}}*left(-3right)log_33=-6 $$ Так как он был в третьей степени, то возведем -6 в нее и получим -216

Задание 939

Известно, что $$log_a b *log_b c = -5$$ . Найдите значение выражения $$log_c a$$

Ответ: -0.2

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

$$log_a b *log_b c = frac{1}{log_b a}*log_b c=frac{log_b c}{log_b a}=log_a c=-5$$ $$log_c a=frac{1}{log_a c}=frac{1}{-5}=-0.2$$

Задание 975

Вычислите $$frac{sin 35cos 35}{sin ^{2} 10-cos ^{2} 10}$$

Ответ: -0.5

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

$$frac{sin 35cos 35}{sin ^{2} 10-cos ^{2} 10}=$$ $$frac{0.5sin 70}{-cos 20}=frac{0.5cos 20}{-cos 20}=-0.5$$

Задание 1015

Найдите значение выражения $$frac{(0.1)^{-1}-(0.1)^{0}}{(frac{3^{2}}{2^{3}})^{-1}*(frac{3}{2})^{3}-(frac{1}{3})^{-2}}$$

Ответ: -1.5

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

$$frac{(0.1)^{-1}-(0.1)^{0}}{(frac{3^{2}}{2^{3}})^{-1}*(frac{3}{2})^{3}-(frac{1}{3})^{-2}}=$$ $$=frac{10-1}{frac{2^{3}}{3^{2}}*frac{27}{8}-9}=frac{9}{frac{8}{9}*frac{27}{8}-9}=$$ $$frac{9}{3-9}=frac{9}{-6}=-1.5$$

Задание 1082

Най­ди­те зна­че­ние вы­ра­же­ния $$(frac{3}{4}+2frac{3}{8})*25,8$$

Ответ: 80,625

Задание 1083

Най­ди­те зна­че­ние вы­ра­же­ния $$(2frac{4}{7}-2,5):frac{1}{10}$$

Ответ: 5

Задание 1084

Най­ди­те зна­че­ние вы­ра­же­ния  $$(432^{2}-568^{2}):1000$$

Ответ: -136

Задание 1085

Най­ди­те зна­че­ние вы­ра­же­ния $$4frac{4}{9}:frac{4}{9}$$

Ответ: 10

Задание 1086

Най­ди­те зна­че­ние вы­ра­же­ния  $$frac{1,23*45,7}{12,3*0,457}$$

Ответ: 10

Задание 1099

Вычислите $$tg alpha $$, если известно, что $$cos 2alpha =0.6$$ и $$frac{3pi }{4}< alpha < pi $$

Ответ: -0.5

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

Воспользуемся формулой косинуса двойного угла: $$cos 2alpha =2cos^{2}alpha-1=0.6$$

С учетом того, что $$alpha$$ — угол второй четверти, то косинус у него отрицательный, а синус положительный.

Значит: $$cos alpha = -sqrt{frac{cos 2alpha+1}{2}}=-sqrt{frac{0.6+1}{2}}=-sqrt{0.8} $$

Воспользуемся основным тригонометрическим тождеством: $$sin alpha = sqrt{1-cos^{2}alpha}=sqrt{0.2}$$

Значит тангенс будет равен: $$tan alpha = frac{sin alpha}{cos alpha}= frac{sqrt{0.2}}{-sqrt{0.8}}=-frac{1}{2}=-0.5$$

Задание 1177

Найдите значение выражения $$(frac{9^{frac{1}{6}}*9^{frac{1}{9}}}{sqrt[18]{9}})^{9}$$

Ответ: 81

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

$$(frac{9^{frac{1}{6}}*9^{frac{1}{9}}}{sqrt[18]{9}})^{9}=(frac{9^{frac{1}{6}+frac{1}{9}}}{9^{frac{1}{18}}})^{9}=(9^{frac{1}{6}+frac{1}{9}-frac{1}{18}})^{9}=9^{2}=81$$

Задание 1238

Известно, что $$frac{cos x-sin x}{cos x+sin x}=-0.8$$. Найдите $$ tg x $$

Ответ: 9

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

$$frac{cos x-sin x}{cos x+sin x}=-0.8=frac{-4}{5}$$ $$(cos x-sin x)*5=-4*(cos x+sin x)$$ $$5cos x-5sin x=-4*cos x-4sin x$$ $$9cos x = sin x $$ Поделим обе части на cos x $$9 = tg x $$

Задание 1279

Известно, что $$ tg x = frac{2}{sqrt{21}}$$ и $$pi < x< frac{3pi }{2}$$. Найдите sin x

Ответ: -0.4

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

Угол располагается в третьей четверти, поэтому sin будет отрицательный. Найдем сначала ctg x: $$ ctg x = frac {1}{tg x}= frac {1}{frac{2}{sqrt{21}}}=frac{sqrt{21}}{2}$$ Выразим sin x из формулы $$ 1 + ctg^{2} x = frac{1}{sin^{2} x} $$ $$ frac{1}{1 + ctg^{2} x} =sin^{2} x $$ $$sin x = — sqrt{ frac{1}{1 + ctg^{2} x} } $$ $$sin x = — sqrt{ frac{1}{1 + (frac{sqrt{21}}{2})^{2}} }=- sqrt{ frac{1}{1 + frac{21}{4}}}=-frac{2}{5}=-0.4 $$

Задание 1444

Найдите значение выражения: $$frac{12sin 11^{circ}*cos 11^{circ}}{sin 22^{circ}}$$.

Ответ: 6

Задание 1445

Найдите значение выражения: $$frac{24(sin^2 17^{circ}-cos^2 17^{circ})}{cos 34^{circ}}$$.

Ответ: -24

Источник

Понравилась статья? Поделить с друзьями:
  • Найти заботливых хозяев егэ
  • Найти вузы по предметам егэ в нижнем новгороде
  • Найти вузы по предметам егэ бюджет
  • Найти вуз по экзамену
  • Найти вуз по экзаменам егэ