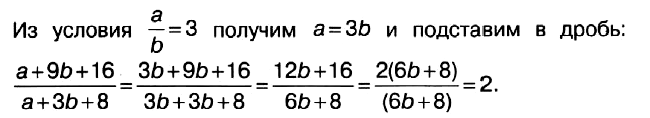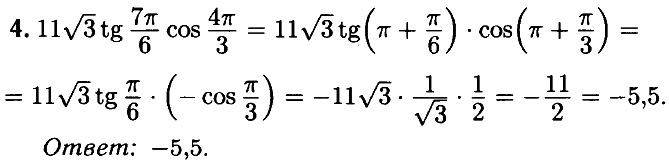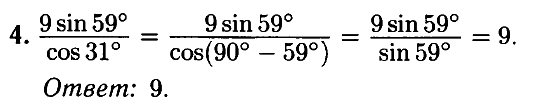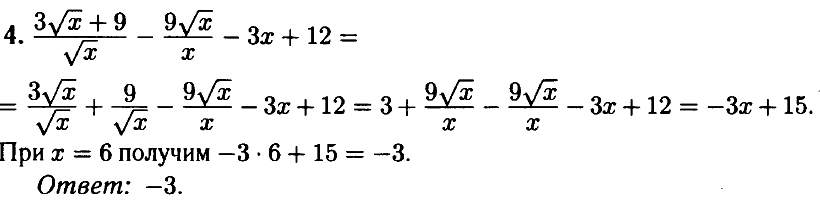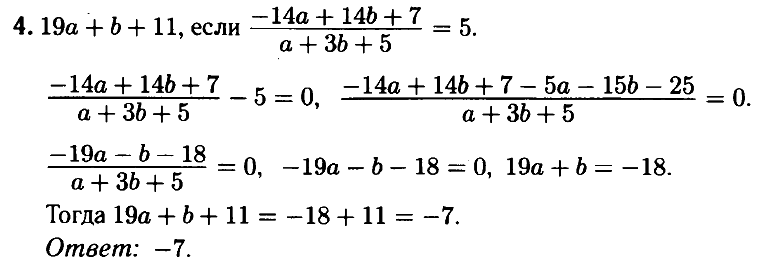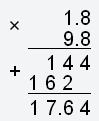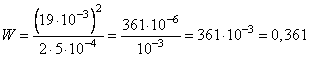ЕГЭ по математике Профиль. Задание 4: Уметь выполнять вычисления и преобразования. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.
Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».
ЕГЭ Профиль. Задание № 4
АЛГОРИТМ ВЫПОЛНЕНИЯ
Задание № 4 проверяет умение производить вычисления и преобразования рациональных, иррациональных, степенных, логарифмических и тригонометрических выражений. Задание состоит из числового или алгебраического выражения, значение которого необходимо найти, применяя математические преобразования. Ответом является целое число или конечная десятичная дробь.
План выполнения:
- Внимательно прочитайте условие задачи.
- Выполните преобразования.
- Найдите числовое значение выражения.
- Запишите полученное число в поле ответа КИМ и бланк ответов № 1.
Вычисление значений рациональных выражений
Задачи этого типа заключаются в вычислении значений рациональных, то есть дробных выражений. При подготовке необходимо повторить правила действий с дробями, формулы сокращённого умножения.
Задача № 4 (1). Найдите значение выражения
Решение:
Ответ: 1.
Задача № 4 (2). Найдите (a + 9b + 16)/(a + 3b + 8), если a/b = 3.
Решение:
Ответ: 2.
Вычисление значений иррациональных выражений
Задачи этого типа заключаются в вычислении значений иррациональных (содержащих корни) выражений. При подготовке следует повторить правила вычисления корней, свойства корней.
Задача № 4 (3). Найдите значение выражения (3√5 • 6√5) : √5.
Решение:
Ответ: 1.
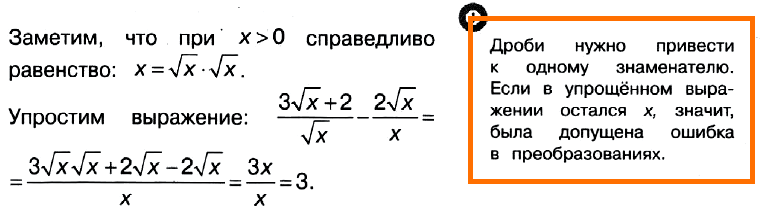
Задача № 4 (4). Найдите значение выражения (3√x + 2)/√x – 2√x/x при х > 0.
Решение:
Ответ: 3.
Вычисление значений степенных выражений
Задачи этого типа заключаются в вычислении значений степенных выражений. При подготовке нужно повторить правила действий со степенями, правило возведения числа в степень.
Задача № 4 (5). Найдите значение выражения 21,5 • 80,5.
Решение:
Ответ: 8.
Задача № 4 (6). Найдите значение выражения (3 – 140,25)(3 + 140,25) : (9 + (70,5 – 21/2)2).
Решение:
Ответ: 27.
Вычисление значений логарифмических выражений
Задачи этого типа заключаются в вычислении значений логарифмических выражений. При подготовке нужно повторить понятие логарифма, основные свойства логарифмов.
Задача № 4 (7). Вычислите log1/2 4√2.
Решение:
Ответ: –0,25.
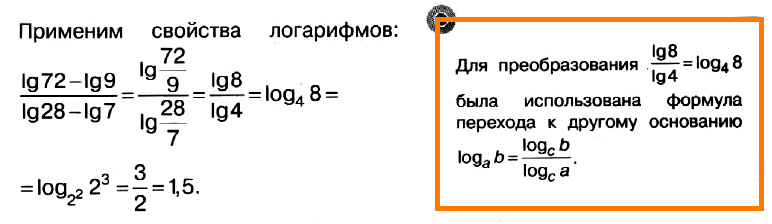
Задача № 4 (8). Найдите значение выражения (lg 72 – lg 9) : (lg 28 – lg 7).
Решение:
Ответ: 1,5.
Вычисление значений тригонометрических выражений
Задачи этого типа заключаются в вычислении значений тригонометрических выражений. При подготовке необходимо повторить основное тригонометрическое тождество, знаки синуса, косинуса, тангенса, формулы приведения, формулы синуса и косинуса двойного аргумента, понятие периодичности тригонометрических функций и табличные значения тригонометрических функций основных углов.
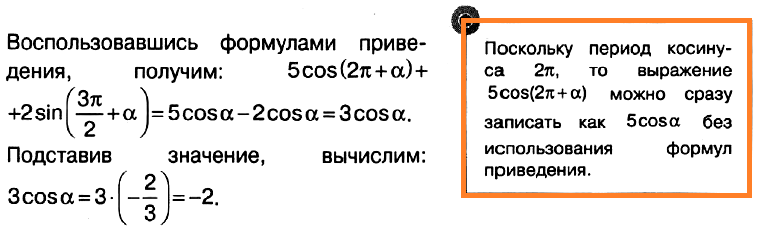
Задача № 4 (9). Найдите значение выражения 5 cos (2π + α) + 2 sin (3π/2 + α), если cos α = –2/3.
Решение:
Ответ: –2.
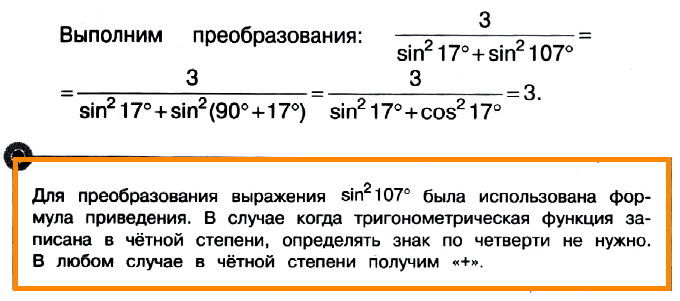
Задача № 4 (10). Найдите значение выражения 3/(sin2 17° + sin2 107°).
Решение:
Ответ: 3.
Тренировочные задания с самопроверкой
№ 4.1. Найдите значение выражения 11√3 • tg (7π/6) • cos (4π/3).
Открыть ОТВЕТ
№ 4.2. Найдите значение выражения (9 sin 59°) / (cos 31°).
Открыть ОТВЕТ
№ 4.3. Найдите значение выражения
Открыть ОТВЕТ
№ 4.4. Найдите значение выражения (3√x + 9)/√x – (9√x)/x – 3x + 12 при х = 6.
Открыть ОТВЕТ
№ 4.5. Найдите значение выражения 19а + b + 11, если (–14a + 14b + 7) : (a + 3b + 5) = 5.
Открыть ОТВЕТ
Вы смотрели: ЕГЭ по математике Профиль. Задание 4: Уметь выполнять вычисления и преобразования. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.
Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».
Просмотров:
14 783
ЕГЭ Профиль №4. Вычисление значений тригонометрических выражений
Скачать файл в формате pdf.
ЕГЭ Профиль №4. Вычисление значений тригонометрических выражений
| Задача 1. Найдите значение выражения (frac{{50sin {{179}^ circ } cdot cos {{179}^ circ }}}{{sin {{358}^ circ }}})
Ответ
ОТВЕТ: 25. |
| Задача 2. Найдите значение выражения (8sin frac{{5{\pi }}}{{12}} cdot cos frac{{5{\pi }}}{{12}})
Ответ
ОТВЕТ: 2. |
| Задача 3. Найдите значение выражения (frac{{24left( {{{sin }^2}{{17}^ circ } — {{cos }^2}{{17}^ circ }} right)}}{{cos {{34}^ circ }}})
Ответ
ОТВЕТ: — 24. |
| Задача 4. Найдите значение выражения (sqrt 3 {cos ^2}frac{{5{pi }}}{{12}} — sqrt 3 {sin ^2}frac{{5pi }}{{12}})
Ответ
ОТВЕТ: — 1,5. |
| Задача 5. Найдите значение выражения (sqrt {12} {cos ^2}frac{{5{pi }}}{{12}} — sqrt 3 )
Ответ
ОТВЕТ: — 1,5. |
| Задача 6. Найдите значение выражения (sqrt 3 — sqrt {12} {sin ^2}frac{{5{pi }}}{{12}})
Ответ
ОТВЕТ: — 1,5. |
| Задача 7. Найдите ( — 47cos 2alpha ), если (cos alpha = — 0,4)
Ответ
ОТВЕТ: 31,96. |
| Задача 8. Найдите значение выражения (frac{{5cos {{29}^ circ }}}{{sin {{61}^ circ }}})
Ответ
ОТВЕТ: 5. |
| Задача 9. Найдите значение выражения (36sqrt 3 {text{tg}}frac{{\pi }}{3}sin frac{{\pi }}{6})
Ответ
ОТВЕТ: 54. |
| Задача 10. Найдите значение выражения (4sqrt 2 cos frac{{\pi }}{4}cos frac{{7{\pi }}}{3})
Ответ
ОТВЕТ: 2. |
| Задача 11. Найдите значение выражения (frac{8}{{sin left( { — frac{{27{\pi }}}{4}} right)cos left( {frac{{31{\pi }}}{4}} right)}})
Ответ
ОТВЕТ: — 16. |
| Задача 12. Найдите значение выражения (33sqrt 2 cos left( {{{495}^ circ }} right))
Ответ
ОТВЕТ: — 33. |
| Задача 13. Найдите значение выражения (2sqrt 3 {text{tg}}left( { — {{300}^ circ }} right))
Ответ
ОТВЕТ: 6. |
| Задача 14. Найдите значение выражения ( — 18sqrt 2 sin left( { — {{135}^ circ }} right))
Ответ
ОТВЕТ: 18. |
| Задача 15. Найдите значение выражения (24sqrt 2 cos left( { — frac{{\pi }}{3}} right)sin left( { — frac{{\pi }}{4}} right))
Ответ
ОТВЕТ: — 12. |
| Задача 16. Найдите значение выражения (frac{{14sin {{19}^ circ }}}{{sin {{341}^ circ }}})
Ответ
ОТВЕТ: — 14. |
| Задача 17. Найдите значение выражения (frac{{36cos {{93}^ circ }}}{{cos {{87}^ circ }}})
Ответ
ОТВЕТ: — 36. |
| Задача 18. Найдите значение выражения (frac{{ — 37{text{tg6}}{{text{3}}^ circ }}}{{{text{tg11}}{{text{7}}^ circ }}})
Ответ
ОТВЕТ: 37. |
| Задача 19. Найдите значение выражения (frac{{14sin {{409}^ circ }}}{{sin {{49}^ circ }}})
Ответ
ОТВЕТ: 14. |
| Задача 20. Найдите значение выражения (5{text{tg1}}{{text{7}}^ circ } cdot {text{tg10}}{{text{7}}^ circ })
Ответ
ОТВЕТ: — 5. |
| Задача 21. Найдите значение выражения ( — 6{text{tg3}}{{text{1}}^ circ } cdot {text{tg5}}{{text{9}}^ circ })
Ответ
ОТВЕТ: — 6. |
| Задача 22. Найдите значение выражения (frac{{ — 12}}{{{{sin }^2}{{131}^ circ } + {{sin }^2}{{221}^ circ }}})
Ответ
ОТВЕТ: — 12. |
| Задача 23. Найдите значение выражения (frac{{27}}{{{{cos }^2}{{116}^ circ } + {{cos }^2}{{206}^ circ }}})
Ответ
ОТВЕТ: 27. |
| Задача 24. Найдите значение выражения (frac{{ — 5}}{{{{sin }^2}{{16}^ circ } + {{cos }^2}{{196}^ circ }}})
Ответ
ОТВЕТ: — 5. |
| Задача 25. Найдите значение выражения (frac{{ — 14sin {{84}^ circ }}}{{sin {{42}^ circ } cdot sin {{48}^ circ }}})
Ответ
ОТВЕТ: — 28. |
| Задача 26. Найдите значение выражения (frac{{5sin {{74}^ circ }}}{{cos {{37}^ circ } cdot cos {{53}^ circ }}})
Ответ
ОТВЕТ: 10. |
| Задача 27. Найдите значение выражения (20sin {135^ circ } cdot cos {45^ circ })
Ответ
ОТВЕТ: 10. |
| Задача 28. Найдите ({text{tg}}alpha ), если (cos alpha = frac{1}{{sqrt {10} }}) и (a in left( {frac{{3{\pi }}}{2};;2{\pi }} right))
Ответ
ОТВЕТ: — 3. |
| Задача 29. Найдите ({text{tg}}alpha ), если (sin alpha = — frac{5}{{sqrt {26} }}) и (alpha in left( {{\pi };;frac{{3{\pi }}}{2}} right))
Ответ
ОТВЕТ: 5. |
| Задача 30. Найдите (3cos alpha ), если (sin alpha = — frac{{2sqrt 2 }}{3}) и (alpha in left( {frac{{3{\pi }}}{2};;2{\pi }} right))
Ответ
ОТВЕТ: 1. |
| Задача 31. Найдите (7sin alpha ), если (cos alpha = frac{{3sqrt 5 }}{7}) и (alpha in left( {1,5{\pi };;2{\pi }} right))
Ответ
ОТВЕТ: — 2. |
| Задача 32. Найдите (24cos 2alpha ), если (sin alpha = — 0,2)
Ответ
ОТВЕТ: 22,08. |
| Задача 33. Найдите (frac{{10sin 6alpha }}{{3cos 3alpha }}), если (sin 3alpha = 0,6)
Ответ
ОТВЕТ: 4. |
| Задача 34. Найдите значение выражения (frac{{3cos left( {{\pi } — beta } right) + sin left( {frac{{\pi }}{2} + beta } right)}}{{cos left( {beta + 3{\pi }} right)}})
Ответ
ОТВЕТ: 2. |
| Задача 35. Найдите значение выражения (frac{{2sin left( {alpha — 7{\pi }} right) + cos left( {frac{{3{\pi }}}{2} + alpha } right)}}{{sin left( {a + {\pi }} right)}})
Ответ
ОТВЕТ: 1. |
| Задача 36. Найдите значение выражения (5{text{tg}}left( {5{\pi } — gamma } right) — {text{tg}}left( { — gamma } right)), если ({text{tg}}gamma {text{ = 7}})
Ответ
ОТВЕТ: — 28. |
| Задача 37. Найдите (sin left( {frac{{7{\pi }}}{2} — alpha } right)), если (sin alpha = 0,8) и (a in left( {frac{{\pi }}{2};;{\pi }} right))
Ответ
ОТВЕТ: 0,6. |
| Задача 38. Найдите (26cos left( {frac{{3{\pi }}}{2} + alpha } right)), если (cos alpha = frac{{12}}{{13}}) и (alpha in left( {frac{{3{\pi }}}{2};;2{\pi}} right))
Ответ
ОТВЕТ: — 10. |
| Задача 39. Найдите ({text{tg}}left( {alpha + frac{{5{\pi }}}{2}} right)), если ({text{tg}}alpha {text{ = 0}}{text{,4}})
Ответ
ОТВЕТ: — 2,5. |
| Задача 40. Найдите ({text{t}}{{text{g}}^2}alpha ), если (4{sin ^2}alpha + 9{cos ^2}alpha = 6)
Ответ
ОТВЕТ: 1,5. |
| Задача 41. Найдите (frac{{3cos alpha — 4sin alpha }}{{2sin alpha — 5cos alpha }}), если ({text{tg}}alpha {text{ = 3}})
Ответ
ОТВЕТ: — 9. |
| Задача 42. Найдите (frac{{10cos alpha + 4sin alpha + 15}}{{2sin alpha + 5cos alpha + 3}}), если ({text{tg}}alpha {text{ = }} — {text{2}}{text{,5}})
Ответ
ОТВЕТ: 5. |
| Задача 43. Найдите ({text{tg}}alpha ), если (frac{{6sin alpha — 2cos alpha }}{{4sin alpha — 4cos alpha }} = — 1)
Ответ
ОТВЕТ: 0,6. |
| Задача 44. Найдите ({text{tg}}alpha ), если (frac{{3sin alpha — 5cos alpha + 2}}{{sin alpha + 3cos alpha + 6}} = frac{1}{3})
Ответ
ОТВЕТ: 2,25. |
| Задача 45. Найдите значение выражения (7cos left( {{\pi } + beta } right) — 2sin left( {frac{{\pi }}{2} + beta } right)), если (cos beta = — frac{1}{3})
Ответ
ОТВЕТ: 3. |
| Задача 46. Найдите значение выражения (5sin left( {alpha — 7{\pi }} right) — 11cos left( {frac{{3{\pi }}}{2} + alpha } right)), если (sin alpha = — 0,25)
Ответ
ОТВЕТ: 4. |
| Задача 47. Найдите (3cos 2alpha ), если (cos alpha = frac{1}{2})
Ответ
ОТВЕТ: — 1,5. |
За это задание ты можешь получить 1 балл. На решение дается около 5 минут. Уровень сложности: повышенный.
Средний процент выполнения: 86.9%
Ответом к заданию 4 по математике (профильной) может быть целое число или конечная десятичная дробь.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
Чтобы поступить в институт на специальность «Комплексное использование и охрана водных ресурсов», абитуриент должен набрать на ЕГЭ не менее $70$ баллов по каждому из трёх предметов — математике, русскому языку и физике. Чтобы поступить на специальность «Безопасность жизнедеятельности в техносфере», нужно набрать не менее $70$ баллов по каждому из трёх предметов — математике, русскому языку и химии. Вероятность того, что абитуриент Э. получит не менее $70$ баллов по математике, равна $0{,}5$, по русскому языку — $0{,}7$, по физике — $0{,}6$ и по химии — $0{,}3$. Найдите вероятность того, что Э. сможет поступить хотя бы на одну из двух упомянутых специальностей.
Решение
Чтобы поступить хотя бы на одну специальность, абитуриенту Э. надо набрать не менее 70 баллов по математике, русскому языку и хотя бы по одному из предметов химия и физика.
Найдём вероятность того, что абитуриент Э. наберёт не менее 70 баллов хотя бы по одному из предметов химия и физика. Сначала отыщем вероятность противоположного события, то есть вероятность того, что абитуриент Э. по обоим этим предметам не наберёт 70 баллов. Результаты экзаменов не зависят друг от друга, вероятность не набрать 70 баллов по физике равна 1 — 0.6 = 0.4, а вероятность не набрать 70 баллов по химия равна 1 — 0.3 = 0.7. Отсюда вероятность того, что абитуриент Э. по обоим этим предметам не наберёт 70 баллов, равна 0.4 · 0.7 = 0.28. Следовательно, вероятность того, что абитуриент Э. наберёт не менее 70 баллов хотя бы по одному из предметов химия и физика, равна 1 — 0.28 = 0.72.
Таким образом, вероятность того, что абитуриент Э. наберёт не менее 70 баллов по математике, русскому языку и хотя бы по одному из предметов химия и физика, равна 0.5 · 0.7 · 0.72 = 0.252.
Ответ: 0.252
Задача 2
Биатлонист Алексей Антонов пять раз стреляет по мишеням. Вероятность попадания при одном выстреле равна $0{,}7$. Найдите вероятность того, что биатлонист Алексей Антонов один раз попал по мишени, а четыре — промахнулся. Результат округлите до сотых.
Решение
Вероятность промахнуться при одном выстреле равна $1 — 0.7 = 0.3$. Обозначим события.
1. $A_1$ — «Алексей попал по мишени при первом выстреле».
2. $A_2$ — «Алексей попал по мишени при втором выстреле».
3. $A_3$ — «Алексей попал по мишени при третьем выстреле».
4. $A_4$ — «Алексей попал по мишени при четвёртом выстреле».
5. $A_5$ — «Алексей попал по мишени при пятом выстреле».
События ${A_1}↖{-}, {A_2}↖{-}, {A_3}↖{-}, {A_4}↖{-}$ и ${A_5}↖{-}$ — означают, что Алексей промахнулся при соответствующем выстреле.
Событие «Алексей Антонов первый раз попал по мишени, а последние четыре промахнулся» означает одновременное наступление (пересечение) независимых событий ${A_1}, {A_2}↖{-}, {A_3}↖{-}, {A_4}↖{-}$ и ${A_5}↖{-}$.
$P (A_1 ∩ {A_2}↖{-} ∩ {A_3}↖{-} ∩ {A_4}↖{-} ∩ {A_5}↖{-}) = P (A_1) · P ({A_2}↖{-}) · P ({A_3}↖{-}) · P ({A_4}↖{-}) · P ({A_5}↖{-}) = 0.7 · 0.3 · 0.3 · 0.3 · 0.3 = 0.00567$.
По условию Алексей мог попасть единожды, но это попадание могло прийтись на любой из пяти выстрелов, не обязательно на первый.
Тогда, аналогично, $P ({A_1}↖{-} ∩ A_2 ∩ {A_3}↖{-} ∩ {A_4}↖{-} ∩ {A_5}↖{-}) = P ({A_1}↖{-}∩ {A_2}↖{-} ∩ A_3 ∩ {A_4}↖{-} ∩ {A_5}↖{-}) =$
$= P ({A_1}↖{-} ∩ {A_2}↖{-} ∩ {A_3}↖{-} ∩ A_4 ∩ {A_5}↖{-}) = P ({A_1}↖{-} ∩ {A_2}↖{-} ∩ {A_3}↖{-} ∩ {A_4}↖{-} ∩ A_5) =$
$= P (A_1 ∩ {A_2}↖{-} ∩ {A_3}↖{-} ∩ {A_4}↖{-} ∩ {A_5}↖{-}) = (0.3)^4 · 0.7 = 0.00567$.
Следовательно, искомая вероятность равна $0.00567 · 5 = 0.02835 ≈0.03$.
Ответ: 0.03
Задача 3
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы $4$ очка в двух играх. Если команда выигрывает, она получает $3$ очка, в случае ничьей — $1$ очко, если проигрывает — $0$ очков. Найдите вероятность того, что команде «Ветерок» удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны $0{,}3$.
Решение
Вероятность ничьей в каждой игре равна 1 — 0.3 — 0.3 = 0.4 (из единицы вычитаем вероятность выигрыша и вероятность проигрыша). «Ветерок» выйдет в следующий круг в одном из трёх следующих случаев.
1. «Ветерок» выиграет обе игры. Вероятность этого равна 0.3 · 0.3 = 0.09.
2. «Ветерок» выиграет первую игру и сыграет вничью вторую. Вероятность этого равна 0.3 · 0.4 = 0.12.
3. «Ветерок» сыграет вничью первую игру и выиграет вторую. Вероятность этого равна 0.4 · 0.3 = 0.12.
Искомая вероятность равна 0.09 + 0.12 + 0.12 = 0.33.
Ответ: 0.33
Задача 4
Помещение торгового дома «Светлый» освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в течение года равна $0{,}6$. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Решение
Найдём вероятность события «перегорели обе лампы», а затем искомую вероятность.
Вероятность события «перегорела первая лампа» равна вероятности события «перегорела вторая лампа» и равна 0.6. Эти два события независимы, значит, вероятность того, что они наступили оба, равна произведению их вероятностей, то есть равна 0.6 · 0.6 = 0.36. Это вероятность события «перегорели обе лампы».
События «перегорели обе лампы» и «хотя бы одна лампа не перегорела» противоположны, следовательно, сумма их вероятностей равна 1. Значит, вероятность события «хотя бы одна лампа не перегорела» равна 1 — 0.36 = 0.64.
Ответ: 0.64
Задача 5
В ларьке на улице Счастья стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью $0{,}1$ независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Решение
Найдём вероятность события «оба автомата неисправны», а затем искомую вероятность.
Вероятность события «неисправен первый автомат» равна вероятности события «неcисправен второй автомат» и равна 0,1. Эти два события независимы, значит, вероятность того, что они наступят оба, равна произведению их вероятностей, то есть равна 0.1 · 0.1 = 0.01. Таким образом, мы нашли вероятность события «оба автомата неисправны».
События «оба автомата неисправны» и «хотя бы один автомат исправен» противоположны, следовательно, сумма их вероятностей равна 1. Значит, вероятность события «хотя бы один автомат исправен» равна 1 — 0.01 = 0.99.
Ответ: 0.99
Задача 6
Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью $0{,}72$. Если А. играет чёрными, то А. выигрывает у Б. с вероятностью $0{,}6$. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Решение
По условию вероятность события «шахматист А. выиграет белыми» равна $0{,}72$, вероятность события «шахматист А. выиграет чёрными» равна $0{,}6$. Эти события независимы. Значит, вероятность того, что оба этих события наступят (А. выиграет оба раза) равна произведению вероятностей, то есть равна $0{,}72⋅ 0{,}6=0{,}432$.
Ответ: 0.432
Задача 7
На железнодорожном вокзале $3$ кассира. Каждый из них занят с клиентом с вероятностью $0{,}2$ независимо от других кассиров. Найдите вероятность того, что в случайный момент времени все три кассира заняты одновременно.
Решение
События «первый кассир занят», «второй кассир занят» и «третий кассир занят» по условию независимы. Тогда вероятность их одновременного наступления (вероятность пересечения событий) равна произведению вероятностей этих событий, то есть равна 0.2 · 0.2 · 0.2 = 0.008.
Ответ: 0.008
Задача 8
В магазине сантехники три продавца. Каждый из них занят с клиентом с вероятностью $0{,}7$ независимо от других продавцов. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно.
Решение
События «первый продавец занят», «второй продавец занят» и «третий продавец занят» по условию независимы.
Тогда вероятность их одновременного наступления (вероятность пересечения событий) равна произведению вероятностей этих событий
То есть равна $0.7 · 0.7 · 0.7 = 0.343$
Ответ: 0.343
Задача 9
Вероятность того, что новый электрический чайник прослужит больше года, равна $0{,}93$. Вероятность того, что он прослужит больше двух лет, равна $0{,}84$. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Решение
Заметим, что из событий «чайник прослужит меньше года», «чайник прослужит от 1 до 2 лет» и «чайник прослужит больше двух лет» произойдёт обязательно ровно одно, то есть, говоря математическим языком, они попарно несовместны, а их объединение — достоверное событие. Следовательно, сумма вероятностей этих событий равна 1.
При этом события «чайник прослужит меньше года» и «чайник прослужит больше года» противоположны, поэтому вероятность события «чайник прослужит меньше года» равна 1 — 0.93 = 0.07. Заполним таблицу.
| Событие | Прослужит меньше года | Прослужит от 1 до 2 лет | Прослужит больше двух лет |
| Вероятность | 0.07 | ? | 0.84 |
Отсюда искомая вероятность равна 1 — 0.07 — 0.84 = 0.09.
Ответ: 0.09
Задача 10
На экзамене по биологии студент отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Млекопитающие», равна $0{,}36$. Вероятность того, что это вопрос по теме «Бактерии», равна $0{,}18$. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене студенту достанется вопрос по одной из этих двух тем.
Решение
Из условия следует, что события A = «достанется вопрос по теме Млекопитающие» и B = «достанется вопрос по теме Бактерии» несовместны. Действительно, нет билетов, относящихся к обоим этим темам одновременно. Событие «достанется вопрос по одной из этих двух тем» — это объединение событий A и B (A $∪$ B). По формуле вероятности объединения несовместных событий получим, что искомая вероятность равна P(A $∪$ B) = P(A) + P(B) = 0.36 + 0.18 = 0.54.
Ответ: 0.54
Задача 11
В торговом центре два одинаковых автомата продают лимонад. Вероятность того, что к концу дня в автомате закончится лимонад, равна $0{,}2$. Вероятность того, что лимонад закончится в обоих автоматах, равна $0{,}09$. Найдите вероятность того, что к концу дня лимонад останется в обоих автоматах.
Решение
По условию вероятность события A =«лимонад закончится в первом автомате» равна вероятности события B =«лимонад закончится во втором автомате» и равна $0.2$. Эти два события зависимые.
В этом случае воспользуемся формулой $P (A + B) = P (A) + P (B) — P (A B)$.
$P (A + B) = 0.2 + 0.2 — 0.09 = 0.31$. Событие $A + B$ — это событие «лимонад закончилась хотя бы в одном автомате». Указанное событие противоположно искомому. Отсюда вероятность события «лимонад останется в обоих автоматах» равна $1 — 0.31 = 0.69$.
Ответ: 0.69
Задача 12
Предприниматель закупает для продажи на рынке куриные яйца в двух хозяйствах. $50%$ яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — $40%$ яиц высшей категории. При продаже яиц на рынке оказалось, что всего получилось $42%$ яиц высшей категории. Найдите вероятность того, что яйцо, купленное у предпринимателя, окажется из второго хозяйства.
Задача 13
Робин Гуд подошел к столу, на котором лежали 3 его старых лука и 2 новых. Он решил сбить стрелой яблоко с дерева. Робин попадает в цель из своего старого лука с вероятностью $0{,}8$, а из нового — с вероятностью $0{,}3$. Робин случайным образом выбирает один лук. Найдите вероятность того, что Робин промахнётся при стрельбе.
Рекомендуемые курсы подготовки
1. Найдите значение выражения (5√6)2/10
2. Найдите значение выражения 2𝑡𝑔15° ∙ 𝑡𝑔105°
3. Найдите значение выражения p(b)/p(1/b), если p(b)=(b+8/b)(8b+1/b)
4. Найдите значение выражения: (52/7*92/3)21/4512
5. Вычислите: (√28 − √12) ⋅ √10 + √84
6.Найдите значение выражения −6√3/ (cos390*sin(-750))
7. Найдите −25 cos 2𝑥, если cos(𝑥) = −0,8
8. Найдите значение выражения 8 cos 34° / sin 56°
9. Найдите значение выражения lognn3/m5
если logmn=3
10.
Найдите значение выражения:
24/ (sin2147+sin2237)
11.
Найдите значение выражения, 4p(x − 4) − p(4x), если p(x) = 2x + 5.

Более 100 тренировочных прототипов задания №4 решу ЕГЭ 2022 по математике 11 класс профильный уровень с ответами и решением для практики. Задание №4 профильного ЕГЭ по математике – вычисления и преобразования.
На ЕГЭ вам могут встретиться и совсем простые задачи (на сложение дробей), и задания, которые не решить без подготовки.
Скачать задания рациональные выражения
Скачать задания иррациональные выражения
Скачать задания степенные выражения
Скачать задания логарифмические выражения
Скачать задания тригонометрические выражения
Рациональные выражения ЕГЭ 2022 по математике профиль:
Иррациональные выражения ЕГЭ 2022 по математике профиль:
Степенные выражения ЕГЭ 2022 по математике профиль:
Логарифмические выражения ЕГЭ 2022 по математике профиль:
Тригонометрические выражения ЕГЭ 2022 по математике профиль:
1)Найдите значение выражения log527⋅log325.
2)Найдите значение выражения 14 sin225°+cos2205° .
3)Найдите значение выражения 5 cos233°+cos2123° .
4)Найдите значение выражения 18(sin216°−cos216°) cos32°
5)Найдите значение выражения (1−log318)(1−log618).
6)Найдите значение выражения log336 2+log34 .
7)Найдите значение выражения log2(log5625).
8)Найдите значение выражения 7log550 7log52 .
9)Найдите значение выражения log723 log4923 .
10)Найдите значение выражения 15cos19° cos341° .
11)Найдите значение выражения 3cos39° sin51° .
12)Найдите значение выражения 15√x−3 √x + 3√x x +2x−8 при x=3.
13)Найдите значение выражения f(x+3) f(x−3) , если f(x)=5x.
14)Найдите значение выражения (√23−√15)(√23+√15).
15)Найдите значение выражения 63√2+2·62√2 65√2−1 .
16)Найдите значение выражения 83√5−1⋅81−√5:82√5−1.
17)Найдите значение выражения 6x⋅(2×9)4:(4×12)3 при x=5.
18)Найдите значение выражения x⋅52x+1⋅25−x при x=3.
19)Найдите значение выражения 3sinβ+15cosβ−8 sinβ+5cosβ+2 , если tgβ=−5.
20)Найдите значение выражения −6√3 cos390°⋅sin(−750°) .
21)Найдите значение выражения 5√14⋅5√16 5√7 .
22)Найдите значение выражения log0,85⋅log51,25.
23)Найдите значение выражения 18 √6 tg π 3 ⋅sin π 4 .
24)Найдите значение выражения 12√6tg π 6 ⋅cos π 4 .
25)Найдите значение выражения 5tg125°⋅tg35°.
26)Найдите значение выражения 7tg27°⋅tg117°.
27)Найдите значение выражения a+7b+12 a+5b+10 , если a b =5.
28)Найдите значение выражения a b , если 5a+2b 2a+5b =3.
29)Найдите значение выражения 14sin13°⋅cos13° sin26° .
30)Найдите значение выражения 44−3,5⋅114,5:4−2,5.
31)Найдите значение выражения √1602−962.
32)Найдите −7cos2α, если cosα=−0.8.
33)Найдите значение выражения 3⋅log0.45·log52.5.
ЕГЭ математика профиль 3 задание все возможные задачи с ответами
Вероятность события задание №2 ЕГЭ 2022 математика профиль с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Задание 903
Найдите значение выражения $$log^{3}_{sqrt{3}}{{frac{1}{3}}^3}$$
Ответ: -216
Скрыть
Рассмотрим сам логарифм: $$ log_{sqrt{3}}{{frac{1}{3}}^3}=log_{3^{1/2}}{3^{-3}}=frac{1}{frac{1}{2}}*left(-3right)log_33=-6 $$ Так как он был в третьей степени, то возведем -6 в нее и получим -216
Задание 939
Известно, что $$log_a b *log_b c = -5$$ . Найдите значение выражения $$log_c a$$
Ответ: -0.2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$log_a b *log_b c = frac{1}{log_b a}*log_b c=frac{log_b c}{log_b a}=log_a c=-5$$ $$log_c a=frac{1}{log_a c}=frac{1}{-5}=-0.2$$
Задание 975
Вычислите $$frac{sin 35cos 35}{sin ^{2} 10-cos ^{2} 10}$$
Ответ: -0.5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$frac{sin 35cos 35}{sin ^{2} 10-cos ^{2} 10}=$$ $$frac{0.5sin 70}{-cos 20}=frac{0.5cos 20}{-cos 20}=-0.5$$
Задание 1015
Найдите значение выражения $$frac{(0.1)^{-1}-(0.1)^{0}}{(frac{3^{2}}{2^{3}})^{-1}*(frac{3}{2})^{3}-(frac{1}{3})^{-2}}$$
Ответ: -1.5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$frac{(0.1)^{-1}-(0.1)^{0}}{(frac{3^{2}}{2^{3}})^{-1}*(frac{3}{2})^{3}-(frac{1}{3})^{-2}}=$$ $$=frac{10-1}{frac{2^{3}}{3^{2}}*frac{27}{8}-9}=frac{9}{frac{8}{9}*frac{27}{8}-9}=$$ $$frac{9}{3-9}=frac{9}{-6}=-1.5$$
Задание 1082
Найдите значение выражения $$(frac{3}{4}+2frac{3}{8})*25,8$$
Ответ: 80,625
Задание 1083
Найдите значение выражения $$(2frac{4}{7}-2,5):frac{1}{10}$$
Ответ: 5
Задание 1084
Найдите значение выражения $$(432^{2}-568^{2}):1000$$
Ответ: -136
Задание 1085
Найдите значение выражения $$4frac{4}{9}:frac{4}{9}$$
Ответ: 10
Задание 1086
Найдите значение выражения $$frac{1,23*45,7}{12,3*0,457}$$
Ответ: 10
Задание 1099
Вычислите $$tg alpha $$, если известно, что $$cos 2alpha =0.6$$ и $$frac{3pi }{4}< alpha < pi $$
Ответ: -0.5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Воспользуемся формулой косинуса двойного угла: $$cos 2alpha =2cos^{2}alpha-1=0.6$$
С учетом того, что $$alpha$$ — угол второй четверти, то косинус у него отрицательный, а синус положительный.
Значит: $$cos alpha = -sqrt{frac{cos 2alpha+1}{2}}=-sqrt{frac{0.6+1}{2}}=-sqrt{0.8} $$
Воспользуемся основным тригонометрическим тождеством: $$sin alpha = sqrt{1-cos^{2}alpha}=sqrt{0.2}$$
Значит тангенс будет равен: $$tan alpha = frac{sin alpha}{cos alpha}= frac{sqrt{0.2}}{-sqrt{0.8}}=-frac{1}{2}=-0.5$$
Задание 1177
Найдите значение выражения $$(frac{9^{frac{1}{6}}*9^{frac{1}{9}}}{sqrt[18]{9}})^{9}$$
Ответ: 81
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$(frac{9^{frac{1}{6}}*9^{frac{1}{9}}}{sqrt[18]{9}})^{9}=(frac{9^{frac{1}{6}+frac{1}{9}}}{9^{frac{1}{18}}})^{9}=(9^{frac{1}{6}+frac{1}{9}-frac{1}{18}})^{9}=9^{2}=81$$
Задание 1238
Известно, что $$frac{cos x-sin x}{cos x+sin x}=-0.8$$. Найдите $$ tg x $$
Ответ: 9
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$frac{cos x-sin x}{cos x+sin x}=-0.8=frac{-4}{5}$$ $$(cos x-sin x)*5=-4*(cos x+sin x)$$ $$5cos x-5sin x=-4*cos x-4sin x$$ $$9cos x = sin x $$ Поделим обе части на cos x $$9 = tg x $$
Задание 1279
Известно, что $$ tg x = frac{2}{sqrt{21}}$$ и $$pi < x< frac{3pi }{2}$$. Найдите sin x
Ответ: -0.4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Угол располагается в третьей четверти, поэтому sin будет отрицательный. Найдем сначала ctg x: $$ ctg x = frac {1}{tg x}= frac {1}{frac{2}{sqrt{21}}}=frac{sqrt{21}}{2}$$ Выразим sin x из формулы $$ 1 + ctg^{2} x = frac{1}{sin^{2} x} $$ $$ frac{1}{1 + ctg^{2} x} =sin^{2} x $$ $$sin x = — sqrt{ frac{1}{1 + ctg^{2} x} } $$ $$sin x = — sqrt{ frac{1}{1 + (frac{sqrt{21}}{2})^{2}} }=- sqrt{ frac{1}{1 + frac{21}{4}}}=-frac{2}{5}=-0.4 $$
Задание 1444
Найдите значение выражения: $$frac{12sin 11^{circ}*cos 11^{circ}}{sin 22^{circ}}$$.
Ответ: 6
Задание 1445
Найдите значение выражения: $$frac{24(sin^2 17^{circ}-cos^2 17^{circ})}{cos 34^{circ}}$$.
Ответ: -24
Преобразование выражений
[su_box title=”Описание задания” style=”soft” box_color=”#c1e8cc” title_color=”#0c0a0a”]
В задании №4 ЕГЭ по математике базового уровня нам необходимо продемонстрировать умения работы с выражениями. В данных задачах необходимо выразить из заданного выражения нужную переменную и вычислить её, подставив значения.
Тематика заданий: преобразования выражений
Бал: 1 из 20
Сложность задания: ♦◊◊
Примерное время выполнения: 3 мин.
[/su_box]
Разбор типовых вариантов заданий №4 ЕГЭ по математике базового уровня
Вариант 4МБ1
[su_note note_color=”#defae6″]
Найдите v0 из равенства v = v0 + at, если v = 20, t = 2, a = 7.
[/su_note]
Алгоритм выполнения:
- Подставить данные значения в выражение.
- Решить уравнение относительно неизвестной.
Решение:
Подставим все значения в данное выражение, получим:
20 = v0 + 7 · 2
Преобразуем:
20 = v0 + 14.
Найдем неизвестное слагаемое. Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
v0 = 20 – 14
v0 = 6
Ответ: v0 = 6
Вариант 4МБ2
[su_note note_color=”#defae6″]
Скорость камня (в м/с), падающего с высоты h (в м), в момент удара о землю можно найти по формуле . Найдите скорость (в м/с), с которой ударится о землю камень, падающий с высоты 0,9 м. Считайте, что ускорение свободного падения g равно 9,8 м/с2.
[/su_note]
Алгоритм выполнения:
- Подставить все значения в данную формулу.
- Произвести вычисления.
Решение:
По условию задания дана высота h=0,9 м и ускорение свободного падения g=9,8 м/с2. Подставим эти значения в формулу вычисления скорости v, получим:
Делаем умножение 1,8 на 9,8, имеем:
Примечание: При умножении в столбик десятичных дробей запятая записывается строго под запятой. В полученном результате справа отсчитывают столько знаков, сколько поле запятой в ОБЕИХ дробях ВМЕСТЕ.
и извлекаем из числа 17,64 квадратный корень:
м/с.
Ответ: 4,2 м/с.
Вариант 4МБ3
[su_note note_color=”#defae6″]
Энергия заряженного конденсатора W (в Дж) вычисляется по формуле , где C — ёмкость конденсатора (в Ф), a q — заряд на одной обкладке конденсатора (в Кл). Найдите энергию конденсатора (в Дж) ёмкостью
Ф, если заряд на его обкладке равен 0,019 Кл.
[/su_note]
Алгоритм выполнения задания:
- Подставить все известные значения в данную формулу.
- Провести вычисления.
Решение:
Подставим в формулу энергии конденсатора значения q=0,019 Кл и C = Ф, получим:
Пояснения:
Если степень стоит за скобкой, а внутри скобки произведение, то степень относится к каждому из множителей. То есть (19 · 10-3)2 = 192 · 10-3·2.
Чтобы найти вторую степень числа нужно умножить число само на себя.
192 = 19 · 19 = 361
Умножить на число в отрицательной степени, значит разделить на это число, но только в положительной степени.
361 · 10-3 = 361/1000 = 0,361
Ответ: 0,361.
Вариант 4МБ4
[su_note note_color=”#defae6″]
Энергия заряженного конденсатора W (в Дж) вычисляется по формуле , где C — ёмкость конденсатора (в Ф), a q — заряд на одной обкладке конденсатора (в Кл). Найдите энергию конденсатора (в Дж) ёмкостью
Ф, если заряд на его обкладке равен 0,07 Кл.
[/su_note]
Алгоритм выполнения:
- Подставить все известные значения в данную формулу.
- Провести вычисления.
Решение:
Подставим в формулу энергии конденсатора значения q=0,07 Кл и C = Ф, получим:
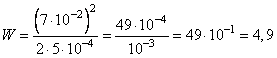
Пояснения:
Если степень стоит за скобкой, а внутри скобки произведение, то степень относится к каждому из множителей. То есть (7 · 10-2)2 = 72 · 10-2·2.
Чтобы найти вторую степень числа нужно умножить число само на себя.
72 = 7 · 7 = 49
Умножить на число в отрицательной степени, значит разделить на это число, но только в положительной степени.
49 · 10-1 = 49/10 = 4,9
Ответ: 4,9.
Вариант 4МБ5 (демо)
[su_note note_color=”#defae6″]
Найдите m из равенства F = ma, если F = 84 и a = 12.
[/su_note]
Алгоритм выполнения:
- Подставить данные значения в выражение.
- Решить уравнение относительно неизвестной.
Решение:
Подставим все значения в данное выражение, получим:
84 = m ·12
2. Найдем неизвестный множитель. Чтобы найти неизвестный множитель нужно разделить произведение на известный множитель.
m = 84 : 12
m = 7
Ответ: 7 кг.
Вариант 4МБ6 (ЕГЭ 2017)
[su_note note_color=”#defae6″]
Найдите m из равенства F = ma , если F = 84 и a =12.
[/su_note]
В начале выразим из формулы m, так как это множитель, то он равен произведению, деленному на второй множитель.
m=F/a
Теперь можем подставить числа из условия:
m=84/12=7
Ответ: 7
Вариант 4МБ7
[su_note note_color=”#defae6″]
Найдите v0 из равенства v = v0 + at , если v = 20 , t = 2 и a = 7 .
[/su_note]
Аналогично выразим v0, перенеся at в левую часть:
v – at = v0
Подставим значения:
20 – 7 • 2 = 6 = v0
Ответ: 6
Вариант 4МБ8
[su_note note_color=”#defae6″]
Найдите S из равенства S = v0t + at2/2 , если v0 = 6 , t = 2 , a = −2.
[/su_note]
В данном случае нам необходимо просто подставить числа и выполнить вычисления:
S = 6 • 2 + (-2) • 22/2 = 12 -4 = 8
Ответ: 8
Вариант 4МБ9
[su_note note_color=”#defae6″]
Перевести температуру из шкалы Фаренгейта в шкалу Цельсия позволяет формула , где tC – температура в градусах по шкале Цельсия, tF – температура в градусах по шкале Фаренгейта. Скольким градусам по шкале Цельсия соответствует 95 градусов по шкале Фаренгейта?
[/su_note]
Алгоритм выполнения
- Подставляем данное в условии для tF значение, равное 95, в формулу для tC.
- Выполняем числовые расчеты в формуле в такой последовательности: 1) вычитание в скобках; 2) внесение в числитель дроби 5/9 полученной в скобках разности; 3) сокращение 63 в числителе и 9 в знаменателе на 9; 4) нахождение конечного результата.
Решение:
Вычисляем вычитание в скобках:
95-32=63
Далее умножаем на 5/9, замечаем, что 63 делится на 9 – это 7, что и умножаем на 5, получаем 35!
Ответ: 35
Вариант 4МБ10
[su_note note_color=”#defae6″]
Кинетическая энергия (в джоулях) вычисляется по формуле , где m – масса тела (в килограммах), а v – его скорость (в м/с). Пользуясь этой формулой, найдите E (в джоулях), если v=4 м/с и m=10 кг.
[/su_note]
Алгоритм выполнения
- Подставляем числовые данные из условия в формулу для Е.
- Производим вычисления. Сначала возводим v в квадрат (получаем 16). Затем сокращаем 16 в числителе и 2 в знаменателе на 2. Далее выполняем умножение.
Решение:
Возводим 4 в квадрат – это 16, умножаем на 10 – 160 и делим на 2 – 80 – вот и ответ!
Ответ:80
Вариант 4МБ11
[su_note note_color=”#defae6″]
Ускорение тела (в м/с2) при равномерном движении по окружности можно вычислить по формуле , где ω – угловая скорость вращения (в с–1), а R – радиус окружности (в метрах). Пользуясь этой формулой, найдите а (в м/с2), если R=4 м и ω=7 с–1.
[/su_note]
Алгоритм выполнения
- Подставляем в формулу числовые значения для R и ω.
- Делаем вычисления в полученном числовом выражении: 1) возводим в квадрат 7; 2) выполняем умножение.
Решение:
Если R=4 и ω=7, то а = 72 · 4 = 49 · 4 = 196 (м/с2)
Ответ:196
Вариант 4МБ12
[su_note note_color=”#defae6″]
Мощность постоянного тока (в ваттах) вычисляется по формуле , где U – напряжение (в вольтах), R – сопротивление (в омах). Пользуясь этой формулой, найдите P (в ваттах), если R= 6 Ом и U=12 В.
[/su_note]
Алгоритм выполнения
- Поскольку все числовые данные приведены в условии в соответствии с СИ, то просто подставляем эти числа в формулу для мощности.
- Вычисляем значение для Р: 1) в числителе 122 представляем как 12·12; 2) выполняем сокращение на 6; 3) находим произведение.
Решение:
Возводим 12 в квадрат – это 144, затем делим на 6 – это 24. Либо замечаем, что 12 можно сократить на 6 – это 2, тогда умножаем оставшуюся от квадрата 12 на 2 – снова получаем 24.
Ответ:24
Вариант 4МБ13
[su_note note_color=”#defae6″]
Зная длину своего шага, человек может приближенно подсчитать пройденное им расстояние s по формуле s=nl, где n – число шагов, l – длина шага. Какое расстояние прошел человек, если l=50 см, n=1600? Ответ дайте в метрах.
[/su_note]
Алгоритм выполнения
- Т.к. ответ требуется дать в метрах, то l тоже необходимо перевести в метры.
- Числовые данные подставляем в формулу для s.
- Производим умножение.
Решение:
l=50 см=0,5 м
Если l=0,5 n=1600, то s=0,5·1600=800 (м)
Ответ:800
Вариант 4МБ14
[su_note note_color=”#defae6″]
Закон Гука можно записать в виде F=kx, где F – сила (в ньютонах), с которой растягивают пружину, х – абсолютное удлинение пружины (в метрах), а k – коэффициент упругости. Пользуясь этой формулой, найдите х (в метрах), если F=51 Н и k=3 Н/м.
[/su_note]
Алгоритм выполнения
- Из приведенной в условии формулы выражаем искомое удлинение х.
- В полученную формулу подставляем данные в условии числовые величины.
- Делаем вычисление.
Решение:
Искомое удлинение x находим как частное – F/k, так как x множитель.
Подставляя значения, получаем:
51/3=17
Ответ:17
Вариант 4МБ15
[su_note note_color=”#defae6″]
Работа постоянного тока (в джоулях) вычисляется по формуле, где I – сила тока (в амперах), R – сопротивление (в омах), t – время (в секундах). Пользуясь этой формулой, найдите A (в джоулях), если t=5 с, I=2 А и R=13 Ом.
[/su_note]
Алгоритм выполнения
- Подставляем в формулу приведенные в условии соответствующие числовые данные.
- Производим вычисления. Делаем это оптимальным способом: сначала находим I2, потом умножаем полученное число на значение для t, и уже затем множим это произведение на значение для R.
Решение:
Если I=2 А, R=13 Ом, t=5 с, то А=22·13·5=4·13·5=(4·5)·13=20·13=260 (Дж)
Ответ:260
Вариант 4МБ16
[su_note note_color=”#defae6″]
Сумма углов выпуклого многоугольника вычисляется по формуле , где n – количество его углов. Пользуясь этой формулой, найдите n, если ∑=15π.
[/su_note]
Алгоритм выполнения
- Преобразовываем формулу и выражаем из нее искомое n.
- Подставляем в полученное уравнение формулу ∑=15π.
- Выполняем сокращение на π. Находим конечный результат.
Решение:
Из ∑=(n–2)π имеем: n–2=∑/π → n=∑/π+2.
Если ∑=15π, то получаем:
15π/π +2 = 17
Ответ:17
Вариант 4МБ17
[su_note note_color=”#defae6″]
Среднее геометрическое трех чисел a, b и c вычисляется по формуле . Вычислите среднее геометрическое чисел 2, 4, 27.
[/su_note]
Алгоритм выполнения
- Подставляем в формулу числовые данные из условия.
- В подкоренном выражении представляем 4 как 22, а 27 как 33.
- Произведение 2·22 представляем как 23. Получаем две степени с показателем 3.
- Выносим степени из-под куб.корня. Получаем произведение оснований этих степеней. Вычисляем произведение.
Решение:
2 при умножении на 4 дает 2 в кубе, а 27 – это три в кубе. По свойству корней избавляемся от кубического корня и степеней для 2 и 3 поочередно (просто сокращая корень на степень), а затем выполняем умножение 2 на 3 – получаем 6.
Ответ:6
Вариант 4МБ18
[su_note note_color=”#defae6″]
Площадь треугольника вычисляется по формуле , где b и c – две стороны треугольника, а α – угол между ними. Пользуясь этой формулой, найдите площадь S, если b=18, c=16 и sinα=1/3.
[/su_note]
Алгоритм выполнения
- Подставляем в формулу приведенные в условии числовые данные.
- Заводим 18 и 16 в числитель, получаем дробь с числителем и знаменателем в виде произведений, соответственно, чисел 18, 16 и 2,3.
- Сокращаем 18 и 3 на 3, а 16 и 2 на 2. Получаем в знаменателе 1, а в числителе произведение 6 и 8. Находим это произведение.
Ответ:48
Даниил Романович | Просмотров: 8.4k