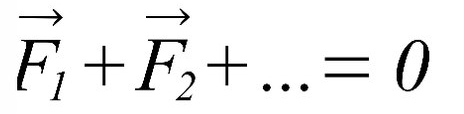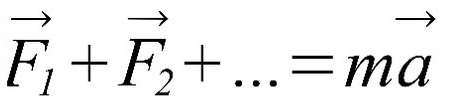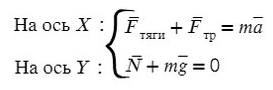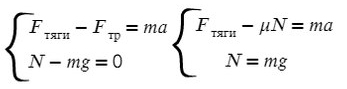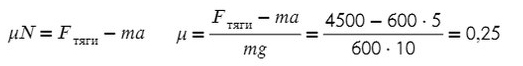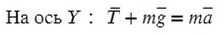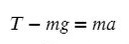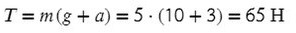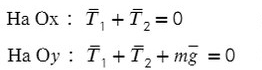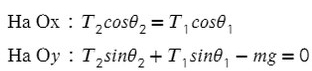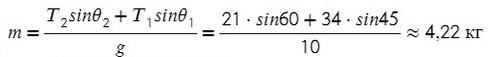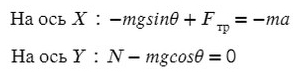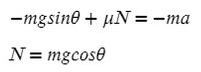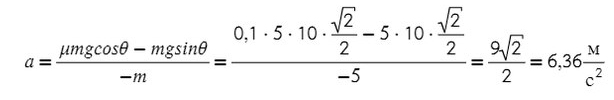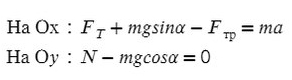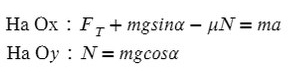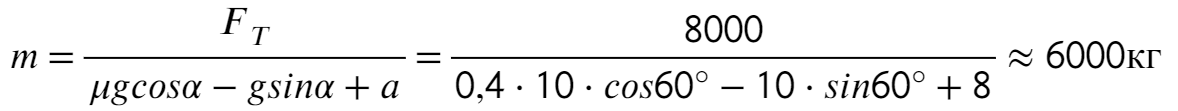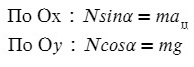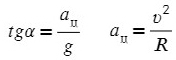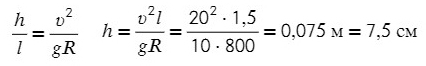Наклонная плоскость решу егэ - Помощь в подготовке к экзаменам и поступлению

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 135 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Небольшая шайба после удара скользит вверх по наклонной плоскости из точки А (см. рис.).

В точке В наклонная плоскость без излома переходит в наружную поверхность горизонтальной трубы радиусом R. Если в точке А скорость шайбы превосходит то в точке В шайба отрывается от опоры. Длина наклонной плоскости угол Коэффициент трения между наклонной плоскостью и шайбой Найдите внешний радиус трубы R.

Какие законы Вы использовали для описания движения тела? Обоснуйте их применимость к данному случаю.

Задания Д29 C2 № 2952

Небольшая шайба после удара скользит вверх по наклонной плоскости из точки А (см. рис.).

Гоночный автомобиль едет по треку, имеющему на повороте радиусом R = 50 м угол наклона полотна дороги к горизонту α = 30° внутрь поворота. С какой максимальной скоростью V может двигаться автомобиль, чтобы не заскользить и не вылететь с трека? Коэффициент трения колёс автомобиля о дорогу μ = 0,8. Ответ выразите в км/ч.

Какие законы Вы используете для описания движения автомобиля? Обоснуйте их применение к данному случаю.

Источник: Тренировочная работа по физике 18.09.2018, вариант ФИ10101

Задания Д29 C2 № 3070

Наклонная плоскость пересекается с горизонтальной плоскостью по прямой AB. Угол между плоскостями Маленькая шайба начинает движение вверх по наклонной плоскости из точки A с начальной скоростью под углом к прямой AB. В ходе движения шайба съезжает на прямую AB в точке B. Пренебрегая трением между шайбой и наклонной плоскостью, найдите расстояние AB.

Брусок скользит по наклонной плоскости вниз без трения. Что происходит при этом с его скоростью, потенциальной энергией, силой реакции наклонной плоскости?

Для каждой величины определите соответствующий характер изменения:

1)  увеличилась;

2)  уменьшилась;

3)  не изменилась.

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Скорость бруска

Потенциальная энергия

бруска

Сила реакции наклонной

плоскости

Небольшой брусок соскальзывает без начальной скорости с наклонной плоскости длиной L. Наклонная плоскость составляет с горизонтом угол α. В процессе движения на брусок со стороны плоскости действует сила нормальной реакции, модуль которой равен N, а модуль силы трения скольжения при этом равен F. Установите соответствие между физическими величинами, характеризующими движение бруска, и формулами, выражающими эти величины в рассматриваемой задаче. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА

А)  кинетическая энергия бруска в конце движения по наклонной плоскости

Б)  время движения бруска до основания наклонной плоскости

Ответ:

Задания Д29 C2 № 2947

Брусок массой соскальзывает по наклонной плоскости с высоты h и, двигаясь по горизонтальной поверхности, сталкивается с неподвижным бруском массой В результате абсолютно неупругого соударения общая кинетическая энергия брусков становится равной 2,5 Дж. Определите высоту наклонной плоскости h. Трением при движении пренебречь. Считать, что наклонная плоскость плавно переходит в горизонтальную.

Задания Д29 C2 № 2948

Брусок массой соскальзывает по наклонной плоскости с высоты h=0,8м и, двигаясь по горизонтальной поверхности, сталкивается с неподвижным бруском массой Считая столкновение абсолютно неупругим, определите общую кинетическую энергию брусков после столкновения. Трением при движении пренебречь. Считать, что наклонная плоскость плавно переходит в горизонтальную.

Задания Д29 C2 № 7160

Брусок массой m₁  =  500 г соскальзывает по наклонной плоскости с некоторой высоты h и, двигаясь по горизонтальной поверхности, сталкивается с неподвижным бруском массой m₂  =  300 г. Считая столкновение абсолютно неупругим, определите высоту h, если общая кинетическая энергия брусков после столкновения равна 2,5 Дж. Трением при движении пренебречь. Считать, что наклонная плоскость плавно переходит в горизонтальную.

Какие законы Вы используете для описания неупругого столкновения брусков? Обоснуйте их применение к данному случаю.

Небольшую шайбу массой 100 г, покоящуюся у основания наклонной плоскости, толкают вдоль неё вверх. В результате шайба поднимается по наклонной плоскости на некоторую высоту. На рисунке показан график зависимости максимальной высоты подъёма h шайбы от начальной кинетической энергии E, которую сообщили шайбе при её толкании. Угол наклона плоскости к горизонту равен 45°.

Из приведённого ниже списка выберите все правильные утверждения.

1)  Если сообщить шайбе начальную скорость 6 м/с, то шайба поднимется по наклонной плоскости на высоту более 2 м.

2)  Для того, чтобы шайба поднялась по наклонной плоскости на высоту 3 м, надо сообщить шайбе начальную кинетическую энергию 4,5 Дж.

3)  Наклонная плоскость гладкая.

4)  Коэффициент трения шайбы о наклонную плоскость равен 0,5.

5)  После подъёма по наклонной плоскости на максимальную высоту шайба остановится.

Из приведённого ниже списка выберите все правильные утверждения.

1)  Для того чтобы шайба поднялась по наклонной плоскости на высоту 1 м, надо сообщить шайбе начальную кинетическую энергию 1,5 Дж.

2)  Если сообщить шайбе начальную скорость 6 м/с, то шайба поднимется по наклонной плоскости на высоту более 1,5 м.

3)  Коэффициент трения шайбы о наклонную плоскость равен 0,5.

4)  Наклонная плоскость гладкая.

5)  После подъёма по наклонной плоскости на максимальную высоту шайба остановится.

Источник: ЕГЭ по физике 06.06.2022. Основная волна. Разные задачи

Всего: 135 1–20 | 21–40 | 41–60 | 61–80 …

Источник

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 165 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Из приведённого ниже списка выберите все правильные утверждения.

3)  Наклонная плоскость гладкая.

4)  Коэффициент трения шайбы о наклонную плоскость равен 0,5.

5)  После подъёма по наклонной плоскости на максимальную высоту шайба остановится.

Из приведённого ниже списка выберите все правильные утверждения.

3)  Коэффициент трения шайбы о наклонную плоскость равен 0,5.

4)  Наклонная плоскость гладкая.

5)  После подъёма по наклонной плоскости на максимальную высоту шайба остановится.

Задания Д2 B2 № 3626

Брусок, находящийся на шероховатой наклонной плоскости, остается в покое, пока угол наклона плоскости не превышает 30°. Из этого следует, что

1)  коэффициент трения между бруском и плоскостью больше

2)  коэффициент трения между бруском и плоскостью меньше

3)  коэффициент трения между бруском и плоскостью равен

4)  коэффициент трения между бруском и плоскостью зависит от угла наклона плоскости

Тело съезжает вниз по гладкой наклонной плоскости с начальной высоты Н до уровня пола. Затем проводят опыт с другой наклонной плоскостью с большим углом наклона к горизонту; при этом начальную высоту H, с которой съезжает тело, оставляют прежней. Как в результате этого изменятся следующие физические величины: время соскальзывания тела до уровня пола, модуль скорости тела вблизи пола, модуль силы нормальной реакции наклонной плоскости?

Для каждой величины определите соответствующий характер изменения: увеличится; уменьшится; не изменится.

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А)  Время соскальзывания тела до уровня пола

Б)  Модуль скорости тела вблизи пола

В)  Модуль силы нормальной реакции наклонной плоскости

ИХ ИЗМЕНЕНИЕ

1)  увеличится

2)  уменьшится

3)  не изменится

Тело съезжает вниз по гладкой наклонной плоскости с начальной высоты Н до уровня пола. Затем проводят опыт с другой наклонной плоскостью с меньшим углом наклона к горизонту; при этом начальную высоту H, с которой съезжает тело, оставляют прежней. Как в результате этого изменятся следующие физические величины: время соскальзывания тела до уровня пола, модуль скорости тела вблизи пола, модуль силы нормальной реакции наклонной плоскости?

Для каждой величины определите соответствующий характер изменения:

1)  увеличится;

2)  уменьшится;

3)  не изменится.

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А)  Время соскальзывания тела до уровня пола

Б)  Модуль скорости тела вблизи пола

В)  Модуль силы нормальной реакции наклонной плоскости

ИХ ИЗМЕНЕНИЕ

1)  увеличится

2)  уменьшится

3)  не изменится

Задания Д29 C2 № 2953

Маленький шарик падает сверху на наклонную плоскость и упруго отражается от неё. Угол наклона плоскости к горизонту равен 30°. На какое расстояние по горизонтали перемещается шарик между первым и вторым ударами о плоскость? Скорость шарика непосредственно перед первым ударом направлена вертикально вниз и равна 1 м/с.

Деревянный брусок толкнули вверх по гладкой наклонной плоскости, и он стал скользить без трения. Что происходит при этом с его скоростью, потенциальной энергией, силой реакции наклонной плоскости?

К каждому элементу первого столбца подберите соответствующий элемент из второго и внесите в строку ответов выбранные цифры под соответствующими буквами.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А)  Скорость

Б)  Потенциальная энергия

В)  Сила реакции наклонной плоскости

ИЗМЕНЕНИЕ ВЕЛИЧИНЫ

1)  Увеличивается

2)  Уменьшается

3)  Не изменяется

Для определения КПД наклонной плоскости использовано оборудование, изображенное на рисунке. Ученик с помощью динамометра поднимает брусок с двумя грузами равномерно вдоль наклонной плоскости.

Данные эксперимента ученик занес в таблицу. Чему равен КПД наклонной плоскости? Ответ выразите в процентах и округлите до целого числа.

Показания динамометра при подъеме груза, Н	1,5
Длина наклонной плоскости, м	1,0
Масса бруска с двумя грузами, кг	0,22
Высота наклонной плоскости, м	0,15

Небольшое тело кладут на наклонную плоскость, угол при основании которой можно изменять. Если угол при основании наклонной плоскости равен 20°, то тело покоится и на него действует такая же по модулю сила трения, как и в случае, когда угол при основании наклонной плоскости равен 47°. Чему равен коэффициент трения между наклонной плоскостью и телом? Ответ округлите до десятых долей.

Небольшое тело кладут на наклонную плоскость, угол при основании которой можно изменять. Если угол при основании наклонной плоскости равен 30°, то тело покоится и на него действует такая же по модулю сила трения, как и в случае, когда угол при основании наклонной плоскости равен 45°. Чему равен коэффициент трения между наклонной плоскостью и телом? Ответ округлите до десятых долей.

На шероховатой наклонной плоскости покоится деревянный брусок. Угол наклона плоскости увеличили, но брусок относительно плоскости остался в покое. Как изменились при этом сила нормального давления бруска на плоскость и коэффициент трения бруска о плоскость?

Для каждой величины определите соответствующий характер изменения:

1)  увеличилась

2)  уменьшилась

3)  не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Сила нормального

давления бруска

на плоскость

Коэффициент трения

бруска о плоскость

Источник: ЕГЭ по физике 2020. Досрочная волна. Вариант 1

Источник: ЕГЭ по физике 06.06.2022. Основная волна. Разные задачи

Шайба лежит на наклонной плоскости, расположенной под углом 30 градусов к горизонту. Масса шайбы 500 грамм, коэффициент трения о поверхность 0,7. Какую минимальную горизонтальную силу, параллельную нижнему ребру наклонной плоскости, нужно приложить, чтобы сдвинуть шайбу с места? Ответ дайте в ньютонах и округлите до десятых долей.

Какие законы Вы используете для описания движения бруска? Обоснуйте их применение к данному случаю.

Источник: ЕГЭ по физике 07.06.2017. Основная волна

Задания Д29 C2 № 3070

Для каждой величины определите соответствующий характер изменения:

1)  увеличилась;

2)  уменьшилась;

3)  не изменилась.

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Скорость бруска

Потенциальная энергия

бруска

Сила реакции наклонной

плоскости

Шайбе массой 100 г, находящейся на наклонной плоскости, сообщили скорость 4 м/с, направленную вверх вдоль наклонной плоскости. Шайба остановилась на расстоянии 1 м от начала движения. Угол наклона плоскости 30°. Чему равна сила трения шайбы о плоскость? Ответ укажите в ньютонах с точностью до одного знака после запятой.

Задания Д14 B25 № 3627

Брусок, находящийся на шероховатой наклонной плоскости, скользит по ней, если угол наклона плоскости больше 30°. Из этого следует, что коэффициент трения равен

При выполнении лабораторной работы по физике ученикам требовалось определить КПД наклонной плоскости при некотором угле её наклона. Для этого им были предоставлены шероховатая прямая доска и брусок. Коэффициент трения между доской и бруском был известен. Какие два предмета из приведённого ниже перечня оборудования необходимо дополнительно использовать для проведения такого исследования?

1)  пружина известной жёсткости

2)  шарик на нити

3)  секундомер

4)  транспортир

5)  штатив с лапкой

В ответ запишите номера выбранных предметов.

На шероховатую наклонную плоскость положили брусок (см. рис.). Коэффициент трения бруска о плоскость равен μ = 0,35, тангенс угла α наклона плоскости к горизонту равен 0,15. В первом случае бруску ударом придали скорость vec v , направленную вдоль плоскости вверх, а во втором  — вниз. Во сколько раз путь, пройденный бруском до остановки на наклонной плоскости во втором случае, будет больше, чем в первом?

Какие законы Вы используете для описания движения бруска? Обоснуйте их применение к данному случаю.

Источник: Тренировочная работа по физике 16.02.2017, вариант ФИ10303

Задания Д29 C2 № 8878

Всего: 165 1–20 | 21–40 | 41–60 | 61–80 …

Источник

Проецирование сил. Движение по наклонной плоскости

Задачи по динамике.

I и II закон Ньютона.

Ввод и направление осей.

Неколлинеарные силы.

Проецирование сил на оси.

Решение систем уравнений.

Самые типовые задачи по динамике

Начнем с I и II законов Ньютона.

Откроем учебник физики и прочтем. I закон Ньютона: существуют такие инерциальные системы отсчета в которых… Закроем такой учебник, я тоже не понимаю. Ладно шучу, понимаю, но объясню проще.

I закон Ньютона: если тело стоит на месте либо движется равномерно (без ускорения), сумма действующих на него сил равна нулю.

Вывод: Если тело движется с постоянной скоростью или стоит на месте векторная сумма сил будет ноль.

II закон Ньютона: если тело движется равноускоренно или равнозамедленно (с ускорением), сумма сил, действующих на него, равна произведению массы на ускорение.

Вывод: Если тело двигается с изменяющейся скоростью, то векторная сумма сил, которые как-то влияют на это тело ( сила тяги, сила трения, сила сопротивления воздуха), равна массе этого тело умножить на ускорение.

При этом одно и то же тело чаще всего движется по-разному (равномерно или с ускорением) в разных осях. Рассмотрим именно такой пример.

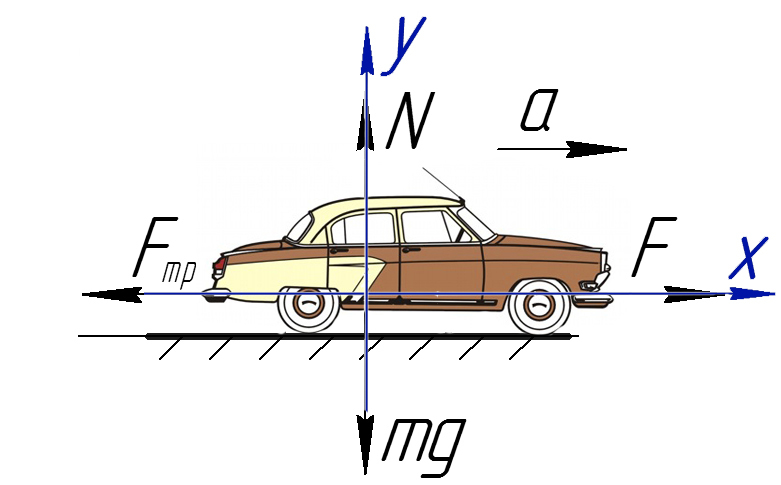
Задача 1. Определите коэффициент трения шин автомобиля массой 600 кг, если сила тяги двигателя 4500 Н вызывает ускорение 5 м/с².

Обязательно в таких задачах делать рисунок, и показывать силы, которые дествуют на машину:

На Ось Х: движение с ускорением

На Ось Y: нет движения (здесь координата, как была ноль так и останется, машина не поднимает в горы или спускается вниз)

Те силы, направление которых совпадает с направлением осей, будут с плюсом, в противоположном случае — с минусом.

По оси X: сила тяги направлена вправо, так же как и ось X, ускорение так же направлено вправо.

Fтр = μN, где N — сила реакции опоры. На оси Y: N = mg, тогда в данной задаче Fтр = μmg.

Получаем, что:

Коэффициент трения — безразмерная величина. Следовательно, единиц измерения нет.

Ответ: 0,25

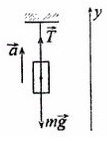
Задача 2. Груз массой 5кг, привязанный к невесомой нерастяжимой нити, поднимают вверх с ускорением 3м/с². Определите силу натяжения нити.

Сделаем рисунок, покажем силы, которые дествуют на груз

T — сила натяжения нити

На ось X: нет сил

Разберемся с направлением сил на ось Y:

Выразим T (силу натяжения) и подставим числительные значения:

Ответ: 65 Н

Самое главное не запутаться с направлением сил (по оси или против), все остальное сделает калькулятор или всеми любимый столбик.

Далеко не всегда все силы, действующие на тело, направлены вдоль осей.

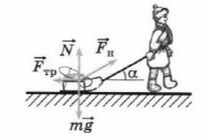
Простой пример: мальчик тянет санки

Если мы так же построим оси X и Y, то сила натяжения (тяги) не будет лежать ни на одной из осей.

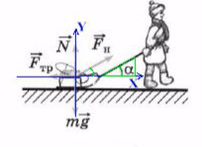
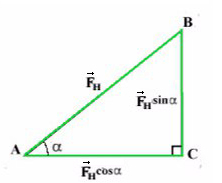
Чтобы спроецировать силу тяги на оси, вспомним прямоугольный треугольник.

Отношение противолежащего катета к гипотенузе — это синус.

Отношение прилежащего катета к гипотенузе — это косинус.

Сила тяги на ось Y — отрезок (вектор) BC.

Сила тяги на ось X — отрезок (вектор) AC.

Если это непонятно, посмотрите задачу №4.

Чем длинее будет верека и, соответсвенно, меньше угол α, тем проще будет тянуть санки. Идеальный вариант, когда веревка параллельна земле, ведь сила, которая действуют на ось X— это Fнcosα. При каком угле косинус максимален? Чем больше будет этот катет, тем сильнее горизонтальная сила.

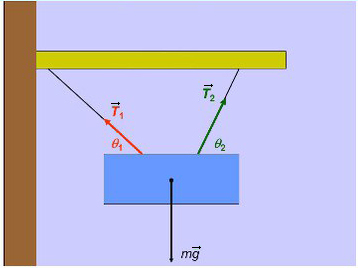
Задача 3. Брусок подвешен на двух нитях. Сила натяжения первой составляет 34 Н, второй — 21Н, θ1 = 45°, θ2 = 60°. Найдите массу бруска.

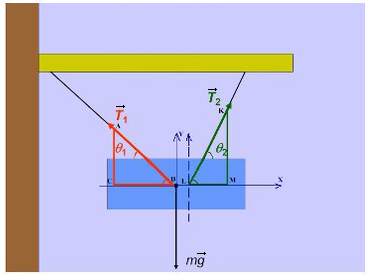
Введем оси и спроецируем силы:

Получаем два прямоугольных треугольника. Гипотенузы AB и KL — силы натяжения. LM и BC — проекции на ось X, AC и KM — на ось Y.

Ответ: 4,22 кг

Задача 4. Брусок массой 5 кг (масса в этой задаче не нужна, но, чтобы в уравнениях все было известно, возьмем конкретное значение) соскальзывает с плоскости, которая наклонена под углом 45°, с коэффициентом трения μ = 0,1. Найдите ускорение движения бруска?

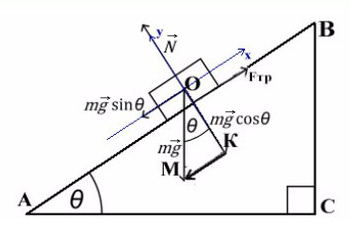
Когда же есть наклонная плоскость, оси (X и Y) лучше всего направить по направлению движения тела. Некоторые силы в данном случае ( здесь это mg) не будут лежать ни на одной из осей. Эту силу нужно спроецировать, чтобы она имела такое же направление, как и взятые оси.
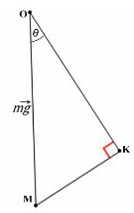
Всегда ΔABC подобен ΔKOM в таких задачах (по прямому углу и углу наклона плоскости).

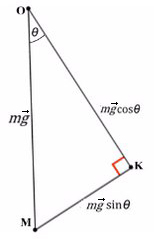
Рассмотрим поподробнее ΔKOM:

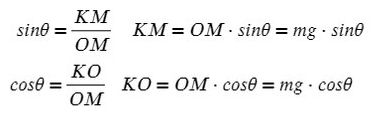
Получим, что KO лежит на оси Y, и проекция mg на ось Y будет с косинусом. А вектор MK коллинеарен (параллелен) оси X, проекция mg на ось X будет с синусом, и вектор МК направлен против оси X (то есть будет с минусом).

Не забываем, что, если направления оси и силы не совпадают, ее нужно взять с минусом!

Из оси Y выражаем N и подставляем в уравнение оси X, находим ускорение:

Ответ: 6,36 м/с²

Как видно, массу в числителе можно вынести за скобки и сократить со знаменаталем. Тогда знать ее не обязательно, получить ответ реально и без нее.
Да-да, в идеальных условиях (когда нет силы сопротивления воздуха и т.п.), что перо, что гиря скатятся (упадут) за одно и тоже время.

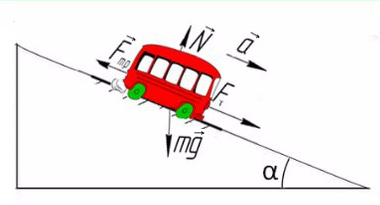
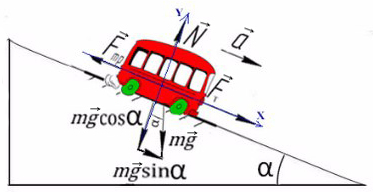
Задача 5. Автобус съезжает с горки под уклоном 60° с ускорением 8 м/с² и с силой тяги 8 кН. Коэффициент трения шин об асфальт равен 0,4. Найдите массу автобуса.

Сделаем рисунок с силами:

Введем оси X и Y. Спроецируем mg на оси:

Запишем второй закон Ньютона на X и Y:

Ответ: 6000 кг

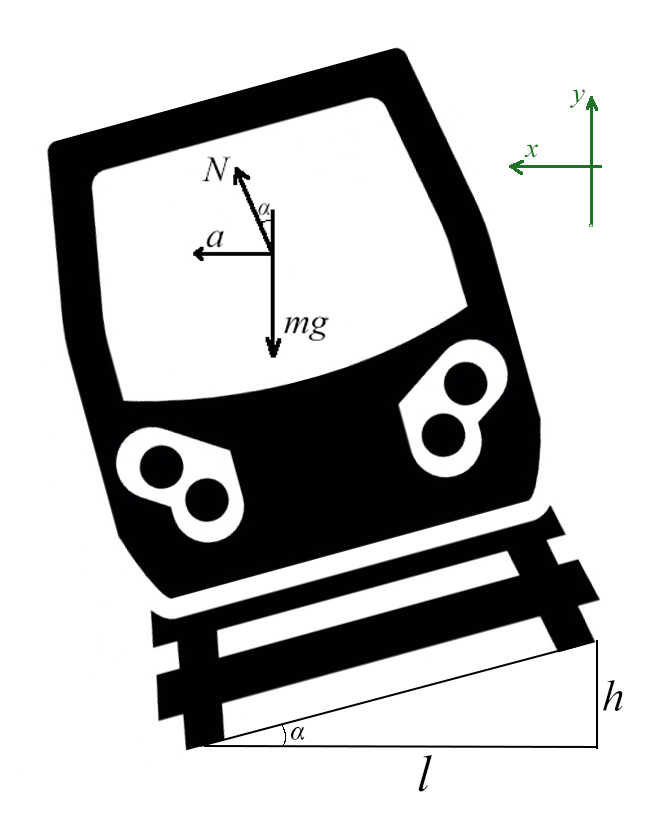
Задача 6. Поезд движется по закруглению радиуса 800 м со скоростью 72 км/ч. Определить, на сколько внешний рельс должен быть выше внутреннего. Расстояние между рельсами 1,5 м.

Самое сложное — понять, какие силы куда действуют, и как угол влияет на них.

Вспомни, когда едешь по кругу на машине или в автобусе, куда тебя выталкивает? Для этого и нужен наклон, чтобы поезд не упал набок!

Угол α задает отношение разницы высоты рельсов к расстоянию между ними (если бы рельсы находились горизонтально)

Запишем какие силы действуют на оси:

Ускорение в данной задачи центростремительное!

Поделим одно уравнение на другое:

Тангенс — это отношение противолежащего катета к прилежащему:

Ответ: 7,5 см

Как мы выяснили, решение подобных задач сводится к расстановке направлений сил, проецированию их на оси и к решению систем уравнений, почти сущий пустяк.

В качестве закрепления материала решите несколько похожих задач с подсказками и ответами.

Будь в курсе новых статеек, видео и легкого технического юмора.

Источник

Эксперт ЕГЭ Н. Л. Точильникова
Задача 29 на ЕГЭ по физике – это расчетная задача на механику. До 2014 года включительно она фигурировала под номером «С2».

Это может быть кинематика, динамика, динамика движения по окружности, задача на законы сохранения в механике, статику или гидростатику.

Например, задача на движение тела, брошенного под углом к горизонту:

1. Маленький шарик падает сверху на наклонную плоскость и упруго отражается от нее. Угол наклона плоскости к горизонту равен $30^{circ}$ . На какое расстояние по горизонтали перемещается шарик между первым и вторым ударами о плоскость? Скорость шарика в момент первого удара направлена вертикально вниз и равна м/с.

Запишем «дано»:
V_0=1 м/с
$alpha = 30^{circ}$

Найти: .

Решение:

В задачах части «С» необходимо описывать все параметры, которых нет в дано, иначе оценку снижают на один балл.
Поэтому пишем:
– расстояние по горизонтали между первым и вторым ударами о плоскость.
Нарисуем наклонную плоскость и начальную скорость шарика $overrightarrow{mkern -5mu V_0}$ . Как известно из геометрии, углы с перпендикулярными сторонами равны. Начальная скорость шарика перпендикулярна основанию наклонной плоскости. Восстановим перпендикуляр к наклонной плоскости в точке падения на нее шарика. Тогда угол между этим перпендикуляром и вектором начальной скорости равен углу наклона плоскости к горизонту (углы с перпендикулярными сторонами, зеленые пунктирные линии на рисунке). Угол падения шарика (с перпендикуляром) равен углу отражения $alpha = 30^{circ}$ . Тогда угол между начальной скоростью отскочившего шарика и наклонной плоскостью равен $beta = 90^{circ} - alpha = 90^{circ} - 30^{circ} = 60^{circ} = 2 alpha$ . Модуль скорости не меняется, так как удар упругий.

Итак, убираем построения, которые нам больше не нужны:

Тело будет двигаться по параболе и упадет на расстоянии от точки бросания вдоль наклонной плоскости. Это не то расстояние, которое нам надо найти, мы ищем — расстояние по горизонтали. Но, если мы знаем , найти очень легко: .

Теперь нужно выбрать систему отсчета. С началом отсчета все ясно, очевидно, мы берем его в точке падения шарика. А вот с направлениями осей все не так просто.

Можно выбрать оси традиционным способом: «» горизонтально и «» вертикально:

Но при таком выборе осей трудно определить точку падения. Поэтому в подобных задачах оси обычно выбирают иначе: «» вдоль наклонной плоскости, а «» перпендикулярно наклонной плоскости:

При таком выборе осей точка падения определяется элементарно: там координата «» обращается в ноль. Зато движение становится равноускоренным по двум осям, поскольку ускорение проектируется на обе оси:

— противолежащий катет;
— прилежащий катет.

Начальная скорость $overrightarrow{mkern -3mu V_0mkern 3mu}$ также проектируется на обе оси:

$V_{0x} = V_0 cdot cos 2 alpha$ – прилежащий катет;
$V_{0y} = V_0 cdot sin 2 alpha$ – противолежащий катет

Зависимости координат от времени при равноускоренном движении выражаются формулами:

$x= x_0 + V_{0x}t + genfrac{}{}{}{0}{alpha_x t^2}{2}$

$y= y_0 + V_{0y}t + genfrac{}{}{}{0}{alpha_y t^2}{2}$

Подставляя значения проекций скорости и ускорения, получаем:

$left{begin{matrix}x=V_0 cdot cos 2 alpha cdot t +g cdot sin alpha cdot genfrac{}{}{}{0}{t^2}{2}=l\y = V_0 cdot sin 2 alpha cdot t - g cdot cos alpha cdot genfrac{}{}{}{0}{t^2}{2}=0end{matrix}right.$

Начальные координаты: ;

Конечная координата y также равна нулю, так как тело падает на наклонную плоскость.

Из второго уравнения получаем:

$tleft ( V_0 sin 2 alpha - g cos alpha genfrac{}{}{}{0}{t}{2}right ) = 0$

Это уравнение равносильно совокупности:

$left[ begin{matrix} t=0 phantom{sin 2 alpha - g cos alpha genfrac{}{}{}{0}{t}{2}}\V_0sin 2 alpha - g cos alpha genfrac{}{}{}{0}{t}{2}=0 end{matrix}right.$

Из второго уравнения находим :

$V_0 sin 2 alpha= g cos alpha genfrac{}{}{}{0}{t}{2}$

$t = genfrac{}{}{}{0}{2V_0 sin 2 alpha}{g cos alpha}$

Подставляем в уравнение для :

$l = V_0 cos 2 alphagenfrac{}{}{}{0}{2V_0 sin 2 alpha}{g cos alpha} + g sin alphagenfrac{}{}{}{0}{left (genfrac{}{}{}{0}{2V_0 sin 2 alpha}{g cos alpha} right ) ^2}{2},$

Откуда:

$l=2{V_0}^2 cos 2 alpha genfrac{}{}{}{0}{sin 2 alpha}{g cos alpha} + g sin alpha genfrac{}{}{}{0}{4{V_0}^2(sin 2 alpha)^2}{2 g^2 (cos alpha)^2},$

$l= genfrac{}{}{}{0}{2{V_0}^2 sin 2 alpha ( cos 2 alpha cos alpha+ sin alphasin 2 alpha)}{g (cos alpha)^2},$

Тогда:

$L=l cos alpha= genfrac{}{}{}{0}{2{V_0}^2 sin 2 alpha ( cos 2 alpha cos alpha+ sin alphasin 2 alpha)}{g (cos alpha)^2}cos alpha=$

$= genfrac{}{}{}{0}{2{V_0}^2 sin 2 alpha ( cos 2 alpha cos alpha+ sin alphasin 2 alpha)}{g cos alpha}$

Но $sin 2 alpha = sin 60^{circ} = cos 30^{circ} = cos alpha$ и $cos 2 alpha = cos 60^{circ} = sin 30^{circ} = sin alpha$

То есть:

$L= genfrac{}{}{}{0}{2{V_0}^2 sin alpha cos alpha }{g}= genfrac{}{}{}{0}{2{V_0}^2 sin 2 alpha}{g}$

$L =genfrac{}{}{}{0}{2{V_0}^2 sin 2 alpha}{g}$

$L = 2 cdot 1^2genfrac{}{}{}{0}{sin 60^{circ}}{10}= 2 cdot genfrac{}{}{}{0}{sqrt{3}}{2}cdot genfrac{}{}{}{0}{1}{10}=0,173$ м

Задача 30 на ЕГЭ по физике

Задача 30 на ЕГЭ по физике (раньше называлась С3) – это задача на газовые законы или термодинамику.

Например:

2. Вертикально расположенный замкнутый цилиндрический сосуд высотой см разделен подвижным поршнем весом 110 H на две части, в каждой из которых содержится одинаковое количество идеального газа при температуре 361 K . Сколько молей газа находится в каждой части цилиндра, если поршень расположен на высоте см от дна сосуда? Толщиной поршня пренебречь.

Дано:

H=50 см = 0,5 м
P=110 H
T=361 K
h=20 см = 0,2 м

Найти: (число молей в каждой части цилиндра.)

p_1 – давление в верхней части цилиндра;

p_2 – давление в нижней части цилиндра;

– площадь сечения поршня.

p_1S – сила давления на поршень газа в верхней части цилиндра;

p_2S — сила давления на поршень газа нижней части цилиндра.

Так как поршень неподвижен, сумма всех действующих на него сил равна нулю.

То есть:

Запишем уравнение Менделеева-Клапейрона для верхней и нижней частей цилиндра:

Где – объем верхней части цилиндра;

V_2=hS — объем нижней части цилиндра.

Выражаем p_1 и p_2 :

$p_1 = genfrac{}{}{}{0}{nu RT}{V_1};$

$p_2 = genfrac{}{}{}{0}{nu RT}{V_2}$

И подставляем в уравнение для сил:

$genfrac{}{}{}{0}{nu RT}{V_2}S=genfrac{}{}{}{0}{nu RT}{V_1}S+P$

Подставляем выражения для объемов:

$genfrac{}{}{}{0}{nu RT}{hS}S=genfrac{}{}{}{0}{nu RT}{(H-h)S}S+P$

Сокращаем :

$genfrac{}{}{}{0}{nu RT}{h}=genfrac{}{}{}{0}{nu RT}{H-h}+P$

$genfrac{}{}{}{0}{nu RT}{h}-genfrac{}{}{}{0}{nu RT}{H-h}=P$

$nu RT left ( genfrac{}{}{}{0}{1}{h}-genfrac{}{}{}{0}{1}{H-h} right ) =P$

$nu RT left ( genfrac{}{}{}{0}{H-h-h}{h(H-h)} right ) =P$

Откуда:

$nu = genfrac{}{}{}{0}{Ph(H-h)}{RT(H-2h)}$

$nu = genfrac{}{}{}{0}{110 cdot 0,5 cdot (0,5-0,2)}{8,31 cdot 361(0,5-2 cdot 0,2)} = 0,022$ моль

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задачи 29 и 30 на ЕГЭ по физике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Канал видеоролика: Физика с АЛ

Смотреть видео:

#физика #егэфизика #огэфизика #термодинамика #репетиторпофизике #фтф #мифи #мфти #физтех

Свежая информация для ЕГЭ и ОГЭ по Физике (листай):

С этим видео ученики смотрят следующие ролики:

Движение по наклонной плоскости двух тел

Физик Воронежский

Движение по наклонной плоскости двух тел

Физик Воронежский

1.04. Движение по наклонной плоскости

Физика с АЛ

Выпуск 177. Решение задач. Движение заряженной частицы в однородных электрическом и магнитном полях

Александр Давыдов

Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):

11.01.2022

Источник

Подробности: Обновлено 30.05.2018 23:11; Просмотров: 1098

Задачи по физике — это просто!

Не забываем
Решать задачи надо всегда в системе СИ!

А теперь к задачам!

Типовые задачи из курса школьной физики по динамике на движение тела по наклонной плоскости под действием нескольких сил.

Задача 1

Сани спускаются с горы высотой 20 метров и длиной 100 метров с ускорением 1 м/с. Определить коэффициент трения.

Задача 2

C каким ускорением будет скользить вниз ящик по наклонной плоскости, если коэффициент трения равен 0,9, а угол наклонной плоскости относительно горизонтали составляет 60^o?

Задача 3

Какую силу надо приложить к тележке массой 200 кг, чтобы она двигалась вверх по наклонной плоскости с ускорением 0,5 м/с², если коэффициент трения равен 0,2, а наклонная плоскость составляет с горизонталью угол 30^o?

Источник

Физика. Рымкевич А.П. Движение по наклонной плоскости.

В данной главе представлены задачи по физике из раздела Движение по наклонной плоскости задачника Рымкевича А.П.

Источник