Нелинейные задачи строительной механики вопросы к экзамену

ММ-7. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ. РЕШЕНИЕ
НЕЛИНЕЙНЫХ ЗАДАЧ СТРОИТЕЛЬНОЙ МЕХАНИКИ

ММ-7. Ключевые
слова и понятия

7.1. Ограниченный
носитель.

7.2. Финитные
функции.

7.3. Конечный
элемент.

7.4. Узел конечного
элемента.

7.5. Узел расчётной
схемы системы.

7.6. Сетка конечных
элементов.

7.7. Сетка узлов
системы.

7.8. Конечноэлементная
расчётная схема системы.

7.9. Координатные
функции МКЭ (функции формы, функции
распределения).

7.10. Матрица
жёсткости конечного элемента..

7.11. Матрица
жёсткости системы.

7.12. Ансамблирование

7.13. Метод переменных
параметров упругости.

7.14. Метод фиктивных
нагрузок и вынужденных деформаций.

7.15. Шагово-итерационные
методы.

Для изучения
данной темы Вам необходимо восстановить
в памяти:

— из курса прикладной
математики — понятия и операции: линейной
алгебры, векторной алгебры; понятия:
интеграла, кратного интеграла, минимума
функции нескольких переменных;

— из курса
сопротивления материалов – понятия:
напряжений, деформаций, обобщённых
усилий, работы обобщёных внутренних
сил, работы нагрузки; деформативные
свойства материалов;

—

из
настоящего спецкурса – понятия:
функционала, координатной функции,
координатной системы, линейной
аппроксимации, функционала энергии,
невязки приближённого решения,
ортогональности функций, последовательности
решений, идея метода Ритца, идея метода
Бубнова-Галёркина, идеи методов
линеаризации. .

6.2. Содержание темы

6 .2.1. Структурно – логическая схема содержания темы

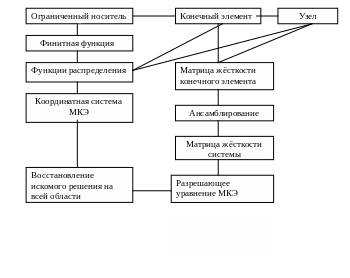
6 .2.2. Тематическое содержание

Методы, изложенные в лекции ММ-6, которые
мы будем называть традиционными прямыми
методами, в своё время сыграли значительную
роль в численном решении ряда важных
практических задач. Однако, при
использовании этих методов расчётчики
столкнулись с рядом трудноразрешимых
проблем. Перечислим некоторые из них.

1. Подбор
координатных систем для неканонических
областей. Расчётная
схема конструкции может представлять
собой область одно-, двух- и трёхмерного
пространства. Так, расчётная схеме
стержня — отрезок прямой линии — является
областью прямой, то-есть, одномерного
пространства; расчётная схема изгибаемой
плиты или нагруженной в своей плоскости
пластинки является областью плоскости,
то-есть, двумерного пространства; равно,
как и областью криволинейной поверхности
(то-есть, также двумерного пространства)
является оболочка. Расчётная схема
массива (например, столбчатого фундамента
или основания) — это область трёхмерного
пространства. Область двух- или
трёхмерного пространства будем относить
к какой-либо фиксированной системе
координат и называть канонической, если
её граница состоит из участков, каждый
из которых проходит:

— для двумерной области — по
координатной линии

-для трёхмерной области — по
координатной поверхности

Для прямоугольной декартовой
системы координат на плоскости это
будет прямоугольник, в пространстве —
паралеллепипед; для полярной системы
координат — часть сектора, выделенная
сторонами

для
цилиндрической системы координат

для сферической системы координат

На канонической области легче проверять
соответствие систем функций требованиям,
предъявляемым к координатным системам,
в особенности, выполнение условий на
границе области. На неканонической
области такая проверка становится
проблематичной. Особенно трудно выполнить
такую проверку, если количество гладких
участков границы не такое, как у
канонических областей, то-есть, не равно
четырём на плоскости или криволинейной
поверхности и шести — у пространственной
области.

2. Скачки или резкие изменения
переменных коэффициентов дифференциального
уравнения задачи. При
расчёте конструкций это обстоятельство
возникает, например, в случаях скаков
или резких изменений свойств материалов
или геометрии конструкций. При этом
следует ожидать скачков или резкого
изменения производных функции, описывающей
перемещения, а придать координатным
функциям способность отражать наличие
таких скачков или резких изменений
невозможно, так как эти функции должны
иметь несколько непрерывных производных
порядка не менее заданного.

3. Скачки или резкие изменения
правой части неоднородного дифференциального
уравнения задачи. Это
обстоятельство возникает, например,
когда интенсивность распределённой
нагрузки описывается функцией, имеющей
такой характер, вплоть до такой абстракции,
как сосредоточенная сила или сосредоточенный
момент. Сосредоточенной силе соответствует
случай бесконечно большой интенсивности
нагрузки на бесконечно малой области
её локализации при конечном значении
равнодействующей. Сосредоточенный
момент моделируется парой состредоточенных
сил с бесконечно малым плечом (величина
момента приэтом конечна). . Для строгого
описания таких нагрузок требуется
аппарат обобщённых функций, но это
выходит за рамки нашего спецкурса. У
координатных функций такие особенности
должны иметь их производные хотя бы
того же порядка, что и порядок уравнения
задачи, то0есть, мы опять сталкиваемся
с проблемой несоответствия ожидаемых
свойств решения и свойств координатных
функций.

3. Сложность задачи
конструирования координатной системы
в общем случае.Для
решения этой задачи в общем случае
требуется достаточно высокая квалификация,
она для большого количества классов
задач не поддаётся стандартизации и
требует эвристического подхода.

4. Трудность учёта различных
краевых условий. При
наличии таких краевых условий, как
податливые опоры, задании на одном
участке граници нескольких типов опор,
применении локальных опор, изменении
нагрузок на край в пределах участка
границы и в ряде других случаев
конструирование функции

(см. лекцию ММ-6) практически невозможно.

5
.
Сложность конструирования кординатной
системы в случае сопряжения областей,
принадлежащих разным пространствам.
На практике часто
сопрягаются такие конструкции, расчётные
схемы которых приналежат разным
пространствам. В качестве примеров
можно привести сопряжение колонн и
ригелей, рачётные схемы которых
принадлежат разным прямым, сопряжение
монолитных железобетонных стен и
перекрытий, расчётные схемы которых
принадлежат разным плоскостям; сопряжение
стенки и купола защитной оболочки
атомного реактора, расчётные схемы
которых принадлежат разным криволинейным
поверхностям, сопряжение элементов,
расчётные схемы которых принадлежат
областям разной размерности (колонны
с плитой, колонны с массивом) и т.д.

Эти проблемы любой степени
сложности достаточно легко преодолеваются
в методе конечных
элементов (МКЭ) – едва
ли не самом мощном и универсальном
численном методе для решения в первую
очередь краевых задач для дифференциальных
уравнений (обыкновенных и в частных
производных) и систем таких уравнений.

Основная идея метода конечных
элементов. Метод конечных
элементов основан на использовании
нового принципа конструирования
координатных систем. В традиционных
вариантах прямых методов координатные
функции задавались на всей области
определения оператора задачи, границы
которой задавались краевыми условиями
и были на этой области достаточно
гладкими. Это как раз и порождало
практически все перечисленные выше
противоречия.

В отличие от этого в МКЭ
используются принципиально новые
координатные функции. Их основной
отличительный признак состоит в том,
что они удовлетворяют заданным условиям
не на всей области определения оператора
задачи, а на её достаточно малой (но всё
же конечной) подобласти, за пределами
которой они тождественно равны нулю.
Иными словами, можно сказать, что они
заданы на этой малой подобласти.

Таким образом, носителем каждой
координатной функции метода конечных
элементов является замыкание подобласти,
на которой она определена, другими
словами, объединение подобласти и её
границы.

7.2. Финитные
функции (Адрес файла Блок
4_____________
)

Финитными функциями называются
кусочно-непрерывные функции с ограниченным
носителем.

Вернитесь к тексту

Таким образом, в качестве координатных
функций в МКЭ выбираются финитные
функции.

Воосоздание искомой функции на её
носителе в МКЭ выполняется по

а) дифференциальному уравнению (системе
дифференциальных уравнений) или
вариационному принципу, как в традиционных
прямых методах;

б) краевым условиям в отдельных точках
границы носителя, а не на всей границе,
как это было в традиционных прямых
методах.

Точки границы носителя, в
которых задаются краевые условия,
называются узлами. Как правило, в узлах
задаются главные краевые условия. Их
достаточно для определения искомой
функции (в случае системы уравнений –
искомой вектор-функции).

Примечание. Иногда
рассматриваются случаи расположения
узлов внутри носителя; мы такими случаями
не занимаемся.

Отсюда естественным образом
можно перейти к ключевому в МКЭ понятию
– конечный элемент
(КЭ).

КЭ могут иметь различную
форму, и это позволяет более точно (хоть
в ряде случаев всё равно приближённо)
отразить форму области на расчётной
схеме, а также некоторые априори известные
особенности искомого решения.

Примеры конечных элементов
для расчётных схем конструкций различной
размерности приведены на рис. 7.1. Здесь
здесь на рис. 7.1а показан КЭ одномерной
области (стержня), на рис. 7.1б – прямоугольный
КЭ двумерной области (изгибаемой плиты
или плосконапряжённой пластины), на
рис. 7.1в – их же треугольный КЭ, на рис.
7.1г, д – КЭ трёхмерной области (массива)
в виде паралеллепипеда или тетраэдра.
На этих рисунках 1 – узлы, 2 – границы,
3 – рёбра границ.

В криволинейных системах координат
границы КЭ также удобно принимать
криволинейными.

Граница одномерного КЭ –
всегда точка; она же является узлом.
Граница двумерного КЭ — линия, которая
состоит из гладких, обычно, прямых,
участков; разделяющая их точка называется
узлом. Граница трёхмерного КЭ –
поверхность, которая состоит из гладких,
часто — плоских, участков. Линии,
разделяющие эти участки, называются
ребрами; точка пересечения рёбер
называется узлом. Узел трёхмерного
элемента, таким образом, это, чаще всего,
вершина многогранника (например,
паралеллепипеда, тетраэдра), двумерного
– вершина многоугольника (например,
прямоугольника, треугольника).

Таким образом, конечный
элемент – ограниченный носитель
координатной функции, узел конечного
элемента является узлом носителя
координатной функции.

Можно сказать, что у одномерного
КЭ понятия узла и границы совпадают; у
двумерного КЭ границей является замкнутая
линия, имеющая изломы (скачки касательной),
и эти изломы являются узлами; у трёхмерного
КЭ границей является замкнутая
поверхность, эта поверхность имеет
изломы, называемые рёбрами, а изломы
рёбер называются узлами. Повторим, что
для воссоздания координатной функции
в пределах КЭ необходимо указать
уравнение или вариационный принцип
задачи и значения функции в узлах.

7.4. Узел конечного
элемента (Адрес файла Блок
4________)

Узлом конечного элемента называется:

а) для одномерного элемента – один из
его концов;

б) для двумерного элемента – одна из
точек излома его границы;

в) для трёхмерного элемента – одна из
точек излома рёбер (в узле могут
встречаться более двух участков рёбер,
например, в вершине тетраэдра встречаются
три ребра.

Вернитесь к тексту

Для выполнения расчёта методом конечных
элементов вся область, на которой задана
краевая задача (вся область, занятая
конструкцией) разбивается на отдельные
КЭ таким образом, что

— вся область занята КЭ без разрывов;

— любые два КЭ либо не имеют
общих точек, либо имеют общий участок
границы (включая узлы), который может
выродиться в одну точку (узел); никакие
внутренние точки двух и более КЭ не
могут быть общими (пересечение двух КЭ
либо пусто, либо состоит только (!) из
точек их общего участка границы). Можно
сказать, что конечные элементы либо не
соприкасаются, либо соприкасаются на
их общем участке границы без нахлёста.

Иногда используются конечноэлементные
разбивки с зазорами между элементами,
однако требуется, чтобы: 1) зазоры в узлах
отсутствовали; 2) зазоры между узлами
стремились к нулю при неограниченном
сгущении узлов. В частности, такое
разбиение на КЭ выполняется иногда при
расчёте оболочек, очерченных по
криволинейным поверхностям, с
использованием плоских КЭ.

Часто бывает удобным, чтобы участки
границы двумерной области были направлены
вдоль координатных линий (особенно,
если таких участков четыре), участки
границы трёхмерной области совпадали
с координатными поверхностями, а рёбра
– с координатными линиями.

Обычно наиболее сложным
вопросом является разбивка двумерной
или трёхмерной области задания задачи
в пределах её приопорной зоны, так как
границу области часто невозможно
составить из участков границы КЭ. В
таких случаях приходится приближённо
аппроксимировать границу области
участками границы КЭ, но так, чтобы зазор
между ними стремился к нулю вместе с
размером самого большого КЭ. При этом
внешние узлы КЭ надо располагать на
границе области. Таким образом мы
получаем конечноэлементную аппроксимацию
границы области.

У КЭ не может быть узлов,
которые бы не совмещались с узлами
соседних элементов или узлами
конечноэлементной аппроксимации границы
области. При этом в процессе разбивки
заданной области на КЭ на указанной
области выделяются точки, на которых
совмещаются либо узлы соприкасающихся
КЭ, либо узлы КЭ и границы; эти узлы
называются узлами рассчитываемой
системы (точнее, её расчётной схемы).
Другие правила разбивки сетки узлов
будут изложены после описания МКЭ.

Рис.7.2. Пример разбивки плоской области
на конечные элементы

7.6. Сетка конечных
элементов (Адрес файла Блок
4________)

Сеткой конечных элементов называется
совокупность области и конечных
элементов, расставленных на ней в
соответствии с изложеными правилами.

Возвратитесь к тексту

Если вычертить схему разбивки
области на КЭ, отметить на ней узлы,
занумеровать и те, и другие, а затем
указать на КЭ информацию о свойствах
системы (отражённых в коэффициентах
этого уравнения), на узлах — данные о
взаимодействии с внешней средой
(отражённые в свободном члене
дифференциального уравнения и в краевых
условиях), то мы получим конечноэлементную
расчётную схему системы. Методы
определения этих данных будут сообщены
ниже.

Нумерация КЭ и узлов позволяет организовать
ввод остальной информации в компьютер.

Обычно широко используемые
программы, реализующие МКЭ, ориентируясь
на конкретную область приложений
(прочностные расчёты, расчёты теплопередачи,
расчёты электрических или гидравлических
сетей и т.п.) содержат библитеки
КЭ, позволяющие вычислить
определённым образом организованные
данные о естественных краевых условиях
КЭ при заданных его главных краевых
усовиях для различных типичных часто
встречающихся случаев. При выполнении
конкретного расчёта необходимо выбрать
тип КЭ, проставить его размеры и указать
величины параметров, характеризующих
физические свойства материала. Информация
о главных и естественных краевых условиях
КЭ по определённым правилам приведена
к его узлам – в каждом узле указывается
некоторая функция искомого решения и
его производных, обычно – сама искомая
функция и её производные.

7.8. Конечноэлементная
расчётная схема системы (Адрес файла
Блок
4_____)

Конечноэлементная расчётная
схема системы – это совмещённая схема
сетки узлов и сетки КЭ; на которой
указаны номера КЭ и узлов и приведены
таблицы с указанием

1) координат узлов;

2) информации о свойствах системы (типах
КЭ из библиотеки и величинах параметров,
определяющих свойства материала; их
размеры программа определит по
координатам узлов);

3) данные о взаимодействии с внешней
средой (о свободном члене и краевых
условиях; эти данные привязаны к узлам)

Возвратитесь к тексту

Одна из центральных идей МКЭ
состоит в том, что приближённое решение
должно полностью определяться конечным
количеством параметров, указываемых в
каждом из конечного числа узлов системы.
Таким образом, мы состояние континуальной
системы описываем дискретным множеством
параметров; в этом и состоит дискретизация
задачи в МКЭ.

Количество параметров,
указываемых в узлах, определяется
порядком дифференциального уравнения
и применяемым методом поиска коэффициентов
линейной аппроксимации решения (в нашем
случае – метод Ритца или метод Галёркина)..

Каждому параметру каждого
узла ставится в соответствие одна
координатная функция. Она равна единице
в этом узле и нулю — в остальных узлах
ЕЭ. Благодаря этому

а) линейная аппроксимация
искомой функции включает слагаемое в
виде произведения параметра на значение
координатной функции, то-есть, узловой
параметр является коэффициентом этой
линейной аппроксимации и одновременно
значением аппроксимации в узле;

б) в других узлах параметр
умножается на нулевое значение
координатной функции, то-есть, не влияет
на значение аппроксимации в других
узлах.

Действительно, выделим одно слагаемое
линейной аппроксимации (см. лекцию ММ-6,
формула (6.4))

(7.1)

где

— один из параметров

-го
узла;

— соответствующая
координатная функция одной, двух или
трёх координат

или

,
или

,
причём

при

.

Отсюда легко заметить, что,
если линейная аппроксимация уже найдена,
то узловой параметр данного узла равен
значению аппроксимации в этом узле и
не влияет на значения аппроксимации в
других узлах.

В случае одномерной области
в качестве параметра могут выступать
искомая функция, её обыкновенные
производные и их линейные комбинации,
а в случае двумерных и трёхмерных
областей – функции и её частные
производные, в том числе – смешанные,
а также их линейные комбинации. Наибольший
порядок указанных производных на единицу
меньше порядка дифференциального
уравнения в методе Галёркина или порядка
дифференциального оператора в методе
Ритца (если он сформулирован в энергетически
сопряжённых переменных — момент —
кривизна, нормальная сила — осевое
удлинение и т.п.). В случае применения
интегрирования по частям при использовании
метода Галёркина этот порядок может
быть уменьшен вдвое. При
наличии общего участка границы у двух
смежных КЭ координатная система должна
обеспечить возможность приравнивания
хотя бы главных краевых условий данной
задачи. В задачах строительной механики
обычно это перемещения точек границы
и (при наличии изгибного состояния)
повороты нормали в этой точке вокруг
границы. Таким образом, в условиях
сопряжения КЭ участвуют искомая функция
и (при наличии изгиба) её производные
вдоль нормали к границе. Для того, чтобы
обеспечить возможность приравнивания
производных, взятых по нормали к границе
в сопрягаемых КЭ, на всём их общем участке
границы, приходится использовать в
качестве узловых параметров смешанные
производные. Однако, это требование
иногда нарушается и возникают так
называемые несогласованные координатные
функции.

Ещё одно условие, накладываемое
на координатные функции в МКЭ: при
стремлении размеров КЭ к нулю они должны
обеспечивать возможность соответствующим
подбором узловых параметров получать
любые постоянные (в том числе – нулевые)
значения искомой функции и её производных
(порядка менее порядка дифференциального
оператора) на КЭ и его границе.

Часто наиболее удобными для
использования в качестве координатных
функций являются многочлены. В случае
одномерной области полные многочлены
степени

имеют

независимых параметров — его коэффициентов.
Следовательно, если порядок старшей
производной оператора задачи равен

(и таково же количество параметров), то
необходим полином степени

.

Каждая координатная функция имеет вид
многочлена и его коэффициенты должны
обеспечивать выполнение заданного
набора граничных условий в узлах (когда
один из узловых параметров равен единице,
а осталбные – нулю, а данная координатная
функция равна единице на одном узле и
нлую – на остальных).

Для определения его коэффициентов
в простых случаях удобно использовать
метод неопределённых коэффициентов –
записывается общий вид такого многочлена
и определяются дифференцированием все
его производные, участвующие в
формулировании граничных условий КЭ
(если производные участвуют в формулировании
граничных условий).

Это позволяет записать
граничные условия в узлах КЭ, выраженные
через общий вид многочлена и его
производных, и получить систему

линейных
алгебраических уравнений относительно

неизвестных
коэффициентов полинома. Рещение этой
системы – коэффициенты полинома, который
должен стать координатной функцией,
отвечающей заданному набору краевых
условий.

Следует отметить, что в
различных источниках при изложении МКЭ
координатные функции
называются также функциями
формы или функциями
распределения.

Пример 1. Дано:
одномерная область, порядок дифференциального
уравнения

.
В этом случае число степеней свободы
КЭ

.
Конечный элемент — отрезок прямой длиной

Задавая на каждом конце КЭ по одному
параметру — значению искомой функции
на границе элементов, мы полностью
определим приближённое решение на
носителе. Выберем в качестве координатных
функций многочлены степени

,
то-есть, линейные функции. Первая из них
удовлетворяет условию

вторая
—

.

Общий вид многочлена первой степени

.

Для первой функции:

откуда

и , следовательно,

.

Для второй функции

откуда

и , следовательно,

.

Пример 2.
Дано: одномерная область, порядок
дифференциального уравнения

.
В этом случае число степеней свободы
КЭ

.
Конечный элемент — отрезок прямой длиной

.
Задавая на каждом конце КЭ по два
параметра — значению искомой функции и
её производной на границе элементов,
мы полностью определим приближённое
решение на носителе. Выберем в качестве
координатных функций многочлены степени

,
то-есть, кубические многочлены.

Общий вид кубического
многочлена

,
его производная —

.

Первый из них удовлетворяет
условиям

,

второй –

,

третий –

,

четвёртый –

.

Составляем поочерёдно для каждой из
этих координатных функций систему
уравнений, отражающих граничные условия
на узлах:

,

,

,

;

,

,

,

;

,

,

,

;

,

,

,

.

Вектора решений этих систем представим
в виде таблицы (табл. 7.1).

Таблица 7.1.

Номер координатной функции	Коэффициенты многочлена – -ой координатной функции
1			0	1
2		—	1	0
3			0	0
4			0	0

Введём удобное для анализа
свойств координатных функций относительное
независимое переменное

.
Тогда четыре координатные функции этого
КЭ примут вид:

;

;

;

.

Пример 3. Дано:
двумерная область, порядок дифференциального
уравнения по каждой координате

.
Тогда число степеней свободы КЭ

.
Конечный элемент –
прямоуглльник

.
Задавая на каждом узле КЭ по одному
параметру — значению искомой функции,
мы полностью определим приближённое
решение на носителе. Выберем в качестве
координатных функций многочлены степени

по каждой координате
(то-есть, функции, линейные по каждой
координате). Общий вид таких функций:

.

Первая из них удовлетворяет условиям

вторая —

третья –

четвёртая –

Составляем поочерёдно для
каждой из этих координатных функций
систему уравнений, отражающих граничные
условия на узлах:

Вектора решений этих систем представим
в виде таблицы (табл. 7.1).

Таблица 7.1.

Номер координатной функции	Коэффициенты многочлена – -ой координатной функции
1				1
2		0		0
3			0	0
4			0	0

Введём удобные для анализа
свойств координатных функций относительные
независимые переменные

.
Тогда четыре координатные функции этого
КЭ примут вид:

;

;

;

.

Работа с несогласованными координатными
функциями требует, как правило, более
глубокого анализа, иногда с физическим
осмыслением пренебрегаемых условий
сопряжения, поэтому примеры таких
функций мы не приводим.

Существенно, что в наших
задачах количество главных и естественных
краевых условий одинаково и это
энергетически сопряжённые величины –
интеграл от произведения естественного
условия на вариацию главного условия
равен вариации работы обобщённого
усилия (естественного условия) на
соответствующем возможном обобщённом
перемещении (главном условии). В процессе
расчёта подбираются такие значения
главных краевых условий в узлах
(одинаковые для всех узлов КЭ, которые
совмещены с данным узлом системы), чтобы
в этих же узлах выполнялись (в приближённом
смысле) естественные краевые условия.
В задачах строительной механики это
означает, что узлы должны находиться в
равновесии, при этом условия равновесия
могут записываться в трёх эквивалентных
вариантах:

либо в виде равенства нулю обощённой
силы, действующей на узел,

либо в виде равенства нулю работы
обобщённой силы на соответствующем
обобщённом перемещении,

либо как условие минимума функционала
энергии.

Если среди краевых условий
есть главные и естественные, то, как мы
выяснили, главные условия должны
выполняться точно, а естественные –
приближённо. В прямых методах это
означает, что главные условия должны
выполняться уже во время конструирования
координатной системы, а приближённое
соблюдение естественных уловий должно
обеспечиваться в результате расчёта..Исходя
из этого, условия сопряжения подобластей
в узлах обеспечивается:

— строгим равенством величин, задающих
главные условия (в строительной механике
– обобщённых перемещений нормали и её
поворотов для балок и плит и перемещений
для массивов);

— возможностью выполнения
любых заданных естественных условий в
форме условий сопряжения соответствующим
подбором величин, при помощи которых
формулируются главные условия; связь
между главными и естественными условиями
может быть приближённой (из-за того, что
используется только конечное число
координатных функций), но любому сочетанию
естественных условий должно соответствовать
создающее его сочетание главных условий.

Строгое равенство главных
условий в налагаемых друг на друга узлах
смежных элементов (можно сказать – в
совмещаемых узлах смежных элементов)
обеспечивается в алгоритме (и программе)
тем, что неизвестными
являются приближённые значения искомой
функции в узлах системы, и этим значениям
приравниваются узловые параметры КЭ
для их узлов, попадающих в эти узлы
системы.

Рассмотрим, какой вид
приобретают коэффициенты системы
уравнений методов Ритца или Галёркина,
когда эти методы сочетаются с МКЭ.
Согласно традиции, установившейся в
литературе по МКЭ, будем обозначать эти
коэффициенты как

,
если речь идёт овсей системе, и

,
если речь идёт о КЭ с номером

(вместо

по ММ-6).

Вначале выберем КЭ, занимающий всю
рассматриваемую область.

Введём обозначения:

— номер выбранного КЭ;

— множество номеров узловых параметров
этого КЭ (нумерация в пределах КЭ);

— носитель всех координатных функций,
связанных с выбранным КЭ;

— вся область (вначале

).
Согласно (6.30), обобщая эту формулу, в
случае необходимости, на случай
пространств большей размерности, и
обозначая аргумент аналогично тому,
как это сделано в пояснениях к формуле
(7.1), получим

.
(7.2)

Этот интеграл в случае
неодномерной области – кратный,

или

.
При вычислении этого интеграла может
быть выполнено понижение порядка
дифференциального оператора вдвое
путём применения интегрирования по
частям или его обобщения для неодномерной
области (формул Грина, Стокса или
Гаусса-Остроградского) или с учётом
физического смысла соотношений метода
Ритца..

Количество элементов множества

— это количество узловых параметров КЭ,
число его степеней свободы

.
Наборы

при каждом фиксированном значении

можно считать

—
ми столбцами, а наборы

при каждом фиксированном значении

—
ми строками некоторой матрицы

.
Эта матрица называется матрицей
жёсткости конечного элемента №

— МЖ КЭ №

.Если
оператор задачи симметричен, то эта
матрица также симметрична. Если КЭ
предствляет собой неклассическую
область, вычисление интегралов (7.2) может
представлять собой нетривиальнуюи уж
во всяком случае трудоёмкую задачу. Все
промышленные программы МКЭ имеют
библиотеки конечных
элементов с формулами
для определения элементов МЖ КЭ.

7.10. Матрица
жёсткости конечного элемента (Адрес
файла Блок
4_______).

Матрицей жёсткости конечного
элемента называется матрица

,
элементы которой определяются поформуле

или её
аналогу, полученному путём понижения
порядка дифференциального оператора.

В случае задач строительной
механики МЖ КЭ связывает вектор узловых
обобщённых усилий

с вектором узловых обобщённых перемещений

формулой

.

(7.3)

Вернитесь к тексту

В ряде случаев различные КЭ
одной конечноэлементной сетки могут
быть сориентированы по-разному. В этих
случаях целесообразно вводить на каждом
КЭ свою систему координат. Такая система
координат называется
местной (локальной)
системой координат данного КЭ.

Если ввести общую
(глобальную) систему
координат, то взаимное положение этой
системы и каждой из местных систем может
быть охарактеризовано углом взаимного
поворота

. Тогда компоненты векторов

,

,
заданные в местной системе, могут быть
преобразованы к общей системе по формуле,
повторяющей пребразование координат

,

(7.4)

,

(7.5)

где

— матрица преобразования
координат (матрица
поворота) от местной системы к глобальной;

,

— узловые параметры КЭ, соответствующие
главным граничным условиям;

— узловые параметры КЭ,
соответствующие естественным граничным
условиям,

В аналитической геометрии
доказывается, что

— ортогональная матрица, то-есть, она
обратима и её обратная матрица равна
её транспонированной матрице

.

(7.6)

Тогда из (7.4) с учётом (7.6) можно
записать

.

(7.7)

Подставим (7.7) в (7.3), после чего
— преобразованное выражение (7.3) в (7.5)

,
(7.8)

где

— МЖ КЭ в глобальной системе координат.

В МКЭ принято определять естественные
граничные условия КЭ, приведенные к его
узлам (узловые обобщённые силы КЭ в
случае задачи строительной механики)

.

(7.9)

Теперь перейдём к случаю
сетки КЭ с произвольным количеством
элементов. Узлы, принадлежащие какому-либо
КЭ либо совпадающие с его узлами, в МКЭ
называют инцидентными
ему. Соответствие между
номерами КЭ и номерами инцидентных им
узлов системы задаётся расчётчиком в
исходных данных в виде специальной
таблицы инциденций.

Ненулевому значению любого
узлового параметра узла системы,
инцидентного нескольким КЭ, соответствует
в этих КЭ аппроксимация решения

,

(7.10)

где

—
номер КЭ;

—
множество номеров КЭ, которым инцидентен
узел

системы;

—
номер узла КЭ в его местной нумерации;

—
количество узлов в

-ом
КЭ;

—
номер узлового параметра данного узла;

-количество узловых параметров в

-ом
узле;

—

—
ый узловой параметр

—
го узла;

—
координатная функция, соответствующая
этому параметру; многоточием показаны
нулевые слагаемые (связанные с нулевыми
узловыми параметрами).

Пусть теперь в некотором узле
системы с глобальным номером

задан своими координатами в глобальной
системе координат вектор узловых
параметров

.
По аналогии с (7.10), вспоминая понятие
скалярного произведения векторов из
линейной алгебры, запишем (с учётом
(7.7)) соответствующий вектор аппроксимаций

,
(7.11)

где

— транспонированный вектор координатных
функций, соответствующих заданному
вектору узловых параметров;

—
номер узла КЭ, накладываемого на

-ый
узел системы.

Учитывая, что за пределами носителя
координатные функции тождественно
равны нулю, (7.11) можно записать в виде

.

(7.12)

По аналогии с формулами
(6.30), (6.38) и сучётом (7.8) десь следует иметь
иметь ввиду,запишем блоки матрицы
коэффициентов МКЭ в форме методов Ритца
или Бубнова-Галёркина (опять согласно
традиции МКЭ заменим обозначение
коэффициентов на

;
блок

,

)

(7.13)

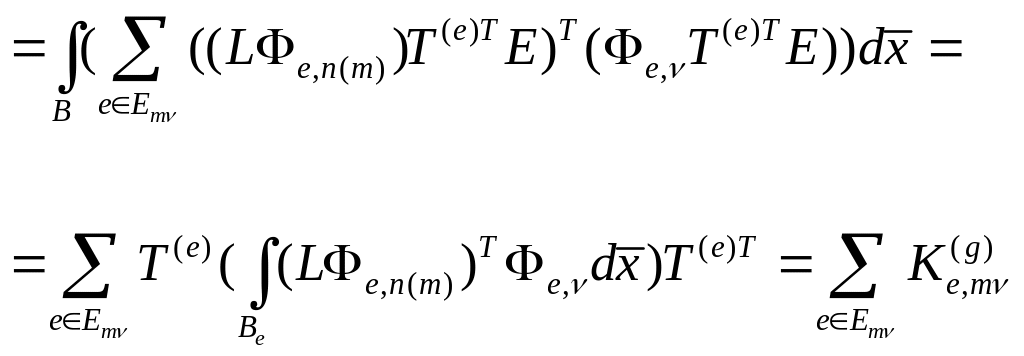
Здесь

;

—
отдельные блоки МЖ КЭ

,
расположенные на пересечении её

-ой
блочной строки и

-го
блочного столбца;

,
где

— множество номеров узлов системы,
инцидентных тем же КЭ, что и узел

,

.

Для столбцов свободных членов
аналогично (7.9) получаем выражение для

-го
блочного подвектора

.
(7.14)

Для матрицы коэффициентов
всей системы уравнений для определения
узловых параметров рассчитываемого
объекта и её столбца свободных членов
естественно получаем, используя (7.13) и
(7.14)

,

(7.15)

.

(7.16)

Упомянутая система уравнений в матричной
записи имеет вид

.

(7.17)

Это разрешающая
система уравнений МКЭ.

7.11. Матрица
жёсткости системы (МЖС) (Адрес файла
Блок
4_____________)

Матрицей жёсткости системы
называется матрица

коэффициентов её разрешающей системы
уравнений, вычисляемая по формулам

,

.

Она связывает узловые параметры системы
и нагрузку разрешающей системой
уравнений.

При симметричном операторе задачи она
симметрична.

Вернитесь к тексту

7.12. Ансамблирование
(Адрес файла Блок
4_____________)

Ансамблированием
в МКЭ называется процесс объединения
конечных элементов в сеть КЭ (ансамбль
конечных элементов), при котором
формируется МЖС из блоков отдельных
МЭ КЭ по формуле

и
свободный вектор по формуле

Вернитесь к тексту

Обычно при рациональной
нумерации узлов и конечных элементов
разность

между номерами узлов системы, инцидентных
одному КЭ, ограничена и существенно
меньше половины дляны строки. Поэтому
все ненулевые элементы МЖС сосредоточены
в пределах ленты шириной

,
где

—
длина строки (говорят,
что матрица имеет ленточную структуру).
Это в сочетании с симметрией МЖС позволяет
снизить требуемые ресурсы памяти
компьютера и время счёта.

Решая систему (7.17), получаем
приближённые значения
искомой функции в узлах системы

,
(7.18)

где

,

—
номер узла.

Её производные порядка до

включительно (здесь

—
количество узловых параметров

—
го узла системы) определяются по формуле
(7.18) при

,

(7.19)

где

— порядок разыскиваемой производной.

Обычно необходимы не только
значения искомой функции в отдельных
узлах системы, получаемые в результате
решения системы (7.17), но также и значения
функции и её производных (или их линейных
комбинаций) между узлами, то-есть, внутри
КЭ. В этих случаях для каждого КЭ строятся
аппроксимации искомой вектор-функции
(7.11).

В случае решения граничных
задач для систем уравнений с несколькими
неизвестными функциями идея МКЭ
сохраняется, но требуется соответствующее
обобщение расчётных соотношений.

В теории МКЭ доказывается,
что при правильной разбивке сетки КЭ
погрешность метода падает при уменьшении
диаметра (наибольшего размера) самого
большого КЭ, или сгущении
узлов системы, и
приближённое решение стремится к
точному. При рациональной разбивке
сетки узлов адекватность расчётной
схемы МКЭ растёт при сгущении узлов, в
первую очередь — в окрестности источников
возмущения решения (входящие углы,
проёмы, местные воздействия, резкие
изменения геометрии системы или свойств
материала ит.д.).

Следует подчеркнуть, что
предварительная (априорная)
оценка погрешности практически
невозможна, и единственная возможность
получить приближённое решение с
погрешностью,не превосходящей заданную
– организавать последовательнось
процессов решения задачи при сгущении
узлов и измельчении КЭ от расчёта к
расчёту. При грамотной подготовке
исходных данных последовательность
полученных приближённых решени должна
сходится к точному решению, а разность
двух решений может послужить для оценки
погрешности (апостериорной),
если, например, сгущение узлов осуществлять
только путём добавления новых узлов и
сравнивать вектора значений неизвестнойо
функции в тех узлах, которые есть в
нескольких последовательных сетках
узлов.

Методы решения нелинейных
задач в строительной механике приобретают
специфические формы. Рассмотрим их на
примере нелинейных задач, в которых
дискретизация выпоняется методом
Бубнова-Галёркина в форме МКЭ.

Общим для этих задач является
зависимость матрицы жёсткости системы
от решения

.
Как было показано в лекции ММ-1, эта
зависимость проявляется вследствие
того, что коэффициенты дифференциального
уравнения задачи несут информацию о
свйствах рассчитываемого объекта — его
геометрии и механических свойствах
материала. В частности, геометрия объекта
влияет на вид и коэффициенты уравнений
равновесия и уравнений связи деформаций
с перемещениями и их лроизводными по
координатам, а также в некоторых случаях
— на выражения для определения внутренних
усилий в сечениях по напряжениям в них.
При достаточно больших деформациях
проявляетсянелинейность их связи с
напряжениями.В то же время метод
Бубнова-Галёркина предусматривает: а)
определение таких перемещений, при
которых уравнения равновесия оказывются
ортогональными к функциям заданной
системы координатных функций; б) выражение
усилий через деформации и деформаций
через премещения. Таким образом, указанные
уравнения и зависимости оказываются
нелинейными. В процессе применения
метода дискретизации соответствующие
разрешающие уравнения также становятся
нелинейными; при этом, как правило,
зависимости элементов МЖ от решения
записать в виде аналитических выражений
невозможно. Эти коэффициенты должны
вычисляться каждый раз при новых
значениях решения (то-есть, перемещений)
по достаточно сложному алгоритму. Такие
зависимости естественно называть
алгоритмическими.

Уравнение (7.17) принимает вид

.

(7.20)

Конкретизируем пути применения
изученных нами ранее методов линеаризации
(лекции ММ-4 и ММ-5).

1. Метод
простых итераций.
Запишем (7.20) в виде

.

(7.21)

Это попрежнему уравнение,
так как оно не разрешено относительно

,
однако, оно приведено к виду, ориентированному
на применение метода простых итераций
(лекция ММ-4):

.

(7.22)

В механике деформируемого
твёрдого тела, в строительной механике
такой итерационный процесс называется
методом переменных
параметров упругости,
так как он предусматривает пересчёт
коэффициентов уравнения (7.20) на каждой
итерации в соответствии с заданными
зависимостями напряжений от деформаций.

Естественно, приведение к
виду (7.21) нам понадобилось только для
пояснения связи междц понятиями метод
простых итераций и
метод переменных
параметров упругости.
При выполнении реальных
расчётов записывать решение в таком
виде нецелесообразно,
нужно просто решать
систему уравнений,
ставших линейными
после подстановки
предыдущей
итерации в выражение
для

.

(7.23)

2. Модифицированный метод
Ньютона. Использование
обычного метода Ньютона при выполнении
реальных расчётов практически невозможно
из-за отсутствия аналитических выражений
для отмеченных выше нелинейных
зависимостей и необходимости их
определения в большом количестве точек
– узлов системы. Его замена аналогом –
многомерным вариантом метода секущих
в отмеченных случаях также чрезмерно
трудоёмка. В то же время модифицированный
метод Ньютона в ряде случаев может быть
применён (и действительно применяется).

Запишем (7.20) в виде

,

(7.24)

где

—
нулевой вектор.

Найдём матрицу Якоби левой части (7.24)

.
(7.25)

Её значение в точке естественного
состояния (
)

(7.26)

Теперь мы можем записать
итерационный процесс модифицированного
метода Ньютона

.

(7.27)

Введём обозначения

,

и
подставим их в (7.27):

.

(7.28)

Таким образом, итерационный
процесс модифицированного метода
Ньютона принял форму
метода фиктивных нагрузок
Ильюшина

,

(7.28`)

где

—
фиктивная нагрузка по Ильюшину.

Иногда этот метод называют
методом упругих решений, но в настоящее
время чаще это название употребляют
для обоих описанных выше методов.

Применяемые иногда методы
начальных напряжений и начальных
деформаций также
приводятся к виду метода фиктивных
нагрузок.

3. Шагово-итерационные
методы. Итерационный
метод может применяться в случае, если
порождаемый им итерационный процесс в
условиях решаемой задачи сходится. В
общем случае одним из необходимых
условий, обеспчивающих сходимость,
является принадлежность начального
приближения области сходимости
неподвижной точки оператора задачи
(то-есть, решения данной нелинейной
задачи). Кроме того, при выполнении
практических расчётов важно, чтобы
итерационный процесс сходился достаточно
быстро. В то же время, чем выше нагрузка
и, следовательно, чем выше уровень
напряжений и деформаций, тем сильнее
отклоняются упомянутые выше нелинейные
зависимости от линейных и тем меньшей
и труднее оцениваемой оказывается
область сходимости и тем медленнее
сходится вычислительный процесс. Для
ускорения этого процесса нужно начальное
приближение располагать как можно ближе
к искомому (неизвестному заранее!)
решению. Этого можно достигнуть, если
в качестве начального приближения при
данном уровне нагрузки использовать
пусть приближённое, но достаточно точное
решение, которое можно получить при
несколько меньшей нагрузке. Можно
построить процесс постепенного пошагового
увеличения нагрузки,
начиная со столь малой нагрузки, что
начальным приближением для неё могло
бы служить решение, полученное в
предположении линейноупругой работы
материала. При этом окончательное (на
последней итерации) решение, полученное
на предыдущем шаге нагрузки, принимается
в качестве начального приближения для
последующего шага нагрузки. Такие методы
линеаризации называются в строительной
механике шагово-итерационными
и в математике — методами
продолжения по параметру (в
даннгом случае — по параметру нагрузки)
с итерационным уточнением
на каждом шаге.

Шагово-итерационные методы,
использующие на каждом шаге процессы
(7.23) и (7.28`), выглядят следующим образом

;

(7.29)

.

(7.30)

Здесь

—
номер шага по нагрузке;

—
индекс

—
ой итерации

—
го шага по нагрузке. Как указыно выше,
в качестве начального приближения

—
го шага принимается последняя итерация
предыдущего

—
го шага, на которой условие прекращения
итераций было выполнено

,

(7.31)

где

—
номер итерации, на которой выполнилось
условие выхода из итерационного цикла
при выполнении

—
го шага.

При выполнении расчётов реальных
объектов обычно используются
шагово-итерационные методы.

4. Инкрементальные методы.
Идея постепенного
наращивания нагрузки используется и в
инкрементальнхы методах, однако, их
главное отличие заключается в том, что
на каждом шаге определяется приращение
решения при заданном приращении нагрузки,
а соответствующие коэффициенты
разрешающей системы уравнений отвечают
этой новой постановке задачи. Обозначим
матрицу этих коэффициентов

,
где

—
номер шага, на котором началось заданное
приращение нагрузки. Эта матрица зависит
от неизвестных, определённых на предыдущем
шаге, и их приращений. Так как эти
приращения неизвестны (их только надлежит
определить), зависимостью коэффициентов
от них обычно пренебрегают, по крайней
мере, для определения начального
приближения на данном шаге. Разрешающая
система уравнений в этом случае принимает
вид

.

(7.32)

Простейшим путём построения новой
матрицы коэффициентов является
использование для вычисления приращений
соотношения для дифференциала
вектор-функции, заданной уравнением
(7.20)

,
(7.33)

где

—
по-прежнему якобиан матрицы жёсткости

Ограничиваясь линейной частью
приращения (при условии, что приращения
нагрузки и неизвестных достаточно малы,
а связь между ними непрерывна), запишем

,

(7.34)

где

— приращения векторов неизвестных и
нагрузок, которые начались при

.
Таким образом, сравнение (7.32) и (7.34)
приводит к выражению для матрицы
коэффициентов

.

(7.35)

Для реальных сложных систем построение
дифференцируемых матриц коэффициентов
практически невозможно, поэтому
записывают в приращениях исходные
зависимости «напряжения – деформации»
и «перемещения – деформации», а затем
осуществляют процедуру МКЭ. При таком
дифференцировании определяются
производные механических и геометрических
параметров, которые после этого называют
иногда касательными модулями.

Сама матрица

называется касательной МЖ.

Метод простых итераций –
метод переменных параметров упругости

Метод Ньютона,
модифицированный метод Ньютона-фиктивных
нагрузок, начальных напряжений

Метод продолжения по
параметру нагрузки-инкрементальный
метод

метод Ньютона

Шагово-итерационные методы

История термина
“метод упругих решений”

О проверке сходимости (аппроксимация
заданных нелинейных функций близкими
функциями с достаточным количеством
производных) – ведь нет дифференцирования

МЖ системы

Ансамблирование-некоторые
элементы матриц жёст. сопрягаемых КЭ
суммируются (совпадающие реакции
налагаемых друг на друга (совмещаемых)узлов),
так как они занимают одинаковые места
в МЖ; некоторые элементы занимают разные
местаи записываются на своих местах.

Свободные члены.

СГУЩЕНИЕ УЗЛОВ!!!!!!!!!!

Нелинейность

.

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)

Предмет и задачи строительной механики и понятие нелинейности

При решении задач строительной механики применяются разные численные методы. Наиболее распространенным стал метод конечных элементов. В решении большинства задач статики, устойчивости сооружений и динамики первоочередно определяется полная потенциальная энергия $U$:

$U=W–V$

Где $W$ представляет работу внешних сил, а $V$ – работу внутренних. Все эти силы обычно записываются в виде функций, зависимых от таких процессов, как: перемещение, деформация, напряжение элементов для расчетной модели сооружений.

Стажировки для студентов

Начни получать реальный опыт работы по специальности и полезные навыки для дальнейшей карьеры

Найти стажировку

В строительной механике различают такие типы задач:

• одномерные (позволяют установить зависимость между одной функцией и пространственной координатой);
• плоские (допускают решение в двух измерениях);
• пространственные (рассматривают решение в трех измерениях).

Геометрическая нелинейность уравнений строительной механики свойственна большим перемещениям и деформациям элементов, что довольно редко наблюдается в строительных конструкциях (исключение составляют вантовые).

Возникновение физической нелинейности связано с отсутствием пропорциональности между деформациями и усилиями (когда используются неупругие материалы). Свойством физической нелинейности в определенной степени обладают все строительные конструкции и материалы.

Любое сооружение считается в строительной механике пространственным объектом. Воздействующая на такой объект также будет считаться пространственной, соответственно, и расчетная схема сооружения выбирается как пространственная. Наряду с тем, подобная схема соответствует более сложной задаче с составлением и решением большого количества уравнений. По этой причине для реального сооружения в строительной механике выбирается плоская система.

«Нелинейная строительная механика» 👇

Решение нелинейных задач в строительной механике

При значительных перемещениях, которые соизмеримы с размерами конструкций, учитывается геометрическая нелинейность (при продольном и продольно-поперечном изгибе стержней, измененных координатах точек конструкции по причине сравнительно больших перемещений).

Особое место в строительной механике занимает конструктивная нелинейность. Она связана с изменениями расчетной схемы конструкции при нагрузке (при этом учитываются односторонние связи):

• при контактном типе взаимодействия деформируемых тел (трещины, одностороннее основание);
• при расчете конструкций (вантовые, с затяжками и т. п.).

Расчет нелинейных систем представляет более сложную задачу, в отличие от линейных. Это объясняется тем, что в первом варианте нужно:

• обязательно учитывать деформированное состояние нужной области конструкции;
• отказываться от принципа независимости для действующих сил;
• задействовать специальные методы поиска и анализа решений.

Аналитическое решение задачи при таких условиях требует проведение расчетов с применением численных методов (МКЭ), при этом используются процедуры последовательных приближений.

Если в решении задачи учитывается физическая нелинейность, напряжений и деформаций в общем виде будет выражать следующая формула:

$sigma=E(e) e$

где $E(e)$ – матрица физических свойств материала, элементы которой представляют функции компонент для вектора деформаций $e$.

Таким образом, если учитывать геометрическую и физическую нелинейность, при решении задачи получается система нелинейных алгебраических уравнений, требующих применения шаговых или других методов. Стоит учитывать, что не существует универсального метода среди широко используемых алгоритмов расчета для нелинейных систем. Эффективность того или иного из них будет, главным образом, зависеть от типа и параметров нелинейности.

Шаговые методы решения нелинейных задач

Каждый шаг при нагружении допускает конкретную физическую интерпретацию. Поскольку приращение нагрузки оказывается достаточно незначительным, поведение конструкции на каждом шаге принимается за линейное. После осуществления шага нагружения начинает формироваться новая нелинейная составляющая для матрицы жесткости и далее выполняется следующее приращение нагрузки. Нелинейное поведение конструкции, таким образом, полностью представляет собой последовательность кусочно-линейных шагов.

Недостаток задействования шаговых методов проявляется в накоплении ошибок (неувязки решений) в момент перехода от одного шага нагружения к следующему. При условии сильной нелинейности требуется уменьшение величины приращения нагрузки (большое количество шагов). Это, в свою очередь, усложняет нелинейный расчет. Улучшению точности решения также способствует регулирование невязки узловых сил (через каждые последующие несколько шагов нагружения).