Неполные квадратные уравнения егэ - Помощь в подготовке к экзаменам и поступлению

Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением. Выражение, стоящее слева от знака равенства, называется левой частью уравнения, а выражение, стоящее справа, — правой частью уравнения.

Линейные уравнения

Линейным называется такое уравнение, в котором неизвестное $x$ находится в числителе уравнения и без показателей. Например: $2х – 5 = 3$

Линейные уравнения сводятся к виду $ax = b$, которое получается при помощи раскрытия скобок, приведения подобных слагаемых, переноса слагаемых из одной части уравнения в другую, а также умножения или деления обеих частей уравнения на число, отличное от нуля.

$5 (5 + 3х) — 10х = 8$

Раскроем скобки.

$25 + 15х — 10х = 8$

Перенесем неизвестные слагаемые в левую часть уравнения, а известные в правую. При переносе из одной части в другую, у слагаемого меняется знак на противоположный.

$15х — 10х = 8 — 25$

Приведем подобные слагаемые.

$5х = -17$ — это конечный результат преобразований.

После преобразований к виду $ax = b$, где, a=0, корень уравнения находим по формуле $х = {b}/{a}$

$х=-{17}/{5}$

$х = — 3,4$

Ответ: $- 3,4$

Квадратные уравнения

Квадратное уравнение — уравнение вида $ax^2 + bx + c = 0$, где $a, b, c$ — некоторые числа a$≠0$, $x$ — неизвестное. Перед тем как решать уравнение, необходимо раскрыть скобки и собрать все слагаемые в левой части уравнения.

Числа $a, b, c$ называются коэффициентами квадратного уравнения.

$a$ — старший коэффициент;
$b$ — средний коэффициент;
$c$ — свободный член.

Если в квадратном уравнении коэффициенты $b$ и $c$ не равны нулю, то уравнение называется полным квадратным уравнением. Например, уравнение $2x^2 – 8x + 3 = 0$. Если один из коэффициентов $b$ или $c$ равен нулю или оба коэффициента равны нулю, то квадратное уравнение называется неполным. Например, $5x^2 – 2x = 0$.

Решение неполных квадратных уравнений

Неполное квадратное уравнение имеет вид $ax^2 + bx = 0$, если $a$≠0$; $c$=0$. В левой части этого уравнения есть общий множитель $x$.

1. Вынесем общий множитель $x$ за скобки.

Мы получим $x (ax + b) = 0$. Произведение равно нулю, если хотя бы один из множителей равен нулю. Поэтому получаем $x = 0$ или $ax + b =0$. Таким образом, данное уравнение эквивалентно двум уравнениям:

$x = 0; ax + b = 0$

2. Решаем получившиеся уравнения каждое отдельно.

Мы получим $x = 0$ и $x={-b}/{a}$. Следовательно, данное квадратное уравнение имеет два корня $x = 0$ и $x={-b}/{a}$

$4х^2 — 5х = 0$

Вынесем х как общий множитель за скобки:

$х (4х — 5) = 0$

Приравняем каждый множитель к нулю и найдем корни уравнения.

$x = 0$ или $4х — 5 = 0$

$х_1 = 0 х_2 = 1,25$

Ответ: $х_1 = 0; х_2 = 1,25$

Неполное квадратное уравнение вида $ax^2 + c = 0, a≠0, b=0$

Для решения данного неполного квадратного уравнения выразим $x^2$.

$ax^2 + c = 0$

$ax^2 = — c$

$x_2 = {-c}/{a}$

При решении последнего уравнения возможны два случая:

если ${-c}/{a}>0$, то получаем два корня: $x = ±v{{-c}/{a}}$

если ${-c}/{a}<0$, то уравнение во множестве действительных числе не имеет решений.

$x^2 — 16 = 0$

$x^2 = 16$

$x = ±4$

Ответ: $х_1 = 4, х_2 = — 4$

Решение полного квадратного уравнения

Решение с помощью дискриминанта

Дискриминантом квадратного уравнения D называется выражение

$b^2 — 4ac$.

При решении уравнения с помощью дискриминанта возможны три случая:

1. $D > 0$. Тогда корни уравнения равны:

$x_{1,2}={-b±√D}/{2a}$

2. $D = 0$. В данном случае решение даёт два двукратных корня:

$x_{1}=x_{2}={-b}/{2a}$

3. $D < 0$. В этом случае уравнение не имеет корней.

$3х^2 — 11 = -8х$

Соберем все слагаемые в левую часть уравнения и расставим в порядке убывания степеней

$3х^2 + 8х — 11 = 0$

$a = 3 ,b = 8, c = — 11$

$D = b^2- 4ac = 82- 4 · 3 · (-11) = 196 = 142$

$x_{1}={-b+√D}/{2a}={-8+14}/{6}=1$

$x_{2}={-b-√D}/{2a}={-8-14}/{6}=-3{2}/{3}$

Ответ: $x_1=1, x_2=-3{2}/{3}$

Устные способы

Если сумма коэффициентов равна нулю $(а + b + c = 0)$, то $х_1= 1, х_2={с}/{а}$

$4х^2+ 3х — 7 = 0$

$4 + 3 — 7 = 0$, следовательно $х_1= 1, х_2=-{7}/{4}$

Ответ: $х_1= 1, х_2 = -{7}/{4}$

Если старший коэффициент в сумме со свободным равен среднему коэффициенту $(a + c = b)$, то $х_1= — 1, х_2=-{с}/{а}$

$5х^2+ 7х + 2 = 0$

$5 + 2 = 7$, следовательно, $х_1= -1, х_2 =-{2}/{5}$

Ответ: $х_1= -1, х_2 = -{2}/{5}$

Кубические уравнения

Для решения простых кубических уравнений необходимо обе части представить в виде основания в третьей степени. Далее извлечь кубический корень и получить простое линейное уравнение.

$(x — 3)^3 = 27$

Представим обе части как основания в третьей степени

$(x — 3)^3 = $3³

Извлечем кубический корень из обеих частей

$х — 3 = 3$

Соберем известные слагаемые в правой части

$x = 6$

Ответ: $х = 6$

Дробно рациональные уравнения

Рациональное уравнение, в котором левая или правая части являются дробными выражениями, называется дробным.

Чтобы решить дробное уравнение, необходимо:

найти общий знаменатель дробей, входящих в уравнение;
умножить обе части уравнения на общий знаменатель;
решить получившееся целое уравнение;
исключить из его корней те, которые обращают в ноль общий знаменатель.

$4x + 1 — {3}/{x} = 0$

1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)

$x≠0$

2. находим общий знаменатель дробей и умножаем на него обе части уравнения

$4x + 1 — {3}/{x}= 0¦· x$

$4x · x + 1 · x — {3·x}/{x} = 0$

3. решаем полученное уравнение

$4x^2 + x — 3 = 0$

Решим вторым устным способом, т.к. $а + с = b$

Тогда $х_1 = — 1, х_2 = {3}/{4}$

4. исключаем те корни, при которых общий знаменатель равен нулю В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.

Ответ: $х_1 = — 1, х_2 = {3}/{4}$

При решении уравнения с двумя дробями можно использовать основное свойство пропорции.

Основное свойство пропорции: Если ${a}/{b} = {c}/{d}$, то $a · d = b · c$

${3х-5}/{-2}={1}/{х}$

Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)

$x≠0$

Воспользуемся основным свойством пропорции

$х (3х — 5) = -2$

Раскроем скобки и соберем все слагаемые в левой части уравнения

$3х^2- 5х + 2 = 0$

Решим данное квадратное уравнение первым устным способом, т.к.

$a + b + c = 0$

$x_1 = 1, x_2 = {2}/{3}$

В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.

Ответ: $x_1 = 1, x_2 = {2}/{3}$

Рациональное уравнение – это уравнение вида $f(x)=g(x)$, где $f(x)$ и $g(x)$ — рациональные выражения.

Рациональные выражения — это целые и дробные выражения, соединённые между собой знаками арифметических действий: деления, умножения, сложения или вычитания, возведения в целую степень и знаками последовательности этих выражений.

Например,

${2}/{x}+5x=7$ – рациональное уравнение

$3x+√x=7$ — иррациональное уравнение (содержит корень)

Если хотя бы в одной части рационального уравнения содержится дробь, то уравнение называется дробно рациональным.

Чтобы решить дробно рациональное уравнение, необходимо:

Найти значения переменной, при которых уравнение не имеет смысл (ОДЗ);
Найти общий знаменатель дробей, входящих в уравнение;
Умножить обе части уравнения на общий знаменатель;
Решить получившееся целое уравнение;
Исключить из его корней те, которые обращают в ноль общий знаменатель.

Решить уравнение: $4x+1-{3}/{x}=0$

Решение:

1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)

$x ≠ 0$

2. находим общий знаменатель дробей и умножаем на него обе части уравнения

$4x+1-{3}/{x}=0|·x$

$4x·x+1·x-{3·x}/{x}=0$

3. решаем полученное уравнение

$4x^2+x-3=0$

Решим вторым устным способом, т.к. $а+с=b$

Тогда, $x_1=-1, x_2=-{3}/{4}$

4. исключаем те корни, при которых общий знаменатель равен нулю

Ответ: $x_1=-1, x_2=-{3}/{4}$

При решении уравнения с двумя дробями, можно использовать основное свойство пропорции.

Основное свойство пропорции: Если ${a}/{b}={c}/{d}$ — пропорция, то $a·d=b·c$

Решить уравнение ${3x-5}/{-2}={1}/{x}$

Решение:

Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)

$x≠0$

Воспользуемся основным свойством пропорции

$х(3х-5)=-2$

Раскроем скобки и соберем все слагаемые в левой стороне

$3х^2-5х+2=0$

Решим данное квадратное уравнение первым устным способом, т.к. $a+b+c=0$

$x_1=1, x_2={2}/{3}$

В первом пункте получилось, что при x = 0 уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.

Ответ: $x_1=1, x_2={2}/{3}$

Уравнения, содержащие неизвестную под знаком корня, называются иррациональными.

Чтобы решить иррациональное уравнение, необходимо:

Преобразовать заданное иррациональное уравнение к виду: $√{f(x)}=g(x)$ или $√{f(x)}=√{g(x)}$
Обе части уравнение возвести в квадрат: $√{f(x)}^2=(g(x))^2$ или $√{f(x)}^2=√{g(x)}^2$
Решить полученное рациональное уравнение.
Сделать проверку корней, так как возведение в четную степень может привести к появлению посторонних корней. (Проверку можно сделать при помощи подстановки найденных корней в исходное уравнение.)

Решите уравнение $√{4х-3}=х$. Если уравнение имеет более одного корня, укажите наименьший из них.

Решение:

Обе части уравнение возведем в квадрат:

$√{4х-3}^2=х^2$

Получаем квадратное уравнение:

$4х-3=х^2$

Перенесем все слагаемые в левую часть уравнения:

${-х}^2+4х-3=0$

Решим данное квадратное уравнение устным способом, так как

$a+b+c=0$

$-1+4-3=0$, следовательно $х_1 = 1; х_2={с}/{а}={-3}/{-1}=3$

Проведем проверку корней, подставив их вместо икса в исходное уравнение

$√{4·1-3}=1$

$1=1$, получили в результате проверки верное равенство, следовательно $х_1=1$ подходит.

$√{4·(3)-3}=3$

$√9=3$

$3=3$, получили в результате проверки верное равенство, следовательно корень $х_2=3$ подходит

$х_1=1$ наименьший корень.

Ответ: $1$

Так как в иррациональных уравнениях иногда необходимо возводить в квадрат не только число, но и целое выражение, необходимо вспомнить формулы сокращенного умножения:

Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе число плюс квадрат второго числа. $(a-b)^2=a^2-2ab+b^2$
Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа. $(a+b)^2=a^2+2ab+b^2$

Решить уравнение: $х-6=√{8-х}$

Возведем обе части уравнения в квадрат

$(х-6)^2=8-х$

В левой части уравнения при возведении в квадрат получаем формулу сокращенного умножения квадрат разности. В правой части уравнения квадрат и корень компенсируют друг друга и в результате остается только подкоренное выражение

$х^2-2·6·х+6^2=8-х$

$х^2-12х+36=8-х$

Получили квадратное уравнение. Все слагаемые переносим в левую часть уравнения. При переносе слагаемых через знак равно их знаки меняются на противоположные.

$х^2-12х+36-8+х=0$

Приводим подобные слагаемые:

$х^2-11х+28=0$

Найдем корни уравнения через дискриминант:

$D=b^2-4ac=121-4·28=121-112=9=3^2$

$x_{1,2}={-b±√D}/{2a}={11±3}/{2}$

$x_1=7; x_2=4$

Проведем проверку корней, подставив их вместо икса в исходное уравнение

$x_1=7$

$7-6=√{8-7}$

$1=1$, получили верное равенство, следовательно, корень нам подходит.

$x_2=4$

$4-6=√{8-4}$

$-2=2$, получили неверное равенство, следовательно, данный корень посторонний.

Ответ: $7$

Показательными называют такие уравнения, в которых неизвестное содержится в показателе степени.

$a^x=b$

При решении показательных уравнений используются свойства степеней, вспомним некоторые из них:

1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.

$a^n⋅a^m=a^{n+m}$

2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели вычитаются

$a^n:a^m=a^{n-m}$

3. При возведении степени в степень основание остается прежним, а показатели перемножаются

$(a^n)^m=a^{n·m}$

4. При возведении в степень произведения в эту степень возводится каждый множитель

$(a·b)^n=a^n·b^n$

5. При возведении в степень дроби в эту степень возводиться числитель и знаменатель

$({a}/{b})^n={a^n}/{b^n}$

6. При возведении любого основания в нулевой показатель степени результат равен единице

$a^0=1$

7. Основание в любом отрицательном показателе степени можно представить в виде основания в таком же положительном показателе степени, изменив положение основания относительно черты дроби

$a^{-n}={1}/{a^n}$

${a^{-n}}/{b^{-k}}={b^k}/{a^n}$

8. Радикал (корень) можно представить в виде степени с дробным показателем

$√^n{a^k}=a^{{k}/{n}}$

Показательные уравнения часто сводятся к решению уравнения $a^x=a^m$, где, $а >0, a≠1, x$ — неизвестное. Для решения таких уравнений воспользуемся свойством степеней: степени с одинаковым основанием $(а >0, a≠1)$ равны только тогда, когда равны их показатели.

Решить уравнение $25·5^х=1$

Решение:

В левой части уравнения необходимо сделать одну степень с основанием $5$ и в правой части уравнения представить число $1$ в виде степени с основанием $5$

$5^2·5^х=5^0$

При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются

$5^{2+х}=5^0$

Далее проговариваем: степени с одинаковым основанием $(а >0, a≠1)$ равны только тогда, когда равны их показатели

$2+х=0$

$х=-2$

Ответ: $-2$

Решить уравнение $2^{3х+2}-2^{3х-2}=30$

Решение:

Чтобы решить данное уравнение, вынесем степень с наименьшим показателем как общий множитель

$2^{3x+2}-2^{3x-2}=30$

$2^{3x-2}({2^{3x+2}}/{2^{3x-2}}-{2^{3x-2}}/{2^{3x-2}})=30$

$2^{3x-2}(2^{3x+2-(3x-2)}-1)=30$

$2^{3x-2}(2^4-1)=30$

$2^{3x-2}·15=30$

Разделим обе части уравнения на $15$

$2^{3х-2}=2$

$2^{3х-2}=2^1$

$3х-2=1$

$3х=3$

$х=1$

Ответ: $1$

Источник

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.

Квадратное уравнение — это ax² + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b² − 4ac. А вот свойства дискриминанта:

Неполное квадратное уравнение — это уравнение вида ax² + bx + c = 0, где хотя бы один из коэффициентов b или c равен нулю.

Неполные квадратные уравнения бывают трех видов:

Если b = 0, то квадратное уравнение принимает вид ax² + 0x+c=0 и оно равносильно ax² + c = 0.
Если c = 0, то квадратное уравнение выглядит так ax² + bx + 0 = 0, иначе его можно написать как ax² + bx = 0.
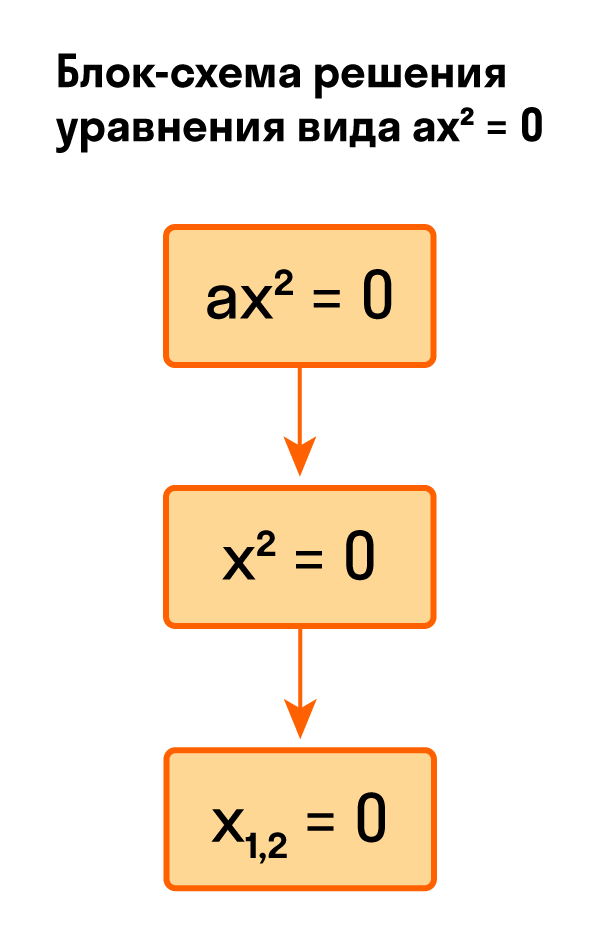
Если b = 0 и c = 0, то квадратное уравнение выглядит так ax² = 0.

Такие уравнения отличаются от полного квадратного тем, что их левые части не содержат слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.

Решение неполных квадратных уравнений

Как мы уже знаем, есть три формулы неполных квадратных уравнений:

ax² = 0, ему отвечают коэффициенты b = 0 и c = 0;
ax² + c = 0, при b = 0;
ax² + bx = 0, при c = 0.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Как решить уравнение ax² = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax² = 0.

Уравнение ax² = 0 равносильно x² = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x² = 0 является нуль, так как 0² = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax² = 0 имеет единственный корень x = 0.

Пример 1. Решить −5x² = 0.

Замечаем, что данному уравнению равносильно x2 = 0, значит исходное уравнение имеет единственный корень — нуль.
По шагам решение выглядит так:

Записывайся на дополнительные уроки по математике онлайн, с нашими лучшими преподавателями! Для учеников с 1 по 11 класса!

Как решить уравнение ax² + с = 0

Обратим внимание на неполные квадратные уравнения вида ax² + c = 0, в которых b = 0, c ≠ 0. Мы знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. То есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax² + c = 0:

перенесем c в правую часть: ax² = — c,
разделим обе части на a: x² = — c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если — c/а 0, то корни уравнения x² = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)² = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)² = — c/а. Ура, больше у этого уравнения нет корней.

В двух словах

Неполное квадратное уравнение ax² + c = 0 равносильно уравнению ax² + c = 0, которое:

не имеет корней при — c/а 0.

Пример 1. Найти решение уравнения 9x² + 4 = 0.

Перенесем свободный член в правую часть:

Разделим обе части на 9:

В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 9x² + 4 = 0 не имеет корней.

Пример 2. Решить -x² + 9 = 0.

Перенесем свободный член в правую часть:

Разделим обе части на -1:

Ответ: уравнение -x² + 9 = 0 имеет два корня -3; 3.

Как решить уравнение ax² + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Квадратное уравнение без с непривычно решать только первые несколько примеров. Запомнив алгоритм, будет значительно проще щелкать задачки из учебника.

Неполное квадратное уравнение ax² + bx = 0 можно решить методом разложения на множители. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.

Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax² + bx = 0 имеет два корня:

Пример 1. Решить уравнение 2x² — 32x = 0

Вынести х за скобки

Это уравнение равносильно х = 0 и 2x — 32 = 0.

Решить линейное уравнение:

Значит корни исходного уравнения — 0 и 16.

Ответ: х = 0 и х = 16.

Пример 2. Решить уравнение 3x² — 12x = 0

Разложить левую часть уравнения на множители и найти корни:

#115 Урок 1. Квадратные уравнения. Дискриминант. Алгебра 8 класс.

Квадратные уравнения. Какое квадратное уравнение называется полным? Формула дискриминанта и корней полного квадратного уравнения. Уравнения с дробями. Как избавиться от всех знаменателей сразу. Алгебра 8 класс. Примеры с решением и объяснением. Видеоуроки по математике. Устранение пробелов в знаниях. Подготовка к ЗНО ( ВНО ) по математике. Подготовка к ЕГЭ, ДПА ( ГИА ), ОГЭ по математике.

#116 Урок 2. Неполные квадратные уравнения. Решение через дискриминант. Алгебра 8 класс.Математика.

Квадратные уравнения. Какое квадратное уравнение называется полным? Какое квадратное уравнение называется неполным? Формула дискриминанта и корней полного квадратного уравнения. Как решать неполное квадратное уравнение через дискриминант. Алгебра 8 класс. Примеры с решением и объяснением.

#117 Урок 3. Квадратные уравнения. Текстовые задачи. Алгебра 8 класс.

Решение текстовых задач составлением квадратного уравнения. Алгебра 8 класс. Примеры с решением.

Пример 1: Найдите три последовательных целых числа, если удвоенный квадрат первого из них на 26 больше произведения второго и третьего чисел.
Пример 2: Найдите четыре последовательных четных числа, если утроенное произведение второго и третьего чисел на 344 больше произведения первого и четвертого.
Пример 3: Найдите стороны прямоугольника, если их разность равна 23 дм, а диагональ 37 дм.
Пример 4: Сколько сторон имеет многоугольник, если в нем можно провести 77 диагоналей.

Задачи с объяснением. Видеоуроки по математике. Устранение пробелов в знаниях. Подготовка к ЗНО ( ВНО ) по математике. Подготовка к ЕГЭ, ДПА ( ГИА ), ОГЭ по математике.

#118 Урок 4 Квадратные уравнения. Параметры. При каком значении параметра уравнение имеет 1 корень.

Квадратные уравнения. Параметры. Алгебра 8 класс. Что такое параметр? Понятие параметра в математике. Определение параметра: Если в уравнение или неравенство наряду с неизвестной величиной входят неизвестные, но фиксированные числа, обозначаемые буквами, то они называются параметрами. Пример: 10х2 +4х+b=0; х — переменная; b — параметр; В уравнениях (неравенствах) коэффициенты при неизвестных или свободные члены заданные не конкретными числовыми значениями, а обозначенные буквами называются параметрами. Примеры с решением и объяснением.

Пример 1: При каком значении а, число 1/3 является корнем уравнения.
Пример 2: При каком значении b имеет единственный корень уравнение? Условие единственности корня. Видеоуроки по математике. Устранение пробелов в знаниях. Подготовка к ЗНО ( ВНО ) по математике. Подготовка к ЕГЭ, ДПА ( ГИА ), ОГЭ по математике.

#119 Урок 5. Параметры. Решение квадратных уравнений с параметрами. Алгебра 8 класс. Математика.

Параметры. Решение квадратных уравнений с параметрами. Алгебра 8 класс. Квадратные уравнения. Примеры с решением и объяснением.

Пример 1: Решить квадратное уравнение с параметром, если коэффициент при х2 фиксированное число.
Пример 2: Решить квадратное уравнение с параметром, если коэффициент при х2 записано с использованием параметра.

#120 Урок 6. Квадратные уравнения с модулем. Алгебра 8 класс. Решить уравнение. Модуль. Математика.

Решение квадратных уравнений с модулем. Алгебра 8 класс. Примеры с решением.

Пример 1: Решить квадратное уравнение с модулем, раскрыв модуль по определению.
Пример 2: Решить квадратное уравнение с модулем, раскрыв модуль, используя свойства модуля.

Квадратные уравнения с модулем 8 класс; квадратное уравнение под модулем; квадратные уравнения с модулем примеры; решение квадратных уравнений с модулем 8 класс; квадратные уравнения с модулем примеры решения; решение квадратных уравнений содержащих модуль; как раскрыть модуль квадратного уравнения. Как решать квадратное уравнение с модулем. Как раскрыть модуль, используя его определение. Определение модуля. Свойства модуля. Решить квадратное уравнение. Решить через дискриминант. Сделать проверку. Посторонние корни. Как убрать посторонние корни. Математика. Образование. Подготовка к егэ, егэ математика, видео уроки, подготовка к зно, вно математика. Видео уроки алгебра, алгебра видеоуроки, онлайн урок, математика видео уроки, онлайн урок, инфо урок, огэ, огэ математика. Дистанционное обучение.

#121 Урок 7. Решение квадратных уравнений с использованием свойств функций. Алгебра 8 класс.

Квадратные уравнения. Использование свойств функций для решения квадратных уравнений. Оценка левой и правой частей уравнения. Сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю. Примеры с решением.

Пример 1: Решить иррациональное уравнение, приводящееся к квадратному, используя свойства функций.
Пример 2: Решить уравнение, преобразовав условие по формулам сокращенного умножения и оценив левую и правую части уравнения.
Пример 3: Решить уравнение с корнем и модулем.

#122 Урок 8. Решение квадратных уравнений с учетом ОДЗ. Область определения. Алгебра 8 класс.

Область определения функции, 4 случая: многочлен, дробь, квадратный корень и квадратные корень в знаменателе. ОДЗ дроби. ОДЗ корня. ОДЗ уравнения. Область определения квадратного корня. Область определения квадратного дроби. Область определения квадратного корня в знаменателе. Что такое область определения. Область определения теория. Область определения, табличка. Примеры с решением. Алгебра 8 класс. Решить квадратное уравнение с учетом ОДЗ. ОДЗ квадратного уравнения; как найти одз в квадратном уравнении; одз корня квадратного уравнения; 2 квадратных уравнения; решение квадратных уравнений; произведение квадратных уравнений; 3 квадратных уравнения. Математика. Образование. Подготовка к егэ, егэ математика, видео уроки, подготовка к зно, вно математика. Видео уроки алгебра, алгебра видеоуроки, онлайн урок, математика видео уроки, онлайн урок, инфо урок, огэ, огэ математика. Дистанционное обучение.

#62 Урок 9. Решение квадратных и кубических уравнений разложением на множители.

Как решить квадратное или кубическое уравнение, разложив его на множители?

Разложить на множители (вынести общий множитель за скобки, посмотреть формулы, посмотреть способ группировки).
Приравнять каждый множитель к нулю.
Решить полученные уравнения.

Формулы сокращенного умножения. Разность квадратов, разность кубов, квадрат разности.Примеры с решением. Решение кубических уравнений. Уравнение четвертой степени. Как решить уравнение?

Пример 1: Решить кубическое уравнение разложением на множители.
Пример 2: Решить кубическое уравнение, используя формулы сокращенного умножения.
Пример 3: Решить кубическое уравнение, используя способ группировки.
Пример 4: Решить уравнение 4-й степени разложением на множители.

Квадратные уравнения. Полное квадратное уравнение. Неполное квадратное уравнение. Дискриминант.

Как решить квадратное уравнение?
Как выглядит формула квадратного уравнения?
Какие бывают квадратные уравнения?
Что такое полное квадратное уравнение?
Что такое неполное квадратное уравнение?
Что такое дискриминант?
Сколько корней имеет квадратное уравнение?
Эти вопросы вас больше не будут мучить, после изучения материала.

Формула квадратного уравнения:

где x — переменная,
a,b,c — числовые коэффициенты.

Виды квадратного уравнения

Пример полного квадратного уравнения:

3x 2 -3x+2=0
x 2 -16x+64=0

Решение полных квадратных уравнений сводится к нахождению дискриминанта:

Если D>0, то уравнение имеет два корня и находим эти корни по формуле:

Корни квадратного уравнения

Если D=0, уравнение имеет один корень

корень уравнения

Записываем сначала, чему равны числовые коэффициенты a, b и c.

Коэффициент a всегда стоит перед x 2 , коэффициент b всегда перед переменной x, а коэффициент c – это свободный член.
a=1,b=-1,c=-6

Находим дискриминант:
D=b 2 -4ac=(-1) 2 -4∙1∙(-6)=1+24=25

Дискриминант больше нуля, следовательно, у нас два корня, найдем их:

Нахождения корней по дискриминанту

Пример №2:
x 2 +2x+1=0
Записываем, чему равны числовые коэффициенты a,b и c.
a=1,b=2,c=1
Далее находи дискриминант.
D=b 2 -4ac=(2) 2 -4∙1∙1=4-4=0
Дискриминант равен нулю, следовательно, один корень:
x=-b/2a=-2/(2∙1)=-1

Пример №3:
7x 2 -x+2=0
Записываем, чему равны числовые коэффициенты a,b и c.
a=7,b=-1,c=2
Далее находи дискриминант.
D=b 2 -4ac=(-1) 2 -4∙7∙2=1-56=-55
Дискриминант меньше нуля, следовательно, корней нет.

Рассмотрим неполное квадратное уравнение:
ax 2 +bx=0, где числовой коэффициент c=0.

Пример как выглядят такие уравнения:
x 2 -8x=0
5x 2 +4x=0

Чтобы решить такое уравнение необходимо переменную x вынести за скобки. А потом каждый множитель приравнять к нулю и решить уже простые уравнения.

ax 2 +bx=0
x(ax+b)=0
x₁=0 x₂=-b/a

Пример №1:
3x 2 +6x=0
Выносим переменную x за скобку,
x(3x+6)=0
Приравниваем каждый множитель к нулю,
x₁=0

3x+6=0
3x=-6
Делим все уравнение на 3, чтобы получить у переменной x коэффициент равный 1.
x=(-6)/3
x₂=-2

Пример №2:
x 2 -x=0
Выносим переменную x за скобку,
x(x-1)=0
Приравниваем каждый множитель к нулю,
x₁=0

Рассмотрим неполное квадратное уравнение:
ax 2 +c=0, где числовой коэффициент b=0.

Чтобы решить это уравнение, нужно записать так:
x 2 =c/a , если число c/a будет отрицательным числом, то уравнение не имеет решения.
А если c/a положительное число, то решение выглядит таким образом:

корень квадратного уравнения

Пример №1:
x 2 +5=0
x 2 =-5, видно, что -5 2 -12=0
3x 2 =12
x 2 =12/3
x 2 =4

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

источники:

http://math.xfresh.info/index.php/8-klass/algebra-8-klass/38-kvadratnye-uravneniya

http://tutomath.ru/baza-znanij/kvadratnye-uravneniya-polnoe-kvadratnoe-uravnenie-nepolnoe-kvadratnoe-uravnenie-diskriminant.html

Источник

Каталог заданий.
1. Решите неполное квадратное уравнение

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Тип 4 № 122