Тип 18 № 505251
Целое число S является суммой не менее пяти последовательных членов непостоянной арифметической прогрессии, состоящей из целых чисел.
а) Может ли S равняться 9?
б) Может ли S равняться 2?
в) Найдите все значения, которые может принимать S.
Аналоги к заданию № 505245: 505251 Все
Источник: ЕГЭ по математике 08.05.2014. Досрочная волна, резервная волна. Вариант 2, Задания 19 (С7) ЕГЭ 2014
Классификатор алгебры: Последовательности и прогрессии
Решение
а) Один из самых простых способов проверить, является ли натуральное число простым, — это проверить его чётность. Среди чётных чисел простым является только 2.
Пусть d — разность арифметической прогрессии. Тогда a_{n+2}=a_n+2d и d — целое ненулевое число (d=a_2 -a_1 ), значит, a_n и a_{n+2} — различные числа одинаковой чётности.
Отсюда c_n=a_n ^2 +a_{n+2} ^2 чётно и больше 2 (действительно, сумма квадратов двух различных нечётных натуральных чисел не меньше 1^2+3^{2}, аналогично рассматриваются квадраты чётных чисел). Значит, c_n не является простым ни при каком n.
б) S_k=b_1 (1+q+. . . +q^{k-1} ), где q — знаменатель прогрессии. Будем рассматривать только случай b_1=1 (иначе существует не более одного простого числа среди S_k , хотя ровно одно (b_1 ) может быть простым). Вспомним, что число 1 к простым по определению не относится.
Заметим, что если q — нечётно, то все b_k нечетны, а потому чётность чисел S_k будет чередоваться, при этом при k > 2 для всех S_k выполняется неравенство S_k geqslant 1+3 > 2. Значит, среди S_k существует не более одного простого числа подряд.
Если же q — чётное и простое, то q=2. Тогда S_k=2^k -1. В частности, S_1=1, S_2=3, S_3=7, S_4=15 и т.д.
Но 2^{2n} имеет остаток 1 при делении на 3, значит, S_{2n} делится на 3. То есть при k > 2 любые члены S_k и S_{k+1} больше 3 и один из них делится на 3, то есть не более 1 простого числа подряд. При k=2 числа S_k и S_{k+1} равны соответственно числам 3 и 7, то есть являются простыми. Таким образом, два простых числа подряд. Так как число 1 не является простым, то трёх простых членов подряд среди S_k нет.
Итак, среди чисел S_k возможно не более двух простых чисел подряд. Пример: b_1=1, q=2; члены S_2 и S_3 — простые числа.
в) Здесь также будем рассматривать только случай b_1=1.
c_n=n+q^n+q^{n+1}.
Очевидно, что в последовательности чисел c_n чередуется чётность членов. Так как при этом все c_n > 2, то возможно не более одного простого числа c_n подряд.
Пример простого члена c_{n}:, q=2, n=1, c_1=7.
Ответ
а) 0; б) 2; в) 1.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
Заголовок сообщения: Сумма первых членов НЕПОСТОЯННОЙ арифметической прогрессии
|
|||
|
Так, задачка для настоящих матанофагов Непостоянная значит что разность (d) это не одно и тоже число, у меня случай когда разность сама идёт как прогрессия но уже простая сами разности раскладываются как простая арифметическая прогрессия. Аноны нерды, надеюсь на вас!
|
||
| Вернуться к началу |
|
||
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Сумма квадратных корней членов арифметической прогрессии
в форуме Задачи со школьных и студенческих олимпиад |
NICO |
1 |
275 |
25 мар 2020, 16:04 |
|
Найти 1-й член и сумму 10 членов арифметической прогрессии
в форуме Алгебра |
Anastoisia |
1 |
461 |
12 дек 2013, 12:47 |
|
Количество первых членов прогрессии по их сумме
в форуме Алгебра |
EnderWiggin |
13 |
326 |
28 дек 2019, 13:58 |
|
Сумма арифметической прогрессии n от 1 до 10
в форуме Алгебра |
afraumar |
6 |
500 |
02 апр 2015, 12:59 |
|
Сумма утроенного второго и четвертого членов арифметической
в форуме Алгебра |
Dima Rudik |
1 |
453 |
16 мар 2020, 11:10 |
|
Сумма n членов геометрической прогрессии
в форуме Алгебра |
Gorbunov Stepan |
1 |
103 |
25 фев 2021, 15:26 |
|
Три последовательных члена арифметической прогрессии
в форуме Алгебра |
metallcort |
2 |
704 |
12 дек 2013, 18:47 |
|
Найти разность и первый член арифметической прогрессии
в форуме Алгебра |
Anastoisia |
1 |
481 |
12 дек 2013, 12:46 |
|
Несколько первых членов разложения в степенной ряд
в форуме Дифференциальное исчисление |
graft |
6 |
352 |
15 дек 2015, 09:31 |
|
Найти сумму n первых членов ряда
в форуме Ряды |
makc2299 |
1 |
287 |
24 янв 2019, 20:07 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 3 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Определение числовой последовательности
Числовая последовательность — это множество чисел, каждому из которых можно присвоить уникальный номер.
Последовательности можно задавать разными способами:
- Словесно — когда правило последовательности объясняется словами:
«Последовательность простых чисел: 4, 6, 10, 19, 21, 33…»
- Аналитически — когда указана формула ее n-го члена: yn = f(n).
Последовательность yn = C называют постоянной или стационарной.
- Рекуррентно — когда указывается правило, которое помогает вычислить n-й член последовательности, если известны её предыдущие члены.
Арифметическая прогрессия — (an), задана таким соотношением:
a1 = a, an+1= an + d.Последовательность Фибоначчи — когда каждое следующее число равно сумме двух предыдущих чисел: an+1 = an
+ an-1.
Пример: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…
- Графически — когда график последовательности состоит из точек с абсциссами
1, 2, 3, 4…
Так как алгебраическая числовая последовательность — это частный случай числовой функции, то ряд свойств функций рассматриваются и для последовательностей.
Свойства числовых последовательностей:
- Последовательность {yn} называют возрастающей, если каждый ее член кроме первого больше предыдущего:
y1 < y2 < y3 < … < yn < yn+1 < …
- Последовательность {yn} называют убывающей, если каждый ее член кроме первого меньше предыдущего:
y1 > y2 > y3 > … > yn > yn+1 > …
Возрастающие и убывающие последовательности называют монотонными последовательностями.
- Последовательность можно назвать периодической, если существует такое натуральное число T, что начиная с некоторого N, выполняется равенство: yn = yn+T.
Число T — длина периода.
Запишем числа, которые первые пришли в голову: 7, 19, 0, -1, 2, -11, 0… Сколько бы чисел не написали, всегда можно сказать, какое из них первое, какое — второе и так до последнего. То есть мы можем их пронумеровать.
Пример числовой последовательности выглядит так:
В такой математической последовательности каждый номер соответствует одному числу. Это значит, что в последовательности не может быть двух первых чисел и т.д. Первое число (как и любое другое) — всегда одно.
N-ный член алгебраической последовательности — это число с порядковым номером n.
Всю последовательность можно обозначить любой буквой латинского алфавита, например, a. Каждый член этой последовательности — той же буквой с индексом, который равен номеру этого члена: a1, a2,…, a10…, an.
N-ый член последовательности можно задать формулой.
- Формула an = 3n — 5 задает последовательность: −2, 1, 4, 7, 10…
- Формула an = 1 : (n + 2) задает последовательность: 13, 14, 15, 16…
Определение арифметической прогрессии
Так как числовая последовательность — это частный случай функции, которая определена на множестве натуральных чисел, арифметическую прогрессию можно назвать частным случаем числовой последовательности.
Рассмотрим основные определения и как найти арифметическую прогрессию.
an+1= an + d, где d — это разность арифметической прогрессии.
Описать словами эту формулу можно так: каждый член арифметической прогрессии равен предыдущему, сложенному с одним и тем же числом d.
Разность между последующим и предыдущим членами, то есть разность арифметической прогрессии можно найти по формуле:
Если известны первый член a1 и n-ый член прогрессии, разность можно найти так:
Арифметическая прогрессия бывает трех видов:
- Возрастающая — арифметическая прогрессия, у которой положительная разность, то есть d > 0.
Пример: последовательность чисел 11, 14, 17, 20, 23… — это возрастающая арифметическая прогрессия, так как ее разность d = 3 > 0.
- Убывающая — арифметическая прогрессия, у которой отрицательная разность, то есть d < 0.
Пример: последовательность чисел 50, 48, 46, 44, 43… — это убывающая арифметическая прогрессия, так как ее разность d = –2 < 0.
- Стационарная — арифметическая прогрессия, у которой разность равна нулю, то есть d = 0.
Пример: последовательность чисел 23, 23, 23, 23, 23… — это стационарная арифметическая прогрессия, так как ее разность d = 0.
Свойство арифметической прогрессии
Переведем с языка формул на русский: каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних с ним членов. Что как раз объясняет название «арифметическая» прогрессия.
Рассмотрим пример арифметической прогрессии.
Дано: арифметическая прогрессия (an), где a1 = 0 и d = 2.
Найти: первые пять членов прогрессии и десятый член прогрессии.
Решение арифметической прогрессии:
- Чтобы найти последующий член прогрессии, нужно к предыдущему прибавить разность:
a2 = a1 + d = 0 + 2 = 2;
a3 = a2 + d = 2 + 2 = 4;
a4 = a3 + d = 4 + 2 = 6;
a5 = a4 + d = 6 + 2 = 8.
- Используем общую формулу an = a1 + d * (n — 1).
По условиям задачи n = 10, подставляем в формулу:
a10 = a1 + 2 * (10 — 1) = 0 + 2⋅9 = 18.
Формулы арифметической прогрессии
В 9 классе проходят все формулы арифметической прогрессии. Давайте узнаем, какими способами ее можно задать:
- Рекуррентной формулой:
- Формулой n-го члена: an = a1+ d · (n — 1).
- Формулой вида an = kn + b, где k и b — числа, n — число членов последовательности.
Сумма первых n членов арифметической прогрессии (аn) обозначается Sn:
Формулы нахождения суммы n членов арифметической прогрессии:
Чтобы быстрее запомнить формулы можно использовать такую табличку с основными определениями:
Формула n-го члена арифметической прогрессии
Из определения арифметической прогрессии следует, что равенство истинно:
Поэтому:
и т.д.
Значит,
Переведем с языка формул на русский: если мы знаем первый член и разность арифметической прогрессии, то можем найти любой ее член.
Арифметическую прогрессию можно назвать заданной, если известен ее первый член и разность.
Формулу an = a1 + d * (n — 1) называют формулой n-го члена арифметической прогрессии.
Доказательство формулы n-го члена арифметической прогрессии
Формулу n-го члена арифметической прогрессии можно доказать при помощи метода математической индукции.
Пусть дано:
Нужно доказать:
Как доказываем:
- Формула верна при n = 1.
Действительно,
- Предположим, что формула верна при n = k, то есть
- Докажем, что формула верна и при n = k + 1, то есть
- Из условия и предположения получаем:
Согласно принципу математической индукции формула верна для любого натурального числа.
Геометрическая прогрессия
Геометрическая прогрессия — это последовательность (bn), в которой каждый последующий член можно найти, если предыдущий член умножить на одно и то же число q.
Если последовательность (bn) является геометрической прогрессией, то для любого натурального значения n справедлива зависимость:
bn+1 = bn * q, где q — знаменатель геометрической прогрессии
Если в геометрической прогрессии (bn) известен первый член b1 и знаменатель q, то можно найти любой член прогрессии:
- b2 = b1 * q;
- b3 = b2 * q = b1 * q * q = b1 * q²;
- b4 = b1 * q³;
- и т. д.
Общий член геометрической прогрессии bn можно вычислить при помощи формулы:
bn = b1 * qn−1, где n — порядковый номер члена прогрессии, b1 — первый член последовательности, q — знаменатель.
Пример 1. 2, 6, 18, 54,… — геометрическая прогрессия b = 2, q = 3.
Пример 2.
Пример 3. 7, 7, 7, 7,… — геометрическая прогрессия b = 7, q = 1.
формула n-го члена прогрессии 9 класс онлайн-подготовка на Ростелеком Лицей |
Тема 10.
Определение арифметической прогрессии: формула n-го члена прогрессии.
Сегодня познакомимся с последовательностью, которая получается по определенному закону (правилу).
Рассмотрим последовательность натуральных чисел, которые при делении на 5 дают в остатке 2.
Каждый ее член, начиная со второго, получается прибавлением к предыдущему члену числа 5. Эта последовательность является примером арифметической прогрессии.
Итак, арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.
Другими словами, последовательность an – арифметическая прогрессия, если для любого натурального n выполняется условие an+1=an+d, где d – некоторое число.
Из определения арифметической прогрессии следует, что разность между любым ее членом, начиная со второго, и предыдущим членом равна d, то есть при любом натуральном n верно равенство:an+1-an=d. Это число d называют разностью арифметической прогрессии.
Чтобы задать арифметическую прогрессию достаточно указать ее первый член и разность.
a1=1 и d=2, то получим арифметическую прогрессию: 1,3,5,7,…
a1=-5 и d=3, то получим арифметическую прогрессию: -5,-2,1,4,7,…
a1=-3 и d=-2, то получим арифметическую прогрессию: -3,-5,-7,…
a1=4 и d=0, то получим арифметическую прогрессию: 4,4,4,4,…
Итак, зная первый член и разность арифметической прогрессии, можно найти любой ее член, вычисляя последовательно второй, третий, четвертый и т.д. Но если надо будет найти сотый, или двухсотый члены, то этот способ не очень удобен.
Давай попробуем вывести формулу для нахождения любого члена арифметической прогрессии.
a2=a1+d
a3=a2+d=a1+d+d=a1+2d
a4=a3+d=a1+2d+d=a1+3d
a5=a4+d=a1+3d+d=a1+4d
Что же мы видим? Что любой член арифметической прогрессии можно найти по формуле: an=a1+dn-1 – это и есть формула n — го члена арифметической прогрессии.
Рассмотрим примеры.
1) Последовательность an – арифметическая прогрессия, в которой a1=2,3 и d=0,36. Найти 101-й член этой прогрессии.
Воспользуемся формулой: an=a1+dn-1
a101=2,3+0,36100-1=2,3+0,36∙100=2,3+36=38,3
Ответ: 38,3
2) Выясним являются ли числа -31,5 и 16 членами арифметической прогрессии (an): 27, 4; 24,3; 21,2; …
В данной арифметической прогрессии
a1=27,4
d=a2-a1=24,3-27,4=-3,1
Запишем формулу n-го члена арифметической прогрессии:
an=a1+dn-1
an=27,4-3,1n-1, то есть
an=27,4-3,1n+3,1
an=30,5-3,1n
Числа -31,5 и 16 будут членами арифметической прогрессии, если существует такое натуральное число n, при котором значение выражения 30,5 — 3,1n = -31,5 (1)
30,5 — 3,1n = 16 (2)
Решим эти уравнения.
А, значит, число -31,5 является двадцатым членом арифметической прогрессии. Число 16 не является членом арифметической прогрессии.
Отсюда понятно, что любую арифметическую прогрессию можно задать формулой an = kn + b, где k и b некоторые числа.
Верно и обратное, если последовательность (an), заданная формулой an = kn + b, где k и b некоторые числа, является арифметической прогрессией.
Рассмотрим еще один пример.
Найти 25-й член и n-й член арифметической прогрессии: -2; -0,5; 1; 2,5; 4;…
Итак, a1 = -2; d = 2,5 — 1 = 1,5.
Воспользуемся формулой n-го члена арифметической прогрессии:
an=a1+dn-1
a25=-2+1,525-1=-2+1,5∙24=34
an=-2+1,5n-1=-2+1,5n-1,5=1,5n-3,5.
Отметим важное свойство арифметической прогрессии.
Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому предыдущего и последующего членов, то есть своих соседей.
Например, дана арифметическая прогрессия: an: … ; 11; x; 27;…
x=11+272=19
Итак, в арифметической прогрессии
an=an-1+an+12.
Итак, сегодня мы познакомились с арифметической прогрессией, ее свойством, а так же вывели формулу n-го члена арифметической прогрессии. А в следующий раз мы выведем формулу нахождения суммы первых n-членов арифметической прогрессии.
Арифметическая прогрессия (ЕГЭ — 2021)
На самом деле формула суммы членов арифметической прогрессии была доказана древнегреческим ученым Диофантом еще в 3 веке, да и на протяжении всего этого времени остроумные люди вовсю пользовались свойствами арифметической прогрессии.
Например, представь Древний Египет и самую масштабную стройку того времени – строительство пирамиды… На рисунке представлена одна ее сторона.
Где же здесь прогрессия скажешь ты? Посмотри внимательно и найди закономерность в количестве песчаных блоков в каждом ряде стены пирамиды.
Чем не арифметическая прогрессия? Посчитай, сколько всего блоков необходимо для строительства одной стены, если в основание кладется ( displaystyle 6) блочных кирпичей.
Надеюсь, ты не будешь считать, водя пальцем по монитору, ты же помнишь последнюю формулу и все, что мы говорили об арифметической прогрессии?
В данном случае прогрессия выглядит следующим образом:
( displaystyle 6;text{ }5;text{ }4;text{ }3;text{ }2; 1).
Разность арифметической прогрессии ( displaystyle ~=text{ }dtext{ }=text{ }-1).
Количество членов арифметической прогрессии ( displaystyle=6).
Подставим в последние формулы наши данные (посчитаем количество блоков 2 способами).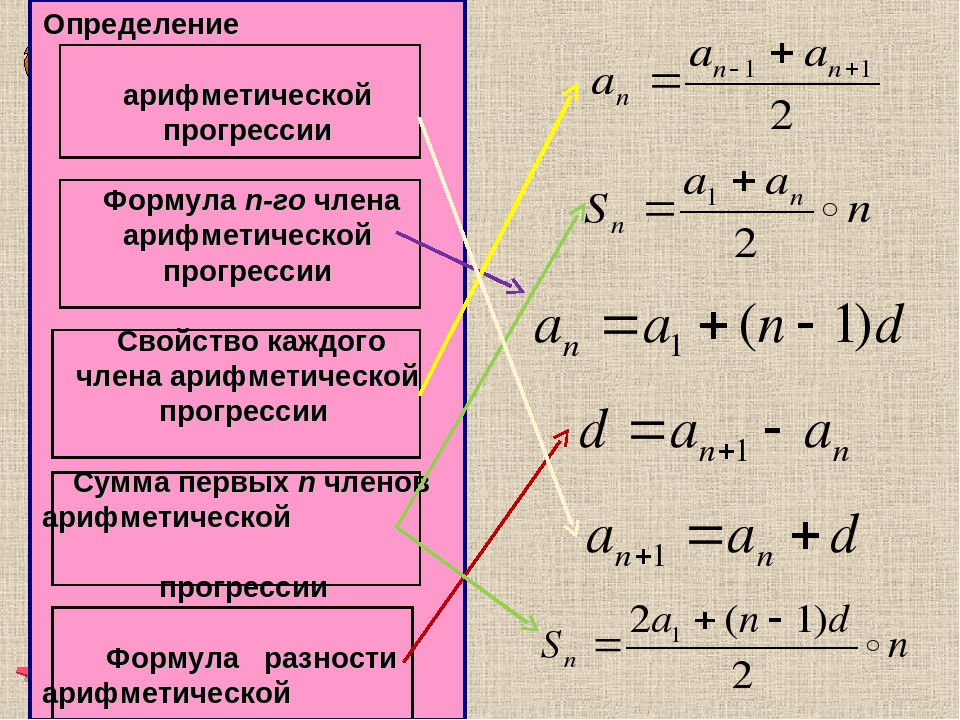
Разность арифметической прогрессии ( displaystyle ~=text{ }dtext{ }=text{ }-1).
Количество членов арифметической прогрессии ( displaystyle=6).
Подставим в последние формулы наши данные (посчитаем количество блоков 2 способами).
Способ 1.
( begin{array}{l}{{S}_{n}}=frac{left( {{a}_{1}}+{{a}_{n}} right)cdot n}{2}\~~{{S}_{6}}=frac{left( 6+1 right)cdot 6}{2}=frac{7cdot 6}{2}=21\~end{array})
Способ 2.
( displaystyle {{S}_{n}}=frac{2{{a}_{1}}+dleft( n-1 right)}{2}cdot n)
( {{S}_{n}}=frac{2cdot 6+1left( 6-1 right)}{2}cdot 6=frac{12+5cdot 6}{2}=frac{7cdot 6}{2}=frac{42}{2}=21)
А теперь можно и на мониторе посчитать: сравни полученные значения с тем количеством блоков, которое есть в нашей пирамиде.
Сошлось?
Молодец, ты освоил сумму ( displaystyle n)-ных членов арифметической прогрессии.
Конечно, из ( displaystyle 6) блоков в основании пирамиду не построишь, а вот из ( displaystyle 60)?
Попробуй рассчитать, сколько необходимо песчаных кирпичей, чтобы построить стену с таким условием.
Справился?
Верный ответ – ( displaystyle 1830) блоков:
( begin{array}{l}{{S}_{n}}=frac{left( {{a}_{1}}+{{a}_{n}} right)cdot n}{2}\{{S}_{60}}=frac{left( 60+1 right)cdot 60}{2}=frac{61cdot 60}{2}=61cdot 30=1830.end{array})
Арифметическая прогрессия. Формула n-го члена и суммы первых n членов арифметической прогрессии
Арифметической прогрессией называется последовательность чисел, в которой каждый член (начиная со второго) получается из предыдущего путем прибавления к нему одного и того же числа d. Число d называют разностью арифметической прогрессии. Для того, чтобы задать арифметическую прогрессию, нужно задать ее первый член a1 и разность.
Примеры арифметических прогрессий:
1. 5, 8, 11, 14, 17… . Здесь первый член равен 5, а разность равна 3.
2 . 10, 8, 6, 4, 2, 0, -2… . Здесь первый член равен 10, а разность равна -2.
Итак, первый член прогрессии равен a1, второй — a1+d, третий a1+d+d = a1+2d, четвертый a1+2d+d = a1+3d ….
Утверждение: Сумма n членов арифметической прогрессии вычисляется по формуле
Докажем это утверждение сначала для четных n.
Рассмотрим последовательность a1, a1+d, a1+2d … a1+(n-3)d, a1+(n-2)d, a1+(n-1)d.
Найдем сумму этой последовательности, группирую слагаемые таким образом: первый член складываем с n-ым, второй с (n-1)-ым, третий с (n-2)-ым, и т. д.
Получим сумму:
Sn = (a1+a1+(n-1)d)+(a1+d+a1+(n-2)d)+(a1+2d+a1+(n-3)d)+ … = (a1+a1+(n-1)d)+(a1+a1+d+nd-2d)+(a1+a1+2d+nd-3d)+ … = (a1+a1+(n-1)d)+(a1+a1+nd-d)+(a1+a1+nd-d)+ .
видим, что получились одинаковые слагаемые. Всего таких слагаемых n/2.
Значит
Докажем теперь это утверждение для нечетных n.
Если n нечетное, значит (n-1)-четное.
Примеры задач на арифметическую прогрессию.
1.Найдите сумму первых 50 членов арифметической прогрессии, если известно, что a1=-2, d=3.
Решение.
Ответ: 3575.
2. Начинающий пловец первый раз проплыл дистанцию за 1 минуту и 55 секунд. Тренер предполагает, что он будет улучшать результат на 1,5 секунды каждый месяц. С каким результатом пловец проплывет эту же дистанцию через 10 месяцев.
Решение.
В этой задаче мы имеем дело с арифметической прогрессией, в которой a1 = 1 мин. 55 сек = 115 сек., d = 1,5 сек.
a11 = a1+(11-1)d = 115-1,5*10 = 100 сек. = 1 мин. 40 сек.
Ответ: 1мин. 40 сек.
Сумма арифметической прогрессии | Онлайн калькулятор
Когда речь идет о таком параметре, как сумма арифметической прогрессии, подразумевается всегда сумма первых членов арифметической прогрессии или сумма членов прогрессии с k по n, то есть количество членов, которые берутся для суммы, строго ограничено в заданных условием пределах. В противном случае задание не будет иметь решения, так как вся числовая последовательность именно арифметической прогрессии начинается с конкретного числа — первого члена a1, и продолжается бесконечно.
Бытует мнение, что формула суммы арифметической прогрессии была открыта еще Гауссом, как быстрый и точный способ расчета суммы чисел в определенной последовательности.
a1+an=a2+a(n-1)=a3+a(n-2)=⋯
Соответственно, он нашел данную сумму и умножил ее на половину от общего количества чисел в последовательности, участвующих в расчете суммы. Таким образом, была выведена формула суммы арифметической прогрессии
Пример. Предположим, задано условие: «Найдите сумму первых десяти (10) членов арифметической прогрессии». Для этого понадобится следующие данные: разность прогрессии и первый ее член. Если в задаче дан какой-либо n член арифметической прогрессии вместо первого, тогда сначала нужно воспользоваться разделом, где представлена формула нахождения первого члена прогрессии, и найти его. Затем исходные данные вбиваются в калькулятор и он производит расчеты, складывая первый и десятый члены, и умножая полученную сумму на половину от общего количества складываемых членов – на 5.
В случае, когда необходимо найти сумму членов арифметической прогрессии, начинающихся не с первого, а с пятого члена, к примеру, тогда среднее арифметическое остается тем же, а общее количество членов берется как увеличенная на единицу разность между порядковыми номерами взятых членов.
Смотрите также
Внеклассный урок — Арифметическая прогрессия
Арифметическая прогрессия
Прогрессия – это определенная последовательность чисел.
Последовательность обозначается так: (an)
Числа, образующие последовательность, называют членами последовательности.
Члены последовательности обычно обозначают буквами с индексами, указывающими порядковый номер члена (a1, a2, a3 и т.д.- читается так: «а первое», «а второе», «а третье» и т.
Последовательность может быть бесконечной или конечной.
Понятие арифметической прогрессии.
Арифметическая прогрессия – это такая последовательность чисел, которая получается в результате сложения каждого последующего члена с одним и тем же числом.
Пример:
Возьмем последовательность чисел 3; 10; 17; 24; 31.
Здесь каждое последующее число на 7 больше предыдущего. То есть последовательность получилась в результате прибавления одного и того же числа 7 к каждому последующему члену. Это и есть арифметическая прогрессия:
3+7=10
10+7=17
17+7=24
24+7=31
Формула арифметической прогрессии.
Любая арифметическая прогрессия может быть задана формулой:
an = kn + b,
где k и b – некоторые числа.
И наоборот: если последовательность задана подобной формулой, то эта последовательность точно является арифметической прогрессией.
Пример: формула an = 8n – 2 является формулой арифметической прогрессии, так как она задана формулой типа an = kn + b. В ней k = 8, b = –2.
Разность арифметической прогрессии.
Разность арифметической прогрессии – это разность между последующим и предыдущим членами прогрессии. Ее обычно обозначают буквой d.
Пример:
Вернемся к нашей прогрессии 3; 10; 17; 24; 31. В ней разность между второй и первой, третьей и второй и т.д. членами равна 7. Число 7 и является разностью данной арифметической прогрессии.
Свойства арифметической прогрессии.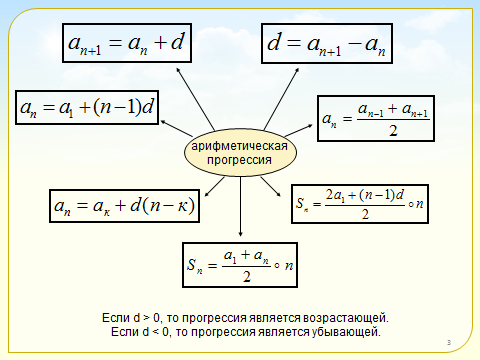
1) Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому предыдущего и последующего членов.
2) Верно и обратное утверждение: если в последовательности чисел каждый член, начиная со второго, равен среднему арифметическому предыдущего и последующего членов, то эта последовательность является арифметической прогрессией.
В нашем примере второй член равен средней арифметической первого и третьего членов:
3 + 17
——— = 10.
2
Точно так же третий член равен средней арифметической второго и четвертого членов и т.д.
Как найти определенный член арифметической прогрессии.
Чтобы найти n-й член арифметической прогрессии, следует применить формулу:
an = a1 + d(n – 1)
Пример:
Возьмем некую арифметическую прогрессию, в которой первый член равен 3, а разность арифметической прогрессии составляет 4.
Дано:
b1 = 3
d = 4
n = 45
———
b45 — ?
Решение.
Применим формулу bn = b1 + d(n – 1):
b45 = 3 + 4(45 – 1) = 3 + 4 · 44 = 3 + 176 = 179.
Ответ: 45-й член заданной арифметической прогрессии – число 179.
Как найти сумму первых n членов арифметической прогрессии.
Сумму любого количества первых членов арифметической прогрессии можно найти
с помощью формулы:
(a1 + an) n
Sn = —————
2
Если заданы первый член и разность арифметической прогрессии, то удобно пользоваться другой формулой:
2a1 + d(n – 1)
Sn = —————— n
2
Пример 1: Найдем сумму первых ста членов арифметической прогрессии 1+2+3+4+5 и т.
Дано:
a1 = 1
n = 100
an = 100
————
S100 — ?
Решение:
(1 + 100) · 100 101 · 100
S100 = ——————— = ————— = 5050
2 2
Ответ: Сумма первых ста членов заданной арифметической прогрессии равна 5050.
Пример 2: Найдем сумму первых двадцати членов арифметической прогрессии, в которой первый член равен 5, разность арифметической прогрессии составляет 3.
Дано:
a1 = 5
d = 3
————
S20 — ?
Решение:
1) Найдем сначала двадцатый член по уже известной нам формуле an = a1 + d(n – 1):
a20 = 5 + 3 (20 – 1) = 5 + 3 · 19 = 62.
2) Теперь уже легко решить нашу задачу.
По формуле 1:
(5 + 62) · 20
S20 = ——————— = 670
2
По формуле 2:
2 · 5 + 3 · (20 – 1)
S20 = ————————— · 20 = 670
2
Ответ: Сумма первых двадцати членов заданной арифметической прогрессии равна 670.
Арифметическая прогрессия и сумма ее членов 🐲 СПАДИЛО.РУ
Определение
Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом.
Другими словами, последовательность (аn) – арифметическая прогрессия, если для любого натурального числа n выполняется условие аn+1=аn+d, где d – некоторое число. Из данного равенства следует, что можно найти это число d, если вычесть из последующего члена предыдущий, то есть d = аn+1–аn. Число d называют разностью арифметической прогрессии.
Арифметической прогрессией, например, является ряд чисел 3; 8; 13; 18….., так как разница между числами равна 5, мы видим, что каждое последующее на 5 больше предыдущего.
Если известен первый член арифметической прогрессии a1 и разность d, то можно вычислить любой член арифметической прогрессии:
a2 = a1 + d;
a3 = a2 + d = a1+2d;
a4 = a3 + d = a1+3d.
Этот ряд можно продолжать до бесконечности, поэтому надо запомнить, что n-ый член арифметической прогрессии можем получить быстрее, если к первому члену прогрессии добавить (n−1) разностей, то есть:
Формула n-ого члена арифметической прогрессии
an = a1 + d(n−1)
где n – порядковый номер члена арифметической прогрессии, a1 – первый член прогрессии, d – разность арифметической прогрессии
Формулу используют, чтобы вычислить заданный член арифметической прогрессии (например, пятнадцатый, двухсотый и т.д.), если известны первый член последовательности и ее разность. Рассмотрим на примерах применение данной формулы.
Пример №1. Найти а20 арифметической прогрессии (аn), если а1=14, d=5. Составляем формулу для а20 и подставляем в нее данные: а20= a1 + d(20−1)=14+5(20−1)=109. Таким образом, мы вычислили, что на 20-ом месте в данной арифметической прогрессии стоит число 109.
Найти а7 арифметической прогрессии (аn), если а1=−8, d=−3. Аналогично работаем, составляя формулу и подставляя в нее данные значения (обращаем внимание на знаки чисел, чтобы не допустить ошибок): а7= a1 + d(7−1)= −8−3(7−1)= −26.
Дана арифметическая прогрессия 10; 12; 14;…… Найти а12. Здесь для нахождения а12 надо сначала найти разность d: d=12−10=2, то есть из последующего вычтем предыдущее. Можно было 14−12, порядок здесь не имеет значения, главное берем два соседних члена прогрессии. Теперь можем составлять формулу и находить а12: а12= a1 + d(12−1)=10+2(12−1)=32.
Утверждение
Любая арифметическая прогрессия может быть задана формулой вида an=kn+b, где k и b некоторые числа. Верно и обратное утверждение: если последовательность чисел задана формулой вида an=kn+b, где k и b некоторые числа, то она является арифметической.
Так, например, формула an=5n+1 задает арифметическую прогрессию, в которой разность d равна 1; по данной формуле можно найти любой член последовательности, например, найдем 20-ый член, подставляя в формулу число 20: a20=5×20+1=101.
Свойство арифметической прогрессии
Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому предыдущего и последующего членов. Формула:
аn=(аn-1+ аn+1):2
Другими словами, используя данное свойство, мы можем найти член арифметической прогрессии, стоящий между двумя известными членами, без использования разности d. Рассмотрим это на примерах.
Пример №2. Найти а10 арифметической прогрессии (аn), если а9=24; а11=38. Здесь используем свойство, так как видим, что у а10 известны соседние члены. Значит, а10=(а9+а11):2=(24+38):2=31. Таким образом, десятый член равен 31.
Дана арифметическая прогрессия …..23; х; 35. Найти х. Применяем свойство для нахождения х: х=(23+35):2=29. Для наглядности запишем, что ряд чисел выглядит так: …23; 29; 35.
Формулы суммы n первых членов арифметической прогрессии
Для нахождения суммы (обозначим ее буквой S) большого количества членов арифметической прогрессии существует формула, позволяющая это сделать быстро.Формула суммы членов арифметической прогрессии с известными членами
Sn= (a1+an )n2.
В данной формуле мы видим, что для нахождения суммы нужны первый и последний член прогрессии. Но встречаются случаи, когда аn не известно, но известна разность. Тогда для нахождения суммы применяют вторую формулу.
Формула суммы членов арифметической прогрессии с первым членом и разностью
Sn=2a1+d(n−1)2..n
Рассмотрим на примерах применение данных формул.
Пример №3. Найти сумму первых пятидесяти членов арифметической прогрессии (аn), если а1=11, а50=39.
Для решения лучше использовать первую формулу, так как здесь есть первый и последний члены: а1=11, а50=39. Поэтому составляем формулу, подставляем в нее данные значения и вычисляем:
S50=(a1+a50 )502..=(11+39)502..=25002..=1250
Найти сумму первых десяти членов арифметической последовательности 3; 18; …. В данном случае задание можно выполнить двумя способами, как по первой формуле, так и по второй, а затем выяснить, какой способ короче, а значит, рациональнее.
Способ №1 (по первой формуле): надо найти разность d, затем десятый член прогрессии, а затем сумму:
d=18-3=15; а10=3+15(10-1)=138
S10=(a1+a10 )102..=(3+138)102..=705
Способ №2 (по второй формуле): надо знать разность d, d=18-3=15. Теперь подставим значения во вторую формулу и сосчитаем результат:
S10=2a1+d(10−1)2..10=2×3+15(10−1)2..10=705
Результаты в обоих случаях получились у нас одинаковые. А если сравнить два способа, то видно, что второй способ быстрее, тем более что в большинстве случаев разность арифметической прогрессии можно вычислить устно.
Таким образом, выбор формулы для нахождения суммы n первых членов арифметической прогрессии зависит от заданного условия.
n-й член арифметической последовательности
Учитывая
арифметическая последовательность
с первым сроком
а
1
и
общая разница
d
, то
п
th
(или общий) термин
дан кем-то
а
п
знак равно
а
1
+
(
п
—
1
)
d
.
Пример 1:
Найти
27
th
член арифметической последовательности
5
,
8
,
11
,
54
,
…
.
а
1
знак равно
5
,
d
знак равно
8
—
5
знак равно
3
Так,
а
27
знак равно
5
+
(
27
—
1
)
(
3
)
знак равно
83
Пример 2:
Найти
40
th
термин для арифметической последовательности, в которой
а
8
знак равно
60
а также
а
12
знак равно
48
.
Заменять
60
для
а
8
а также
48
для
а
12
в формуле
а
п
знак равно
а
1
+
(
п
—
1
)
d
получить
система линейных уравнений
с точки зрения
а
1
а также
d
.
а
8
знак равно
а
1
+
(
8
—
1
)
d
→
60
знак равно
а
1
+
7
d
а
12
знак равно
а
1
+
(
12
—
1
)
d
→
48
знак равно
а
1
+
11
d
Вычтите второе уравнение из первого и решите относительно
d
.
12
знак равно
—
4
d
—
3
знак равно
d
потом
60
знак равно
а
1
+
7
(
—
3
)
. Решить для
а
.
60
знак равно
а
1
—
21 год
81 год
знак равно
а
1
Теперь используйте формулу, чтобы найти
а
40
.
а
40
знак равно
81 год
+
39
(
—
3
)
знак равно
81 год
—
117
знак равно
—
36
.
Смотрите также:
сигма-обозначение ряда
а также
п
th
член геометрической последовательности
Сумма N условий AP | Решенные примеры | Алгебра
Содержание
Мы в Cuemath считаем, что математика — это жизненный навык.Наши эксперты по математике сосредотачиваются на том, «почему» стоит за «что». Учащиеся могут исследовать огромное количество интерактивных листов, наглядных пособий, симуляторов, практических тестов и многого другого, чтобы глубже понять концепцию.
Забронируйте БЕСПЛАТНОЕ пробное занятие сегодня! и поучаствуйте в онлайн-классе Cuemath LIVE вместе со своим ребенком.
Введение
В 19 годах в Германии преподавали математику для 10 класса.
Учитель попросила своих учеников просуммировать все числа от (1 ) до (100 ).
Студенты пытались подсчитать сумму всех этих чисел.
Один мальчик выкрикнул ответ (5050 ), в то время как другие ученики все еще находились на начальных этапах подсчета суммы.
Этим мальчиком был великий немецкий математик Карл Фридрих Гаусс.
Как он так быстро пришел к сумме?
Ну, он заметил, что члены, равноотстоящие от начала и до конца ряда, имеют постоянную сумму, равную (101 ).
Мы видим, что в последовательности (1,2,3 ,.{th} ) срок, (a_n ) известен:
[S_n = frac {n} {2} [a_1 + a_n] ]
Как получить эти формулы?
Мы будем использовать ту же логику, которую использовал выше Карл Фридрих Гаусс.
Рассмотрим арифметическую прогрессию с (n ) членами:
[a, a + d, a + 2d, … (a + (n-2) d), (a + (n-1) d) ]
Сумма (n ) членов этой прогрессии составляет:
[S_n = a + (a + d) + ldots + (a + (n-2) d) + (a + (n-1) d) , , , , , , rightarrow (1) ]
Путем изменения порядка членов этого уравнения:
[S_n = (a + (n-1) d) + (a + (n-2) d) + ldots + (a + d) + a , , , , , , rightarrow (2 ) ]
Мы видим, что сумма соответствующих членов уравнения (1) и уравнения (2) дает ту же сумму, которая равна (2a + (n-1) d ).
Мы знаем, что в указанном выше AP есть полностью (n ) терминов.
Итак, сложив (1) и (2), мы получим:
[ begin {align}
2S_n & = n (2a + (n-1) d) \ [0,3 см]
S_n & = frac {n} {2} (2a + (n-1) d)
end {align} ]
Вышеупомянутая сумма уравнения арифметической прогрессии может быть записана как:
[ begin {align}
S_n & = frac {n} {2} (2a + (n-1) d) \ [0,3 см]
S_n & = frac {n} {2} (a + a + (n-1) d) \ [0.3см]
S_n & = frac {n} {2} (a_1 + a_n) [ потому что a_n = a + (n-1) d text {и} a = a_1]
end {align} ]
Таким образом, сумма уравнений арифметической прогрессии равна:
( begin {align}
S_n & = frac {n} {2} (2a + (n-1) d) \ [0,3 см]
S_n & = frac {n} {2} (a_1 + a_n)
end {align} )
Давайте взглянем на следующую блок-схему, чтобы получить представление о формуле, которая должна использоваться для нахождения суммы арифметической прогрессии в соответствии с доступной нам информацией.
CLUEless по математике? Узнайте, как учителя CUEMATH объяснят вашему ребенку Сумма из n условий AP , используя интерактивное моделирование и рабочие листы, чтобы им больше никогда не пришлось запоминать что-либо по математике!
Изучите интерактивные и персонализированные онлайн-классы Cuemath, которые сделают вашего ребенка экспертом по математике. Забронируйте БЕСПЛАТНОЕ пробное занятие сегодня!
Сумма AP натуральных чисел
AP натуральных чисел:
[1,2,3 ,…, п, … ]
Найдем сумму (n ) членов AP натуральных чисел.
Это будет:
[1 + 2 + 3 + … + n ]
Мы можем найти сумму двумя способами, используя две приведенные выше формулы.
Метод 1
Здесь,
Первый член — (a = 1 ).
Общая разница: (d = 1 ).
Количество терминов (n ).
Подставьте все эти значения в первую сумму формулы AP:
[ begin {align}
S_n & = frac {n} {2} (2a + (n-1) d) \ [0.3см]
S_n & = frac {n} {2} (2 (1) + (n-1) 1) \ [0,3 см]
S_n & = frac {n} {2} (2 + n-1) \ [0,3 см]
S_n & = frac {n (n + 1)} {2}
end {align} ]
Метод 2
Здесь,
Первый член — (a_1 = 1 ).
n-й член вышеуказанного AP равен (a_n = n ).
Подставьте все эти значения во вторую сумму формулы AP:
[ begin {align}
S_n & = frac {n} {2} (a_1 + a_n) \ [0,3 см]
S_n & = frac {n} {2} (1 + n) \ [0.3см]
S_n & = frac {n (n + 1)} {2}
end {align} ]
Таким образом, из описанных выше методов сумма AP натуральных чисел равна:
Сумма AP натуральных чисел (= dfrac {n (n + 1)} {2} )
Сумма бесконечных AP
Рассмотрим пример суммы бесконечной AP.
[2+ 5 + 8 + … ]
Здесь первый член (a = 2 ).
Общая разница: (d = 3 ).
Количество терминов: (n = infty ).
Подставьте все эти значения в формулу суммы AP:
[ begin {align}
S_n & = frac {n} {2} (2a + (n-1) d) \ [0,3 см]
S_n & = frac { infty} {2} (2 (2) + ( infty-1) 3) \ [0,3 см]
S_n & = infty
end {align} ]
Мы обнаружили, что сумма бесконечных AP равна ( infty ), когда
(d> 0 ).
Таким же образом, сумма бесконечных AP равна (- infty ), когда
(d <0 ).
Таким образом,
( text {Сумма бесконечных чисел} A P = left { begin {array} {ll}
infty, & text {if} quad d> 0 [0,3 см]
— infty, & text {if} quad d <0
end {array} right.
)
Важные примечания
- Сумма арифметической прогрессии, первый член которой равен (a ), а общая разница равна (d ), может быть вычислена по одной из следующих формул:
[ begin {align}
S_n & = frac {n} {2} (2a + (n-1) d) \ [0.3см]
S_n & = frac {n} {2} (a_1 + a_n)
end {align} ] -
Сумма AP натуральных чисел:
[ Dfrac {n (n + 1)} {2} ] -
Сумма бесконечных AP:
[ left { begin {array} {ll}
infty, & text {if} quad d> 0 [0,3 см]
— infty, & text {if} quad d <0
end {array} right.
]
Калькулятор суммы AP
Мы можем узнать сумму AP, используя следующий «Калькулятор суммы AP», введя первый член, общую разницу и количество членов.
Помогите своему ребенку набрать больше баллов с помощью запатентованного БЕСПЛАТНОГО диагностического теста Cuemath. Получите доступ к подробным отчетам, индивидуальным планам обучения и БЕСПЛАТНОЙ консультации. Попытайтесь пройти тест сейчас.
Решенные примеры
Вычислите следующую сумму:
[S = underbrace {190 + 167 + 144 + 121 + ldots} _ {20 text {terms}} ]
Решение:
Нам неизвестен последний член в этой последовательности, поэтому мы будем использовать первую формулу для вычисления этой суммы, которая составляет:
[S = frac {n} {2} (2a + (n-1) d) ]
Здесь имеем:
[a = 190, quad d = -23, quad n = 20 ]
Подставляя все эти значения в формулу выше,
[ begin {align} S & = frac {20} {2} (2 (190) + (20-1) (- 23)) \ [0.3см]
& = 10 (380-437) \ [0,3 см]
& = 10 (-57) \ [0,3 см]
& = — 570
end {align} ]
Рассмотрим следующую точку доступа:
[24,21,18, ldots ]
Сколько членов этой AP нужно учесть, чтобы их сумма была (78 )?
Решение:
Обозначим количество членов, дающих сумму (78 ), как (n ).
У нас:
[a = 24, d = -3, quad S = 78 ]
Подставляя все эти значения в первую формулу суммы AP,
[ begin {align}
S = & frac {n} {2} (2 a + (n-1) d) \ [0.{2} -17 n + 52 = 0 \ [0,3 см]
Rightarrow & (n-4) (n-13) = 0 \ [0,3 см]
Rightarrow & n = 4, , , 13
end {align}
]
( поэтому begin {align}
text {Сумма 4-х членов} & = 78 \
text {Сумма 13 членов} & = 78 \
end {align} )
Учитывая (a = 5 ), (d = 3 ) и (a_n = 50 ), найдите значение (S_n ).{th} ) член AP, мы используем следующую формулу, чтобы найти сумму:
[ begin {align} S_n & = frac {n} {2} (a_1 + a_n) \ [0,3 см] S_n & = frac {16} {2} (5 + 50) \ [0,3 см ] S_n & = 8 (55) \ [0,3 см] S_n & = 440 end {align} ]
Сложные вопросы
- Найдите сумму (7 + 10 frac {1} {2} +14+ ldots + 84 ).
- Найдите сумму ( frac {1} {15}, frac {1} {12}, frac {1} {10}, ldots, text {to} 13 text {terms.} )
- Сколько членов АП (9,17,25, ldots ).нужно взять, чтобы получить сумму (636 )?
Практические вопросы
Образцы материалов олимпиады по математике
IMO (Международная олимпиада по математике) — это конкурсный экзамен по математике, который ежегодно проводится для школьников. Он побуждает детей развивать свои навыки решения математических задач с точки зрения соревнований.
Вы можете БЕСПЛАТНО скачать образцы работ по оценкам ниже:
Чтобы узнать больше об олимпиаде по математике щелкните здесь
Часто задаваемые вопросы (FAQ)
1. Какова сумма арифметической последовательности?
Сумма арифметической последовательности — это «сумма первых (n ) членов» последовательности, и ее можно найти с помощью одной из следующих формул:
[ begin {align}
S_n & = frac {n} {2} (2a + (n-1) d) \ [0.{th} ) срок
(S_n ) = сумма первых (n ) членов.
2. Какова сумма n членов AP?
Сумма арифметической последовательности — это «сумма первых (n ) членов» последовательности, и ее можно найти с помощью одной из следующих формул:
[ begin {align}
S_n & = frac {n} {2} (2a + (n-1) d) \ [0,3 см]
S_n & = frac {n} {2} (a_1 + a_n)
end {align} ]
Здесь,
(a = a_1 ) = первый член
(d ) = общая разница
(n ) = количество терминов
(a_n = n ^ {th} ) срок
(S_n ) = сумма первых (n ) членов. {th} ) член
(S_n ) = сумма первых (n ) членов.{n} -1 right)} {r-1} ]
Здесь
(a ) = первый член
(r ) = общее отношение
(n ) = количество терминов
(S_n ) = сумма первых (n ) членов.
4. Какова формула (S_n )?
Мы используем несколько формул при нахождении суммы ряда, представленного как (S_n ).
- Если серия AP, то мы используем следующие формулы, чтобы найти сумму.
[ begin {align}
S_n & = frac {n} {2} (2a + (n-1) d) \ [0.{n} -1 right)} {r-1} ]
Здесь
(a ) = первый член
(r ) = общее отношение
(n ) = количество терминов
(S_n ) = сумма первых (n ) членов.
N-й срок ап | Арифметическая прогрессия | Решенные примеры
Йохана Карла Фредриха Гаусса, отца арифметических прогрессий, попросили найти сумму целых чисел от 1 до 100 без использования счетной рамки.
Он перечислил первые 50 целых чисел и записал следующие 50 в обратном порядке под первым набором.
К его удивлению, сумма чисел рядом друг с другом составила 101, т.е. 100 + 1, 99 + 2, 51 + 50 и т. Д.
Он обнаружил, что таких пар 50, и в итоге умножил 101 на 50, чтобы получить выход 5050
Следите за обновлениями, чтобы узнать больше о n-м члене арифметической прогрессии.
Арифметическая прогрессия может быть определена как последовательность, в которой различия между каждыми двумя последовательными членами одинаковы.
Первый член a этой AP равен 2, второй член равен 5, третий член равен 8 и так далее.Запишем это так:
n-й член этой AP будет обозначен T n .
Важные примечания
- Первый член, как следует из названия, первый член AP — это первое число в прогрессии. Обычно он представлен расширением.
- Поскольку арифметическая прогрессия представляет собой последовательность, в которой каждый член, кроме первого, получается добавлением фиксированного числа к его предыдущему члену, здесь «фиксированное число» называется «общей разницей» и обозначается d.
- n-й член арифметической прогрессии зависит от первого члена и общей разности арифметической прогрессии.
Как определить N-й срок AP?
Мы не можем оценить каждый термин AP, чтобы определить эти конкретные условия. Вместо этого мы должны разработать отношения, которые позволят нам найти n-й член для любого значения n.
Для этого рассмотрим следующие отношения для терминов в AP:
T 1 = a
T 2 = a + d
Т 3 = a + d + d = a + 2d
Т 4 = a + 2d + d = a + 3d
Т 5 = a + 3d + d = a + 4d
Т 6 = a + 4d + d = a + 5d
Какую закономерность вы наблюдаете?
Если нам нужно вычислить, например, шестой член, то мы должны добавить пять раз d (общая разница) к первому члену a.Точно так же, если нам нужно вычислить член n th , сколько раз мы добавим d к a?
Ответ должен быть простым: на единицу меньше n.
Таким образом, формула n-го члена числа ap:
T n = a + (n — 1) d
Это соотношение помогает нам вычислить любой член AP, учитывая его первый член и его общую разницу.
Таким образом, для AP выше имеем:
Т 20 = 2 + (20-1) 3 = 2 + 57 = 59
Т 45 = 2 + (45-1) 3 = 2 + 132 = 134
Т 90 = 2 + (90-1) 3 = 2 + 267 = 269
Т 200 = 2 + (200 — 1) 3 = 2 + 597 = 599
Примеры
Пример 1: Какой 11-й член для данной арифметической прогрессии?
2, 6, 10, 14, 18 ,….
Решение:
В данной арифметической прогрессии
Первый член = а = 2
Общая разница = d = 4
Срок, который предстоит определить, n = 11
Следовательно, 11-й член данной прогрессии равен
T n = a + (n — 1) d
Т 11 = 2 + (11-1) 4 = 2 + 40 = 42
( следовательно ) 11-й член AP составляет 42
Пример 2: Если 5-й член AP равен 40 с общей разницей 6.Узнайте арифметическую прогрессию.
Решение:
Данные значения для точки доступа:
Пятый член = T 5 = 40
Общая разница = d = 6
Следовательно, пятый член можно записать как,
Т 5 = а + (5-1) 6 = а + 24 = 40
( подразумевает ) a = 40-24 = 16
Следовательно, арифметическая прогрессия равна
.
Т 1 = а = 16
Т 2 = a + d = 16 + 6 = 22
T 3 = a + 2d = 16 + (2) (6) = 28
T 4 = a + 3d = 16 + (3) (6) = 34
T 5 = a + 4d = 16 + (4) (6) = 40
T 6 = a + 5d = 16 + (5) (6) = 46
Арифметическая прогрессия: 16, 22, 28, 34, 40, 46 и так далее.
( следовательно ) AP — это 16, 22, 28, 34, 40, 46 и т. Д.
Советы и хитрости
- Общая разница не всегда должна быть положительной.
- Общее различие AP — это разница между двумя последовательными терминами AP, взятыми в этом порядке.
- Согласно формуле n-го члена числа ap, первый член можно найти, используя a = T n — (n — 1) d.
Решенные примеры
Как Джастин может найти 20-й член AP, 3-й член которого равен 5, а 7-й член равен 13?
Решение
Из данной задачи Джастин может найти n-й член числа ap, где n = 20, следующим образом:
Он знает, согласно n-му члену формулы p,
Т 3 = a + 2d = 5
Т 7 = a + 6d = 13
( подразумевает ) 4d = 8
( подразумевает ) d = 2
Поскольку третий член равен 5, значение a может быть задано как,
а + (2) 2 = 5
( подразумевает ) a = 1
Теперь срок можно рассчитать как,
T 20 = a + 19d = 1 + 19 (2) = 39
( следовательно ) Двадцатый член AP равен 39.
Помогите Джеку определить, сколько трехзначных чисел делятся на 3?
Решение
Джек знает, что наименьшее трехзначное число, которое делится на 3, равно 102, а наибольшее трехзначное число, делимое на 3, — 999.
Чтобы найти количество терминов в следующей AP:
102, 105, 108, .., 999
Он возьмет 999 как n-й член AP, видно, что a равно 102, а d равно 3.
Таким образом, согласно n-му члену формулы p,
Т n = a + (n — 1) d = 102 + (n — 1) 3 = 999
( подразумевает ) 3 (n — 1) = 999-102 = 897
( подразумевает ) n — 1 = ( dfrac {897} {3} )
( подразумевает ) n = 300
( следовательно ) Есть 300 трехзначных чисел, которые делятся на 3
Мария считала AP:
7, 11, 15, 19 ,…
Как она определит, является ли число 301 частью этой AP?
Решение
Мария знает, что a равно 7, а d равно 4.
Чтобы определить, является ли 301 частью AP,
Мария будет считать 301 n-м членом этой AP, где n — положительное целое число.
По n-му члену формулы p,
Т n = a + (n — 1) d = 7 + (n — 1) 4 = 301
( подразумевает ) 4 (n — 1) = 301-7 = 294
( подразумевает ) n — 1 = ( dfrac {294} {4} = dfrac {147} {2} )
( подразумевает ) n = ( dfrac {149} {2} )
Мария получила n как нецелое число, тогда как n должно было быть целым числом.
Это может означать только то, что 301 не является частью данной AP.
( следовательно ) 301 не является частью этой AP
Интерактивные вопросы
Вот несколько занятий для вас.
Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Подведем итоги
Мы надеемся, что вам понравилось узнать о n-м члене арифметической прогрессии и n-м члене формулы p с помощью практических вопросов.Теперь вы можете найти n-й член числа ap, используя формулу n-го члена числа ap.
Мини-урок был посвящен увлекательной концепции n-го члена арифметической прогрессии. Математическое путешествие по графическим функциям начинается с того, что студент уже знает, и переходит к творческому созданию новой концепции в молодых умах. Сделано таким образом, чтобы оно не только было понятным и понятным, но и навсегда осталось с ними. В этом заключается магия Куэмат.
О компании Cuemath
В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу «обучение-обучение-обучение» учителя исследуют тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, мы в Cuemath верим в логическое мышление и интеллектуальный подход к обучению.
Часто задаваемые вопросы по N-му сроку AP
1. Что такое AP по математике?
AP разработан как арифметическая прогрессия по математике. Он определяется как последовательность, в которой каждый член, кроме первого, получается добавлением фиксированного числа к его предыдущему члену.
2. Что такое А в AP?
A в AP определяется как арифметический.
3. Какова формула n-го члена AP?
Формула для n-го члена AP: T n = a + (n — 1) d.
4. Какова формула суммы AP?
Формула суммы AP: S n = ( frac {n} {2} ) (2a + (n — 1) d).
5. Какова формула суммы n натуральных чисел?
Формула суммы n натуральных чисел: ( frac {n (n + 1)} {2} )
6. Бесконечна ли арифметическая прогрессия?
Арифметическая прогрессия может быть бесконечной или конечной.
7. Что такое конечная точка доступа и бесконечная точка доступа?
- Точка доступа, в которой количество элементов в последовательности ограничено, называется конечной точкой доступа. Например, 2, 4, 6, 8
- Точка доступа, в которой нет ограничений на количество элементов в последовательности, называется бесконечной точкой доступа. Например, 5, 10, 15, 20, ….
8. Что такое непостоянная арифметическая прогрессия?
Непостоянная арифметическая прогрессия определяется как последовательность, имеющая общие отличия, отличные от 0.Например, 1, 2, 3, 4 и т. Д.
9. Как найти n-й член последовательности с разными различиями?
Шаги, чтобы найти n-й член последовательности с разными различиями:
- Берем разницу между последовательными сроками.
- Если разница между последовательными терминами непостоянна, мы проверяем произошедшее изменение разницы.
- Если происходит изменение разности a, то n-й член задается как ( ( dfrac {a} {2} )) n 2 .
10. В чем разница между арифметической последовательностью и арифметической серией?
- Арифметическая последовательность определяется как последовательность, в которой общая разница между последовательными членами постоянна.
- Арифметический ряд, представляющий собой сумму всех членов арифметической последовательности.
Арифметико-геометрическая прогрессия | Блестящая вики по математике и науке
Теперь, когда мы нашли сумму конечного числа членов, давайте рассмотрим случай бесконечного числа членов.Мы, конечно, не можем вручную суммировать бесконечные числа, поэтому нам придется найти общий подход. Начнем с обсуждения проблемы, с которой вы столкнулись в верхней части этой страницы:
12 + 24 + 38 + 416 + 532 + ⋯ =? Large dfrac { color {# 3D99F6} {1}} { color {# D61F06} {2}} + dfrac { color {# 3D99F6} { 2}} { color {# D61F06} {4}} + dfrac { color {# 3D99F6} {3}} { color {# D61F06} {8}} + dfrac { color {# 3D99F6} { 4}} { color {# D61F06} {16}} + dfrac { color {# 3D99F6} {5}} { color {# D61F06} {32}} + cdots = ,? 21 +42 +83 +164 +325 + ⋯ =?
Допустим, данная серия является SSS, тогда
S = 12 + 24 + 38 + 416 + 532 + ⋯.S = dfrac 12 + dfrac 24 + dfrac 38+ dfrac {4} {16} + dfrac {5} {32} + cdots.S = 21 +42 +83 +164 +325 + ⋯.
Умножая SSS на 12 frac 1221, получаем
S2 = 14 + 28 + 316 + 432 + 564 + ⋯. dfrac S2 = dfrac 14 + dfrac 28 + dfrac {3} {16} + dfrac {4} {32} + dfrac {5} {64} + cdots.2S = 41 +82 +163 +324 +645 + ⋯.
Теперь вычитая S2 frac S22S из SSS, получаем
S = 12 + 24 + 38 + 416 + 532 + ⋯ S2 = 0 + 14 + 28 + 316 + 432 + 564 + ⋯ S (1−12) = 12 + 14 + 18 + 116 + 132 + ⋯ ⇒S2 = 12 + 14 + 18 + 116 + 132 + ⋯, begin {array} {rlllllllll}
S & = dfrac 12 & + dfrac 24 & + dfrac 38 & + dfrac {4} {16} & + dfrac {5} {32} + cdots \
dfrac S2 & = 0 & + dfrac 14 & + dfrac 28 & + dfrac {3} {16} & + dfrac {4} {32} + dfrac {5} {64} + cdots \
hline
S left (1- dfrac 12 right) & = dfrac 12 & + dfrac 14 & + dfrac 18 & + dfrac {1} {16} & + dfrac {1} {32} + cdots
Rightarrow dfrac S2 & = dfrac 12 & + dfrac 14 & + dfrac 18 & + dfrac {1} {16} & + dfrac {1} {32} + cdots,
end {array} S2S S (1-21) ⇒2S = 21 = 0 = 21 = 21 +42 +41 +41 +41 +83 +82 + 81 +81 +164 +163 +161 +161 +325 + ⋯ + 324 +645 + ⋯ + 321 + ⋯ + 321 + ⋯,, который является GP.2} = 2 1−21 21 + (1−21) 21 × 21 = 2.
Второе суммирование — это геометрическая прогрессия с суммой до бесконечности 141−12 = 12 frac { frac {1} {4}} {1 — frac {1} {2}} = frac {1} { 2} 1−21 41 = 21.
Следовательно, общая сумма равна 2−12 = 1,5 □ 2 — frac {1} {2} = 1,5 _ square 2−21 = 1,5 □.Решение 2:
Данную серию можно записать как
14 + 38 + 516 + 732 + ⋯. Dfrac 14+ dfrac 38 + dfrac {5} {16} + dfrac {7} {32} + cdots .41 +83 +165 +327 + ⋯.
Умножив и разделив ряд на 444, получим
14 (1 + 32 + 54 + 78 + ⋯).2} right) = dfrac 14 left (2 + 4 right) = 1,5. _ квадрат S = 41 ⎝⎜⎜⎜⎛ 1−21 1 + (1−21) 22⋅21 ⎠⎟⎟⎟⎞ = 41 (2 + 4) = 1,5. □
Решение проблем, указанных ниже, позволит проверить, хорошо ли вы разбираетесь в концепциях и способах решения проблем:
Найдите значение ppp для данного
3 + 14 (3 + p) +142 (3 + 2p) +143 (3 + 3p) + ⋯ = 8. n} n = 1∑∞ 3n2n может быть выражено в форме ab frac { a} {b} ba, где aaa и bbb взаимно простые положительные целые числа.Найдите a − b a — b a − b.
арифметических последовательностей и рядов | Безграничная алгебра
Арифметические последовательности
Арифметическая последовательность — это последовательность чисел, в которой разница между последовательными членами постоянна.
Цели обучения
Вычислить n-й член арифметической последовательности и описать свойства арифметической последовательности
Основные выводы
Ключевые моменты
- Поведение арифметической последовательности зависит от общей разницы [латекс] d [/ латекс].
- Арифметические последовательности могут быть конечными или бесконечными.
Ключевые термины
- арифметическая последовательность : упорядоченный список чисел, в котором разница между последовательными членами постоянна.
- бесконечное : Безграничное, бесконечное, без конца или ограничений; бесчисленное множество.
Арифметическая прогрессия или арифметическая последовательность — это последовательность чисел, такая, что разница между следующими друг за другом членами постоянна.Например, последовательность [латекс] 5, 7, 9, 11, 13, cdots [/ latex] является арифметической последовательностью с общей разницей [латекс] 2 [/ латекс].
- [латекс] a_1 [/ латекс]: первый член последовательности
- [латекс] d [/ латекс]: Общее различие последовательных терминов
- [latex] a_n [/ latex]: [latex] n [/ latex] -й член последовательности
Поведение арифметической последовательности зависит от общей разницы [латекс] d [/ латекс].
Если общая разница, [латекс] d [/ латекс], составляет:
- Положительно, последовательность будет увеличиваться до бесконечности ([latex] + infty [/ latex])
- Отрицательно, последовательность будет регрессировать к отрицательной бесконечности ([latex] — infty [/ latex])
Обратите внимание, что первый член в последовательности можно представить как [латекс] a_1 + 0 cdot d, [/ latex], второй член можно представить как [латекс] a_1 + 1 cdot d, [/ latex ] третий член можно представить как [латекс] a_1 + 2 cdot d, [/ latex], и поэтому следующее уравнение дает [латекс] a_n [/ latex]:
[латекс] a_n = a_1 + (n − 1) cdot d [/ латекс]
Конечно, всегда можно записать каждый термин, пока не будет получен искомый термин, но если нужен 50-й член, это может быть обременительно.
арифметических и геометрических прогрессий | S-cool, сайт доработки
Если у вас есть последовательность 2, 8, 14, 20, 26, то каждый член на 6 больше, чем предыдущий. Это пример арифметической прогрессии (AP) , а постоянное значение, определяющее разницу между любыми двумя последовательными членами, называется общей разницей .
Если арифметическая разность имеет первый член a и общую разность d , то мы можем записать
a, (a + d), (a + 2d) ,… {a + (n-1) d}
, где n -й член = a + (n − 1) d
Сумма арифметических рядов
Сумма арифметических Ряд из n членов находится путем составления n / 2 пар, каждая со значением суммы первого и последнего члена. (Попробуйте это с суммой первых 10 целых чисел, составив 5 пар из 11.)
Это дает нам формулу:
, где a = первый член и l = последний член.
Поскольку последним членом является n th term = a + (n — 1) d, мы можем переписать это как:
(Используйте первую формулу, если вы знаете первый и последний члены; используйте второй, если вы знаете первый член и общее различие.)
Если у вас есть такая последовательность, как: 81, 27, 9, 3, 1, 1/3, 1/9, … , то каждый член составляет одну треть от срок до.
Это можно записать как 81, 81 (1/3), 81 (1/3) 2 , 81 (1/3) 3 , 81 (1/3) 4 ,…
Это пример геометрической прогрессии (GP) , где каждый член кратен предыдущему. Коэффициент умножения называется общим соотношением .
Таким образом, GP с первым членом a и общим соотношением r с n членов может быть обозначен как
a, ar, ar 2 , ar 3 , ar 4 . ..ar n-1 , где n th term = ar n-1
Пример:
В последовательности 400, 200, 100, 50 ,… найдите термин 8 th .
a = 400, r = 0,5, поэтому 8 th term = 400 × 0.5 7 = 3,125
Примечание: Чтобы определить, какой член имеет определенное значение, вам нужно будет использовать логарифмов .
Пример:
В последовательности 2, 6, 18, 54 … какой член первым превышает 1 000 000?
a = 2, r = 3.
2 × 3 n-1 > 1000000
3 n-1 > 500000
(n — 1) log 3> log 500000
n> 12.94
Следовательно:
n = 13
Пример:
В предыдущей последовательности 400, 200, 100, 50 … какой первый член меньше 1?
400 × 0,5 (n-1] <1
0,5 (n-1) <0,0025
(n-1) log 0,5
Следовательно:
n> 9, или n = 10
Примечание: Знак неравенства изменился, потому что мы разделили на отрицательное значение (log 0.5 <0)
Сумма геометрического ряда
Сумму членов можно записать двумя способами.
где a = первый член,
r = обычное отношение и r 1.
(используйте эту формулу, когда r <1).
Пример:
Оценить,
( Примечание: есть 9 членов.)
Первый член — это когда n = 2
(т.е. 2,36 2 = 5,5696)
Используя формулу для сумма геометрической прогрессии дает:
, что составляет примерно 9300 (до 3 с.е.).
Сходимость
Сумма бесконечного ряда существует, если:
-1
Это связано с тем, что каждый последующий член становится меньше, и поэтому ряд будет стремиться к определенному пределу. Этот предел находится с помощью второй из двух формул:
If | г | <1, то при n → ∞ r n → 0
и так:
Пример:
серия 1/3 + (1/3) 2 + (1/3) 3 + (1/3) 4 +… сходится и его сумма равна 1, когда n приближается к ∞.
(Последовательность, такая как n 3 , имеет первые 6 членов как 1 + 8 + 27 + 64 + 125 + 216. По мере приближения n к бесконечности сумма также увеличивается. Следовательно, она не сходится. Этот ряд равен расходящийся .
Каждая точка доступа имеет сумму, которая приближается к бесконечности с увеличением n, поэтому каждая точка доступа расходится.)
Пример
Найти 1 — 1/2 + 1/4 — 1/8 + …
1 — 1/2 + 1/4 — 1/8 + … = 1 + (-1/2) + (-1/2) 2 + (-1/2) 3 +…
Это геометрическая прогрессия, где r = -½, поэтому | г | <1.
Таким образом, этот ряд сходится к:
Два последних элемента информации, которые могут быть полезны:
Среднее арифметическое
Среднее арифметическое двух чисел m и n определяется как:
Среднее арифметическое = ½ (m + n)
Это способ найти пропущенный член между двумя известными терминами.
Пример:
Термин 4 AP равен 14, 6 -й член равен 22.Член 5 th будет средним арифметическим этих двух значений.
то есть (14 + 22) / 2 = 18 (здесь d = 4 и a = 2).
Среднее геометрическое
Среднее геометрическое двух чисел m и n определяется как:
Среднее геометрическое = √ (mn)
Это значение между двумя другими в GP.
Пример:
7 -й член GP равен 6, 9 -й равен 1.5. Срок 8 th :
√ (6 × 1,5) = √9 = 3
Здесь r = 0,5 и a = 384.
Формулы арифметической прогрессии PDF: Получить всю формулу
Формулы арифметической прогрессии : Арифметическая прогрессия (AP) или арифметическая последовательность — это последовательность чисел, такая, что разница между последовательными членами является постоянной. Например: 3, 6, 9, 12, 15,…, 30. Здесь каждое последующее число отличается от предыдущего на 3. Итак, это арифметическая прогрессия с общей разницей 3.
В этой статье мы предоставили определение арифметической прогрессии вместе со всей формулой AP и решенными примерами.
Формулы арифметической прогрессии: что такое арифметическая прогрессия?
Что такое AP? Арифметическая последовательность или прогрессия определяется как последовательность чисел, в которой для каждой пары следующих друг за другом членов мы получаем второе число, добавляя фиксированное число к первому. Фиксированное число, которое должно быть добавлено к любому члену AP, чтобы получить следующий член, известно как общая разница арифметической прогрессии.
AP полная форма — это арифметическая прогрессия. В AP есть 3 основных термина, которые используются для решения математических задач:
- (i) Общая разница (d)
- (ii) n-й срок (a n )
- (iii) сумма первых n условий (S n )
Эти три термина определяют свойство Арифметическая прогрессия. Мы можем понять концепцию арифметической прогрессии на примере.
2, 6, 10, 14, 18, 22,…, 50
Эта AP имеет первый член, a = 2, общую разность, d = 4, и последний член, l = 50.
5, 10, 15, 20, 25, 30,…, 60
Эта AP имеет первый член, a = 5, общую разность, d = 5, и последний член, l = 60.
Получите формулы алгебры ниже:
Формулы арифметической прогрессии
Это основная формула арифметической прогрессии Класс 10:
- (i) Последовательность
- (ii) Общая разница
- (iii) n-й член AP
- (iv) n-й член из последнего члена
- (v) Сумма первых n членов
Давайте посмотрим все формулы подробно.
Формула серии AP
Бесконечная арифметическая последовательность обозначается следующей формулой:
Поведение последовательности зависит от значения общей разности d.
- (i) Если значение «d» равно положительному , то члены увеличиваются до положительной бесконечности .
- Если значение «d» равно отрицательному , то члены увеличиваются до отрицательной бесконечности .
Формула общей разности
Общим отличием является фиксированная константа, значение которой остается неизменным на протяжении всей последовательности. Это разница между любыми двумя последовательными сроками AP. Формула общей разницы AP:
Здесь n + 1 и n — это два последовательных элемента AP.
Энтерпрайз AP Formula
Формула для нахождения n-го члена AP:
Здесь,
a = Первый член
d = Общая разница
n = Количество терминов
a n
38 Давайте разберемся с этой формулой на примере:
Пример: Найдите n-й член AP: 5, 8, 11, 14, 17,…, a n , если количество членов равно 12.
Решение: AP: 5, 8, 11, 14, 17,…, a n (дано)
n = 12
По известной нам формуле a n = a + (n — 1) d
Первый член, a = 5
Общая разница, d = (8-5)
= 3
Следовательно, a n = 5 + (12-1) 3
= 5 + 33
= 38Сумма n членов формулы AP
Для AP сумма первых n членов может быть вычислена, если известны первый член и общее количество членов.Формула для суммы AP:
Здесь,
S = Сумма n членов AP
n = Общее количество терминов
a = Первый член
d = Общая разница
38
Формула суммы арифметической прогрессии, когда даны первые и последние члены:
Когда мы знаем первый и последний член AP, мы можем вычислить сумму AP по следующей формуле:
Деривация:
Рассмотрим AP, состоящий из n членов, имеющих последовательность a, a + d, a + 2d,…, a + (n — 1) × d
Сумма первых n членов = a + (a + d) + (a + 2г) + ……….+ [a + (n — 1) × d] —— (i)
Записывая члены в обратном порядке, получаем:
S = [a + (n — 1) × d] + [a + (n — 2 ) × d] + [a + (n — 3) × d] + ……. (а) —— (ii)Складывая оба уравнения почленно, получаем:
2S = [2a + (n — 1) × d] + [2a + (n — 1) × d] + [2a + (n — 1) × d] +… + [2a + (n — 1) × d] (n-член)
2S = n × [2a + (n — 1) × d] S = n / 2 [2a + (n — 1) × d]Давайте разберемся с этой формулой на примерах:
Пример 1: Найдите сумму следующей арифметической прогрессии: 9, 15, 21, 27,… Общее количество членов — 14.
Решение: AP = 9, 15, 21, 27,…
Имеем: a = 9, d = (15 — 9) = 6 и n = 14
По формуле суммы AP мы знаем:
S = n / 2 [2a + (n — 1) × d]
= 14/2 [2 x 9 + (14 — 1) x 6] = 14/2 [18 + 78]
= 14/2 [96]
= 7 x 96
= 672
Следовательно, сумма AP составляет 672.Пример 2: Найдите сумму следующих AP: 15, 19, 23, 27,…, 75.
Решение: AP: 15, 19, 23, 27,…, 75
У нас есть: a = 15, d = (19-15) = 4 и l = 75
Мы должны найти n.Итак, используя формулу: l = a + (n — 1) d, получаем
75 = 15 + (n — 1) x 4
60 = (n — 1) x 4
n — 1 = 15
n = 16
Здесь даны первый и последний члены, поэтому по формуле суммы AP мы знаем:
S = n / 2 [первый член + последний член]
Подставляя значения, получаем:
S = 16/2 [15 + 75] = 8 x 90
= 720
Следовательно, сумма AP равна 720.n-й срок из формулы последнего срока
Когда нам нужно узнать n-й член AP не с самого начала, а с последнего, мы используем следующую формулу:
Здесь,
a n = n-й срок из последнего
l = Последний срок
n = всего = Общая разница
Список формул арифметической прогрессии
Здесь мы представили все арифметические формулы в таблице ниже для вашего удобства.Ознакомьтесь с этими формулами здесь или вы также можете загрузить их в формате PDF.
Последовательность a, a + d, a + 2d, ……, a + (n — 1) d,…. Общая разница d = (a 2 — a 1 ), где 2 и 1 являются последовательным термином и предшествующим термином соответственно. Общий срок (n th term) a n = a + (n — 1) d n th от последний член a n ‘ = l — (n — 1) d, где l последний член Сумма первых n членов S n = n / 2 [2a + (n — 1) d] Сумма первых n членов, если заданы первый и последний член S n = n / 2 [первый член + последний член] Загрузить — Формула арифметической прогрессии PDF
Решенные примеры формул, относящихся к арифметической прогрессии
Давайте посмотрим на некоторые примеры арифметической прогрессии с решениями:
Вопрос 1: Первый член арифметической последовательности равен 4, а десятый член — 67.Какая общая разница?
Решение: Пусть первый член будет a, а общая разность d
Используйте формулу для n-го члена: x n = a + d (n — 1)
Первый член = 4
⇒ a = 4 — —- (1)
Десятый член = 67
⇒ x 10 = a + d (10-1)
= 67
⇒ a + 9d = 67 ——- (2)
Заменить a = 4 из (1 ) в (2)
⇒ 4 + 9d = 67
⇒ 9d = 63
⇒ d = 63 ÷ 9
= 7
Общая разница равна 7.Вопрос 2: Какой тридцать второй член арифметической последовательности -12, -7, -2, 3,…?
Решение: Эта последовательность имеет разность в 5 между каждой парой чисел.
Значения a и d:
a = -12 (первый член)
d = 5 («общая разница»)
Правило может быть вычислено:
x n = a + d (n — 1 )
= -12 + 5 (n — 1)
= -12 + 5n — 5
= 5n — 17
Итак, 32-й член:
x 32 = 5 × 32-17
= 160-17
= 143Вопрос 3: Какой двадцатый член арифметической последовательности 21, 18, 15, 12,…?
Решение: Эта последовательность убывающая, поэтому разница между каждой парой чисел составляет -3.
Значения a и d:
a = 21 (первый член)
d = -3 («общая разница»)
Правило может быть вычислено:
x n = a + d (n-1 )
= 21 + -3 (n-1)
= 21 — 3n + 3
= 24 — 3n
Итак, 20 член:
x 20 = 24 — 3 × 20
= 24-60
= -36Вопрос 4: Какова сумма первых тридцати членов арифметической последовательности: 50, 45, 40, 35,…?
Решение: 50, 45, 40, 35,…
Значения a, d и n:
a = 50 (первый член)
d = -5 (обычная разница)
n = 30 (сколько условия суммирования)Используя формулу суммы AP — S n = n / 2 (2a + (n — 1) d), получаем:
S 30 = 30/2 (2 × 50 + 29 × -5))
= 15 (100 — 145)
= 15 × -45
= -675Вопрос 5: Какова сумма от одиннадцатого до двадцатого (включительно) членов арифметической последовательности: 7, 12, 17, 22,…?
Решение: даны AP: 7, 12, 17, 22,…
Значения a и d:
a = 7 (первый член)
d = 5 (обычная разница)
Чтобы найти сумму с одиннадцатого по двадцатый член вычитаем сумму первых десяти членов из суммы первых 20 членовСледовательно, сумма с одиннадцатого по двадцатый слагаемые = 1090 — 295
= 795Другие важные статьи по математике:
Задачи арифметической прогрессии
Вот несколько вопросов по арифметической прогрессии для практики.
Вопрос 1: Какой седьмой член арифметической прогрессии 2, 7, 12, 17,…?Вопрос 2: Какова сумма первых 50 нечетных положительных целых чисел?
Вопрос 3: 13 + 28 + 43 + ⋯ + a n = 68210
Члены n , добавляемые в левой части приведенного выше уравнения, образуют арифметическую прогрессию в этом порядке. Что такое n ?Вопрос 4: Рассмотрим арифметическую прогрессию, у которой первый член и общая разность равны 100.Если n -й член этой прогрессии равен 100 !, найдите n .
Вопрос 5: Вы стоите рядом с ведром, и вам поручено собрать 100 картошек, но вы можете нести только одну картошку за раз. Картофель выстроен в линию перед вами, первый картофель находится на расстоянии 1 метра, а каждый последующий картофель расположен еще на расстоянии одного метра. Какое расстояние вы бы преодолели, выполняя эту задачу?
Вопрос 6: Решите следующее выражение:
(100001 + 100003 + 100005+ ⋯ + 199999) / (1 + 3 + 5 + 7 + ⋯ + 99999) =?Вопрос 7: Для определенной арифметической прогрессии с S 1729 = S 29 , где S n обозначает сумму первых n членов, найдите S 1758 .
Вопрос 8: Сунил получил -10 баллов на своем первом экзамене и 15 баллов на 15-м экзамене. Если все его оценки соответствуют арифметической прогрессии с положительной общей разницей, на каком экзамене он получил нулевые оценки?
Также чек
Часто задаваемые вопросы, связанные с формулами арифметической прогрессии
Вот некоторые из часто задаваемых вопросов:
Q1: Что такое арифметическая прогрессия?
A: Арифметическая прогрессия определяется как последовательность чисел, в которой каждое число отличается от предыдущего на постоянную величину (известную как общее различие).
Q2: Что такое формула арифметической прогрессии?
A: Арифметическая последовательность задается как a, a + d, a + 2d, a + 3d,…. Следовательно, формула для нахождения n-го члена:
a n = a + (n — 1) × d.
Сумма n членов AP = n / 2 [2a + (n — 1) × d].Q3: Что такое d в формуле AP?
A: d — общая разница. Арифметическая последовательность — это последовательность чисел, в которой каждый член после первого получается добавлением константы d к предыдущему члену.
Q4: Какова сумма первых n натуральных чисел?
A: С помощью формулы суммы AP мы можем вычислить сумму первых n натуральных чисел.
S = n (n + 1) / 2Q5: Какова сумма первых n четных чисел?
A: Пусть сумма первых n четных чисел равна S n
S n = 2 + 4 + 6 + 8 + 10 + ………………… .. + (2n)
Решение уравнения используя формулу суммы AP, мы получаем:
Сумма n четных чисел = n (n + 1)Q6: Сколько формул имеется в классе 10 арифметической прогрессии?
A: В основном есть две формулы, связанные с арифметической прогрессией:
(i) n-й член AP
(ii) сумма n членов APТеперь вам предоставлена вся необходимая информация о формулах арифметической прогрессии.
Все задачи на прогрессии и последовательности ЕГЭ 2022 математика 11 класс профильный уровень 35 задач с ответами для проверки, подготовка к ЕГЭ 2022 по математике.
Скачать задачи на прогрессии ЕГЭ 2022 с ответами
1)Даны n различных натуральных чисел, составляющих арифметическую прогрессию (3)n . а) Может ли сумма всех данных чисел быть равной 14? б) Каково наибольшее значение n, если сумма всех данных чисел меньше 900? в) Найдите все возможные значения n, если сумма всех данных чисел равна 123.
Ответ: а) да; б) 41; в) 3; 6.
2)Пусть K n( ) обозначает сумму квадратов всех цифр натурального числа n. а) Существует ли такое трёхзначное число n, что K n( ) 171? б) Существует ли такое трёхзначное число n, что K n( ) 172 ? в) Какое наименьшее значение может принимать выражение 4 ( ) K n n , если n — трёхзначное число?
Ответ: а) Да; б) нет; в) −582.
3)Даны две последовательности: 2, 4, 8, 16, 14, 10, 2 и 3, 6, 12. В каждой из них каждое число получено из предыдущего по одному и тому же закону. а) Найдите этот закон. б) Найдите все натуральные числа, переходящие сами в себя (по этому закону). в) Докажите, что число 21991 после нескольких переходов станет однозначным.
Ответ: а) удвоенная сумма цифр; б) 18.
4)В последовательности 19752… каждая цифра, начиная с пятой, равна последней цифре суммы предыдущих четырёх цифр. Встретится ли в этой последовательности: а) набор цифр 1234; 3269; б) вторично набор 1975; в) набор 8197?
Ответ: а) нет; б) да; в) да.
5)Целые числа от 1 до n записаны в строчку. Под ними записаны те же числа в другом порядке. Может ли случиться так, что сумма каждого числа и записанного под ним есть точный квадрат а) при n 9 , б) при n 11, в) при n 1996 .
Ответ: а) да; б) нет; в) да.
6)Рассматривается последовательность 1, 1/ 2, 1/ 3, 1/ 4, . а) Существует ли арифметическая прогрессия длины 5 составленная из членов этой последовательности? б) Можно ли составить арифметическую прогрессию бесконечной длины из этих чисел? в) Может ли в прогрессии быть 2013 членов?
Ответ: а) да; б) нет; в) да.
7)Можно ли привести пример пяти различных натуральных чисел, произведение которых равно 792 и а) пять; б) четыре; в) три из них образуют геометрическую прогрессию?
Ответ: а) нет; б) нет; в) да.
8)Возрастающая конечная арифметическая прогрессия состоит из различных целых неотрицательных чисел. Математик вычислил разность между квадратом суммы всех членов прогрессии и суммой их квадратов. Затем математик добавил к этой прогрессии следующий еѐ член и снова вычислил такую же разность. а) Приведите пример такой прогрессии, если во второй раз разность оказалась на 40 больше, чем в первый раз. б) Во второй раз разность оказалась на 1768 больше, чем в первый раз. Могла ли прогрессия сначала состоять из 13 членов? в) Во второй раз разность оказалась на 1768 больше, чем в первый раз. Какое наибольшее количество членов могло быть в прогрессии сначала?
Ответ: а) 2, 3; б) нет; в) 8.
9)Можно ли привести пример пяти различных натуральных чисел, произведение которых равно 1008 и а) пять; б) четыре; в) три из них образуют геометрическую прогрессию?
Ответ: а) нет; б) нет; в) да.
10)а) Существует ли конечная арифметическая прогрессия, состоящая из пяти натуральных чисел, такая, что сумма наибольшего и наименьшего членов этой прогрессии равна 99? б) Конечная арифметическая прогрессия состоит из шести натуральных чисел. Сумма наибольшего и наименьшего членов этой прогрессии равна 9. Найдите все числа, из которых состоит эта прогрессия. в) Среднее арифметическое членов конечной арифметической прогрессии, состоящей из натуральных чисел, равно 6,5. Какое наибольшее количество членов может быть в этой прогрессии?
Ответ: а) нет; б) 2, 3, 4, 5, 6, 7; в) 12.
11)Целое число S является суммой не менее трех последовательных членов непостоянной арифметической прогрессии, состоящей из целых чисел. а) Может ли S равняться 8? б) Может ли S равняться 1? в) Найдите все значения, которые может принимать S.
Ответ: а) да; б) нет; в) любые целые значения, кроме −1 и 1.
12)В возрастающей последовательности натуральных чисел каждые три последовательных члена образуют либо арифметическую, либо геометрическую прогрессию. Первый член последовательности равен 1, а последний 2076. а) может ли в последовательности быть три члена? б) может ли в последовательности быть четыре члена? в) может ли в последовательности быть меньше 2076 членов?
Ответ: а) нет; б) нет; в) да.
13)Число S таково, что для любого представления S в виде суммы положительных слагаемых, каждое из которых не превосходит 1 эти слагаемые можно разделить на две группы так, что каждое слагаемое попадает только в одну группу и сумма слагаемых в каждой группе не превосходит 19 . а) Может ли число S быть равным 38 ? б) Может ли число S быть больше 37,05 ? в) Найдите максимально возможное значение S
Ответ: а) нет; б) нет; в) 37,05
14)Можно ли привести пример пяти различных натуральных чисел, произведение которых равно 1512 и а) пять; б) четыре; в) три из них образуют геометрическую прогрессию?
Ответ: а) нет; б) нет; в) да.
15)Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 10 раз больше, либо в 10 раз меньше предыдущего. Сумма всех членов последовательности равна 3024. а) Может ли последовательность состоять из двух членов? б) Может ли последовательность состоять из трѐх членов? в) Какое наибольшее количество членов может быть в последовательности?
Ответ: а) нет; б) да; в) 549.
16)Возрастающая конечная арифметическая прогрессия состоит из различных целых неотрицательных чисел. Математик вычислил разность между квадратом суммы всех членов прогрессии и суммой их квадратов. Затем математик добавил к этой прогрессии следующий еѐ член и снова вычислил такую же разность. а) Приведите пример такой прогрессии, если во второй раз разность оказалась на 48 больше, чем в первый раз. б) Во второй раз разность оказалась на 1440 больше, чем в первый раз. Могла ли прогрессия сначала состоять из 12 членов? в) Во второй раз разность оказалась на 1440 больше, чем в первый раз. Какое наибольшее количество членов могло быть в прогрессии сначала?
Ответ: а) 1, 2, 3; б) нет; в) 8.
17)Первый член конечной геометрической прогрессии, состоящей из трѐхзначных натуральных чисел, равен 128. Известно, что в прогрессии не меньше трѐх чисел. а) Может ли число 686 являться членом такой прогрессии? б) Может ли число 496 являться членом такой прогрессии? в) Какое наибольшее число может являться членом такой прогрессии?
Ответ: а) да; б) нет; в) 972.
Смотрите также на нашем сайте:
Задание 16 планиметрия ЕГЭ 2022 математика профиль задачи с ответами
Задание 14 ЕГЭ 2022 математика профиль неравенства практика с ответами







 Число T — длина периода.
Число T — длина периода.

