Неравенства и сравнения
В семнадцатом задании нам необходимо сравнить данные числа с положением на координатной прямой или решить и сопоставить решения неравенств с областью на прямой. В данном задании можно пользоваться правилом исключения, поэтому достаточно правильно определить три решения из четырех, выбирая в первую очередь простые. Итак, приступим к разбору 17 задания базового варианта ЕГЭ по математике.
Разбор типовых вариантов заданий №17 ЕГЭ по математике базового уровня
Вариант 17МБ1
[su_note note_color=”#defae6″]
На координатной прямой отмечены точки A, B, C и D.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
| ТОЧКИ
А В С D |
ЧИСЛА
1) log2 10 2) 7/3 3) √26 4) (3/5)-1 |
[/su_note]
Алгоритм выполнения:
- Проанализировать рядом с каким из целых чисел стоит данная точка.
- Проанализировать на каком интервале лежат числа из правого столбца.
- Сравнить полученные интервалы и поставить в соответствие.
Решение:
- Рассмотрим точку А. Ее значение больше 1 и меньше 2.
- Рассмотрим точку B. Ее значение больше 2 и меньше 3.
- Рассмотрим точку С. Ее значение больше 3 и меньше 4.
- Рассмотрим точку D. Ее значение больше 5 и меньше 6.
- Вспомним что такое логарифм.
Логарифм по основанию a от аргумента x — это степень, в которую надо возвести число a, чтобы получить число x.
Обозначение: loga x = b, где a — основание, x — аргумент, b — собственно, чему равен логарифм.
В нашем случае а = 2, x = 10.
То есть нас интересует число 2b = 10. 23 = 8 и 24 = 16, следовательно, b лежит в промежутке от 3 до 4.
Следовательно, 7/3 больше 2 и меньше 3.
Рассмотрим √26. √25 = 5, √36 = 6. Значит, √26 больше 5 и меньше 6.
То есть (3/5)-1 больше 1 и меньше 2.
Поставим в соответствие полученные интервалы.
А – (3/5)-1 – 4
В – 7/3 – 2
С – log2 10 – 1
D – √26 – 3
Ответ: 4213.
Вариант 17МБ2
[su_note note_color=”#defae6″]
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
[/su_note]
Алгоритм выполнения:
- Представить правые и левые части неравенств в виде степени одного и того же числа.
- Сравнить степени, так как основания равны.
- Поставить в соответствие предложенные интервалы.
Решение:
А)
Представим 4 в виде степени с основанием 2. 22 = 4.
Неравенство примет вид:
Основания степеней одинаковы, следовательно, степени соотносятся так же.
то есть, – вариант под номером 2.
Б)
Число 0,5 можно представить как , значит (0,5)x = (2-1) x = 2-x
Неравенство примет вид:
Основания степеней одинаковы, следовательно, степени соотносятся так же.
Если умножить и правую и левую часть неравенства на -1, то знак изменится на противоположный.
то есть, – вариант под номером 1.
В)
Аналогично с вариантом Б.
Число 0,5 можно представить как , значит (0,5)x = (2-1) x = 2-x
Неравенство примет вид:
Основания степеней одинаковы, следовательно, степени соотносятся так же.
Если умножить и правую и левую часть неравенства на -1, то знак изменится на противоположный.
то есть, – вариант под номером 4.
Г)
Представим 4 в виде степени с основанием 2. 22 = 4.
Неравенство примет вид:
Основания степеней одинаковы, следовательно, степени соотносятся так же.
и – вариант под номером 3.
Ответ: 2143.
Вариант 17МБ3
[su_note note_color=”#defae6″]
На прямой отмечены числа m и n.
Каждому из четырёх чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами и отрезками из правого столбца.
[/su_note]
Алгоритм выполнения:
- Найти промежутки в которых лежат числа m и n.
- Оценить интервалы, в которых лежат выражения в левом столбце.
- Поставить им в соответствие интервалы из правого столбца.
Решение:
Из рисунка видно, что число n немного меньше 0, а число m много больше отстоит от 1. Следовательно, их сумма m+n даст число в пределах [1; 2] – вариант ответа под номером 3.
Число m>1, следовательно, при делении на 1 получим положительное число меньше 1. Добавляя небольшое отрицательное значение n останемся в диапазоне [0; 1]. Вариант ответа 2.
Произведение mn положительного и отрицательного чисел дают отрицательное число. Подходит только один вариант [-1; 0] под номером 1.
Г) Квадрат числа m много больше квадрата числа n, поэтому их разница будет положительной и принадлежать диапазону [2; 3] – вариант под номером 4.
Ответ: 3214.
Вариант 17МБ4
[su_note note_color=”#defae6″]
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
[/su_note]
Рассмотрим первое неравенство:
2x≥4
представим 4 как 22, тогда:
2x ≥ 22
x ≥ 2
Остальные неравенства решаются аналогичным образом, достаточно вспомнить, что 0,5 = ½ = 2-1:
2-x ≥ 4
2-x ≥ 22
-x ≥ 2
x≤-2
Ответ: А-4, Б-3, В-2, А-1.
Вариант 17МБ5
[su_note note_color=”#defae6″]
Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установить соответствие между неравенствами и их решениями.
[/su_note]
Алгоритм выполнения
- Решаем по очереди каждое из неравенств (А–Г). При необходимости (для наглядности) отображаем полученное решение на координатной прямой.
- Записываем результаты в форме, которая предложена в столбце «Решения». Находим соответствующие пары «буква–число».
Решение:
А. 2–х+1 < 0,5 → 2–x+1 < 2–1 → –x+1 < –1 → –x < –2 → x > 2. Ответ: х ϵ (2; +∞). Получаем: А–3.
Б.
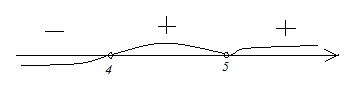
Неравенство преобразований не требует, поэтому сразу применяем метод интервалов, отобразив корни неравенства на координатной прямой.
Корни в данном случае – это х=4 и х=5. Имеем в виду, что неравенство строгое, т.е. значения корней в промежуток для ответа не включаем. В точке х=5 перехода знака не происходит, т.к. по условию (х–5) дано в квадрате. Поскольку нам нужен промежуток, где х<0, то ответ в данном случае: х ϵ (–∞; 4).
Соответственно, имеем: Б–4.
В. log4x > 1 → log4x > log44 → x > 4. Т.е.: х ϵ (4; +∞). Ответ: В–1.
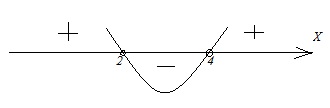
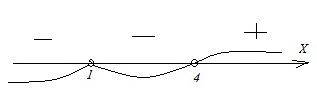
Г. (х–4)(х–2) < 0. Здесь так же, как и в неравенстве Б, нужно сразу отобразить решение на координатной прямой.
Неравенство дано квадратное, его корни – х=2 и х=4. Для получения промежутков с положительными и отрицательными значениями схематически изображаем параболу, пересекающую координатную прямую в точках корней. Промежуток «внутри» параболы отрицательный, промежутки «вне» ее положительны. Т.к. в неравенстве дано «<0», то для ответа следует взять промежуток отрицательных значений. Учитываем, что неравенство строгое. Получаем: х ϵ (2; 4).
Ответ: Г–2.
Вариант 17МБ6
[su_note note_color=”#defae6″]
На координатной прямой отмечены точки А, В, С и D.

Число m равно √2.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
[/su_note]
Алгоритм выполнения
Для каждого из выражений правого столбца делаем следующее:
- Подставляем вместо m его числовое значение (√2). Вычисляем приблизительное значение.
- Ориентируясь на целую часть полученного числа, находим соответствующее значение на координатной прямой.
- Фиксируем пару «буква–число».
Решение:
Это значение на прямой находится между значениями –3 и –2 и соответствует точке А. Получили: А–1.
Число находится между значениями 2 и 3 и соответствует точке D. Имеем: D–2.
Число находится на прямой между 0 и 1. Это – точка С. Имеем: С–3.
Число размещается на прямой между значениями –1 и 0, что отображает т.В. Получаем: В–4.
Вариант 17МБ7
[su_note note_color=”#defae6″]
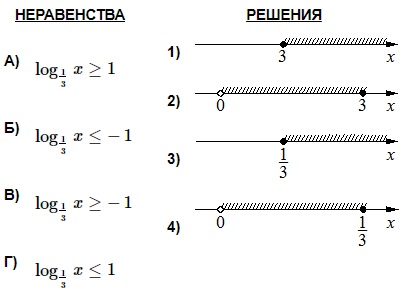
Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установить соответствие между неравенствами и их решениями.
[/su_note]
Алгоритм выполнения
- Последовательно решаем каждое неравенство (А–Г), получая в ответе промежуток значений. Находим соответствующее ему графическое отображение в правой колонке (Решения).
- При решении неравенств учитываем, что: 1) при снятии знаков логарифма с основанием, меньшим 1, знак неравенства меняется на противоположный; 2) выражение под знаком логарифма всегда больше 0.
Решение:
А.
Полученный промежуток-ответ отображен на 4-й координатной прямой. Поэтому имеем: А–4.
Б.
Полученный промежуток представлен на 1-й прямой. Отсюда имеем: Б–1.
В. Это неравенство аналогично предыдущему (Б) с разницей исключительно в знаке. Поэтому и ответ будет подобен с той только разницей, что в конечном неравенстве будет противоположный знак. Т.е. получим: х ≤ 3, х > 0 → x ϵ (0; 3]. Соответственно, получаем пару: В–2.
Г. Это неравенство аналогично 1-му (А), но с противоположным знаком. Поэтому ответ здесь будет таким: х ≥ 1/3, х > 0 → х ϵ [1/3; +∞). Т.о., ответ: Г–3.
Вариант 17МБ8
[su_note note_color=”#defae6″]
Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установить соответствие между неравенствами и их решениями.
[/su_note]
Алгоритм выполнения
- Решаем неравенство А. Находим номер соответствующего ответу решения из правой колонки.
- Рассматриваем неравенство Г как подобное неравенству А. Определяем для него номер решения из правого столбца.
- Решаем неравенство Б, перейдя к основанию 2. Определяем соответствующий для него номер варианта решения.
- По аналогии с неравенством Б решаем неравенство В.
Решение:
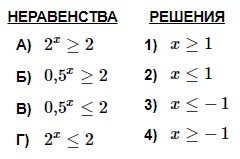
А. 2х ≥ 2 → 2х ≥ 21 → х ≥ 1. Имеем: А–1.
Г. По аналогии с неравенством А получаем в ответе: х ≤ 1. Имеем: Г–2.
Б. 0,5х ≥ 2 → (1/2)х ≥ 2 →2–х ≥ 21 х ≤ –1. Имеем: Б–3.
В. По аналогии с неравенством Б получаем в ответе: х ≥ –1. Имеем: В–4.
Вариант 17МБ9
[su_note note_color=”#defae6″]
Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
[/su_note]
Алгоритм выполнения
- Подобные неравенства решаются методом интервалов. На координатной прямой отмечаются точки, являющиеся корнями соответствующего кв.ур-ния; промежутки между этими точками имеют определенные знаки, причем 1-й из них справа (от +∞ до самого большого корня) всегда имеет знак «+». Далее, продвигаясь справа налево, знаки чередуем, т.е. 2-й справа промежуток будет иметь знак «–», 3-й – «+» и т.д.
- Если в неравенстве имеется выражение вида (х–а)2, то знак промежутка при прохождении точки а не меняется.
- Поскольку все неравенства строгие, то точки-корни в промежутки для ответов не включаются, что в результате фиксируется посредством круглых скобок.
- Знак «ᴗ» является объединяющим и должен прочитываться как «или».
Решение:
Корнями в этих неравенствах являются х=1 и х=4.
Для неравенства А на прямой имеем:
Результатом здесь будут промежутки с отрицательным знаком, т.е. х < 1 или 1 < x < 4. Ответ: А–3.
Для неравенств Б и В получаем на прямой:
Для ответа в неравенстве Б следует взять промежутки со знаком «+». Получим: х < 1 или x > 4. Ответ: Б–1.
В неравенстве В нужно взять промежуток с отрицательным знаком. Тогда имеем: 1 < x < 4. Ответ: В–4.
Б. Отмечаем на прямой корни и промежутки с соответствующими знаками:
Для неравенства Г на прямой получили:
Результат – промежутки с положительным знаком. Тогда имеем: 1 < x < 4 или x > 4. Ответ: Г–2.
Вариант 17МБ10
[su_note note_color=”#defae6″]
На координатной прямой отмечены точки А, В, С и D.
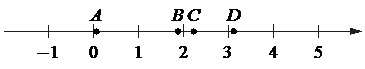
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
[/su_note]
Алгоритм выполнения
- Определяем приблизительное значение чисел, приведенных в правом столбце, или их целую часть, что позволит выяснить, между какими двумя целыми числами на координатной прямой они располагаются.
- Фиксируем пары «буква–число» для заполнения итоговой таблицы ответов.
Решение:
Число 1. log55=1, log525=log552=2log55=2·1=2. Т.к. 5<20<25, то 1<log520<2. Значит, на координатной прямой число log520 отображено точкой В. Ответ: В–1.
Число 2. . Это означает, что число отображено на прямой точкой С. Ответ: С–2.
Число 3. √10 совсем немного больше, чем √9=3. Это число точно меньше 4, поскольку 4=√16. Соответственно, √10 на прямой расположен между 3 и 4 и отображен точкой D. Ответ: D–3.
Число 4. 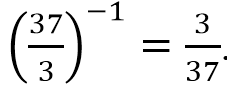
Вариант 17МБ11
[su_note note_color=”#defae6″]
Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
[/su_note]
Алгоритм выполнения
- Решаем последовательно неравенства А–Г, учитывая ОДЗ.
- По результату (полученному простейшему неравенству) находим соответствующее графическое решение из правого столбца.
Решение:
- log2 (x–1) < 1 → log2 (x–1) < log2 2 → x–1 < 2 → x < 3. ОДЗ: х–1 > 0 → x > 1.
Объединяем полученный промежуток с ОДЗ, получаем: x ϵ (1; 3). Это соответствует решению №3. Ответ: А–3.
- . ОДЗ не дает ограничений
Тогда в результате имеем: х ϵ (1; +∞). Ответ: Б–2.
- Здесь не требуются преобразования. Решается неравенство методом интервалов. Точки пересечения с координатной прямой: х=1, х=3. Тогда имеем:
Для решения требуется взять промежутки с положительным знаком. ОДЗ: х≠3. Получаем: х ϵ (1; 3)ᴗ(3; +∞). Ответ: В–4.
- х2 – 4х + 3 > 0 → (x–1)(x–3) > 0. Применив метод интервалов, получим:
ОДЗ не дает ограничений. Значит, х ϵ (–∞; 1)ᴗ(3; +∞). Ответ: Г–1.
Вариант 17МБ12
[su_note note_color=”#defae6″]
На координатной прямой отмечено число m.
Каждому из четырех чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами и отрезками из правого столбца.
[/su_note]
Алгоритм выполнения
- Определяем приблизительное значение для m.
- Подставляем найденное значение для m последовательно в каждое из выражений (А–Г), вычисляем их числовые значения.
- Сопоставляем полученные числа с отрезками, предложенными в правом столбце, находим пары «буква–число» для ответа.
Решение:
Число m располагается на прямой между 1,5 и 2 и немного смещено от середины этого отрезка к двойке. Следовательно, наиболее точным для него является 1,8.
Число А. Имеем: √1,8. Известно, что √1=1, √2≈1,4. Т.е. √1,8 наверняка располагается на отрезке между 1 и 2. Ответ: А–1.
Число Б. Оно равно: 1,83=5,832, т.е. это число принадлежит промежутку [5; 6]. Ответ: Б–4.
Число В. Это число равно: 1,8+1=2,8, что соответствует отрезку [2; 3]. Ответ: В–2.
Число Г. Тут получаем: 6/1,8≈3,33. Этому значению соответствует отрезок [3; 4]. Ответ: Г–3.
Вариант 17МБ13
[su_note note_color=”#defae6″]
Число m равно √0,15.
Каждому из четырех чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами и отрезками из правого столбца.
[/su_note]
Алгоритм выполнения
- Преобразуем число m так, чтобы вынести значение из-под корня.
- Подставляем последовательно полученную величину для m в каждое из выражений в левом столбце. Получаемые результаты соотносим с подходящим отрезком из правого.
Решение:
Число √0,15 очень немногим отличается от √0,16, а из 0,16 можно точно извлечь корень. Делая подобное приближение – всего на 0,01 – мы не выходим за пределы приемлемой абсолютной погрешности. Поэтому имеем право принять, что √0,15≈√0,16=0,4.
Находим значения выражений А–Г и определяем их соответствия отрезкам:
А. –1/0,4=–2,5. Результат соответствует отрезку [–3; –2]. Ответ: А–1.
Б. 0,42=0,16. Число входит в промежуток [0; 1]. Ответ: Б–3.
В. 4·0,4=1,6. Это число находится в интервале [1; 2]. Ответ: В–4.
Г. 0,4–1=–0,6. Результат попадает на отрезок [–1; 0]. Ответ: Г–2.
Вариант семнадцатого задания 2019 года (10)
[su_note note_color=”#defae6″]
На координатной прямой отмечено число m и точки А, В, С и D.
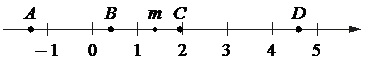
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
[/su_note]
Алгоритм выполнения
- Определяем приблизительное значение для m.
- Вычисляем значения выражений 1–4, находим соответствие между полученными результатами и точками А–D на координатной прямой.
Решение:
Точка m располагается почти посередине между 1 и 2, но немного ближе к 1, чем к 2. Максимально приближенным к реальному в данном случае следует считать значение m=1,4.
Определяем соответствие чисел и точек на прямой:
- 6–1,4=4,6. Это значение отображено точкой D. Ответ: D–1.
- 1,42=1,96. Такое число отображается в точке С. Ответ: С–2.
- 1,4–1=0,4. Это число соответствует точке В. Ответ: В–3.
- Здесь можно не вычислять результат, поскольку имеет место единственное отрицательное число, а на прямой обозначена единственная точка слева от 0 – т.А. Ответ: А–4.
Даниил Романович | Просмотров: 18.6k
Алгебра и начала математического анализа, 11 класс
Урок №51. Неравенства. Методы решения неравенств.
Перечень вопросов, рассматриваемых в теме:
- Методы решения неравенств.
- Применение методов решения к неравенствам различного вида.
- Примеры решения задач государственной итоговой аттестации
Глоссарий по теме
Неравенство. Пусть заданы функции f(x) и g(x). Если относительно неравенства 
Система неравенств. Если ставится задача найти множество общих решений двух или нескольких неравенств, то говорят, что надо решить систему неравенств.
Основная литература:
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. Под ред. А.Б. Жижченко. Алгебра и начала математического анализа. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни. – 2-е изд. – М.: Просвещение, 2010.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.
Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.
Теоретический материал для самостоятельного изучения
Основной методы решения неравенств
Итак, можно сделать следующий вывод. Метод интервалов применим к неравенствам различных типов
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Решите неравенство
Выберите верный ответ из предлагаемых.
Решение.
Введем новую переменную
Получим неравенство 
Возвращаясь к первоначальной переменной получим ответ
Ответ:
Пример 2.
Решите неравенство. Найдите значения переменных a, b, c, d
Ответ:
Правильный вариант:
– радикал
- b = 1 — степень
- c = 3- корень
— логарифм
Решение:
Рассмотрим основание логарифма:
Учитывая это условие получим
Решаем квадратное неравенство и получаем ответ

Уравнения
Уравнения содержатся во всех частях контрольных и измерительных материалов. В части 1 – базового уровня трудности, в части 2 – более трудные, в части 3 – самые трудные, требующие хорошего знания теоретического материала, умения проводить исследования различных ситуаций. В частности, предлагаются уравнения следующих типов:
- показательные;
- логарифмические;
- тригонометрические;
- иррациональные;
- уравнения, содержащие неизвестную в основании и показателе степени;
- уравнения смешанного типа, включающие различные функции.
Для выполнения заданий этого раздела нужно владеть определением корня уравнения (решения неравенства), уметь решать простейшие уравнения и простейшие неравенства. Эти умения позволят успешно применить общие методы решения уравнений (метод замены, метод разложения на множители, графический метод, использование свойств функций) к различным видам уравнений.
Решение уравнений (неравенств) любого вида сопряжено с проведением тождественных преобразований различных выражений, входящих в заданное уравнение (неравенство). Владение формулами для тождественных преобразований выражений и теоремами о равносильных уравнениях (неравенствах) поможет в поиске рационального решения.
Если задания базового уровня, используемые в контрольно-измерительных материалах, нередко текстуально совпадают с заданиями учебников, то задания повышенного уровня более разнообразны. Поэтому для подготовки к ЕГЭ полезно специально тренироваться в решении заданий, содержащихся в КИМ, или аналогичных им. Начнем с уравнений смешанного типа, включающих различные функции, содержащихся во второй части КИМ.
Вначале рассмотрим уравнения, в которых равны нулю произведения двух функций. Напомним, что произведение нескольких множителей равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а остальные существуют.
- Найдите сумму корней уравнения .
Ответ: 5.
- Найдите сумму корней уравнения
Ответ: 0,25.
- Найдите количество корней уравнения
Ответ: 4.
В следующем примере необходимо применить функциональный подход: рассмотреть уравнение как равенство значений двух функций. Поскольку функции совершенно различны (относятся к разным классам функций), нужно сравнить множества их значений.
- Решите уравнение
В левой части уравнения – квадратичная функция. Выделим полный квадрат: . Теперь понятно, что множество ее значений – интервал .
В правой части уравнения – функция . Множество ее значений – отрезок . Следовательно, решением исходного уравнения являются те и только те значения переменной, при которых значения левой и правой частей равны числу 4. Квадратичная функция принимает значение только при Найдем значение функции при полученном значении х: Итак, — единственный корень данного уравнения. Ответ: -0,75.
Если рассматривать логарифмические уравнения второй части КИМ, то основная сложность решения их связана с тем, что большинство преобразований, основанных на свойствах логарифмов, не являются тождественными – при их выполнении может изменяться область допустимых значений входящих в выражения переменных. Это может приводить к потере корней (решений) или появлению так называемых посторонних корней (решений). Поэтому желательно выполнять только тождественные преобразования.
- Сколько корней имеет уравнение ?
Воспользуемся основным логарифмическим тождеством и получим систему, равносильному данному уравнению: Очевидно, что полученная система не имеет решений, так как единственный корень уравнения – отрицательное число, которое не удовлетворяет неравенству системы. Итак, исходное уравнение не имеет корней.
Ответ: 0.
- Найдите меньший корень уравнения
Учитывая, что , преобразуем исходное уравнение
или .
Ответ: -30.
- Найдите меньший корень уравнения
Так как логарифмическая функция определена на множестве положительных чисел, то а значит, Поэтому корни надо искать на множестве отрицательных чисел. Но тогда и уравнение принимает вид Сделав замену , приходим к уравнению , корнями которого являются числа и , откуда или . В ответ запишем, как требуется в задании, меньший корень. Ответ: -10.
Как правило, в контрольные измерительные материалы ЕГЭ включают простейшие тригонометрические уравнения. Естественно, они находятся в части 1 и, как правило, представлены заданиями с выбором ответа. Приведем несколько примеров тригонометрических уравнений, аналоги которых могут встретиться среди заданий группы В. Как правило, это тригонометрические уравнения, при решении которых нам придется отбирать корни.
- Сколько корней имеет уравнение
Ответ: 5.
- Определите число корней уравнения на отрезке .
Ответ: 4.
Неравенства
Задания второй части с кратким ответом
- Найдите количество целочисленных решений неравенства
Так как знаменатель дроби при всегда положителен, то данное неравенство равносильно системе В этом отрезке целых чисел 7: -2; -1; 0; 1; 2; 3; 4.
Ответ: 7.
- Сколько целочисленных решений имеет неравенство ?
Из всех целых чисел, принадлежащих отрезку -1; 0; 1; 2; 3; 4, мы должны убрать нечетные. Остаются три числа: 0; 2; 4.
Ответ: 3.
- Найдите количество целочисленных решений неравенства удовлетворяющих условию
Решением неравенства является отрезок . Решением неравенства являются все действительные значения переменной х, при которых определен и не равен нулю, то есть или Таким образом, условию задачи удовлетворяют все нечетные числа из отрезка Таких чисел 3.
Ответ: 3
Задания с развернутым ответом.
1. Найдите все значения х, при каждом из которых расстояние между соответствующими точками графиков функций и меньше, чем 1,5.
Ответ:
2. Найдите все значения х, при каждом из которых расстояние между соответствующими точками графиков функций и меньше, чем 2.
Ответ:
3. Найдите все значения х, для которых точки графика функции лежат выше соответствующих точек графика функции .
Ответ:
4. Решите неравенство
Ответ: .
5. Решите неравенство
.
Ответ: .
Отметим, что выпускник вправе использовать различные способы решения, и ни один из методов не является «более верным», чем другие.
6. Решите неравенство:
Если то , т.е. вторая система не имеет решений. Решением первой системы является объединение двух промежутков Оно и будет решением логарифмического неравенства.
Ответ:
Практикум
1. Решите неравенство
2. Решите неравенство
3. Решите неравенство
4. Найдите все значения х, при каждом из которых расстояние между соответствующими точками графиков функций именьше, чем 0,5.
5. Найдите все значения х, для каждого из которых точка графика функции лежит ниже соответствующей точки графика функции .
6.Найдите все значения х, при которых функция принимает положительные значения.
- Найдите наименьшее целое положительное х, удовлетворяющее неравенству .
Задания повышенного уровня сложности с развернутым ответом С1 и С2
- Решите уравнение ;
504=2
;
;
;
Задачи такого типа отличаются от аналогичных задач, имеющихся практически во всех школьных учебниках лишь наличием трех, а не двух простых сомножителей. В работах учеников встречались весьма разнообразные способы решения. Можно не раскладывать правую часть, а группировать степени в левой части и все приводить к основанию 504. Можно к единице приравнивать отношение правой части к левой, одни простые множители группировать в одной части, а другие – в другой и т.п. Интересен редко, но встречавшийся графический способ решения уравнения : левая часть возрастает, правая убывает и обе они определены на всей числовой прямой. Значит, есть не более одного корня, а его можно найти подбором: .
- Решите уравнение
1)
2) ;
;
;
или
или
3) не удовлетворяет условию
Ответ: -1.
- Решите уравнение
1)
2)
удовлетворяет условию 1)
нет корней.
Ответ: .
- Решите уравнение ;
Т.к. , то . Поэтому,
Ответ: 0;-1,6.
Многие выпускники начинали решение с отыскания ОДЗ уравнения. Однако в данном случае – это отдельная и довольно кропотливая работа. Можно, переходя к уравнениям-следствиям, получить ответы и просто проверить их. Конечно же, многие выпускники, как это часто бывает, делили на х и теряли при этом корень .
- Решите уравнение .
,
Ответ: -8;3.
- Решите уравнение
1)
не удовлетворяет условию
Ответ:
- Решите уравнение
- Решите уравнение:
. (*)
не удовлетворяет условию (*), не является корнем уравнения.
Ответ: .
- Решите уравнение
1)
2) ;
3) ;
;
.
С учетом 1), корень уравнения 64.
Ответ: 64.
- Решите уравнение
1)
2) ;
3), ;
С учетом 1), корень уравнения 0,008.
Ответ: 0,008.
- Решите уравнение
1)
2) ;
или
или
3) не удовлетворяет условию
Ответ:
- Решите уравнение
А) Б)
Ответ:
- Решите уравнение ; 7
А) ;
Очевидно, что при таких значениях х величина и второй множитель имеет смысл.
Б)
нет решений.
Ответ:
14. Найдите все значения p, при которых уравнение не имеет корней.
1)
У этого уравнения нет корней, только если p не лежит во множестве значений левой части.
2) Так как то
Поэтому
3) Функция принимает и значение 7 (при ), и значение -15 (при ). Поэтому -15 – ее наименьшее значение, а 7 – наибольшее. Функция y непрерывна и, значит, принимает все значения от -15 до 7, т.е. . Исключая этот отрезок из числовой прямой, получаем ответ.
Ответ: .
15.Найдите все значения р, при которых уравнение имеет хотя бы один корень.
У этого уравнения есть корни, только если р лежит во множестве значений левой части. Пусть . Требуется найти множество значений функции при .
Найдем производную
.
График есть парабола с ветвями, направленными вниз. Знак меняется с минуса на плюс при прохождении через точку 0 и с плюса на минус при прохождении через точку . Значит, на отрезке функция убывает, а на отрезке она возрастает.
Так как функция непрерывна, то множество ее значений на отрезке равняется отрезку , а множество ее значений на отрезке равняется отрезку . Поэтому множество ее значений на отрезке — отрезок . Значит, множество значений функции при есть промежуток .
Ответ: .
16. Решите уравнение ;
1) Пусть , тогда
или
или .
Учитывая, что , получим .
2) Пусть , тогда .
или
или .
Но найденные значения х не удовлетворяют условию .
Ответ: .
17.Решите уравнение
Ответ: 0.
19. Решите уравнение
или
нет корней
Ответ:
18. Найдите нули функции .
1) Нули функции – это те значения х, при которых y=0.
и , значит, их сумма равна нулю, если каждое слагаемое обращается в ноль.
.
Ответ:-2.
Практикум
- Решите уравнение .
- Решите уравнение
- Решите уравнение
- Решите уравнение
- Решите уравнение
- Решите уравнение
- Найдите все значения р, при которых уравнение имеет хотя бы один корень.
- Найдите все значения р, при которых уравнение не имеет корней.
- Решите уравнение
- Решите уравнение
- Решите уравнение
- Решите уравнение
- Решите уравнение
- Решите уравнение
- Решите уравнение
- Решите уравнение .
- Решите уравнение
-
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
-
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
РЕШЕНИЯ
А)
Б)
В)
Г)
-
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.

-
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) Б) В) Г) |
|
-
Каждому из четырёх неравенств в левом столбце соответствует одно из решений из правого столбца. Установите соответствие между неравенствами и множествами их решениями.
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) Б) В) Г) |
|
-
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) Б) В) Г) |
1) 2) 3) 4) |
-
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
РЕШЕНИЯ
А)
Б)
В)
Г)
1) 1 x
2) x 1
3) x 2
4) x
-
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
РЕШЕНИЯ
А)
Б)
В)
Г)
1)
2)
3)
4)
-
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) Б) В) Г) |
1) 2) 3) 4) |
-
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
ВЕЛИЧИНЫ
ЗНАЧЕНИЯ
А)
Б)
В)
Г)
1)
2)
3)
4)
-
Каждое из четырёх неравенств в левом столбце соответствует одному из решений в праве столбца. Установить соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
РЕШЕНИЯ
А)
Б)
В)
Г)
-
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
РЕШЕНИЯ
А)
Б)
В)
Г)
1)
2)
3)
4)
-
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
-
Каждому из четырех неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) Б) В) Г) |
1) 2) 3) 4) |
На прямой отмечено число m и точки A, B, C и D.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами. Впишите в приведённую в ответе таблицу под каждой буквой соответствующий числу номер.
|
ТОЧКИ |
ЧИСЛА |
|
|
А) A Б) B В) C Г) D |
1) 2) 3) 4) |
На прямой отмечено число m и точки A, B, C и D.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами. Впишите в приведённую в ответе таблицу под каждой буквой соответствующий числу номер.
|
ТОЧКИ |
ЧИСЛА |
|
|
А) A Б) B В) C Г) D |
1) 2) 3) 4) |
На координатной прямой отмечены точки A, B, C и D.
Установите соответствие между указанными точками и числами из правого столбца, которые им соответствуют.
|
ТОЧКИ |
ЧИСЛА |
|
|
А) A Б) B В) C Г) D |
1) 2) 3) 4) |
На координатной прямой отмечены точки A, B, C и D.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
|
ТОЧКИ |
ЧИСЛА |
|
|
А) A Б) B В) C Г) D |
1) 2) 3) 4) |
На координатной прямой отмечены точки A, B, C и D.
Число m равно Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами. Впишите в приведённую в ответе таблицу под каждой буквой соответствующий числу номер.
|
ТОЧКИ |
ЧИСЛА |
|
|
А) A Б) B В) C Г) D |
1) 2) 3) 4) |
На координатной прямой отмечены точки A, B, C и D.
Число m равно Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
|
ТОЧКИ |
ЧИСЛА |
|
|
А) A Б) B В) C Г) D |
1) 2) 3) 4) |
На прямой отмечены точки A, B, C и D.
Каждой точке соответствует одно из чисел из правого столбца. Установите соответствие между указанными точками и числами.
|
ТОЧКИ |
ЧИСЛА |
|
|
A B C D |
1) 2) 3) 4) |
На координатной прямой отмечены точки A, B, C и D.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
|
ТОЧКИ |
ЧИСЛА |
|
|
А) A Б) B В) C Г) D |
1) 2) 3) 4) |
Каждому из четырёх чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами и отрезками из правого столбца.
|
ВЕЛИЧИНЫ |
ЗНАЧЕНИЯ |
|
|
А) Б) В) Г) |
1) [1; 2] 2) [2; 3] 3) [3; 4] 4) [4; 5] |
Каждому из четырёх чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами и отрезками из правого столбца.
|
ВЕЛИЧИНЫ |
ЗНАЧЕНИЯ |
|
|
А) Б) В) Г) |
1) [−1: 0] 2) [0; 1] 3) [2; 3] 4) [4; 5] |
На координатной прямой отмечено число
Каждому из четырёх чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами и отрезками из правого столбца.
|
ТОЧКИ |
ЧИСЛА |
|
|
А) Б) В) Г) |
1) [0;1] 2) [1; 2] 3) [2; 3] 4) [4; 5] |
На прямой отмечены числа m и n.
Каждому из четырёх чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите соответствие между числами и отрезками из правого столбца.
|
ЧИСЛА |
ОТРЕЗКИ |
|
|
А) m + n Б) В) mn Г) |
1) [−1; 0] 2) [0; 1] 3) [1; 2] 4) [2; 3] |
Методические рекомендации по решению алгебраических неравенств .
Готовимся к ЕГЭ.
Учитель математики МОУ «СОШ №61»
Ленинского района г.Саратова
Вахлаева Ольга Васильевна
Содержание
Введение …………………………………………………………………………2
Глава 1 Теоретико-методические аспекты изучения темы «Алгебраические неравенства» в школьном курсе математики…………………………………..2
1.1 Анализ изложения темы «Алгебраические неравенства» в учебно-методической и научно-популярной литературе……………………………….3
1.2 Функционально-графические методы решения неравенств………………4
1.2.1 Метод интервалов…………………………………………………….4
1.2.2 Использование свойств монотонности функций в решении неравенств………………………………………………………………………..6
1.2.3 Метод рационализации………………………………………………7
1.3 Алгебраические методы решения неравенств…………………………….7
1.3.1 Метод равносильных переходов…………………………………… 7
1.3.2 Метод введения новых переменных…………………………………9
1.3.3 Разбиение области определения неравенства на подмножества…..9
1.4.Геометрический подход в решении неравенств……………………………10
Глава 2 Алгебраические неравенства в контрольно-измерительных материалах государственной итоговой аттестации по математике………….11
2.1.1 Типы алгебраических неравенств, используемые на ГИА ……………..12
2.2.2Типичные ошибки при решении алгебраических неравенств и способы их устранения………………………………………………………………..……14
Заключение .………………………………………………………………………17
Список использованной литературы………………………………………..….28
Введение
Выпускной экзамен по математике — сложное, но необходимое испытание для всех выпускников, потому что успешная его сдача-обязательное условие для получения аттестата о среднем полном образовании, а набранные баллы по математике профильного уровня- пропускной билет в высшую школу. Поэтому выпускники серьезно и основательно готовятся к его сдаче.
В соответствии с распространенными рекомендациями все задания экзамена по математике и базового и профильного уровня условно делят на группы: самые простые, решая которые можно набрать минимальное количество баллов, перешагнуть «порог», задания среднего уровня сложности, решая которые можно набрать «хорошее» количество баллов, сложные задания, решив которые, выпускник набирает максимальное количество баллов. Задания первой группы решают все- это необходимая данность, а вот задания второй группы-для ребят знающих, творческих, амбициозных, трудолюбивых. К этой второй важной, сложной, но интересной группе заданий можно отнести и задания, связанные с решением алгебраических неравенств (задания № 18 базового уровня, задания №17 — профильного уровня). Поэтому в работе рассмотрены основные методы решения этого типа заданий.
Поскольку тема «алгебраические неравенства» обширна, в своей работе я остановлюсь на решении рациональных, дробно-рациональных неравенствах и неравенствах, содержащих знак модуля.
Глава 1 Теоретико-методические аспекты изучения темы «Алгебраические неравенства» в школьном курсе математики
При решении неравенств в школьном курсе используют такие основные методы: метод интервалов (обобщенный метод интервалов), метод равносильных переходов, метод введения новых переменных, метод рационализации, метод оценки и другие.
-
Анализ изложения темы «алгебраические неравенства» в
учебно-методической и научно-популярной литературе
Неравенства и методы их решения включены в обязательный минимум содержания образовательных программ основного общего и среднего полного образования, поэтому эта тема изложена в школьных учебниках по математике. В УМК по алгебре для 7–9 классов Мордковича А.Г., Никольского С.М., Дорофеева В.Г., Макарычева Ю.Н., Колягина Ю. М. , а также в УМК по алгебре и началам математического анализа для 10–11 Мордковича А.Г., Никольского С.М., Дорофеева В.Г., Колягина Ю. М. . Виленкина Н.Я. и др. в полном объеме изложены основные методы решения алгебраических неравенств. В многочисленных математических справочниках, например «Повторяем и систематизируем школьный курс алгебры и начал анализа» Крамора В.С., «Математика» Гусева В.А., Мордковича А.Г. и других, эта тема также подробно изложена. В научно-популярной литературе много публикаций, связанных с нестандартными методами решения неравенств. Например, это статья Олехник, С. Н. « Уравнения и неравенства. Нестандартные методы решения. 10-11 классы» в учебно-методическом пособии, посвященном задачам, которые для школьников считаются задачами повышенной трудности или публикация «Нестандартные методы решения неравенств и их систем» Короповец З.П. Много публикаций связано с методом рационализации, его еще называют метод декомпозиции (Моденов В.П.), метод замены множителей (Голубев В.И) который получил достаточно широкое распространение, хотя в школьных учебниках он, как правило, не рассматривается. Мне показалась интересной классификация методов, представленная в работе Прокофьева А.А. и Корянова А.Г. «Решение неравенств с одной переменной». Авторы предлагают в зависимости от трактовки или интерпретации неравенства различать алгебраический, функциональный или геометрический подходы в решении неравенств. Первые два подхода различаются в понятии неравенства, которое рассматривается либо как сравнение двух выражений, либо как сравнение двух функций. При алгебраическом подходе выполняют равносильные общие (над обеими частями неравенства) или частичные преобразования неравенств (отдельных выражений, входящих в неравенство). При функциональном подходе используют свойства функций (монотонность, ограниченность и т.д.), входящих в данное неравенство. В некоторых случаях алгебраический и функциональный подходы взаимно заменяемы. Основой геометрического подхода является интерпретация неравенств и их решений на координатной прямой, координатной плоскости или в пространстве, что позволяет перейти к равносильным неравенствам, опираясь на геометрические утверждения.
1.2 Функционально-графические методы решения неравенств Функциональный подход в решении неравенств использует свойства функций.
1.2.1 Один из наиболее распространенных методов решения неравенств- метод интервалов основан на свойстве непрерывности функции.
Пример1(Базовый уровень)
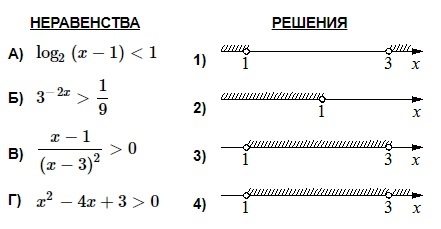
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
Решим каждое из неравенств (предварительно приравняв левую часть к нулю) методом интервалов.
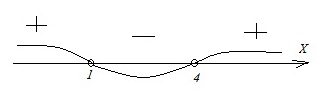
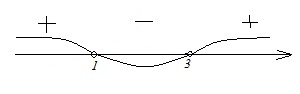
А) ,
Отметим данные решения на числовой прямой и расставим знаки на соответствующих интервалах:
Данному решению соответствует 1)
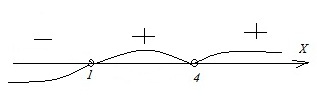
Б) ,
Отметим данные решения на числовой прямой и расставим знаки на соответствующих интервалах:
Данному решению соответствует 4)
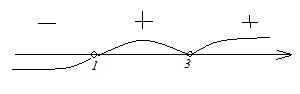
В) ,
Отметим данные решения на числовой прямой и расставим знаки на соответствующих интервалах:
Данному решению соответствует 3)
Г),
Отметим данные решения на числовой прямой и расставим знаки на соответствующих интервалах:
Данному решению соответствует 2)
Ответ: 1432
В рациональных неравенствах профильного уровня часто используется обобщенный метод интервалов, например, для которых при переходе из одного интервала в смежный интервал знак функции f (х) может не меняться.
Пример 2. Решите неравенство:
Преобразуем неравенство:
Ответ:
1.2.2 Свойство монотонности при решении неравенств используют для случаев, когда функции, стоящие в обеих частях неравенства, имеют одинаковую монотонность или разную монотонность. Например:
Пример 3. Решите неравенство: х7+1<0.
Его можно записать его в виде х7<-17, и рассматривая функцию у= х7, которая возрастает на всей области определения, можно сделать вывод, что последнее неравенство равносильно неравенству х <-1.
Ответ: (-∞; -1).
Пример 4. Решите неравенство: (2х2+1)5 — (3х)5 >3х — 2х2-1.
Запишем неравенство как
(2х2+1)5+ 2х2+1> (3х)5+3х
Рассмотрим функцию у = t5 + t, определенную при всех действительных значениях t. Так как у ′ (t) =5t4 +1 • 0 для любого t из области определения, то функция у(t) возрастает на всей области определения . Для возрастающей функции, определенной на всей числовой прямой, неравенство у(t1) • у(t2) равносильно неравенству t1• t2.Значит, наше неравенство равносильно неравенству 2х2+1>3х,
2х2-3х +1>0, откуда х <0,5 или х>1.
Ответ: (-∞;0,5) (1; + ∞).
1.2.3При решении неравенств методом интервалов могут возникать трудности вычислительного характера. Чтобы расширить возможности применения метода интервалов при решении неравенств, используют идею рационализации неравенств. Метод рационализации заключается в замене сложного выражения на более простое выражение, при которой более сложное неравенство равносильно более простому неравенству на области определения исходного неравенства.
Пример 5. Решите неравенство: (х2-1)2+х > (х2-1)5х-3
Запишем его как (х2-1)2+х — (х2-1)5х-3>0 и используем метод рационализации.
Ответ: (−∞ ; ) ∪ (1, 25;
)
1.3 Алгебраические методы решения неравенств
1.3.1 При решении неравенств алгебраическими методами используют преобразования, позволяющие привести неравенство к более простому виду. При выполнении преобразований множество решений исходного неравенства или не меняется, или расширяется (можно получить посторонние решения), или сужается (можно потерять решения). Поэтому важно знать, какие преобразования неравенства являются равносильными и при каких условиях. Например, решая неравенство с модулем методом сведения его к равносильной системе или совокупности систем можно использовать стандартные схемы для решения, которые опираются на определение модуля, его геометрический смысл и свойства
Пример 6. Решите неравенство:
Согласно одной из стандартных схем неравенство равносильно совокупности неравенств:
Ответ:
1.3.2 Для решения неравенств часто используют метод введения новой переменной, решают неравенство относительно этой переменной, а и затем решают полученные неравенства (или неравенство) с первоначальной переменной х.
Пример 7. Решите неравенство:
Сделаем замену решим неравенство методом интервалов.
Возвратимся к исходной переменной и получим:
1(х+1)
3
(х+1)
или
Ответ:
1.3.3 Разбиение области определения неравенства на подмножества Разбиение области определения неравенства на промежутки позволяет упростить некоторые неравенства. Решение неравенства рассматривают отдельно на каждом промежутке. Особенно наглядно этот метод работает при решении неравенств с модулями, когда модуль раскрываем на каждом промежутке.
Пример 8. Решите неравенство:
Числа 2 и -1 разбивают числовую прямую на три промежутка (−∞;1) ,
[1; 2) и [2; + ∞) . Освобождаясь от знаков модулей, с учетом знаков выражений под знаком модуля решим данное неравенство на каждом из этих промежутков.
Первый случай.
Второй случай.
Третий случай.
Объединяя промежутки, получаем
Ответ:
1.4 Геометрический подход в решении неравенств
Геометрические методы решения неравенств не часто используются на практике. Однако, геометрическая интерпретация неравенств позволяет легко и красиво решать, как простые, так и сложные задачи.
Пример 9. Решите неравенство: | x − 5 | > | x + 2 |.
Геометрическая интерпретация дает простое и красивое решение: так как |x − 5 | и | x + 2 | = | x − (−2) | – это расстояния от точки x до точек 5 и – 2 соответственно, то из данного равенства следует, что точка x – середина отрезка [−2;5], и поэтому х= . Значит, решениями данного неравенства являются все числа x ∈(−∞;1,5), т.е. все точки, расстояния от каждой из которых до точки 5 больше расстояния до точки (–2).
Ответ: (−∞;1,5).
В материалах для дистанционного обучения нашей группы в блоке «Методы решения уравнений. Модуль», представленном доцентом кафедры математического образования Конник О.Ю. этот подход развивается. Анализируя различные способы решения уравнений, содержащих модуль, Ольга Юрьевна делает вывод: обобщением решения вышеприведенных уравнений являются следующие равносильные переходы:
, которые можно использовать в решении неравенств.
Пример 10. 1Решите неравенство: .
Решим неравенство, используя координатную прямую. Данное неравенство выполняется для всех точек c координатой х, которые находятся ближе к точке с координатой-2000, чем к точке с координатой -2001. Так как , то искомыми являются все точки, расположенные левее точки с координатой
.
Ответ:.
Глава 2. Алгебраические неравенства в контрольно-измерительных материалах государственной итоговой аттестации по математике
Все представленные выше методы используются при решении неравенств на государственной итоговой аттестации. В математике базового уровня задания с неравенствами однотипны: они на установление соответствия между неравенствами(простейшими) и их решениями. В математике профильного уровня неравенства могут встретиться в различных заданиях, но в основном они представлены в заданиях №13. Эти задания занимают одну из важнейших позиций в структуре КИМ. К их выполнению в 2015 г. приступало более 60% участников профильного единого государственного экзамена (ЕГЭ), а положительные баллы получили более 30% всех участников. Успешность выполнения заданий этого типа является характеристическим свойством, различающим базовый и профильный уровни подготовки учащихся. Поэтому при подготовке выпускников к экзамену решению заданий подобного уровня следует уделять много внимания.
2.1.1 Все задания, связанные с неравенствами, на базовом уровне (задания №17) зависимости от формы записи решений неравенств можно условно разделить на следующие прототипы: неравенства, в которых решения записаны в виде числовых промежутков, в виде неравенств, на геометрической модели.
— Решения записаны в виде числовых промежутков:
Поставьте в соответствие каждому неравенству множество его решений.
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) Б) В) Г) |
1) 2) 3) 4) |
— Решения записаны в виде неравенств:
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) Б) В) Г) |
1) 2) 3) 4) |
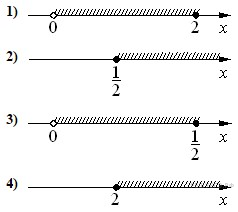
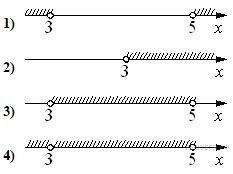
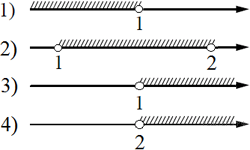
-Решения представлены на числовой прямой:
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) Б) В) Г) |
|
Чтобы ученик мог справиться с этими заданиями, надо отрабатывать различные формы записи ответа.
К типичным ошибкам можно отнести ошибки в расстановке знаков, ошибки в правильной записи луча, отрезка, интервала. Для профилактики таких ошибок можно использовать упражнения типа: «Составить неравенство, решение которого — (-∞, -10) U [-7, -4]», на которых отрабатываются эти понятия.
Рассматриваемые в этой работе рациональные, дробно-рациональные неравенства и неравенства, содержащие знак модуля, представленные в заданиях №13 профильного уровня можно условно разбить на прототипы.
К прототипу1 можно отнести неравенства, состоящие из алгебраических дробей, их суммы, произведения множителей. Например:
а)
б)
в)
г)
Такие неравенства надо преобразовать, чтобы свести их к решению методом интервалов (наиболее часто применяемый метод). Типичные ошибки в таких заданиях:
— последовательность шагов решения неверная или выполнена не до конца;
-формальное перенесение приемов решения уравнений на неравенство того же типа;
— не исключаются из ответа точки, в которых знаменатель обращается в 0;
-ошибки в расстановке знаков;
— в нестрогих неравенствах исключается из ответа точки (как правило, конечное их число), при которых числитель обращается в 0;
— последовательность шагов решения преобразования выполняются «в лоб» (например, алгебраические дроби складываются без учета разложения квадратного трехчлена на множители или по формуле), что приводит к тупиковой ситуации или неверному решению.
К прототипу 2 можно отнести сложные дробно-рациональные неравенства, которые решаются методом введения новых переменных.
а)
б)
в)
Типичные ошибки:
— используют преобразования, нарушающие равносильность;
— последовательность шагов решения выполнена не до конца (не выполнена обратная замена или ошибки в обратном переходе).
К прототипу 3 можно отнести неравенства, содержащие знак модуля, которые решаются методом равносильных переходов.
К прототипу 4 можно отнести неравенства, содержащие знак модуля такого типа:
Типичные ошибки:
— ошибки при применении равносильных переходов и в знаках при раскрытии модуля.
2.2.2К типичным ошибкам, относящимся ко всем неравенствам можно отнести неверное использование логической символики. Т.к. «конъюнкция» и «дизъюнкция» в школьном курсе математики не изучаются, зачастую эти символы применяются неверно, поэтому лучше их заменить словами «и», «или».
Чтобы ошибок при решении неравенств было меньше, необходима система устной работы для формирования вычислительной грамотности, которая в том числе поможет и безошибочно расставлять знаки в методе интервалов, нужно более тщательно отрабатывать применение метода введения вспомогательной переменной при решении неравенств, указывая на отличия от уравнений, решаемых тем же способом. Надо обращать внимание учащихся на то, что множество решений неравенства, полученного при введении вспомогательной переменной, целесообразно записать в виде одного или нескольких элементарных неравенств, в которых и возвращаться к исходной переменной. Запись же решений промежуточного неравенства в виде числовых промежутков часто не позволяет ученикам продолжить решение.
Учителю надо сформировать набор дидактических материалов по данной теме с учетом типичных ошибок и по индивидуальному маршруту совершенствовать с учащимися навыки решения неравенств.
Задача учителя-помочь ученику овладеть методикой решения неравенств, научился видеть «изюминки», тогда и решения получаются красивые, и результаты экзамена радуют.
Решите неравенство:
.
Решение:
Преобразуем неравенство:
Сделав замену получаем неравенство
откуда
Тогда: откуда
или
Ответ:
Заключение.
В своей работе я постаралась проанализировать изложение темы «алгебраические неравенства» в учебно-методической и научно-популярной литературе, систематизировать методы решения алгебраических неравенств по общему подходу к их решению (функциональный, алгебраический и геометрический подходы). Учитывая разнообразие неравенств, в данной работе были рассмотрены рациональные, дробно-рациональные неравенства и неравенства, содержащие знак модуля. Основные типы неравенств по данной теме, встречающиеся на государственной итоговой аттестации по математике, сгруппированы по прототипам, рассмотрены типичные ошибки каждой группы и способы их устранения.
Список использованных источников
1.Алгебра и начала анализа. 10-11 классы. В 2 частях. Ч. 1: Учебник для общеобразовательных учреждений. : учебник / Под. ред. А. Г. Мордковича. — М.: Мнемозина, 2013.
2. Алгебра и начала анализа. 10-11 классы. В 2 частях. Ч. 2: Задачник для общеобразовательных учреждений. : учебник / Под. ред. А. Г. Мордковича. — М.: Мнемозина, 2013.
3. Олехник С. Н. Уравнения и неравенства. Нестандартные методы решения. 10-11 классы : учебно-методическое пособие . — М.: Дрофа, 2004. — 192 с.
4.Прокофьев А. А., Корянов А. Г. Решение неравенств с одной переменной. Серия: Готовимся к ЕГЭ .-Р.Легион,2015,-93с.
5.Математика.Нестандартные методы решения неравенств и их систем/З.Л.Коронец, А.А.Коронец, Т.А.Алексеева_Орел,2012,-125с.
6.Прокофьев А.А., Корянов А.Г. Готовим к ЕГЭ хорошистов и отличников. Лекция 3. Решение неравенств алгебраическими методами. // Математика. – М., 2011, – №16, − С. 50-61
7.Прокофьев А.А., Корянов А.Г. Готовим к ЕГЭ хорошистов и отличников. Лекция 4. Решение неравенств функционально графическим методом. // Математика. – М., 2011, – №17, − С. 49-61.
Интернетресурсы
Математика ЕГЭ 2016 (открытый банк заданий)- www.mathege.ru
ЕГЭ по математике: подготовка к тестированию -www.alexlarin.narod.ru
ЕГЭ по математике: подготовка к тестированию- www. ege.sdamgia.ru
Открытый банк заданий ЕГЭ по математике на сайте- fipi.ru

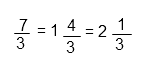
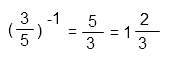
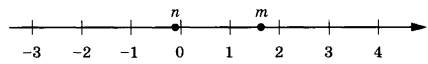



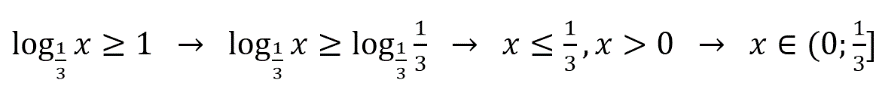
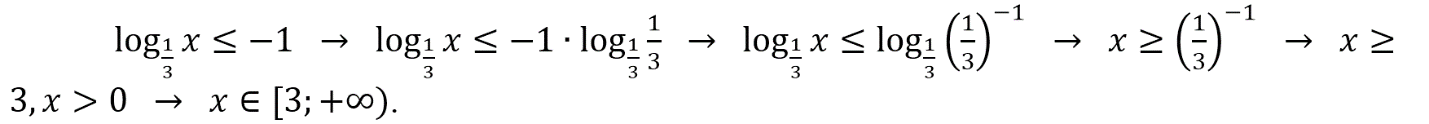


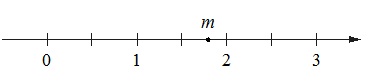













 – радикал
– радикал — логарифм
— логарифм