Неравенства с двумя переменными егэ

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

Алгебра и начала математического анализа, 11 класс

Урок №42. Линейные уравнения и неравенства с двумя переменными

Перечень вопросов, рассматриваемых в теме:

• Решение уравнений, неравенств, систем уравнений и систем неравенств с двумя переменными;
• Изображение в координатной плоскости множества решений уравнений, неравенств, систем уравнений, систем неравенств;
• Нахождение площади получившейся фигуры.

Глоссарий по теме

Уравнение вида     ax + by + c = 0 называется линейным уравнением с двумя переменными, где   a, b и c   —   некоторые числа (a ≠ 0 ,   b ≠0), а, х и у   —   переменные. 

Основная литература:

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. Учебник: Алгебра 9 кл с углубленным изучением математики Мнемозина, 2014.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.

Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.

Теоретический материал для самостоятельного изучения

Историческая справка

Уравнения, а также системы уравнений имеют давнюю историю. Нам известно, что уже в Древнем Вавилоне и Индии повседневные задачи, связанные с земляными работами или планированием военных расходов, а также астрономическими наблюдениями решались с помощью уравнений и их систем.

В то время еще не существовало привычного нам формального языка математики. Вавилоняне, также, как и индусы не использовали в своих трактатах привычные нам «икс» и «игрек». Не обозначали степень надстрочными индексами. И т.д. Их уравнения записаны в виде текстовых задач. Также, как и решения, не похожи на современные, а скорее напоминают цепочку логических рассуждений.

Вместе с тем, если перевести в привычный нам вид те уравнения, которые умели решать в Древнем Вавилоне, то мы увидим: . И в древнем индийском манускрипте «Ариабхаттиам», датируемом 499 годом нашей эры, также встречаются задачи, решаемые с помощью квадратных уравнений. Индийские мудрецы (слово ученый тоже еще не существовало) уже не ограничивались решением конкретных житейских задач, но и работали над решением квадратного уравнения в общем виде.

Привычный нам вид уравнения обретают только в конце шестнадцатого века, благодаря трудам Франсу Виета (1540 – 1603 гг.). Именно он, помимо прочих своих научных достижений обладает и неофициальным титулом «создатель алгебры». Поскольку разработал и активно внедрял символический язык алгебры – те самые, привычные нам «иксы и игреки».

Актуализация знаний

1.Найдите уравнения, которые являются линейными.

4х + 5у = 10; ; у = 7х +4

Ответ: 4х + 5у = 10; у = 7х +4

Сегодня на уроке мы вспомним что такое линейные уравнения и неравенства с двумя переменными; системы линейный уравнений и неравенств, а также научимся изображать множество на плоскости, задаваемое линейным уравнением и неравенством.

1. Линейные уравнения с двумя переменными.

Уравнение вида ах + by +с =0, где а,b,с – некоторые числа, называется линейным уравнением с двумя переменными х и у.

Решением уравнения ах + by +с =0, где а,b,с – некоторые числа, называется пара значений обращающая уравнение в верное числовое равенство.

Если одновременно а и b, то уравнение ах + by +с =0 является уравнением некоторой прямой. Для построения прямой достаточно найти две точки этой прямой.

Пример

Построить график уравнения 2х+у =1

у = -2х + 1

Если х=0, то у=1;

Если х=2, то у=-3.

На координатной плоскости отметим точки с координатами (0;1) и (2;-3). Через две точки на плоскости проведем прямую. Полученная прямая является геометрической моделью уравнения 2х+у =1.

1. Линейные неравенства с двумя переменными.

Линейным неравенством с двумя переменными называется неравенство вида ах + bу + с < 0 или ах + bу + с > 0, где х и у – переменные, а, b, c – некоторые числа.

Решением неравенства с двумя переменными называется пара значений переменных, обращающая его в верное равенство.

Является ли пара (2;1) решением неравенства 5х + 2у > 4 . Является, тк при подстановке в него вместо х числа 2, а вместо у числа 1 получается верное равенство 10 + 2 > 4.

Если каждое решение неравенства с двумя переменными изобразить точкой в координатной плоскости, то получится график этого неравенства. Он является некоторой фигурой.

Пример

Найти множество точек координатной плоскости, удовлетворяющих неравенству 3х – 2у +6 > 0.

1. Уравнение 3х – 2у +6 = 0 является уравнением прямой, проходящей через точки(- 2; 0) и (0; 3).
2. Пусть точка М₁(х_1,у₁) лежит в заштрихованной полуплоскости (ниже прямой 3х – 2у +6 = 0, а М₂(х_1,у₂)лежит на прямой 3х – 2у +6 = 0_. Тогда 2у₂ – 3х₁ – 6 = 0, а 2у₁ – 3х₁ – 6 < 0, т.к. у₁< у₂

Изобразим множество точек координатной плоскости, удовлетворяющих неравенству 3х – 2у +6 > 0 штриховкой (рис. 1)

Рисунок 1 – решение неравенства 3х – 2у +6 > 0

Если в линейном неравенстве с двумя переменными знак неравенства заменить знаком равенства, то получится линейное уравнение ах + by +с =0, графиком которого является прямая при условии, что и . Прямая разбивает плоскость на две полуплоскости. Одна из них является графиком неравенства ах + bу + с < 0, а другая – графиком неравенства ах + bу + с > 0

Чтобы решить неравенство ах + bу + c < 0 или aх + bу + c > 0, достаточно взять какую-нибудь точку М₁(х₁; у₁), не лежащую на прямой aх + bу + c = 0, и определить знак числа aх₁ + bу₁ + c.

Пример

Изобразите в координатной плоскости множества решений неравенства 2х + 3у < 6

Начертим график уравнения 2х + 3у = 6.

Пара (0;0) является решением неравенства 2х + 3у < 6, и принадлежит нижней полуплоскости, значит графиком неравенства 2х + 3у < 6 является нижняя полуплоскость (рис. 2).

Рисунок 2 – решение неравенства 2х + 3у < 6

1. Система линейных уравнений с двумя переменными.

Система вида , где а,b,с,d,e,f – некоторые числа, называется линейной системой с двумя переменными х и у.

Пара значений переменных, обращающая каждое уравнение системы уравнений с двумя переменными в верное равенство называют решением системы.

Решить систему – значит найти множество ее решений.

Пример

Решите систему:

Каждое решение уравнения с двумя переменными представляет координаты некоторой его точки его графика. Каждое решение системы есть координаты общих точек графиков уравнений системы. Построим графики этих уравнений и найдем координаты точки пересечения (рис.3). 

Рисунок 3 – решение системы

Система имеет единственное решение: x = 4 ,   y = 4 .

1. Система линейных неравенств с двумя переменными.

Системой линейных неравенств с двумя переменными называется такая система неравенств, которая в своем составе имеет два и более линейных неравенств с двумя переменными.
Рассмотрим систему линейных неравенств с двумя переменными на примере:

1. Построим прямые х – у = 2 и х + 3у = 6
2. Пара (4;1) является решением как первого, так и второго неравенства, те является общим решением неравенств системы. Такую пару чисел называют решением системы неравенств с двумя переменными. Множество общих решений неравенств есть множество решений системы (пересечение множеств решений неравенств, составляющих систему).

Множество решение системы изображается двойной штриховкой. (плоской угол) (рис. 4).

Рисунок 4 – решение системы

Примеры и разбор решения заданий тренировочного модуля

Пример 1

Изобразите в координатной плоскости множества решений неравенства 3х – 2у + 6 0.

1. Начертим график уравнения 3х – 2у + 6 = 0
2. Отметим в какой-нибудь полуплоскости, например, точку (1;2).

Пара (1;2) не является решением неравенства и принадлежит нижней полуплоскости, значит графиком неравенства является верхняя полуплоскость вместе с прямой 3х – 2у + 6 = 0. 9 (рис. 5)

Рисунок 5 – решение неравенства

Пример 2

Изобразим на координатной плоскости множество решений системы

Построим прямые х + у = 3 и 4х – 5у = 20.

Множество решений первого неравенства показано горизонтальной штриховкой, а множество решений второго неравенства – вертикальной штриховкой. Двойная штриховка – множество решений системы. Система задает плоский угол (рис. 6)

Рисунок 6 – решение системы

Если к системе добавить еще одно неравенство

, то получится система трех неравенств с двумя переменными

Этой системой задается треугольник (рис. 7)

Рисунок 7 – решение системы

Точка О принадлежит , левая часть неравенства положительна, и поэтому множество его решений – объединение множеств .

Решение неравенства с двумя переменными, а тем более системы неравенств с двумя переменными, представляется достаточно сложной задачей. Однако есть простой алгоритм, который помогает легко и без особых усилий решать на первый взгляд очень сложные задачи такого рода. Попробуем в нем разобраться.

Пусть мы имеем неравенство с двумя переменными одного из следующих видов:

y > f(x); y ≥ f(x); y < f(x); y ≤ f(x).

Для изображения множества решений такого неравенства на координатной плоскости поступают следующим образом:

1. Строим график функции y = f(x), который разбивает плоскость на две области.

2. Выбираем любую из полученных областей и рассматриваем в ней произвольную точку. Проверяем выполнимость исходного неравенства для этой точки. Если в результате проверки получается верное числовое неравенство, то заключаем, что исходное неравенство выполняется во всей области, которой принадлежит выбранная точка. Таким образом, множеством решений неравенства – область, которой принадлежит выбранная точка. Если в результате проверки получается неверное числовое неравенство, то множеством решений неравенства будет вторая область, которой выбранная точка не принадлежит.

3. Если неравенство строгое, то границы области, то есть точки графика функции y = f(x), не включают в множество решений и границу изображают пунктиром. Если неравенство нестрогое, то границы области, то есть точки графика функции y = f(x), включают в множество решений данного неравенства и границу в таком случае изображают сплошной линией.
А теперь рассмотрим несколько задач на эту тему.

Задача 1.

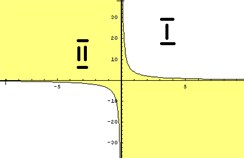
Какое множество точек задается неравенством x · y ≤ 4?

Решение.

1) Строим график уравнения x · y = 4. Для этого сначала преобразуем его. Очевидно, что x в данном случае не обращается в 0, так как иначе мы бы имели 0 · y = 4, что неверно. Значит, можем разделить наше уравнение на x. Получим: y = 4/x. Графиком данной функции является гипербола. Она разбивает всю плоскость на две области: ту, что между двумя ветвями гиперболы и ту, что снаружи их.

2) Выберем из первой области произвольную точку, пусть это будет точка (4; 2).
Проверяем неравенство: 4 · 2 ≤ 4 – неверно.

Значит, точки данной области не удовлетворяют исходному неравенству. Тогда можем сделать вывод о том, что множеством решений неравенства будет вторая область, которой выбранная точка не принадлежит.

3) Так как неравенство нестрогое, то граничные точки, то есть точки графика функции y = 4/x, рисуем сплошной линией.

Закрасим множество точек, которое задает исходное неравенство, желтым цветом (рис. 1).

Задача 2.

Изобразить область, заданную на координатной плоскости системой
{ y > x² + 2;
{y + x > 1;
{ x² + y² ≤ 9.

Решение.

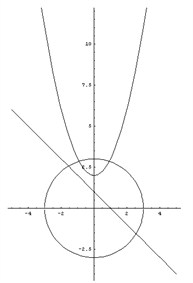
Строим для начала графики следующих функций (рис. 2):

y = x² + 2 – парабола,

y + x = 1 – прямая

x² + y² = 9 – окружность.

Теперь разбираемся с каждым неравенством в отдельности.

1) y > x² + 2.

Берем точку (0; 5), которая лежит выше графика функции.
Проверяем неравенство: 5 > 0² + 2 – верно.

Следовательно, все точки, лежащие выше данной параболы y = x² + 2, удовлетворяют первому неравенству системы. Закрасим их желтым цветом.

2) y + x > 1.

Берем точку (0; 3), которая лежит выше графика функции.
Проверяем неравенство: 3 + 0 > 1 – верно.

Следовательно, все точки, лежащие выше прямой y + x = 1, удовлетворяют  второму неравенству системы. Закрасим их зеленой штриховкой.

3) x² + y² ≤ 9.

Берем точку (0; -4), которая лежит вне окружности x² + y² = 9.
Проверяем неравенство: 0² + (-4)² ≤ 9 – неверно.

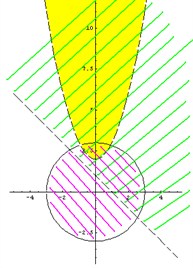
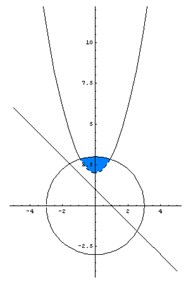
Следовательно, все точки, лежащие вне окружности x² + y² = 9, не удовлетворяют  третьему неравенству системы. Тогда можем сделать вывод о том, что все точки, лежащие внутри окружности x² + y² = 9, удовлетворяют  третьему неравенству системы. Закрасим их фиолетовой штриховкой.

Не забываем о том, что если неравенство строгое, то соответствующую граничную линию следует рисовать пунктиром. Получаем следующую картинку (рис. 3).

Искомая область – это область, где все три раскрашенных области пересекаются друг с другом (рис. 4).

Задача 3.

Изобразить область, заданную на координатной плоскости системой:
{x² + y² ≤ 16;
{x ≥ -y;
{x² + y² ≥ 4.

Решение.

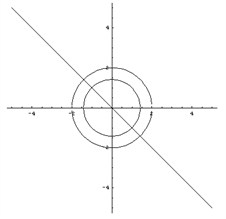
Строим для начала графики следующих функций:

x² + y² = 16 – окружность,

x = -y – прямая

x² + y² = 4 – окружность (рис. 5).

Теперь разбираемся с каждым неравенством в отдельности.

1) x² + y² ≤ 16.

Берем точку (0; 0), которая лежит внутри окружности x² + y² = 16.
Проверяем неравенство: 0² + (0)² ≤ 16 – верно.

Следовательно, все точки, лежащие внутри окружности x² + y² = 16, удовлетворяют  первому неравенству системы.
Закрасим их красной штриховкой.         

2) x ≥ -y.

Берем точку (1; 1), которая лежит выше графика функции.
Проверяем неравенство: 1 ≥ -1 – верно.

Следовательно, все точки, лежащие выше прямой x = -y, удовлетворяют  второму неравенству системы. Закрасим их синей штриховкой.

3) x² + y² ≥ 4.

Берем точку (0; 5), которая лежит вне окружности x² + y² = 4.
Проверяем неравенство: 0² + 5² ≥ 4 – верно.

Следовательно, все точки, лежащие вне окружности x² + y² = 4, удовлетворяют  третьему неравенству системы. Закрасим их голубым цветом.

В данной задаче все неравенства нестрогие, значит, все границы рисуем сплошной линией. Получаем следующую картинку (рис. 6).

Искомая область – это область, где все три раскрашенных области пересекаются друг с другом (рис 7).

Остались вопросы? Не знаете, как решить систему неравенств с двумя переменными?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Определение и примеры неравенств с двумя переменными

Соотношение между алгебраическими выражениями (функциями с переменными x, y), которое указывает, что одно больше или меньше другого, называют неравенством.

Неравные соотношения различают строгие (>, <) и нестрогие (≥, ≤), простейшие (х≥0, y≤0), линейные (прямые) и нелинейные (например, со степенями). Решение с одним переменным отмечают на числовой оси. По аналогии можно решать неравенства с двумя переменными, но использовать две оси (x, y) на координатной плоскости; поскольку решения (пары действительных чисел) определяют область (множество) точек на этой плоскости.

Пример двух линейных нестрогих и одного строгого отношения:

. X-3y≥-12, 4x+3y≤27, 2x+2y>0.

Квадратичные неравенства с 2 переменными:

y-x^2≥0, х^2 – 8х + 12< y.

Искать ответ можно несколькими способами; прежде всего, решить уравнение, определенное неравенством, используя методы преобразования, разбить оси по данным решения на предполагаемые участки, определить верные интервалы, пользуясь методом «подопытной» точки.

Сколько и какие могут быть решения?

Если по условию несколько неравенств объединены в систему, то для выводов решается каждое отдельно. По результатам находится область их пересечения (множество решений может быть открытым бесконечным, либо ограниченным), или же «перекрытие» решений отсутствует. При упрощении выражений используются способы преобразований уравнений. Идеи преобразований неравенств в системе надо суметь догадаться «увидеть».

Система неравенств не имеет решений, в случае отсутствия таковых у одного из неравенств. Если у неравенства выполняется условие для любого значения аргумента, тогда решением системы является решение в других соседних неравенствах.

Существует несколько методов решения:

• Геометрически, с построением точек в четырех квадрантах плоскости координат по их ординатам и абсциссам.

• Для квадратного неравенства используют разложение на множители с найденными корнями и

определяют необходимые участки методом интервалов.

• Иногда решают способом через оценку получившегося знака разности. Для этого выполняют вычитание частей неравенства и приводят доказательства требуемого знака (>, <, ≥, ≤).

• Применяют общеизвестное доказательство методом «от противного» (истина, ложь). Предполагают противоположное требуемому изначально доказательству (хотя бы одни переменные делают его истинным). Если преобразования приведут к ложному неравенству, то сделанное предположение неверное, но верно изначальное.

• Доказывают неравенства «синтетическим» методом, преобразуя известные неравенства (опорные) до требуемого.

Примеры решения неравенства с двумя переменными

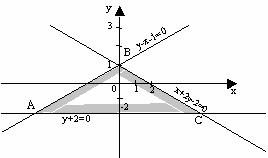
Задача 1.

Найти решение системы неравенств с двумя переменными:

Решается система графическим способом, вначале преобразуются уравнения, определяются места пересечения осей координат.

2y=-x+2; х=-2; у=0; х=0; у=1;

y=x+1; x=0; y=1; x=-1; y=0;

y=-2

По двум точкам каждой линии строятся две прямые. Неравенства нестрогие. Устанавливая при каждой прямой линии направление области определения (1/2 плоскости), находится общая для них область:

внутри треугольника, включительно с его границами все многие точки плоскости координат. Проверка заданных отношений в точке (0;0): (-2<0, -1<0, 2>0)

Решая попарно уравнения прямых (пересечение), находятся три вершины треугольника С, В, А.

Для С – у=-2; х=6. Для В – х=0;у=1. Для А – у=-2; х=-3.

Задача 2.

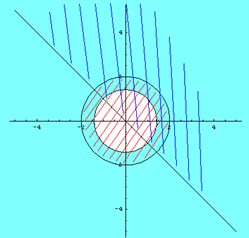
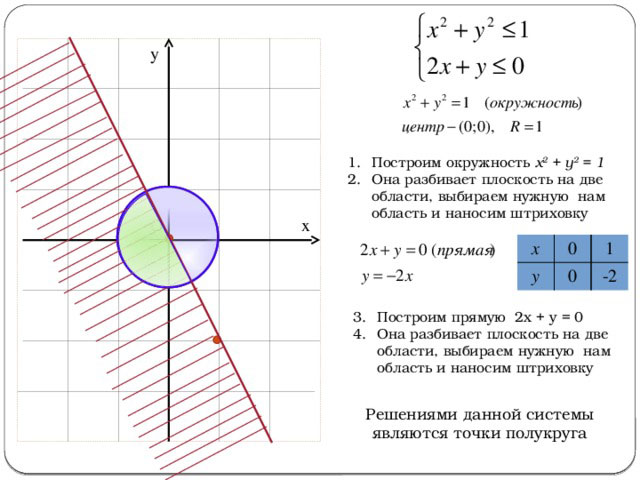
Найти подходящий к системе неравенств участок координатной плоскости.

Решаем уравнение для каждого отношения. Первое выражение — окружность с точкой центра в начале координат, единичным r. Строится линия x^2 + у^ 2 = 1, с пересечением осей (1; 0),(-1;0). Она делит плоскость на круг и вне круга; выбирается нужная область внутри круга (наносится штриховка).

Второе уравнение – прямая линия y=-2x. Строится по точкам (1;2), (-1;-2). Она разделяет плоскость пополам, выбирается область ниже прямой (заштриховывается). Пробное место с координатами -1, 1 удовлетворяет второму отношению (-1≤0).

Неравенства в системе верны в области точек нижнего полукруга и линии контура.

Проверим подстановкой (-0.2;-0.2) 0.08<1, -0.4-0.2=-0.6<0. Условия выполнены.

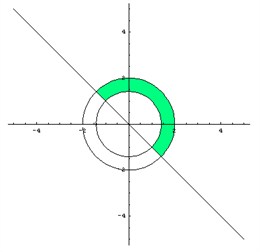
Задача 3.

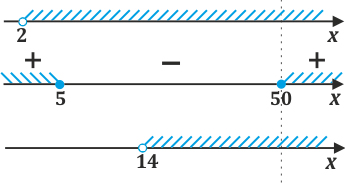
Определить общий участок для трех отношений:

Преобразуются исходные неравенства в уравнения, раскрываются скобки, вводятся множители, приводятся подобные слагаемые:

27(x-2)>0,

(x-5)(x-50)≥0,

x>14.

Отмечаются на числовой оси промежутки по результатам трех отношений.

После объединения для всех неравенств подходит «луч» из точки ≥50.

Ответ: [50;+∞)

Для помощи при решении квадратичных неравенств, используя равнозначно соответствующее уравнение ax² + bx + c = у, с дискриминантом D = b² − 4ac, предлагается табличный алгоритм нахождения участков переменных x в зависимости от знаков коэффициента a и D. Причем старший коэффициент а≠0. Необходимо находить корни при положительном D для разложения на множители, упрощения, использования метода интервалов.

Как записать общее решение?

Сообразно четкой математической формулировке, отображению решения используются дополнительные условные символы. При вычислении результатов объединенных неравенств ищется пересечение решений, когда их нет, то ответом является пустое множество x: 

Если встречается «пустое» неравенство, то результат находится хотя бы из одного уравнения системы.

Итог будет:

Если отношение строгое, тогда отрезок решения считается открытым, со скобками ( ), без включения на отрезки пограничных точек. Если – нестрогое, то решение будет закрытым отрезком, включающим граничные точки.

Х>23,

Х≤0,6.

Результат:

Применение знака ;– объединение двух множеств решений. Если неравенство второе нестрогое, тогда отрезок справа закрыт.

Ответ:

Если из всего целого интервала исключают точку 5, то возможно оформление со знаком :

Откроется еще много новых понятий, определений, знаковых обозначений благодаря осознанному изучению математических наук.

Приведены не все типы из многообразия неравенств, могут быть более сложные. Для их решения необходимо научиться разбираться в применяемых методах и способах специалистам, которые встречаются с необходимостью оптимизации процессов, допусками и ограничениями, учетом влияния нескольких параметров (математики, программисты, физики, экономисты).

ПРИМЕР: