Неравенства с радикалами егэ профиль - Помощь в подготовке к экзаменам и поступлению

Иррациональные неравенства

Так называются неравенства, содержащие знак корня.

В решении иррациональных неравенств главное – логика и внимательность.

И конечно, надо повторить следующие темы:

1) Арифметический квадратный корень.

2) Решение неравенств. Основные ошибки и полезные лайфхаки.

Напоминаем, что решение лучше всего записывать в виде цепочки равносильных переходов.

1.Решите неравенство

Правая часть неравенства неотрицательна:
(по определению корня квадратного).

Поскольку левая часть положительна:

Выражение под корнем должно быть неотрицательным. Неравенство равносильно системе:

Ответ: (5;+∞)

2.Решите неравенство .

Как вы думаете – это неравенство такое же, как предыдущее, или отличается от него? Ведь здесь правая часть может быть и положительной, и отрицательной, и равной нулю. И надо рассмотреть все эти случаи.

1) Пусть правая часть неравенства неотрицательна. И левая тоже неотрицательна (по определению арифметического квадратного корня). И подкоренное выражение неотрицательно. Значит, при обе части неравенства можно возвести в квадрат.

Получим:

$left{begin{matrix}x-5geq 0\4x-8geq 0\4x-8geq left ( x-5 right )^{2}end{matrix}right.Leftrightarrow left{begin{matrix}!!!!!!!!!!!xgeq 5\!!!!!!!!!!!xgeq 2\x^{2}-14x+33leq 0end{matrix}right.$

Разложим выражение $x^{2}-14x+33$ на множители. Корни уравнения $x^{2}-14x+33=0$ – это x=3 и x=11 .

Получаем систему:

$left{begin{matrix}xgeq 5\xgeq 2\left ( x-3 right )left ( x-11 right )leq 0end{matrix}right.Leftrightarrow 5leq xleq 11$

2) Пусть теперь правая часть неравенства отрицательна. Если то неравенство выполняется. В самом деле, по определению. Значит,

Нам нужно только, чтобы подкоренное выражение было неотрицательно: .

Получим:

Объединим полученные интервалы и запишем ответ.

Ответ: .

3.Решите неравенство

Ответ:

4.Решите неравенство

Ответ:

5.Решите неравенство $frac{1}{8x^{2}+6x}geq frac{1}{sqrt{8x^{2}+6x+1}-1}$

Сделаем замену $sqrt{8x^{2}+6x+1}=t, ;tgeq 0$ , тогда $8x^{2}+6x=t^{2}-1$

$left{begin{matrix}frac{1}{t^{2}-1}geq frac{1}{t-1}\tgeq 0end{matrix}right.Leftrightarrow left{begin{matrix}frac{1}{left ( t-1 right )left ( t+1 right )}-frac{1}{t-1}geq 0\tgeq 0end{matrix}right.Leftrightarrowleft{begin{matrix}frac{1-t-1}{left ( t-1 right )left ( t+1 right )}geq 0\tgeq 0end{matrix}right.Leftrightarrow$

$8x^{2}+6x+1=0$

$x_{1}=frac{-6+2}{16}=-frac{1}{4}$

$x_{2}=frac{-6-2}{16}=-frac{1}{2}$

Ответ: $x in left ( -frac{3}{4};;-frac{1}{2} right )cup left ( -frac{1}{4} ;;0right )$

6. Решите неравенство

$left ( frac{1}{x^{2}-7x+12} +frac{x-4}{3-x}right )sqrt{6x-x^{2}}leq 0$

$left ( frac{1}{x^{2}-7x+12} +frac{x-4}{3-x}right )sqrt{6x-x^{2}}leq 0Leftrightarrow left{begin{matrix}x^{2}-7x+12neq 0\xneq 3\6x-x^{2}geq 0\left[begin{array}{ccc}6x-x^{2}=0 \frac{1}{x^{2}-7x+12}+frac{x-4}{3-x} leq 0 \end{array}right.end{matrix}right.$
$left{begin{matrix}xneq 4\xneq 3\6x-x^{2}geq 0\left[begin{array}{ccc}x=0 \x=6\frac{1}{left ( x-3 right )left ( x-4 right )}-frac{x-4}{x-3} leq 0 \end{array}right.end{matrix}right.$

$left{begin{matrix}xneq 4\xneq 3\xleft ( x-6 right )leq 0\left[begin{array}{ccc}x=0 \x=6\frac{1-left ( x-4 right )^{2}}{left ( x-3 right )left ( x-4 right )} leq 0\end{array}right.end{matrix}right.Leftrightarrowleft{begin{matrix}xneq 4\xneq 3\xleft ( x-6 right )leq 0\left[begin{array}{ccc}x=0 \x=6\frac{left ( 1-x+4 right )left ( 1+x-4 right )}{left ( x-3 right )left ( x-4 right )} leq 0\end{array}right.end{matrix}right.Leftrightarrowleft{begin{matrix}xneq 4\xneq 3\xleft ( x-6 right )leq 0\left[begin{array}{ccc}x=0 \x=6\frac{left ( x-3 right )left ( x-5 right )}{left ( x-3 right )left ( x-4 right )} geq 0\end{array}right.end{matrix}right.$

Ответ:

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Иррациональные неравенства» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Особенности решения неравенств с корнями

3 мая 2014

Сегодня мы вернемся к решению неравенств методом интервалов, однако рассмотрим не обычные неравенства (где просто перемножаются скобки), а нестандартные, в которых присутствуют корни.

Итак, первая задача:

Задача 1. Решите неравенство:

В чем особенность такого неравенства? Какие ограничения для нас вносит наличие радикала? Все очень просто. Согласно определению, арифметический квадратный корень из любой функции f (x) всегда неотрицателен, т.е. больше или равен нуля.

А это значит, что мы можем без всяких затруднений избавиться от корня, просто зачеркнув его. Но при условии, что это выражение отлично от нуля. Потому что, напомню:

Основное свойство неравенства: обе части неравенства можно умножать и делить на любое число, отличное от нуля.

Таким образом, случай, когда корень (а значит — и подкоренное выражение) равняется нулю, следует проверять отдельно. Имеем:

15 − 5x = 0;
15 = 5x;
x = 3.

Подставим найденное число в исходное неравенство — получим:

(3 − 5) ∙ 0 < 0;
0 < 0.

Последнее неравенство, очевидно, является полным бредом. Следовательно, x = 3 не является решением исходного неравенства. А это значит, что мы можем спокойно разделить все неравенство на корень. Получим:

x − 8 < 0
x < 8

Однако если мы просто запишем такой ответ — (−∞; — то, как вы уже поняли, это будет неправильным решением. Все дело в том, что, избавляясь от корня в исходном неравенстве, мы одновременно расширяем область определения.

Судите сами: в неравенстве x < 0 переменная x может принимать абсолютно любые значения, потому что линейная функция определена на всей числовой прямой. А вот в исходном неравенстве подкоренное выражение должно быть неотрицательным, потому что корень из отрицательного числа не определен.

Поэтому возникает еще одно требование:

15 − 5x ≥ 0
15 ≥ 5x
x ≤ 3

Обратите внимание знак «больше или равно» никак не связан с тем, что стояло в исходном неравенстве — это просто требование области определения корня.

При решении неравенств, содержащих корни, подкоренная функция должна быть неотрицательной в любом случае — независимо от знака исходного неравенства.

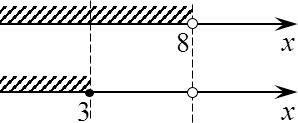
Теперь отметим наши требования на двух параллельных прямых:

Итак, с одной стороны, x должен быть меньше 8 (т.е. левее восьмерки). С другой — не больше 3 (опять же левее). Пересекаем наши множества и получаем интервал:

x ∈ (−∞; 3]

Но и это не является окончательным и правильным ответом! Дело в том, что в самом начале решения мы убедились, что x = 3 нас не устраивает. Следовательно, эту точку надо выколоть. Поэтому окончательным ответом будет множество:

x ∈ (−∞; 3)

Решение второго неравенства

Итак, переходим ко второму неравенству.

Задача 2. Решите неравенство:

Выполняем все те же самые действия, как и в прошлый раз. Для начала проверяем: является ли ответом тот случай, когда подкоренное выражение равно нулю.

16 − x² = 0
x² = 16
x = ± 4

Подставляем полученные числа в исходное неравенство и получаем:

(16 − 9) ∙ 0 > 0
0 > 0

Очевидно, мы вновь получили неверное неравенство (ноль больше нуля — полный бред). А это значит, что корни x = 4 и x = −4 не являются решением. Эти точки нужно будет выколоть.

С учетом данного факта нужно просто выполоть эти точки и решить обычное неравенство:

x² − 9 > 0
(x − 3)(x + 3) > 0

Чертим прямую, отмечаем нули выражения, стоящего справа — получаем:

Поскольку нас интересуют положительные области, отмечаем интервалы по бокам.

С другой стороны, в исходном неравенстве у нас есть корень. Поэтому нельзя забывать про определение:

16 − x² ≥ 0
x² ≤ 4
−4 < x < 4

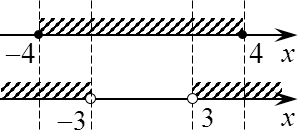
Осталось начертить на двух параллельных прямых полученные множества:

Пересекаем заштрихованные области (потому что указанные требования должны выполняться одновременно). Кроме того, вспоминаем, что значения x = ±4 нас не устраивают. Следовательно, эти точки нужно выколоть из итогового ответа. Получим:

x ∈ (−4; −3) ∪ (3; 4)

Вот такому множеству должно принадлежать число x, чтобы выполнялось исходное неравенство. Все точки при этом выколоты. Все, задача решена.

Надеюсь, этот урок поможет вам не запутаться при решении задач, содержащих корни. Тренируйтесь в решении неравенство методом интервалов — и до новых встреч.

Смотрите также:

Иррациональные неравенства. Часть 1
Иррациональные неравенства. Часть 2
Решение задач B12: №440—447
Преобразование уравнений
Задачи на проценты: формула, упрощающая вычисления
Задача B4: Семья из трех человек едет из Москвы в Нижний Новгород

Источник

Иррациональные неравенства.

1.Решите неравенство

Правая часть неравенства неотрицательна:
(по определению корня квадратного).

Поскольку левая часть положительна:

Выражение под корнем должно быть неотрицательным. Неравенство равносильно системе:

Ответ: (5;+∞)

2.Решите неравенство .

Здесь правая часть может быть и положительной, и отрицательной, и равной нулю. И надо рассмотреть все эти случаи.

Получим:

Разложим выражение $x^{2}-14x+33$ на множители. Корни уравнения $x^{2}-14x+33=0$ – это x=3 и x=11 .

Получаем систему:

Нам нужно только, чтобы подкоренное выражение было неотрицательно: .

Получим:

Объединим полученные интервалы и запишем ответ.

Ответ: .

3.Решите неравенство

Ответ:

4.Решите неравенство

Ответ:

5.Решите неравенство $frac{1}{8x^{2}+6x}geq frac{1}{sqrt{8x^{2}+6x+1}-1}$

Сделаем замену $sqrt{8x^{2}+6x+1}=t, ;tgeq 0$ , тогда $8x^{2}+6x=t^{2}-1$

$8x^{2}+6x+1=0$

$x_{1}=frac{-6+2}{16}=-frac{1}{4}$

$x_{2}=frac{-6-2}{16}=-frac{1}{2}$

Ответ: $x in left ( -frac{3}{4};;-frac{1}{2} right )cup left ( -frac{1}{4} ;;0right )$

6. Решите неравенство

$left ( frac{1}{x^{2}-7x+12} +frac{x-4}{3-x}right )sqrt{6x-x^{2}}leq 0$

Ответ:

Неравенства, содержащие радикалы. По материалам ЕГЭ.

1. Задание 15 № 507582

Решите неравенство

Решение.

Решение неравенства ищем при условиях: откуда

Рассмотрим два случая:

1) т. е. и, значит, или Тем самым, — решение задачи.

2) Разделив обе части неравенства на получим: откуда

Решим это неравенство, получим: или

Учитывая ограничения, получаем множество решений исходного неравенства:

Ответ:

2. Задание 15 № 507612

Решите неравенство

Решение.

Имеем:

Ответ:

Примечание.

Напомним, что При этом условие избыточно, так как величина, большая неотрицательной, заведомо положительна. Существенным моментом решения является хорошее понимание этого обстоятельства. Именно поэтому, решая неравенство нет необходимости дополнительно решать неравенство

3. Задание 15 № 507792

Решите неравенство

Решение.

Пусть Получаем систему неравенств:

Следовательно:

Таким образом, решением исходного неравенства является множество

Ответ:

4. Задание 15 № 507894

Решите неравенство

Решение.

Перейдем к равносильной системе:

Из первого неравенства получаем или

Второе неравенство выполняется при всех

Из третьего неравенства получаем или

Таким образом, множество решений исходного неравенства:

Ответ:

5. Задание 15 № 508431

Решите неравенство:

Решение.

Неравенство имеет смысл при

1. Пусть Тогда и неравенство равносильно неравенству Решим систему:

2. Заметим, теперь, что также является решением.

Ответ:

6. Задание 15 № 511239

Решите неравенство

Решение.

Последовательно получаем:

И решим это неравенство методом интервалов, учитывая, что

Ответ:

7. Задание 15 № 485951

Решите неравенство

Решение.

Если то или При этих значениях выражение имеет смысл, поэтому и являются решениями неравенства.

Если то при этом Тогда

Пересекая полученное решение с множеством и учитывая, что точки 0 и 6 также входят в являются решениями неравенства, получим множество решений исходного неравенства:

Ответ:

8. Задание 15 № 507175

Решите неравенство

Решение.

Данное неравенство эквивалентно системе неравенств:

Решим второе неравенство системы методом интервалов:

Отметим на прямой точки, как показано на рисунке:

Учитывая неравенство получаем решение:

Ответ:

9. Задание 15 № 539881

Решите неравенство

Решение.

Корень существует на отрезке [1; 5]. Преобразуем неравенство на этом множестве: приведем к общему знаменателю, и воспользуемся методом интервалов (см. рис.):

Ответ:

Источник

Иррациональные неравенства.

1.Решите неравенство

Правая часть неравенства неотрицательна:

(по определению корня квадратного).

Поскольку левая часть положительна:

Выражение под корнем должно быть неотрицательным. Неравенство равносильно системе:

Ответ: (5;+∞)

2.Решите неравенство .

1) Пусть правая часть неравенства неотрицательна. И левая тоже неотрицательна (по определению арифметического

квадратного корня). И подкоренное выражение неотрицательно. Значит, при обе части неравенства можно возвести

в квадрат.

Получим:

Разложим выражение на множители. Корни уравнения – это и .

Получаем систему:

2) Пусть теперь правая часть неравенства отрицательна. Если то неравенство выполняется. В самом

деле, по определению. Значит,

Нам нужно только, чтобы подкоренное выражение было неотрицательно: .

Получим:

Объединим полученные интервалы и запишем ответ.

Ответ: .

3.Решите неравенство

Ответ:

4.Решите неравенство

Ответ:

5.Решите неравенство

Сделаем замену , тогда

Ответ:

6. Решите неравенство

Ответ:

Неравенства, содержащие радикалы. По материалам ЕГЭ.

1. Задание 15 № 507582

Решите неравенство

Решение.

Решение неравенства ищем при условиях: откуда

Рассмотрим два случая:

1) т. е. и, значит, или Тем самым, — решение задачи.

2) Разделив обе части неравенства на получим: откуда

Решим это неравенство, получим: или

Учитывая ограничения, получаем множество решений исходного неравенства:

О т в е т :

2. Задание 15 № 507612

Решите неравенство

Решение.

Имеем:

О т в е т :

Примечание.

Напомним, что При этом условие избыточно, так как величина, большая неотрицательной, заведомо положительна.

Существенным моментом решения является хорошее понимание этого обстоятельства. Именно поэтому, решая

неравенство нет необходимости дополнительно решать неравенство

3. Задание 15 № 507792

Решите неравенство

Решение.

Пусть Получаем систему неравенств:

Следовательно:

Таким образом, решением исходного неравенства является множество

О т в е т :

4. Задание 15 № 507894

Решите неравенство

Решение.

Перейдем к равносильной системе:

Из первого неравенства получаем или

Второе неравенство выполняется при всех

Из третьего неравенства получаем или

Таким образом, множество решений исходного неравенства:

О т в е т :

5. Задание 15 № 508431

Решите неравенство:

Решение.

Неравенство имеет смысл при

1. Пусть Тогда и неравенство равносильно неравенству Решим систему:

2. Заметим, теперь, что также является решением.

О т в е т :

6. Задание 15 № 511239

Решите неравенство

Решение.

Последовательно получаем:

И решим это неравенство методом интервалов, учитывая, что

О т в е т :

7. Задание 15 № 485951

Решите неравенство

Решение.

Если то или При этих значениях выражение имеет смысл,

поэтому и являются решениями неравенства.

Если то при этом Тогда

Пересекая полученное решение с множеством и учитывая, что точки 0 и 6 также входят в являются решениями неравенства, получим

множество решений исходного неравенства:

О т в е т :

8. Задание 15 № 507175

Решите неравенство

Решение.

Данное неравенство эквивалентно системе неравенств:

Решим второе неравенство системы методом интервалов:

Отметим на прямой точки, как показано на рисунке:

Учитывая неравенство получаем решение:

О т в е т :

9. Задание 15 № 539881

Решите неравенство

Решение.

Корень существует на отрезке [1; 5]. Преобразуем неравенство на этом множестве: приведем к общему знаменателю, и воспользуемся методом

интервалов (см. рис.):

О т в е т :

Источник

21
Окт 2013

Категория: Иррациональные выражения, уравнения и неравенства

Иррациональные неравенства

2013-10-21
2019-08-13

Давайте учиться решать иррациональные неравенства. Будем решать методом равносильных переходов в иррациональных неравенствах. Хотя зачастую, возможно, будет легче решить отдельное неравенство обобщенным методом интервалов или методом рационализации.

Задание 1.

Решить неравенство: $sqrt{x^2+5x}<sqrt{1-x^2+4x}.$

Решение: + показать

Задание 2.

Решить неравенство: $sqrt{x^2-3x-10}<8-x.$

Решение: + показать

Задание 3.

Решить неравенство: $sqrt{x^2-5x-24}>x+2.$

Решение: + показать

Задание 4.

Решить неравенство: $(x+1)sqrt{x^2+1}>x^2-1.$

Решение: + показать

Задание 5.

Решить неравенство: $frac{sqrt{6+x-x^2}}{2x+5}geq frac{sqrt{6+x-x^2}}{x+4}.$

Решение: + показать

Задание 6.

Решить неравенство: .

Решение: + показать

Задание 7.

Решить неравенство: $sqrt{4x^2+x+9}+sqrt{4x^2+x}>3.$

Решение: + показать

Задания для самостоятельной работы

Решить неравенства:

1. $sqrt{2x^2+5x-6}>sqrt{-x-3};$

Ответ: + показать

2. $sqrt{x^2-3x-18}<4-x;$

Ответ: + показать

3. $sqrt{2x^2+5x-6}>2-x;$

Ответ: + показать

4. $(x-3)sqrt{x^2+4}leq x^2-9;$

Ответ: + показать

5. $frac{sqrt{2-x-x^2}}{x-4}geq frac{sqrt{2-x-x^2}}{2x+11};$

Ответ: + показать

8. $sqrt{x^2-2x-2}+sqrt{x^2-2x+6}<4;$

Ответ: + показать

Автор: egeMax |

комментариев 6

Источник

Иррациональные неравенства

Привет!

Говоря об иррациональности, может показаться, что сложнее иррациональных уравнений есть лишь одна вещь — иррациональные неравенства.

И сейчас ты поймешь, что это не так!

Если ты хорошо разобрался в предыдущих темах (я скажу, в каких в начале статьи), то иррациональные уравнения покажутся тебе легкими.

Мы рассмотрим все виды неравенств и разберем различные примеры, так, чтобы ты смог решить любое иррациональное неравенство.

Иррациональные неравенства – коротко о главном

Определение

Иррациональное неравенство – это неравенство, содержащее переменную под корнем

Неравенства вида ( sqrt{A}ge sqrt{B})

( sqrt{A}ge sqrt{B}text{ }Leftrightarrow text{ }left{ begin{array}{l}Age B\Bge 0end{array} right.)

или

( sqrt{A}>sqrt{B}text{ }Leftrightarrow text{ }left{ begin{array}{l}A>B\Bge 0end{array} right.)

Неравенства вида ( Asqrt{B}>0) или ( Asqrt{B}<0)

( Asqrt{B}>0text{ }Leftrightarrow text{ }left{ begin{array}{l}B>0\A>0end{array} right.)

или

( Asqrt{B}<0text{ }Leftrightarrow text{ }left{ begin{array}{l}B>0\A<0end{array} right.)

Неравенства вида ( Asqrt{B}ge 0)

( Asqrt{B}ge 0text{ }Leftrightarrow text{ }left[ begin{array}{l}B=0\left{ begin{array}{l}Age 0\Bge 0end{array} right.end{array} right.)

или

( Asqrt{B}le 0text{ }Leftrightarrow text{ }left[ begin{array}{l}B=0\left{ begin{array}{l}Ale 0\Bge 0end{array} right.end{array} right.)

Неравенства вида ( sqrt{A}ge B)

( sqrt{A}ge Btext{ }Leftrightarrow text{ }left[ begin{array}{l}left{ begin{array}{l}Ble 0\Age 0end{array} right.\left{ begin{array}{l}B>0\Age {{B}^{2}}end{array} right.end{array} right.)

или

( sqrt{A}>Btext{ }Leftrightarrow text{ }left[ begin{array}{l}left{ begin{array}{l}B<0\Age 0end{array} right.\left{ begin{array}{l}Bge 0\A>{{B}^{2}}end{array} right.end{array} right.)

Неравенства вида ( sqrt{A}le B)

( sqrt{A}le Btext{ }Leftrightarrow text{ }left{ begin{array}{l}Age 0\Bge 0\Ale {{B}^{2}}end{array} right.)

или

( sqrt{A}<Btext{ }Leftrightarrow text{ }left{ begin{array}{l}Age 0\B>0\A<{{B}^{2}}end{array} right.)

Корни четной степени

Например:

( displaystyle sqrt[4]{A}le Btext{ }Leftrightarrow text{ }left{ begin{array}{l}Ale {{B}^{4}}\Bge 0\Age 0end{array} right.)

Корни нечетной степени

Корень нечетной степени можно извлекать из любого числа!

( displaystyle begin{array}{l}sqrt[3]{A}>Btext{ }Leftrightarrow text{ }A>{{B}^{3}}\sqrt[5]{A}<Btext{ }Leftrightarrow text{ }A<{{B}^{5}},end{array}) и т.д.

ОДЗ (Область допустимых значений)

Помнишь, что такое ОДЗ?

ОДЗ (область допустимых значений) неравенства или неравенств – это множество значений переменной, при которых обе части данного неравенства (или неравенств) имеют смысл.

Например, в уравнении ( sqrt{x+2}=3) присутствует квадратный корень. А квадратный корень не имеет смысла, если подкоренное выражение отрицательно.

То есть, в данном случае ОДЗ – это решения неравенства ( x+2ge 0).

Нет необходимости искать ОДЗ в каждой задаче, содержащей корень.

Взять, например, такую задачу:

( sqrt{{{x}^{2}}+3x}>2).

При возведении в квадрат получаем ( {{x}^{2}}+3x>4), то есть подкоренное выражение автоматически неотрицательно! Так зачем лишняя писанина?

Но в некоторых случаях это может быть очень полезно. Более того, иногда можно решить пример, просто найдя ОДЗ. Например:

( sqrt{2{x}-6}>-2).

Но ведь мы помним, что квадратный корень всегда неотрицателен. Поэтому он всегда будет больше ( -2). Значит, решением задачи будет ОДЗ:

( 2{x}-6ge 0text{ }Leftrightarrow text{ }xge 3).

Ответ: ( left[ 3;+infty right)).

Пять видов неравенств и способы их решений

Первый вид неравенств

( sqrt{A}ge sqrt{B})

Естественно, знак неравенства может быть и нестрогим.

Здесь и далее большими буквами ( A), ( B), ( C) и т.д. я буду обозначать не переменные или параметры, а целые выражения, содержащие переменную.

Так, общая запись ( sqrt{A}>sqrt{B}) соответствует, например, уравнению ( sqrt{{{x}^{2}}-{x}-2}>sqrt{{x}-1}).

Здесь ( A={{x}^{2}}-{x}-2) и ( B={x}-1).

Как решить такое неравенство?

Для начала вспомним, что функция ( fleft( x right)=sqrt{x}) – монотонна, то есть, чем больше подкоренное выражение, тем больше сам корень.

Поэтому из двух корней больше тот, у которого подкоренное выражение больше.

Но недаром мы недавно вспоминали про ОДЗ. Есть ли какие-нибудь ограничения в этом неравенстве?

Действительно, чтобы неравенство имело смысл, необходимо, чтобы оба подкоренных выражения были неотрицательны:

( left{ begin{array}{l}Age 0\Bge 0end{array} right.)

Но поскольку первое выражение больше второго, достаточно потребовать неотрицательности только второго:

( sqrt{A}ge sqrt{B}text{ }Leftrightarrow text{ }left{ begin{array}{l}Age B\Bge 0end{array} right.)

или

( sqrt{A}>sqrt{B}text{ }Leftrightarrow text{ }left{ begin{array}{l}A>B\Bge 0end{array} right.)

Три примера на закрепление материала:

Пример №1. ( sqrt{{{x}^{2}}-{x}+2}>sqrt{{x}+1})

Пример №2. ( sqrt{2{{x}^{2}}-6{x}-17}ge sqrt{{x}-2})

Пример №3. ( sqrt{2{{x}^{2}}-x-6}le sqrt{3{{x}^{2}}-{8x}})

Решение примера №1

Применим только что выученное правило:

( displaystyle sqrt{{{x}^{2}}-x+2}>sqrt{x+1}text{ }Leftrightarrow text{ }left{ begin{array}{l}{{x}^{2}}-x+2>x+1\x+1ge 0end{array} right.text{ }Leftrightarrow text{ }left{ begin{array}{l}{{x}^{2}}-2x+1>0\xge -1end{array} right.Leftrightarrow )

( displaystyle Leftrightarrow text{ }left{ begin{array}{l}{{left( {x}-1 right)}^{2}}>0\xge -1end{array} right.text{ }Leftrightarrow left{ begin{array}{l}xne 1\xge -1end{array} right.text{ }Leftrightarrow text{ }xin left[ -1;1 right)cup left( 1;+infty right)).

Решение примера №2

( displaystyle sqrt{2{{x}^{2}}-6{x}-17}ge sqrt{{x}-2}text{ }Leftrightarrow text{ }left{ begin{array}{l}2{{x}^{2}}-6{x}-17ge {x}-2\{x}-2ge 0end{array} right. Leftrightarrow )

Решение примера №3

( displaystyle sqrt{2{{x}^{2}}-{x}-6}le sqrt{3{{x}^{2}}-8x}text{ }Leftrightarrow text{ }left{ begin{array}{l}3{{x}^{2}}-8xge 2{{x}^{2}}-{x}-6\2{{x}^{2}}-{x}-6ge 0end{array} right.text{ }Leftrightarrow )

( displaystyle Leftrightarrow text{ }left{ begin{array}{l}left( {x}-6 right)left( {x}-1 right)ge 0\2left( {x}-2 right)left( x+frac{3}{2} right)ge 0end{array} right.).

Далее поставим знаки…

Второй вид неравенств

( Asqrt{B}>0) или ( Asqrt{B}<0)

Корень всегда принимает неотрицательные значения, поэтому, он влияет на это неравенство, только если равен нулю. То есть нужно ограничить корень, чтобы он не был равен нулю, а в остальном – дело за выражением ( A).

И не забываем про ОДЗ, подкоренное выражение неотрицательно. А если оно неотрицательно, и при этом не должно быть равно нулю, то оно строго болше нуля:

( Asqrt{B}>0text{ }Leftrightarrow text{ }left{ begin{array}{l}B>0\A>0end{array} right.)

или

( Asqrt{B}<0text{ }Leftrightarrow text{ }left{ begin{array}{l}B>0\A<0end{array} right.)

Три примера на закрепление материала

Пример №1. ( xsqrt{x+5}>0)

Пример №2. ( ({{x}^{2}}-{x}-2)cdot sqrt{{x}-2}<0)

Пример №3. ( ({{x}^{2}}-9)sqrt{{{x}^{2}}-4}>0)

Решение примера №1

( xsqrt{x+5}>0)

( left{ begin{array}{l}x+5>0\x>0end{array} right. Rightarrow left{ begin{array}{l}x>-5\x>0end{array} right.Rightarrow x>0).

Решение примера №2

( ({{x}^{2}}-{x}-2)cdot sqrt{{x}-2}<0)

Решение примера №3

( ({{x}^{2}}-9)sqrt{{{x}^{2}}-4}>0)

Третий вид неравенств

( Asqrt{B}ge 0)

В случае нестрогого неравенства условие, что подкоренное выражение не равно нулю теперь лишнее. Но это только добавило нам проблем, ведь при этом выражение ( displaystyle A) может быть любым. Значит, надо отдельно рассмотреть случай, когда корень равен нулю:

( Asqrt{B}ge 0text{ }Leftrightarrow text{ }left[ begin{array}{l}B=0\left{ begin{array}{l}Age 0\Bge 0end{array} right.end{array} right.)

или

( Asqrt{B}le 0text{ }Leftrightarrow text{ }left[ begin{array}{l}B=0\left{ begin{array}{l}Ale 0\Bge 0end{array} right.end{array} right.)

Три примера на закрепление материала

Пример №1. ( xsqrt{{x}-1}ge 0)

Пример №2. ( left( {{x}^{2}}-4 right)sqrt{x+1}le 0)

Пример №3. ( left( {{x}^{2}}-3{x}-4 right)sqrt{x+1}>0)

Решение примера №1

( xsqrt{{x}-1}ge 0text{ }Leftrightarrow text{ }left[ begin{array}{l}{x}-1=0\left{ begin{array}{l}xge 0\{x}-1ge 0end{array} right.end{array} right.text{ }Leftrightarrow text{ }left[ begin{array}{l}x=1\xge 1end{array} right.text{ }Leftrightarrow text{ }xge 1.).

Решение примера №2

( displaystyle left( {{x}^{2}}-4 right)sqrt{x+1}le 0text{ }Leftrightarrow text{ })

Решение примера №3

( displaystyle left( {{x}^{2}}-3{x}-4 right)sqrt{x+1}>0text{ }Leftrightarrow text{ })

Четвертый вид неравенств

( sqrt{A}le B)

Здесь все немного проще: поскольку корень неотрицателен, то и правая часть этого неравенства должна быть неотрицательной:

( sqrt{A}le Btext{ }Leftrightarrow text{ }left{ begin{array}{l}Age 0\Bge 0\Ale {{B}^{2}}end{array} right.) или ( sqrt{A}<Btext{ }Leftrightarrow text{ }left{ begin{array}{l}Age 0\B>0\A<{{B}^{2}}end{array} right.).

Три примера на закрепление материала

Пример №1. ( sqrt{15-2x}le x)

Пример №2. ( x+3>sqrt{4x})

Пример №3. ( sqrt{x+7}+3x<4{x}-5)

Решение примера №1

( sqrt{15-2x}le x)

( left{ begin{array}{l}15-2x ge 0\xge 0\15-2xle {{x}^{2}}end{array} right.Rightarrow left{ begin{array}{l}x le 7,5\xge 0\{{x}^{2}}+2{x}-15ge 0end{array} right.Rightarrow left{ begin{array}{l}x le 7,5\xge 0\({x}-3)cdot ({x}+5)ge 0end{array} right.Rightarrow )

( left{ begin{array}{l}x le 7,5\xge 0\xin (-infty ;left. -5 right]cup left[ 3 right.;+infty )end{array} right.Rightarrow xin left[ 3; right.left. 7,5 right]).

Решение примера №2

( x+3>sqrt{4x})

Решение примера №3

( sqrt{x+7}+3x<4{x}-5)

Пятый вид неравенств

( sqrt{A}ge B)

Рассмотрим пример:

( sqrt{x+2}ge x)

Тут возможны два варианта. Если ( xle 0), неравенство выполнится при всех допустимых ( x), ведь корень неотрицателен, значит, он автоматически больше (или равен) неположительного числа:

( left{ begin{array}{l}xle 0\x+2ge 0end{array} right.)

Если же правая часть положительна (( x>0)), имеем право возводить в квадрат:

( x+2ge {{x}^{2}}).

ОДЗ, как видим, здесь учтено автоматически. Итак, собираем все в кучу:

( left[ begin{array}{l}left{ begin{array}{l}xle 0\x+2ge 0end{array} right.\left{ begin{array}{l}x>0\x+2ge {{x}^{2}}end{array} right.end{array} right.)

Запомни, прежде чем возводить в квадрат, нужно убедиться, что обе части неравенства неотрицательны! Тоже своего рода ОДЗ.

Итак, правило в общем виде:

( sqrt{A}ge Btext{ }Leftrightarrow text{ }left[ begin{array}{l}left{ begin{array}{l}Ble 0\Age 0end{array} right.\left{ begin{array}{l}B>0\Age {{B}^{2}}end{array} right.end{array} right.)

А как будет выглядеть это правило, если неравенство строгое? Вот так:

( sqrt{A}>Btext{ }Leftrightarrow text{ }left[ begin{array}{l}left{ begin{array}{l}B<0\Age 0end{array} right.\left{ begin{array}{l}Bge 0\A>{{B}^{2}}end{array} right.end{array} right.)

Подумай сам, почему именно так.

Три примера на закрепление материала

Пример №1. ( sqrt{4x+1}ge {x}-1)

Пример №2. ( sqrt{2{x}-1}-sqrt{x+2}<1)

Пример №3. ( displaystyle 3sqrt{6+2{x}-4{{x}^{2}}}+2>8x)

Решение примера №1

( displaystyle sqrt{4x+1}ge {x}-1text{ }Leftrightarrow )

( displaystyle Leftrightarrow left[ begin{array}{l}left{ begin{array}{l}{x}-1le 0\4x+1ge 0end{array} right.\left{ begin{array}{l}4x+1ge {{x}^{2}}-2x+1\{x}-1>0end{array} right.end{array} right.text{ }Leftrightarrow left[ begin{array}{l}-frac{1}{4}le xle 1\left{ begin{array}{l}xleft( {x}-6 right)le 0\x>1end{array} right.end{array} right.text{ }Leftrightarrow )

( displaystyle Leftrightarrow left[ begin{array}{l}-frac{1}{4}le xle 1\left{ begin{array}{l}0le xle 6\x>1end{array} right.end{array} right.text{ }Leftrightarrow text{ }xin left[ -frac{1}{4};6 right]text{.}).

Решение примера №2

( sqrt{2{x}-1}-sqrt{x+2}<1text{ }Leftrightarrow text{ }sqrt{2{x}-1}<1+sqrt{x+2})

Теперь обе части неравенства неотрицательны, значит, можно возвести их в квадрат (не забыв также, что подкоренное выражение в левой части должно быть неотрицательным):

Решение примера №3

( displaystyle 3sqrt{6+2{x}-4{{x}^{2}}}+2>8x)

Корни степени больше 2

Если же корень в неравенстве не квадратный, важна четность его степени.

Корни чётной степени

Корни ( 2), ( 4), ( 6) и т.д. степеней очень похожи друг на друга, и принцип решения уравнений с ними абсолютно одинаковый. Дело в том, что корень четной степени можно всегда привести к квадратному (вспоминаем тему «Корень и его свойства»!):

( sqrt[4]{x}=sqrt{sqrt{x}};text{ }sqrt[6]{x}=sqrt{sqrt[3]{x}};text{ }sqrt[2k]{x}=sqrt{sqrt[k]{x}})

Например:

( displaystyle sqrt[4]{A}le Btext{ }Leftrightarrow text{ }left{ begin{array}{l}Ale {{B}^{4}}\Bge 0\Age 0end{array} right.).

Корни нечётной степени

С нечетными степенями (( 3), ( 5), …) все намного проще!

Дело в том, что корень нечетной степени можно извлекать из любого числа! (И снова, если ты этого не знал, вспомни тему «Корень и его свойства»!)

Что это значит?

Теперь никаких дополнительных условий, никаких ограничений – просто возводим все в нужную степень и решаем:

( displaystyle begin{array}{l}sqrt[3]{A}>Btext{ }Leftrightarrow text{ }A>{{B}^{3}}\sqrt[5]{A}<Btext{ }Leftrightarrow text{ }A<{{B}^{5}},end{array}) и т.д.

Три примера на закрепление материала

Пример №1. ( displaystyle sqrt[5]{2-x}>-2)

Пример №2. ( displaystyle sqrt[3]{{{x}^{3}}+3x+5}ge x)

Пример №3. ( displaystyle sqrt[3]{{{x}^{2}}-{x}-7}<sqrt[3]{1-x})

( displaystyle sqrt[5]{2-x}>-2text{ }Leftrightarrow text{ }2-x>{{left( -2 right)}^{5}}text{ }Leftrightarrow text{ }2-x>-32text{ }Leftrightarrow text{ }x<34).

Решение примера №3

( displaystyle sqrt[3]{{{x}^{2}}-{x}-7}<sqrt[3]{1-x}text{ }Leftrightarrow text{ }{{x}^{2}}-{x}-7<1-xtext{ }Leftrightarrow )

Самые бюджетные курсы по подготовке к ЕГЭ на 90+

Алексей Шевчук – ведущий мини-групп

математика, информатика, физика

+7 (905) 541-39-06 – WhatsApp/Телеграм для записи

alexei.shevchuk@youclever.org – email для записи

тысячи учеников, поступивших в лучшие ВУЗы страны
автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
закончил МФТИ, преподавал на малом физтехе;
репетиторский стаж – c 2003 года;
в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов – как обычно дурацкая ошибка:);
отзыв на Профи.ру: “Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами”.

Источник