Неравенство егэ 2 часть - Помощь в подготовке к экзаменам и поступлению

Неравенства. Метод замены множителя (метод рационализации)

Полезный прием для решения сложных неравенств на ЕГЭ по математике – метод рационализации неравенства. Другое название — метод замены множителя. Это один из тех секретов, о которых ученику рассказывает репетитор. В учебниках о таком не написано.

Суть метода в том, чтобы от неравенства, содержащего в качестве множителей сложные показательные или логарифмические выражения, перейти к равносильному ему более простому рациональному неравенству.

Давайте для начала вспомним, что такое равносильные уравнения (или неравенства). В школьной программе этот важный вопрос почти не обсуждается. Поэтому запишем определение.

Равносильными называются уравнения, множества решений которых совпадают.

Заметим, что внешне уравнения могут быть и не похожи друг на друга.

Например, уравнения (x − 3)² = 0 и x − 3 = 0 равносильны. Число 3 является единственным решением и того, и другого.

Уравнения $x^{2}=-1$ и также равносильны. Оба они не имеют решений. Другими словами, множество решений каждого из них – пусто.

Уравнения и $2x-1=(x-2)^{2}$ не являются равносильными. Решением первого уравнения является только x = 5. Решения второго – два числа: x = 5 и x = 1. Получается, что возведение обеих частей уравнения в квадрат в общем случае приводит к уравнению, неравносильному исходному.

Аналогичное определение – для неравенств.

Равносильными называются неравенства, множества решений которых совпадают.

Например, неравенства и $frac{x-1}{x-3}>0$ равносильны – ведь множества их решений совпадают. В этом легко убедиться с помощью метода интервалов.

Неравенства $log_{2}x>log_{2}5$ и x> 5 также равносильны при x> 0 . Заметим, что внешне эти неравенства не похожи – одно из них логарифмическое, другое алгебраическое.

Другими словами, при x > 0 неравенства $log_{2}x-log_{2}5>0$ и x-5>0 имеют одинаковые решения. Если какое-либо число x > 0 является решением одного из них, то оно будет и решением второго.

А это значит, что при любом x > 0 выражение $log_{2}x-log_{2}5$ будет иметь такой же знак, как и выражение x − 5. Следовательно, если в какое-либо сложное неравенство входит в качестве множителя выражение $log_{2}x-log_{2}5$ , то при выполнении условия x > 0 его можно заменить на более простое x − 5 и получить неравенство, равносильное исходному.

Вот ключевой момент. На этом и основан метод рационализации – замены множителей, содержащих сложные логарифмические или показательные выражения, на более простые алгебраические множители.

Например, выражение вида $log_{a}f-log_{a}g$ , где f и g – функции от x, a – число, можно заменить на более простое (f − g) (a − 1) – конечно, при условии, что f(x) > 0 и g(x) > 0. Доказательство легко провести самостоятельно.

А сейчас – самое главное: волшебная таблица, позволяющая заменять сложные логарифмические (или показательные) множители в неравенствах на более простые. Эта таблица является ключом к задаче С3. Вот увидите, она выручит вас на ЕГЭ по математике:

Сложный множитель	На что заменить
log_h f − log_h g	(h − 1) (f − g)
log_h f − 1	(h − 1) (f − h)
log_h f	(h − 1) (f − 1)
h^f − h^g	(h − 1) (f − g)
h^f − 1	(h − 1) · f
f^h − g^h	(f − g) · h
f, g — функции от x. h — функция или число.

Конечно же, все выражения, которые содержат логарифмы, существуют при f, g, h > 0 и h ≠ 1.

Когда на ЕГЭ по математике вы применяете метод рационализации (замены множителя), – обязательно поясните, что вы им воспользовались. И не забудьте доказать соответствующую формулу. Иначе можно потерять балл.

Обратите внимание, что мы говорим о замене множителя в неравенствах вида Знак здесь может быть любой: >, ≥, ≤. Правая часть обязательно должна быть равна нулю. И заменяем мы именно множитель (а не слагаемое, например). Иначе ничего не получится.

Перейдем к практике – к решению задач из вариантов ЕГЭ по математике Профильного уровня.

1. $log_{2-x}(x+2)cdot log_{x+3}(3-x)leq 0$ .

ОДЗ неравенства: .

Применим метод рационализации. В соответствии с нашей таблицей, множитель $log_{2-x}(x+2)$ заменим на (2 − x − 1)(x + 2 − 1). Множитель вида $log_{x+3}(3-x)$ заменим на (x + 3 − 1)(3 − x − 1). Таким образом, от логарифмического неравенства мы перешли к рациональному:

(1 − x) (x + 1) (x + 2) (2 − x) ≤ 0.

Решим его методом интервалов:

Ответ: .

2. $frac{10^{x}}{2cdot log^{2}_{2}(x+1)^{2}cdot log_{3}(x+2)}leq frac{(15cdot 3^{x})^{x}}{9cdot log^{2}_{2}(x+1)^{2}cdot log_{3}(x+2)}.$

Начнем с ОДЗ.

$left{begin{matrix} xneq 0;\ x>-2;\ xneq -1. end{matrix}right.$

Заметим, что выражение $log^{2}_{2}(x+1)^{2}$ положительно при x ∈ ОДЗ. Умножим обе части неравенства на это выражение.
Упростим числитель правой части неравенства:

$(15cdot 3^{x})^{x}=5^{x}cdot 3^{x}cdot 3^{x^{2}}=5^{x}cdot 3^{x^{2}+x}$
Поделим обе части неравенства на 5^x > 0:

$frac{2^{x}}{2log_{3}(x+2)}leq frac{3^{x^{2}+x}}{9log_{3}(x+2)}: : Leftrightarrow \ , , \ : : \ Leftrightarrow frac{2^{x-1}-3^{x^{2}+x-2}}{log_{3}(x+2)}leq 0: : Leftrightarrow \ , , \ : : \ Leftrightarrow frac{2^{x-1}-3^{(x-1)(x+2)}}{log_{3}(x+2)}leq 0.$ Неравенство уже намного проще, чем исходное. Но основания степеней разные! Чтобы применить метод рационализации, нам придется представить 2^{x − 1} в виде степени с основанием 3.

$2^{x-1}=3^{log_{3}2^{x-1}}=3^{(x-1)log_{3}2}.$ Неравенство примет вид:

$frac{3^{(x-1)log_{3}2}-3^{(x-1)(x+2)}}{log_{3}(x+2)}leq 0.$ Воспользуемся методом замены множителя. Множитель вида h^f −h^g можно заменить на (h − 1) (f − g). Да и логарифм в знаменателе можно заменить на выражение x + 1.

$frac{(x-1)(x-(log_{3}2-2))}{x+1}geq 0.$ Оценим $log_{3}2-2$ . Это необходимо сделать, чтобы правильно расставить точки на числовой прямой.

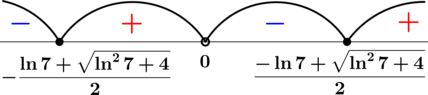
$log_{3}1<log_{3}2<log_{3}3;$ $0<log_{3}2<1$ $-2<log_{3}2-2<-1$ Ответ:

3. $frac{10^{log_{2}x}}{2x^{2}(x+1)}leq frac{(15cdot 3^{log_{2}x})^{log_{2}x}}{9x^{2}(x+1)}$ .

Постараемся упростить это неравенство. Область допустимых значений

$left{begin{matrix} x>0;\ x+1neq 0. end{matrix}right.$ Отсюда следует, что x > 0. Это хорошо, потому что при данных значениях x выражение x + 1 строго положительно, следовательно, мы можем умножить на него обе части неравенства. Да и на x² тоже можно умножить обе части неравенства, и тогда оно станет проще:

$frac{10^{log_{2}x}}{2}leq frac{15^{log_{2}x}cdot 3^{log^{2}_{2}x}}{9}$ Преобразуем числители выражений в левой и правой части и сделаем замену log₂x = t:

$frac{2^{t}cdot 5^{t}}{2}leq frac{3^{t}cdot 5^{t}cdot 3^{t^{2}}}{9}$ Теперь обе части неравенства можно сократить на 5^t > 0:

$2^{t-1}leq 3^{t^{2}+t-2};$
$2^{t-1}-3^{(t+2)(t-1)}leq 0.$

Поскольку $2=3^{log_{3}2}$ , выражение 2^t−1 можно записать как 3^{(t−1)·log₃2}:

$3^{(t-1)cdot log_{3}2}leq 3^{(t+2)(t-1)};$ $(t-1)cdot log_{3}2leq (t-1)(t+2);$ $(t-1)cdot log_{3}2-(t-1)(t+2)leq 0.$ $(t-1)(log_{3}2-t-2)leq 0;$ $(t-1)(t-(log_{3}2-2))leq 0.$ Заметим, что log₃2 − 2 < 0.

Мы получили квадратичное неравенство относительно t. Решим его:

Итак, t ≥ 1 или t ≤ log₃2 − 2.

Вернемся к переменной x:

$: \ log_{2}xgeq 1\ xgeq 2;$ или $: \ log_{2}xleq log_{3}2-2;\ 0<xleq 2^{log_{3}2-2}.$

Ответ: $x in (0;2^{log_3 2-2}]cup[2;+infty).$

4. Еще одна задача из той же серии:

$frac{14^{log_{2}(4x)}}{7cdot log^{2}_{2}(32x)cdot log_{2}(0,25x)}geq frac{(4cdot 2^{log_{2}(4x)})^{log_{2}(4x)}}{4cdot log^{2}_{2}(32x)cdot log_{2}(0,25x)}.$ Запишем ОДЗ:

$left{begin{matrix} x>0;\ 32xneq 1;\ 0,25xneq 1. end{matrix}right.$

$xin left ( 0;frac{1}{32} right )cup left ( frac{1}{32};4 right )cup left (4;+infty right ) .$

Умножим обе части неравенства на $log^{2}_{2}32x>0$ . Постараемся упростить числители выражений в левой и правой части:

$frac{7^{log_{2}(4x)}cdot 2^{log_{2}(4x)}}{7cdot log_{2}(0,25x)}geq frac{4^{log_{2}(4x)}cdot 2^{(log_{2}(4x))^{2}}}{4cdot log_{2}(0,25x)}$
Поделим обе части неравенства на $2^{log_{2}(4x)}>0.$

$frac{7^{log_{2}(4x)}}{7cdot log_{2}(0,25x)}geq frac{2^{(log_{2}(4x))^{2}+log_{2}(4x)}}{4cdot log_{2}(0,25x)};$

$frac{7^{log_{2}(4x)-1}-2^{left ((log_{2}(4x))^{2}+log_{2}(4x)-2 right )}}{ log_{2}(0,25x)} geq 0$
Хорошо бы сделать замену. Пусть log₂(4x) = t. Тогда:

$log_{2}x=t-2;$

$log_{2}(0,25x)=log_{2}left ( frac{1}{4} right )+log_{2}x=log_{2}x-2=t-4.$ Неравенство примет вид:

$frac{7^{t-1}-2^{t^{2}+t-2}}{t-4}geq 0.$
Мы уже знаем, как представить число 7 в виде степени числа 2: $7=2^{log_{2}7}.$

$frac{2^{(t-1)cdot log_{2}7}-2^{(t-1)(t+2)}}{t-4}geq 0.$ Применим метод рационализации:

$frac{(t-1)cdot log_{2}7-(t-1)(t+2)}{t-4}geq 0;$

$frac{(t-1) (log_{2}7-t-2)}{t-4}geq 0;$

Оценим $log_{2}7-2:$

4 < 7 < 8;

$log_{2}4<log_{2}7<log_{2}8;$

$2<log_{2}7<3$

$0<log_{2}7-2<1$

$tleq log_{2}7-2\ , \ log_{2}(4x)leq log_{2}7-2;\ , \ log_{2}(4x)leq log_{2}frac{7}{4};\ , \ 0<xleq frac{7}{16};$ или $1leq t<4;\ , \ 1leq log_{2}(4x)<4;\ , \ log_{2}2leq log_{2}(4x)<log_{2}16;\ , \ frac{1}{2}leq x<4;$

Ответ: $xin left ( 0;frac{1}{32} right )cup left ( frac{1}{32};frac{7}{16} right ]cup left [ frac{1}{2};4 right ).$

5. Еще одна задача-страшилка из того же сборника:

$frac{log_{2^{left ( left ( x-1 right )^{2}-1 right )}}left ( log_{(2x^{2}+10x+15)}(x^{2}+2x) right )}{log_{2^{left ( left ( x-1 right )^{2}-1 right )}}left ( x^{2}+10x+26 right )}geq 0.$ Начнем с ОДЗ. Условий будет много – все выражения под логарифмами должны быть положительны, все основания логарифмов положительны и не равны единице, и еще знаменатель не равен нулю

$left{begin{matrix} (x-1)^{2}-1neq 0;\ x(x+2)>0;\ xneq -5. end{matrix}right.$

Применим в левой части неравенства формулу перехода к другому основанию:

$frac{log_{c}b}{log_{c}a}=log_{a}b;$

$log_{x^{2}+10x+26}left ( log_{2x^{2}+10x+15} left ( x^{2}+2x right )right )geq 0.$

Последовательно применим метод замены множителя, то есть метод рационализации.

Напомним, что множитель log_h f можно заменить на (h-1)( f-1), а множитель (log_h f — 1) — на (h — 1)( f — h):

$(x^{2}+10x+25)(log_{2x^{2}+10x+15}(x^{2}+2x)-1)geq 0;$

Поскольку $(x+5)^{2}>0$ при x ∈ ОДЗ, а $2x^{2}+10x+14>0$ при всех x, получим:

С учетом ОДЗ:

Ответ: x ∈ (-5; -3].

Посмотрим, чем поможет метод замены множителя в решении сложного показательного неравенства.

6. Решите неравенство: $displaystyle frac{{rm 2}cdot {{rm 3}}^{{rm 2x+1}}{rm -}{{rm 6}}^{{rm x}}{rm -}{{rm 4}}^{{rm x+1}}{rm -}{rm 9}}{{{rm 9}}^{{rm x}}{rm -}{rm 3}}le {rm 3.}$

$displaystyle frac{{rm 2}cdot {{rm 3}cdot {rm 3}}^{{rm 2x}}{rm -}{{rm 6}}^{{rm x}}{rm -}{rm 4}cdot {{rm 2}}^{{rm 2x}}{rm -}{rm 3}cdot {{rm 3}}^{{rm 2x}}{rm -}{rm 9+9}}{{{rm 3}}^{{rm 2x}}{rm -}{rm 3}}le {rm 0}.$

$displaystyle frac{{{rm 3}cdot {rm 3}}^{{rm 2x}}{rm -}{{rm 3}}^{{rm x}}cdot {{rm 2}}^{{rm x}}{rm -}{rm 4}cdot {{rm 2}}^{{rm 2x}}}{{{rm 3}}^{{rm 2x}}{rm -}{rm 3}}le {rm 0}.$

Числитель дроби в левой части — однородное выражение, где каждое слагаемое имеет степень 2х. Поделим обе части неравенства на ${{rm 2}}^{{rm 2}{rm x}}{rm textgreater 0.}$

Получим:

$displaystyle newline frac{3 cdot left (frac{3}{2} right )^{2x}-left (frac{3}{2} right )^{x}-4}{3^{2x}-3}leq 0;$

$displaystyle newline , newline 3 cdot left (frac{3}{2} right )^{2x}-left (frac{3}{2} right )^{x}-4=0;$

$displaystyle newline , newline frac{3left ( left ( frac{3}{2} right )^x+1 right )left ( left ( frac{3}{2} right )^x-frac{4}{3} right )}{3^{2x}-3}leq 0.$

Разложим числитель на множители.

Сделаем замену:

$displaystyle newline left ( frac{3}{2} right )^x=t; , ,3t^2-t-4=0;$

$displaystyle newline , newline t=frac{1pm 7}{6}; , t_1=-1; , t_2=frac{4}{3};$

$displaystyle newline , newline 3t^2-t-4=3left ( t+1 right )left ( t-frac{4}{3} right ).$

Вернемся к неравенству:

$displaystyle frac{3left ( left ( frac{3}{2} right )^x+1 right )left ( left ( frac{3}{2} right )^x-frac{4}{3} right )}{3^{2x}-3}leq 0.$

Поскольку $displaystyle {left(frac{3}{2}right)}^x textgreater 0$ , поделим обе части неравенства на $displaystyle {left(frac{3}{2}right)}^x+1 textgreater 0.$

$displaystyle frac{{left(frac{3}{2}right)}^x-frac{4}{3}}{3^{2x}-3}le 0.$

Применяя метод рационализации, множитель вида h^f-h^g заменяем на

Получим: $displaystyle newline frac{left ( frac{3}{2} -1right )left ( x-log_{frac{3}{2}}frac{4}{3} right )}{left ( 3-1 right )left ( 2x-1 right )} leq 0;$

$displaystyle newline , newline frac{x-log_{frac{3}{2}}frac{4}{3}}{x-frac{1}{2}}leq 0.$

Остается решить неравенство методом интервалов. Но как сравнить $displaystyle frac{1}{2}$ и ${{log}_{frac{3}{2}} frac{4}{3} }$ ?

Что больше? Давайте представим $displaystyle frac{1}{2}$ как логарифм с основанием $displaystyle frac{3}{2}:$

$displaystyle frac{1}{2}={{log}_{frac{3}{2}} {left(frac{3}{2}right)}^{frac{1}{2}} }={{log}_{frac{3}{2}} sqrt{frac{3}{2}} };$

$displaystyle frac{4}{3} vee sqrt{frac{3}{2}};$

$displaystyle frac{16}{9} vee frac{3}{2};$

Значит, $displaystyle {{log}_{frac{3}{2}} frac{4}{3} } textgreater frac{1}{2}.$

Ответ: $displaystyle xin left(frac{1}{2}; {{log}_{frac{3}{2}} frac{4}{3} }right].$

7. Теперь логарифмическое неравенство. Обратите внимание, что здесь лучше всего записывать решение в виде цепочки равносильных переходов. И само неравенство, которое мы упрощаем, и область его допустимых значений мы записываем в одну систему. И решаем ее.

Решите неравенство: $displaystyle {{log}_{3-x} frac{x+4}{{left(x-3right)}^2} }ge -2.$

$displaystyle {{log}_{3-x} frac{x+4}{{left(x-3right)}^2} }ge -2 textless = textgreater left{ begin{array}{c}3-x textgreater 0 \3-xne 1 \displaystyle frac{x+4}{{left(x-3right)}^2} textgreater 0 \displaystyle {{log}_{3-x} frac{x+4}{{left(x-3right)}^2} }+2ge 0 end{array}right. .$

Мы объединили в систему и область допустимых значений, и само неравенство. Применим формулу логарифма частного, учитывая, что ${left(a-bright)}^2={left(b-aright)}^2 .$

Используем также условия

$left{ begin{array}{c}x textless 3 \xne 2 \x+4 textgreater 0 \{log}_{3-x}left(x+4right)-{log}_{3-x}{left(3-xright)}^2+2ge 0 end{array}right. textless = textgreater left{ begin{array}{c}x textless 3 \xne 2 \x textgreater -4 \{log}_{3-x}left(x+4right)ge 0 end{array}right. .$

Обратите внимание, как мы применили формулу для логарифма степени. Строго говоря, ${{log}_a {left(bleft(xright)right)}^2=2{{log}_a left|bleft(xright)right| } }.$

Поскольку $3-x textgreater 0, { log}_{3-x}{left(3-xright)}^2=2{{log}_{3-x} left|3-xright|= }2{{log}_{3-x} left(3-xright)=2. }$

Согласно методу замены множителя, выражение ${log}_{3-x}left(x+4right)$ заменим на

Получим систему:

$left{ begin{array}{c}xne 2 \-4 textless x textless 3 \left(2-xright)left(x+3right)ge 0 end{array}right. .$

Решить ее легко.

Ответ:

8. А теперь неравенство с ловушкой. Мы надеемся, что вы помните — нельзя извлекать корень из неравенства.

Решите неравенство: $displaystyle {{lg}^2 frac{{left(x+2right)}^2left(x+5right)}{5} textless {lg}^2frac{x+5}{20} }.$

Извлекать корень из неравенства нельзя! Можно перенести все в левую часть неравенства и разложить на множители как разность квадратов:

$displaystyle left ( lgfrac{left ( x+2 right )^2left ( x+5 right )}{5}-lgfrac{x+5}{20} right )left ( lgfrac{left ( x+2 right )^2left ( x+5 right )}{5}+lgfrac{x+5}{20} right ) textless 0.$

Применим формулы разности и суммы логарифмов, следя за областью допустимых значений. Все выражения под логарифмами в исходном неравенстве должны быть положительны.

$left{ begin{array}{c}displaystyle lgfrac{{left(x+2right)}^2left(x+5right)cdot 20}{5cdot left(x+5right)}cdot {lg left(frac{{left(x+2right)}^2cdot {left(x+5right)}^2}{100}right) } textless 0 \displaystyle {left(x+2right)}^2left(x+5right) textgreater 0 \x+5 textgreater 0 end{array}right. .$

Посмотрим на второе и третье неравенства системы. Поскольку х+5 положительно, то и выражение (x+2)^2 должно быть положительно.

Заметим, что решения неравенства — это все числа, кроме x= - 2.

Получим:

$left{ begin{array}{c}displaystyle lgleft ( 4cdotleft ( x+2 right )^2 right ) cdot lg left ( frac{left ( x+2 right )^2 cdot left ( x+5 right )^2}{100} right ) textless 0\x textgreater -5 \xne -2 end{array}right..$

По методу рационализации, каждый из множителей вида ${{log}_h f }$ заменяем на

$newline left{ begin{array}{c}displaystyle left(10-1right)cdot left(4{left(x+2right)}^2-1right)cdot left(10-1right)left(frac{{left(x+2right)}^2cdot {left(x+5right)}^2}{100}-1right) textless 0 \x textgreater -5 \xne -2 end{array}right.newline textless = textgreater left{ begin{array}{c}left(2x+4-1right)left(2x+4+1right)left(left(x+2right)left(x+5right)-10right)left(left(x+2right)left(x+5right)+10right) textless 0 \x textgreater -5 \xne -2 end{array}right.newlinetextless = textgreater left{ begin{array}{c}left(2x+3right)left(2x+5right)cdot xcdot left(x+7right)cdot left(x^2+7x+20right) textless 0 \x textgreater -5 \xne -2 end{array}right.newline textless = textgreater left{ begin{array}{c}left(2x+3right)left(2x+5right)cdot xcdot left(x+7right) textless 0 \x textgreater -5 \xne -2 end{array}right. .$

Просто равносильные преобразования. Выражение положительно всегда — так как в уравнении дискриминант отрицателен. Осталось применить метод интервалов.

Ответ: $displaystyle xin left(-5;-frac{5}{2}right)cup left(-frac{3}{2};0right).$

Больше неравенств: Задание 15 Профильного ЕГЭ по математике

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Неравенства. Метод замены множителя (метод рационализации)» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Тема 14.

Решение неравенств

Смешанные неравенства

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

решение неравенств

14.01Задачи из ЕГЭ прошлых лет

14.02Задачи из сборника И.В. Ященко ЕГЭ 2023

14.03Рациональные неравенства и метод интервалов

14.04Показательные неравенства

14.05Логарифмические неравенства с числовым основанием

14.06Логарифмические неравенства с переменным основанием

14.07Метод рационализации

14.08Смешанные неравенства

14.09Системы неравенств

Решаем задачи

Решите неравенство

Показать ответ и решение

Ответ:

Решите неравенство

x 1-
ln(7e ) ≥ x

Показать ответ и решение

ОДЗ:

{
7ex > 0
⇔ x ⁄= 0.
x ⁄= 0

На ОДЗ:

x 1- x 1x x 1x ln7 x 1x
ln (7e ) ≥ x ⇔ ln(7e ) ≥ lne ⇔ 7e ≥ e ⇔ e e ≥ e ⇔
1x 2
⇔ ex ≥ -e-- ⇔ ex ≥ e 1x−ln7 ⇔ x ≥ 1-− ln7 ⇔ x--+-xln-7 −-1 ≥ 0.
eln7 x x

По методу интервалов

Таким образом, с учётом ОДЗ

Ответ:

Решите неравенство

Показать ответ и решение

Ответ:

Решите неравенство:

-1 9log16(7−x) log216(x− 7)2
32 ⋅2 ≥ 2 .

Показать ответ и решение

-1 9log16(7−x) log216(x−7)2
32 ⋅2 ≥ 2

Найдем ОДЗ данного неравенства:

(
{7 − x > 0 ⇔ 7 − x > 0 ⇔ x < 7
((x− 7)2 > 0

Преобразуем левую часть неравенства:

Преобразуем показатель степени в правой части неравенства:

На ОДЗ и исходное неравенство примет вид:

Обозначим , тогда

Перепишем неравенство в виде

pict

Решим неравенство методом интервалов:

Произведем обратную замену:

Учтем ОДЗ:

(
{ x < 7
( ⇔ − 25 ≤ x ≤ − 9 ⇔ x ∈ [− 25;− 9]
− 25 ≤ x ≤ − 9

Ответ:

Решите неравенство

( 35 x−1 x− 1)
2x≥ log2 3-⋅6 − 2⋅9 2

Показать ответ и решение

Преобразуем неравенство

({ 2x 35 x 2 x ({ x x x
2 ≥ 18 ⋅6 − 3 ⋅9 ⇔ 18⋅4( − 35⋅6 + 1)2⋅9 ≥ 0
( 3518-⋅6x − 23 ⋅9x > 0 ( 3x3- 356-⋅2x − 2 ⋅3x > 0

Из второго неравенства получаем

( )x
35⋅2x− 2⋅3x > 0 ⇔ 2 > 12 ⇔ x <log212
6 3 35 335

Из первого неравенства получаем

(2)2x ( 2)x
18⋅ 3 − 35 ⋅ 3 +12 ≥0

Замена ( )x
t= 2
3 дает:

( ] [ )
18 ⋅t2− 35t+ 12≥ 0 ⇔ t∈ −∞; 4 ∪ 3;+ ∞
9 2

Сделаем обратную замену:

⌊(2)x ≤ 4
⌈(3)x 9 ⇔ x∈ (− ∞;− 1]∪ [2;+ ∞)
23 ≥ 32

log23 12 > 2
35 , т.к. ( )2
2 = 4= 4-⋅35 = 140> 108 = 9⋅12= 12-
3 9 9 ⋅35 315 315 9⋅35 35 , и основание логарифма меньше 1.

Поскольку x < log2 12-
3 35 , получаем [ )
x∈ (−∞; −1]∪ 2;log2 12
3 35 .

Ответ:

[ 12)
(−∞; −1]∪ 2;log2335

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	2

Обоснованно получен ответ, отличающийся от верного исключением/включением граничных точек,	1
ИЛИ
получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

При этом в первом случае выставления 1 балла допускаются только ошибки
в строгости неравенства: «» вместо «» или наоборот. Если в
ответ включено значение переменной, при котором одна из
частей неравенства не имеет смысла, то выставляется оценка «0
баллов».

Решите неравенство

log1log3(−2x) log1log5(−2x)
5 5 < 3 3

Показать ответ и решение

По свойствам логарифма исходное неравенство равносильно:

pict

Последний переход корректен, так как первое неравенство системы выполняется при всех из ОДЗ: ведь
основание логарифма левой части больше основания логарифма правой части, а аргументы равны.

Ответ:

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	2

Обоснованно получен ответ, отличающийся от верного исключением/включением граничных точек,	1
ИЛИ
получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

Решите неравенство

Показать ответ и решение

ОДЗ: x > 0.

Решим неравенство на ОДЗ.

Сделаем замену .

Тогда

16 t2-−-17t+-16
t+ t < 17 ⇔ t < 0

Решая неравенство методом интервалов, получим:

[
t < 0
1 < t < 16

Так как из-за замены t > 0 , то неравенство t < 0 не имеет решений.

Делаем обратную замену:

lnx⋅logx 0 lnx⋅log x ln 16
1 < e 2 < 16 ⇔ e < e 2 < e ⇔ 0 < lnx ⋅log2x < ln16

Решим данное двойное неравенство как два неравенства по отдельности и затем пересечем решения.

1) Решим с помощью метода рационализации:

2
(e− 1)(x − 1)(2 − 1)(x− 1) > 0 ⇔ (x − 1) > 0 ⇔ x ⁄= 1

2) . Разделим обе части неравенства на положительное число ln16 :

Пересекая решения этих двух неравенств между собой и с ОДЗ, получаем окончательный ответ.

Ответ:

Решите неравенство

∘ -----
x+ 1⋅log0,5(log2|1− x|)≥ 0
2

Показать ответ и решение

При левая часть неравенства имеет смысл и равна нулю. Тогда
пойдет в ответ.

При условии получаем неравенство

log (log |1 − x|)≥ 0
0,5 2

Отсюда имеем:

Следовательно, или

Учитывая условие находим:

1
− 2< x< 0 или 2< x ≤3

Объединяя полученные множества c получаем

[ )
x ∈ − 1;0 ∪(2;3]
2

Ответ:

[ )
− 1;0 ∪(2;3]
2

Найдите все такие , которые являются решениями неравенства

N ⋅ log 3 ⋅ log (1 + x) ≥ 1
(1+Nx) 3

при любых

Показать ответ и решение

ОДЗ:

(
|{ 1 + N x > 0

|( 1 + N x ⁄= 1 — при лю бы х N ∈ ℕ
1 + x > 0

Покажем, что x < 0 не подходят по ОДЗ:
зафиксируем произвольное x < 0 , тогда . Существует , такое что

1
n > ----.
− x

Положим N = n , тогда

что
не подходит по ОДЗ. Таким образом, x ≥ 0 .

Также по ОДЗ не подходит x = 0 , а x > 0 подходят по ОДЗ, следовательно,
ОДЗ:

x > 0.

На
ОДЗ:
исходное неравенство равносильно неравенству

Так как на ОДЗ

то
, следовательно,

------1------ N N
log (1 + N x) ⋅ log3(1 + x) ≥ 1 ⇔ log3(1 + x) ≥ log3(1 + N x) ⇔
3 N
⇔ (1 + x ) ≥ (1 + N x).

Зафиксируем произвольный x > 0 .
Докажем по индукции, что данное неравенство выполнено для всех :

1) N = 1 :

–
верно.

2) Рассмотрим произвольное , такое что , тогда

m+1 m 2
(1 + x) = (1 + x) ⋅ (1 + x) ≥ (1 + x) ⋅ (1 + mx ) = 1 + mx + x + mx ≥ 1 + x(m + 1),

таким образом, мы доказали, что рассматриваемый подходит. Так как мы фиксировали
произвольный x > 0 , то все x > 0 являются решениями исходной задачи.

Ответ:

Решите неравенство

( )log (2x+3)
3log2(x2)+ 2⋅|x|log29 ≤ 3⋅ 1 0,5
3

Показать ответ и решение

Запишем ОДЗ:

{
x2 >0 ⇒ x∈ (−1,5;0)∪ (0;+∞ )
2x +3 > 0

Тогда на ОДЗ второе слагаемое левой части можно преобразовать так:

( ) ( )
2⋅|x|log29 = 2 ⋅|x|log23 2 = 2 ⋅3log2|x| 2 = 2⋅3log2x2

Правую часть можно преобразовать так:

Тогда все неравенство перепишется в виде

Получили квадратичное неравенство

Пересекая полученное множество с ОДЗ, получим

Ответ:

Решите неравенство

Показать ответ и решение

ОДЗ:

На ОДЗ:
исходное неравенство равносильно неравенству

x log (--1- ) x 1 x
2 ⋅ 2 21+xln2 ≥ 1 ⇔ 2 ⋅--------- ≥ 1 ⇔ 2 ≥ 1 + xln 2 ⇔
x 1 + x ln 2
⇔ 2 − 1 − xln 2 ≥ 0.

Рассмотрим функцию

Найдём её промежутки возрастания/убывания:

Легко проверить, что x = 0 – единственная точка локального минимума функции , тогда она
является точкой минимума и наименьшее значение равно

0
f(0) = 2 − 1 − 0 ⋅ ln 2 = 0.

Таким образом, x
2 − 1 − xln2 ≥ 0 – верно при всех , тогда ответ совпадает с
ОДЗ:

x > − -1--.
ln2

Ответ:

( )
− -1--;+ ∞
ln 2

Решите неравенство

Показать ответ и решение

Найдем ОДЗ неравенства:

(
| 5x > 0
||{ x
5 ⁄= 1 ⇔ x ∈ (− ∞; − 1) ∪ (− 1; 0) ∪ (0;+ ∞ )
|| 25x+1 > 0
|( x+1
25 ⁄= 1

Сделаем замену :

{
1 y2 − 2y + 1 (y − 1 )2 y > 0
y + --− 2 > 0 ⇔ ------------> 0 ⇔ --------> 0 ⇔
y y y y ⁄= 1,

откуда

(
{ | 2x + 2
log5x 25x+1 > 0 { ---x---> 0
x+1 ⇔ | 2x + 2
log5x 25 ⁄= 1 ( -------⁄= 1
x

Решая первое неравенство последней системы, получаем

Решая второе неравенство последней системы, получаем

В
итоге

–
входит в ОДЗ

Ответ:

Решите неравенство

x log π (x + 3 ) ≤ 0
x+2

Показать ответ и решение

ОДЗ:

(
| x + π-> 0 ( π
|{ 2π { x > − --
x + --⁄= 1 ⇔ 2π
||( 2 ( x ⁄= − --+ 1
x + 3 > 0 2

Заметим, что

x + 3 > x + π- + 1
2

Рассмотрим два случая:
1) x > − π-+ 1
2 , тогда

π
logx+ 2(x + 3) > 0

и
исходное неравенство равносильно

то
есть в этом случае подходят

( ]
x ∈ − π-+ 1;0
2

2)
π π
− --< x < − --+ 1
2 2 , тогда

и
исходное неравенство равносильно

то
есть в этом случае подходящих нет.
В итоге ответ с учётом ОДЗ:

( π ]
x ∈ − --+ 1;0 .
2

Ответ:

( π ]
− --+ 1;0
2

Решите неравенство

(2x + 15)log (x2 + 7x) ≤ 0
x+2

Показать ответ и решение

ОДЗ:

(
| x + 2 > 0
{
| x + 2 ⁄= 1 ⇔ x > 0
( x2 + 7x > 0

На ОДЗ , , следовательно, исходное неравенство на ОДЗ равносильно

2 2
logx+2(x + 7x) ≤ logx+2 1 ⇔ x + 7x − 1 ≤ 0

По методу интервалов:

откуда [ √ --- √---]
− 7-−--53- −-7 +--53-
x ∈ 2 ; 2 .
Пересечём ответ с ОДЗ:

( √ --]
x ∈ 0; −-7-+--53
2

Ответ:

√ ---
(0;− 3,5 + 0,5 53]

Решите неравенство

2
2 (( )log3x+12) 9x4−4-
49x4-− 3-x + 1 2 ≤ 3
2

Показать ответ и решение

Найдем ОДЗ неравенства:

(
|| 3x + 1 > 0 ( )
{ 2 2-
| 3 ⇔ x ∈ − 3;0 ∪ (0;+ ∞ )
|( -x + 1 ⁄= 1
2

Решим неравенство на ОДЗ. Так как по основному логарифмическому свойству ,
то

9x24- 9x42−1
4 − 2 ≤ 3

Сделаем замену 9x42-
t = 2 , t > 0 , тогда

( 3 ) [ 3 ]
t2 − 0,5t − 3 ≤ 0 ⇔ t +-- (t − 2) ≤ 0 ⇔ t ∈ − --;2
2 2

Так
как согласно замене t > 0 , то получаем . Сделаем обратную замену:

2 2 ( ) ( )
0 < 2 9x4--≤ 2 ⇔ 9x--≤ 1 ⇔ x − 2- x + 2- ≤ 0 ⇔
4 3 3
[ ]
2 2
x ∈ − --;--
3 3

Пересечем ответ с ОДЗ и получим

( ) ( ]
x ∈ − 2;0 ∪ 0; 2
3 3

Ответ:

( ) ( ]
x ∈ − 23;0 ∪ 0; 23

Решите неравенство

Показать ответ и решение

Выпишем ОДЗ:

(
|| sinx + cos x + 4 > 0
||||
{ sinx + cos x + 4 ⁄= 1
x2 + 1 > 0
|||| 2 sin x cosx + 4,5 > 0
||(
2 sin x cosx + 4,5 ⁄= 1

Так
как по формуле вспомогательного аргумента

√--( √ -- √ -- ) √ -- ( )
sin x + cosx = 2 --2-sin x + --2-cosx = 2 sin x + π- ,
2 2 4

а по
формуле двойного угла , то

( ( π) √ --
||| sin x + -- > − 2 2
||| ( 4)
|{ π- 3√ --
sin x + 4 ⁄= − 2 2 ⇔ x ∈ ℝ.
|||
|||| sin2x > − 4,5
( sin2x ⁄= − 3,5

Заметим, что при одинаковых аргументах один логарифм будет другого логарифма в одном из
двух случаев:

1) Аргументы этих логарифмов равны . Тогда .
Тогда неравенство принимает вид: что на ОДЗ равносильно

что
является верным неравенством. Следовательно, x = 0 является решением неравенства.

2) При .
Заметим, что функция f (x) = log a
x является убывающей (докажите это самостоятельно) при a > 1 и
возрастающей при a < 1 . В нашем случае 2
x + 1 > 1 , следовательно, функция убывает. Значит, чем
больше значение функции, тем меньше значение . Следовательно, при неравенство
равносильно

Данное неравенство равносильно совокупности систем:

⌊ (
||{ sin x ≥ 1-
|| 2
| || 1
|| ( cosx ≥ --
|| ( 2
| ||{ sin x ≤ 1-
|| 2
⌈ | 1
|( cosx ≤ --
2

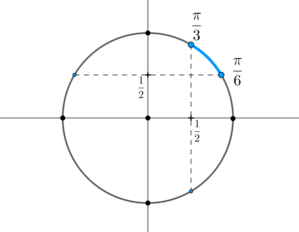
Решим каждую систему по окружности:
первая система:

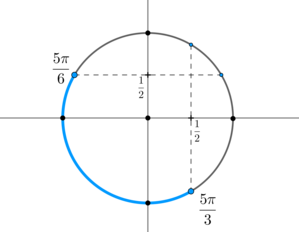
вторая система:

Тогда ответом будут [ ]
[π- π- ] 5-π 5π-
x ∈ 6 + 2πn; 3 + 2πn ∪ 6 + 2πn; 3 + 2 πn , .

Тогда окончательный ответ – это объединение решений x = 0 и [ ]
[π- π- ] 5-π 5π-
x ∈ 6 + 2πn; 3 + 2πn ∪ 6 + 2πn; 3 + 2πn ,
, то есть

[π π ] [ 5π 5π ]
x ∈ --+ 2πn; --+ 2πn ∪ ---+ 2πn; ---+ 2πn ∪ {0 }, n ∈ ℤ.
6 3 6 3

Ответ:

[ ] [ ]
x ∈ π6 + 2 πn; π3 + 2 πn ∪ 56π+ 2πn; 53π+ 2πn ∪ {0}, n ∈ ℤ

Решите неравенство

−|x− 2| 2
2 ⋅log2(4x− x − 2)≥ 1

Показать ответ и решение

Рассмотрим первый множитель левой части Так как модуль при всех значениях неотрицателен, то

Следовательно,

Рассмотрим второй множитель log(4x− x2− 2).
2 Выделим полный квадрат:

Так как квадрат любого выражения — число неотрицательное, то

Следовательно,

Получили, что оба множителя в левой части ≤ 1, а значит и их произведение ≤ 1.

Значит, неравенство будет иметь решения тогда и только тогда, когда оба они равны по 1.

Таким образом, получаем, что x = 2 — единственное решение неравенства.

Ответ:

{2}

Решите неравенство

при каждом .

Показать ответ и решение

ОДЗ:

(
| x > 0
||||
||| x ⁄= 1
||| x + 1 > 0
||||
||| x + 2 > 0 {
{ x + 2 ⁄= 1 x > 0
| ⇔
||| x + 3 > 0 x ⁄= 1
||| ...
|||| x + 2n > 0
|||
||| x + 2n ⁄= 1
|( x + 2n + 1 > 0

По методу рационализации: на ОДЗ

С учётом ОДЗ последнее неравенство равносильно

Таким образом, с учётом ОДЗ:

Ответ:

(0;1)

Решите неравенство

Показать ответ и решение

ОДЗ:

(
|| x2 > 0
|||
||| 2x + 7 > 0
|||{ 2x + 7 ⁄= 1 {
x > 0
| x + 7 > 0 ⇔ x ⁄= 0,5
|||| 5x − 1 ⁄= 0
|||
||| x > 0
( lg 2x ⁄= 0

На ОДЗ , тогда исходное неравенство на ОДЗ равносильно

На ОДЗ , следовательно, , тогда на ОДЗ

и
исходное неравенство на ОДЗ равносильно

lg2x2-
lg 2x ≤ 0

Найдём нули числителя:

2 2 2
lg x = 0 ⇔ lg x = lg1 ⇔ x = ±1

Найдём нули знаменателя:

По методу интервалов на ОДЗ:

откуда

Ответ:

Решите неравенство

Показать ответ и решение

ОДЗ:

(
|| x2 + 1 > 0
||| (
|{ 4x > 0 |{ x ⁄= log3 2
3x − 2 ⁄= 0 ⇔ x > 0
||| |(
||| x > 0 x ⁄= 1
( x ⁄= 1

На ОДЗ , следовательно, , тогда исходное неравенство на ОДЗ
равносильно

2
log24x-+-log24x-−--log2-4 ≤ 0
(3x − 2)lnx

Найдём нули числителя:

2
log24x + log24x − log2 4 = 0

Сделаем замену :

t2 + t − 2 = 0 ⇔ t = −-1-±-3
2

1
log2 4x = − 2 ⇔ log2 4x = log20,25 ⇔ 4x = 0,25 ⇔ x = ---
16

Найдём нули знаменателя:
1)

По методу интервалов:

откуда [ ]
1 1
x ∈ 16;2- ∪ (log32;1 )
пересечём ответ с ОДЗ:

[ ]
-1- 1-
x ∈ 16 ;2 ∪ (log32;1 ).

Ответ:

Источник

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Решение неравенств

Задание
1

#2500

Уровень задания: Легче ЕГЭ

Решите неравенство [x+10<3x^2]

Перенесем слагаемые в левую часть: [-3x^2+x+10<0] Разложим на множители выражение (-3x^2+x+10): [-3x^2+x+10=0 quad Rightarrow quad x_1=2quadtext{и}quad x_2=-dfrac53] Следовательно, (-3x^2+x+10=-3(x-2)left(x-frac53right)=-(x-2)(3x+5)).
Тогда неравенство примет вид [-(x-2)(3x+5)< 0quad Rightarrow
quad (x-2)(3x+5)>0] Решим его методом интервалов:

Таким образом, подходят (xin
left(-infty;-frac53right)cup(2;+infty)).

Ответ:

(left(-infty;-frac53right)cup(2;+infty))

Задание
2

#2501

Уровень задания: Легче ЕГЭ

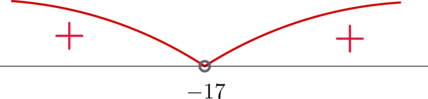
Решите неравенство [x^2+34x+289>0]

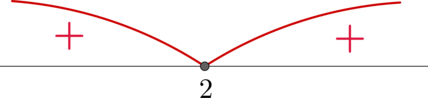
Заметим, что по формуле квадрата суммы (x^2+34x+289=(x+17)^2), следовательно, неравенство принимает вид: [(x+17)^2>0] Решим его методом интервалов:

Таким образом, нам подходят (xin(-infty;-17)cup(-17;+infty)).

Ответ:

((-infty;-17)cup(-17;+infty))

Задание
3

#2502

Уровень задания: Легче ЕГЭ

Решите неравенство [x^2-4x+4leqslant 0]

Заметим, что по формуле квадрата разности (x^2-4x+4=(x-2)^2), следовательно, неравенство принимает вид: [(x-2)^2leqslant 0] Решим его методом интервалов:

Таким образом, нам подходят (xin{2}).

Ответ:

({2})

Задание
4

#2503

Уровень задания: Легче ЕГЭ

Решите неравенство [x^2+3x+3geqslant 0]

Разложим на множители выражение (x^2+3x+3), для этого решим уравнение (x^2+3x+3=0). Оно имеет отрицательный дискриминант, следовательно, не разлагается на множители и принимает значения одного знака: либо положительно, либо отрицательно при всех (x). Проверить его знак можно, подставив вместо (x) любое число, например, (x=0): получим (3), следовательно, выражение всегда (>0).

Таким образом, нам подходят (xin mathbb{R}).

Ответ:

(mathbb{R})

Задание
5

#2412

Уровень задания: Легче ЕГЭ

Решите неравенство

[begin{aligned}
dfrac{(x — 1)(x + 2)}{(x — 3)(x + 4)}leqslant 0
end{aligned}]

ОДЗ:

[begin{aligned}
(x — 3)(x + 4)neq 0
end{aligned}]

Решим исходное неравенство методом интервалов. Для этого найдём нули числителя и знаменателя.

1) Нули числителя находятся из уравнения [(x — 1)(x + 2) = 0] Произведение выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл, тогда нули числителя: [x = 1,qquadqquad x = -2]

2) Найдём нули знаменателя: [(x — 3)(x + 4) = 0qquadLeftrightarrowqquad
left[
begin{gathered}
x = 3\
x = -4
end{gathered}
right.]

По методу интервалов:

откуда [xin(-4; -2]cup[1; 3),.] В этом ответе ОДЗ уже учтено (мы учли его, когда выкололи на числовой прямой нули знаменателя).

Ответ:

((-4; -2]cup[1; 3))

Задание
6

#3762

Уровень задания: Легче ЕГЭ

Решить неравенство [dfrac 6{xsqrt3-3}+dfrac{xsqrt3-6}{xsqrt3-9}geqslant 2]

(Задача от подписчиков)

Пусть (xsqrt3-3=t). Тогда [dfrac 6t+dfrac{t-3}{t-6}geqslant 2quadLeftrightarrowquad
dfrac{t^2-15t+36}{t(t-6)}leqslant 0quadLeftrightarrowquad
dfrac{(t-3)(t-12)}{t(t-6)}leqslant 0] Решая данное неравенство методом интервалов, получим (0<tleqslant 3) или (6<tleqslant 12). Следовательно, [left[begin{gathered}begin{aligned}
&0<xsqrt3-3leqslant 3\
&6<xsqrt3-3leqslant
12end{aligned}end{gathered}right.quadLeftrightarrowquad
left[begin{gathered}begin{aligned}
&sqrt3<xleqslant 2sqrt3\
&3sqrt3<xleqslant 5sqrt3
end{aligned}end{gathered}right.]

Ответ:

((sqrt3;2sqrt3]cup(3sqrt3;5sqrt3])

Задание
7

#2413

Уровень задания: Легче ЕГЭ

Решите неравенство

[begin{aligned}
dfrac{(x + 1)(x — 2)}{(x + 3)(x^2 + 4)}leqslant 0
end{aligned}]

ОДЗ:

[begin{aligned}
(x — 3)(x^2 + 4)neq 0
end{aligned}]

Решим исходное неравенство методом интервалов. Для этого найдём нули числителя и знаменателя.

1) Нули числителя находятся из уравнения [(x + 1)(x — 2) = 0] Произведение выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл, тогда нули числителя: [x = -1,qquadqquad x = 2]

2) Найдём нули знаменателя: [(x + 3)(x^2 + 4) = 0] так как (x^2geqslant 0), то (x^2 + 4geqslant 4), следовательно, нули знаменателя: [x = -3]

По методу интервалов:

откуда [xin(-infty; -3)cup[-1; 2],.] В этом ответе ОДЗ уже учтено (мы учли его, когда выкололи на числовой прямой нули знаменателя).

Ответ:

((-infty; -3)cup[-1; 2])

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Решение неравенств (Базакина А.В.)

Решение. Преобразуем
логарифмическое неравенство

Обозначим Тогда

или Следовательно

или Ответ:
или

2. Решите неравенство .

Решение. Неравенство имеет смысл при

и Преобразуем

следовательно,
значит, Ответ:

3. Решите неравенство

В
соответствии с определением логарифма, входящие в неравенство выражения имеют
смысл при выполнении условий:

а) Если

То

Следовательно нет решения.

б) Если и

То

и Учитывая
условие

Получаем ответ (-0,5;0]; [1;4). Ответ: (-0,5;0]; [1;4).

4. Решите неравенство

Решение. В соответствии с определением логарифма, входящие в
неравенство выражения имеют смысл при выполнении условий:

а) Если

то

б) Если

то значит

С учетом условия получаем ответ х=1; (1,5;3).

Ответ: х=1; (1,5;3).

5. Решите неравенство

Воспользуемся тождеством Для доказательства этого тождества
достаточно рассмотреть разность логарифмов левой и правой части: Значит, Второе
неравенство примет вид при
условии

Ответ: [-1;0); (0;3].

Источник

Блок 1. Логарифмические неравенства. Равносильные преобразования (схемы) для простых неравенств

Блок 2. Логарифмические неравенства. Равносильные преобразования (схемы) для более сложных неравенств

Блок 3. Логарифмические неравенства. Метод замены множителей (метод рационализации)

Блок 4. Логарифмические неравенства. Метод замены множителей (метод рационализации) и замена переменных

Блок 5. Логарифмические неравенства. Закрепление метода замены множителей (метода рационализации) и метода замены переменных

Блок 6. Логарифмические неравенства. Использование свойств логарифмической функции

Источник