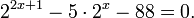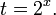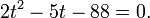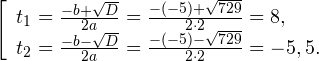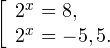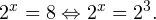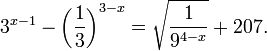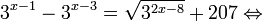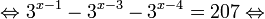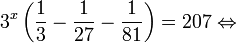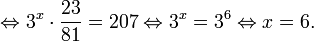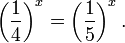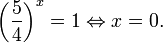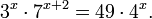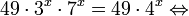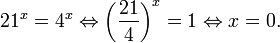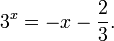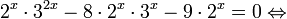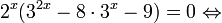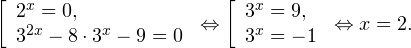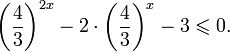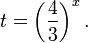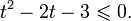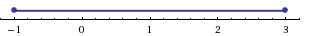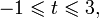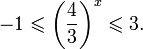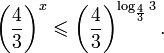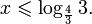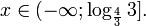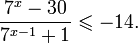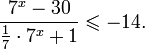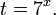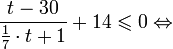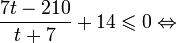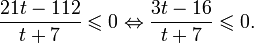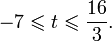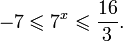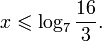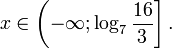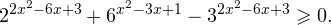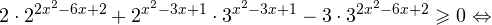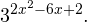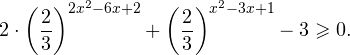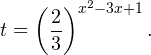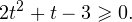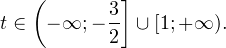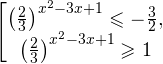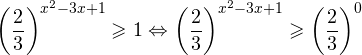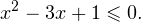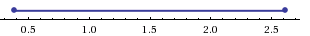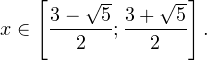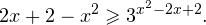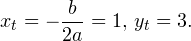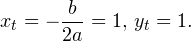1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Решение неравенств
Задание
1
#2500
Уровень задания: Легче ЕГЭ
Решите неравенство [x+10<3x^2]
Перенесем слагаемые в левую часть: [-3x^2+x+10<0] Разложим на множители выражение (-3x^2+x+10): [-3x^2+x+10=0 quad Rightarrow quad x_1=2quadtext{и}quad x_2=-dfrac53] Следовательно, (-3x^2+x+10=-3(x-2)left(x-frac53right)=-(x-2)(3x+5)).
Тогда неравенство примет вид [-(x-2)(3x+5)< 0quad Rightarrow
quad (x-2)(3x+5)>0] Решим его методом интервалов:
Таким образом, подходят (xin
left(-infty;-frac53right)cup(2;+infty)).
Ответ:
(left(-infty;-frac53right)cup(2;+infty))
Задание
2
#2501
Уровень задания: Легче ЕГЭ
Решите неравенство [x^2+34x+289>0]
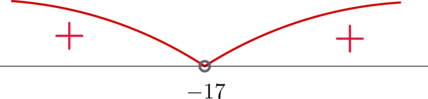
Заметим, что по формуле квадрата суммы (x^2+34x+289=(x+17)^2), следовательно, неравенство принимает вид: [(x+17)^2>0] Решим его методом интервалов:
Таким образом, нам подходят (xin(-infty;-17)cup(-17;+infty)).
Ответ:
((-infty;-17)cup(-17;+infty))
Задание
3
#2502
Уровень задания: Легче ЕГЭ
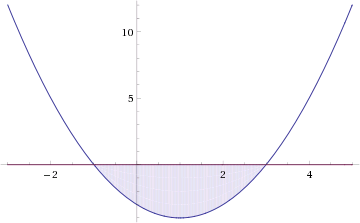
Решите неравенство [x^2-4x+4leqslant 0]
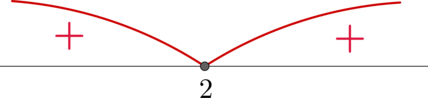
Заметим, что по формуле квадрата разности (x^2-4x+4=(x-2)^2), следовательно, неравенство принимает вид: [(x-2)^2leqslant 0] Решим его методом интервалов:
Таким образом, нам подходят (xin{2}).
Ответ:
({2})
Задание
4
#2503
Уровень задания: Легче ЕГЭ
Решите неравенство [x^2+3x+3geqslant 0]
Разложим на множители выражение (x^2+3x+3), для этого решим уравнение (x^2+3x+3=0). Оно имеет отрицательный дискриминант, следовательно, не разлагается на множители и принимает значения одного знака: либо положительно, либо отрицательно при всех (x). Проверить его знак можно, подставив вместо (x) любое число, например, (x=0): получим (3), следовательно, выражение всегда (>0).
Таким образом, нам подходят (xin mathbb{R}).
Ответ:
(mathbb{R})
Задание
5
#2412
Уровень задания: Легче ЕГЭ
Решите неравенство
[begin{aligned}
dfrac{(x — 1)(x + 2)}{(x — 3)(x + 4)}leqslant 0
end{aligned}]
ОДЗ:
[begin{aligned}
(x — 3)(x + 4)neq 0
end{aligned}]
Решим исходное неравенство методом интервалов. Для этого найдём нули числителя и знаменателя.
1) Нули числителя находятся из уравнения [(x — 1)(x + 2) = 0] Произведение выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл, тогда нули числителя: [x = 1,qquadqquad x = -2]
2) Найдём нули знаменателя: [(x — 3)(x + 4) = 0qquadLeftrightarrowqquad
left[
begin{gathered}
x = 3\
x = -4
end{gathered}
right.]
По методу интервалов:
откуда [xin(-4; -2]cup[1; 3),.] В этом ответе ОДЗ уже учтено (мы учли его, когда выкололи на числовой прямой нули знаменателя).
Ответ:
((-4; -2]cup[1; 3))
Задание
6
#3762
Уровень задания: Легче ЕГЭ
Решить неравенство [dfrac 6{xsqrt3-3}+dfrac{xsqrt3-6}{xsqrt3-9}geqslant 2]
(Задача от подписчиков)
Пусть (xsqrt3-3=t). Тогда [dfrac 6t+dfrac{t-3}{t-6}geqslant 2quadLeftrightarrowquad
dfrac{t^2-15t+36}{t(t-6)}leqslant 0quadLeftrightarrowquad
dfrac{(t-3)(t-12)}{t(t-6)}leqslant 0] Решая данное неравенство методом интервалов, получим (0<tleqslant 3) или (6<tleqslant 12). Следовательно, [left[begin{gathered}begin{aligned}
&0<xsqrt3-3leqslant 3\
&6<xsqrt3-3leqslant
12end{aligned}end{gathered}right.quadLeftrightarrowquad
left[begin{gathered}begin{aligned}
&sqrt3<xleqslant 2sqrt3\
&3sqrt3<xleqslant 5sqrt3
end{aligned}end{gathered}right.]
Ответ:
((sqrt3;2sqrt3]cup(3sqrt3;5sqrt3])
Задание
7
#2413
Уровень задания: Легче ЕГЭ
Решите неравенство
[begin{aligned}
dfrac{(x + 1)(x — 2)}{(x + 3)(x^2 + 4)}leqslant 0
end{aligned}]
ОДЗ:
[begin{aligned}
(x — 3)(x^2 + 4)neq 0
end{aligned}]
Решим исходное неравенство методом интервалов. Для этого найдём нули числителя и знаменателя.
1) Нули числителя находятся из уравнения [(x + 1)(x — 2) = 0] Произведение выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл, тогда нули числителя: [x = -1,qquadqquad x = 2]
2) Найдём нули знаменателя: [(x + 3)(x^2 + 4) = 0] так как (x^2geqslant 0), то (x^2 + 4geqslant 4), следовательно, нули знаменателя: [x = -3]
По методу интервалов:
откуда [xin(-infty; -3)cup[-1; 2],.] В этом ответе ОДЗ уже учтено (мы учли его, когда выкололи на числовой прямой нули знаменателя).
Ответ:
((-infty; -3)cup[-1; 2])

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
В (14) задании ЕГЭ предлагается решить неравенство. За это задание можно получить (2) балла.
Алгоритм выполнения задания
1. Определи вид неравенства, выбери метод решения.
2. Найди ОДЗ неравенства или используй равносильные преобразования неравенств.
3. Реши неравенство, используя соответствующие виду неравенства свойства и правила. Все найденные решения должны принадлежать области определения неравенства.
4. Запиши все шаги решения на чистовик разборчиво и кратко.
5. Запиши ответ.
Если ход решения верный и обоснованно получен верный ответ, то решение оценивается в (2) балла. Если верна последовательность всех шагов решения, но допущена описка или вычислительная ошибка, и в результате получен неверный ответ, можно получить (1) балл. Если в ответ по ошибке не включена одна точка из правильного решения (в результате того, что поставлена круглая скобка вместо квадратной), то также можно получить (1) балл. При включении в ответ хотя бы одной точки, не входящей в ОДЗ, ставится (0) баллов.
Как решить задание из примера
1.
log0,4(x2−6x+8)−log0,4(12−6x)≤−log0,4(x+3).
Неравенство является логарифмическим. Логарифмы имеют одинаковое основание.
Нам пригодится формула:
loga(b⋅c)=logab⋅logac.
Применение этой формулы может сузить ОДЗ, поэтому его лучше найти.
2. Найдём ОДЗ:
.
3. Преобразуем неравенство:
log0,4((4−x)(2−x))−log0,4(6(2−x))≤−log0,4(x+3).
При
−3<x<2
неравенство примет вид:
log0,4(4−x)+log0,4(2−x)−log0,46−log0,4(2−x)+log0,4(x+3)≤0;
log0,4(4−x)−log0,46+log0,4(x+3)≤0;log0,4((4−x)(x+3))≤log0,46;(4−x)(x+3)≥6;−x2+x+12≥6;x2−x−6≤0;−2≤x<2.
4. Перепишем шаги решения в чистовик.
5. Запишем ответ.
Для решения показательных уравнений требуется знать и уметь использовать следующую несложную теорему:
Помимо этого, полезно помнить об основных формулах и действиях со степенями:
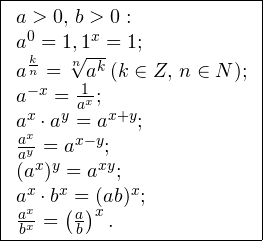
Пример 1. Решите уравнение:
Решение: используем приведенные выше формулы и подстановку:
Уравнение тогда принимает вид:
Дискриминант полученного квадратного уравнения положителен:
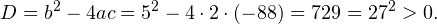
Это означает, что данное уравнение имеет два корня. Находим их:
Переходя к обратной подстановке, получаем:
Второе уравнение корней не имеет, поскольку показательная функция строго положительна на всей области определения. Решаем второе:
С учетом сказанного в теореме 1 переходим к эквивалентному уравнению: x = 3. Это и будет являться ответом к заданию.
Ответ: x = 3.
Пример 2. Решите уравнение:
Решение: ограничений на область допустимых значений у уравнения нет, так как подкоренное выражение имеет смысл при любом значении x (показательная функция y = 9 4 -x положительна и не равна нулю).
Решаем уравнение путем равносильных преобразований с использованием правил умножения и деления степеней:
Последний переход был осуществлен в соответствии с теоремой 1.
Пример 3. Решите уравнение:
Решение: обе части исходного уравнения можно поделить на 0,2 x . Данный переход будет являться равносильным, поскольку это выражение больше нуля при любом значении x (показательная функция строго положительна на своей области определения). Тогда уравнение принимает вид:
Ответ: x = 0.
Пример 4. Решите уравнение:
Решение: упрощаем уравнение до элементарного путем равносильных преобразований с использованием приведенных в начале статьи правил деления и умножения степеней:
Деление обеих частей уравнения на 4 x , как и в предыдущем примере, является равносильным преобразованием, поскольку данное выражение не равно нулю ни при каких значениях x.
Ответ: x = 0.
Пример 5. Решите уравнение:
Решение: функция y = 3 x , стоящая в левой части уравнения, является возрастающей. Функция y = —x-2/3, стоящая в правой части уравнения, является убывающей. Это означает, что если графики этих функций пересекаются, то не более чем в одной точке. В данном случае нетрудно догадаться, что графики пересекаются в точке x = -1. Других корней не будет.
Ответ: x = -1.
Пример 6. Решите уравнение:
Решение: упрощаем уравнение путем равносильных преобразований, имея в виду везде, что показательная функция строго больше нуля при любом значении x и используя правила вычисления произведения и частного степеней, приведенные в начале статьи:
Ответ: x = 2.
Решение показательных неравенств
Показательными называются неравенства, в которых неизвестная переменная содержится только в показателях каких-либо степеней.
Для решения показательных неравенств требуется знание следующей теоремы:
Теорема 2. Если a > 1, то неравенство a f(x) > a g(x) равносильно неравенству того же смысла: f(x) > g(x). Если 0 f(x) > a g(x) равносильно неравенству противоположного смысла: f(x) 2x , при этом (в силу положительности функции y = 3 2x ) знак неравенства не изменится:
Тогда неравенство примет вид:
Итак, решением неравенства является промежуток:
переходя к обратной подстановке, получаем:
Левое неравенства в силу положительности показательной функции выполняется автоматически. Воспользовавшись известным свойством логарифма, переходим к эквивалентному неравенству:
Поскольку в основании степени стоит число, большее единицы, эквивалентным (по теореме 2) будет переход к следующему неравенству:
Итак, окончательно получаем ответ:
Пример 8. Решите неравенство:
Решение: используя свойства умножения и деления степеней, перепишем неравенство в виде:
Введем новую переменную:
С учетом этой подстановки неравенство принимает вид:
Умножим числитель и знаменатель дроби на 7, получаем следующее равносильное неравенство:
Итак, неравенству удовлетворяют следующие значения переменной t:
Тогда, переходя к обратной подстановке, получаем:
Поскольку основание степени здесь больше единицы, равносильным (по теореме 2) будет переход к неравенству:
Окончательно получаем ответ:
Пример 9. Решите неравенство:
Решение:
Делим обе части неравенства на выражение:
Оно всегда больше нуля (из-за положительности показательной функции), поэтому знак неравенства изменять не нужно. Получаем:
Воспользуемся заменой переменной:
Исходное уравнение тогда принимает вид:
Итак, неравенству удовлетворяют значения t, находящиеся в промежутке:
Переходя к обратной подстановке получаем, что исходное неравенство распадается на два случая:
Первое неравенство решений не имеет в силу положительности показательной функции. Решаем второе:
Поскольку основание степени в данном случае оказалось меньше единицы, но больше нуля, равносильным (по теореме 2) будет переход к следующему неравенству:
Итак, окончательный ответ:
Пример 10. Решите неравенство:
Решение:
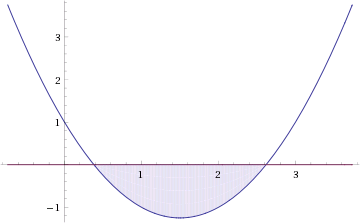
Ветви параболы y = 2x+2-x 2 направлены вниз, следовательно она ограничена сверху значением, которое она достигает в своей вершине:
Ветви параболы y = x 2 -2x+2, стоящей в показателе, направлены вверх, значит она ограничена снизу значением, которое она достигает в своей вершине:
Вместе с этим ограниченной снизу оказывается и функция y = 3 x 2 -2x+2 , стоящая в правой части уравнения. Она достигает своего наименьшего значения в той же точке, что и парабола, стоящая в показателе, и это значение равно 3 1 = 3. Итак, исходное неравенство может оказаться верным только в том случае, если функция слева и функция справа принимают в одной точке значение, равное 3 (пересечением областей значений этих функций является только это число). Это условие выполняется в единственной точке x = 1.
Ответ: x = 1.
Для того, чтобы научиться решать показательные уравнения и неравенства, необходимо постоянно тренироваться в их решении. В этом нелегком деле вам могут помочь различные методические пособия, задачники по элементарной математике, сборники конкурсных задач, занятия по математике в школе, а также индивидуальные занятия с профессиональным репетитором. Искренне желаю вам успехов в подготовке и блестящих результатов на экзамене.
P. S. Уважаемые гости! Пожалуйста, не пишите в комментариях заявки на решение ваших уравнений. К сожалению, на это у меня совершенно нет времени. Такие сообщения будут удалены. Пожалуйста, ознакомьтесь со статьёй. Возможно, в ней вы найдёте ответы на вопросы, которые не позволили вам решить своё задание самостоятельно.
Задание 14. Неравенства — профильный ЕГЭ по математике
Задание 14 Профильного ЕГЭ по математике можно считать границей между «неплохо сдал ЕГЭ» и «поступил в вуз с профильной математикой». Здесь не обойтись без отличного знания алгебры. Потому что встретиться вам может любое неравенство: показательное, логарифмическое, комбинированное (например, логарифмы и тригонометрия). И еще бывают неравенства с модулем и иррациональные неравенства. Некоторые из них мы разберем в этой статье.
Хотите получить на Профильном ЕГЭ не менее 70 баллов? Учитесь решать неравенства!
Темы для повторения:
Разберем неравенства разных типов из вариантов ЕГЭ по математике.
Дробно-рациональные неравенства
1. Решите неравенство:
Решим неравенство относительно t методом интервалов:
Вернемся к переменной x:
Показательные неравенства
2. Решите неравенство
Сделаем замену Получим:
Умножим неравенство на
Дискриминант квадратного уравнения
Значит, корни этого уравнения:
Разложим квадратный трехчлен на множители.
. Вернемся к переменной x.
Внимание. Сначала решаем неравенство относительно переменной t. Только после этого возвращаемся к переменной x. Запомнили?
Следующая задача — с секретом. Да, такие тоже встречаются в вариантах ЕГЭ,
3. Решите неравенство
Сделаем замену Получим:
Вернемся к переменной
Первое неравенство решим легко: С неравенством тоже все просто. Но что делать с неравенством ? Ведь Представляете, как трудно будет выразить х?
Оценим Для этого рассмотрим функцию
Сначала оценим показатель степени. Пусть Это парабола с ветвями вниз, и наибольшее значение этой функции достигается в вершине параболы, при х = 1. При этом
Мы получили, что
Тогда , и это значит, что Значение не достигается ни при каких х.
Логарифмические неравенства
4. Решите неравенство
Запишем решение как цепочку равносильных переходов. Лучше всего оформлять решение неравенства именно так.
Следующее неравенство — комбинированное. И логарифмы, и тригонометрия!
5. Решите неравенство
А вот и метод замены множителя (рационализации). Смотрите, как он применяется. А на ЕГЭ не забудьте доказать формулы, по которым мы заменяем логарифмический множитель на алгебраический.
6. Решите неравенство:
Мы объединили в систему и область допустимых значений, и само неравенство. Применим формулу логарифма частного, учитывая, что . Используем также условия
Обратите внимание, как мы применили формулу для логарифма степени. Строго говоря,
Согласно методу замены множителя, выражение заменим на
Решить ее легко.
Разберем какое-нибудь нестандартное неравенство. Такое, что не решается обычными способами.
7. Решите неравенство:
Привести обе части к одному основанию не получается. Ищем другой способ.
Заметим, что при x = 9 оба слагаемых равны 2 и их сумма равна 4.
Функции и — монотонно возрастающие, следовательно, их сумма также является монотонно возрастающей функцией и каждое свое значение принимает только один раз.
Поскольку при x=9 значение монотонно возрастающей функции равно 4, при значения этой функции меньше 4. Конечно, при этом , то есть x принадлежит ОДЗ.
ЕГЭ Профиль №15. Показательные неравенства
15 заданием профильного ЕГЭ по математике является неравенство. Одним, из наиболее часто встречаемых неравенств, которое может оказаться в 15 задание, является показательное неравенство. Большая часть показательных неравенств предлагаемых на реальных экзаменах решается с помощью замен, методом интервалов или разложением на множители. Прежде чем решать показательные неравенства необходимо знать свойства показательной функции и уметь решать показательные уравнения (см. задание 13 профильного ЕГЭ « Показательные уравнения »). В данном разделе представлены показательные неравенства (всего 109) разбитые на два уровня сложности. Уровень А — это простейшие показательные неравенства, которые являются подготовительными для решения реальных показательных неравенств предлагаемых на ЕГЭ по профильной математике. Уровень В — состоит из неравенств, которые предлагали на реальных ЕГЭ и в диагностических работах прошлых лет.
источники:
http://ege-study.ru/ru/ege/materialy/matematika/zadanie-15-profilnogo-ege-po-matematike-neravenstva/
http://math100.ru/prof-ege15-4/