Неравномерное кодирование егэ - Помощь в подготовке к экзаменам и поступлению

Урок посвящен тому, как решать 4 задание ЕГЭ по информатике

Содержание:

Кодирование информации
- Кодирование и расшифровка сообщений
Решение 4 заданий ЕГЭ

Кодирование информации

4-е задание: «Кодирование и декодирование информации»

Уровень сложности

— базовый,

Требуется использование специализированного программного обеспечения

— нет,

Максимальный балл

— 1,

Примерное время выполнения

— 2 минуты.

Проверяемые элементы содержания: Умение кодировать и декодировать информацию

До ЕГЭ 2021 года — это было задание № 5 ЕГЭ

Типичные ошибки и рекомендации по их предотвращению:

«Из-за невнимательного чтения условия задания экзаменуемые иногда не замечают, что требуется найти кодовое слово минимальной длины с максимальным (минимальным) числовым значением.

Кроме того, если в задании указано, что несколько букв остались без кодовых слов (как, например, в задании демоварианта), то кодовое слово для указанной буквы должно быть подобрано таким образом, чтобы осталась возможность найти кодовые слова, удовлетворяющие условию Фано, и для других букв. Так, например, если мы букву А закодируем нулём, а букву Б единицей, то букву В мы уже никак не сможем закодировать с соблюдением условия Фано, поэтому длину кодового слова для А или Б следует увеличить»

ФГБНУ «Федеральный институт педагогических измерений»

Кодирование — это представление информации в форме, удобной для её хранения, передачи и обработки. Правило преобразования информации к такому представлению называется кодом.
Кодирование бывает равномерным и неравномерным:
при равномерном кодировании всем символам соответствуют коды одинаковой длины;
при неравномерном кодировании разным символам соответствуют коды разной длины, это затрудняет декодирование.

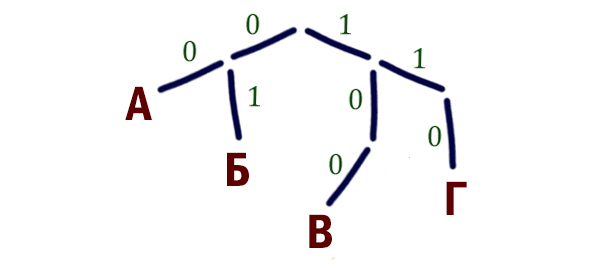
Пример: Зашифруем буквы А, Б, В, Г при помощи двоичного кодирования равномерным кодом и посчитаем количество возможных сообщений:

Таким образом, мы получили равномерный код, т.к. длина каждого кодового слова одинакова для всех кодов (2).

Кодирование и расшифровка сообщений

Декодирование (расшифровка) — это восстановление сообщения из последовательности кодов.

Для решения задач с декодированием, необходимо знать условие Фано:

Условие Фано: ни одно кодовое слово не должно являться началом другого кодового слова (что обеспечивает однозначное декодирование сообщений с начала)

Префиксный код — это код, в котором ни одно кодовое слово не совпадает с началом другого кодового слова. Сообщения при использовании такого кода декодируются однозначно.

если сообщение декодируется с конца, то его можно однозначно декодировать, если выполняется обратное условие Фано:

Обратное условие Фано: никакое кодовое слово не является окончанием другого кодового слова

Постфиксный код — это код, в котором ни одно кодовое слово не совпадает с концом другого кодового слова. Сообщения при использовании такого кода декодируются однозначно и только с конца.

условие Фано – это достаточное, но не необходимое условие однозначного декодирования.

Однозначное декодирование обеспечивается:

Однозначное декодирование

Декодирование

Егифка ©:

Задание демонстрационного варианта 2022 года ФИПИ
Плейлист видеоразборов задания на YouTube:

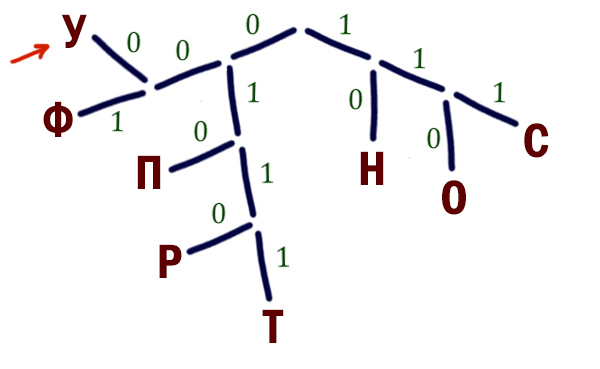
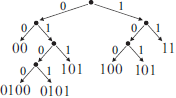
ЕГЭ 4.1: Для кодирования букв О, В, Д, П, А решили использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления).

Закодируйте последовательность букв ВОДОПАД таким способом и результат запишите восьмеричным кодом.

✍ Решение:

Переведем числа в двоичные коды и поставим их в соответствие нашим буквам:

О -> 0 -> 00
В -> 1 -> 01
Д -> 2 -> 10
П -> 3 -> 11
А -> 4 -> 100

Теперь закодируем последовательность букв из слова ВОДОПАД:

010010001110010

Разобьем результат на группы из трех символов справа налево, чтобы перевести их в восьмеричную систему счисления:

010 010 001 110 010
 ↓   ↓   ↓   ↓   ↓
 2   2   1   6   2

Результат: 22162

Теоретическое решение ЕГЭ данного задания по информатике, видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Рассмотрим еще разбор 4 задания ЕГЭ:

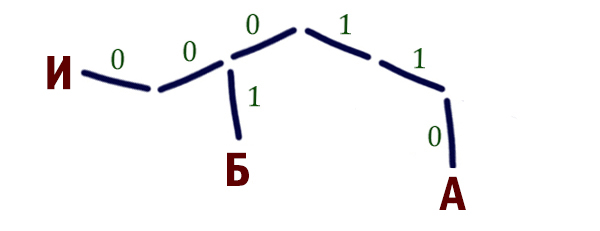
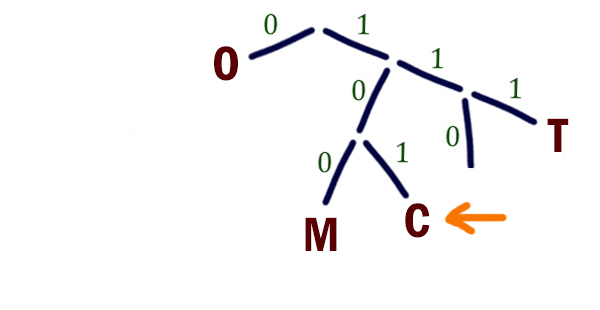
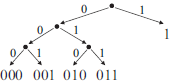
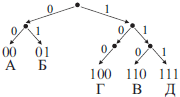
ЕГЭ 4.2: Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв — из двух бит, для некоторых — из трех). Эти коды представлены в таблице:

a	b	c	d	e
000	110	01	001	10

Какой набор букв закодирован двоичной строкой 1100000100110?

✍ Решение:

Во-первых, проверяем условие Фано: никакое кодовое слово не является началом другого кодового слова. Условие верно.

✎ 1 вариант решения:

Код разбиваем слева направо согласно данным, представленным в таблице. Затем переведём его в буквы:

110 000 01 001 10
 ↓   ↓   ↓  ↓  ↓
 b   a  c   d  e

Результат: b a c d e.

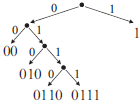
✎ 2 вариант решения:

Сделаем дерево, согласно кодам в таблице:

Сопоставим закодированное сообщение с кодами в дереве:

110 000 01 001 10

Результат: b a c d e.

Кроме того, вы можете посмотреть видеорешение этого задания ЕГЭ по информатике (теоретическое решение):

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Решим следующее 4 задание:

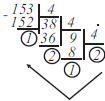
ЕГЭ 4.3:
Для передачи чисел по каналу с помехами используется код проверки четности. Каждая его цифра записывается в двоичном представлении, с добавлением ведущих нулей до длины 4, и к получившейся последовательности дописывается сумма её элементов по модулю 2 (например, если передаём 23, то получим последовательность 0010100110).

Определите, какое число передавалось по каналу в виде 01100010100100100110.

✍ Решение:

Рассмотрим пример из условия задачи:

Было 23₁₀
Стало 0010100110₂

Где сами цифры исходного числа (выделим их красным цветом):

 0010100110  (0010 - 2, 0011 - 3)

Первая добавленная цифра 1 после двоичной двойки — это проверка четности (1 единица в 0010 — значит нечетное), 0 после двоичной тройки — это также проверка нечетности (2 единицы в 0011, значит — четное).
Исходя из разбора примера решаем нашу задачу так: поскольку «нужные» нам цифры образуются из групп по 4 числа в каждой плюс одно число на проверку четности, то разобьем закодированное сообщение на группы по 5, и отбросим из каждой группы последний символ:
разбиваем по 5:

01100 01010 01001 00110

отбрасываем из каждой группы последний символ:

0110 0101 0100 0011

Результат переводим в десятичную систему:

0110 0101 0100 0011
 ↓    ↓     ↓    ↓
 6    5     4    3

Ответ: 6 5 4 3

Вы можете посмотреть видеорешение этого задания ЕГЭ по информатике, теоретическое решение:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

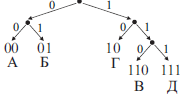
ЕГЭ 4.4:

Для кодирования некоторой последовательности, состоящей из букв К, Л, М, Н решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Н использовали кодовое слово 0, для буквы К — кодовое слово 10.

Какова наименьшая возможная суммарная длина всех четырёх кодовых слов?

Подобные задания для тренировки

✍ Решение:

✎

1 вариант решения

основан на логических умозаключениях:

Найдём самые короткие возможные кодовые слова для всех букв.
Кодовые слова 01 и 00 использовать нельзя, так как тогда нарушается условие Фано (начинаются с 0, а 0 — это Н).
Начнем с двухразрядных кодовых слов. Возьмем для буквы Л кодовое слово 11. Тогда для четвёртой буквы нельзя подобрать кодовое слово, не нарушая условие Фано (если потом взять 110 или 111, то они начинаются с 11).
Значит, надо использовать трёхзначные кодовые слова. Закодируем буквы Л и М кодовыми словами 110 и 111. Условие Фано соблюдается.
Суммарная длина всех четырёх кодовых слов равна:

(Н)1 + (К)2 + (Л)3 + (М)3 = 9

✎ 2 вариант решения:

Будем использовать дерево. Влево откладываем 0, вправо — 1:

Теперь выпишем соответствие каждой буквы ее кодового слова согласно дереву:

(Н) -> 0   -> 1 символ
(К) -> 10  -> 2 символа
(Л) -> 110 -> 3 символа
(М) -> 111 -> 3 символа

Суммарная длина всех четырёх кодовых слов равна:

(Н)1 + (К)2 + (Л)3 + (М)3 = 9

Ответ: 9

4.5:

По каналу связи передаются сообщения, содержащие только 4 буквы: А, Б, В, Г; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв А, Б, В используются такие кодовые слова:

А: 101010, 
Б: 011011, 
В: 01000

Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Подобные задания для тренировки

✍ Решение:

Наименьшие коды могли бы выглядеть, как 0 и 1 (одноразрядные). Но это не удовлетворяло бы условию Фано (А начинается с единицы — 101010, Б начинается с нуля — 011011).
Следующим наименьшим кодом было бы двухбуквенное слово 00. Так как оно не является префиксом ни одного из представленных кодовых слов, то Г = 00.

Результат: 00

4.6:

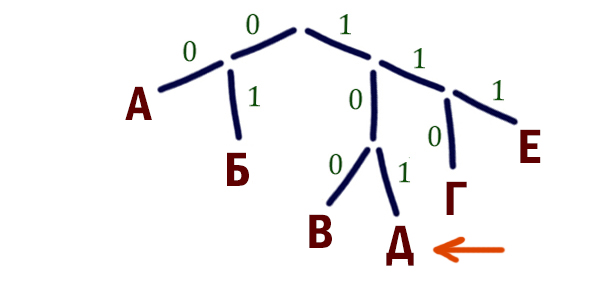
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приемной стороне канала связи. Использовали код:

А - 01 
Б - 00
В - 11
Г - 100

Укажите, каким кодовым словом должна быть закодирована буква Д. Длина этого кодового слова должна быть наименьшей из всех возможных. Код должен удовлетворять свойству однозначного декодирования. Если таких кодов несколько, укажите код с наименьшим числовым значением.

✍ Решение:

Так как необходимо найти кодовое слово наименьшей длины, воспользуемся деревом. Влево будем откладывать нули, а вправо — единицы:

Поскольку у нас все ветви завершены листьями, т.е. буквами, кроме одной ветви, то остается единственный вариант, куда можно поставить букву Д:

Перепишем сверху вниз получившееся кодовое слово для Д: 101

Результат: 101

Подробней разбор урока можно посмотреть на видео ЕГЭ по информатике 2017:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

4.7: Демоверсия ЕГЭ 2018 информатика (ФИПИ):

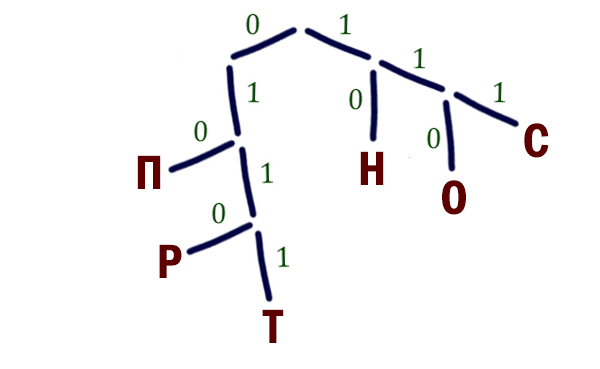
По каналу связи передаются шифрованные сообщения, содержащие только десять букв: А, Б, Е, И, К, Л, Р, С, Т, У. Для передачи используется неравномерный двоичный код. Для девяти букв используются кодовые слова.

Укажите кратчайшее кодовое слово для буквы Б, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Подобные задания для тренировки

✍ Решение:

Для решения будем использовать дерево. Ветви, соответствующие нулю, будем откладывать влево, единице — вправо.

При рассмотрении дерева видим, что все ветви «закрыты» листьями, кроме одной ветви — 1100:

Результат: 1100

Подробное теоретическое решение данного 4 (раньше №5) задания из демоверсии ЕГЭ 2018 года смотрите на видео:

📹 Видеорешение на RuTube здесь

4.8:

По каналу связи передаются шифрованные сообщения, содержащие только четыре букв: А, Б, В, Г; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв А, Б, В используются кодовые слова:

А: 00011 
Б: 111 
В: 1010

Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

✍ Решение:

Для решения будем использовать дерево. Ветви, соответствующие нулю, будем откладывать влево, единице — вправо.
Поскольку в задании явно не указано о том, что код должен удовлетворять условию Фано, то дерево нужно построить как с начала (по условию Фано), так и с конца (обратное условие Фано).

Дерево по условию Фано (однозначно декодируется с начала):

Получившееся числовое значение кодового слова для буквы Г — 01.

Дерево по обратному условию Фано (однозначно декодируется с конца):

Получившееся числовое значение кодового слова для буквы Г — 00.
После сравнения двух кодовых слов (01 и 00), код с наименьшим числовым значением — это 00.

Результат: 00

4.9:

По каналу связи передаются сообщения, содержащие только буквы: А, Е, Д, К, М, Р; для передачи используется двоичный код, удовлетворяющий условию Фано. Известно, что используются следующие коды:

Е – 000
Д – 10
К – 111

Укажите наименьшую возможную длину закодированного сообщения ДЕДМАКАР.
В ответе напишите число – количество бит.

Подобные задания для тренировки

✍ Решение:

С помощью дерева отобразим известные коды для букв:

В результирующем слове — ДЕДМАКАР — вде буквы А. Значит, для получения наименьшей длины необходимо для буквы А выбрать наименьший код в дереве. Учтем это и достроим дерево для остальных трех букв А, М и Р:

Расположим буквы в порядке их следования в слове и подставим их кодовые слова:

Д   Е   Д   М   А   К   А   Р
10 000 10  001 01  111 01  110

Посчитаем количество цифр в итоговом коде и получим 20.

Результат: 20

Смотрите виде решения задания:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Источник

Всего: 114 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

По каналу связи передаются сообщения, содержащие только восемь букв: К, Л, М, Н, О, П, Р, С. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: К  — 001, Н  — 100, Р  — 111. Какое наименьшее количество двоичных знаков потребуется для кодирования слова МОЛОКОСОС?

Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.

По каналу связи передаются сообщения, содержащие только семь букв: А, Б, В, Д, О, Р, Т. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: Б  — 01, Д  — 001, Р  — 100. Какое наименьшее количество двоичных знаков потребуется для кодирования слова ВОДОВОРОТ?

Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.

По каналу связи передаются сообщения, содержащие только заглавные русские буквы. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А  — 000, Б  — 01, В  — 1101, Г  — 111, Д  — 0010, Е  — 100. Для кодирования слова ГОРОД потребовалось 17 двоичных знаков. Какое кодовое слово соответствует букве О?

Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.

По каналу связи передаются сообщения, содержащие только заглавные русские буквы. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А  — 010, Б  — 101, В  — 1001, Г  — 111, Д  — 0110, Е  — 110. Для кодирования слова ОГОРОД потребовалось 17 двоичных знаков. Какое кодовое слово соответствует букве О?

По каналу связи передаются сообщения, содержащие только семь букв: А, Б, Г, И, М, Р, Я. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А  — 010, Б  — 011, Г  — 100. Какое наименьшее количество двоичных знаков потребуется для кодирования слова МАГИЯ?

Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.

По каналу связи передаются сообщения, содержащие только семь букв: А, Б, Г, И, М, Р, Я. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А  — 010, Б  — 00, Г  — 101. Какое наименьшее количество двоичных знаков потребуется для кодирования слова МАГИЯ?

Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.

Для кодирования растрового рисунка, напечатанного с использованием шести красок, применили неравномерный двоичный код. Для кодирования цветов используются кодовые слова.

Белый  — 0, Зелёный  — 11111, Фиолетовый  — 11110, Красный  — 1110, Чёрный  — 10. Укажите кратчайшее кодовое слово для кодирования синего цвета, при котором код будет допускать однозначное декодирование.

Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.

Источник: ЕГЭ по информатике 13.06.2019. Основная волна. Юг-Центр.

По каналу связи передаются сообщения, содержащие только заглавные русские буквы. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: В  — 1110, Г  — 110, Д  — 0000, Е  — 01. Известно, что для кодирования слова БАОБАБ потребовалось 16 двоичных знаков. Какое кодовое слово соответствует букве А?

По каналу связи передаются сообщения, содержащие только заглавные русские буквы. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: Б  — 10, Г  — 1110, Д  — 0111, Е  — 010. Известно, что для кодирования слова АНАНАС потребовалось 16 двоичных знаков. Какое кодовое слово соответствует букве Н?

По каналу связи передаются сообщения, содержащие только заглавные русские буквы. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А  — 000, Б  — 01, В  — 1101, Г  — 111, Д  — 0010, Е  — 100. Какое наименьшее количество двоичных знаков потребуется для кодирования слова КОКОС?

По каналу связи передаются сообщения, содержащие только четыре буквы: П, О, С, Т; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв Т, О, П используются такие кодовые слова: Т: 111, О: 0, П: 100.

Укажите кратчайшее кодовое слово для буквы С, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Источник: Демонстрационная версия ЕГЭ—2016 по информатике.

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В, Г использовали соответственно кодовые слова 000, 001, 10, 11. Укажите кратчайшее возможное кодовое слово для буквы Д, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением. Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.

Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 29 ноября 2016 года Вариант ИН10203

По каналу связи передаются сообщения, содержащие только семь букв: А, Б, Г, И, М, Р, Я. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А  — 010, Б  — 011, И  — 10. Какое наименьшее количество двоичных знаков потребуется для кодирования слова ГРАММ?

Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.

Для передачи сообщений, составленных из заглавных букв русского алфавита, используется неравномерный двоичный код, в котором никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Известны кодовые слова, назначенные для некоторых букв: А  — 000, Б  — 0010, В  — 101, Г  — 11. Какое наименьшее количество двоичных знаков может содержать сообщение, кодирующее слово КОЛОБОК?

Все заглавные буквы русского алфавита закодированы неравномерным двоичным кодом, в котором никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Известно, что слову КАША соответствует код 011011010. Какое наименьшее количество двоичных знаков может содержать сообщение, кодирующее слово ОСОКА?

По каналу связи передаются сообщения, содержащие только семь букв: А, Б, Г, И, М, Р, Я. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А  — 010, Б  — 00, Г  — 101. Какое наименьшее количество двоичных знаков потребуется для кодирования слова ГРАММ?

Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.

По каналу связи передаются сообщения, содержащие только семь букв: А, Б, В, Д, Е, И, Н. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А  — 110, Б  — 01, И  — 000. Какое наименьшее количество двоичных знаков потребуется для кодирования слова ВВЕДЕНИЕ?

Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.

По каналу связи передаются сообщения, содержащие только заглавные русские буквы. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А  — 010, Б  — 101, В  — 1001, Г  — 111, Д  — 0110, Е  — 110. Какое наименьшее количество двоичных знаков потребуется для кодирования слова ЛИЛИЯ?

Все заглавные буквы русского алфавита закодированы неравномерным двоичным кодом, в котором никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Известно, что слову УДОД соответствует код 100011101. Какое наименьшее количество двоичных знаков может содержать сообщение, кодирующее слово УДАЧА?

По каналу связи передаются сообщения, содержащие только пять букв: A, B, С, D, E. Для передачи используется двоичный код, допускающий однозначное декодирование. Для букв A, B, C используются такие кодовые слова: A  — 1, B  — 010, C  — 000.

Укажите кратчайшее кодовое слово для буквы E, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Всего: 114 1–20 | 21–40 | 41–60 | 61–80 …

Источник

В этом уроке мы поговорим о задании 4 из ЕГЭ по информатике 2022.

Задание 4 включает в себя понятие кодирование и декодирование информации.

Приступим к тренировочным заданиям из ЕГЭ по информатике 2022.

Задача (Стандартная)

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е. решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В, Г использовали соответственно кодовые слова 00, 01, 100, 110. Укажите кратчайшее возможное кодовое слово для буквы Д, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.

Решение:

Используем приём Дерево Фано. Расставим на этом дереве те буквы, для которых уже известны кодовые слова.

Дерево рисуется обычно сверху вниз. В начале от дерева рисуются две ветки: ветка 0 и ветка 1. От каждой ветки можно нарисовать ещё две ветки, так же 0 и 1, и т. д.

Для удобства ветки с 1 будем направлять вправо, а ветки с 0 будем направлять влево.

В конце каждой ветки можно размещать буквы, но если мы разместили букву, то эта ветка блокируется, и от этой ветки больше нельзя делать новые ответвления.

Нам осталось закодировать (расположить на дереве) две буквы: Д и Е.

Мы можем нарастить ещё две ветки от точки 1-1. Тогда получится код 111. И от точки 1-0. Тогда получится код 101.

Для буквы Д нужно выбрать код с наименьшим числовым значением. Значит, для буквы Д выбираем код 101, а для буквы Е выбираем код 111.

Ответ: 101

Закрепим приём дерево Фано на ещё одной примерной задаче из ЕГЭ по информатике 2022.

Задача(Стандартная, закрепление)

Для кодирования некоторой последовательности, состоящей из букв Н, О, П, Р, С, Т, У, Ф решили использовать неравномерный двоичный код, удовлетворяющий условию, что ни одно кодовое слово не является началом другого кодового слова. Для букв Н, О, П, Р, С, Т использовали соответственно кодовые слова 10, 110, 010, 0110, 111, 0111. Укажите кратчайшее возможное кодовое слово для буквы У, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение:

Здесь код так же должен удовлетворять Условию Фано, т.к. сказано, что ни одно кодовое слово не является началом другого кодового слова.

Значит, можем воспользоваться Деревом Фано. Расположим на Дереве Фано буквы, для которых уже известны кодовые слова.

Нам нужно закодировать ещё две буквы: У, Ф. У нас единственная возможность осталась прорастить ветку от точки 0. От этой точки проращиваем ветку 0 и от этой ветки проращиваем ещё две ветки 0 и 1.

Букву У размещаем на позиции 000, потому что для этой буквы нужно выбрать код с наименьшим числовым значением.

Ответ: 000

Ещё одна примерная задача из ЕГЭ по информатике 2022 является частым гостем в различных тренировочных вариантах.

Задача (Стандартная, закрепление)

По каналу связи передаются сообщения, содержащие только семь букв: А, Б, Д, Л, Е, И, Н. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А – 110, Б – 01, И – 000. Какое наименьшее количество двоичных знаков потребуется для кодирования слова ДЕЛЕНИЕ?

Решение:

Расставим на дереве Фано буквы, для которых известны коды.

Нам осталось расположить 4 буквы: Д, Л, E, Н.

Буква Е встречается три раза в слове ДЕЛЕНИЕ, значит, ей нужно постараться присвоить самый короткий код. По дереву видно, что можно букве Е присвоить код 10.

Буквы Д, Л, Н встречаются в слове ДЕЛЕНИЕ 1 раз. Одну букву можно разместить на позицию 111. Так же можно продлить ветку из точки 00, а затем от позиции 001 сделать два отростка. У нас получатся ещё два свободных места: 0011 и 0010.

Можно оставшиеся буквы разместить следующим образом:

Подсчитаем какое количество двоичных знаков потребуется для кодирования слова ДЕЛЕНИЕ.

3+2+4+2+4+3+2=20

Ответ: 20

Далее решим непростую задачу из тренировочных вариантов ЕГЭ по информатике 2022. Похожая задача была в сборнике С. С. Крылова в 2021 году.

Задача (Непростая)

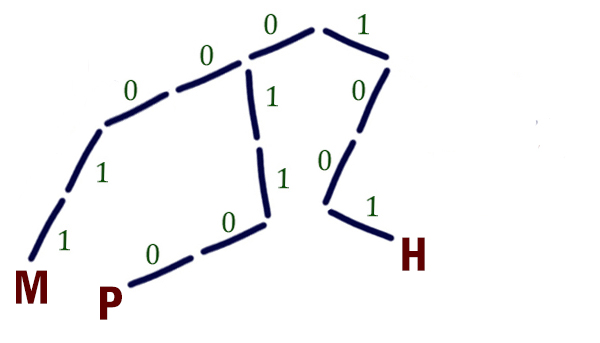
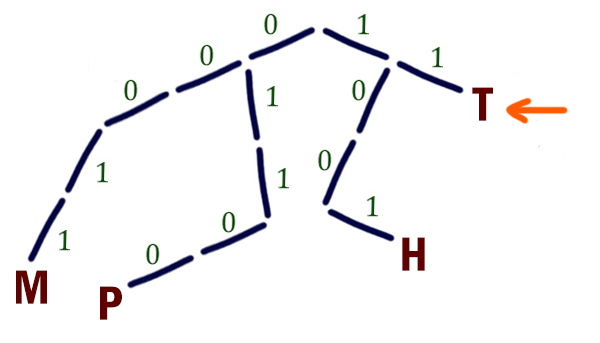
По каналу связи передаются сообщения, содержащие только четыре буквы: М, Н, Р, Т; для передачи используется двоичный код, допускающий однозначное декодирование.

Для букв М, Н, Р используются такие кодовые слова: М: 00011, Н: 1001, Р: 01100.

Укажите кратчайшее кодовое слово для буквы Т, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение:

Нужно, чтобы код декодировался однозначно. Чтобы код декодировался однозначно, можно использовать условие Фано. Мы видим, что в уже известных кода не нарушается условие Фано. Узнаем код для буквы Т по дереву Фано. Отметим известные буквы.

Куда разместить букву Т? Чтобы кодовое слово было кратчайшее, разместим букву Т на позицию 11.

Сложность этой задачи заключается в том, что явно не указано, что нужно использовать условие Фано. Так же однозначное декодирование будет, если используется обратное условие Фано.

Обратное условие Фано: никакое кодовое слово не является окончанием другого кодового слова. Сообщения при использовании такого кода декодируются однозначно и только с конца.

Т. е. сообщения нужно такие раскодировать справа налево. Здесь про то, как будут раскодировать сообщения, ничего не сказано, поэтому мы должны проверить, какой код получится для буквы Т, если здесь используется обратное условие Фано.

Кодовое слово 0 мы использовать не можем, потому что 0 — это окончание кодового слова буквы Р. Кодовое слово 1 — это окончание кодовых слов букв М и Н. Кодовое слово 00 — это окончание кодового слова буквы Р. А вот 10 подходит для буквы Т.

Получилась следующая ситуация. Если кодовые слова будут удовлетворяют условию Фано, то для буквы Т можно написать кратчайшее кодовое слово 11 с минимальным числовым значением. Если кодовые слова будут удовлетворяют обратному условию Фано, то для буквы Т можно написать кратчайшее кодовое слово 10 с минимальным числовым значением.

И в том и в другом случае будет однозначное декодирование. Но мы выбираем тот случай, когда кодовое слово будет наименьшим числовым значением. Таким образом, в ответе напишем 10.

Ответ: 10

Разберём ещё один нюанс в подобных задах из ЕГЭ по информатике.

Задача (Ещё раз про однозначное декодирование)

По каналу связи передаются сообщения, содержащие только четыре буквы: М, О, С, Т; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв Т, О, М используются такие кодовые слова: Т: 111, О: 0, М: 100. Укажите кратчайшее кодовое слово для буквы С, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение:

Здесь условие похоже на то, которое было в предыдущей задаче. Но обратное условие Фано здесь не применимо, т.к. код для буквы О является окончанием для кода буквы М.

Значит, у нас остаётся единственный инструмент, чтобы сообщения декодировались однозначно — это условие Фано. Теперь задачу решаем как обычно по дереву Фано.

Выбираем из двух вариантов: 110 и 101. Но останавливаемся на 101, т.к. это кодовое слово с наименьшим числовым значением.

Ответ: 101

Решим задачу, которая часто встречается в бумажных сборниках по подготовке к ЕГЭ по информатике.

Задача (код не удовлетворяет условию Фано)

По каналу связи передаются шифрованные сообщения, содержащие только пять латинских букв: A, B, С, D, E. Для передачи используется неравномерный двоичный код. Для некоторых букв известны кодовые слова: A: 01, B: 10, C: 11, D: 000.

Укажите самое короткое кодовое слово для буквы E, при котором код не будет удовлетворять условию Фано, при этом в записи самого этого слова должно использоваться более одного символа, а само слово не должно совпадать ни с одним из используемых слов для букв с известными кодами.

Если таких слов несколько, то укажите слово с наименьшим числовым значением.

Решение:

Здесь код не должен однозначно декодироваться.

Подходит код 00, т.к. длина этого кодового слова больше чем 1 символ. Этот код не совпадает ни с одним кодом для известных букв. Этот код нарушает принцип условия Фано, видно, что он является началом кодового слова буквы D. И этот код имеет самое маленькое числовое значение.

Ответ: 00

В 4 задании из ЕГЭ по информатике 2022 не обязательно может попасться задача, связанная с условием Фано. Может просто быть задача на кодирование и декодирование информации.

Задача (Заключительная)

Для кодирования букв X, К, Л, О, Д решили использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления). Закодируйте последовательность букв ХОЛОДОК таким способом и результат запишите шестнадцатеричным кодом.

Решение:

Распишем, как кодируются все буквы в двоичной системе. Ноль и один кодируются одним разрядом, поэтому к ним слева приписывается ноль, как написано в условии.

Буква	Десятичное Представление	Двоичное Представление
Х	0	00
К	1	01
Л	2	10
О	3	11
Д	4	100

Выписываем слово ХОЛОДОК и под ним кодовые слова букв.

Чтобы перевести из двоичной системы число в шестнадцатиричную систему, мы должны двоичные цифры разбить по четвёркам, начиная с правого края. Каждая четвёрка превращается в цифру в шестандцатиричной системе. Таблицу перевода четвёрок двоичных цифр в шестнадцатиричную систему можно посмотреть в этой статье.

Т.к. ЕГЭ по информатике сдаётся в компьютерной форме, то можно воспользоваться стандартным калькулятором в режиме программист.

Ответ: 1DCD

На этом всё! Пусть Вам повезёт на ЕГЭ по информатике 2022.

В последней задаче буква К шифруется как 01, тогда почему в самом слове ХОЛОДОК она кодируется как 00?

Источник

ЕГЭ информатика 4 задание разбор, теория, как решать

Кодирование и декодирование информации, (Б) — 1 балл

Е4.41 Какое количество двоичных знаков потребуется для кодирования слова КАЗАЧКА

По каналу связи передаются сообщения, содержащие только буквы из набора: А, З, К, Н, Ч. Для передачи используется двоичный код, удовлетворяющий прямому условию Фано, согласно которому никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: Н – 1111, З – 110. …

Е4.40 Определите наименьшую возможную сумму длин всех семи кодовых слов

Для кодирования некоторой последовательности, состоящей из букв N, P, R, Q, X, W, Z, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв Q и R использовали кодовые слова 11 и 100 соответственно. Определите наименьшую возможную сумму длин всех семи кодовых слов, учитывая, что кодовые слова оставшихся букв имеют одинаковую длину. Примечание. Условие Фано …

Е4.39 Какую наименьшую длину может иметь код слова ВОДОПРОВОД

Все заглавные буквы русского алфавита закодированы неравномерным двоичным кодом, в котором никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Известны кодовые слова первых букв алфавита: А – 001, Б – 011, В – 110. Какую наименьшую длину может иметь код слова ВОДОПРОВОД? Ответ: СтатГрад Вариант …

Е4.38 слово КАШКА закодировали с помощью последовательности 1110110011101

Известно, что слово КАШКА закодировали с помощью последовательности 1110110011101. При этом код удовлетворяет условию Фано. Найдите минимальную длину кодовой последовательности для слова ПАМПУШКА? Известно, что другие буквы в кодируемой последовательности встретиться не могут. Ответ: «Некрыловские варианты» от Евгения Джобса — Вариант 5

Е4.37 Какой код соответствует слову СУП?

Заглавные буквы русского алфавита закодированы неравномерным двоичным кодом, в котором никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Известно, что все кодовые слова содержат не меньше двух двоичных знаков, а слову СПУСК соответствует код 01010110010111. Какой код соответствует слову СУП? Ответ: СтатГрад Вариант ИН2010401 17.03.2021– …

Е4.36 а слову БАРАН соответствует код 10011111011010

Все заглавные буквы русского алфавита закодированы неравномерным двоичным кодом, в котором никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Известно, что все кодовые слова содержат не меньше двух двоичных знаков, а слову БАРАН соответствует код 10011111011010. Какое наименьшее количество двоичных знаков может содержать сообщение, кодирующее слово …

Е4.35 Какой код соответствует слову ШОК

Заглавные буквы русского алфавита закодированы неравномерным двоичным кодом, в котором никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Известно, что все кодовые слова содержат не меньше двух двоичных знаков, а слову КОШКА соответствует код 10101001101000. Какой код соответствует слову ШОК? Ответ: СтатГрад Вариант ИН2010401 17.03.2021– …

Е4.34 Какое наименьшее количество двоичных знаков может содержать код слова ПАНАМА?

Все заглавные буквы русского алфавита закодированы неравномерным двоичным кодом, в котором никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: П – 00, Е – 01, Н – 110. Какое наименьшее количество двоичных знаков может содержать код слова ПАНАМА? Ответ: …

Е4.33 наименьшую возможную длину закодированной последовательности для слова СУСТАВ

Укажите наименьшую возможную длину закодированной последовательности для слова СУСТАВ. По каналу связи передаются сообщения, содержащие только шесть букв: А, В, Г, У, С, Т; для передачи используется двоичный код, удовлетворяющий условию Фано. Буквы Т, У, С, А имеют коды 10, 000, 11, 001 соответственно. Укажите наименьшую возможную длину закодированной последовательности для слова СУСТАВ. Ответ: …

Е4.32 Для букв А, Б, В, Г использовали соответственно кодовые слова 000, 001, 010, 011

Для букв А, Б, В, Г использовали соответственно кодовые слова 000, 001, 010, 011. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В, Г использовали соответственно кодовые слова 000, 001, 010, 011. Укажите кратчайшее возможное кодовое слово для буквы …

Источник

Уроки Информатики
11 класс
Подготовка к ЕГЭ

Основано на: демонстрационных вариантах ЕГЭ по информатике за 2015 год, http://wiki.vspu.ru/

Задание:

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код: А – 0; Б – 100; В – 1010; Г – 111; Д – 110. Требуется сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно. Коды остальных букв меняться не должны. Как это можно сделать?

Для того чтобы понять что от нас требуют, давайте разберемся с каждым словом в этом задании. Кодирование, последовательность, — это всем нам с вами знакомые и хорошо понятные слова и что они означяают, мы прекрасно понимаем. И вот после перечисления букв мы сталкиваемся с не всем знакомым словосочетанием НЕРАВНОМЕРНЫЙ двоичный код. Неравномерное двоичное кодирование — кодирование при котором символы некоторого первичного алфавита кодируются комбинациями символов двоичного алфавита (т.е. 0 и 1), причем, длина кодов и, соответственно, длительность передачи отдельного кода, могут различаться. Данная идея двоичного кодирования положена в основу Кода Хаффмана, в котором символ, который встречается в последовательности чаще всего, получает очень маленький код, а символ, который встречается реже всего, получает, наоборот, очень длинный код, тем самым позволяя уменьшить объем информации.

Предположим, у нас есть строка «тор тут тёр», для которой, в её текущем виде, на каждый знак тратится по одному байту. Это означает, что вся строка целиком занимает 11*8 = 88 бит памяти. После кодирования строка займёт 27 бит.

Чтобы получить код для каждого символа строки «тор тут тёр», на основе его частотности, нам надо построить дерево (граф), такое, что каждый лист этого дерева будет содержать символ . Дерево будет строиться от листьев к корню, в том смысле, что символы с меньшей частотой будут дальше от корня, чем символы с большей.

Чтобы построить дерево, мы воспользуемся слегка модифицированной очередью с приоритетами — первыми из неё будут извлекаться элементы с наименьшим приоритетом, а не наибольшим. Это нужно, чтобы строить дерево от листьев к корню.

И так, подсчитаем частотность символов Т Р пробел О У Е

Символ	Частотность
Т	4
Р	2
‘ ‘	2
У	1
О	1
Е	1

После вычисления частот мы создадим узлы бинарного дерева для каждого знака и добавим их в очередь, используя частоту в качестве приоритета:

Теперь мы достаём два первых элемента из очереди и связываем их, создавая новый узел дерева, в котором они оба будут потомками, а приоритет нового узла будет равен сумме их приоритетов. После этого мы добавим получившийся новый узел обратно в очередь.

Повторим те же шаги и в итоге мы получим:

После связывания веток в одно дерево, мы с вами получим следующие коды для наших символов

Т — 00; Р — 10; пробел -01; О — 1110; У — 110; Е — 1111 более подробно можно прочитать вот тут

Задание 1 ЕГЭ:

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код: А – 0; Б – 100; В – 1010; Г – 111; Д – 110. Требуется сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно. Коды остальных букв меняться не должны. Как это можно сделать?

Решение:

Как и в теории мы с вами должны составить дерево кода для соблюдения условия Фано (Никакое кодовое слово не может быть началом другого кодового слова) с целью кодирования по Хоффману

Далее подпишем данные нам кодовые фразы, и соответствующие им буквы

По условию Фано: Никакое кодовое слово не может быть началом другого кодового слова, — следует, что целиком ветка 0 у нас не используется (0 используется для кодирования А), сократить коды для букв Г, Д, Б, так же не представляется возможным. И связано это с тем, что если мы используем кодовое слово для шифрования некоторого символа, то вся ветка шифра ниже этого символа более использоваться не может! (как в случае с А)

И в нашем случае сократить мы можем только код для символа В — 101 вместо 1010

Все статьи раздела

Коменты VK
Анонимные коменты, G+ или Facebook

Источник

За это задание ты можешь получить 1 балл. На решение дается около 3 минут. Уровень сложности: базовый.
Средний процент выполнения: 84.4%
Ответом к заданию 4 по информатике может быть цифра (число) или слово.

Разбор сложных заданий в тг-канале

Задачи для практики

Задача 1

По каналу связи передаются сообщения, каждое из которых содержит 15 букв А, 10 букв Б, 7 букв В и 5 букв Г (других букв в сообщениях нет). Каждую букву кодируют двоичной последовательностью.При выборе кода учитывались два требования: а) ни одно кодовое слово не является началом другого (это нужно, чтобы код допускал однозначное декодирование); б) общая длина закодированного сообщения должна быть как можно меньше.

Определите, чему равна длина кодового сообщения для кода, удовлетворяющего перечисленным условиям.

Решение

Условие однозначного декодирования (условие Фано) заключается в том, что однозначное декодирование возможно, только если ни одно кодовое слово не является началом другого кодового слова. В данной задаче требуется получить минимальную длину закодированного сообщения, поэтому кодовые слова следует подбирать так, чтобы самая часто встречающаяся буква кодировалась самым коротким кодовым словом. Исходя из этого, можно построить код следующего вида: А – 00, Б – 01, В – 10, Г – 11. Этот код удовлетворяет условию Фано, и длина всего сообщения, закодированного этим кодом, будет равна 15$·$2+10$·$2+7$·$2+5$·$2=74. Для проверки имеет смысл составить ещё один код, удовлетворяющий условию Фано, который мог бы быть оптимальным для некоторых сообщений. Например, рассмотрим такой код: А – 0, Б – 10, В – 110, Г – 111. Тогда длина закодированного сообщения будет 15$·$1+10$·$2+7$·$3+5$·$3=71. Следовательно, такой вариант нас устраивает, данный код является более выгодным, и длина сообщения, закодированного этими кодовыми словами, рана 71.

Ответ: 71

Задача 2

По каналу связи передаются сообщения, каждое из которых содержит 15 букв А, 14 букв Б, 12 букв В и 4 буквы Г (других букв в сообщениях нет). Каждую букву кодируют двоичной последовательностью.При выборе кода учитывались два требования: а) ни одно кодовое слово не является началом другого (это нужно, чтобы код допускал однозначное декодирование); б) общая длина закодированного сообщения должна быть как можно меньше.

Определите, чему равна длина кодового сообщения для кода, удовлетворяющего перечисленным условиям.

Решение

Условие однозначного декодирования (условие Фано) заключается в том, что однозначное декодирование возможно, только если ни одно кодовое слово не является началом другого кодового слова. В данной задаче требуется получить минимальную длину закодированного сообщения, поэтому кодовые слова следует подбирать так, чтобы самая часто встречающаяся буква кодировалась самым коротким кодовым словом. Исходя из этого, можно построить код следующего вида: А – 00, Б – 01, В – 10, Г – 11. Этот код удовлетворяет условию Фано, и длина всего сообщения, закодированного этим кодом, будет равна 15$·$2+14$·$2+12$·$2+4$·$2=90. Для проверки имеет смысл составить ещё один код, удовлетворяющий условию Фано, который мог бы быть оптимальным для некоторых сообщений. Например, рассмотрим такой код: А – 0, Б – 10, В – 110, Г – 111. Тогда длина закодированного сообщения будет 15$·$1+14$·$2+12$·$3+4$·$3=91. Следовательно, такой вариант нас не устраивает, первый код является более выгодным, и длина сообщения, закодированного этими кодовыми словами, рана 90.

Ответ: 90

Задача 3

По каналу связи передаются сообщения, каждое из которых содержит 20 букв Е, 18 букв И, 16 букв К и 10 букв П (других букв в сообщениях нет). Каждую букву кодируют двоичной последовательностью. При выборе кода учитывались два требования: а) ни одно кодовое слово не является началом другого (это нужно, чтобы код допускал однозначное декодирование); б) общая длина закодированного сообщения должна быть как можно меньше.

Определите, чему равна длина кодового сообщения для кода, удовлетворяющего перечисленным условиям.

Решение

Условие однозначного декодирования (условие Фано) заключается в том, что однозначное декодирование возможно, только если ни одно кодовое слово не является началом другого кодового слова. В данной задаче требуется получить минимальную длину закодированного сообщения, поэтому кодовые слова следует подбирать так, чтобы самая часто встречающаяся буква кодировалась самым коротким кодовым словом. Исходя из этого, можно построить код следующего вида: Е – 00, И – 01, К – 10, П – 11. Этот код удовлетворяет условию Фано, и длина всего сообщения, закодированного этим кодом, будет равна 20$·$2+18$·$2+16$·$2+10$·$2=128. Для проверки имеет смысл составить ещё один код, удовлетворяющий условию Фано, который мог бы быть оптимальным для некоторых сообщений. Например, рассмотрим такой код: Е – 0, И – 10, К – 110, П – 111. Тогда длина закодированного сообщения будет 20$·$1+18$·$2+16$·$3+10$·$3=134. Следовательно, такой вариант нас не устраивает, первый код является более выгодным, и длина сообщения, закодированного этими кодовыми словами, рана 128.

Ответ: 128

Задача 4

По каналу связи передаются сообщения, каждое из которых содержит 18 букв Е, 10 букв И, 8 букв К и 6 букв П (других букв в сообщениях нет). Каждую букву кодируют двоичной последовательностью.При выборе кода учитывались два требования: а) ни одно кодовое слово не является началом другого (это нужно, чтобы код допускал однозначное декодирование); б) общая длина закодированного сообщения должна быть как можно меньше.

Определите, чему равна длина кодового сообщения для кода, удовлетворяющего перечисленным условиям.

Решение

Для решения данной задачи рассмотрим дерево, у которого из корня и любой вершины выходят по две ветви. Сопоставим каждой левой ветви 0, а каждой правой — 1. Тогда, проходя от вершины к каждому из листьев (узлов, из которых не выходят ветви) и выписывая последовательность нулей и единиц, соответствующих обходу дерева, получим набор кодовых слов, образующих префиксный код (код, в котором ни одно кодовое слово не является началом другого). Префиксный код является однозначно декодируемым.

По условию задачи в сообщении используются только 4 различные буквы. Следовательно, для построения кодовых слов возможно использование одного из двух деревьев. При использовании других кодовых деревьев длины кодовых слов будут или совпадать с длинами кодовых слов дерева (в этом случае общая длина кодового сообщения так же будет совпадать), или будут больше, и, следовательно, не будут удовлетворять условию наименьшей длины кодового сообщения.

На основе дерева получим кодовые слова 00, 01, 10 и 11. Все слова имеют длину 2. Учитывая количество вхождений каждой из букв в сообщение, получим, что в этом случае длина закодированного сообщения равна 2 · (18 + 10 + 8 + 6) = 84.

На основе дерева получим кодовые слова 0, 01, 110 и 111.

Чтобы общая длина кодового сообщения была наименьшей, следует назначить букве, встречающейся наибольшее число раз, кодовое слово наименьшей длины. Например, Е — 0, И — 01, К — 110 и П — 111.

В этом коде длины кодовых слов для букв Е, И, К и П равны 1, 2, 3 и 3 соответственно. Учитывая количество вхождений каждой из букв в сообщение, получим, что в этом длина закодированного сообщения равна 1 · 18 + 2 · 10 + 3 · 8 + 3 · 6 = 80.

Следовательно, наименьшая длина кодового сообщения, для кода удовлетворяющего условиям задачи, равна 80.

Ответ: 80

Задача 5

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, в котором ни одно кодовое слово не является началом другого (это нужно, чтобы код допускал однозначное декодирование). Известно, что для двух букв были использованы кодовые слова 10 и 110. Определите наименьшую возможную суммарную длину всех шести кодовых слов.

Решение

Условие однозначного декодирования (условие Фано) заключается в том, что однозначное декодирование возможно, только если ни одно кодовое слово не является началом другого кодового слова. Известны кодовые слова 10 и 110, следовательно, для других кодовых слов мы можем использовать только коды, начинающиеся с 0 или 111. Взять в качестве кодового слова 0 нельзя, т.к. в таком случае невозможно будет найти другие кодовые слова, удовлетворяющие условию Фано для оставшихся сообщений. Таким образом, можем использовать 00, 010, 011, 111. Суммарная длина всех кодовых слов – 16.

Ответ: 16

Задача 6

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, решили использовать неравномерный двоичный код, в котором ни одно кодовое слово не является началом другого (это нужно, чтобы код допускал однозначное декодирование). Известно, что для двух букв были использованы кодовые слова 10 и 111.

Определите наименьшую возможную суммарную длину всех пяти кодовых слов.

Решение

Условие однозначного декодирования (условие Фано) заключается в том, что однозначное декодирование возможно, только если ни одно кодовое слово не является началом другого кодового слова. Известны кодовые слова 10 и 111, следовательно, для других кодовых слов мы можем использовать только коды, начинающиеся с 0 или 110. Взять в качестве кодового слова 0 нельзя, т.к. в таком случае невозможно будет найти другие кодовые слова, удовлетворяющие условию Фано для оставшихся сообщений. Таким образом, можем использовать 00, 01, 110. Суммарная длина всех кодовых слов – 12.

Ответ: 12

Задача 7

Определите наименьшую возможную суммарную длину всех пяти кодовых слов.

Решение

Согласно условию задачи, искомый код должен содержать кодовые слова 1 и 010. Значит, узлы, соответствующие эти кодовым словам, должны быть листьями. На основе этих данных построим дерево.

Однако построенное дерево соответствует коду, содержащему только 4 кодовых слова. По условию задачи требуется пять кодовых слов. Для этого следует продолжить построение дерева для одного из узлов: 00 или 011.

Продолжив построение из узла 00, мы получим кодовые слова 000, 001, 010, 011, 1. Суммарная длина всех кодовых слов равна 3 + 3 + 3 + 3 + 1 = 13.

Продолжив построение из узла 0110, мы получим кодовые слова 00, 010, 0011, 0111, 1. Суммарная длина всех кодовых слов равна 2 + 3 + 4 + 4 + 1 = 14.

Следовательно, наименьшая возможная длина всех кодовых слов равна 13.

Ответ: 13

Задача 8

Определите букву, для которой можно сократить длину кодового слова так, чтобы код по-прежнему можно было однозначно декодировать. Коды остальных букв меняться не должны. В ответе укажите букву и её сокращенное кодовое слово без пробелов и запятых. Например, А0.

Решение

Условие однозначного декодирования (условие Фано) заключается в том, что однозначное декодирование возможно, только если ни одно кодовое слово не является началом другого кодового слова. В данной задаче нужно просмотреть кодовые слова для каждой из букв и проверить будет ли выполняться условие Фано, если мы каким-нибудь образом сократим данное кодовое слово. Например, рассмотрим букву А – 01. Если заменить её код на 1, то он будет являться началом кода буквы Б. Если заменить код на 0, то он будет являться началом кодов букв В, Г и Д. Таким образом, при любом сокращении кода буквы А условие Фано нарушается. Проверив подобным образом все буквы, приходим к выводу, что можно сократить букву Б, закодировав её словом 1. В таком случае нарушения условия Фано не произойдёт.

Ответ: б1

Задача 9

Определите букву, для которой можно сократить длину кодового слова так, чтобы код по-прежнему можно было однозначно декодировать. Коды остальных букв меняться не должны.

В ответе укажите букву и её сокращенное кодовое слово без пробелов и запятых. Например, А0.

Решение

Условие однозначного декодирования (условие Фано) заключается в том, что однозначное декодирование возможно, только если ни одно кодовое слово не является началом другого кодового слова. В данной задаче нужно просмотреть кодовые слова для каждой из букв и проверить будет ли выполняться условие Фано, если мы каким-нибудь образом сократим данное кодовое слово. Например, рассмотрим букву А – 01. Если заменить её код на 1, то он будет являться началом кодов букв Б и В. Если заменить код на 0, то он будет являться началом кодов букв Г и Д. Таким образом, при любом сокращении кода буквы А условие Фано нарушается. Проверив подобным образом все буквы, приходим к выводу, что можно сократить букву В, закодировав её словом 11. В таком случае нарушения условия Фано не произойдёт.

Ответ: в11

Задача 10

Решение

Условие однозначного декодирования (условие Фано) заключается в том, что однозначное декодирование возможно, только если ни одно кодовое слово не является началом другого кодового слова. В данной задаче нужно просмотреть кодовые слова для каждой из букв и проверить будет ли выполняться условие Фано, если мы каким-нибудь образом сократим данное кодовое слово. Например, рассмотрим букву А – 01. Если заменить её код на 1, то он будет являться началом кодов букв Б, Г и Д. Если заменить код на 0, то он будет являться началом кода буквы В. Таким образом, при любом сокращении кода буквы А условие Фано нарушается. Проверив подобным образом все буквы, приходим к выводу, что можно сократить букву В, закодировав её словом 00. В таком случае нарушения условия Фано не произойдёт.

Ответ: в00

Задача 11

Решение

Для решения данной задачи построим дерево, у которого из корня и любой вершины выходят по две ветви. Сопоставим каждой левой ветви 0, а каждой правой — 1. Тогда, проходя от вершины к каждому из листьев (узлов, из которых не выходят ветви) и выписывая последовательность нулей и единиц, соответствующих обходу дерева, получим набор кодовых слов, образующих префиксный код (код, в котором ни одно кодовое слово не является началом другого). Префиксный код является однозначно декодируемым. На рисунке представлено дерево, соответствующее заданному коду.

При сокращении кодового слова в дереве нужно заменить один из полученных листьев узлом более высокого уровня. Такая возможность есть только для кодового слова буквы Г. Вместо листа 100 можно взять узел более высокого уровня 10.

В этом случае полученный код: А — 00, Б — 01, В — 110, Г — 10, Д — 111 — будет префиксным и однозначно декодируемым.

Ответ: г10

Задача 12

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный двоичный код, допускающий однозначное декодирование. Для букв А, Б, В и Г используются следующие кодовые слова: А − 10, Б − 11, В − 000, Г − 001. Укажите, каким кодовым словом может быть закодирована буква Д, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение

Условие однозначного декодирования (условие Фано) заключается в том, что однозначное декодирование возможно, только если ни одно кодовое слово не является началом другого кодового слова. Известны кодовые слова 10, 11, 000, 001, следовательно, для других кодовых слов мы можем использовать только коды, начинающиеся с 01. Слово 01 можно использовать в качестве кодового, т.к. условие Фано для него выполняется. Это кодовое слово является минимальным, т.к. любой код меньший длины в данном случае не будет удовлетворять условию Фано.

Ответ: 01

Задача 13

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный двоичный код, допускающий однозначное декодирование. Для букв А, Б, В и Г используются следующие кодовые слова: А − 00, Б − 011, В − 010, Г − 10. Укажите, каким кодовым словом может быть закодирована буква Д, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение

Условие однозначного декодирования (условие Фано) заключается в том, что однозначное декодирование возможно, только если ни одно кодовое слово не является началом другого кодового слова. Известны кодовые слова 00, 011, 010, 10, следовательно, для других кодовых слов мы можем использовать только коды, начинающиеся с 11. Слово 11 можно использовать в качестве кодового, т.к. условие Фано для него выполняется. Это кодовое слово является минимальным, т.к. любой код меньший длины в данном случае не будет удовлетворять условию Фано.

Ответ: 11

Задача 14

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный двоичный код, допускающий однозначное декодирование. Для букв А, Б, В и Г используются следующие кодовые слова: А − 000, Б − 001, В − 010, Г − 011. Укажите, каким кодовым словом может быть закодирована буква Д, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение

Условие однозначного декодирования (условие Фано) заключается в том, что однозначное декодирование возможно, только если ни одно кодовое слово не является началом другого кодового слова. Известны кодовые слова 000, 001, 010, 011, следовательно, для других кодовых слов мы можем использовать только коды, начинающиеся с 1. Слово 1 можно использовать в качестве кодового, т.к. условие Фано для него выполняется.

Ответ: 1

Задача 15

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Известно, что для двух букв были использованы кодовые слова 00 и 10. Определите наименьшую возможную суммарную длину всех кодовых слов.

Задача 16

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы А использовали кодовое слово 1, для буквы Б — кодовое слово 01. Какова наименьшая возможная сумма длин всех шести кодовых слов?

Примечание: Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки кодированных сообщений.

Задача 17

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы А использовали кодовое слово 100, для буквы Б — кодовое слово 01. Укажите наименьшую сумму длин кодовых слов для букв В, Г, Д и Е, при котором код будет допускать однозначное декодирование.

Примечание: Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки кодированных сообщений.

Описание презентации по отдельным слайдам:

1 слайд

ЕГЭ-2022
Разбор задания 4 Информатика
Кодирование и декодирование информации
2 слайд

Введение
В данном уроке мы рассмотрим такие понятия как «Условие Фано» и «Префиксный код» , научимся строить бинарные деревья, а так же рассмотрим разные типы задач на тему «Кодирование и декодирование информации».
3 слайд

Теория
Условие Фано и Префиксный код
4 слайд

Условие Фано
Прямое условие Фано.
Неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с началом (префиксом) какого-либо другого, более длинного кода.
Такой код называют «префиксным».
5 слайд

Условие Фано
Обратное условие Фано.
Неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с окончанием (постфиксом) какоголибо другого, более длинного кода.
Такой код называют «постфиксным».
6 слайд

Префиксный код
Префиксный код— код со словом переменной длины, имеющий такое свойство (выполнение условия Фано): если в код входит слово a, то для любой непустой строки b слова ab в коде не существует.

Например, код, состоящий из слов 0, 10 и 11, является префиксным, и сообщение 01001101110 можно разбить на слова единственным образом:
0 10 0 11 0 11 10
Код, состоящий из слов 0, 10, 11 и 100, префиксным не является, и то же сообщение можно трактовать несколькими способами.
0 10 0 11 0 11 10
0 100 11 0 11 10
7 слайд

Бинарное дерево
Бинарное дерево— это иерархическая структура данных, в которой каждый узел имеет значение и ссылки на левого и правого потомка. Узел, находящийся на самом верхнем уровне называется корнем. Узлы, не имеющие потомков называются листьями.
8 слайд

Бинарное дерево. Термины
Узел (вершина) — это каждый элемент бинарного дерева;
Ветви — связи между узлами;
Глубина (высота) — наибольший уровень какого-нибудь элемента;
Лист (терминальный узел) — термин применяется, если элемент не имеет потомков;
Внутренние узлы — узлы ветвления;
Степень внутреннего узла — число его потомков (наибольшая степень всех существующих узлов — это степень всего бинарного дерева);
Длина пути к x — количество ветвей, которые необходимо пройти от корня до текущего узла x. Длина пути самого корня равна нулю, а узел на уровне i обладает длиной пути, которая равна i.
9 слайд

Построение Бинарного дерева
Задача: Необходимо закодировать буква А, Б, В, Г, Д так что бы полученный код удовлетворял Условию Фано.
Нарисуем корень нашего дерева из которого будут расти ветви.
10 слайд

Построение Бинарного дерева
Задача: Необходимо закодировать буква А, Б, В, Г, Д так что бы полученный код удовлетворял Условию Фано.

Вырастим две ветки
* Из одного корня могу выходить только две ветки
11 слайд

Построение Бинарного дерева
Задача: Необходимо закодировать буква А, Б, В, Г, Д так что бы полученный код удовлетворял Условию Фано.
Пронумеруем ветки двоичным кодом слева → направо
0
1
12 слайд

Построение Бинарного дерева
Задача: Необходимо закодировать буква А, Б, В, Г, Д так что бы полученный код удовлетворял Условию Фано.
0
1
Вырастим два листика.
В дереве появилось два места для двух букв.
13 слайд

Построение Бинарного дерева
Задача: Необходимо закодировать буква А, Б, В, Г, Д так что бы полученный код удовлетворял Условию Фано.
0
1
Как мы видим место больше нет что бы добавить листик дерева.
В этом случаем листик превращаем в узел и растим ещё две ветки.
14 слайд

Построение Бинарного дерева
Задача: Необходимо закодировать буква А, Б, В, Г, Д так что бы полученный код удовлетворял Условию Фано.
Левый лист превращён в узел и теперь он имеет двух потомков
0
1
15 слайд

Построение Бинарного дерева
Задача: Необходимо закодировать буква А, Б, В, Г, Д так что бы полученный код удовлетворял Условию Фано.
И пронумерую ветки двоичным кодом
слева → направо
0
1
0
1
16 слайд

Построение Бинарного дерева
Задача: Необходимо закодировать буква А, Б, В, Г, Д так что бы полученный код удовлетворял Условию Фано.
0
1
0
1
Теперь есть место для трёх букв.
17 слайд

Построение Бинарного дерева
Задача: Необходимо закодировать буква А, Б, В, Г, Д так что бы полученный код удовлетворял Условию Фано.
0
1
0
1
Это корень сюда букву ставить нельзя
Это узел сюда букву ставить нельзя
Это листик сюда можно поставить букву
18 слайд

Построение Бинарного дерева
Задача: Необходимо закодировать буква А, Б, В, Г, Д так что бы полученный код удовлетворял Условию Фано.
0
1
0
1
Места всё ещё не хватает
Правый лист превращу в узел и выращу две ветки.
19 слайд

Построение Бинарного дерева
Задача: Необходимо закодировать буква А, Б, В, Г, Д так что бы полученный код удовлетворял Условию Фано.
0
1
0
1
Пронумеруем ветки двоичным кодом
слева → направо
0
1
20 слайд

Построение Бинарного дерева
Задача: Необходимо закодировать буква А, Б, В, Г, Д так что бы полученный код удовлетворял Условию Фано.
0
1
0
1
Выращу два листа
21 слайд

Построение Бинарного дерева
Задача: Необходимо закодировать буква А, Б, В, Г, Д так что бы полученный код удовлетворял Условию Фано.
0
1
0
1
Пронумерую двоичным кодом ветки
слева → направо
0
1
22 слайд

Построение Бинарного дерева
Задача: Необходимо закодировать буква А, Б, В, Г, Д так что бы полученный код удовлетворял Условию Фано.
Место хватает для 4 букв
0
1
0
1
0
1
23 слайд

Построение Бинарного дерева
Задача: Необходимо закодировать буква А, Б, В, Г, Д так что бы полученный код удовлетворял Условию Фано.
0
1
0
1
0
1
Места всё ещё не хватает
Правый лист превращу в узел и выращу две ветки
24 слайд

Построение Бинарного дерева
Задача: Необходимо закодировать буква А, Б, В, Г, Д так что бы полученный код удовлетворял Условию Фано.
0
1
0
1
0
1
Пронумерую двоичным кодом ветки
слева → направо
0
1
25 слайд

Построение Бинарного дерева
Задача: Необходимо закодировать буква А, Б, В, Г, Д так что бы полученный код удовлетворял Условию Фано.
0
1
0
1
0
1
0
Место есть для пяти букв
1
26 слайд

Построение Бинарного дерева
Задача: Необходимо закодировать буква А, Б, В, Г, Д так что бы полученный код удовлетворял Условию Фано.
В
Г
Д
0
1
0
1
0
1
А
Б
0
Заполню листья буквами
А, Б, В, Г, Д
1
27 слайд

Построение Бинарного дерева
Задача: Необходимо закодировать буква А, Б, В, Г, Д так что бы полученный код удовлетворял Условию Фано.
Бинарное дерево закончено
В
Г
Д
0
1
0
1
0
1
А
Б
0
1
28 слайд

Найти Код символа с помощью бинарного дерева
29 слайд

Код символа по бинарному дереву
Для того что бы найти код символа посмотрим на наш корень
В
Г
Д
0
1
0
1
0
1
А
Б
0
1
30 слайд

Код символа по бинарному дереву
В
Г
Д
0
1
0
1
0
1
А
Б
0
1
Что бы добрать до листика А от корня – необходимо двигаться по левой стороне.
31 слайд

Код символа по бинарному дереву
В
Г
Д
0
1
0
1
0
1
А
Б
0
1
От корня спускаюсь в левый узел.
Запишу в таблицу нумерацию ветки от корня к узлу.
32 слайд

Код символа по бинарному дереву
В
Г
Д
0
1
0
1
0
1
А
Б
0
1
От узла спускаюсь ниже на 1 уровень в левый узел.
Запишу в таблицу нумерацию ветки от узла к узлу.
33 слайд

Код символа по бинарному дереву
В
Г
Д
0
1
0
1
0
1
А
Б
0
1
От узла спускаюсь в листик А.
Запишу в таблицу нумерацию ветки от узла к листику А.
34 слайд

Код символа по бинарному дереву
В
Г
Д
0
1
0
1
0
1
А
Б
0
1
Получился маршрут от корня до листика А которые равен 000.
35 слайд

В
Г
Д
0
1
0
1
0
1
А
Б
0
1
Код символа по бинарному дереву
Аналогично найду код символа Б.
36 слайд

В
Г
Д
0
1
0
1
0
1
А
Б
0
1
Код символа по бинарному дереву
37 слайд

В
Г
Д
0
1
0
1
0
1
А
Б
0
1
Код символа по бинарному дереву
38 слайд

В
Г
Д
0
1
0
1
0
1
А
Б
0
1
Код символа по бинарному дереву
39 слайд

В
Г
Д
0
1
0
1
0
1
А
Б
0
1
Код символа по бинарному дереву
Код для буквы В
40 слайд

В
Г
Д
0
1
0
1
0
1
А
Б
0
1
Код символа по бинарному дереву
Код для буквы Г
41 слайд

В
Г
Д
0
1
0
1
0
1
А
Б
0
1
Код символа по бинарному дереву
Код для буквы Г
42 слайд

Код символа по бинарному дереву
43 слайд

Сокращение двоичного кода
Тип задачи №1
44 слайд

Задача 1
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность.
Вот этот код: А – 10; Б – 11; В – 000; Г – 001; Д – 010.
Как можно сократить длину кодового слова для буквы Д так, чтобы код по-прежнему можно было декодировать однозначно?
Коды остальных букв меняться не должны. Если есть несколько вариантов, выберите кодовое слово с минимальным значением.
45 слайд

Задача 1
Код: А – 10; Б – 11; В – 000; Г – 001; Д – 010.

Построим бинарное дерево.
Коды листов известны по условию задачи
46 слайд

Задача 1
Код:
А – 10;
Б – 11;
В – 000;
Г – 001;
Д – 010.

А
Б
0
1
0
1
0
1
В
Г
0
1
Д
0
1
47 слайд

Задача 1
Как можно сократить длину кодового слова для буквы Д так, чтобы код по-прежнему можно было декодировать однозначно?
А
Б
0
1
0
1
0
1
В
Г
0
1
Д
0
1
Как видим у этого узла два листочка.
Левый листок Д, а правый листок пустой.
48 слайд

Задача 1
Как можно сократить длину кодового слова для буквы Д так, чтобы код по-прежнему можно было декодировать однозначно?
А
Б
0
1
0
1
0
1
В
Г
0
1
Д
0
1
Как видим у этого узла два листочка.
Левый листок Д, а правый листок пустой.
49 слайд

Задача 1
Как можно сократить длину кодового слова для буквы Д так, чтобы код по-прежнему можно было декодировать однозначно?
А
Б
0
1
0
1
0
1
В
Г
0
1
Д
0
1

Пустой листочек мы не используем в кодирование сообщений, следовательно его можно отбросить
50 слайд

Задача 1
Как можно сократить длину кодового слова для буквы Д так, чтобы код по-прежнему можно было декодировать однозначно?
А
Б
0
1
0
1
0
1
В
Г
0
1
Д
0
1
51 слайд

Задача 1
Как можно сократить длину кодового слова для буквы Д так, чтобы код по-прежнему можно было декодировать однозначно?
А
Б
0
1
0
1
0
1
В
Г
0
1
Д
После порезав ветки узел превратился в листок
52 слайд

Задача 1
Как можно сократить длину кодового слова для буквы Д так, чтобы код по-прежнему можно было декодировать однозначно?
А
Б
0
1
0
1
0
1
В
Г
0
1
Д
После порезав ветки узел превратился в листок (одно свободное место)
53 слайд

Задача 1
Как можно сократить длину кодового слова для буквы Д так, чтобы код по-прежнему можно было декодировать однозначно?
А
Б
0
1
0
1
0
1
В
Г
0
1
Д
Перемещаем опавшую Д в пустой листок
54 слайд

Задача 1
Как можно сократить длину кодового слова для буквы Д так, чтобы код по-прежнему можно было декодировать однозначно?
Д
А
Б
0
1
0
1
0
1
В
Г
0
1
Теперь
код буквы Д равен 01
55 слайд

Ответ
Длину кодового слова для буквы Д
можно сократить до 01
56 слайд

Выбор кода для одной буквы
Тип задачи №2
57 слайд

Задача 2
По каналу связи передаются сообщения, содержащие только шесть букв: У, Р, А, Е, Г, Э; для передачи используется двоичный код, удовлетворяющий условию Фано.
Буквы Е, Р, А, Г, У имеют коды 01, 000, 100, 101, 110 соответственно. Укажите код наименьшей длины для буквы Э.
Если в качестве кода может быть использовано несколько кодов одинаковой длины, выбрать тот, числовое значение которого меньше.
58 слайд

Задача 2
Буквы Е, Р, А, Г, У имеют коды 01, 000, 100, 101, 110 соответственно.
Е
0
1
0
1
0
1
Р
0
1
А
Г
0
1
У
1
0
59 слайд

Задача 2
Укажите код наименьшей длины для буквы Э.
Е
0
1
0
1
0
1
Р
Э
0
1
А
Г
0
1
У
Э
1
0
Букву Э можно поставить в один из двух листочков
001
111
60 слайд

Задача 2
Сравним два получившихся числа

Для удобства можно перевести в десятичную систему счисления
001 2 = 1 10
111 2 = 7 10
61 слайд

Задача 2
Сравним два получившихся числа
62 слайд

Задача 2
Сравним два получившихся числа

1 меньше 7, следовательно 001 меньше 111
Ответ: код наименьшей длины для буквы Э — 001
63 слайд

Помехоустойчивые коды
Тип задачи №3
64 слайд

Задача 3
По каналу связи с помощью равномерного двоичного кода передаются сообщения, содержащие только 4 буквы: А, Б, В, Г.
Каждой букве соответствует своё кодовое слово, при этом для набора кодовых слов выполнено такое свойство: любые два слова из набора отличаются не менее чем в трёх позициях. Это свойство важно для расшифровки сообщений при наличии помех.
Для кодирования букв Б, В, Г используются 5-битовые кодовые слова: Б – 00001, В – 01111, Г – 10110.
5-битовый код для буквы А начинается с 1 и заканчивается на 0. Определите кодовое слово для буквы А.
65 слайд

Задача 3
Пример
0 0 0 0 1
кодовое слово
позиция
66 слайд

Задача 3
Сравним позиции кодовых слов Б, В, Г с позициями кодового слова А
67 слайд

Задача 3
Сравним первые позиции
кодовых слов А и Б
1 0
1 = 0 ?
68 слайд

Задача 3
Сравним первые позиции кодовых слов А и В
1 0
1 = 0 ?
69 слайд

Задача 3
Сравним первые позиции кодовых слов А и Г
1 1
1 = 1 ?
70 слайд

Задача 3
Теперь сравниваем последние позиции
71 слайд

Задача 3
0
1
1
0
?
А=Б
0=1
?
А=В
0=1
?
А=Г
0=0
73 слайд

Задача 3
У кодового слова буква Б сошлись две позиции.
По условию: любые два слова из набора отличаются не менее чем в трёх позициях.
У нас уже есть две одинаковые позиции значит остальные три должны быть различные.
74 слайд

Задача 3
У кодового слова буква Б сошлись две позиции.
По условию: любые два слова из набора отличаются не менее чем в трёх позициях.
У нас уже есть две одинаковые позиции значит остальные три должны быть различные.
75 слайд

Задача 3
Если вторая позиция у кодового слова Г равна 0, следовательно вторая позиция у кодового слова А равна НЕ Г (¬ г).
¬0 (НЕ 0)
76 слайд

Задача 3
Если вторая позиция у кодового слова Г равна 0, следовательно вторая позиция у кодового слова А равна НЕ Г (¬ г).
¬0 (НЕ 0)
77 слайд

Задача 3
¬1 (НЕ 1)
78 слайд

Задача 3
¬1 (НЕ 1)
79 слайд

Задача 3
Ответ: кодовое слово для буквы А равно 11000
80 слайд

Выбор кодов для нескольких букв
Тип задачи №4
81 слайд

Задача 4
Для кодирования некоторой последовательности, состоящей из букв П, О, Е, Х, А, Л, И, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано.
Для букв О, Е, А, И использовали соответственно кодовые слова 01, 110, 1010, 001.
Найдите наименьшую возможную суммарную длину всех кодовых слов.
82 слайд

Задача 4
Для букв О, Е, А, И использовали соответственно кодовые слова 01, 110, 1010, 001.

О
0
1
0
1
0
1
И
0
1
Е
0
1
0
1
А
0
1
83 слайд

Задача 4
Некоторая последовательность, состоит из букв П, О, Е, Х, А, Л, И
О
0
1
0
1
0
1
П
И
0
1
Е
Л
0
1
Х
0
1
А
0
1
Для букв П Х Л нет кода.
Добавим его самостоятельно.
84 слайд

Задача 4
Некоторая последовательность, состоит из букв П, О, Е, Х, А, Л, И
О
0
1
0
1
0
1
П
И
0
1
Е
Л
0
1
Х
0
1
А
0
1
Оставшийся листик 1011 мы не берём т.к в нём самое большое количество знаков чем в остальных
85 слайд

Задача 4
Допишем оставшиеся коды.
86 слайд

Задача 4
Подсчитаю количество знаков
87 слайд

Задача 4
П+О+Е+Х+А+Л+И = 3+2+3+3+4+3+3 = 21
Ответ: наименьшая возможная суммарная длина всех кодовых слов равна 21
88 слайд

Примечание
Предположим для буквы Л выбрали код 1011 вместо кода 111, тогда
О
0
1
0
1
0
1
П
И
0
1
Е
0
1
Х
0
1
А
Л
0
1
П+О+Е+Х+А+Л+И = 3+2+3+3+4+4+3 = 22
89 слайд

Декодирование
Тип задачи №5
90 слайд

Задача 5
Заглавные буквы русского алфавита закодированы неравномерным двоичным кодом, в котором никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений.
Известно, что все кодовые слова содержат не меньше двух и не больше трёх двоичных знаков, а слову КАПОТ соответствует код 11000111110011. Какой код соответствует слову ТОК?
91 слайд

Задача 5
Рассмотрим внимательно код 11000111110011
С первого взгляда можно сказать что количество 1 больше чем количество 0, из чего можно сделать вывод что левая ветка будет иметь минимум третий уровень, т.к. одна буква шифруется тремя знаками.
Набрасываем бинарное дерево
1
1
0
1
0
0
92 слайд

Задача 5
Про просмотре кода
1 1 0 0 0 1 1 1 1 1 0 0 1 1
В глаза бросается большое скопление 1 в середине.
1
1
0
1
0
0
93 слайд

Задача 5
Предположим что код 111 — П
1 1 0 0 0 1 1 1 1 1 0 0 1 1
Тогда
1 1 0 0 0 1 .1 1 1 .1 0 0 1 1

* Если 111 листок, следовательно 11 и 1 это узел, в которых не может быть букв.

1
1
П
0
1
0
0
94 слайд

Задача 5
От 111 справа на лево распределим ещё две буквы под два символа
1 1 0 . 0 0 1 . 1 1 1 . 1 0 0 1 1
Поскольку кодовое слово начинается на К,
то 110 – К, следовательно 001 – А.
Дорисовываем дерево.
*Если 110 или 001 листок,
следовательно 11 и 1 это узел, в которых не может быть букв.

1
1
К
П
0
1
0
0
0
1
А
0
1
95 слайд

Задача 5
Осталось 5 символов которые можно разложить на 100 и 11, или на 10 и 011
1 1 0 . 0 0 1 . 1 1 1 . 1 0 0 1 1
Листок 100 существует А вот листочка 11 быть не может. Мы уже сказали что это узел, а в узле не может быть буквы. Это вариант вычёркиваем.
1
1
К
П
0
1
0
0
0
1
А
0
1
0
1
96 слайд

0
Задача 5
Остался вариант 10 и 011
1 1 0 . 0 0 1 . 1 1 1 . 1 0 . 0 1 1
Подставлю буквы соответственно О и Т.
О
1
1
К
П
0
1
0
0
1
А
0
1
0
1
Т
97 слайд

Задача 5
Запишем результат в таблицу
98 слайд

Задача 5
С помощью таблицы закодируем слово ТОК

Ответ: слову ТОК соответствует код 01110110
99 слайд

Список литературы
100 слайд

Список литературы
1. Учебник для 11 класса : в 2 ч. Ч. 1 / К. Ю. Поляков, Е. А. Ере- мин. — М. : БИНОМ. Лаборатория знаний, 2020
2. Богомолова О.Б., Усенков Д.Ю. Фано и его «коллеги»: растим дерево. // компьютерные инструменты в школе – 2017 – Выпуск №2 — С. 26-31. Режим доступа: http://ipo.spb.ru/journal/index.php?article/1873/, свободный.
3. Задачи для подготовки ЕГЭ https://kpolyakov.spb.ru/school/ege/generate.htm

Краткое описание документа:

ЕГЭ-2022 информатикаРазбор задания 4 — Кодирование и декодирование информацииВ материале представлены теория, пять видов задач и список одновной литературы, необходимые для решения задания 4 ЕГЭ информатика.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 154 652 материала в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Материал подходит для УМК

Другие материалы

29.10.2021
92
0

Вам будут интересны эти курсы:

Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
Курс повышения квалификации «Облачные технологии в образовании»
Курс повышения квалификации «Развитие информационно-коммуникационных компетенций учителя в процессе внедрения ФГОС: работа в Московской электронной школе»
Курс профессиональной переподготовки «Информационные технологии в профессиональной деятельности: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Введение в программирование на языке С (СИ)»
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
Курс повышения квалификации «Современные тенденции цифровизации образования»
Курс повышения квалификации «Современные языки программирования интегрированной оболочки Microsoft Visual Studio C# NET., C++. NET, VB.NET. с использованием структурного и объектно-ориентированного методов разработки корпоративных систем»
Курс повышения квалификации «Применение интерактивных образовательных платформ на примере платформы Moodle»

Источник

Кодирование информации

Кодирование и расшифровка сообщений

Е4.41 Какое количество двоичных знаков потребуется для кодирования слова КАЗАЧКА

Е4.40 Определите наименьшую возможную сумму длин всех семи кодовых слов

Е4.39 Какую наименьшую длину может иметь код слова ВОДОПРОВОД

Е4.38 слово КАШКА закодировали с помощью последовательности 1110110011101

Е4.37 Какой код соответствует слову СУП?

Е4.36 а слову БАРАН соответствует код 10011111011010

Е4.35 Какой код соответствует слову ШОК

Е4.34 Какое наименьшее количество двоичных знаков может содержать код слова ПАНАМА?

Е4.33 наименьшую возможную длину закодированной последовательности для слова СУСТАВ

Е4.32 Для букв А, Б, В, Г использовали соответственно кодовые слова 000, 001, 010, 011

Все статьи раздела

Задачи для практики

Задача 1

Решение

Задача 2

Решение

Задача 3

Решение

Задача 4

Решение

Задача 5

Решение

Задача 6

Решение

Задача 7

Решение

Задача 8

Решение

Задача 9

Решение

Задача 10

Решение

Задача 11

Решение

Задача 12

Решение

Задача 13

Решение

Задача 14

Решение

Задача 15

Задача 16

Задача 17

Рекомендуемые курсы подготовки

Описание презентации по отдельным слайдам:

Краткое описание документа:

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

Материал подходит для УМК

Другие материалы

Вам будут интересны эти курсы: