Номер 12 егэ математика профиль 2022

а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

а)  Решите уравнение:

б)  Определите, какие из его корней принадлежат отрезку

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

а)  Решите уравнение

б)  Укажите корни уравнения, принадлежащие отрезку

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

а) $11cos 2x=7sin (x-{π} / {2})-9$,

$11(2cos^2 x-1)=-7cos x-9$,

$22cos^2 x -11+7cos x +9=0$,

$22cos^2 x+7cos x -2=0$.

Обозначим $cos x=t$, $|t|⩽1$.

Тогда уравнение примет вид: $22t^2+7t-2=0$.

Решим его. $22t^2+7t-2=0$,

$D=49+2⋅ 4⋅ 22=225$. $t_{1,2}={-7±15} / {44}$,

$t_1=-{1} / {2}$, $t_2={8} / {44}={2} / {11}$.

$1$. $cos x=-{1} / {2}$, $x=±(π-{π} / {3})+2π n$;

$x=± {2π} / {3}+2π n$, $n∈ Z$.

$2$. $cos x={2} / {11}$, $x=± arccos {2} / {11}+2π k$, $k∈ Z$.

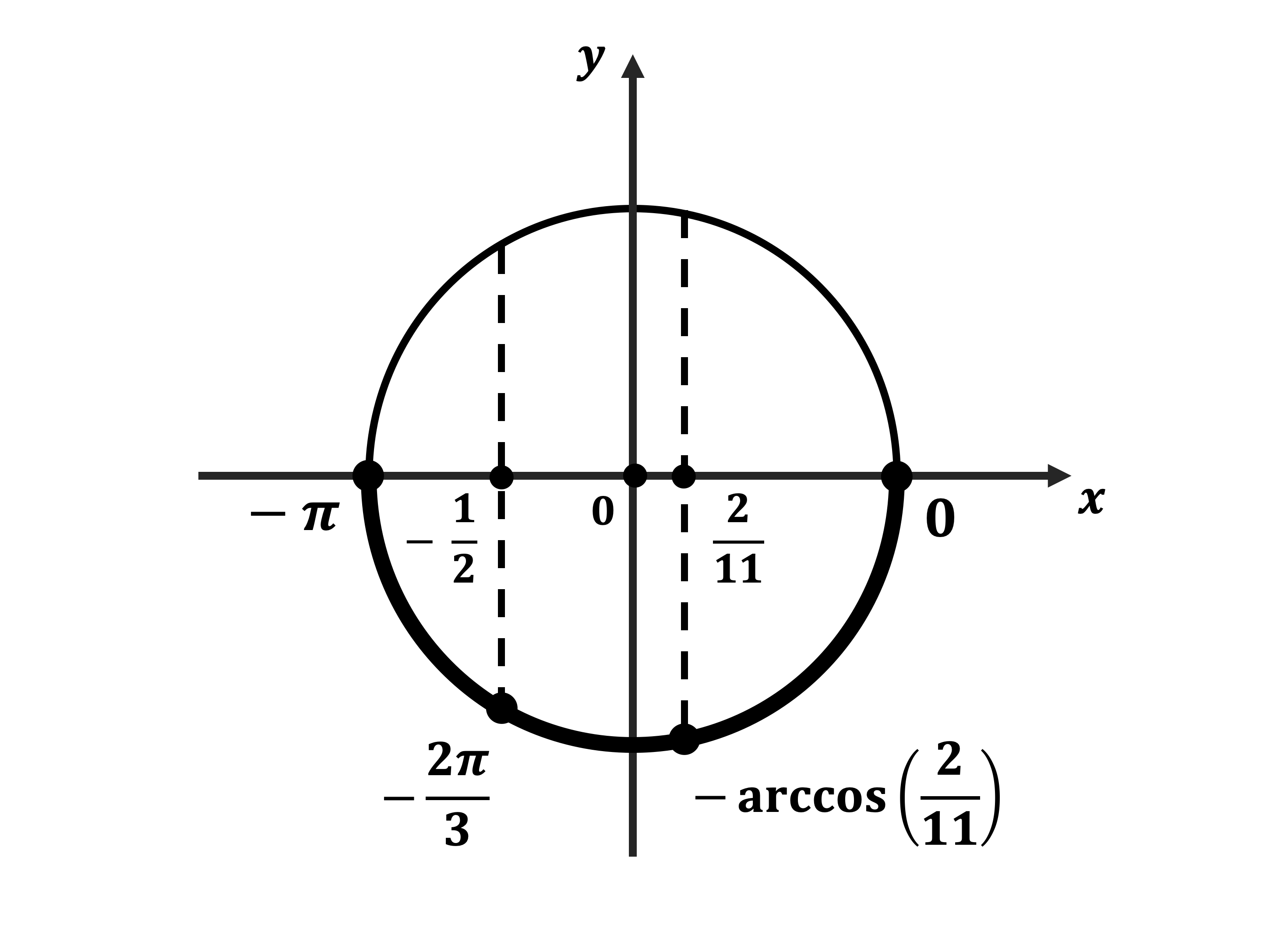
б) Найдём корни этого уравнения, принадлежащие промежутку $[-π;0]$.

$x_1=-π+{π} / {3}=-{2π} / {3}$

$x_2=-arccos {2} / {11}$.

а) Преобразуем уравнение, согласно формуле приведения:

$cos(x+{π}/{2})=-sinx,$

$2sin^2x + 7sinx -4 = 0$

Обозначим $sin x = t, −1 ≤ t ≤ 1$, получим

$2t^2 + 7t -4 = 0.$

$t_1 = {−7 − 9}/{2·2} = −4$ — не удовлетворяет условию $−1 ≤ t ≤ 1. $

$t_2 = {−7 + 9}/{2·2} = {1}/{2}$.

Вернёмся к исходной переменной:

$sinx ={1}/{2}$,

$x = {π}/{6} + 2πn, n ∈ Z$

$x = {5π}/{6} + 2πk, k ∈ Z$

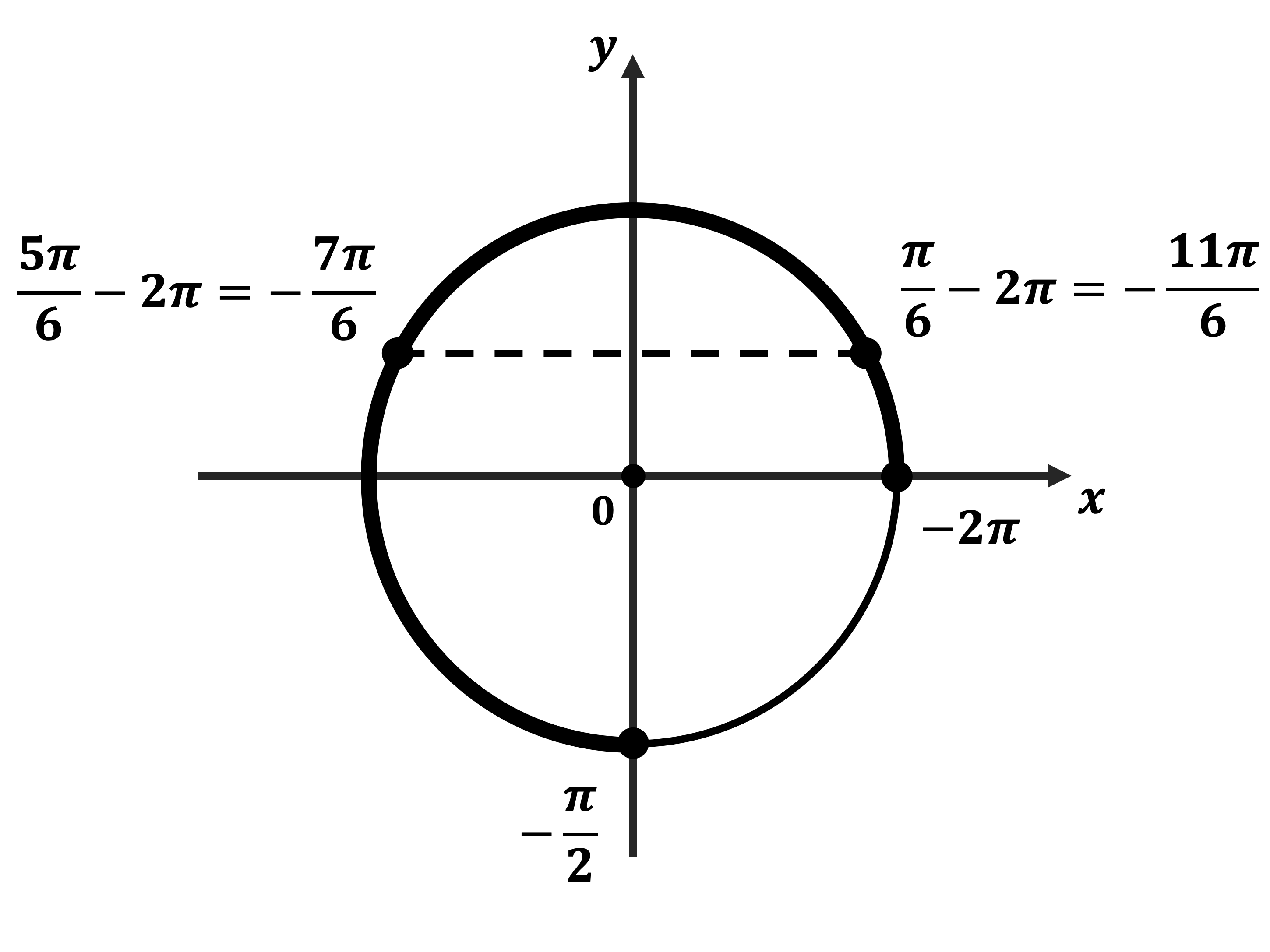
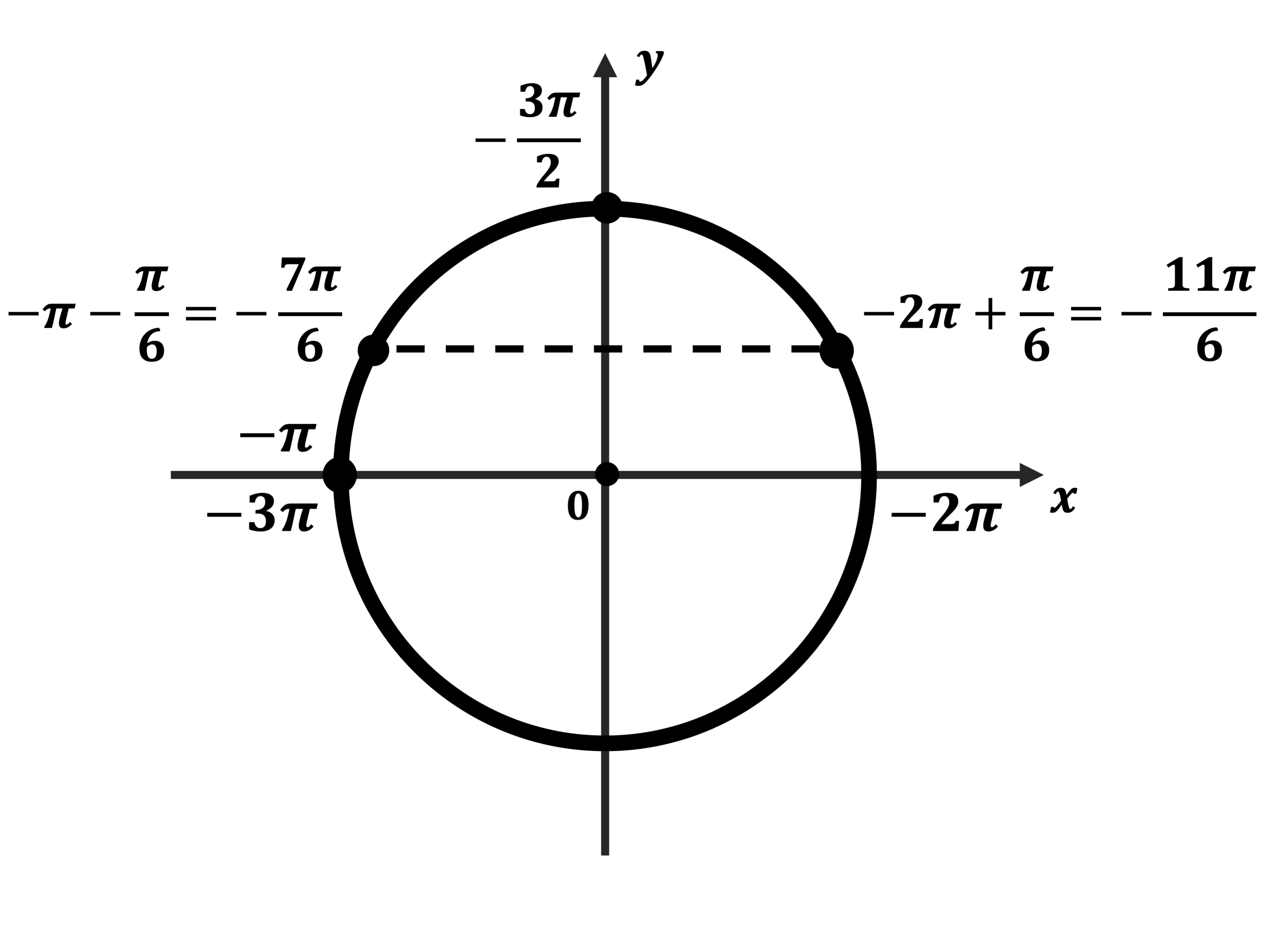
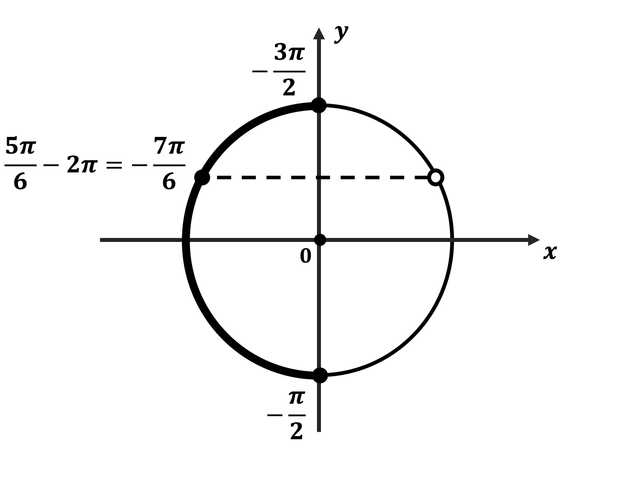
б) Корни, принадлежащие отрезку $[-2π; -{π}/{2}]$, найдём с помощью единичной окружности. Получим: ${π}/{6}-2π=-{11π}/{6}; {5π}/{6}-2π=-{7π}/{6}$.

а) Преобразуем уравнение, согласно формуле приведения:

$sin(x+{3π}/{2})=-cosx,$

$2cos^2x + 5 cos x + 2 = 0$

Обозначим $cos x = t, −1 ≤ t ≤ 1$, получим $2t^2 + 5t + 2 = 0. t_1 = {−5 − 3}/{2·2} = −2$ — не удовлетворяет условию $−1 ≤ t ≤ 1. t_2 = {−5 + 3}/{2· 2} = −{1}/{2}$.

Вернёмся к исходной переменной: $cos x = − {1}/{2}$,

$x = ±(π − {π}/{3}) + 2πn, n ∈ Z , x = ±{2π}/{3} + 2πn, n ∈ Z.$

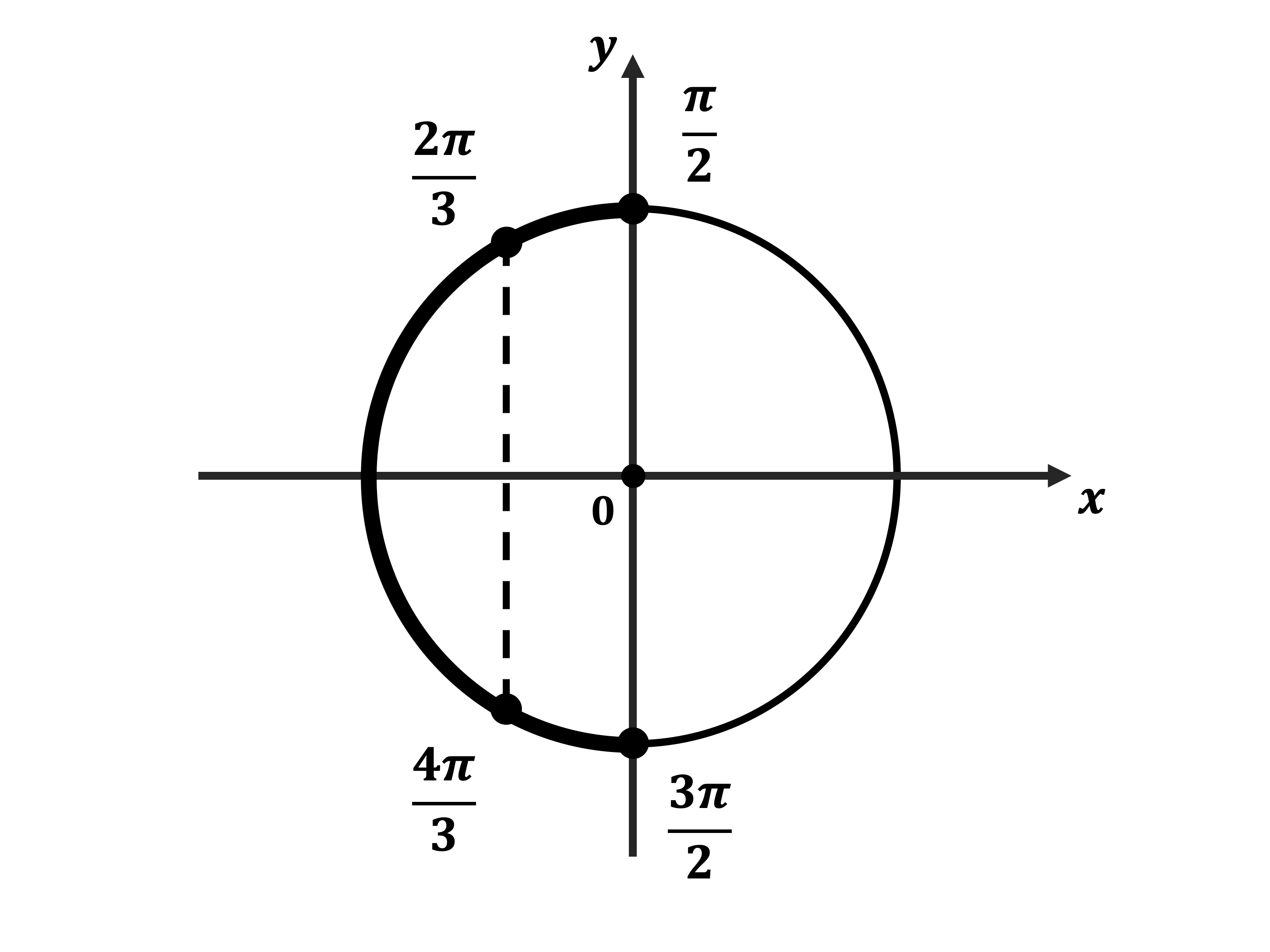
б) Корни, принадлежащие отрезку $[{π}/{2}; {3π}/{2}]$, найдём с помощью единичной окружности. Получим числа ${2π}/{3}; {4π}/{3}$.

а) Преобразуем уравнение:

$−sin x = sin 2x,$

$sinx + 2 sin x cos x = 0,$

$sinx(1 + 2 cos x) = 0,$

$sin x = 0;x = πn, n ∈ Z,$

$cosx = -{1}/{2}; x = ±{2π}/{3} + 2πk, k ∈ Z .,$

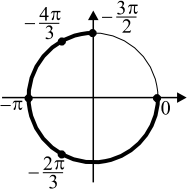
б) Корни, принадлежащие отрезку $[-{3π}/{2};0]$, найдём с помощью единичной окружности. Получим числа $−{4π}/{3}; −π; −{2π}/{3}; 0$.

а) Преобразуем уравнение:

$cos x = − sin 2x,$

$cos x + 2 sin x cos x = 0,$

$cos x(1 + 2 sin x) = 0,$

$cos x = 0;$

$x = (−1)^{k+1}·{π}/{6} + πk, k ∈ Z$

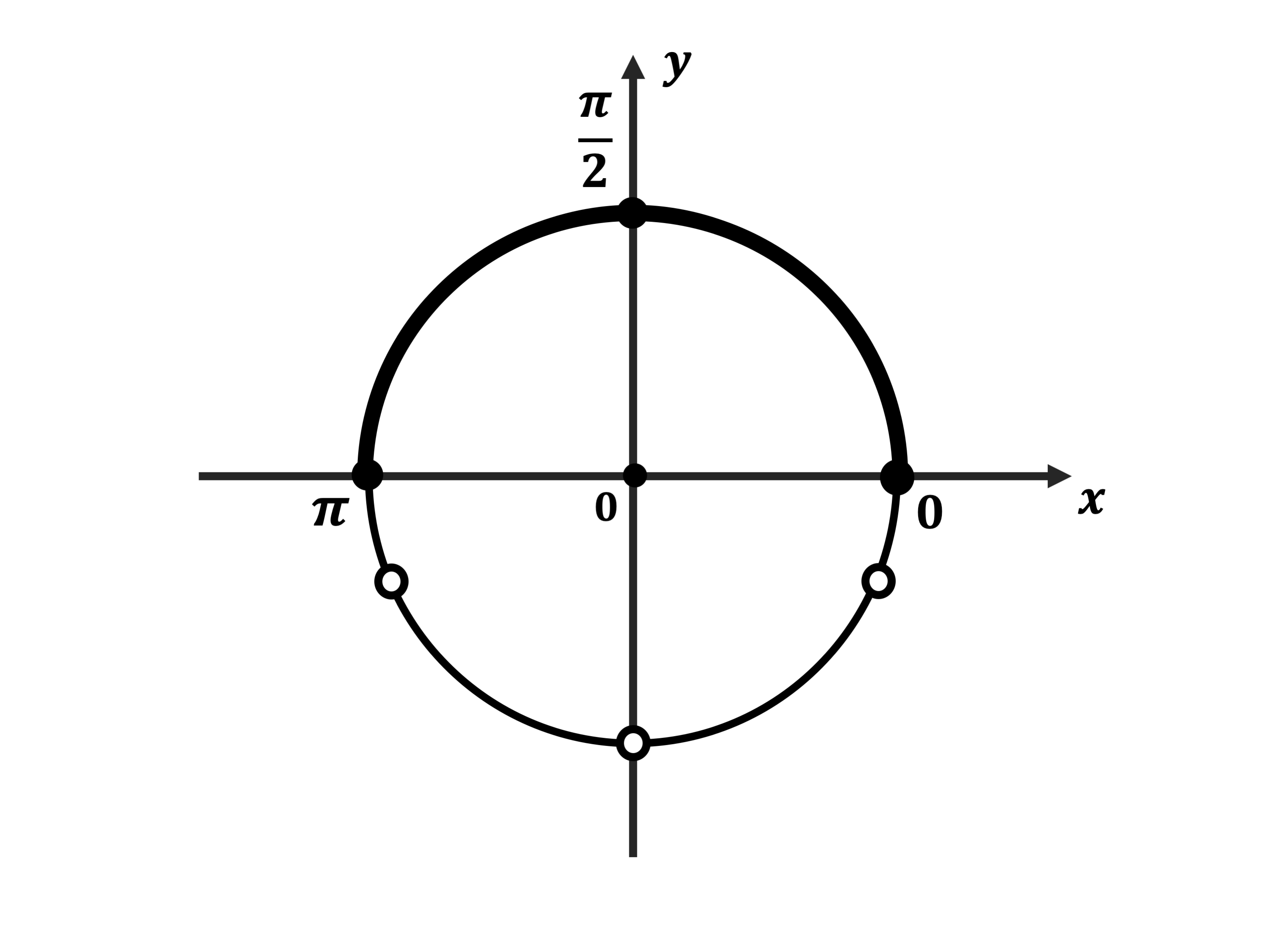
б) Корни, принадлежащие отрезку $[0; π]$, найдём с помощью единичной окружности.

Указанному промежутку принадлежит единственное число ${π}/{2}$.

а) Решим уравнение $sinx(2sinx-1) +√3sinx + sin{4π}/{3} = 0$.

Так как $sin{4π}/{3} = sin(π +{π}/{3}) = − sin{π}/{3} = −{√3}/{2}$, то уравнение примет вид $sin x(2 sin x-1) +√3 sin x-{√3}/{2} = 0$. Отсюда $2 sin x(sin x-{1}/{2})+ √3(sin x-{1}/{2}) = 0; (2sinx+√3)(sin x-{1}/{2}) = 0$.

Тогда $sin x = {1}/{2}; x = (−1)^n{π}/{6} + πn$ или $sin x = −{√3}/{2}; x = (−1)^{n+1}{π}/{3} + πn$, где $n ∈ Z.$

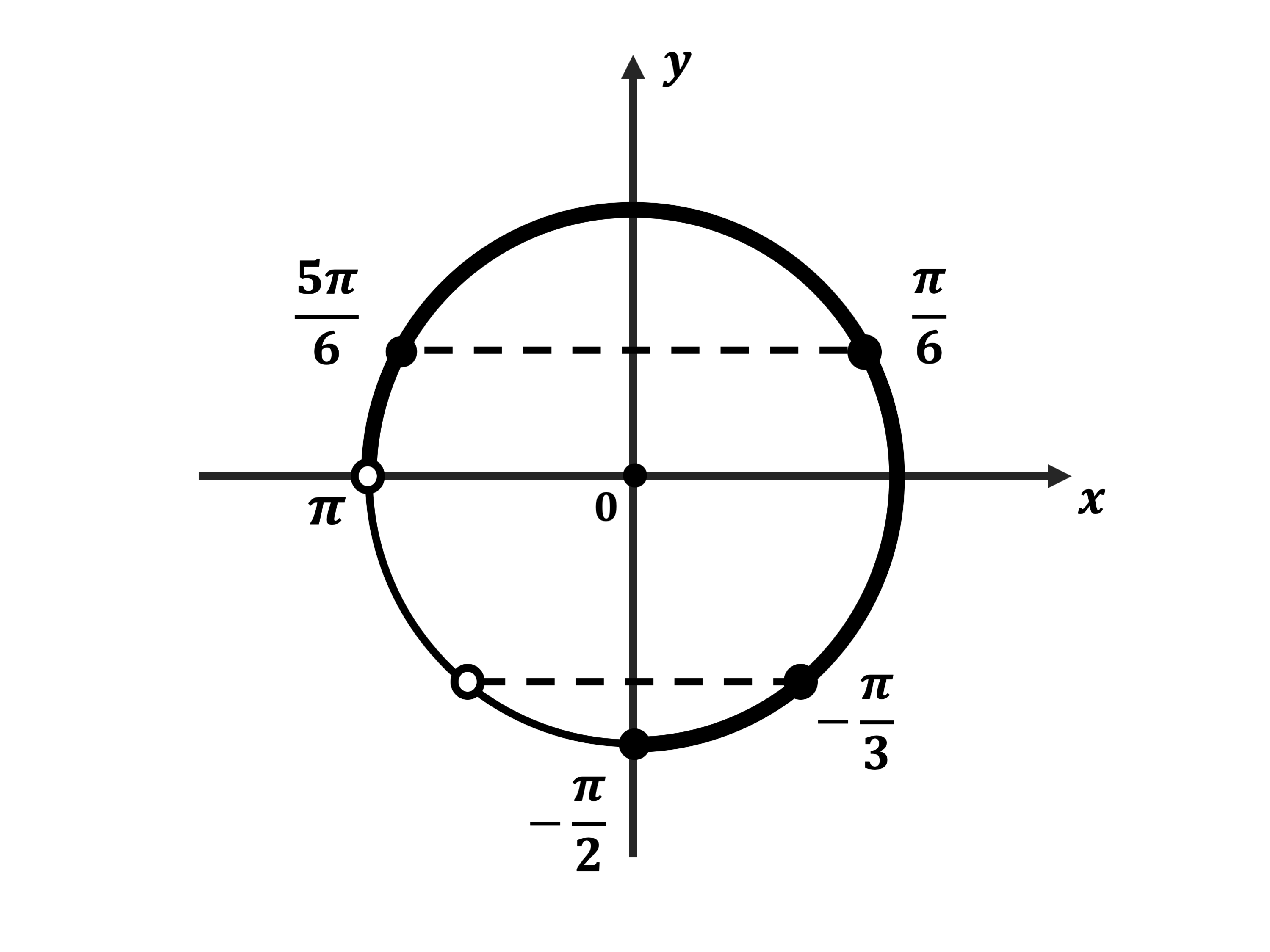
б) Корни, принадлежащие промежутку $[−{π}/{2}; π]$, найдём с помощью числовой окружности: $−{π}/{3}; {π}/{6}; {5π}/{6}$.

a) $4cos^{2}x = 3cos2x+1$,

$4cos^{2}x = 3(2cos^{2}x-1)+1$,

$4cos^{2}x=6cos^{2}x-3+1$,

$cos^{2}x=1, [tablecosx=1; cosx=-1;$ $[tablex=2πn, n ∈ Z; x=π+2πk, k ∈ Z;$ $x=πk, k ∈ Z$

б) Корни, принадлежащие промежутку $[-4π;-{5π}/{4})$, найдем из неравенства $-4π ≤ πk < -{5π}/{4}; k=-4, -3, -2$

$x_1=-4π, x_2=-3π, x_3=-2π$.

a) $cos(2x) + 3sinx-2=0$,

$1 — 2sin^{2}x + 3 sin x -2 = 0$,

$2 sin^{2}x — 3sin x +1 = 0$,

Пусть $sin x = y, |sinx| ≤ 1$, уравнение примет вид

$2y^2 — 3y + 1 = 0$,

$y_{1,2} = {3±√{9-8}}/{4} = {3±1}/{4};$

$ y_1=1, y_2={1}/{2}$.

$sin x = 1, x = {π}/{2}+2πn, n ∈ Z; sinx={1}/{2}, x=(-1)^{k}{π}/{6} + πk, k ∈ Z$.

б) Найдём корни уравнения на отрезке $[-3π;-π]$.

С помощью числовой окружности отберём корни уравнения, принадлежащие $[-3π;-π]$.

Это числа $-{11π}/{6}, -{3π}/{2}, -{7π}/{6}$.

a) $2 cos^{2}x + 19sinx+8=0$,

$2(1 — sin^{2}x) + 19 sin x +8 = 0$,

$-2 sin^{2}x + 19 sin x +10 = 0$,

$2 sin^{2}x — 19 sin x -10 = 0$.

Пусть $sin x = y, |y| ≤ 1$, уравнение примет вид $2y^2 — 19y -10 = 0$, решим его: $y_{1,2} = {19±√{361 + 80}}/{4} = {19±21}/{4}$.

$y_1 = 10$ или $y_2 = -{1}/{2}$. $y_1=10$ не удовлетворяет условию $|y| ≤ 1$. $sin x = -{1}/{2}, x = (-1)^{n+1}{π}/{6} + πn, n ∈ Z$.

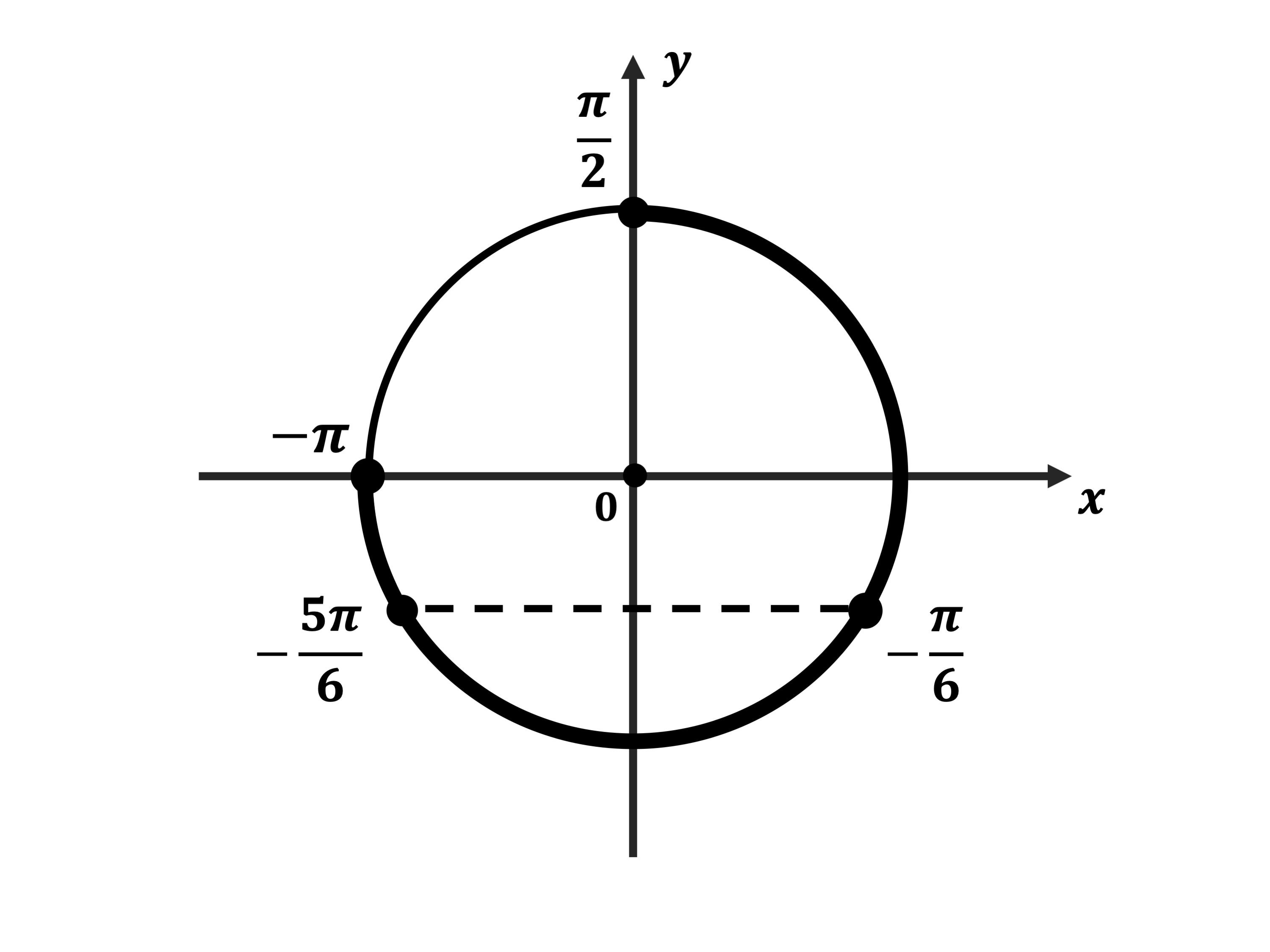
б) Найдём корни уравнения на отрезке $[-π;{π}/{2}]$.

Это числа $-{5π}/{6}$ и $-{π}/{6}$.

a) $8 sin x + 4 cos^{2} x = 7$,

$4(1 — sin^{2}x) + 8 sin x — 7 = 0$,

$-4 sin^{2}x + 8 sin x — 3 = 0$,

$4 sin^{2}x — 8 sin x + 3 = 0$.

Пусть $sin x = t, |t| ≤ 1$, уравнение примет вид $4t^2 — 8t + 3 = 0$, решим его: $t_{1,2} = {8±√{64 — 48}}/{8} = {8±√{16}}/{8} = {8±4}/{8} = 1±{1}/{2}$.

$t_1 = {1}/{2}$ или $t_2 = {3}/{2}$. $t_2$ не удовлетворяет условию $|t| ≤ 1$. $sin x = {1}/{2}, x = (-1)^{n}{π}/{6} + πn, n ∈ Z$.

б) Найдём корни уравнения на отрезке $[-{3π}/{2};-{π}/{2}]$.

Это число ${5π}/{6} — 2π = -{7π}/{6}$.

а) ${{sin2x}/{sin({3π}/{2} + x)} = 1$.

Зная, что $sin2x = 2sinxcosx$ и $sin({3π}/{2}+ x)= −cosx$, получим: ${2sinxcosx}/{−cosx}= 1$, где $cosx≠0, x≠{π}/{2}+ πm, m ∈ Z$.

$−2sinx = 1, sinx =−{1}/{2}$.

$x=−{π}/{6}+2πn, n ∈ Z;$

$x=-{5π}/{6}+ 2πk, k ∈ Z$.

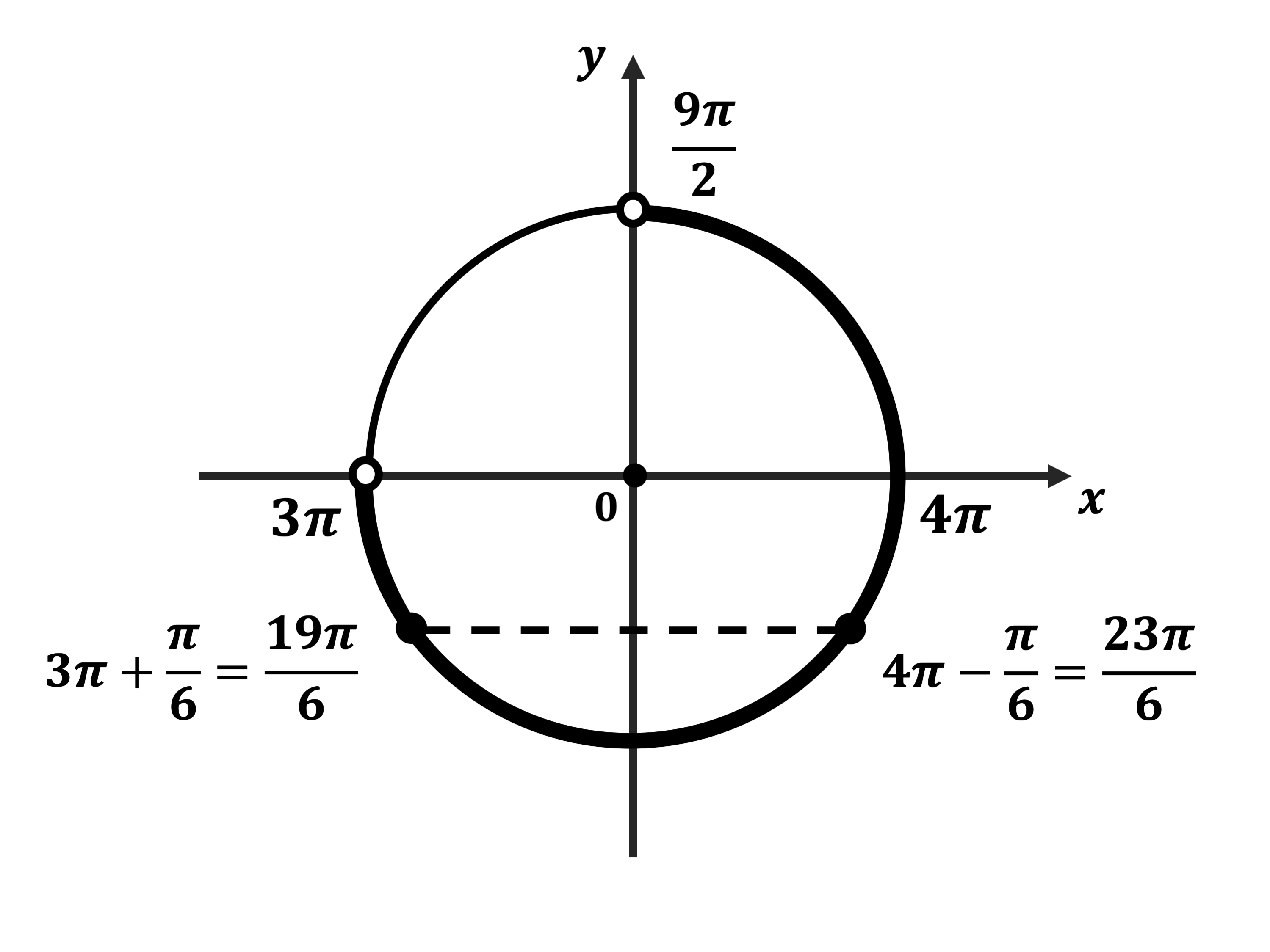
б) Отберём корни уравнения, принадлежащие промежутку $(3π; {9π}/{2})$,с помощью числовой окружности.

$x_1=3π+{π}/{6}={19π}/{6}$,

$x_2=4π−{π}/{6}={23π}/{6}$.

а)${sin2x}/{sin(π — x)}=√2$.

а) Применим формулу синуса двойного аргумента $sin2x = 2sinxcosx$ и формулу приведения $sin(π — x) = sin x$.

Уравнение примет вид: ${2sinxcosx}/{sinx} = √2$.

Учитывая, что $sinx≠0, x≠πn, n∈Z$, получим:

$2cosx=√2$,

$cosx = {√2}/{2}$,

$x = ±{π}/{4} + 2πk, k∈Z$;

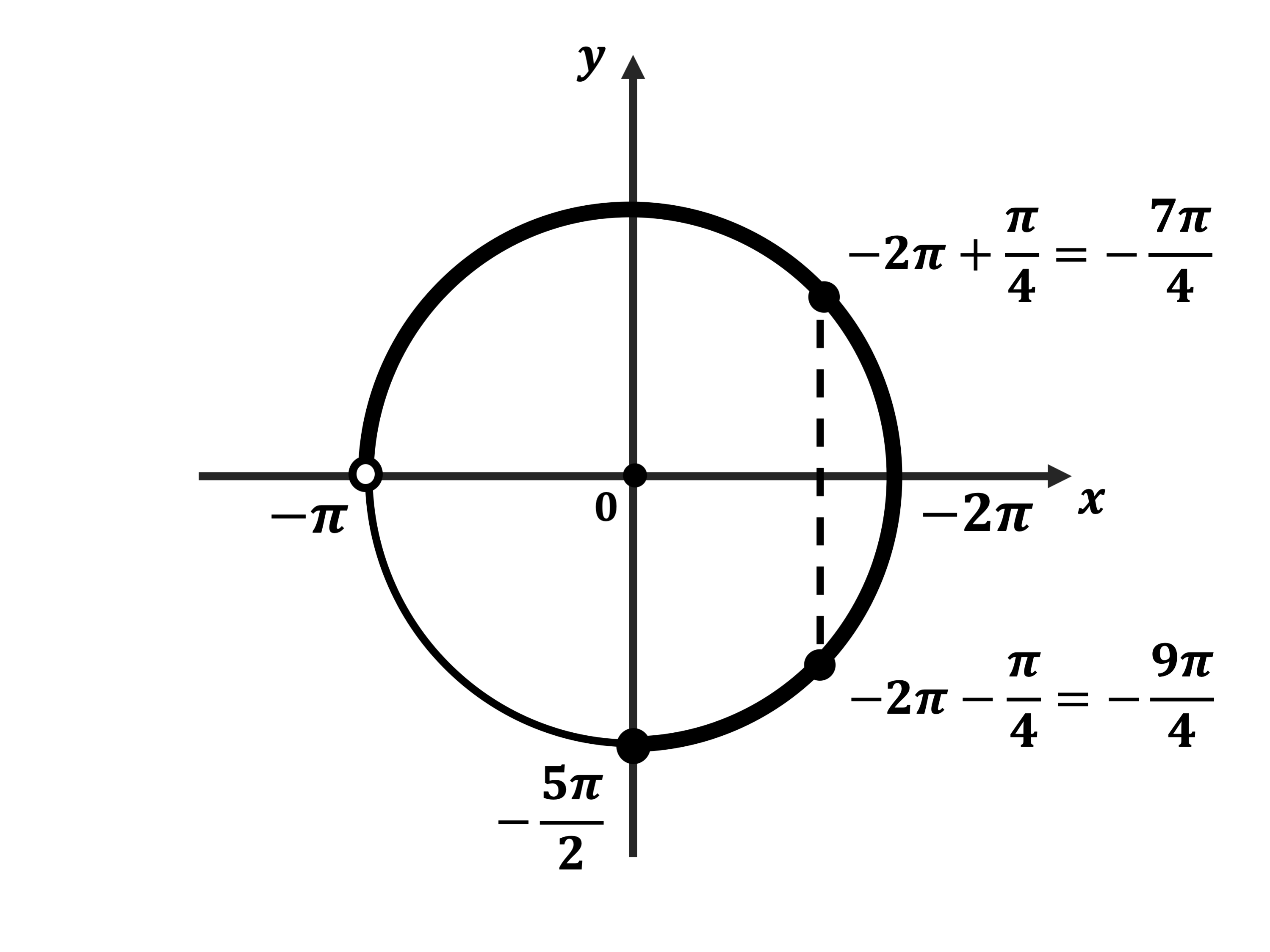
б) Отберём корни уравнения, принадлежащие промежутку $[-{5π}/{2};-π)$, с помощью окружности.

$x_1=-2π+{π}/{4}=-{7π}/{4}$

$x_2=-2π-{π}/{4}=-{9π}/{4}$

а)${sin2x}/{cos(π + x)}=-√2$.

Зная, что $sin2x = 2sinxcosx, cos(π + x)=-cosx$, получим: ${2sinxcosx}/{-cosx}=-√2$.

Учитывая, что $cosx≠0, x≠{π}/{2} + πm, m∈Z$, имеем:

$2sinx=√2$,

$sinx = {√2}/{2}$,

$x = {π}/{4} + 2πn, n∈Z$;

$x = {3π}/{4} + 2πk, k∈Z$.

б) Отберём корни уравнения, принадлежащие промежутку $(-2π;-{π}/{2})$.

1. $x = {π}/{4} + 2πn, n∈Z$.

$-2π < {π}/{4} + 2πn < -{π}/{2},$

$-2 < {1}/{4} + 2n < -{1}/{2},$

$-2-{1}/{4} < 2n < -{1}/{2}-{1}/{4},$

$-{9}/{4} < 2n < -{3}/{4},$

$-{9}/{8} < n < -{3}/{8},$

$n = -1$.

При $n =-1$

$x = {π}/{4}-2π=-{7π}/{4}$.

2. $x = {3π}/{4} + 2πk, k∈Z$.

$-2π < {3π}/{4} + 2πk < -{π}/{2}$,

$-2 < {3}/{4} + 2k < -{1}/{2}$,

$-2-{3}/{4} < 2k < -{1}/{2}-{3}/{4}$,

$-{11}/{4} < 2k < -{5}/{4}$,

$-{11}/{8} < k < -{5}/{8}$,

$k = -1$.

При $k = -1$

$x = {3π}/{4}-2π = -{5π}/{4}$.

а) После замены $t = 3^{cosx}$ исходное уравнение примет вид $9t^2 — 10√3t + 3 = 0$. Корни этого уравнения $t = √3; t = {√3}/{9}$. Возвращаясь к переменной $x$, получим

$[table3^{cosx}=√3; 3^{cosx}={√3}/{9};$ $[table3^{cosx}=3^{{1}/{2}}; 3^{cosx}=3^{-{3}/{2}};$ $[tablecosx={1}/{2}; cosx=-{3}/{2};$

Второе уравнение совокупности не имеет корней. Решая первое уравнение, получим $x =±{π}/{3} + 2πn; n ∈ Z$.

б) Запишем решение уравнения в виде $x =-{π}/{3} + 2πn; n ∈ Z$ или $x ={π}/{3} + 2πk; k ∈ Z$ и выясним, для каких целых значений $n$ и $k$ справедливы неравенства ${3π}/{2}≤-{π}/{3}+2πn≤4π$ и ${3π}/{2}≤{π}/{3}+2πk≤4π$.

Получим ${11}/{12} ≤ n ≤ {26}/{12}$ и ${7}/{12} ≤ k ≤{22}/{12}$.

Откуда следует, что два целых значения $n = 1$ и $n = 2$ удовлетворяют неравенству ${11}/{12} ≤ n ≤ {26}/{12}; k = 1$ — единственное целое $k$, удовлетворяющее неравенству ${7}/{12} ≤ k ≤{22}/{12}$.

При $n = 1$ $x = -{π}/{3} + 2π·1 = {5π}/{3}$.

При $n = 2$ $x = -{π}/{3} + 2π·2 = {11π}/{3}$.

При $k = 1$ $x = {π}/{3} + 2π·1 = {7π}/{3}$. Итак, ${5π}/{3}; {7π}/{3}; {11π}/{3}$ — корни уравнения, принадлежащие промежутку $[{3π}/{2};4π]$.

а) После замены $t = log_2(2 sin x+1)$ исходное уравнение примет вид $t^2-17t+16 = 0$. Корни этого уравнения $t = 1, t = 16$. Возвращаясь к переменной $x$, получим:

$[tablelog_2(2 sin x + 1) = 1; log_2(2 sin x + 1) = 16;$ $[table2 sin x + 1 = 2;; 2sin x + 1 = 2^{16};$

Второе уравнение совокупности не имеет корней. Решая первое уравнение, получим: $sin x = {1}/{2}; x = (-1)^n{π}/{6} + πn; n ∈ Z$.

б) Запишем решение уравнения в виде $x = {π}/{6} + 2πn; n ∈ Z$ или $x = {5π}/{6} + 2πk; k ∈ Z$ и выясним, для каких целых значений $n$ и $k$ справедливы неравенства ${π}/{4}≤{π}/{6}+2πn≤2π$ и ${π}/{4}≤{5π}/{6}+2πk≤2π$.

Получим: ${1}/{24}≤n≤{11}/{12}$ и $-{7}/{24}≤k≤{7}/{12}$, откуда следует, что нет целых значений $n$, удовлетворяющих неравенству ${1}/{24}≤n≤{11}/{12}; k = 0$ — единственное целое $k$, удовлетворяющее неравенству $-{7}/{24}≤k≤{7}/{12}$.

При $k = 0$ $x = {5π}/{6} + 2π·0 = {5π}/{6}$. Итак, ${5π}/{6}$ — корень уравнения, принадлежащий отрезку $[{π}/{4};2π]$.

а) Решим уравнение $6log_2^2(2 cos x)-9 log_2(2 cos x)+3 = 0$. Обозначим $log_2(2 cos x) = t$ и решим получившееся квадратное уравнение.

$6t^2 — 9t + 3 = 0, t = {9±3}/{12}; t_1 = {1}/{2}; t_2 = 1$.

$[tablelog_2(2 cos x) ={1}/{2}; log_2(2 cos x) = 1;$ $[table2 cos x = √2; 2 cos x = 2;$

$[tablecos x = {√2}/{2}; cos x= 1;$ $[tablex = ±{π}/{4}+ 2π n; n ∊ Z; x = 2πk; k ∊ Z;$

б) Корни, принадлежащие отрезку $[-{π}/{2};π]$, найдём с помощью числовой окружности:

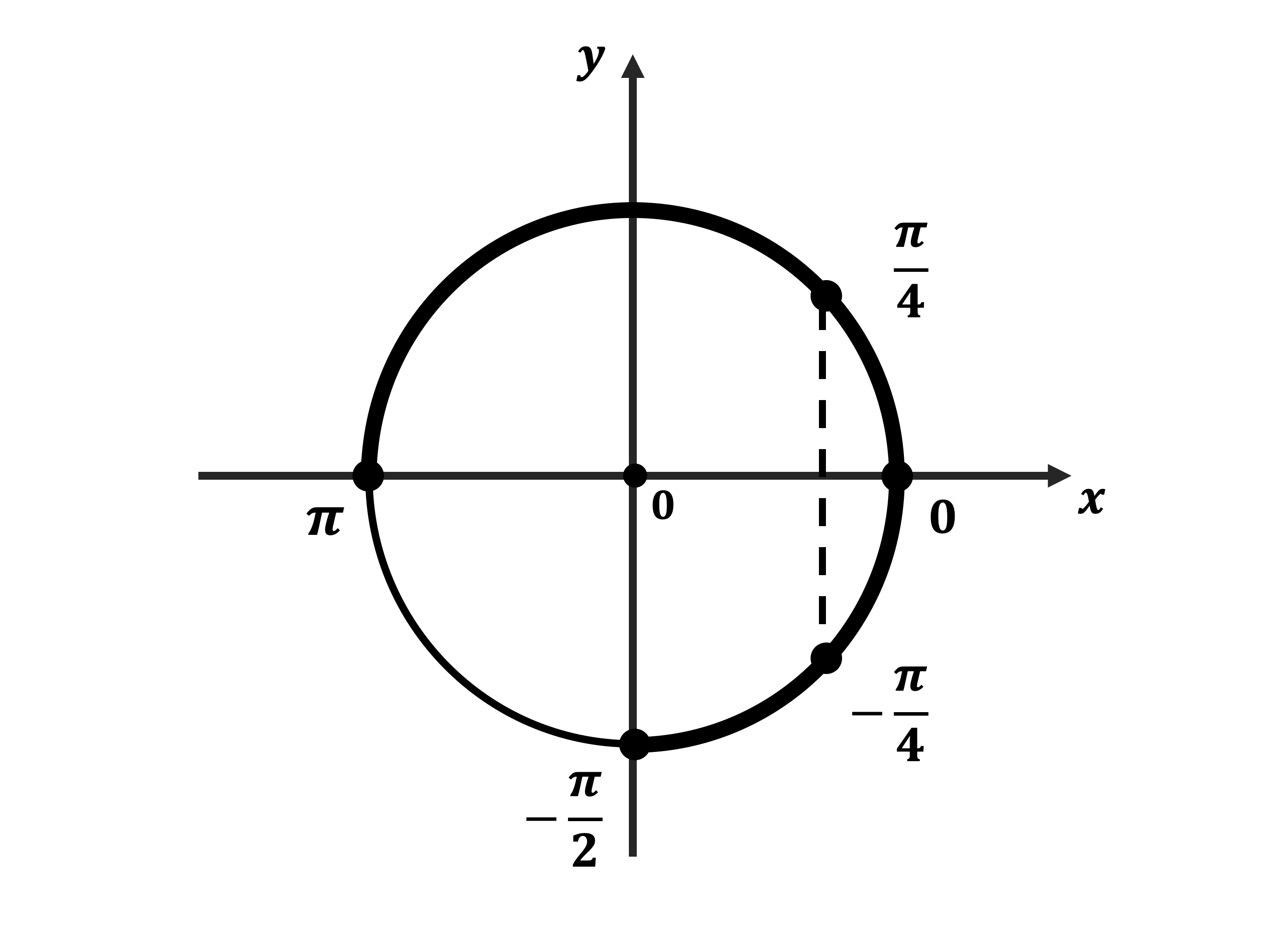
$x_1 = -{π}/{4}; x_2 = 0; x_3 ={π}/{4}$.

а) Решим уравнение $2log_2^2(2 sin x) — 3 log_2(2 sin x) + 1 = 0$. Обозначим $log_2(2 sin x) = t$ и решим получившееся уравнение. $2t^2 — 3t + 1 = 0, t = {3±1}/{4}; t_1 = 1; t_2 ={1}/{2}$

$[tablelog_2(2 sin x) = 1; log_2(2 sin x) ={1}/{2};$ $[table2 sin x = 2; 2 sin x=√2;$

$[tablesin x = 1; sin x = {√2}/{2};$ $[tablex={π}/{2}+2πn; x=(-1)^k{π}/{4}+πk;$ $n,k∈Z$

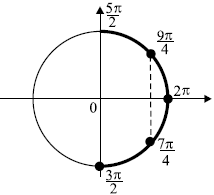
б) Корни, принадлежащие отрезку $[{3π}/{2}; 3π]$, найдём с помощью числовой окружности:

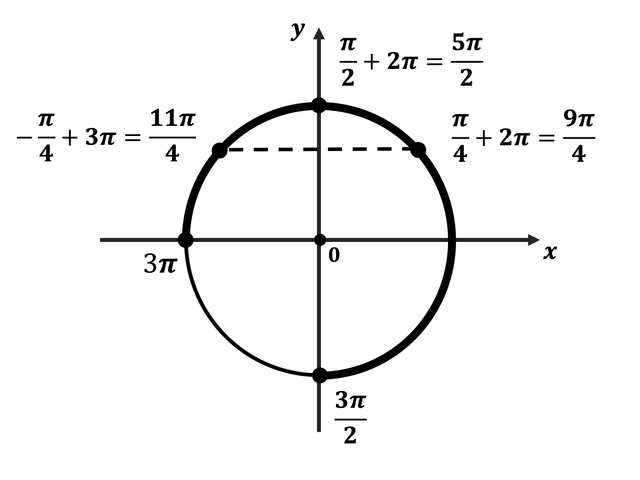
$x_1 = 2π + {π}/{4} = {9π}/{4}; x_2 = 2π + {π}/{2} ={5π}/{2}; x_3 = 3π -{π}/{4} = {11π}/{4}$.

а) Преобразуем исходное уравнение и разложим на множители его левую часть.

$3^{3x} — 5·3^{2x} — 81·3^x + 405 = 0$,

$3^{2x}(3^x — 5) — 81(3^x — 5) = 0$,

$(3^{2x} — 81)(3^x — 5) = 0$.

Получаем: $3^{2x} -81 = 0$ или $3^x -5 = 0$. Значит, $3^{2x} = 81$, откуда $x = 2$ или $3^x = 5$, откуда $x = log_{3}5$.

б) Нам нужно выбрать те корни уравнения, которые принадлежат отрезку $[log_{3}6; log_{3}10]$. Заметим, что $2 = log_{3}9$. Тогда $log_{3}5 < log_{3}6 < 2 < log_{3}10$. Значит, указанному отрезку принадлежит корень $x = 2$.

а) Запишем исходное уравнение в виде $2 cos^2 x — 3√2 cos x + 2 = 0$.

Решая это уравнение как квадратное относительно $cos x$, получим $(cos x)_{1,2} ={3√2±√{18 — 16}}/{4}={3√2± √2}/{4}$.

Значит, $(cos x)_1 = {√2}/{2}$, откуда $x =π/4 + 2πn, n ∈ Z$ или $x =-π/4 + 2πn, n ∈ Z$.

Уравнение $(cosx)_2 = √2$ корней не имеет.

б) Отберём корни, принадлежащие отрезку $[{3π}/{2};{5π}/{2}]$ с помощью числовой окружности.

Получим числа

$2π -{π}/{4} ={7π}/{4}$;

$2π + {π}/{4} = {9π}/{4}$.

а) Запишем исходное уравнение в виде $2sin^2 x — 3√3 sin x + 3 = 0$.

Решая это уравнение как квадратное относительно $sin x$, получим $(sin x)_{1,2} = {3√3±√{27-24}}/{4}= {3√3±√3}/{4}$.

Значит,$(sin x)_1 ={√3}/{2}$, откуда $x ={π}/{3} +2πn, n ∈ Z$ или $x ={2π}/{3}+2πm, m ∈ Z$.

Уравнение $(sin x)_2 = √3$ корней не имеет.

б) С помощью числовой окружности отберём корни, принадлежащие отрезку: $[2π; 3π]$

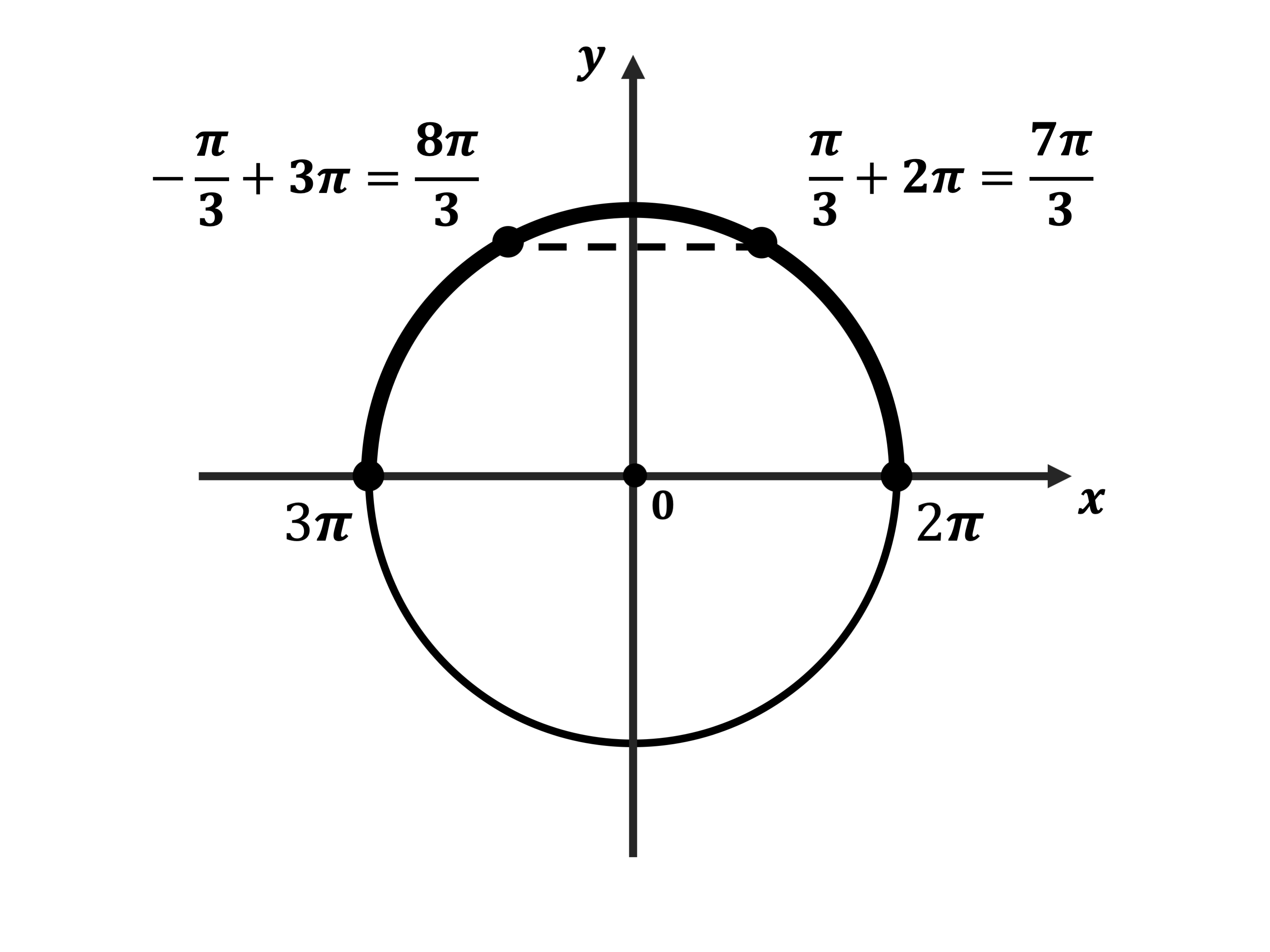
Получим числа:

$2π +{π}/{3}={7π}/{3}$;

$3π -{π}/{3}={8π}/{3}$.