Номер 245342 математика егэ - Помощь в подготовке к экзаменам и поступлению

СДАМ ГИА:

РЕШУ ЕГЭ

Образовательный портал для подготовки к экзаменам

Математика профильного уровня

≡ Математика

Базовый уровень

Профильный уровень

Информатика

Русский язык

Английский язык

Немецкий язык

Французский язык

Испанский язык

Физика

Химия

Биология

География

Обществознание

Литература

История

Сайты, меню, вход, новости

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Об экзамене

Каталог заданий

Варианты

Ученику

Учителю

Школа

Эксперту

Справочник

Карточки

Теория

Сказать спасибо

Вопрос — ответ

Чужой компьютер

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

Играть в ЕГЭ-игрушку

Новости

10 марта

Как подготовиться к ЕГЭ и ОГЭ за 45 дней

6 марта

Изменения ВПР 2023

3 марта

Разместили утвержденное расписание ЕГЭ

27 января

Вариант экзамена блокадного Ленинграда

23 января

ДДОС-атака на Решу ЕГЭ. Шантаж.

6 января

Открываем новый сервис: «папки в избранном»

22 декабря

Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!

4 ноября

Материалы для подготовки к итоговому сочинению 2022–2023

31 октября

Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР

21 марта

Новый сервис: рисование

31 января

Внедрили тёмную тему!

НАШИ БОТЫ

Все новости

ЧУЖОЕ НЕ БРАТЬ!

Экзамер из Таганрога

10 апреля

Предприниматель Щеголихин скопировал сайт Решу ЕГЭ

Наша группа

Задания

Версия для печати и копирования в MS Word

Тип 2 № 245342

Найдите объем многогранника, вершинами которого являются точки A_1, B_1, B, C правильной треугольной призмы площадь основания которой равна 4, а боковое ребро равно 3.

Спрятать решение

Решение.

Заметим, что искомый объём равен разности объема призмы и двух треугольных пирамид, основания и высоты которых совпадают с основанием и высотой призмы:

Поэтому

Ответ: 4.

Аналоги к заданию № 245342: 266981 266983 266985 266987 266989 266991 266993 266995 266997 266999 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы

Спрятать решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

О проекте · Редакция · Правовая информация · О рекламе

Источник

Дана правильная треугольная призма

Дата: 2020-10-16

1493

Категория: Стерео Призма

Метка: ЕГЭ-№2

245340. Дана правильная треугольная призма АВСА₁В₁С₁, площадь основания которой равна 2, а боковое ребро равно 3. Найдите объем многогранника, вершинами которого являются точки А, В, С, А₁Построим указанный многогранник на эскизе: Получили пирамиду с основанием АВС и вершиной А₁. Площадь её основания равна площади основания призмы (основание общее). Высота также общая. Объём пирамиды равен: Ответ: 2

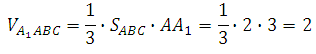
245341. Найдите объем многогранника, вершинами которого являются точки А, В, С, А₁, С₁, правильной треугольной призмы АВСА₁В₁С₁, площадь основания которой равна 3, а боковое ребро равно 2.Построим указанный многогранник на эскизе:Это пирамида с основанием АА₁С₁С и высотой равной расстоянию между ребром АС и вершиной В. Но в данном случае вычислять площадь этого основания и указанную высоту слишком долгий путь к результату. Проще поступить следующим образом:

Чтобы получить объём указанного многогранника необходимо из объёма данной призмы АВСА₁В₁С₁ вычесть объём пирамиды ВА₁В₁С₁.

Запишем:

Ответ: 4

245342.. Найдите объем многогранника, вершинами которого являются точки А₁, В₁, В, С, правильной треугольной призмы АВСА₁В₁С₁, площадь основания которой равна 4, а боковое ребро равно 3.

Построим указанный многогранник на эскизе:

Чтобы получить объём указанного многогранника необходимо из объёма призмы АВСА₁В₁С₁ вычесть объёмы двух тел – пирамиды ABCА₁ и пирамиды CА₁В₁С₁. Запишем: Ответ: 4

Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.

Источник

Задание 12 Профильного ЕГЭ по математике – это решение уравнений. Чаще всего, конечно, это тригонометрические уравнения. Но встречаются и другие типы – показательные, логарифмические, комбинированные.

Сейчас задание 12 Профильного ЕГЭ на решение уравнения состоят из двух пунктов: собственно решения и отбора корней на определенном отрезке.

Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.

Задачи из сборников Ященко, 2021 год

Квадратные уравнения

Показательные уравнения

Логарифмические уравнения

Модуль числа

Уравнения с модулем

Тригонометрический круг

Формулы тригонометрии

Формулы приведения

Простейшие тригонометрические уравнения 1

Простейшие тригонометрические уравнения 2

Тригонометрические уравнения

Что необходимо помнить при решении уравнений?

1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть tg x — помним, что он существует, только если

2) Стараемся записывать решение в виде цепочки равносильных переходов.

3) Если есть возможность сделать замену переменной — делаем замену переменной! Уравнение сразу станет проще.

4) Если еще не выучили формулы тригонометрии — пора это сделать! Много формул не нужно. Самое главное — тригонометрический круг, формулы синусов и косинусов двойных углов, синусов и косинусов суммы (разности), понижения степени. Формулы приведения не надо зубрить наизусть! Надо знать, как они получаются.

5) Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений $x=frac{pi}{3}+2pi n$ , где — целое, а найти надо корни на отрезке $left [frac{5 pi}{2};frac{9 pi}{2} right ].$ На указанном промежутке лежит точка 4 pi . От нее и будем отсчитывать. Получим: $x=4 pi +frac{pi}{3}=frac{13 pi}{3}.$

6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!

Давайте потренируемся.

а) Решите уравнение $2{{sin}^2 left(frac{pi }{2}+xright)}=-sqrt{3}{cos x}$

б) Найдите все корни этого уравнения, принадлежащие промежутку $left[-3pi right.;left.-frac{3pi }{2}right]$

$2{{sin}^2 left(frac{pi }{2}+xright)}=-sqrt{3}{cos x}$

Упростим левую часть по формуле приведения.

$2{{cos}^2 x+sqrt{3}{cos x}=0}$

Вынесем {cos x} за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

б) Отметим на тригонометрическом круге найденные серии решений и отрезок $left[-3pi right.;left.-frac{3pi }{2}right].$

Видим, что указанному отрезку принадлежат решения $-frac{17pi }{6};-frac{5pi }{2};-frac{3pi }{2}.$

Ответ: $-frac{17pi }{6};-frac{5pi }{2};-frac{3pi }{2}.$

Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений $x=frac{pi }{3}+2pi n$ , где — целое, а найти надо корни на отрезке $[frac{5pi }{2};frac{9pi }{2}].$ На указанном промежутке лежит точка 4 pi. От нее и отсчитываем.

Получим: $x=4pi +frac{pi }{3}=frac{13pi }{3}.$

2. а) Решите уравнение ${({27}^{{cos x}})}^{{sin x}}=3^{frac{3{cos x}}{2}}$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-pi ;frac{pi }{2}right].$

Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.

а) $3^{3{cos x{sin x}}}=3^{frac{3{cos x}}{2}}$

Степени равны, их основания равны. Значит, равны и показатели.

$3{cos x{sin x}}=frac{3{cos x}}{2}$

${cos x({sin x-frac{1}{2})=0}}$

Это ответ в пункте (а).

б) Отберем корни, принадлежащие отрезку $left[-pi ;frac{pi }{2}right].$

Отметим на тригонометрическом круге отрезок $left[-pi ;frac{pi }{2}right]$ и найденные серии решений.

Видим, что указанному отрезку принадлежат точки $x=-frac{pi }{2}$ и $x=frac{pi }{2}$ из серии $x=frac{pi }{2}+pi n,nin z.$

Точки серии $x=frac{5pi }{6}+2pi n,nin z$ не входят в указанный отрезок.

А из серии $x=frac{pi }{6}+2pi n,nin z$ в указанный отрезок входит точка $x=frac{pi }{6}.$

Ответ в пункте (б): $-frac{pi }{2},frac{pi }{6} , frac{pi }{2}.$

3. а) Решите уравнение ${cos 2x}+{{sin}^2 x=0,5}$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-frac{7pi }{2}right.;left.-2pi right].$

а)
${cos 2x}+{{sin}^2 x=0,5}$

Применим формулу косинуса двойного угла: $boldsymbol{cos2alpha =1-{2sin}^2alpha }$

$1-2{{sin}^2 x}+{{sin}^2 x}=0,5$

${{-sin}^2 x=-0,5}$

${{sin}^2 x=0,5}$

Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.

Обратите внимание: мы отметили серии решений на тригонометрическом круге. Это помогло нам увидеть, как их записать одной формулой.

б) Для разнообразия отберем корни на отрезке $left[-frac{7pi }{2}right.;left.-2pi right]$ с помощью двойного неравенства.

Сначала серия $x=frac{pi }{4}+pi n,nin Z.$

$-frac{7pi }{2}le frac{pi }{4}+pi nle -2pi$

$-frac{7}{2}le frac{1}{4}+nle -2$

$n=-3, x_1=frac{pi }{4}-3pi =-frac{11pi }{4}$

Теперь серия $x=-frac{pi }{4}+pi n,nin Z$

$-frac{7pi }{2}le -frac{pi }{4}+pi nle -2pi$

$-frac{7}{2}le -frac{1}{4}+nle -2$

$n=-3, x_2=-frac{pi }{4}-3pi =-frac{13pi }{4}$

$n=-2, x_3=-frac{pi }{4}-2pi =-frac{9pi }{4}$

Ответ: $-frac{13pi }{4};-frac{11pi }{4};-frac{9pi }{4}$ .

Какой способ отбора корней лучше — с помощью тригонометрического круга или с помощью двойного неравенства? У каждого из них есть «плюсы» и «минусы».

Пользуясь тригонометрическим кругом, вы не ошибетесь. Вы видите и интервал, и сами серии решений. Это наглядный способ.

Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии $x=-frac{pi }{4}+2pi n,nin Z$ на отрезке $left[-frac{pi }{2}right.;left.20pi right].$ Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.

4. а) Решите уравнение $left({tg}^2x-3right)sqrt{11{cos x}}=0.$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-frac{5pi }{2};-pi right].$

Самое сложное здесь — область допустимых значений (ОДЗ). Условие заметно сразу. А условие появляется, поскольку в уравнении есть ${tg x=frac{{sin x}}{{cos x}}}.$

ОДЗ:

Уравнение равносильно системе:

Отберем решения с помощью тригонометрического круга. Нам нужны те серии решений, для которых , то есть те, что соответствуют точкам справа от оси .

Ответ в пункте а) $x=pm frac{pi }{3}+2pi n, nin z$

б) Отметим на тригонометрическом круге найденные серии решений и отрезок $left[-frac{5pi }{2};-pi right].$

Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки

$x=frac{pi }{3}-2pi =-frac{5pi }{3}$ и $x=-frac{pi }{3}-2pi =-frac{7pi }{3}.$

5. а) Решите уравнение $sqrt{{cos x+{sin x}}}({{cos}^2 x-frac{1}{2})=0}$

б) Найдите корни, принадлежащие отрезку

Выражение под корнем должно быть неотрицательно, а произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

Это значит, что уравнение равносильно системе:

Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых ${cos x}=frac{sqrt{2}}{2}$ или ${cos x}=-frac{sqrt{2}}{2}$ . Заметим, что среди них находятся и углы, для которых tgx=-1.

Числа серии $x=-frac{3pi }{4}+2pi n$ не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие . Остальные серии решений нас устраивают.

Тогда в ответ в пункте (а) войдут серии решений:

б) Отберем корни, принадлежащие отрезку любым способом — с помощью тригонометрического круга или с помощью двойного неравенства.

На отрезке нам подходит корень $x =-frac{pi }{4}$ .

На отрезке нам подходят корни $x=frac{pi }{4};frac{3pi }{4};frac{7pi }{4}$ .

На отрезке — корни $x= frac{9pi }{4} ; frac{11pi }{4};frac{15pi }{4}.$

Ответ в пункте б): $-frac{pi }{4};frac{3pi }{4};frac{7pi }{4};frac{pi }{4};frac{9pi }{4} ; frac{11pi }{4};frac{15pi }{4}.$

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание №12. Уравнения u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

��

�� , � �� .

��-��

�� -�� , �� , ��, �� , �� , ��.

��

�� , �� , �� .

��-��

�� -�� , � �� , ��; �� (� ��) �� .

��

� �� 12600 �� , �� .

��

�� , �� , �� , �� .

��

�� , �� .

��

�� , �� ,
��, ��, �� ,
��, ��,
��,
��, ��, ��

��

�� -�� .

� ��

�� — �� , �� , �� , �� .

��-��

��

��	��
��	��-��
��	��-��
��	��
��	��
��	��
��	��
��ԣ�� .�.-�� .�.	��
��	��
��	��-��, ��
��	��
��	��-��
��	��
��	��
��	��
��	��-��
��	��-��
��	��
��	��
��	��

��

�� , �� , �� -�� .

Источник

ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
АНГЛИЙСКИЙ без ГРАНИЦ

2012-07-26

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Конструктор упражнений для позвоночника!

Отзывов (3)

Маша

2013-05-08 в 22:46

В задаче 245179 ответ не 20, а 2!

Ответить
- Александр Крутицких
  
  2013-05-09 в 09:00
  
  Спасибо, исправим.
  
  Ответить
- Александр Крутицких
  
  2013-05-09 в 11:06
  
  Исправлено!
  
  Ответить

Добавить комментарий

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

РубрикиРубрики
Задачи по номерам!

№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
МЕТКИ

БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
ОСТЕОХОНДРОЗУ-НЕТ!

Источник

егэ 2023 сборник ященко профиль 36 вариантов

4 вариант с ответами и решением из нового сборника Ященко И.В ЕГЭ 2023 профильный уровень математика 11 класс 36 тренировочных вариантов с полным видео разбором варианта, данный вариант вы можете скачать или решать онлайн.

Скачать 4 вариант Ященко

4 вариант Ященко ЕГЭ 2023 профиль с ответами

4вариант-егэ2023-ященко-профиль

Полное видео решение заданий варианта

Задания и ответы с варианта

1.Площадь ромба равна 9. Одна из его диагоналей в 8 раз больше другой. Найдите меньшую диагональ.

Ответ: 1,5

2.Длина окружности основания конуса равна 6, образующая равна 4. Найдите площадь боковой поверхности конуса.

Ответ: 12

3.Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 18 пассажиров, равна 0,9. Вероятность того, что окажется меньше 9 пассажиров, равна 0,66. Найдите вероятность того, что число пассажиров будет от 9 до 17 включительно.

Ответ: 0,24

4.Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Стартер» по очереди играет с командами «Ротор», «Мотор» и «Монтёр». Найдите вероятность того, что «Стартер» будет начинать только вторую игру.

Ответ: 0,125

9.Заказ на изготовление 216 деталей первый рабочий выполняет на 6 часов быстрее, чем второй. Сколько деталей за час изготавливает первый рабочий, если известно, что он за час изготавливает на 6 деталей больше второго?

Ответ: 18

15.В июле Борис планирует взять кредит в банке на некоторую сумму. Банк предложил Борису два варианта кредитования.

1-й вариант; — кредит предоставляется на 3 года; — в январе каждого года действия кредита долг увеличивается на 10 % от суммы долга на конец предыдущего года; — в период с февраля по июнь каждого года действия кредита выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью.
2-й вариант: — кредит предоставляется на 2 года; — в январе каждого года действия кредита долг увеличивается на 16 % от суммы долга на конец предыдущего года; — в период с февраля по июнь каждого года действия кредита выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью. Когда Борис подсчитал, то выяснил, что по 1-му варианту кредитования ему придётся выплачивать на 353 740 рублей меньше, чем по 2-му варианту. Какую сумму Борис планирует взять в кредит?

Ответ: 8937 тыс. рублей

16.Четырёхугольник АВСР со сторонами ВС =14 и AB=CD=40 вписан в окружность радиусом В=25. а) Докажите, что прямые ВС и AD параллельны. 6) Найдите AD.

Ответ: 42,16

18.Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 8 раз больше, либо в 8 раз меньше предыдущего. Сумма всех членов последовательности равна 4040.

а) Может ли последовательность состоять из трёх членов?
б) Может ли последовательность состоять из четырёх членов?
в) Какое наибольшее количество членов может быть в последовательности?

Ответ: а-да, б-нет, в-897

Вариант 1 Ященко ЕГЭ 2023 математика профиль с ответами
Вариант 2 Ященко ЕГЭ 2023 математика профиль с ответами

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Источник

Дана правильная треугольная призма

������� ����������

������� ������� ����������

������-������������ ����������

����� � ��������

��������-������

��������

��������� � �����

��������

������������ �����

��������� �� �������

Добавить комментарий

4 вариант Ященко ЕГЭ 2023 профиль с ответами

Полное видео решение заданий варианта

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

��

��

��-��

��

��-��

��

��

��

��

��