Всего: 7 1–7
Добавить в вариант
В треугольнике ABC угол ABC тупой, H — точка пересечения продолжений высот, угол AHC равен 60°.
а) Докажите, что угол ABC равен 120°.
б) Найдите BH, если и
Источник: Досрочный ЕГЭ по математике (Центр) 30.03.2018
В остроугольном треугольнике ABC, Высоты BN и CM треугольника ABC пересекаются в точке H. Точка O — центр окружности, описанной около
а) Докажите, что
б) Найдите площадь если
Источник: Основная волна ЕГЭ по математике 29.05.2019. Вариант 405, Основная волна ЕГЭ по математике 29.05.2019. Вариант 409, Задания 16 (С4) ЕГЭ 2019
Около остроугольного треугольника ABC с различными сторонами описали окружность с диаметром BN. Высота BH пересекает эту окружность в точке K.
а) Докажите, что
б) Найдите KN, если
а радиус окружности равен 12.
Источник: Основная волна ЕГЭ по математике 29.05.2019. Центр, Задания 16 (С4) ЕГЭ 2019
Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке H.
а) Докажите, что ∠AHB1 = ∠ACB.
б) Найдите BC, если AH = 4 и ∠BAC = 60°.
Источник: ЕГЭ по математике 05.06.2014. Основная волна. Запад. Вариант 302.
Около описана окружность. Прямая BO, где O — центр вписанной окружности, вторично пересекает описанную окружность в точке P.
а) Докажите, что
б) Найдите расстояние от точки P до прямой AC, если а радиус описанной окружности равен 18.
Источник: Основная волна ЕГЭ по математике 29.05.2019. Дальний восток, Задания 16 (С4) ЕГЭ 2019
Точка O — центр вписанной в треугольник ABC окружности. Прямая OB вторично пересекает описанную около этого треугольника окружность в точке P.
а) Докажите, что
б) Найдите площадь треугольника APC, если радиус описанной около треугольника ABC окружности равен 4, а
Источник: Основная волна ЕГЭ по математике 29.05.2019. Санкт-Петербург, Основная волна ЕГЭ по математике 29.05.2019. Вариант 316, Задания 16 (С4) ЕГЭ 2019
Точка O — центр вписанной в треугольник ABC окружности. Прямая BO вторично пересекает описанную около этого треугольника окружность в точке P.
а) Докажите, что
б) Найдите площадь треугольника APC, если радиус описанной около треугольника ABC окружности равен 8, а
Источник: Основная волна ЕГЭ по математике 29.05.2019. Вариант 324, Задания 16 (С4) ЕГЭ 2019
Всего: 7 1–7
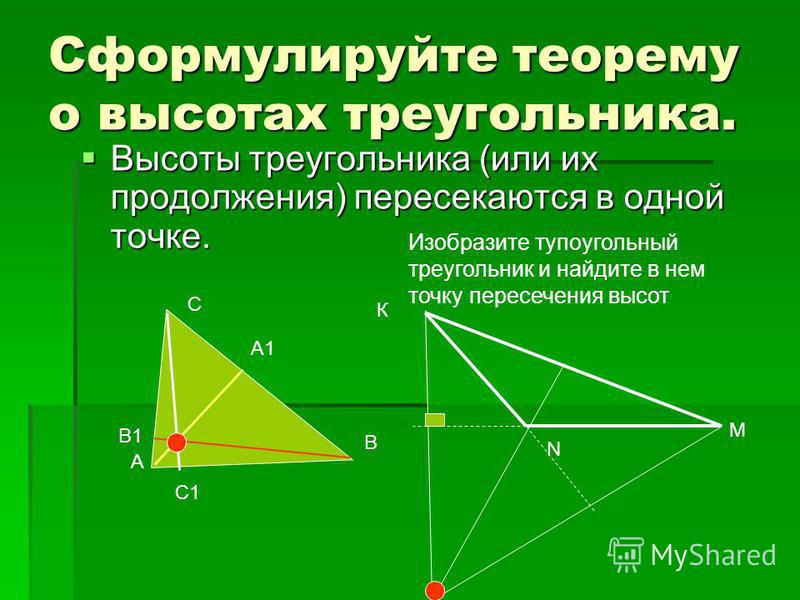
Свойства высот треугольника. Ортоцентр
Анна Малкова
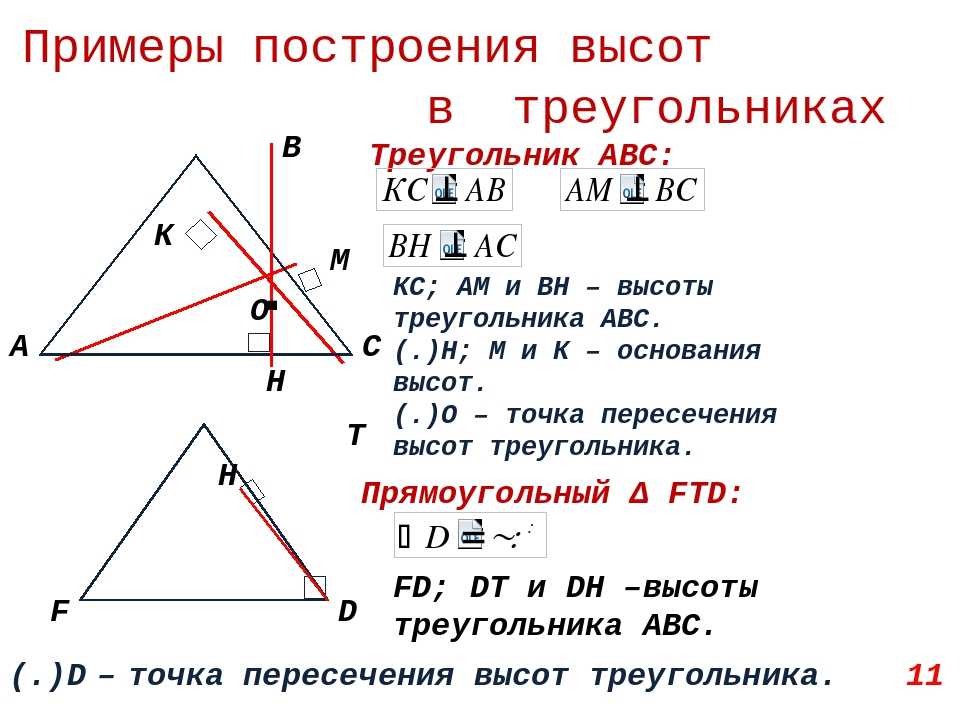
Схема 1. В треугольнике АВС проведены высоты АМ и СК.
Н – точка пересечения высот треугольника (ортоцентр), Н=АМ∩СК
Запомните этот рисунок. Перед вами – схема, из которой можно получить сразу несколько полезных фактов.
1. Треугольники МВК и △АВС, подобны, причем коэффициент подобия
, если
, и
, если
- Четырехугольник АКМС можно вписать в окружность. Эта вспомогательная окружность поможет решить множество задач.
- Четырехугольник ВКМН также можно вписать в окружность.
- Радиусы окружностей, описанных вокруг треугольников АВС, АНС, ВНС и АВН, равны.
,где R – радиус описанной окружности
.
Докажем эти факты по порядку.
1) Заметим, что на рисунке есть подобные треугольники. Это АВМ и СВК, прямоугольные треугольники с общим углом В, и они подобны по двум углам
Мы получили, что в треугольниках МВК и АВС стороны, прилежащие к углу В, пропорциональны. Получаем, что по углу и двум сторонам.
2) Докажем, что вокруг четырехугольника АКМС можно описать окружность. Для этого необходимо и достаточно, чтобы суммы противоположных углов четырехугольника АКМС были равны .
Пусть ∠ACB=∠BKM=γ (поскольку треугольники МВК и АВС подобны), тогда
– как смежный с углом ВКМ. Получили, что
, и это значит, что четырехугольник AKMC можно вписать в окружность.
3) Рассмотрим четырехугольник KBMH. Его противоположные углы ВКН и ВМН — прямые, их сумма равна , и значит, четырехугольник КВМН можно вписать в окружность.
4) По теореме синусов, радиус окружности, описанной вокруг треугольника АВС,
Радиус окружности, описанной вокруг треугольника АНС,
Мы помним, что . Значит, синусы углов АВС и АНС равны, и радиусы окружностей, описанных вокруг треугольников АВС и АНС равны.
5) Докажем, что ,где R – радиус описанной окружности
. Поскольку четырехугольник КВМН можно вписать в окружность и углы ВКН и ВМН – прямые, отрезок ВН является диаметром этой окружности. Треугольник МВК также вписан в эту окружность, и по теореме синусов,
.
Диаметр окружности, описанной вокруг треугольника АВС, равен Поскольку треугольники МВК и АВС подобны, отношение диаметров описанных вокруг них окружностей равно
. Получили, что
Задача ЕГЭ по теме «Высоты треугольника» (Профильный уровень, №16)
2. В остроугольном треугольнике KMN проведены высоты KB и NA.
а) Докажите, что угол ABK равен углу ANK.
б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и
а) Докажем, что
(по двум углам). Запишем отношение сходственных сторон:
Но это значит, что (по углу и двум сторонам), причем
.
— смежный с углом
,
,
,четырехугольник ABNK можно вписать в окружность.
(опираются на одну дугу).
б) Найдем , если
и
По теореме синусов,
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Свойства высот треугольника. Ортоцентр» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
5 февраля 2018
В закладки
Обсудить
Жалоба
Какие геометрические факты можно использовать на ЕГЭ без доказательства?
Начнём с того, что для ЕГЭ не нужны сколько-нибудь редкие теоремы, особенно где-нибудь на шпаргалке.
Нужно уметь применять всем знакомые факты, видеть рисунок и решать больше задач. Но вопрос из заголовка задают очень часто, и ответить на него нужно. Естественно, все сотни признаков и свойств, что есть в вашем школьном учебнике можно использовать. Но как насчет более редких фактов: что можно применять без доказательства, а что нет? Точный ответ: любые факты из школьных учебников, рекомендованных минобром на 2017-2018 год.
Ну а вот заветный список того, что мне все-таки удалось обнаружить в соответствующих учебниках:
→ Теорема Менелая (Атанасян. Геометрия 7-9 классы)
→ Теорема Чевы (Атанасян. Геометрия 7-9 классы)
→ Теорема Птолемея (Мерзляк. Геометрия 8 класс)
→ Прямая Эйлера (Мерзляк. Геометрия 8 класс)
→ Теорема об окружности Эйлера (Бутузов. Геометрия 8 класс)
→ Формула медианы треугольника (Шарыгин. Геометрия 7-9 классы)
→ Формула биссектрисы треугольника (Шарыгин. Геометрия 7-9 классы)
→ Теорема о четырех замечательных точках трапеции (Шарыгин. Геометрия 7-9 классы)
Формулу радиуса вневписанной окружности используйте. Каноническое уравнение эллипса — да пожалуйста! Ключевые формулы метода координат для задачи №14, опять же, есть
Но если здесь есть коллеги по цеху, которые могут уточнить еще несколько популярных вопросов насчет непопулярной теории — черкните, буду признателен! Вот интересующие факты: формула Брахмагупты, теорема Стюарта, формула Эйлера для расстояния между центрами вписанной и описанной окружностями треугольника, понятие определителя квадратной матрицы.
Ну и еще раз в заключение. Вероятность того, что задача ЕГЭ не решается без экзотики, равна нулю (такие события называются невозможными). Вероятность того, что вам вообще попадется конфигурация, для которой актуальна, например, теорема о девяти точках окружности, приблизительно равна 0,015. Вероятность того, что школьник в целом знает что-то «запрещенное», приблизительно равна, не кидайтесь камнями, 0,000037.
Источник: vk.com/wildmathing
Ольга Гончарова
2 недели назад
Спасибо за занятия
Связи На
1 месяц назад
Максим Олегович Ваши обьяснения гениальны!!!! Так великолепно доходчиво, внятно, чётко, понятно!!! Спасибо Вам за ваш труд. ВЫ заразили нас жаждой знаний….а Ваше «смотрите какое красивенькое решение получается»… Я стала понимать что это значит! Действительно красивые решения… Спасибо Вам не только за знания, но и за невероятные эмоции…
Василий Гумпылов
3 месяца назад
Мощная заставка)
Всеросс за месяц
3 месяца назад
спасибо, чувствую всеросс не за горами МО лучший!
GL1N0M3S
3 месяца назад
Не подскажете, можно ли не доказывая пользоваться этими свойствами, т.е. написать, что a=b, по свойству ортоцентра?
Наталья К.
5 месяцев назад
Название только очень нехорошее. Не надо никому вкладывать в голову эти слова. К чему?
Павел Демьяненко
7 месяцев назад
👍
Роман Как
7 месяцев назад
Заставка супер
Олег Паутов
8 месяцев назад
Подскажите пожалуйста, как доказать свойство обратное второму
Семён Валов
8 месяцев назад
Интро — бомба!
Иринка Пироженкова
9 месяцев назад
оооооочень быстро
TQ Project
10 месяцев назад
Так матешу я ещё никогда эпично не повторял
пинки тинки
10 месяцев назад
МО, напишите тайм коды пожалуйста по свойствам, чтобы удобнее было смотреть
Stanokey
10 месяцев назад
Максим Олегович, скажите, а на ЕГЭ нужно доказывать эти свойства?
Максим Еремин
10 месяцев назад
Просто ПУШКА!
MARTYNOV T
11 месяцев назад
у меня есть вопрос один. возможно он глупый. стоит доказывать все эти свойства на егэ или можно просто писать по свойтсву ортоцентра …….?
katalonskiy dr
1 год назад
а можно просто писать по свойству ортоцентра, или надо его доказывать на ЕГЭ?
пинки тинки
1 год назад
Это офигенно!!!
Kirill Kasimov
1 год назад
Мощь от подачи материала так и прёт ,уже от одного видео зарядился.
Регистрация Форум Текущее время: 11 мар 2023, 18:39 Сообщения без ответов | Активные темы Страница 1 из 2 [ Сообщений: 14 ] На страницу 1, 2 След. Начать новую тему»> Ответить Школьная программа.
Школьная программа.
Страница 1 из 2 [ Сообщений: 14 ] На страницу 1, 2 След. Текущее время: 11 мар 2023, 18:39 | Часовой пояс: UTC + 3 часа Удалить cookies форума | Наша команда | Вернуться наверх Кто сейчас на форуме
|
свойства, теоремы и основные соотношения для различных фигур
Геометрия
12.11.21
11 мин.
Решение задач по геометрии часто сводится к самой простой фигуре, называемой треугольником, точка пересечения высот которого обладает важными свойствами, помогающими найти неизвестные величины: стороны, углы, периметр и площадь. В интернете можно найти немало информации по этой теме, но, как правило, она не систематизирована. В результате тратится много времени на поиск формул и важных утверждений.
Оглавление:
- Общие сведения
- Информация об ортоцентре
- Полезные свойства и формулы
Общие сведения
Перед переходом к основным соотношениям высот с другими параметрами треугольника нужно ознакомиться с теоретическими сведениями об этой фигуре. Треугольник — фигура, состоящая из трех вершин, не лежащих на одной прямой, и отрезков, соединяющих их. Упрощенная форма записи в математике — символ «тильда», т. е. Δ. После последнего идут названия трех вершин, например, ΔPTS. Угол обозначается символом ∠, а после него указывается полная запись (∠РТS) или сокращенная (∠a).
Специалисты рекомендуют не называть вершины русскими буквами, поскольку эта запись не является верной. Треугольники бывают нескольких типов, на основании которых можно применить некоторые свойства, утверждения (теоремы) и формулы.
Типы треугольников
Математики классифицируют треугольные фигуры по определенным правилам или критериям. Они отличаются между собой по сторонам и углам. В первом случае фигуры бывают:
- произвольными;
- равнобедренными;
- равносторонними.
К первым принадлежат все фигуры с различными сторонами, ко вторым — с двумя равными, а к третьим — с тремя. Если классифицировать Δ по углам, то фигуры можно разделить на три типа. К ним принадлежат:
- прямоугольные;
- тупоугольные;
- остроугольные.
В прямоугольном Δ один из углов является прямым, т. е. равным 90 градусам. Тогда, используя свойство суммы его ∠, можно сделать вывод, что при сложении последних получается величина, равная 90°. Если Δ тупоугольный, то один из его ∠ эквивалентен величине, которая больше 90°. В остроугольном Δ все ∠ имеют градусную меру меньше 90°.
Следует отметить, что произвольные и равнобедренные Δ бывают прямоугольными и тупоугольными. Однако равносторонние (правильные) могут быть только остроугольными, поскольку все их углы эквивалентны значению 60°. Это можно определить по формуле: ∠K = ∠L = ∠M = 180 / 3 = 60. Кроме того, только вокруг этого типа фигуры можно описать окружность.
Основные и дополнительные параметры
У каждой фигуры, а треугольник не является исключением, существуют основные и дополнительные параметры. К первым относятся стороны и углы, ко вторым — периметр, площадь, высота, медиана и биссектриса.
Периметр — совокупность или алгебраическая сумма значений длин всех его сторон. Площадью является размерность фигуры, которая рассчитывается по некоторому соотношению. Она может быть только у плоских элементов геометрии, кроме точки, прямой, угла, луча и отрезка.
Следует отметить, что при решении задач в фигуре проводятся дополнительные элементы: высота, биссектриса и медиана. Первой называется отрезок, который проводится из вершины треугольника на противоположную сторону под углом 90 градусов. Высота образует подобный Δ относительного того, где она проведена. Это утверждение следует из равенства двух углов и пропорциональности сторон.
Все высоты в остроугольном треугольнике расположены внутри него. Если Δ является прямоугольным, то высоты, которые проводятся из вершин его острых углов, совпадают с катетами. В тупоугольном Δ высота, проведенная из вершины любого острого ∠, всегда находится вне фигуры.
Следующим вспомогательным отрезком является медиана.
В произвольном Δ количество высот, медиан и биссектрис эквивалентно числу его вершин, то есть можно провести по три элемента. Однако бывают исключения из этого правила: если фигура равнобедренная или равносторонняя, то ее высота является медианой и биссектрисой.
Теорема об ортоцентре позволяет вывести важные свойства высот треугольника, пересекающихся в одной точке. Ее формулировка следующая: высоты, проведенные в произвольном Δ, пересекаются в одной точке. Для доказательства требуется начертить произвольный ΔKLM. Он не должен содержать прямой или тупой угол.
Далее нужно действовать по такому алгоритму:
- Из двух вершин следует провести высоты, которые пересекают противоположную сторону под прямым углом, то есть из вершины L опустить LN на сторону КМ.
Аналогичную операцию нужно выполнить для вершины К (KU к LM).
- Высоты пересекутся в некоторой точке — будущем ортоцентре треугольника. Ее следует обозначить W.
- Предположим, что высоты не пересекаются. Следовательно, они параллельны. Это записывается таким образом: LN || KU. Сторона KL является секущей по определению.
- Исходя из третьего пункта, алгебраическая сумма значений углов (∠К/2 и ∠L/2) эквивалентна 180. Из равенства получается, что ∠К + ∠L = 360. Если ∠К и ∠L — внутренние углы ΔKLM, то их сумма не может составлять 360 градусов. Следовательно, предположение ошибочно.
- На основании доказанного в четвертом пункте утверждения можно сделать вывод, что высоты пересекаются в точке W.
- Аналогичным образом доказывается, что высота MV, опущенная из вершины M, проходит через ортоцентр. Для этого нужно повторить 1—5 пункты алгоритма, но вместо KU провести MV.
- Утверждение доказано.
Однако теоремы о высотах недостаточно для решения задач по геометрии.
Для этого случая математики вывели полезные свойства и соотношения, облегчающие нахождение неизвестной величины или доказательства нового утверждения.
Полезные свойства и формулы
При решении задач могут потребоваться некоторые свойства ортоцентра, которые были доказаны математиками. К ним относятся следующие:
- Расположение ортоцентра: остроугольный — в центре, прямоугольный — совпадает с образующей прямой угол вершиной, тупоугольный — внешний (находится за пределами треугольника).
- Ортоцентр остроугольного Δ — центр окружности, вписанной в него.
- Алгебраическая сумма квадратов расстояний от вершин до ортоцентра (KW, LW и MW) с учетом квадратов сторон (KL, LM и KM) эквивалентна двенадцати квадратам радиуса окружности R, которая описана вокруг треугольника: KW2 + LW2 + MW2 + KL2 + LM2 + KM2 = 12 * R2.
- Расстояние (К{kl}) от ортоцентра до середины стороны KL: К{kl} = KL / (2 * tg (∠K)). Для других величин (К{lm} и К{mk}): К{lm} = LM / (2 * tg (∠L)) и К{mk} = MK / (2 * tg (∠M)) соответственно.
- Величина расстояний от W до вершин (KW, LW и MW): KW = KL / tg (∠K), LW = LM / tg (∠L) и MW = KM / tg (∠M).
- Площадь S: S = KL2 * sin (∠K) / 2 = LM2 * sin (∠L) / 2 = KM2 * sin (∠M) / 2.
Существует определенный класс задач, в которых требуется найти координаты ортоцентра. В этом случае нужно начертить декартовую систему координат и отметить на ней вершины, а затем соединить их отрезками. Далее необходимо провести высоты и найти ортоцентр треугольника, а затем начертить из искомой точки проекции на координатные прямые.
Таким образом, расположение ортоцентра треугольника зависит от его вида и является важным параметром для построения вписанных и описанных окружностей.
Точка пересечения высот треугольника — свойства, координаты и расположение ортоцентра » Kupuk.

Точка пересечения высот треугольника называется ортоцентром и традиционно обозначается латинской буквой H. «Ортос» в переводе с греческого означает «прямой», «правильный». Ортоцентр может находиться внутри фигуры и вне ее. Местоположение зависит только от самой фигуры и не зависит от порядка расположения сторон и вершин.
Что такое высота
Если из вершины опустить перпендикуляр на противоположную сторону, получится отрезок, который именуется высотой. В равнобедренном треугольнике 2 отрезка равны, а в равностороннем равны все 3.
У фигур с углами 90 и более градусов высота попадает на противоположную сторону. В случае острого угла дело обстоит иначе. Прямая попадет только на продолжение противоположной стороны и будет находиться вне самой фигуры. Таким образом, если все углы острые, отрезки будут находиться внутри, как и ортоцентр. В тупоугольной фигуре два из трех отрезков будут проходить за его пределами — ортоцентр окажется вне фигуры.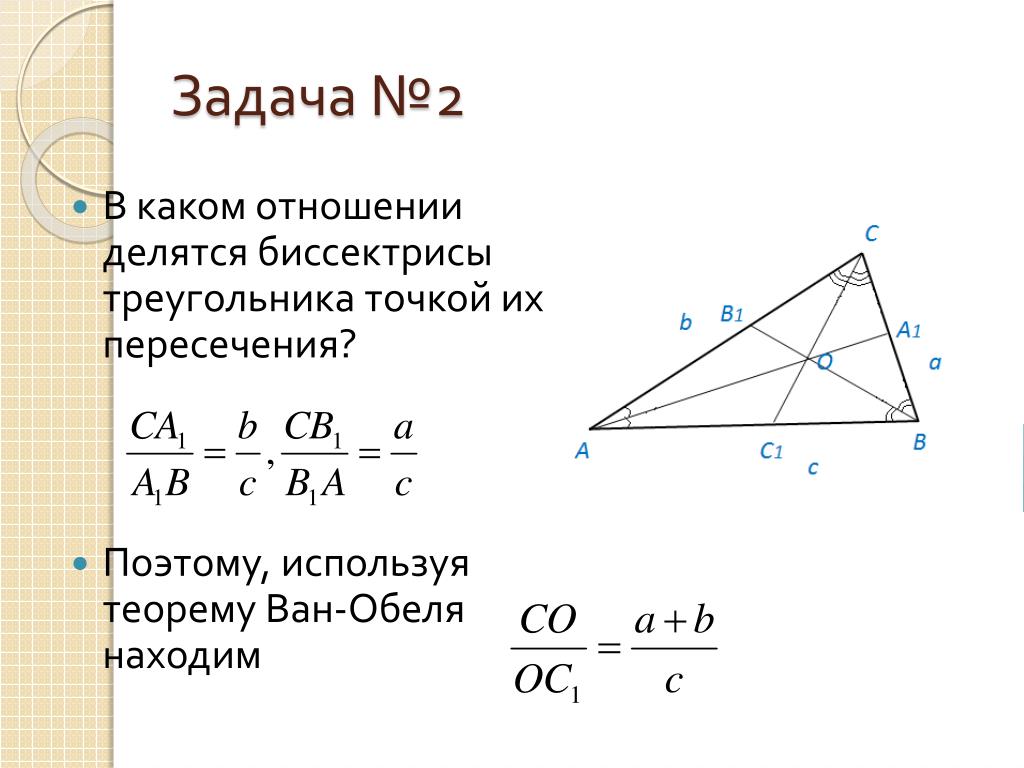
Свойства ортоцентра
Свойства высот треугольника, пересекающихся в одной точке, давно изучены и описаны. Согласно основному из них, все 3 высоты всегда пересекаются в одном месте. Иногда, чтобы найти это место, отрезки нужно продлить, превратив в ортогональные прямые.
Ортоцентр по отношению к фигуре может быть расположен:
- внутри;
- снаружи;
- в вершине (у прямоугольных треугольников)
Ортоцентр — важная в геометрии характеристика, влияющая на нахождение золотого сечения.
Так называется маленький треугольник, расположенный внутри основного, находящийся на пересечении его трех параметров:
- биссектрис,
- высот,
- медиан.
Золотое сечение может представлять собой не только треугольную фигуру, но и отрезок.
В правильном треугольнике медианы, биссектрисы и высоты совпадают, значит, золотое сечение превращается в точку.
Полезные факты
Местонахождение ортоцентра имеет некоторые закономерности. Их знание принесет пользу при решении задач.
Пусть:
- H — ортоцентр в ABC;
- О — центр описанной окружности.
Тогда:
- окружности, описанные вокруг АБС, АНВ, CHB, HCA, равны:
- отрезок BH вдвое длиннее отрезка АС;
- середины отрезков AC и BH разделены расстоянием, равным радиусу описанной окружности.
Задача Фаньяно
Это классическая теорема. Она возникла в процессе поиска фигур с наименьшим периметром. Теорему доказал Фаньяно — итальянский математик и инженер. Это произошло еще в начале XVIII века.
Формулировка: ортотреугольник, то есть фигура, полученная соединением трех оснований треугольника, проведенный внутри остроугольного треугольника, имеет самый маленький периметр изо всех возможных, вписанных в данную фигуру.
Площадь ортотреугольника рассчитывается по формуле:
Здесь S — площадь, а, b, c — стороны.
Существует понятие ортоцентрической системы. Оно включает в себя 3 вершины и место пересечения их высот. Любая из данных четырех точек будет являться ортоцентром треугольника, образованного тремя остальными.
История изучения
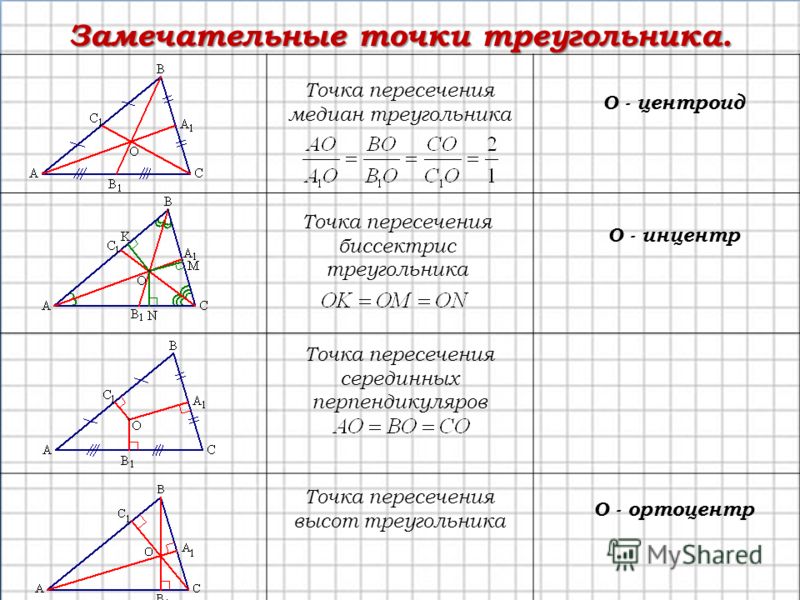
Важное значение имеет место пересечения медиан или центр тяжести. Вместе с ортоцентром это еще одна «замечательная точка», которая была известна еще древним грекам. Так их стали называть начиная с 18 века, другое название «особенные».
Исследование этих точек стало началом для создания геометрии треугольника, основателем которой считается Леонард Эйлер. Ученый показал, что в любом треугольнике точки соединения высот, медиан и центр описанного круга находятся на одной линии, которую позже назвали прямой Эйлера.
В позапрошлом веке была обнаружена окружность 9 точек или Фейербаха.
Каждый отрезок, прочерченный из ортоцентра до соединения с описанной окружностью, всегда будет делиться линией Эйлера на 2 равные части.
Треугольник — удивительная фигура, изучением которой занимается целый раздел геометрии. Ортоцентр и его свойства имеют широкое применение в практической жизни, например, в строительстве. Этот показатель настолько важен и распространен, что существуют калькуляторы, позволяющие определить местонахождение точки по координатам вершин.
Точка пересечения высот треугольника — свойства, координаты и расположение ортоцентра
Точка пересечения высот треугольника называется ортоцентром и традиционно обозначается латинской буквой H. «Ортос» в переводе с греческого означает «прямой», «правильный».
Содержание
- Что такое высота
- Свойства ортоцентра
- Полезные факты
- Задача Фаньяно
- История изучения
Что такое высота
Если из вершины опустить перпендикуляр на противоположную сторону, получится отрезок, который именуется высотой. В равнобедренном треугольнике 2 отрезка равны, а в равностороннем равны все 3.
У фигур с углами 90 и более градусов высота попадает на противоположную сторону. В случае острого угла дело обстоит иначе. Прямая попадет только на продолжение противоположной стороны и будет находиться вне самой фигуры. Таким образом, если все углы острые, отрезки будут находиться внутри, как и ортоцентр. В тупоугольной фигуре два из трех отрезков будут проходить за его пределами — ортоцентр окажется вне фигуры.
Свойства ортоцентра
Свойства высот треугольника, пересекающихся в одной точке, давно изучены и описаны. Согласно основному из них, все 3 высоты всегда пересекаются в одном месте. Иногда, чтобы найти это место, отрезки нужно продлить, превратив в ортогональные прямые.
Ортоцентр по отношению к фигуре может быть расположен:
- внутри;
- снаружи;
- в вершине (у прямоугольных треугольников)
Ортоцентр — важная в геометрии характеристика, влияющая на нахождение золотого сечения.
Так называется маленький треугольник, расположенный внутри основного, находящийся на пересечении его трех параметров:
- биссектрис,
- высот,
- медиан.
Золотое сечение может представлять собой не только треугольную фигуру, но и отрезок.
В правильном треугольнике медианы, биссектрисы и высоты совпадают, значит, золотое сечение превращается в точку.
Полезные факты
Местонахождение ортоцентра имеет некоторые закономерности. Их знание принесет пользу при решении задач.
Пусть:
- H — ортоцентр в ABC;
- О — центр описанной окружности.
Тогда:
- окружности, описанные вокруг АБС, АНВ, CHB, HCA, равны:
- отрезок BH вдвое длиннее отрезка АС;
- середины отрезков AC и BH разделены расстоянием, равным радиусу описанной окружности.
Задача Фаньяно
Это классическая теорема. Она возникла в процессе поиска фигур с наименьшим периметром. Теорему доказал Фаньяно — итальянский математик и инженер. Это произошло еще в начале XVIII века.
Формулировка: ортотреугольник, то есть фигура, полученная соединением трех оснований треугольника, проведенный внутри остроугольного треугольника, имеет самый маленький периметр изо всех возможных, вписанных в данную фигуру.
Площадь ортотреугольника рассчитывается по формуле:
Здесь S — площадь, а, b, c — стороны.
Существует понятие ортоцентрической системы. Оно включает в себя 3 вершины и место пересечения их высот. Любая из данных четырех точек будет являться ортоцентром треугольника, образованного тремя остальными.
История изучения
Важное значение имеет место пересечения медиан или центр тяжести. Вместе с ортоцентром это еще одна «замечательная точка», которая была известна еще древним грекам. Так их стали называть начиная с 18 века, другое название «особенные».
Исследование этих точек стало началом для создания геометрии треугольника, основателем которой считается Леонард Эйлер. Ученый показал, что в любом треугольнике точки соединения высот, медиан и центр описанного круга находятся на одной линии, которую позже назвали прямой Эйлера.
В позапрошлом веке была обнаружена окружность 9 точек или Фейербаха.
Каждый отрезок, прочерченный из ортоцентра до соединения с описанной окружностью, всегда будет делиться линией Эйлера на 2 равные части.
Треугольник — удивительная фигура, изучением которой занимается целый раздел геометрии. Ортоцентр и его свойства имеют широкое применение в практической жизни, например, в строительстве. Этот показатель настолько важен и распространен, что существуют калькуляторы, позволяющие определить местонахождение точки по координатам вершин.
Предыдущая
ГеометрияТеорема Чевы и Менелая — формулировка, применение и примеры решения
Следующая
ГеометрияТочка пересечения биссектрис — свойства, теорема и соотношения
Определение, свойства, формула, примеры, часто задаваемые вопросы
Ортоцентр указывает центр всех прямых углов от вершин к противоположным сторонам, т.
е. высоты. Термин «орто» означает «право», и считается, что это точка пересечения трех высот, проведенных из трех вершин треугольника. Ортоцентр имеет большое значение при изучении различных свойств треугольника по отношению к другим его измерениям. Давайте узнаем больше о свойствах ортоцентра, формуле ортоцентра, определении ортоцентра и решим несколько примеров.
| 1. | Определение ортоцентра |
| 2. | Свойства ортоцентра |
| 3. | Как построить ортоцентр? |
| 4. | Ортоцентр формулы треугольника |
| 5. | Часто задаваемые вопросы об Ортоцентре |
Определение ортоцентра
Ортоцентр можно определить как точку пересечения высот, проведенных перпендикулярно от вершины к противоположным сторонам треугольника. В треугольнике это та точка, где пересекаются все три высоты треугольника.
Три основных аспекта ортоцентра:
- Треугольник — многоугольник с тремя вершинами и тремя ребрами.
- Высота — Высотой треугольника называется линия, проходящая через его вершину и перпендикулярная противоположной стороне. Следовательно, треугольник может иметь три высоты, по одной из каждой вершины.
- Вершина. Точка, в которой встречаются две или более линий, называется вершиной.
Посмотрите на изображение ниже, △ABC — треугольник, △ABC имеет три высоты, а именно, AE, BF и, CD, △ABC имеет три вершины, а именно, A, B и, C, и точку пересечения H — ортоцентр.
Свойства ортоцентра
Свойства ортоцентра различаются в зависимости от типа треугольника, такого как равнобедренный треугольник, разносторонний треугольник, прямоугольный треугольник и т. д. Для некоторых треугольников ортоцентр не обязательно должен лежать внутри треугольника, но может быть размещен снаружи. Например, для равностороннего треугольника ортоцентр является центром тяжести.
Свойства следующие:
Свойство 1: Ортоцентр лежит внутри остроугольного треугольника. Как видно на рисунке ниже, ортоцентр — это точка пересечения линий PF, QS и RJ.
Свойство 2: Ортоцентр лежит вне треугольника тупоугольного треугольника. Как видно на изображении ниже, ортоцентр, образованный тремя пересекающимися линиями или высотами, лежит вне треугольника.
Свойство 3: Ортоцентр лежит в вершине прямого угла прямоугольного треугольника. Как видно на изображении ниже, точка пересечения лежит в точке C.
Свойство 4: Ортоцентр делит высоту на разные части. Произведение длин всех этих частей эквивалентно для всех трех перпендикуляров.
Как построить ортоцентр?
Чтобы построить ортоцентр треугольника геометрически, мы должны сделать следующее:
- Найти перпендикуляр из любых двух вершин к противоположным сторонам.
- Чтобы нарисовать перпендикуляр или высоту, используйте вершину C как центр и радиус, равный стороне BC.
Проведите дуги на противоположных сторонах АВ и АС.
- Нарисуйте пересекающиеся дуги из B и D в точке F. Соедините CF.
- Аналогичным образом проведите пересекающиеся дуги из точек C и E в точке G. Соедините BG.
- CF и BG — высоты или перпендикуляры к сторонам AB и AC соответственно.
- Точка пересечения любых двух высот треугольника дает ортоцентр.
- Таким образом, найдите точку пересечения двух высот.
- В этой точке H считается ортоцентром треугольника.
Ортоцентр формулы треугольника
Формула ортоцентра помогает определить координаты ортоцентра треугольника. Рассмотрим треугольник PQR, как показано на рисунке ниже.
PA, QB, RC — перпендикуляры, проведенные из трех вершин P[(x) 1 , (y) 1 ], Q[(x) 2 , (y) 2 ] и R[(x) 3 , (y) 3 ] соответственно △PQR.
H ( x, y) — точка пересечения трех высот треугольника.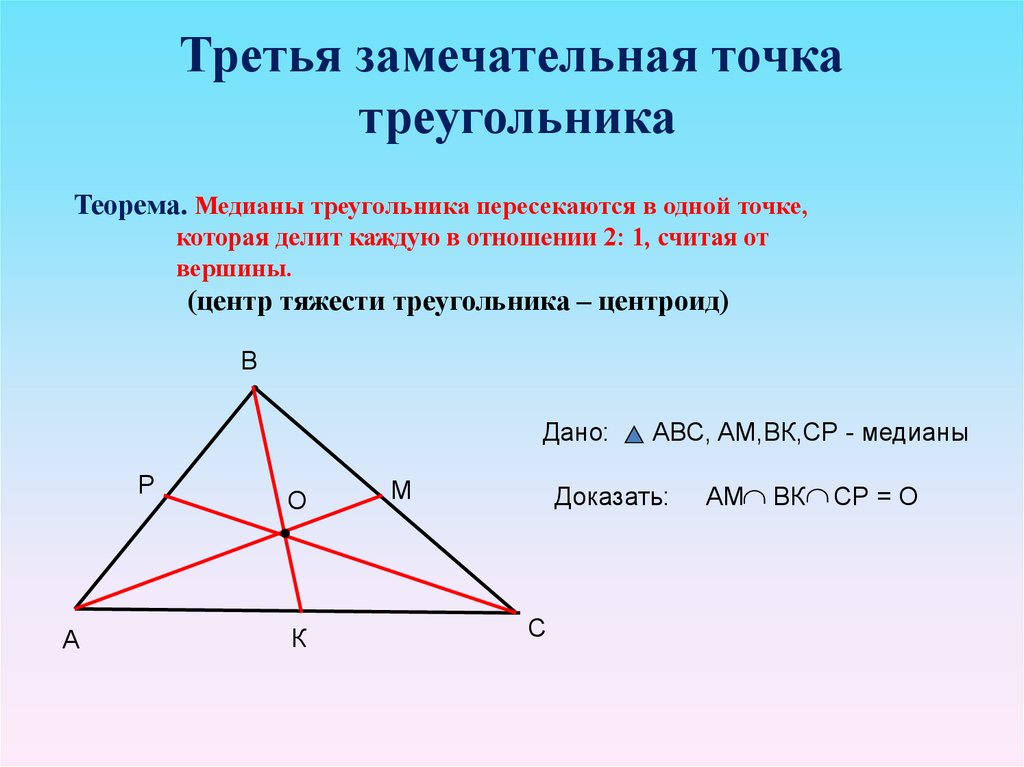
Шаг 1: Рассчитайте наклон сторон треугольника по формуле:
м(наклон) = ( frac{y_{2} — y_{1}}{x_{2} — x_{1}} )
Пусть наклон PR определяется mPR.
Следовательно,
mPR = ( frac{ y_3 — y_1 }{ x_3 — x_1 })
Аналогично,
mQR = ( frac{ y_3 — y_2 }{ x_3 — x_2 })
Шаг 2 Наклон высот △PQR будет перпендикулярен наклону сторон треугольника.
Мы знаем,
( begin{align*} text {Перпендикулярный наклон линии} &= \frac{-1}{ text {наклон линии}} \ &= frac{ -1}{ text m} end{align*})
Наклон соответствующих высот:
Наклон PA, mPA = ( frac{-1}{ text {mQR}})
Наклон QB, mQB = ( frac{ -1}{ text {mPR}})
Используем уравнение формы точки наклона как прямой для расчета уравнений линий, совпадающих с PA и КБ.
Обобщенное уравнение, сформированное с использованием произвольных точек (x) и (y), имеет вид:
( begin{align*} text {mPA} &= frac{( y — y_1 )}{( x — x_1 )} \ text {mQB} &= frac{( y — y_2)}{( x — x_2 )} end{align*} )
Таким образом, решение два уравнения для любых заданных значений можно вычислить ортоцентр треугольника.
Связанные темы
Ниже перечислены некоторые темы, связанные с ортоцентрированием, посмотрите.
- Инцентр
- Циркумцентр
- Части круга
- Типы треугольников
Часто задаваемые вопросы об ортоцентре
Что такое ортоцентр треугольника?
Ортоцентр треугольника — это точка пересечения высот, проведенных перпендикулярно из вершины к противоположным сторонам треугольника. Треугольник обычно имеет 3 высоты, и пересечение всех 3 высот называется ортоцентром. Размещение ортоцентра зависит от типа треугольника. Например, тупоугольный треугольник имеет ортоцентр вне треугольника. Ортоцентр обычно обозначается H.
Каковы свойства ортоцентра?
Свойства ортоцентра треугольника различаются в зависимости от типа треугольника, следовательно, свойства следующие:
- Ортоцентр лежит внутри треугольника остроугольного треугольника.
- Ортоцентр лежит вне треугольника тупоугольного треугольника.
- Ортоцентр лежит в вершине прямого угла прямоугольного треугольника.
- Ортоцентр делит высоту на разные части. Произведение длин всех этих частей эквивалентно для всех трех перпендикуляров.
Что такое формула ортоцентра?
Формула для вычисления ортоцентра треугольника заданных точек:
( begin{align*} text {mPA} &= frac{( y — y_1 )}{( x — x_1 )} \ text {mQB} &= frac{( y — y_2)}{( x — x_2 )} end{align*} )
Почему это называется ортоцентром?
Термин «орто» означает «право», а центр означает середину. Таким образом, объединение двух слов здесь означает центр высот (прямых углов) треугольника. Следовательно, он называется ортоцентром.
Почему важен ортоцентр?
Ортоцентр треугольника — это точка пересечения всех трех высот, проведенных от вершин треугольника к противоположным сторонам. Это важная центральная точка треугольника и, таким образом, помогает в изучении различных свойств треугольника по отношению к сторонам, вершинам, другим важным точкам, таким как центр описанной окружности, центр тяжести и т.
Ортоцентр и центр окружности — одно и то же?
Нет, ортоцентр и центр описанной окружности треугольника различны. Ортоцентр треугольника — это точка пересечения всех трех высот, проведенных от вершин треугольника к противоположным сторонам. Центр описанной окружности треугольника — это точка пересечения биссектрисы трех сторон.
В чем разница между ортоцентром и инцентром?
Центр вписанной окружности — это точка, в которой сходятся три биссектрисы трех вершин треугольника. Эта точка также считается началом круга, вписанного внутрь этого круга. Тогда как ортоцентр — это точка пересечения трех высот треугольника.
В чем разница между центроидом, ортоцентром, центром окружности и вписанным центром?
Центр описанной окружности — это точка, равноудаленная от всех вершин треугольника и обозначаемая как O. Центр вписанной окружности — это точка, равноудаленная от сторон треугольника и обозначаемая как I. Ортоцентр — это точка где все высоты треугольника пересекаются, и он обозначается как H.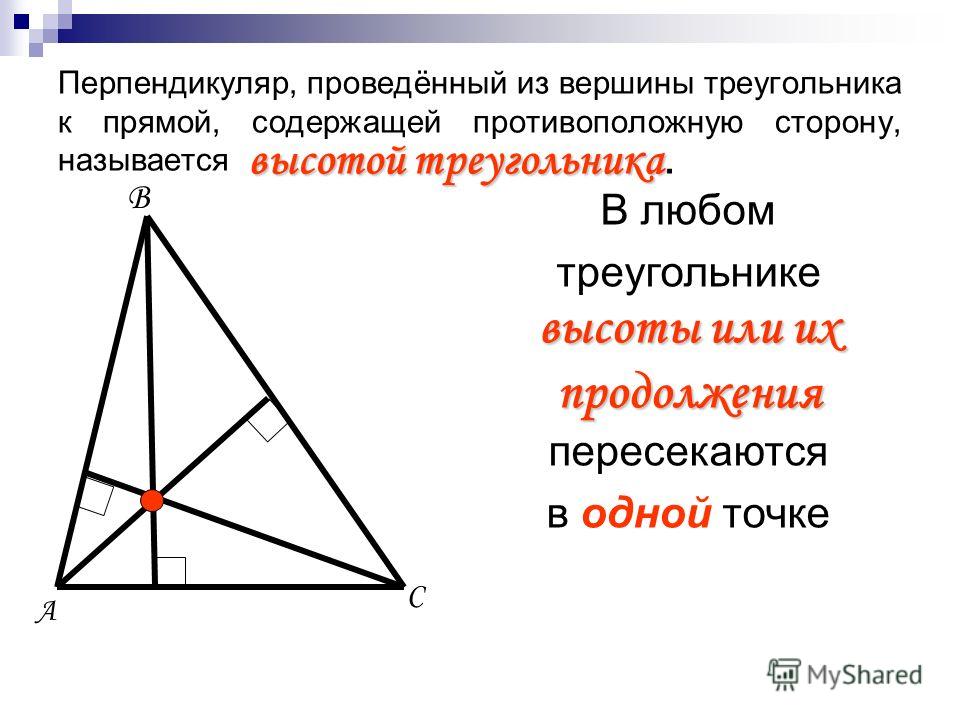
Ортоцентр, центроид, центр окружности и центр вписанной треугольника
В этой статье мы обсудим ортоцентр, центроид, центр описанной окружности и центр вписанной треугольника. Но прежде чем обсуждать эти важные характеристики треугольника, сначала давайте посмотрим, что такое треугольник.
Введение
Треугольник определяется как:
Трехсторонний многоугольник с тремя ребрами и тремя вершинами
Одной из наиболее важных характеристик треугольника является то, что сумма внутренних углов треугольника всегда равна равен 180 градусам. Если XYZ — треугольник, то мы можем обозначить его как . Здесь X, Y и Z — три вершины треугольника XYZ.
Как мы уже упоминали выше, треугольник — это многоугольник, имеющий три стороны. Две стороны треугольника соединяются встык, образуя вершину треугольника. Также создается угол между двумя сторонами. Треугольник классифицируется на различные типы в зависимости от его углов.
В следующем разделе мы обобщили некоторые важные свойства треугольника.
Лучшие репетиторы по математике
Поехали
Свойства треугольника
Каждая геометрическая фигура в математике обладает некоторыми уникальными свойствами, которые отличают эту фигуру от других. Треугольник также имеет свои уникальные свойства, которые отличают его от других фигур. Некоторые свойства треугольника обсуждаются ниже:
- Треугольник состоит из трех сторон и трех углов. Сумма трех внутренних углов треугольника всегда равна 180 градусам.
- Сумма внешних углов треугольника всегда равна 360 градусам.
- Сумма последовательных внутренних и внешних углов всегда равна 180 градусам, что означает, что они являются дополнительными
- Если сложить длины двух сторон треугольника, то полученная сумма всегда больше длины третьей стороны .
- Разница между длинами двух сторон треугольника всегда меньше длины третьей стороны.
- Сторона, противоположная наименьшему внутреннему углу треугольника, всегда является самой короткой стороной треугольника.
- Сторона, противоположная наибольшему внутреннему углу треугольника, всегда является самой длинной стороной треугольника
В следующем разделе мы обсудим ортоцентр, центроид, центр описанной окружности и центр вписанной треугольника.
Ортоцентр
Ортоцентр треугольника определяется как:
точка пересечения трех высот треугольника
Или
Точка, в которой все три высоты треугольника встречаются или пересекают друг друга.
Высота или высота — это каждая из перпендикулярных линий , проведенных от одной вершины к противоположной стороне (или ее продолжению).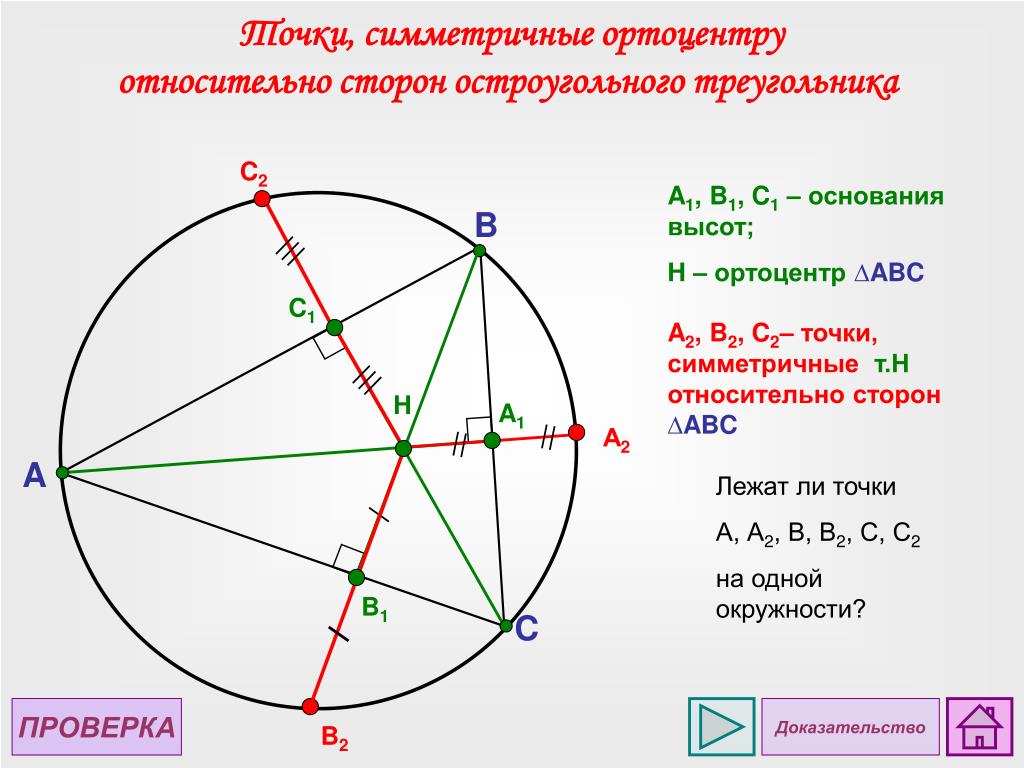
См. следующий треугольник. Точка H является ортоцентром этого треугольника, потому что это точка, в которой все три высоты треугольника пересекаются друг с другом.
Ортоцентр различен для различных треугольников, таких как равнобедренный, разносторонний, равносторонний, остроугольный и т. д. Для равностороннего треугольника центр тяжести будет ортоцентром. В случае других типов треугольников положение точки пересечения всех трех высот будет разным.
- Ортоцентр остроугольного треугольника лежит внутри треугольника
- Ортоцентр тупоугольного треугольника лежит outside the triangle
- The orthocenter of a right-angled triangle lies on the vertex of the right angle
Centroid
The centroid is defined as:
The point of пересечение трех медиан .

Медиана относится к прямой линии , которая соединяет среднюю точку стороны с противоположная вершина.
Центроид обладает следующими свойствами:
- Центроид относится к центру объекта и является центром тяжести
- Он всегда лежит внутри треугольника
- Это точка пересечения или совпадения трех медиан треугольника
Центроид треугольника показан на рисунке ниже:
Центроид делит каждую медиану на два сегмента , отрезок, соединяющий центр тяжести с вершиной, в два раза длиннее отрезка, соединяющего среднюю точку с противоположной стороной. В случае приведенного выше треугольника мы можем обозначить его как:
BG = 2GA
Следовательно, мы можем заключить, что центроид разделяет медиану треугольника в отношении 2 : 1. Мы можем найти центроид треугольника путем вычисления среднего значения x-координатных точек и y-координатных точек всех трех вершин треугольника.
Например, рассмотрим следующий пример:
Найдите центроид треугольника с вершинами (3, 4), (5, 7) и (4, 7).
Чтобы найти центр тяжести, нам нужно взять среднее значение x-координат и y-координат отдельно. (4, 6) Точка пересечения из три перпендикулярных биссектрисы .
биссектриса треугольника — это каждая линия, проведенная перпендикулярно из его середины. Центр описанной окружности является центром описанной окружности треугольника (описанной окружности). Центр описанной окружности треугольника показан на рисунке ниже:
Другими словами, мы можем сказать, что точка пересечения биссектрис трех сторон треугольника называется центром описанной окружности треугольника.
Некоторые свойства центра описанной окружности треугольника обсуждаются ниже:
- Центр описанной окружности треугольника является центром описанной окружности
- Все три вершины треугольника равноудалены от центра описанной окружности треугольника
- центр описанной окружности лежит внутри остроугольного треугольника
- центр описанной окружности лежит вне тупоугольного треугольника
- центр описанной окружности в прямоугольном треугольнике лежит в середине гипотенузы стороны
Центр вписанной окружности
Центр треугольника определяется как:
Точка пересечения трех биссектрис угла
Биссектрисы угла треугольника — это каждая из линий, которые делят угол на две части равные углы.
Таким образом, мы можем сказать, что центр вписанной треугольника является точкой пересечения всех трех биссектрис треугольника. Центр вписанной стороны всегда равноудален от трех сторон треугольника.
Центр треугольника показан на рисунке ниже:
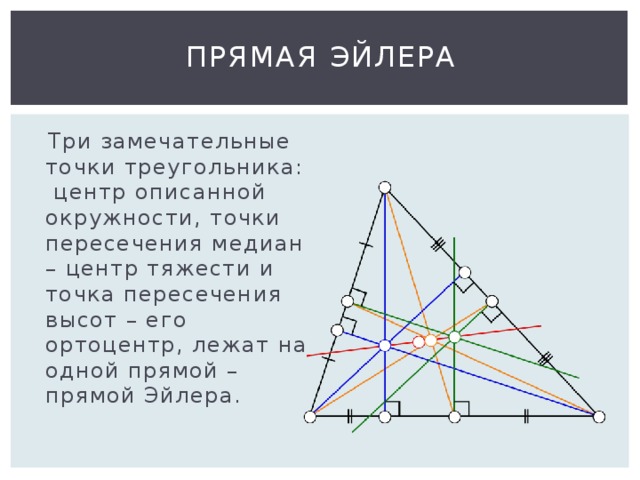
Линия Эйлера
Ортоцентр , центр тяжести , и центр описанной окружности неравностороннего треугольника выровнены. Это означает, что они лежат на одной прямой, называемой прямой Эйлера .
На приведенном ниже рисунке видно, что ортоцентр, центр тяжести и центр описанной окружности лежат на одной прямой и представлены буквами O, G и H. Эта прямая является линией Эйлера.
Свойства треугольника
Треугольник — это многоугольник с тремя вершинами. Вершина — это точка, в которой сходятся две или более линий или ребер.
Типы треугольников
Треугольники можно классифицировать в зависимости от длины их сторон. Тремя наиболее распространенными типами треугольников являются равносторонний треугольник, равнобедренный треугольник и разносторонний треугольник. У равностороннего треугольника все стороны одинаковой длины. У равнобедренного треугольника две стороны одинаковой длины. Разносторонний треугольник имеет разную длину с каждой стороны.
Равенство и конгруэнтность
Для любого заданного угла градусная мера этого угла определяет его отношение к другим углам того же треугольника. Сумма углов треугольника равна 180 градусов. Если два угла в треугольнике имеют одинаковую меру, то говорят, что такие треугольники равны. Треугольники также можно разделить на остроугольные, прямоугольные и тупоугольные в зависимости от величины их наибольшего угла.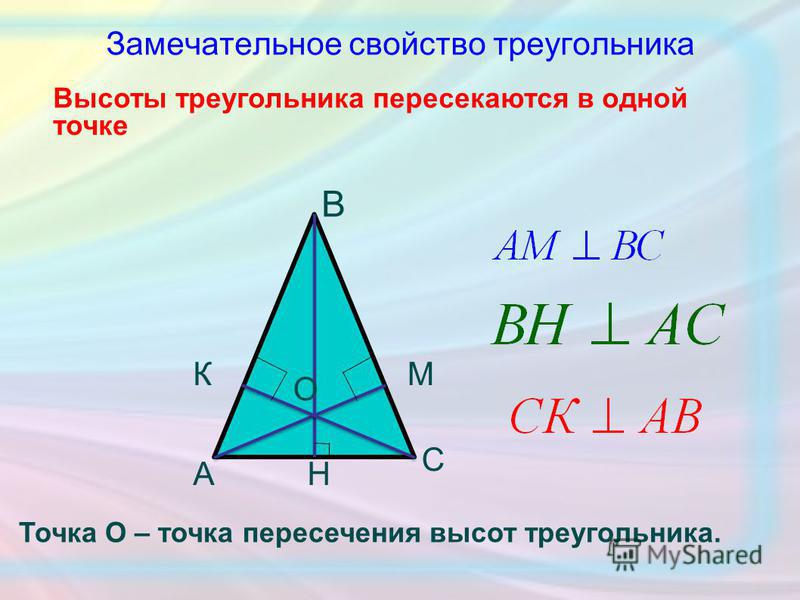
В равностороннем треугольнике все стороны имеют одинаковую длину, а каждый угол равен 60 градусов. В равнобедренном треугольнике две стороны одинаковой длины и два равных угла. Стороны разностороннего треугольника имеют разную длину, а углы разностороннего треугольника имеют разную величину.
Угол в треугольнике считается острым, если его размер меньше 90 градусов. Угол в треугольнике тупой, если он больше 90 градусов и меньше 180 градусов.
Введение
Термины, относящиеся к треугольникам
Медиана: Отрезок, соединяющий вершину с серединой противоположной стороны треугольника, называется медианой треугольника. На рисунке ABC D является серединой AB. Таким образом, AD образует медиану треугольника ABC. Точно так же медиану можно провести как из середины BC, так и из CA. Другими словами, треугольник может иметь три медианы.
Центроид: Точка пересечения трех медиан треугольника называется центроидом.
Высота: Длина перпендикуляра из вершины к противоположной стороне треугольника называется его высотой, а сторона, на которую проведен перпендикуляр, называется его основанием. В треугольнике ABC перпендикуляр, проведенный к BC, то есть AL, является высотой. Сторона ВС называется основанием треугольника.
Ортоцентр: Точка пересечения (или совпадения) трех высот треугольника называется его ортоцентром. Точка встречи (H) высот AL, CN и BM треугольника называется ортоцентром.
В центре и вписанной окружности: Точка пересечения внутренних биссектрис угла треугольника называется центром. Здесь точка I, являющаяся точкой пересечения биссектрис углов A, B и C, называется центром. Центр окружности также является центром окружности, которая касается всех сторон треугольника.
Центр окружности и окружность: Точка пересечения серединных перпендикуляров к сторонам треугольника ABC называется центром описанной окружности.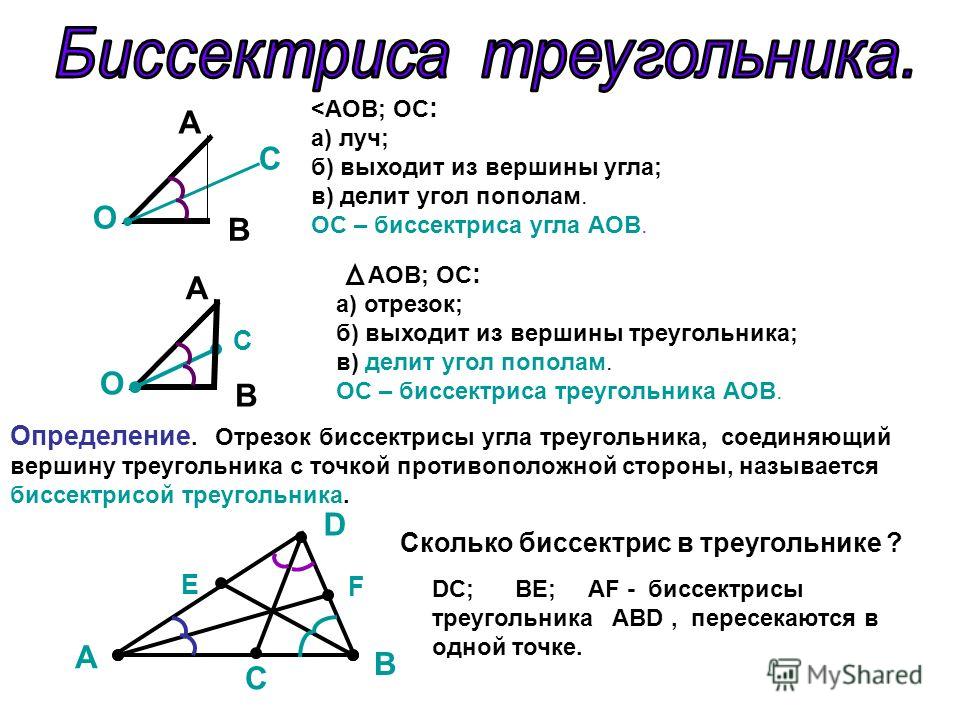
Свойства треугольника
Свойство суммы углов треугольника: Сумма углов Свойство треугольника гласит, что сумма всех трех углов треугольника равна 180 градусам.
Внешний угол Свойство: Каждую сторону треугольника можно продолжить в обе стороны. Три стороны треугольника порождают шесть расширенных сторон, каждая из которых образует расширенные стороны. Внешний угол — это угол между одной стороной и одной продолженной стороной треугольника. В треугольнике три вытянутые стороны, и каждая вытянутая сторона дает один внешний угол, следовательно, у треугольника шесть внешних углов. На приведенной ниже диаграмме углы 1, 2, 3, 4, 5 и 6 являются внешними углами треугольника.
Примечание. Углы между двумя вытянутыми сторонами не являются внешними углами.
Внешний угол Свойство утверждает, что:
-
Сумма любых двух внутренних углов треугольника равна противоположному внешнему углу.
-
Сумма эквивалентных внешних углов треугольника всегда равна 360 градусам.
Свойства подобных треугольников
Подобные треугольники имеют одинаковые основные формы. Треугольники с одинаковыми углами, но разными размерами называются подобными треугольниками, так как отношение сторон остается неизменным. Повернутые треугольники или треугольники зеркального отображения также называются подобными треугольниками, поскольку углы и размеры одинаковы.
Подобные треугольники можно определить тремя способами:
-
Угол Угол Угол: Два треугольника называются подобными, если все три стороны одного треугольника равны соответствующим углам другого треугольника.
-
Сторона Сторона Сторона: два треугольника называются подобными, если стороны одного треугольника равны или находятся в таком же отношении к соответствующим сторонам другого треугольника.
-
Сторона Угол Сторона: Два треугольника называются подобными, если две стороны одного треугольника равны или находятся в отношении к соответствующим сторонам другого треугольника при условии, что углы между ними равны.
Срединное свойство треугольника
-
Делит пополам угол при вершине равнобедренного и равностороннего треугольника, смежные стороны которого равны.
-
Он также делит пополам угол при вершине равнобедренного и равностороннего треугольника.
-
В треугольнике всего три медианы.
-
Точка пересечения медиан называется центроидом.
-
Делит площадь треугольника на две половины.
-
Длина каждой медианы делится в соотношении 2:1 на центр тяжести.
-
Центроид делит треугольник на 6 меньших треугольников равной площади.
-
Все медианы равносторонних треугольников равны.
-
Медианы, проведенные из вершин равнобедренного треугольника с равными углами, равны по длине.
-
Длина всех медиан разностороннего треугольника различна.
-
Теорему Аполлония можно использовать для нахождения длины медиан.
Свойства центра описанной окружности треугольника
-
Центр описанной окружности является центром описанной окружности треугольника.
-
Вершины находятся на одинаковом расстоянии от центра описанной окружности треугольника.
-
В остроугольном треугольнике центр описанной окружности всегда находится внутри треугольника.
-
В тупоугольном треугольнике центр описанной окружности находится вне треугольника.
-
В прямоугольном треугольнике центр окружности находится в середине гипотенузы.
Свойства центра окружности треугольника
Свойства биссектрисы угла треугольника
-
Точка на биссектрисе угла треугольника равноудалена от его сторон.
-
Всегда есть общая точка, в которой пересекаются биссектрисы треугольника.
-
Доказывает соответствие между двумя углами.
Свойства центра треугольника
Свойства центра тяжести треугольника
-
Это пересечение трех медиан треугольника.
-
Это точка конгруэнтности треугольника.
-
Всегда находится внутри треугольника.
-
Действует как центр тяжести треугольника.
-
Каждая медиана делится в отношении 2:1.
Классификация треугольников на основе сторон и их свойств
Разносторонний треугольник: Треугольник, в котором все стороны имеют разную длину, называется разносторонним треугольником.
Свойства
-
У разностороннего треугольника все стороны разные.
-
Имеет неравные углы.
-
Самая длинная сторона находится прямо напротив наибольшего угла.
-
Его нельзя разделить на две равные половины.
-
Не имеет оси симметрии.
-
Разносторонний треугольник может быть остро разносторонним треугольником, тупым разносторонним треугольником или прямоугольным разносторонним треугольником.
-
Площадь разностороннего треугольника можно вычислить по формуле Герона, если известны все стороны.
-
Когда разносторонний треугольник вписан в окружность, каждый угол равен половине угла, опирающегося на противоположную сторону.
-
Центр описанной окружности лежит внутри треугольника, если все три угла острые.
Равнобедренный треугольник: Треугольник, две стороны которого имеют одинаковую длину, называется равнобедренным треугольником. В равнобедренном треугольнике углы, лежащие при равных сторонах, равны. В приведенном ниже треугольнике две стороны равны 5 дюймам, а одна сторона равна 3 дюймам. Таким образом, это равнобедренный треугольник.
Свойства:
-
Две стороны конгруэнтны друг другу.
-
Неравная сторона равнобедренного треугольника называется основанием.
-
Два угла, противоположные равным сторонам, равны друг другу. Значит, у него два равных угла при основании.
-
Угол при вершине — это угол, который не равен двум конгруэнтным углам при основании.
-
Высота, проведенная из вершины равнобедренного треугольника, делит основание на две равные части, а также делит угол при вершине на два равных угла.
-
Площадь равнобедренного треугольника = ½ × основание × высота
-
Периметр равнобедренного треугольника = сумма всех трех сторон
-
Третий неравный угол равнобедренного может быть острым или тупым.
-
Центр описанной окружности равнобедренного треугольника лежит внутри треугольника, если все три угла трех треугольников острые.
-
Стороны треугольника являются хордами описанной окружности.
-
Если один из углов равен 90 градусов, то центр описанной окружности лежит вне треугольника.
-
Центр тяжести – это пересечение медиан равнобедренного треугольника.
-
Медиана, проведенная из вершины, делит треугольник под прямым углом.
-
Биссектрисы равнобедренного треугольника пересекаются в центре описанной окружности.
-
Биссектрисы равнобедренного треугольника пересекаются в центре вписанной стороны.
-
Окружность, нарисованная с центром в центре, касается трех сторон треугольника внутри.
-
Каждая медиана делит равнобедренный треугольник на два равных треугольника, имеющих одинаковую площадь.
-
Площадь треугольника можно оценить:
-
Если известны меры одного угла и одной стороны
-
Если даны три стороны треугольника.
-
Если даны две стороны равнобедренного треугольника и углы между ними.
-
Соединение середины трех сторон делит треугольник на 4 меньших треугольника той же площади.
-
Когда нарисована окружность с диаметром, равным основанию:
-
Для тупоугольного равнобедренного треугольника вершина лежит внутри окружности.
-
В прямоугольном равнобедренном треугольнике вершина лежит на окружности.
-
Для остроугольного равнобедренного треугольника вершина лежит вне треугольника.
-
Когда вершина средней точки принимается за радиус и рисуется окружность с серединой основания в качестве центра
-
Для остроугольных равнобедренных вершин вершины основания лежат внутри окружности.
-
Для прямоугольного равнобедренного треугольника вершины основания лежат на окружности
-
Для тупоугольного равнобедренного треугольника вершины основания лежат вне окружности.
Равносторонний треугольник
Треугольник, у которого все три стороны имеют одинаковую длину, называется равносторонним треугольником.
Свойства:
-
Все стороны равностороннего треугольника всегда одинаковы.
-
Все углы равностороннего треугольника равны.
-
Медиана, высота, биссектриса угла, биссектриса перпендикуляра совпадают на одной линии.
-
Медиана, высота, биссектриса и биссектриса угла образуют линию симметрии равностороннего треугольника.
-
Длина всех медиан, высоты, биссектрисы перпендикуляра и биссектрисы угла одинакова.
-
Площадь равностороннего треугольника равна 23/4 с2.
Здесь s — стороны равностороннего треугольника.
-
Ортоцентр, центр описанной окружности, центр вписанной окружности и центр тяжести лежат в одной и той же точке.
-
Каждая высота является медианой равностороннего треугольника.
-
Центр тяжести – это точка пересечения биссектрисы угла, медианы, а также серединного перпендикуляра треугольника.
-
Центр вписанной окружности и центр окружности равностороннего треугольника совпадают.
-
Площадь равностороннего треугольника можно оценить:
-
Если известны меры одного угла и одной стороны
-
Если даны три стороны треугольника.
-
Если даны две стороны треугольника и углы между ними.
Классификация треугольников на основе углов и их свойств
Остроугольный треугольник: треугольник, в котором каждый угол больше нуля градусов, но меньше 9 градусов.0 градусов называется остроугольным треугольником. Все внутренние углы приведенного ниже треугольника равны 30, 70 и 80 градусов, т. е. все меньше 90 градусов.
Свойства:
-
Все три угла острые.
-
Его серединные перпендикуляры пересекаются в центре описанной окружности, а медиана пересекается в центре тяжести.
-
Центр описанной окружности остроугольного треугольника лежит внутри треугольника.
-
Биссектрисы пересекаются в центре окружности. Можно нарисовать круг с центром треугольника в качестве центра круга, чтобы он касался трех сторон треугольника внутри.
-
Если соединить середины трех сторон треугольника, то получится 3 параллелограмма одинаковой площади и 4 треугольника одинаковой площади.
Тупоугольный треугольник: Треугольник, в котором один из углов больше 90 градусов, но меньше 180 градусов, называется тупоугольным треугольником. В данном треугольнике один угол равен 120 градусам, что больше 90 градусов, а два других угла меньше 90 градусов.
Свойства:
-
Имеет два острых и один тупой угол.
-
Серединные перпендикуляры пересекаются в центре описанной окружности.
-
Медианы пересекаются в центре тяжести.
-
Центр описанной окружности всегда лежит вне треугольника.
-
Биссектрисы пересекаются в центре треугольника. Нарисован круг с центром, так как его центр касается трех сторон треугольника внутри.
-
Медианы делят треугольник на два меньших треугольника, имеющих одинаковую площадь.
-
Если соединить середины трех сторон треугольника, получится 3 параллелограмма одинаковой площади и 4 треугольника одинаковой площади.
Прямоугольный треугольник: Прямоугольным треугольником называется треугольник, в котором одна из мер углов ровно 90 градусов. В приведенном ниже треугольнике один из трех углов треугольника равен 90 градусов, а два других угла меньше 9 градусов.






 Для печати
Для печати
 Предыдущая тема | Следующая тема
Предыдущая тема | Следующая тема 





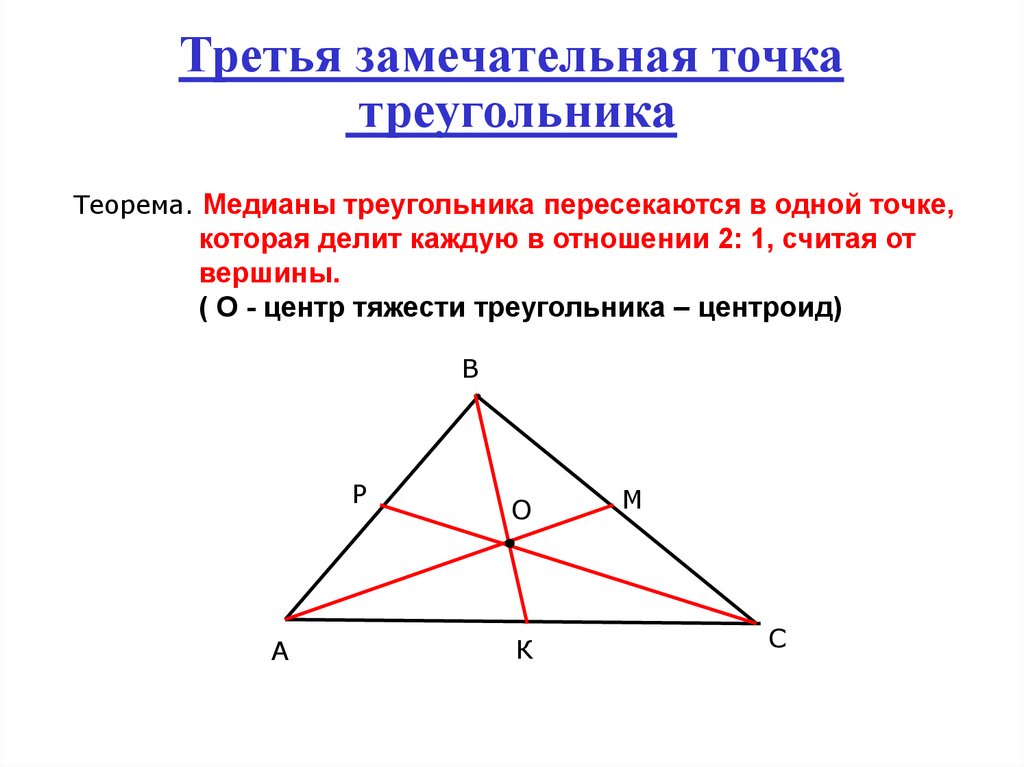
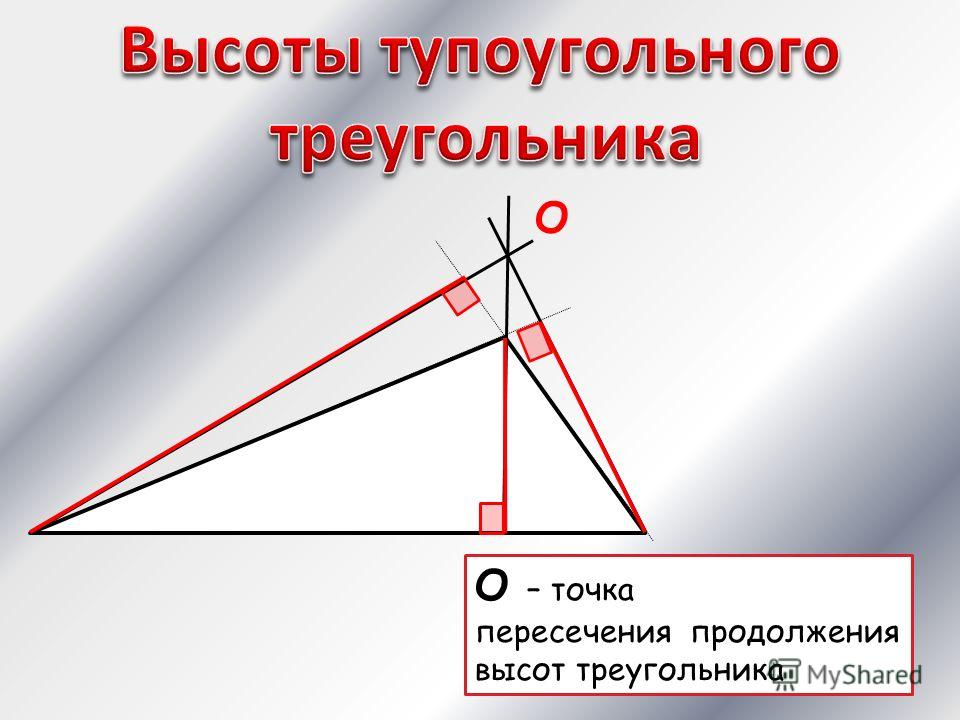
 Аналогичную операцию нужно выполнить для вершины К (KU к LM).
Аналогичную операцию нужно выполнить для вершины К (KU к LM). Для этого случая математики вывели полезные свойства и соотношения, облегчающие нахождение неизвестной величины или доказательства нового утверждения.
Для этого случая математики вывели полезные свойства и соотношения, облегчающие нахождение неизвестной величины или доказательства нового утверждения.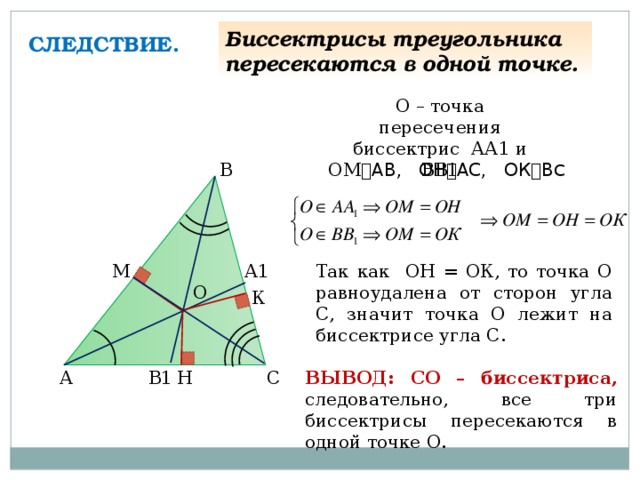
 В правильном треугольнике медианы, биссектрисы и высоты совпадают, значит, золотое сечение превращается в точку.
В правильном треугольнике медианы, биссектрисы и высоты совпадают, значит, золотое сечение превращается в точку. 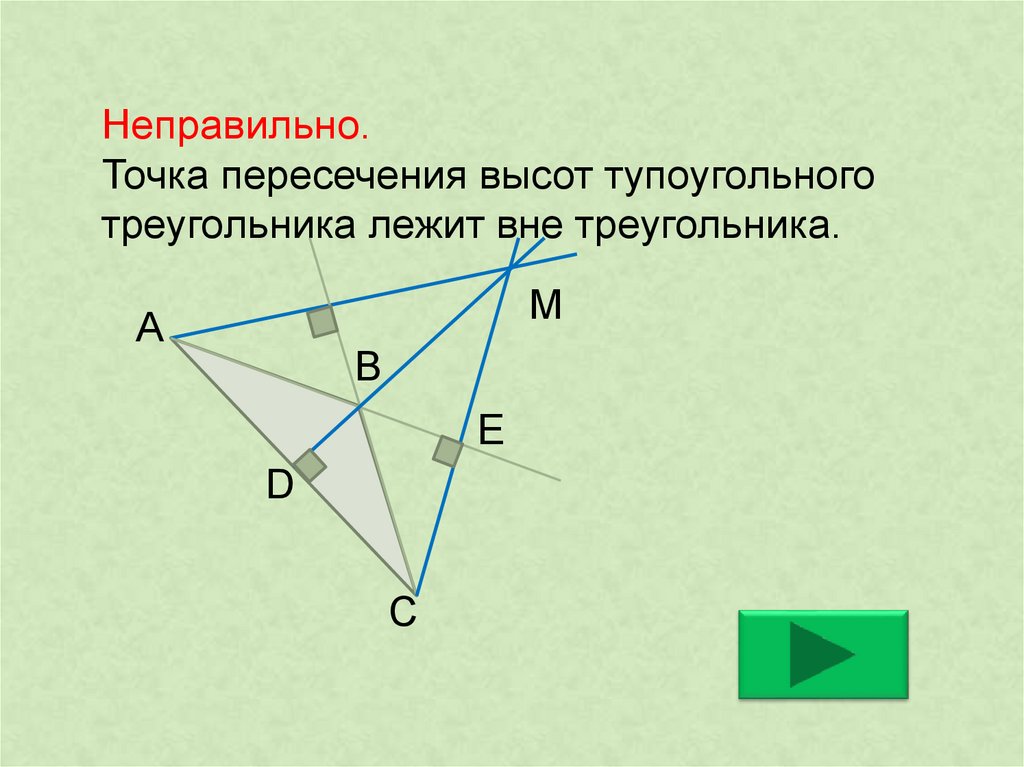 В правильном треугольнике медианы, биссектрисы и высоты совпадают, значит, золотое сечение превращается в точку.
В правильном треугольнике медианы, биссектрисы и высоты совпадают, значит, золотое сечение превращается в точку. 


 Проведите дуги на противоположных сторонах АВ и АС.
Проведите дуги на противоположных сторонах АВ и АС. 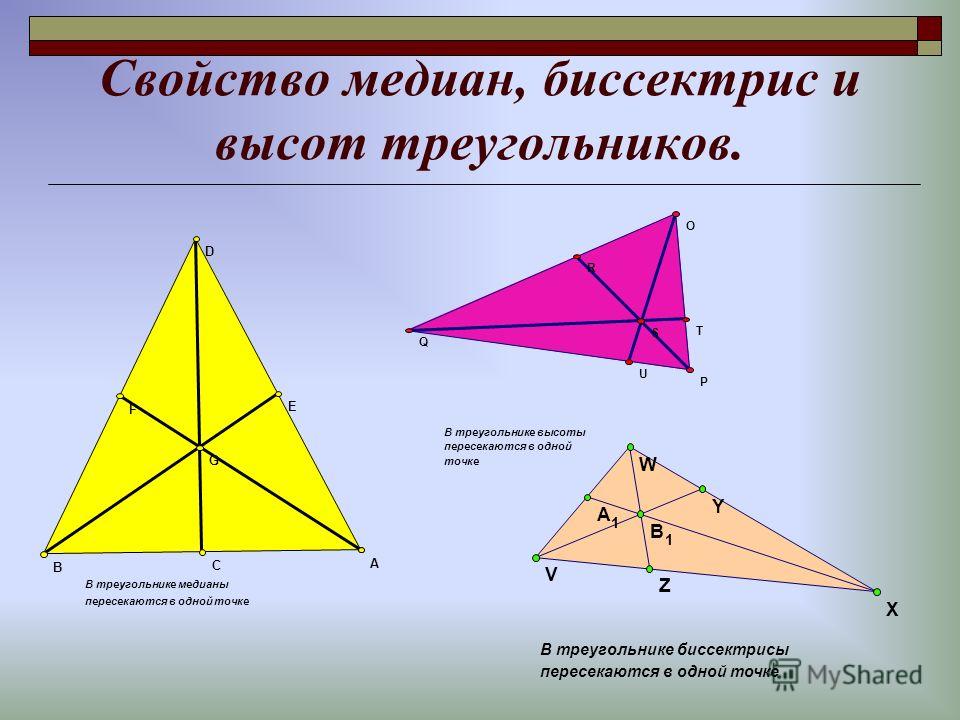






 Здесь s — стороны равностороннего треугольника.
Здесь s — стороны равностороннего треугольника.