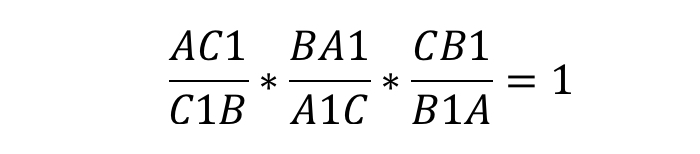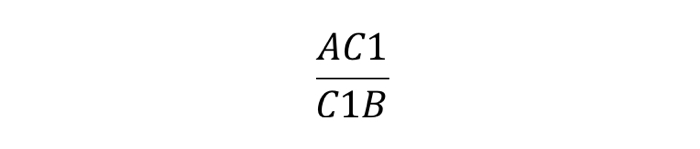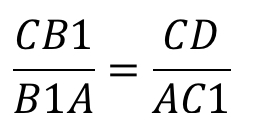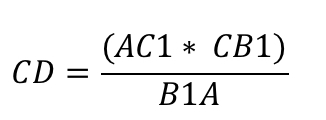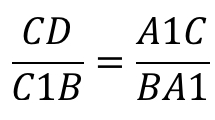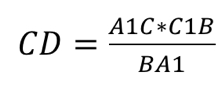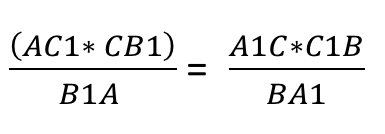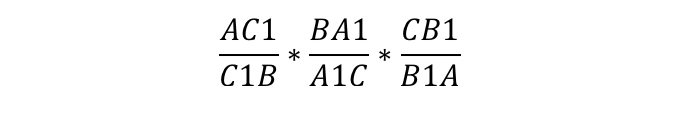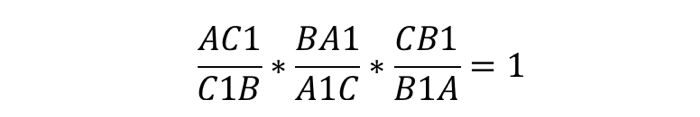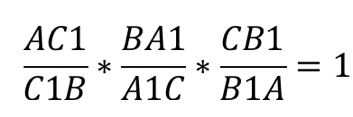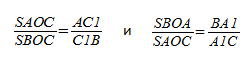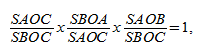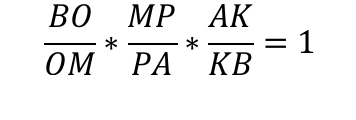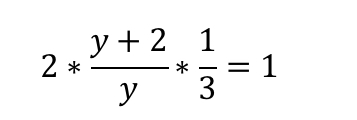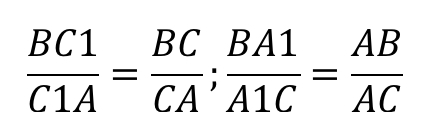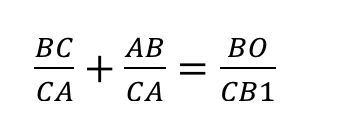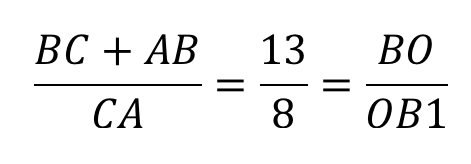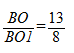Нужно ли доказывать теорему чевы в егэ - Помощь в подготовке к экзаменам и поступлению

Анна Малкова

Эти две полезные теоремы – теорема Менелая и теорема Чевы — чаще применяются при решении олимпиадных задач, чем на ЕГЭ по математике. Однако в 2020 году в ряде вариантов ЕГЭ обнаружилась задача по планиметрии (№16), которую на первый взгляд невозможно решить без теоремы Менелая или теоремы Чевы. Но на самом деле, конечно, возможно. Например, в Санкт-Петербурге попались такие задачи.

Разберемся, что это за теоремы и как применяются. И действительно ли на ЕГЭ дали задачи на применение теорем, выходящих за рамки школьной программы. И можно ли эти задачи решить по-другому?

Теорема Менелая:

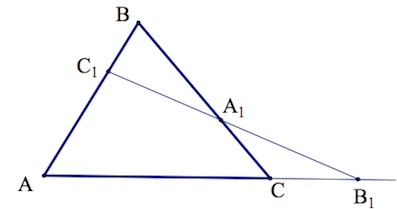
Пусть прямая пересекает произвольный треугольник ABC, причем C_1 – точка ее пересечения со стороной AB, A_1 – точка ее пересечения со стороной BC, и B_1 – точка ее пересечения с продолжением стороны AC.

Тогда выполняется равенство:

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_1}{A_1C} cdot frac{CB_1}{B_1A} = 1.$

Как это запомнить? Сначала рисуем треугольник ABC. Затем прямую, пересекающую две его стороны и продолжение третьей. На этой прямой лежат точки и B_1, причем на стороне должна лежать точка C_1, на стороне – точка A_1 и на продолжении – точка B_1.

Затем записываем равенство так, как будто «обходим» весь треугольник ABC, от точки к точкам и и затем возвращаемся в точку Но по дороге нам встречаются точки и B_1 – их тоже включаем в формулу.

Один из учащихся нашей ЕГЭ-Студии предложил такое мнемоническое правило: пусть точки A, B и – это города, а точки и B_1 – заправки, где можно пополнить запас бензина. Тогда правило звучит так: «Едем из города в город, заезжаем на заправку!»Возможно, вы придумаете свое правило : -)

В некоторых задачах полезна обратная теорема Менелая.

Теорема (Менелая, обратная). Пусть дан треугольник Предположим, что точка лежит на стороне точка лежит на стороне а точка лежит на продолжении стороны причём про эти точки известно, что

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_1}{A_1C} cdot frac{CB_1}{B_1A} = 1.$

Тогда эти точки лежат на одной прямой.

Как правило, не так-то просто бывает доказать, что три точки лежат на одной прямой. Обычно мы используем для доказательства такого факта косвенные методы. Например, если для точек A, , B и выполняется равенство: – то это означает, что точка лежит на отрезке AC. Или, если нам удается доказать, что угол ABC – развернутый, это и будет означать, что точки A, , B и лежат на одной прямой. Обратная теорема Менелая дает еще один способ доказательства того, что три точки – в данном случае и C_1 – лежат на одной прямой.

Теорема Чевы

Пусть точки и C_1 лежат соответственно на сторонах и треугольника ABC, причем отрезки и CC_1 пересекаются в одной точке. В этом случае выполняется равенство:

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_1}{A_1C} cdot frac{CB_1}{B_1A} = 1.$

Обратная теорема Чевы:

Теорема (Чевы, обратная). Пусть точки лежат соответственно на сторонах и треугольника причём

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_1}{A_1C} cdot frac{CB_1}{B_1A} = 1.$

Тогда отрезки и пересекаются в одной точке.

Как применяются теоремы Менелая и Чевы?

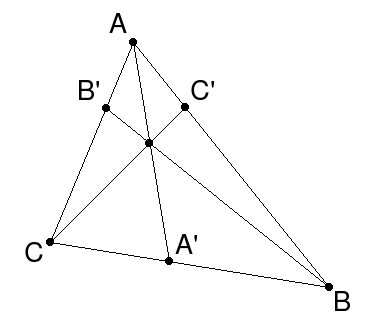
Вот задача Профильного ЕГЭ по математике 2020 года (№16), Санкт-Петербургский вариант.

На сторонах и треугольника отмечены точки и соответственно, причём Отрезки и пересекаются в точке

а) Докажите, что — параллелограмм.
б) Найдите если отрезки и перпендикулярны,

Докажем пункт (а) с помощью теоремы Менелая:

Пусть

По теореме Чевы,

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_2}{A_2C} cdot frac{CB_1}{B_1A} = 1.$

$displaystyle frac{8}{3} cdot frac{BA_2}{A_2C} cdot frac{3}{1} = 1$

$displaystyle frac{BA_2}{A_2C} = frac{1}{8},$ тогда

$displaystyle BA_2 = frac{1}{9}BC$

$displaystyle A_2A_1 = left ( frac{1}{3} - frac{1}{9} right ) BC = frac{2}{9}BC,$

$displaystyle A_1C = frac{2}{3}BC,$ тогда $displaystyle A_2A_1 = frac{1}{3}A_1C$

$displaystyle A_1C : A_2C = B_1C : AC = frac{3}{4},$

Это значит, что по двум углам и то есть

Рассмотрим треугольник ABB_1.

Прямая C_1C пересекает две его стороны и продолжение третьей стороны AB_1.

По теореме Менелая,

$displaystyle frac{AC_1}{C_1B} cdot frac{BD}{DB_1} cdot frac{B_1C}{AC} = 1$

$displaystyle frac{8}{3} cdot frac{BD}{DB_1} = frac{3}{4} = 1;$

$displaystyle frac{BD}{DB_1} = frac{1}{2} = frac{BA_1}{A_1C};$

тогда $displaystyle frac{BD}{BB_1} = frac{BA_1}{BC} = frac{1}{3},$

по углу и двум сторонам, отсюда

Мы получили:

— параллелограмм по определению.

Мы доказали то, что требовалось в пункте (а).
Но что делать, если теоремы Менелая и Чевы вы не проходили в школе? Ничего страшного, докажем без теорем Менелая и Чевы. Их легко заменят подобные треугольники.

Обозначим

Докажем, что — параллелограмм.

Пусть — середина AC.

Тогда

Тогда по углу и двум пропорциональным сторонам,

Проведём

По теореме Фалеса BN = y.

Пусть

по двум углам;

$displaystyle frac{AP}{BD} = frac{AC_1}{BC_1} = frac{8}{3}.$

Пусть

по 2 углам, $displaystyle frac{AP}{B_1D} = frac{AC}{B_1C} = frac{4}{3},$
тогда $displaystyle B_1D = frac{3}{4}AP = 6k,$

$displaystyle frac{BD}{B_1D} = frac{1}{2}.$

Это значит, что по углу и двум сторонам и

При этом $displaystyle A_1D = frac{1}{3}B_1C = Z = AB_1.$

Получим, что в четырёхугольнике :

Значит, — параллелограмм.

Как видим, эти решения примерно одного уровня сложности.
А вот в пункте (б) нет необходимости применять теоремы Чевы и Менелая. Он легко решается с помощью обычной школьной геометрии.

б) Найдём , если

Поскольку получим, что — прямоугольный.

Мы доказали в пункте (а), что — трапеция, причём

По условию,

Тогда $displaystyle A_1D = frac{28}{4} = 7,$

$displaystyle B_1C = frac{28}{4} cdot 3 = 21,$

$displaystyle A_1C = frac{2}{3}BC = frac{2}{3} cdot 18 = 12.$

Пусть

Тогда A_1MCD — параллелограмм (по признаку паралелограмма)

по теореме Пифагора из

$displaystyle B_1A_1 = sqrt{21^2-12^2} = 3 sqrt{7^2 - 4^2} = 3 sqrt{33},$

$displaystyle cos angle A_1B_1C = cos angle A_1B_1M = frac{B_1A_1}{B_1C} = frac{sqrt{33}}{7}$

Найдём A_1M из по теореме косинусов.

$displaystyle A_1M^2 = 9 cdot 33 + 28^2 - frac{2 cdot 28 cdot 3 sqrt{33} cdot sqrt{33}}{7} = 28^2 - 15cdot 33 = 784 - 495 = 289;$

Ответ: 17.

Вот еще одна задача, которую можно решить как с помощью теоремы Чевы, так и без нее.

На сторонах прямоугольного треугольника с прямым углом построены во внешнюю сторону квадраты и Докажите, что:

а) прямые и отсекают от катетов треугольника равные отрезки
б) прямые и высота треугольника проведённая из вершины пересекаются в одной точке.

Пункт (а) доказывается легко.

а) Пусть ,
.

Докажем, что CE=CF .

Обозначим

по 2 углам,

$displaystyle frac{FC}{A_2C_1}=frac{BC}{BC_1}$ , так как

получим:

$displaystyle frac{FC}{b}=frac{a}{a+b}. ,$ (1)

по 2 углам,

$displaystyle frac{CE}{C_2B_2}=frac{AC}{AC_2}; , , frac{CE}{a}=frac{b}{a+b}. ,$ (2)

$displaystyle frac{FC cdot a}{CE cdot b} = frac{a}{b},$ отсюда FC=CE.

Решим пункт (б) с помощью теоремы Чевы:

Запишем, чему равны длины отрезков Для длин и воспользуемся тем, что в прямоугольном треугольнике каждый катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.

$displaystyle AH = frac{b^2}{sqrt{a^2 + b^2}}$

$displaystyle HB = frac{a^2}{sqrt{a^2 + b^2}}$

$displaystyle BE = a - frac{ab}{a+b}$

$displaystyle CE = frac{ab}{a+b}$

$displaystyle CF = frac{ab}{a+b}$

$displaystyle AF = b - frac{ab}{a+b}$

Проверим выполнение равенства

$displaystyle frac{AH}{HB} cdot frac{BE}{CE} cdot frac{CF}{AF} = 1.$

$displaystyle frac{frac{b^2}{sqrt{a^2+b^2}}}{frac{a^2}{sqrt{a^2+b^2}}} cdot frac{a - frac{ab}{a+b}}{frac{ab}{a+b}} cdot frac{frac{ab}{a+b}}{b - frac{ab}{a+b}} = 1.$

Равенство выполняется.
Согласно теореме Чевы, это значит, что и пересекаются в одной точке.
А вот как решается эта задача без теоремы Чевы, с помощью векторов:

Смотрите решение: https://ege-study.ru/zadacha-na-dokazatelstvo-planimetriya/

Математик Менелай Александрийский жил в I веке до нашей эры (Древний Рим).
Математик и инженер Джованни Чева – XVII век, Италия.

Как видим, теоремы Менелая и Чевы оказываются полезны в некоторых задачах. Очень хорошо, если вы знаете эти теоремы. Однако если они для вас непривычны, можно применить простой школьный прием – пары подобных треугольников.

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Теорема Менелая, теорема Чевы – нужны на ЕГЭ или нет?» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.03.2023

Источник

5 февраля 2018

В закладки

Обсудить

Жалоба

Какие геометрические факты можно использовать на ЕГЭ без доказательства?

Начнём с того, что для ЕГЭ не нужны сколько-нибудь редкие теоремы, особенно где-нибудь на шпаргалке.

Нужно уметь применять всем знакомые факты, видеть рисунок и решать больше задач. Но вопрос из заголовка задают очень часто, и ответить на него нужно. Естественно, все сотни признаков и свойств, что есть в вашем школьном учебнике можно использовать. Но как насчет более редких фактов: что можно применять без доказательства, а что нет? Точный ответ: любые факты из школьных учебников, рекомендованных минобром на 2017-2018 год.

Ну а вот заветный список того, что мне все-таки удалось обнаружить в соответствующих учебниках:

→ Теорема Менелая (Атанасян. Геометрия 7-9 классы)
→ Теорема Чевы (Атанасян. Геометрия 7-9 классы)
→ Теорема Птолемея (Мерзляк. Геометрия 8 класс)
→ Прямая Эйлера (Мерзляк. Геометрия 8 класс)
→ Теорема об окружности Эйлера (Бутузов. Геометрия 8 класс)
→ Формула медианы треугольника (Шарыгин. Геометрия 7-9 классы)
→ Формула биссектрисы треугольника (Шарыгин. Геометрия 7-9 классы)
→ Теорема о четырех замечательных точках трапеции (Шарыгин. Геометрия 7-9 классы)

Формулу радиуса вневписанной окружности используйте. Каноническое уравнение эллипса — да пожалуйста! Ключевые формулы метода координат для задачи №14, опять же, есть

Но если здесь есть коллеги по цеху, которые могут уточнить еще несколько популярных вопросов насчет непопулярной теории — черкните, буду признателен! Вот интересующие факты: формула Брахмагупты, теорема Стюарта, формула Эйлера для расстояния между центрами вписанной и описанной окружностями треугольника, понятие определителя квадратной матрицы.

Ну и еще раз в заключение. Вероятность того, что задача ЕГЭ не решается без экзотики, равна нулю (такие события называются невозможными). Вероятность того, что вам вообще попадется конфигурация, для которой актуальна, например, теорема о девяти точках окружности, приблизительно равна 0,015. Вероятность того, что школьник в целом знает что-то «запрещенное», приблизительно равна, не кидайтесь камнями, 0,000037.

Источник: vk.com/wildmathing

Источник

Теоремы Чевы и Менелая – одни из базовых основ планиметрии и геометрии, которым репетиторы и школьные учителя уделяют особое внимание, а ученикам задают писать научные доклады и рефераты на эту тему в качестве домашнего задания.

Их изучение рекомендуется не только в том случае, если вы – математик, но и в помощь ученикам старшего уровня (по уровню сложности может подойти и любой средний класс) и студентам профильных специальностей, которые всерьёз интересуются данной наукой.

Именно для этого мы подготовили данный материал. В нем вы узнаете, чем интересны данные основы, принципы их доказательств и рассмотрите решения некоторых задач из ЕГЭ.

Формулировка теоремы Менелая

Менелай Александрийский — древнегреческий математик и астроном, живший в I в. Большой вклад внес в развитие сферической тригонометрии, где для получения формул использовал именно эту теорему, которую теперь изучают все школьники.

Прежде чем приступить к проработке, сделаем соответствующий рисунок.

Что мы имеем? Треугольник ABC и прямую, которая пересекает две его стороны и продолжение третьей стороны.

Особенность теоремы заключается и в том, что приведённый рисунок чаще всего встречается в заданиях формата ЕГЭ. Это – весьма распространённая геометрическая конструкция, когда какая-то прямая таким образом пересекает треугольник.

Если мы видим приведённый выше рисунок, можно записать формулу:

Запомнить отношение просто: действуем по принципу «вершина — точка, точка — вершина». То есть, если на стороне AB нам дана некоторая точка C1, их отношенное записывается следующим образом:

Доказательство теоремы

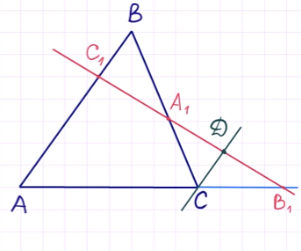
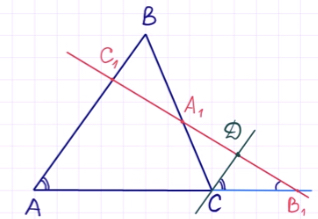
Для доказательства теоремы Менелая проведём через точку C прямую, параллельную AB, таким образом:

Обозначим точку пересечения данной прямой с B₁C₁
через точку D.

В таком случае мы получим несколько пар подобных треугольников.

Сторона CD параллельна AB. Тогда первой парой подобных треугольников будут треугольники B₁CD и B₁AC₁. Они подобны по второму признаку подобия треугольников, то есть по двум пропорциональным сторонам и углу B₁ между ними.

Углы B₁CD и B₁AC₁ равны как соответственные при параллельных прямых CD, AB и секущей AC.

Анализируя данную пару подобных треугольников, можно записать условие пропорциональности сходственных сторон, а именно:

Так как сторона CD не является составляющей исходного равенства, для дальнейшего доказательства её нужно выразить.

Используя описанное равенства, применив свойства пропорции, запишем:

Запишем следующую пару подобных треугольников: треугольники CDA₁ и BC₁A₁ подобны, так как углы CA₁D и BA₁C₁ равны как вертикальные. Кроме этого, угол CDA₁ равен углу BC₁A₁, как накрест лежащие при параллельных прямых CD, AB и секущей C₁D.

Покажем это на рисунке:

Из данного подобия можно записать некоторую пропорциональность сходственных сторон:

Так же выразим CD:

Осталось лишь приравнять. Дроби, с помощью которых мы выразили CD – равны.

Таким образом получаем:

Умножив обе дроби на часть, обратную левой дроби, мы получили исходное равенство:

Что и требовалось доказать.

Формулировка теоремы Чевы

Джованни Чева — итальянский математик, инженер. Годы жизни 1648 — 1734 гг. Основные труды ученого в области геометрии и механики.

Рассматриваемая теорема была доказана ученым в 1678 г.

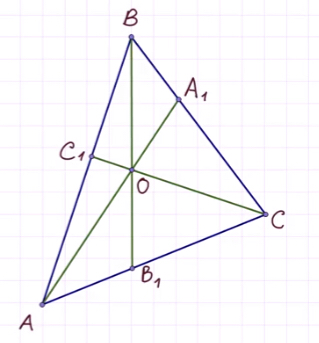
Рассмотрим приведённый ниже рисунок:

Теорема звучит так: любые произвольные отрезки, выходящие из вершин треугольника, (но с одним условием: они должны пересекаться в одной точке) делят противолежащие этим вершинам стороны таким образом, что истинно равенство:

В честь ученого, доказавшего эту теорему, данные отрезки называют «чевианами».

Доказательство теоремы

Рассмотрим рисунок:

Итак, мы имеем треугольник ABC и произвольные чевианы AA1 и BB1.

Третья чевиана CC1 обязательно должна проходить через точку пересечения первых двух. При этом получается, что:

Обозначим за O точку пересечения данных прямых.

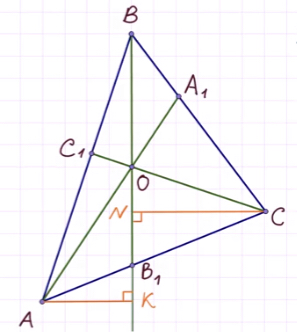
Продлим медиану BB1.

Проведём перпендикуляры из вершин A и С таким образом:

Запишем соотношение:

Треугольники AKB₁ и CNB₁
подобны по острому углу.

Аналогично получаем:

Теперь перемножим равенства:

что и требовалось доказать.

Применение теорем Чевы и Менелая при решении задач ЕГЭ

Теорема Менелая (как и обратная) применима и в первой части экзаменационного бланка, и в 16-м задании. Рассмотрим пару таких задач.

Задача 1

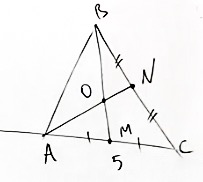
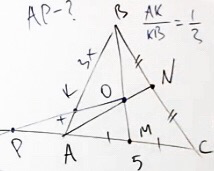
Дан треугольник ABC (см. рисунок ниже) с продолжением стороны CA. Также проведены медианы BM и AN. Точку их пересечения обозначим за O.

Возьмём точку K на стороне AB, такую, что AK относится к AB, как 1/3.

AC = 4 см, AM = 2 см.

Проведём прямую OK до пересечения со стороной AC. Точку их пересечения обозначим за P.

Сторону AP обозначим за y.

Найти: чему равен отрезок AP.

Решение:

Так как отношение сторон AB и AK равно 1/3, следовательно, AK = x, а KB = 3x.

Рассмотрим треугольник ABM. Для него берём прямую OP.

Таким образом мы нашли искомые точки P, A, M, O, K и B.

Запишем теорему Менелая к данному рисунку.

Подставляем в это соотношение известные данные:

В итоге мы получаем, что y = 4.

Ответ: отрезок AP = 4 см.

Задача 2

Задача, связанная со свойствами теоремы Чевы.

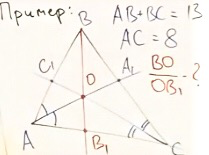
Рассмотрим рисунок:

Дано:

сумма AB и BC равна 13;
AC = 8 см.

Найти: отношение BO и OB1.

Итак, запишем отношение:

Подставляем:

Конечным результатом является дробь 13/8.

Ответ:

Источник

Теорема Менелая, теорема Чевы – нужны на ЕГЭ или нет?

Анна Малкова

Теорема Менелая:

Пусть прямая пересекает произвольный треугольник ABC, причем C_1 – точка ее пересечения со стороной ABC, A_1 – точка ее пересечения со стороной BC, и B_1 – точка ее пересечения с продолжением стороны AC.

Тогда выполняется равенство:

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_1}{A_1C} cdot frac{CB_1}{B_1A} = 1.$

В некоторых задачах полезна обратная теорема Менелая.

Теорема (Менелая, обратная). Пусть дан треугольник ABC. Предположим, что точка C_1 лежит на стороне AB, точка A_1 лежит на стороне BC, а точка B_1 лежит на продолжении стороны AC, причём про эти точки известно, что

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_1}{A_1C} cdot frac{CB_1}{B_1A} = 1.$

Тогда эти точки лежат на одной прямой.

Теорема Чевы

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_1}{A_1C} cdot frac{CB_1}{B_1A} = 1.$

Обратная теорема Чевы:

Теорема (Чевы, обратная). Пусть точки лежат соответственно на сторонах BC, AC и треугольника ABC, причём

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_1}{A_1C} cdot frac{CB_1}{B_1A} = 1.$

Тогда отрезки и CC_1 пересекаются в одной точке.

Как применяются теоремы Менелая и Чевы?

Вот задача Профильного ЕГЭ по математике 2020 года (№16), Санкт-Петербургский вариант.

На сторонах и треугольника ABC отмечены точки и B_1 соответственно, причём Отрезки BB_1 и CC1 пересекаются в точке

а) Докажите, что — параллелограмм.
б) Найдите CD, если отрезки и перпендикулярны,

Докажем пункт (а) с помощью теоремы Менелая:

Пусть

По теореме Чевы,

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_2}{A_2C} cdot frac{CB_1}{B_1A} = 1.$

$displaystyle frac{8}{3} cdot frac{BA_2}{A_2C} cdot frac{3}{1} = 1$

$displaystyle frac{BA_2}{A_2C} = frac{1}{8},$ тогда

$displaystyle BA_2 = frac{1}{9}BC$

$displaystyle A_2A_1 = left ( frac{1}{3} - frac{1}{9} right ) BC = frac{2}{9}BC,$

$displaystyle A_1C = frac{2}{3}BC,$ тогда $displaystyle A_2A_1 = frac{1}{3}A_1C$

$displaystyle A_1C : A_2C = B_1C : AC = frac{3}{4},$

Это значит, что по двум углам и то есть

Рассмотрим треугольник ABB_1.

Прямая C_1C пересекает две его стороны и продолжение третьей стороны AB_1.

По теореме Менелая,

$displaystyle frac{AC_1}{C_1B} cdot frac{BD}{DB_1} cdot frac{B_1C}{AC} = 1$

$displaystyle frac{8}{3} cdot frac{BD}{DB_1} = frac{3}{4} = 1;$

$displaystyle frac{BD}{DB_1} = frac{1}{2} = frac{BA_1}{A_1C};$

тогда $displaystyle frac{BD}{BB_1} = frac{BA_1}{BC} = frac{1}{3},$

по углу и двум сторонам, отсюда

Мы получили:

— параллелограмм по определению.

Обозначим

Докажем, что — параллелограмм.

Пусть — середина AC.

Тогда

Тогда по углу и двум пропорциональным сторонам,

Проведём

По теореме Фалеса BN = y.

Пусть

по двум углам;

$displaystyle frac{AP}{BD} = frac{AC_1}{BC_1} = frac{8}{3}.$

Пусть

по 2 углам, $displaystyle frac{AP}{B_1D} = frac{AC}{B_1C} = frac{4}{3},$
тогда $displaystyle B_1D = frac{3}{4}AP = 6k,$

$displaystyle frac{BD}{B_1D} = frac{1}{2}.$

Это значит, что по углу и двум сторонам и

При этом $displaystyle A_1D = frac{1}{3}B_1C = Z = AB_1.$

Получим, что в четырёхугольнике :

Значит, — параллелограмм.

б) Найдём , если

Поскольку получим, что — прямоугольный.

Мы доказали в пункте (а), что — трапеция, причём

По условию,

Тогда $displaystyle A_1D = frac{28}{4} = 7,$

$displaystyle B_1C = frac{28}{4} cdot 3 = 21,$

$displaystyle A_1C = frac{2}{3}BC = frac{2}{3} cdot 18 = 12.$

Пусть

Тогда A_1MCD — параллелограмм (по признаку паралелограмма)

по теореме Пифагора из

$displaystyle B_1A_1 = sqrt{21^2-12^2} = 3 sqrt{7^2 - 4^2} = 3 sqrt{33},$

$displaystyle cos angle A_1B_1C = cos angle A_1B_1M = frac{B_1A_1}{B_1C} = frac{sqrt{33}}{7}$

Найдём A_1M из по теореме косинусов.

Ответ: 17.

Вот еще одна задача, которую можно решить как с помощью теоремы Чевы, так и без нее.

На сторонах прямоугольного треугольника ABC с прямым углом построены во внешнюю сторону квадраты и Докажите, что:

а) прямые AB_2 и A_2B отсекают от катетов треугольника ABC равные отрезки
б) прямые и высота треугольника ABC, проведённая из вершины пересекаются в одной точке.

Пункт (а) доказывается легко.

а) Пусть ,
.

Докажем, что CE=CF .

Обозначим

по 2 углам,

$displaystyle frac{FC}{A_2C_1}=frac{BC}{BC_1}$ , так как

получим:

$displaystyle frac{FC}{b}=frac{a}{a+b}. ,$ (1)

по 2 углам,

$displaystyle frac{CE}{C_2B_2}=frac{AC}{AC_2}; , , frac{CE}{a}=frac{b}{a+b}. ,$ (2)

$displaystyle frac{FC cdot a}{CE cdot b} = frac{a}{b},$ отсюда FC=CE.

Решим пункт (б) с помощью теоремы Чевы:

$displaystyle AH = frac{b^2}{sqrt{a^2 + b^2}}$

$displaystyle HB = frac{a^2}{sqrt{a^2 + b^2}}$

$displaystyle BE = a - frac{ab}{a+b}$

$displaystyle CE = frac{ab}{a+b}$

$displaystyle CF = frac{ab}{a+b}$

$displaystyle AF = b - frac{ab}{a+b}$

Проверим выполнение равенства

$displaystyle frac{AH}{HB} cdot frac{BE}{CE} cdot frac{CF}{AF} = 1.$

Равенство выполняется.
Согласно теореме Чевы, это значит, что и пересекаются в одной точке.
А

Источник

Всего: 4 1–4

Добавить в вариант

На отрезке BD взята точка C. Биссектриса BL равнобедренного треугольника ABC с основанием BC является боковой стороной равнобедренного треугольника BLD с основанием BD.

а)  Докажите, что треугольник DCL равнобедренный.

б)  Известно, что В каком отношении прямая DL делит сторону AB?

Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016

В треугольной пирамиде SABC точка Е  — середина ребра SA, точка F  — середина ребра SB, О  — точка пересечения медиан треугольника АВС.

а)  Докажите, что плоскость CEF делит отрезок SO в отношении 3 : 2, считая от вершины S.

б)  Найдите косинус угла между плоскостями CEF и EFT, если точка Т  — середина SC, пирамида SABC правильная, площадь треугольника АВС равна а SB  =  10.

Источник: А. Ларин. Тренировочный вариант № 323. (часть C).

Дана правильная четырехугольная пирамида SABCD. Плоскость α параллельна прямой АС, проходит через точку В и середину высоты пирамиды.

а)  Докажите, что плоскость α делит ребро SD в отношении 2 : 1, считая от точки D.

б)  Найдите синус угла между плоскостью α и плоскостью ASC, если угол SAC равен 30°.

Источник: А. Ларин. Тренировочный вариант № 324. (часть C).

В правильной шестиугольной пирамиде SABCDEF сторона основания AB  =  4, а боковое ребро SA  =  7. Точка M лежит на ребре BC, причем BM  =  1, точка K лежит на ребре SC, причем SK  =  4.

а)  Докажите, что плоскость MKD перпендикулярна плоскости основания пирамиды.

б)  Найдите объем пирамиды CDKM.

Источник: А. Ларин. Тренировочный вариант № 397.

Всего: 4 1–4

Источник

Формулировка теоремы Менелая

Прежде чем приступить к проработке, сделаем соответствующий рисунок.

Что мы имеем? Треугольник ABC и прямую, которая пересекает две его стороны и продолжение третьей стороны.

Если мы видим приведённый выше рисунок, можно записать формулу:

Доказательство теоремы

Для доказательства теоремы Менелая проведём через точку C прямую, параллельную AB, таким образом:

Обозначим точку пересечения данной прямой с B1C1
через точку D.

В таком случае мы получим несколько пар подобных треугольников.

Сторона CD параллельна AB. Тогда первой парой подобных треугольников будут треугольники B1CD и B1AC1. Они подобны по второму признаку подобия треугольников, то есть по двум пропорциональным сторонам и углу B1 между ними.

Углы B1CD и B1AC1 равны как соответственные при параллельных прямых CD, AB и секущей AC.

Используя описанное равенства, применив свойства пропорции, запишем:

Запишем следующую пару подобных треугольников: треугольники CDA1 и BC1A1 подобны, так как углы CA1D и BA1C1 равны как вертикальные. Кроме этого, угол CDA1 равен углу BC1A1, как накрест лежащие при параллельных прямых CD, AB и секущей C1D.

Покажем это на рисунке: