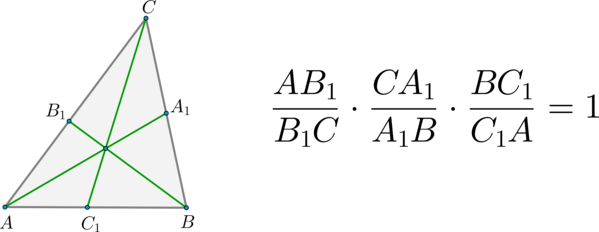Регистрация Форум Текущее время: 11 мар 2023, 18:39 Сообщения без ответов | Активные темы Страница 1 из 2 [ Сообщений: 16 ] На страницу 1, 2 След. Начать новую тему»> Ответить Можно ли пользоваться следующими теоремами на ЕГЭ?
Можно ли пользоваться следующими теоремами на ЕГЭ?
Страница 1 из 2 [ Сообщений: 16 ] На страницу 1, 2 След. Текущее время: 11 мар 2023, 18:39 | Часовой пояс: UTC + 3 часа Удалить cookies форума | Наша команда | Вернуться наверх Кто сейчас на форуме
|
5 февраля 2018
В закладки
Обсудить
Жалоба
Какие геометрические факты можно использовать на ЕГЭ без доказательства?
Начнём с того, что для ЕГЭ не нужны сколько-нибудь редкие теоремы, особенно где-нибудь на шпаргалке.
Нужно уметь применять всем знакомые факты, видеть рисунок и решать больше задач. Но вопрос из заголовка задают очень часто, и ответить на него нужно. Естественно, все сотни признаков и свойств, что есть в вашем школьном учебнике можно использовать. Но как насчет более редких фактов: что можно применять без доказательства, а что нет? Точный ответ: любые факты из школьных учебников, рекомендованных минобром на 2017-2018 год.
Ну а вот заветный список того, что мне все-таки удалось обнаружить в соответствующих учебниках:
→ Теорема Менелая (Атанасян. Геометрия 7-9 классы)
→ Теорема Чевы (Атанасян. Геометрия 7-9 классы)
→ Теорема Птолемея (Мерзляк. Геометрия 8 класс)
→ Прямая Эйлера (Мерзляк. Геометрия 8 класс)
→ Теорема об окружности Эйлера (Бутузов. Геометрия 8 класс)
→ Формула медианы треугольника (Шарыгин. Геометрия 7-9 классы)
→ Формула биссектрисы треугольника (Шарыгин. Геометрия 7-9 классы)
→ Теорема о четырех замечательных точках трапеции (Шарыгин. Геометрия 7-9 классы)
Формулу радиуса вневписанной окружности используйте. Каноническое уравнение эллипса — да пожалуйста! Ключевые формулы метода координат для задачи №14, опять же, есть
Но если здесь есть коллеги по цеху, которые могут уточнить еще несколько популярных вопросов насчет непопулярной теории — черкните, буду признателен! Вот интересующие факты: формула Брахмагупты, теорема Стюарта, формула Эйлера для расстояния между центрами вписанной и описанной окружностями треугольника, понятие определителя квадратной матрицы.
Ну и еще раз в заключение. Вероятность того, что задача ЕГЭ не решается без экзотики, равна нулю (такие события называются невозможными). Вероятность того, что вам вообще попадется конфигурация, для которой актуальна, например, теорема о девяти точках окружности, приблизительно равна 0,015. Вероятность того, что школьник в целом знает что-то «запрещенное», приблизительно равна, не кидайтесь камнями, 0,000037.
Источник: vk.com/wildmathing
Факт 1.
(bullet) Теорема Вариньона:
Середины сторон выпуклого четырехугольника являются вершинами параллелограмма.
Факт 2.
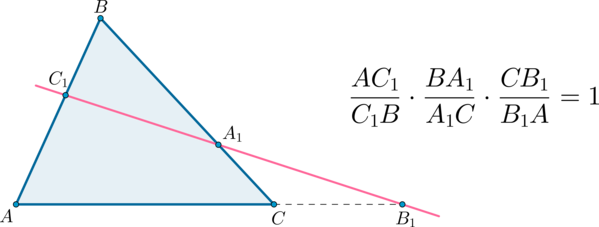
(bullet) Теорема Менелая:
Если прямая пересекает стороны (AB) и (BC) в точках (C_1) и (A_1) соответственно, а также продолжение прямой (AC) в точке (B_1), то выполнено следующее соотношение:
Факт 3.
(bullet) Теорема Чевы:
Если (AA_1, BB_1) и (CC_1) – чевианы, пересекающиеся в одной точке, то для них выполнено следующее соотношение:
(чевиана – отрезок, соединяющий вершину треугольника с точкой на противоположной стороне)
Факт 4.
(bullet) Теорема Ван-Обеля:
Если (AA_1, BB_1) и (CC_1) – чевианы, пересекающиеся в одной точке, то для них выполнено следующее соотношение:
ÐвÑÐ¾Ñ Ð¡Ð¾Ð¾Ð±Ñение
vyv2
Ðаголовок ÑообÑениÑ: ÐлаÑÑиÑеÑкие ÑеоÑÐµÐ¼Ñ Ð¸ задаÑи 4
Ðобавлено: 18 авг 2015, 19:35
ÐаÑегиÑÑÑиÑован: 31 Ñнв 2011, 17:37
СообÑений: 4974
ÐÑкÑда: СанкÑ-ÐеÑеÑбÑÑг
ТеоÑема Ðан-ÐÐ±ÐµÐ»Ñ (van Aubel или van Obel)
ÐоказаÑÑ, ÑÑо `(BP)/(PE)=(BF)/(FA)+(BD)/(DC)`, еÑли AD, BE, CF — ÑÐµÐ²Ð¸Ð°Ð½Ñ ÑÑеÑголÑника ÐÐС, пеÑеÑекаÑÑиеÑÑ Ð² ÑоÑке Ð .
Ðложение:
131.jpg [ 26 KIB | ÐÑоÑмоÑÑов: 6563 ]
СпÑавка:
Ðан-ÐÐ±ÐµÐ»Ñ (Henicus Hubertus van Aubel)(1830-1906) — ÑламандÑкий маÑемаÑик.
Ðложение:
131_1.jpg [ 25.24 KIB | ÐÑоÑмоÑÑов: 6563 ]
ÐÑа ÑеоÑема ÑвÑзана Ñ ÑеоÑемой Ð§ÐµÐ²Ñ Ð¸ баÑиÑенÑÑиÑеÑкими кооÑдинаÑами.
ÐÑÑÑ ÐµÑе одна ÑеоÑема Ðан-ÐбелÑ, ÑвÑÐ·Ð°Ð½Ð½Ð°Ñ Ñ ÑеÑÑÑеÑ
ÑголÑником и квадÑаÑами, коÑоÑÐ°Ñ ÑвлÑеÑÑÑ ÑаÑÑнÑм ÑлÑÑаем ÑеоÑÐµÐ¼Ñ ÐеÑÑа-ÐÑглаÑа-Ðеймана, и из нее ÑледÑÐµÑ ÑеоÑема Тебо. (бÑдÑÑ Ð¿ÑедÑÑÐ°Ð²Ð»ÐµÐ½Ñ Ð¿Ð¾Ð·Ð¶Ðµ).
_________________
СопÑоÑивление беÑполезно.


alex123
Ðаголовок ÑообÑениÑ: Re: ÐлаÑÑиÑеÑкие ÑеоÑÐµÐ¼Ñ Ð¸ задаÑи 4
Ðобавлено: 19 авг 2015, 15:03
ÐаÑегиÑÑÑиÑован: 16 Ñев 2011, 14:13
СообÑений: 1915
vyv2 пиÑал(а):
ТеоÑема Ðан-ÐÐ±ÐµÐ»Ñ (van Aubel или van Obel)
ÐоказаÑÑ, ÑÑо `(BP)/(PE)=(BF)/(FA)+(BD)/(DC)`, еÑли AD, BE, CF — ÑÐµÐ²Ð¸Ð°Ð½Ñ ÑÑеÑголÑника ÐÐС, пеÑеÑекаÑÑиеÑÑ Ð² ÑоÑке Ð .
Ðложение:
СпÑавка:
Ðан-ÐÐ±ÐµÐ»Ñ (Henicus Hubertus van Aubel)(1830-1906) — ÑламандÑкий маÑемаÑик.
Ðложение:
ÐÑа ÑеоÑема ÑвÑзана Ñ ÑеоÑемой Ð§ÐµÐ²Ñ Ð¸ баÑиÑенÑÑиÑеÑкими кооÑдинаÑами.
ÐÑÑÑ ÐµÑе одна ÑеоÑема Ðан-ÐбелÑ, ÑвÑÐ·Ð°Ð½Ð½Ð°Ñ Ñ ÑеÑÑÑеÑ
ÑголÑником и квадÑаÑами, коÑоÑÐ°Ñ ÑвлÑеÑÑÑ ÑаÑÑнÑм ÑлÑÑаем ÑеоÑÐµÐ¼Ñ ÐеÑÑа-ÐÑглаÑа-Ðеймана, и из нее ÑледÑÐµÑ ÑеоÑема Тебо. (бÑдÑÑ Ð¿ÑедÑÑÐ°Ð²Ð»ÐµÐ½Ñ Ð¿Ð¾Ð·Ð¶Ðµ).
ÐÑа ÑеоÑема ÑвÑзана Ñ ÑеоÑемой Ð§ÐµÐ²Ñ Ð¸ баÑиÑенÑÑиÑеÑкими кооÑдинаÑами. — ÑазÑмееÑÑÑ.
Ðо можно и без ниÑ
. ÐоÑÑаÑоÑно понÑÑÑ, ÑÑо ÑÑÑ ÑеоÑÐµÐ¼Ñ Ð´Ð¾ÑÑаÑоÑно доказаÑÑ Ð´Ð»Ñ ÐºÐ°ÐºÐ¾Ð³Ð¾-Ñо ÑикÑиÑованного ÑÑеÑголÑника, напÑÐ¸Ð¼ÐµÑ Ð¿ÑавилÑного или пÑÑмоÑголÑного. РобÑий ÑлÑÑай полÑÑиÑÑÑ Ð´Ð°Ñом из аÑÑинной ÑквиваленÑноÑÑи.


OlG
Ðаголовок ÑообÑениÑ: Re: ÐлаÑÑиÑеÑкие ÑеоÑÐµÐ¼Ñ Ð¸ задаÑи 4
Ðобавлено: 19 авг 2015, 15:44
ÐаÑегиÑÑÑиÑован: 09 Ð°Ð¿Ñ 2011, 14:49
СообÑений: 6463
ÐÑкÑда: ÐоÑква
alex123 пиÑал(а):
ÐÑа ÑеоÑема ÑвÑзана Ñ ÑеоÑемой Ð§ÐµÐ²Ñ Ð¸ баÑиÑенÑÑиÑеÑкими кооÑдинаÑами. — ÑазÑмееÑÑÑ.
Ðо можно и без ниÑ
. ÐоÑÑаÑоÑно понÑÑÑ, ÑÑо ÑÑÑ ÑеоÑÐµÐ¼Ñ Ð´Ð¾ÑÑаÑоÑно доказаÑÑ Ð´Ð»Ñ ÐºÐ°ÐºÐ¾Ð³Ð¾-Ñо ÑикÑиÑованного ÑÑеÑголÑника, напÑÐ¸Ð¼ÐµÑ Ð¿ÑавилÑного или пÑÑмоÑголÑного. РобÑий ÑлÑÑай полÑÑиÑÑÑ Ð´Ð°Ñом из аÑÑинной ÑквиваленÑноÑÑи.
ÐоÑÑаÑоÑно знаÑÑ ÑвойÑÑва пÑопоÑÑий и ÑмеÑÑ Ð²ÑÑажаÑÑ Ð¾ÑноÑение плоÑадей
ÑÑеÑголÑников ÑеÑез оÑноÑение оÑÑезков (вÑÑоÑ, оÑнований …) и ÑеоÑема
доказÑваеÑÑÑ Ð´Ð»Ñ Ð¿ÑоизволÑного ÑÑеÑголÑника в ÑÑи пÑоÑÑÑе ÑÑÑоÑки.
_________________
ÐикÑда не ÑоÑоплÑÑÑ!


alex123
Ðаголовок ÑообÑениÑ: Re: ÐлаÑÑиÑеÑкие ÑеоÑÐµÐ¼Ñ Ð¸ задаÑи 4
Ðобавлено: 19 авг 2015, 15:54
ÐаÑегиÑÑÑиÑован: 16 Ñев 2011, 14:13
СообÑений: 1915
OlG пиÑал(а):
alex123 пиÑал(а):
ÐÑа ÑеоÑема ÑвÑзана Ñ ÑеоÑемой Ð§ÐµÐ²Ñ Ð¸ баÑиÑенÑÑиÑеÑкими кооÑдинаÑами. — ÑазÑмееÑÑÑ.
Ðо можно и без ниÑ
. ÐоÑÑаÑоÑно понÑÑÑ, ÑÑо ÑÑÑ ÑеоÑÐµÐ¼Ñ Ð´Ð¾ÑÑаÑоÑно доказаÑÑ Ð´Ð»Ñ ÐºÐ°ÐºÐ¾Ð³Ð¾-Ñо ÑикÑиÑованного ÑÑеÑголÑника, напÑÐ¸Ð¼ÐµÑ Ð¿ÑавилÑного или пÑÑмоÑголÑного. РобÑий ÑлÑÑай полÑÑиÑÑÑ Ð´Ð°Ñом из аÑÑинной ÑквиваленÑноÑÑи.
ÐоÑÑаÑоÑно знаÑÑ ÑвойÑÑва пÑопоÑÑий и ÑмеÑÑ Ð²ÑÑажаÑÑ Ð¾ÑноÑение плоÑадей
ÑÑеÑголÑников ÑеÑез оÑноÑение оÑÑезков (вÑÑоÑ, оÑнований …) и ÑеоÑема
доказÑваеÑÑÑ Ð´Ð»Ñ Ð¿ÑоизволÑного ÑÑеÑголÑника в ÑÑи пÑоÑÑÑе ÑÑÑоÑки.
Ð ÑÑо Ñоже веÑно. ÐÐ¾Ñ ÑолÑко знаÑиÑелÑно ÑаÑе аÑÑиннÑе задаÑи пÑоÑе ÑеÑиÑÑ Ð¿Ð¾-моемÑ, Ñем в ÑÑи пÑоÑÑÑе ÑÑÑоÑки.


OlG
Ðаголовок ÑообÑениÑ: Re: ÐлаÑÑиÑеÑкие ÑеоÑÐµÐ¼Ñ Ð¸ задаÑи 4
Ðобавлено: 19 авг 2015, 17:19
ÐаÑегиÑÑÑиÑован: 09 Ð°Ð¿Ñ 2011, 14:49
СообÑений: 6463
ÐÑкÑда: ÐоÑква
ÐоказаÑелÑÑÑво ÑеоÑÐµÐ¼Ñ Ðан-ÐÐ±ÐµÐ»Ñ Ð´Ð»Ñ 8-го клаÑÑа.
_________________
ÐикÑда не ÑоÑоплÑÑÑ!


OlG
Ðаголовок ÑообÑениÑ: Re: ÐлаÑÑиÑеÑкие ÑеоÑÐµÐ¼Ñ Ð¸ задаÑи 4
Ðобавлено: 19 авг 2015, 20:25
ÐаÑегиÑÑÑиÑован: 09 Ð°Ð¿Ñ 2011, 14:49
СообÑений: 6463
ÐÑкÑда: ÐоÑква
ÐеомеÑÑÐ¸Ñ 10-11 клаÑÑÑ. УÑебник (базовÑй и пÑоÑилÑнÑй ÑÑовни). СмиÑнова Ð.Ð.,
СмиÑнов Ð.Ð. 5-е изд., иÑпÑ. и доп. — Ð.: 2008. — 288 Ñ. СÑÑ. 237-238.
_________________
ÐикÑда не ÑоÑоплÑÑÑ!


alex123
Ðаголовок ÑообÑениÑ: Re: ÐлаÑÑиÑеÑкие ÑеоÑÐµÐ¼Ñ Ð¸ задаÑи 4
Ðобавлено: 19 авг 2015, 22:56
ÐаÑегиÑÑÑиÑован: 16 Ñев 2011, 14:13
СообÑений: 1915
OlG пиÑал(а):
ÐеомеÑÑÐ¸Ñ 10-11 клаÑÑÑ. УÑебник (базовÑй и пÑоÑилÑнÑй ÑÑовни). СмиÑнова Ð.Ð.,
СмиÑнов Ð.Ð. 5-е изд., иÑпÑ. и доп. — Ð.: 2008. — 288 Ñ. СÑÑ. 237-238.
ÐÑли доказаÑелÑÑÑво ÑеоÑÐµÐ¼Ñ Ð¾ Ð¼ÐµÐ´Ð¸Ð°Ð½Ð°Ñ ÑеÑез ÑеоÑÐµÐ¼Ñ ÐÐ±ÐµÐ»Ñ Ð¿ÐµÑвое — за ÑÑо надо болÑно биÑÑ, а ÑÑебник оÑпÑавиÑÑ Ð² ÑопкÑ. ÐÑли Ð´Ð»Ñ Ð°ÑÑоÑÑименÑа (Ñо еÑÑÑ Ñанее ÑеоÑема о Ð¼ÐµÐ´Ð¸Ð°Ð½Ð°Ñ Ð´Ð¾ÐºÐ°Ð·Ð°Ð½Ð° каким-нибÑÐ´Ñ Ð±Ð¾Ð»ÐµÐµ еÑÑеÑÑвеннÑм пÑÑем) — Ñогда ладно, можно Ñ Ñопкой повÑемениÑÑ.


OlG
Ðаголовок ÑообÑениÑ: Re: ÐлаÑÑиÑеÑкие ÑеоÑÐµÐ¼Ñ Ð¸ задаÑи 4
Ðобавлено: 19 авг 2015, 23:49
ÐаÑегиÑÑÑиÑован: 09 Ð°Ð¿Ñ 2011, 14:49
СообÑений: 6463
ÐÑкÑда: ÐоÑква
alex123 пиÑал(а):
пÑоÑе ÑеÑиÑÑ Ð¿Ð¾-моемÑ
ТеÑпеливо ждем ÐаÑе ÑеÑение. ЧÑоб бÑло понÑÑно и Ð´Ð»Ñ 8, 9, 10, 11-го клаÑÑа.
_________________
ÐикÑда не ÑоÑоплÑÑÑ!


alex123
Ðаголовок ÑообÑениÑ: Re: ÐлаÑÑиÑеÑкие ÑеоÑÐµÐ¼Ñ Ð¸ задаÑи 4
Ðобавлено: 20 авг 2015, 13:05
ÐаÑегиÑÑÑиÑован: 16 Ñев 2011, 14:13
СообÑений: 1915
OlG пиÑал(а):
alex123 пиÑал(а):
пÑоÑе ÑеÑиÑÑ Ð¿Ð¾-моемÑ
ТеÑпеливо ждем ÐаÑе ÑеÑение. ЧÑоб бÑло понÑÑно и Ð´Ð»Ñ 8, 9, 10, 11-го клаÑÑа.
Ðам Ð¼Ð¾Ð³Ñ Ð¿Ð¾ÑекомендоваÑÑ Ð±ÑкваÑÑ.
ÐоÑомÑ, ÑÑо пока 8,9,10 и 11 клаÑÑам понÑÑно, ÑÑо ÑиÑаÑÑ ÐÑ Ð½Ðµ ÑмееÑе.


OlG
Ðаголовок ÑообÑениÑ: Re: ÐлаÑÑиÑеÑкие ÑеоÑÐµÐ¼Ñ Ð¸ задаÑи 4
Ðобавлено: 20 авг 2015, 13:33
ÐаÑегиÑÑÑиÑован: 09 Ð°Ð¿Ñ 2011, 14:49
СообÑений: 6463
ÐÑкÑда: ÐоÑква
ÐÑли Ðам пÑоÑе поÑекомендоваÑÑ Ð±ÑкваÑÑ, Ñем
alex123 пиÑал(а):
пÑоÑе ÑеÑиÑÑ Ð¿Ð¾-моемÑ, Ñем в ÑÑи пÑоÑÑÑе ÑÑÑоÑки.
или пÑоÑе ÑеÑиÑÑ Ð¿Ð¾-ÐаÑемÑ, Ñем в две пÑоÑÑÑе ÑÑÑоÑки в ÑÑебнике СмиÑновÑÑ
, Ñо ÑколÑникам вÑÑепеÑеÑиÑленнÑÑ
клаÑÑов понÑÑно, ÑÑо ÑаздаваÑÑ Ð±ÑкваÑи Ñ ÐÐ°Ñ Ð¿Ð¾Ð»ÑÑаеÑÑÑ ÐµÑе пÑоÑе, Ñем пÑоÑе ÑеÑаÑÑ Ð¿Ð¾-ÐаÑемÑ.
_________________
ÐикÑда не ÑоÑоплÑÑÑ!


Свойство пересекающихся чевиан – теорема Ван-Обеля
Пусть точка F – точка пересечения чевиан АА1, ВВ1 и СС1, тогда:
Теорема Ван-Обеля
Доказательство теоремы Ван-Обеля
Шаг 1
Рассмотрим треугольник АВС.
Проведем в нем три чевианы АА1, ВВ1 и СС1.
Чевианы проведем таким образом, чтобы они пересекались в одной точке. Эту точку обозначим буквой F.
Докажем, что:
Доказательство теоремы Ван-Обеля. Шаг 1
Шаг 2
Через вершину В проведем прямую, параллельную стороне АС.
Доказательство теоремы Ван-Обеля. Шаг 2
Шаг 3
Продолжим отрезки СС1 и АА1 до пересечения с этой прямой. Точки пересечения обозначим А2 и С2.
Доказательство теоремы Ван-Обеля. Шаг 3
Шаг 4
Рассмотрим треугольники АFС и А2FС2.
∠АFС = ∠А2FС2 – как вертикальные;
∠С2А2F = ∠ FАС – как накрест лежащие углы при параллельных прямых АС и С2А2 и секущей АА2.
По признаку подобия треугольников по двум равным углам, рассматриваемые треугольники подобны:
Из подобия треугольников следует пропорция:
Доказательство теоремы Ван-Обеля. Шаг 4
Шаг 5
Рассмотрим треугольники FA2B и FAB1.
∠A2FB = ∠AFB1 – как вертикальные;
∠FAB1 = ∠ FA2B – как накрест лежащие углы при параллельных прямых АС и С2А2 и секущей АА2.
По признаку подобия треугольников по двум равным углам, рассматриваемые треугольники подобны:
Из подобия треугольников следует пропорция:
Доказательство теоремы Ван-Обеля. Шаг 5
Шаг 6
На шагах 4 и 5 получили равенства:
Так как эти равенства имеют равные части, то мы можем приравнять и другие:
По построению:
Следовательно:
Доказательство теоремы Ван-Обеля. Шаг 6
Шаг 7
Рассмотрим треугольники А2ВА1 и АСА1.
∠А2А1В = ∠СА1А – как вертикальные;
∠А1А2В = ∠ А1АС – как накрест лежащие углы при параллельных прямых АС и С2А2 и секущей АА2.
По признаку подобия треугольников по двум равным углам, рассматриваемые треугольники подобны:
Из подобия треугольников следует пропорция:
Доказательство теоремы Ван-Обеля. Шаг 7
Шаг 8
Рассмотрим треугольники BC2C1 и ACC1.
∠C2C1B = ∠AC1C – как вертикальные;
∠CAC1 = ∠ C2BC1 – как накрест лежащие углы при параллельных прямых АС и С2А2 и секущей AB.
По признаку подобия треугольников по двум равным углам, рассматриваемые треугольники подобны:
Из подобия треугольников следует пропорция:
Доказательство теоремы Ван-Обеля. Шаг 8
Шаг 9
Подставим значения равенств, полученных на шагах 7 и 8:
в равенство, полученное на шаге 6:
Получим:
Теорема Ван-Обеля доказана.
Доказательство теоремы Ван-Обеля. Шаг 9
9E09BEAE0A118E93DED3D74128EA2C147A65428915829EB11235F7758F7B38C3
Применение теоремы Вариньона к решению задач
2. 2. Применение теоремы Вариньона к решению задач.
Рассмотрим применение теоремы Вариньона к решению планиметрических задач повышенной трудности. Дело в том, что планиметрические задачи на олимпиадах встречаются значительно чаще.
Мы будем называть параллелограмм KLMN параллелограммом Вариньона, а отрезки КМ и LN, соединяющие середины противоположных сторон четырёхугольника АВСD — средними линиями этого четырёхугольника.
Задача 1. В выпуклом пятиугольнике ABCDE середины сторон AB и CD, BC и DE соединены отрезками. K, L – середины этих отрезков. Доказать, что отрезок KL параллелен пятой стороне AE и составляет ¼ от неё.
Решение: отрежем четырёхугольник ABCD и пусть Р-середина AD, тогда по теореме Вариньона A1B1C1P – параллелограмм, А1С1 – его диагональ и К – середина А1С1, значит, К – середина и второй
диагонали параллелограмма В1Р. Значит, KL – средняя линия треугольника PB1D1, поэтому KL||PD1 и KL=1/2 PD1, но PD1 – средняя линия треугольника ADE, значит, PD1||AE и PD1=1/2AE, поэтому KL||AE и KL=1/4 AE.

Решение: верно, так как параллелограмм Вариньона существует для любого выпуклого четырёхугольника. Например, условию задачи удовлетворяют треугольники KLM и LMN на рис. 10. рис. 10
Задача 3. Средние линии четырёхугольника ABCD равны a и b, а угол между ними 60˚. Найдите диагонали четырёхугольника.
Решение: пусть KM=a, LN=b, 








Ответ: 
Задача 4. Докажите, что сумма квадратов диагоналей четырёхугольника в два раза больше суммы квадратов его средних линий.
Доказательство: в параллелограмме Вариньона, как и в любом другом параллелограмме, сумма квадратов рис. 11 диагоналей равна сумме квадратов всех его сторон, т. е. 
Задача 5. Докажите, что площадь параллелограмма Вариньона равна половине площади четырёхугольника ABCD.


Учитывая, что 

Задача 6. Докажите, что все четырёхугольники, имеющие общие середины
Доказательство: действительно, для всех таких четырёхугольников определён один и тот же параллелограмм Вариньона. Его площадь равна половине площади каждого из исходных четырёхугольников (задача 5), тем самым их равновеликость доказана.

Доказательство: в случае равенства диагоналей AC и BD параллелограмм Вариньона KLMN является ромбом (рис. 13), а рис. 13
площадь ромба равна половине произведения диагоналей:


Задача 8. Диагонали четырёхугольника ABCD равны d1 и d2, а средние линии равны между собой. Найдите площадь четырёхугольника.
Решение: из условия задачи следует, что в параллелограмме Вариньона диагонали KM и LN равны (рис. 12). Значит, KLMN – прямоугольник и SKLMN=1/2 d1d2, а с другой стороны, SKLMN=1/2 SABCD, следовательно, SABCD=1/2d1d2.

Задача 9. Докажите, что площадь четырёхугольника равна произведению средней линии на одну из диагоналей и на синус угла между ними.
Доказательство: согласно рис. 14 необходимо доказать, рис. 14
что 






Задача 10. Докажите, что сумма квадратов сторон четырёхугольника равна сумме квадратов его диагоналей, сложенной с учетверённым квадратом отрезка, соединяющего середину его диагоналей.
Доказательство: согласно рис. 11 надо доказать, что








Кроме того, 
Итак, получаем: 

Решение: пусть в трапеции ABCD, которую необходимо построить, известны длины диагоналей AC и BD, отрезка LN и величина угла А (рис. 15).
Поскольку 

сторонам треугольник KLN. Далее построим его до параллелограмма Вариньона. Затем на отрезке KN построим сегмент, вмещающий угол А, и проведём через точку N параллельно KM прямую, она пересечёт сегмент в точке А. Дальнейшее построение очевидно.
В ходе работы мы прорешали более двадцати пяти задач, формулировки и решения наиболее интересных из них дополнительно приведены в приложении. Мы убедились в том, что теорема Вариньона помогает красиво, оригинально решать задачи, открывать и доказывать новые свойства четырёхугольников.
Исследовательская работа по математике «Теорема Вариньона», 9 класс
«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»
Сертификат и скидка на обучение каждому участнику
Муниципальное бюджетное образовательное учреждение города Абакана «Средняя общеобразовательная школа №26 с углубленным изучением отдельных предметов»
Секция «Мир моих математических исследований»
Применение теоремы Вариньона при решении планиметрических задач .
Тетервова Ирина Вадимовна
Ученица 9 класса В.
Ширяева Нина Анатольевна
Цель работы. Гипотеза.
Основные теоретические сведения.
Теорема Вариньона и ее применение. Практическая часть.
Изучить теорему Вариньона
Научиться использовать теорему Вариньона на практике
Рассмотреть задачи из ЕГЭ.
Развить умение исследовать
Рассмотреть разные методы решения задач.
Сравнить решения одной и той же задачи, применяя теорему Вариньона и традиционный подход.
Применение теоремы Вариньона по сравнению с традиционным решением задач по геометрии упрощает процесс доказательства, вычислений и экономит время, затраченное на решение задачи.
Планиметрия — раздел евклидовой геометрии , изучающий двумерные (одноплоскостные) фигуры , то есть фигуры, которые можно расположить в пределах одной плоскости : треугольники, окружности, параллелограммы и т.п. Одной из знаменитых теорем планиметрии является теорема Вариньона, описывающая удивительный феномен.
Эта теорема иллюстрирует два важных принципа: во-первых, доказательство, которое не объясняет явление, не является достаточным, во-вторых, цель творческого подхода в математике заключается в том, чтобы понять явление, а для этого необходимо всестороннее доказательство. Иными словами, иногда «доказать» не означает «объяснить».
Пьер Вариньон ( фр. Pierre Varignon , Кан , 1654 — 23 декабря , 1722 , Париж )— французский математик и механик , член Парижской Академии наук , профессор математики коллежа Мазарини ( 1688 ), профессор Коллеж де Франс (с 1704). Обучался в иезуитском коллеже и университете в Кане , где стал магистром в 1682 году .
Вариньон был другом Ньютона , Лейбница и Бернулли . Основной вклад Вариньон совершил в статику и механику ; кроме того, труды Вариньона посвящены анализу бесконечно малых ( Анализ бесконечно малых — историческое название математического анализа , раздела высшей математики ), геометрии , гидромеханике . За исключением Лопиталя , Вариньон был самым первым пропагандистом дифференциального исчисления во Франции. В 1687 году дал точную формулировку закона параллелограмма сил , развил понятие момента сил и вывел теорему , получившую имя Вариньона. В 1725 Вариньон дал систематическое изложение учения о сложении и разложении сил, о моментах сил и о правилах оперирования ими.
Четырехугольник, вершины которого совпадают с серединами сторон произвольного четырехугольника, является параллелограммом, стороны которого параллельны диагоналям исходного четырехугольника, площадь которого равна половине площади данного четырехугольника.

ABCD – выпуклый четырехугольник
1) KLMN – параллелограмм;
2) S KLMN = 
К 
KL II AC MN II KL , NK II ML следовательно KLMN параллелограмм.
Учитывая, что 

Основные теоретические сведения.
Бимедианы четырехугольника – это отрезки, соединяющие середины противоположных сторон.
Следствия из теоремы Вариньона:
1. Параллелограмм Вариньона является ромбом тогда и только тогда, когда в исходном четырехугольнике:
а) диагонали равны
б) бимедианы перпендикулярны.
А) Дано: Доказательство:

KLMN – параллелограмм Вариньона
Так как AC=BD (диагонали исходного четырехугольника равны по условию), то стороны параллелограмма Вариньона будут равны KL=LM=MN=NK (используя свойство средних линий треугольников, образованных при пересечении диагоналей исходного четырехугольника). Параллелограмм c равными сторонами является ромбом. ч.т.д.
Б
KLMN – параллелограмм Вариньона;
KM и LN перпендикулярны
Доказать: KLMN – ромб
Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали перпендикулярны, то этот параллелограмм является ромбом (по признаку ромба). ч.т.д.
Параллелограмм Вариньона является прямоугольником тогда и только тогда, когда в исходном четырехугольнике:
а) диагонали перпендикулярны
б) бимедианы равны
А) Дано: Доказательство:
A
KLMN – параллелограмм Вариньона
AC и BD – перпендикулярны
Так как диагонали AC и BD – перпендикулярны, то стороны параллелограмма Вариньона будут перпендикулярны. Следовательно, параллелограмм Вариньона является прямоугольником. ч.т.д.
Б
KLMN – параллелограмм Вариньона;
Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником (по признаку прямоугольника). ч.т.д.
Параллелограмм Вариньона является квадратом тогда и только тогда, когда в исходном четырехугольнике:
а) диагонали равны и перпендикулярны
б) бимедианы равны и перпендикулярны
А) Дано: Доказательство:
A
KLMN – параллелограмм Вариньона;
AC и BD – перпендикулярны
Так как диагонали исходного четырехугольника AC и BD равны и перпендикулярны, то стороны параллелограмма Вариньона будут равны и перпендикулярны. Следовательно, параллелограмм Вариньона является квадратом. ч.т.д.
Б
KLMN – параллелограмм Вариньона
бимедианы KM и LN – перпендикулярны
Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм является квадратом (по признаку квадрата). ч.т.д.
Бимедианы четырехугольника и отрезок, соединяющий середины диагоналей, пересекаются в одной точке и делятся этой точкой пополам.
Пусть KM и LN – бимедианы,
PQ – отрезок, соединяющий АС и BD.
Отрезки PQ и LN их точкой пересечения делятся пополам
То, что бимедианы KM и LN точкой пересечения делятся пополам, следует из того, что эти отрезки являются диагоналями параллелограмма Вариньона. Поэтому нам достаточно доказать, что отрезки PQ и LN их точкой пересечения делятся пополам.
Используя теорему о средней линии треугольника для соответствующих треугольников, имеем:
Тем самым, PLQN – параллелограмм. По свойству параллелограмма следует, что отрезки PQ и LN их точкой пересечения делятся пополам. ч.т.д.
Для четырехугольника сумма квадратов всех сторон равна сумме квадратов диагоналей плюс учетверенный квадрат отрезка, соединяющего середины диагоналей, то есть 
Д
BD и AC диагонали
EF – отрезок, соединяющий АС и BD
Для медианы ET треугольника ELN имеем: 







Кроме того, 
Итак, получаем: 
AB 2 +BC 2 +CD 2 +AD 2 =AC 2 +BD 2 +4EF 2 . ч.т.д.
Следствие 6. (теорема о бабочках).
Суммы площадей накрест лежащих четырехугольников, образованных пересечением бимедиан LN и KM выпуклого четырехугольника ABCD равны.
A
LN и KM бимедианы
Воспользуемся теоремой о средней линии треугольника. Получаем:

Теорема Вариньона и ее применение.
З
Отрежем четырёхугольник ABCD и пусть Р — середина AD, тогда по теореме Вариньона A1B1C1P – параллелограмм, А1С1 – его диагональ и К – середина А1С1, значит, К – середина и второй диагонали параллелограмма В1Р.
Значит, KL – средняя линия треугольника PB1D1, поэтому KL||PD1 и KL=1/2 PD1.
Но PD1 – средняя линия треугольника ADE, значит, PD1||AE и PD1=1/2AE, поэтому KL||AE и KL=1/4 AE.
Задача 2. Средние линии четырёхугольника ABCD равны a и b , а угол между ними 60˚. Найдите диагонали четырёхугольника.
Пусть KM = a , LN = b , 


Из треугольника LTM по теореме косинусов 




О

Задача 3. Докажите, что сумма квадратов диагоналей четырёхугольника в два раза больше суммы квадратов его средних линий.


Задача 4. Докажите, что если диагонали четырёхугольника равны, то его площадь равна произведению средних линий.
В случае равенства диагоналей AC и BD параллелограмм Вариньона KLMN является ромбом (рис.), а площадь ромба равна половине произведения диагоналей:


З
Согласно рис. необходимо доказать, что 






З
Пусть в трапеции ABCD , которую необходимо построить, известны длины диагоналей AC и BD , отрезка LN и величина угла А (рис.).
Поскольку 

Задача 7. (ЕГЭ 2013г.) Медианы АА 1 и ВВ 1 и CC 1 треугольника ABC пересекаются в точке М . Точки А 2 , В 2 и С 2 — середины отрезков MA , MB и МС соответственно.
б) Найдите сумму квадратов всех сторон этого шестиугольника, если известно, что АВ = 6, ВС = 11 и АС = 12.
а) Площадь треугольника А 1 МВ 2 в два раза меньше площади треугольника А 1 МВ , поскольку MB = 2 MB 2 , а высота, проведённая из вершины А 1 у этих треугольников общая: S A 1 MB = 2 SA 1 MB 1 .
Аналогично получаем еще 5 равенств:
С
б) Обозначим длины сторон ВС, АС, АВ треугольника ABC через а, b, с .
Докажем, что квадрат медианы AA 1 равен
Для доказательства на продолжении отрезка AA 1 за точку А 1 отложим отрезок А 1 Р = AA 1 . Получим параллелограмм АСРВ со сторонами АС = РВ = b и АВ = CP = с и диагоналями ВС = а и АР =2 AA 1 . Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон:
Аналогично доказывается, что 
Отрезок C 1 A 2 — средняя линия треугольника АВМ , значит,
Рассуждая аналогично, мы получим, что стороны шестиугольника втрое меньше медиан треугольника ABC : 
Подставляя в эту формулу длины сторон треугольника ABC , получаем ответ: сумма квадратов сторон шестиугольника равна
Ответ:
Задача 8. (ЕГЭ 2014) Дан четырёхугольник ABCD.
а) Докажите, что отрезки LN и KM , соединяющие середины его противоположных сторон, делят друг друга пополам.
б) Найдите площадь четырёхугольника ABCD, если
а

2 способ (теорема Вариньона) По теореме Вариньона KLMN –параллелограмм, KM и LN диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. Ч.т.д.
б) 1 способ ( традиционный ) В треугольнике KLM имеем:
Значит, 
Пусть искомая площадь четырёхугольника ABCD равна S . Отрезок KL является средней линией треугольника ABC, поэтому 
Где 

Поэтому 
2 способ (теорема Вариньона) По теореме Вариньона S ABCD = 2 S KLMN , S KLMN =2 S LMK . S LMK = 


Ответ:
В ходе исследовательской работы я достигла целей, поставленных в начале работы. Я изучила теорему Вариньона и рассмотрела интересующие меня задачи.
Изучение этой теоремы дало мне новые знания о четырехугольниках, которые могут пригодиться мне в 11 классе. Рассматривая задания ЕГЭ 2 части, я поняла, что это полезные знания. Решая планиметрические задачи, связанных с четырехугольниками теорема Вариньона помогает сэкономить время при решении и доказательстве задач.
Теорема Вариньона и её применение к решению задач
В математике самыми трудными считаются геометрические задачи. Почти каждая геометрическая задача нестандартна. Надо подумать, какие нужно сделать дополнительные построения, какими воспользоваться теоремами, при этом очень непросто из их огромного количества выбрать ту, которая наилучшим образом поможет в решении.
Скачать:
| Вложение | Размер |
|---|---|
| Теорема Вариньона и её применение к решению задач | 498.69 КБ |
Предварительный просмотр:
Министерство образования и науки РБ
МОУ «Иволгинская средняя общеобразовательная школа»
Республиканская научно- практическая конференция «Шаг в будущее»
Направление : преобразование фигур
и её применение к решению задач.
ученица 10 класса.
Минеева Ирина Анатольевна,
конт.тел. 8 950 382 7857
Глава 1. Пьер Вариньон и его теорема……………………………………….4
1. 2. Доказательство теоремы Вариньона…………………………………….4
Глава 2. Применение теоремы Вариньона……………………………………6
2. 1. Применение теоремы Вариньона к доказательству основного
свойства медиан треугольника……………………………………………. 6
2. 2. Применение теоремы Вариньона к решению задач………………….7
Список использованной литературы………………………………………..11
Крупное научное открытие даёт
решение крупной проблемы,
но и в решении любой задачи
присутствует крупица открытия.
Д. Пойа, венгерский математик
В математике самыми трудными считаются геометрические задачи. Почти каждая геометрическая задача нестандартна. Надо подумать, какие нужно сделать дополнительные построения, какими воспользоваться теоремами, при этом очень непросто из их огромного количества выбрать ту, которая наилучшим образом поможет в решении.
Цель работы: показать, что теорема Вариньона — надёжный помощник в решении геометрических задач.
Актуальность и новизна работы состоит в том, что область применения теоремы Вариньона не раскрыта в школьных учебниках и не показана её роль в решении задач.
1. Рассмотреть доказательство теоремы Вариньона для различных видов четырёхугольников (выпуклого, вогнутого, пространственного);
2. Продемонстрировать применение теоремы Вариньона для решения важных планиметрических задач.
1. Анализ, систематизация и обобщение данных из различных источников информации (основные источники информации – статьи из периодических изданий по математике (журналы: «Квант», «Математика в школе», «Математика»), энциклопедии, Интернет);
2. Самостоятельное решение задач.
Практическая и теоретическая значимость работы состоит в том, что данное исследование можно использовать при проведении уроков, кружков, факультативов, подготовке к олимпиадам и экзаменам. Решение олимпиадных задач служит хорошей подготовкой к будущей научной деятельности, заостряет интеллект.
1. Пьер Вариньон и его теорема.
1. 1. Историческая справка.
Окружающий нас мир – это мир геометрии, чистой,
истинной, безупречной в наших глазах. Всё вокруг – геометрия.
Пьер Вариньон, руководивший «Журналом учёных» в Париже и написавший учебник по элементарной геометрии, по-видимому, первым заострил внимание на, казалось бы, довольно очевидном факте: середины сторон выпуклого четырёхугольника являются вершинами параллелограмма.
Пьер Вариньон (1654 — 22.12.1722), французский механик и математик, родился в г. Каенне во Франции. Изучал философию и математику. Работал профессором математики в коллеже Мазарини с 1688 г., с 1704 г. – в Коллеже де Франс, член Парижской Академии наук с 1688 г. Труды Вариньона посвящены теоретической механике, анализу бесконечно малых, геометрии, гидромеханике. Наибольшее значение имеют работы Вариньона по геометрической статике. В 1687 г. в работе «Проект новой механики. » Вариньон дал чёткую формулировку закона параллелограмма сил, развил понятие момента сил и вывел, так называемую, теорему Вариньона .
1. 2. Доказательство теоремы Вариньона.
Теорема Вариньона вытекает из теоремы о средней линии треугольника (средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны) и гласит: середины сторон произвольного четырёхугольника являются вершинами параллелограмма. Стороны этого параллелограмма параллельны диагоналям четырёхугольника, а их длины равны половинам длин диагоналей.
Четырёхугольник — это многоугольник , содержащий четыре вершины и четыре стороны ( многоугольник – простая замкнутая ломаная). Различают выпуклые и невыпуклые четырёхугольники.
Рассмотрим доказательство теоремы для выпуклого четырёхугольника.
Четырёхугольник называется выпуклым , если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
1) К и L – середины сторон АD и AB, значит КL – средняя линия треугольника
АВD, поэтому отрезок КL параллелен диагонали BD и равен её половине.
2) M и N – середины сторон BC и CD, значит MN – средняя линия треугольника BDС , поэтому отрезок MN параллелен диагонали BD и равен её половине.
3) Таким образом, MN || KL и KL = MN , значит четырехугольник KLMN –
параллелограмм по признаку. Теорема доказана.
Следствие. В любом четырёхугольнике отрезки, соединяющие середины противоположных сторон, делятся точкой пересечения пополам.
Действительно, в этих отрезках можно увидеть диагонали параллелограмма, а в параллелограмме диагонали делятся точкой пересечения пополам (эта точка – центр симметрии параллелограмма).
1) Если ABCD – прямоугольник, то KLMN – ромб;
2) Если ABCD — ромб, то KLMN – прямоугольник;
3) Если ABCD — квадрат, то KLMN — квадрат;
4) Если ABCD – равнобедренная трапеция, то KLMN — ромб.
Однако обратные утверждения нельзя считать верными.
Справедливость теоремы Вариньона не зависит от выпуклости четырёхугольника. Теорема Вариньона и следствие из неё остаются верными и для невыпуклого четырехугольника, и для самопересекающейся четырехугольной замкнутой ломаной (рис. 3, 4); в последнем случае может оказаться, что параллелограмм KLMN «вырожденный» — точки K, L, M, N лежат на одной прямой) (доказательство аналогично рассмотренному выше).
Оказывается, что даже не обязательно, чтобы исходный четырёхугольник был плоский, т. е. его вершины не обязаны попадать в одну плоскость, а теорема Вариньона всё равно верна! (рис. 5). Четырёхугольник, вершины которого не лежат в одной плоскости, называют пространственным.
Пространственный четырёхугольник можно получить, вырезав из бумаги четырёхугольник ABCD и согнув его по диагонали под некоторым углом. при этом ясно, что средние линии KL и MN треугольников ABC и ADC остаются по-прежнему их средними линиями и будут параллельны отрезку АС и равны АС/2 (здесь используется тот факт, что для пространства остаётся верным основное свойство параллельных прямых: если две прямые KL и MN параллельны третьей прямой AC, то KL и MN лежат в одной плоскости и параллельны между собой ).
Таким образом, точки K, L, M, N – вершины параллелограмма; тем самым отрезки KM и LN пересекаются и делятся точкой пересечения пополам.
Вместо четырехугольника здесь можно говорить о тетраэдре — треугольной пирамиде АВСD: середины К, L, М, N его ребер АВ, АС, СD и DА всегда лежат в одной плоскости. Разрезав тетраэдр по этой плоскости (рис. 6), получается параллелограмм KLMN, две стороны которого параллельны ребру АС и равны AC/2, а две другие — параллельны ребру ВD и равны BD/2.
Такой же параллелограмм – «среднее сечение» тетраэдра – можно построить и для других пар противоположных рёбер. Каждые два из этих трёх параллелограммов имеют общую диагональ. При этом середины диагоналей совпадают.
Таким образом, получаем интересное свойство тетраэдра: в тетраэдре 3 отрезка, соединяющие середины противоположных рёбер, пересекаются в одной точке и делятся в ней пополам (на чертеже отрезки KM, LN и PQ).
Итак, мы показали, что теорема Вариньона верна для выпуклого, невыпуклого, пространственного четырёхугольников, а также для самопересекающейся четырехугольной замкнутой ломаной и тетраэдра.
2. Применение теоремы Вариньона.
2. 1. Применение теоремы Вариньона к доказательству основного свойства медиан треугольника.
Продемонстрируем применение теоремы Вариньона к доказательству теоремы об основном свойстве медиан треугольника.
Медианы в треугольнике пересекаются в одной точке и делятся в ней в отношении 2:1, считая от вершины.
Доказательство: проведём две медианы AK и BL треугольника ABC . Пусть О – точка их пересечения. Середины сторон невыпуклого четырехугольника АCBО – точки K, L, M и N (рис. 8а) – вершины параллелограмма, причем точкой пересечения его диагоналей KM и LN для этой конфигурации будет точка пересечения медиан О. Итак, AM = MO = OK и BN = NO = OL , т.е. точка О делит каждую из медиан AK и BL в отношении 2:1.
Аналогично доказывается для медианы, проведённой из вершины С.
Для сравнения рассмотрим доказательство этой теоремы, использованное в учебнике геометрии Атанасяна Л.С.
Доказательство: рассмотрим произвольный треугольник ABC (рис. 8б). Обозначим буквой О точку пересечения его медиан AА 1 и ВВ 1 и проведём среднюю линию А 1 В 1 этого треугольника. Отрезок А 1 В 1 параллелен стороне АВ, поэтому 

рис. 8б
параллельных прямых АВ и А 1 В 1 секущими АА 1 и ВВ 1 . Следовательно, треугольники АОВ и А 1 ОВ 1 подобны по двум углам, и, значит, их стороны пропорциональны: 
Но АВ=2А 1 В 1 , поэтому АО=2А 1 О и ВО=2В 1 О. Таким образом, точка О пересечения медиан АА 1 и ВВ 1 делит каждую из них в отношении 2:1, считая от вершины.
Аналогично доказывается, что точка пересечения медиан ВВ 1 и СС 1 делит каждую из них в отношении 2:1 считая от вершины, и, следовательно, совпадает с точкой О. Теорема доказана.
На наш взгляд, доказательство с помощью теоремы Вариньона проще.
2. 2. Применение теоремы Вариньона к решению задач.
Рассмотрим применение теоремы Вариньона к решению планиметрических задач повышенной трудности. Дело в том, что планиметрические задачи на олимпиадах встречаются значительно чаще.
Мы будем называть параллелограмм KLMN параллелограммом Вариньона , а отрезки КМ и LN, соединяющие середины противоположных сторон четырёхугольника АВСD — средними линиями этого четырёхугольника.
Задача 1. В выпуклом пятиугольнике ABCDE середины сторон AB и CD, BC и DE соединены отрезками. K, L – середины этих отрезков. Доказать, что отрезок KL параллелен пятой стороне AE и составляет ¼ от неё.
Решение: отрежем четырёхугольник ABCD и пусть Р-середина AD, тогда по теореме Вариньона A 1 B 1 C 1 P – параллелограмм, А 1 С 1 – его диагональ и К – середина А 1 С 1 , значит, К – середина и второй
диагонали параллелограмма В 1 Р. Значит, KL – средняя линия треугольника PB 1 D 1 , поэтому KL||PD 1 и KL=1/2 PD 1 , но PD 1 –

средняя линия треугольника ADE, значит, PD1||AE и PD 1 =1/2AE, поэтому KL||AE и KL=1/4 AE.
Задача 2. Верно ли, что можно составить треугольник из любой средней линии треугольника и отрезков, вдвое меньших его диагоналей?
Решение: верно, так как параллелограмм Вариньона существует для любого выпуклого четырёхугольника. Например, условию задачи удовлетворяют треугольники KLM и LMN на рис. 10.
Задача 3. Средние линии четырёхугольника ABCD равны a и b, а угол между ними 60˚. Найдите диагонали четырёхугольника.
Решение: пусть KM=a, LN=b, 


Из треугольника LTM по теореме косинусов 




Ответ: 
Задача 4. Докажите, что сумма квадратов диагоналей четырёхугольника в два раза больше суммы квадратов его средних линий.
Доказательство: в параллелограмме Вариньона, как и в
любом другом параллелограмме, сумма квадратов рис. 11 диагоналей равна сумме квадратов всех его сторон, т.е. 
Задача 5. Докажите, что площадь параллелограмма Вариньона равна половине площади четырёхугольника ABCD.
Доказательство: 
Учитывая, что 

Задача 6. Докажите, что все четырёхугольники, имеющие общие середины
Доказательство: действительно, для всех таких четырёхугольников определён один и тот же параллелограмм Вариньона. Его площадь равна половине площади каждого из исходных четырёхугольников (задача 5), тем самым их равновеликость доказана.
Задача 7. Докажите , что если диагонали четырёхугольника равны, то его площадь равна произведению средних линий.
Доказательство: в случае равенства диагоналей AC и BD параллелограмм Вариньона KLMN является ромбом (рис. 13), а
площадь ромба равна половине произведения диагоналей: рис. 13


Задача 8. Диагонали четырёхугольника ABCD равны d 1 и d 2 , а средние линии равны между собой. Найдите площадь четырёхугольника.
Решение: из условия задачи следует, что в параллелограмме Вариньона диагонали KM и LN равны (рис. 12). Значит, KLMN – прямоугольник и S KLMN = 

Ответ: S ABCD = 
Задача 9. Докажите, что площадь четырёхугольника равна произведению средней линии на одну из диагоналей и на синус угла между ними.
Доказательство: согласно рис. 14 необходимо доказать, рис. 14
что 






Задача 10. Докажите, что сумма квадратов сторон четырёхугольника равна сумме квадратов его диагоналей, сложенной с учетверённым квадратом отрезка, соединяющего середину его диагоналей.
Доказательство: согласно рис. 11 надо доказать, что 








Кроме того, 
Итак, получаем: 
AB 2 +BC 2 +CD 2 +AD 2 =AC 2 +BD 2 +4EF 2 .
Задача 11. Постройте трапецию по диагоналям, одному из углов и отрезку, соединяющему середины оснований.
Решение: пусть в трапеции ABCD, которую необходимо построить, известны длины диагоналей AC и BD, отрезка LN и величина угла А (рис. 15). Поскольку 

по трём сторонам треугольник KLN. Далее построим его до параллелограмма рис. 15
Вариньона. Затем на отрезке KN построим сегмент, вмещающий угол А, и проведём через точку N параллельно KM прямую, она пересечёт сегмент в точке А. Дальнейшее построение очевидно.
В ходе работы мы прорешали более двадцати пяти задач, формулировки и решения наиболее интересных из них дополнительно приведены в приложении. Мы убедились в том, что теорема Вариньона помогает красиво, оригинально решать задачи, открывать и доказывать новые свойства четырёхугольников.
В процессе исследования мы узнали о Пьере Вариньоне, его достижениях, рассмотрели доказательство его теоремы для различных видов четырёхугольников; показали, что справедливость теоремы не зависит от выпуклости четырёхугольника, продемонстрировали применение теоремы; убедились в том, что параллелограмм Вариньона – надёжный помощник в решении геометрических задач различной сложности, узнали много нового и интересного о свойствах геометрических фигур. Таким образом, мы считаем, что цель работы достигнута.
Наше исследование поможет систематизировать и углубить теоретические и практические знания учащихся по геометрии. Работа перспективна, т.к. геометрия не остановилась в своём развитии, а играет всё большую роль в познании мира.
Список использованной литературы.
1. Атанасян Л.С. Геометрия, 7-9: учебник. – М.: Просвещение, 2002.
2. Атанасян Л.С. Геометрия, 10-11: учебник. – М.: Просвещение, 2003.
3. Атанасян Л.С. Геометрия. Доп. главы к школьному учебнику 8 кл.: учебное пособие для учащихся школ и классов с углублённым изучением математики. – М.: Вита-Пресс, 2002.
4. Атанасян Л.С. Геометрия. Доп. главы к школьному учебнику 9 кл.: учебное пособие для учащихся школ и классов с углублённым изучением математики. – М.: Вита-Пресс, 2002.
5. Вагутен В.Н. Средние линии// Журнал «Квант». – 1989. – № 6.
6. Глейзер Г.И. История математики в школе, 9-10 кл. – М.: Просвещение, 1983.
7. Зив Б.Г. Задачи к урокам геометрии. 7-11 кл. – СПб: АКАЦИЯ, 1995.
8. Ильин В. Применение теоремы о средней линии треугольника к решению задач// Газета «Математика». Объединение педагогических изданий «1 сентября». – 1998. – № 48.
9. Куланин Е.Д. 3000 конкурсных задач по математике. – М.: Рольф, 1997.
10. Филипповский Г.Б. Параллелограмм Вариньона решает задачи// Журнал «Математика в школе». – 2006. – № 4.
11. Шарыгин И.Ф. Решение задач. Пособие для 10 кл. общеобразоват. учреждений. – М.: Просвещение, 1994.
12. Энциклопедический словарь юного математика// Сост. Савин А.П. –
М.: Педагогика, 1985.
13. Энциклопедия. Т.11. Математика. – М.: Аванта +, 2000.
ЗАДАЧИ, КОТОРЫЕ РЕШАЮТСЯ С ПРИМЕНЕНИЕМ
Задача 1. В выпуклом шестиугольнике середины сторон соединены через одну. Доказать, что центры тяжести двух образовавшихся треугольников совпадают.
Задача 2. Докажите, что периметр параллелограмма Вариньона равен сумме длин диагоналей четырёхугольника ABCD.
Задача 3. Докажите, что средние линии четырёхугольника пересекаются в одной точке и делятся этой точкой пополам.
Задача 4. Верно ли, что можно составить треугольник из любой средней линии четырёхугольника и отрезков, вдвое меньших его диагоналей? (Ответ: верно).
Задача 5. Средние линии четырёхугольника ABCD равны a и b, а угол между ними 60°. Найдите диагонали четырёхугольника. (Ответ: 

Задача 6. Постройте ромб с вершинами на сторонах прямоугольника ABCD.
Задача 7. Докажите, что сумма квадратов диагоналей четырёхугольника в два раза больше суммы квадратов его средних линий.
Задача 8. Докажите, что площадь параллелограмма Вариньона равна половине площади четырёхугольника ABCD.
Задача 9. Докажите, что все четырёхугольники, имеющие общие середины сторон, равновелики.
Задача 10. Докажите, что площадь четырёхугольника равна произведению средней линии на одну из диагоналей и на синус угла между ними.
Задача 11. Докажите, что если диагонали четырёхугольника равны, то его площадь равна произведению средних линий.
Задача 12. В четырёхугольник ABCD вписывают всевозможные параллелограммы, стороны которых параллельны диагоналям четырёхугольника. Какой из этих параллелограммов имеет наибольшую площадь? (Ответ: параллелограмм Вариньона).
Задача 13. Внутри четырёхугольника ABCD, имеющего площадь S, берётся точка E и отражается относительно середин всех его сторон. Получается новый четырёхугольник A 1 B 1 C 1 D 1 . Докажите, что SA 1 B 1 C 1 D 1 =2S .
Задача 14. В четырёхугольнике ABCD отмечены точки E и F – середины диагоналей AC и BD соответственно. Докажите, что S ELFN ABCD
Задача 15. Докажите, что средние линии четырёхугольника ABCD и отрезок, соединяющий середины его диагоналей, пересекаются в одной точке и делятся этой точкой пополам.
Задача 16. Докажите, что сумма квадратов сторон четырёхугольника равна сумме квадратов его диагоналей, сложенной с учетверённым квадратом отрезка, соединяющего середины диагоналей.
Задача 17. Восстановите пятиугольник по серединам его сторон.
Задача 18. Постройте трапецию по диагоналям, одному из углов и отрезку, соединяющему середины оснований.
Задача 19. Восстановите параллелограмм по серединам его сторон.
Задача 20. Докажите, что точка пересечения средних линий четырёхугольника есть центроид системы четырёх точек, лежащих в его вершинах.
Задача 21. При последовательном соединении середин сторон трапеции получился квадрат со стороной а. Найдите площадь трапеции (Ответ: 2а 2 ).
Задача 22. Даны трапеция ABCD и точка Е на её средней линии. С помощью одной линейки постройте параллелограмм Вариньона для трапеции ABCD.
Задача 23. Вершины четырёхугольника являются серединами сторон ромба со стороной, равной 4, и углом 120°. Определите вид четырёхугольника и найдите его площадь. (S= 
Задача 24. Восстановите (2n+1)-угольник по серединам его сторон.
РЕШЕНИЯ НЕКОТОРЫХ ЗАДАЧ.
Задача 13. Внутри четырёхугольника ABCD, имеющего площадь S, берётся точка E и отражается относительно середин всех его сторон. Получается новый четырёхугольник A 1 B 1 C 1 D 1 . Докажите, что SA 1 B 1 C 1 D 1 =2S .
Доказательство: стороны параллелограмма Вариньона и параллелограмма A 1 B 1 C 1 D 1 соответственно параллельны (рис. 16), KL= 


Задача 14. В четырёхугольнике ABCD отмечены точки E и F – середины диагоналей AC и BD соответственно. Докажите, что S ELFN 
Доказательство: так как S KLMN = 
Очевидно, что ТТ 1 =KL= 




S ELFN KLMN = 
Задача 15. Докажите, что средние линии четырёхугольника ABCD и отрезок, соединяющий середины его диагоналей, пересекаются в одной точке и делятся этой точкой пополам.
Доказательство: заметим, что отрезок LN является диагональю и в параллелограмме Вариньона, и в параллелограмме ELFN (см. рис. к задаче 18). Пусть точка Т—середина диагонали LN, тогда в этой точке пересекаются отрезки LN и КМ, а также LN и EF и каждый из них, будучи диагональю параллелограмма, делится точкой T пополам.
Задача 21. При последовательном соединении середин сторон трапеции получился квадрат со стороной а. Найдите площадь трапеции.
Решение: четырёхугольник KLMN-параллелограмм Вариньона (квадрат). (AD+BC)/2=KM (средняя линия трапеции). Треугольник KLM прямоугольник KM= 


Задача 23. Вершины четырёхугольника являются серединами сторон ромба со стороной, равной 4, и углом 120˚. Определите вид четырёхугольника и его площадь.
Решение: Параллелограмм Вариньона KLMN—прямоугольник, так как диагонали ромба AC и BD пересекаются под прямым углом, а значит и параллельные им стороны KN и KL. S KLMN = 



Ответ:
источники:
http://infourok.ru/issledovatelskaya-rabota-po-matematike-teorema-varinona-klass-3150837.html
http://nsportal.ru/ap/library/drugoe/2021/09/18/teorema-varinona-i-eyo-primenenie-k-resheniyu-zadach
Параллелограмм Вариньона
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Лаптева Е.Д. 1
1МБОУ лицей №40 при Ульяновском государственном университете
Гуськова А.Г. 1
1Лицей №40 при ульяновском государственном университете
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
1. Введение.
Цель: исследовать приемы решений планиметрических задач с использованием теоремы Вариньона и следствий из нее.
Задачи:
1.Изучить теорему Вариньона.
2.Сравнить решение планиметрических задач ,применяя теорему Вариньона и традиционный способ решения.
3.Сравнить затраченные временные ресурсы на решение задач с помощью теоремы Вариньона и обычным способом.
4.Практически применить в решении олимпиадных задач и задач ОГЭ и ЕГЭ теоремы Вариньона.
Гипотеза: решать планиметрические задачи с помощью теоремы Вариньона намного эффективнее по сравнению с традиционным способом.
Актуальность: новейшие технологии в математический дисциплинах требуют применения прогрессивных и эффективных способов решения задач.
Объект исследования: параллелограмм Вариньона, бимедианы четырехугольника, теорема Вариньона и ее свойства
Предмет исследования: планиметрические задачи
Методы исследования:
1.Анализ, систематизация и обобщение данных из различных источников информации.
2.Самостоятельное решение задач.
В математике самыми трудными считаются геометрические задачи. Почти каждая геометрическая задача нестандартна. Надо подумать, какие нужно сделать дополнительные построения, какими воспользоваться теоремами, при этом очень непросто из их огромного количества выбрать ту, которая наилучшим образом поможет в решении.
2.Теорема Вариньона и её доказательство.
Пьер Вариньон— французский математик и механик. Обучался в иезуитском колледже и университете в Кане, где стал магистром в 1682 году. Основной вклад Вариньон совершил в статику и механику. В 1687 году в своей работе «Проект новой механики…» Вариньон дал точную формулировку закона параллелограмма сил, развил понятие момента сил и вывел теорему, получившую имя Вариньона.
Пьер Вариньон
Теорема Вариньона
Четырехугольник, образованный путем последовательного соединения середин сторон выпуклого четырехугольника, является параллелограммом, и его площадь равна половине площади данного четырехугольника.
Дано:
ABCD – выпуклый четырехугольник
AK=KB; BL=LC; CM=MD; AN=ND
Доказать:
1) KLMN – параллелограмм;
2) S KLMN = S ABCD:2
Доказательство:
1. Рассмотрим одну из сторон четырехугольника KLMN, например KL. KL – средняя линия треугольника ABC (по определению),следовательно, KL ∥ AC. Аналогично, так как MN – средняя линия треугольника ADC,то MN ∥ AC. Так как KL ∥ AC и MN ∥ AC следовательно, KL ∥ NM и KL=MN=AC:2. Таким образом, KLMN – параллелограмм. Этот параллелограмм называется параллелограммом Вариньона данного четырехугольника.
2. Средняя линия треугольника отсекает от него треугольник, площадь которого в четыре раза меньше площади исходного треугольника,
3. т.е. S KBL = S ABC:4, S MDN=S ADS:4. Следовательно, S 1+S 3=S ABCD:4. Аналогично, S 2+S 4= S ABCD:4. Следовательно, S 1+S 3 + S 2+S 4 = S ABCD :4 + S ABCD:4 = S ABCD:2.
Т.е., S KLMN = S ABCD:2. Что и требовалось доказать.
3. Свойства параллелограмма Вариньона :
1. Каждая пара противоположных сторон параллелограмма Вариньона параллельна диагонали в исходном четырехугольнике.
2. Сторона параллелограмма Вариньона вдвое короче диагонали в исходном четырехугольнике, к которому он параллелен.
3. Площадь параллелограмма Вариньона равна половине площади исходного четырехугольника. Это верно для выпуклых, вогнутых и скрещенных четырехугольников при условии, что площадь последнего определяется как разность площадей двух треугольников, из которых он состоит.
4. Периметр параллелограмма Вариньона равен сумме диагоналей исходного четырехугольника.
5. Диагонали параллелограмма Вариньона — это бимедианы исходного четырехугольника.
Определение: Бимедианы четырехугольника — это отрезки, соединяющие середины противоположных сторон (диагонали параллелограмма Вариньона)
4. Следствия из теоремы Вариньона.
Следствие 1: Параллелограмм Вариньона является ромбом тогда и только тогда, когда в исходном четырехугольнике 1) диагонали равны 2) бимедианы перпендикулярны.
Дано: ABCD – четырехугольник; KLMN – параллелограмм Вариньона; AC=BD
Доказать: KLMN – ромб
Доказательство: Так как AC=BD (диагонали исходного четырехугольника равны по условию), то стороны параллелограмма Вариньона будут равны KL=LM=MN=NK (используя свойство средних линий треугольников, образованных при пересечении диагоналей исходного четырехугольника). Параллелограмм c равными сторонами является ромбом.
Следствие 2: Параллелограмм Вариньона является прямоугольником тогда и только тогда, когда в исходном четырехугольнике: 1) диагонали перпендикулярны; 2) бимедианы равны
Дано: четырехугольник ABCD; KLMN – параллелограмм Вариньона; диагонали AC и BD – перпендикулярны
Доказать: KLMN – прямоугольник
Доказательство: Так как диагонали AC и BD – перпендикулярны, то стороны параллелограмма Вариньона будут перпендикулярны. Следовательно, параллелограмм Вариньона является прямоугольником.
Следствие 3: Параллелограмм Вариньона является квадратом тогда и только тогда, когда в исходном четырехугольнике 1) диагонали равны и перпендикулярны; 2) бимедианы равны и перпендикулярны
Дано: четырехугольник ABCD; KLMN – параллелограмм Вариньона; диагонали AC и BD – перпендикулярны; AC=BD
Доказать: KLMN – квадрат
Доказательство : Так как диагонали исходного четырехугольника AC и BD равны и перпендикулярны, то стороны параллелограмма Вариньона будут равны и перпендикулярны. Следовательно, параллелограмм Вариньона является квадратом.
5. Основная часть работы. Применение теоремы Вариньона при решении задач.
Эффективность и удобство применения теоремы Вариньона рассмотрю на задачах , которые я составила сама и подобрала из сборников ОГЭ прошлых лет.
Задача 1.
Докажите, что если диагонали четырехугольника равны, то его площадь равна произведению средних линий .
Дано: ABCD – четырехугольник; AC = BD
Доказать: S ABCD = KM*LN
Доказательство: Так как диагонали AC = BD, параллелограмм Вариньона является ромбом, площадь ромба равна половине произведения его диагоналей. Что и требовалось доказать.
Задача 2
Найдите площадь четырехугольника ABCD ,если его диагонали равны 12 см и 14 см , а его бимедиана равняется 9 см
Дано:AC–диагональ=12см
BD-диагональ=14см
KP=9см
Найти:SABCD
Решение: 1)построим внутри ABCD параллелограмм Вариньона — MKNP
По теореме Вариньона SMKNP= 0,5SABCD
Т.к. бимедиана является диагональю параллелорамма MKNP =) она разделяет параллелограмм на 2 треугольника- PMK и PNK =)
SMKNP=SPMK + SPNK
2)MK = 0,5 BD т.к. BD является средней линией треугольника DAB = 7см
PM = 0,5 AC т.к. является средней линией треугольника ADC = 6см
3) По теореме Герона S=√p(p-a)(p-b)(p-c),где p=a+b+c/2- полупериметр треугольника =11см
SMKNP = √11(11-7)(11-6)(11-9)=√11*4*5*2=√440=2√110*2 =4√110 =)
SABCD = 4√110*2=8√110см
Ответ :SABCD =8√110см
Задача 3
Докажите , что площадь параллелограмма ,образованного прямыми , проходящими через вершины выпуклого четырехугольника и параллельными его диагоналям , в два раза больше площади исходного четырехугольника
Решение:
SABCD=SLMNK+SLKD+SALM+SBMN+SKNC
Так как AMOL,MONB,CKON,DKOL-параллелограммы , то
SALM=SMOL,SMBN=SMON,SNCK=SKON,SLKD=SLOK
Отсюда получаем , что SABCD=2SKLMN,что и требовалось доказать.
Задача 4
В четырехугольнике ABCD обозначены точки E и F – середины диагоналей AC и BD соответственно. Докажите , что SELFN<0,5SABCD
Доказательство :
1) Достаточно доказать, что точки E и F лежат строго внутри параллелограмма Вариньона KLMN, поскольку SKLMN=0,5SABCD.
Очевидно , что T1T2=KL=0,5AC и AE=EC=0,5AC .
2) Пусть точка Е совпадает с точкой G и лежит вне KLMN. Но тогда GC=0,5AC>T1T2 ,
А T1T2=0,5AC- противоречие
Если же E=T1,то T1С=0,5AC=T1T2 , чего также быть не может.
3) Значит, точка Е лежит внутри KLMN .
Аналогично показываем , что точка F лежит внутри параллелограмма KLMN.
Тогда SELFN<SKLMN=0,5SABCD , что и требовалось доказать .
Задача 5
Докажите , что 1)середины сторон прямоугольника являются вершинами ромба. И наоборот , 2 )середины сторон ромба являются вершинами прямоугольника.
Доказательство:
1)Диагонали прямоугольника равны , поэтому середины сторон прямоугольника являются вершинами ромба( из следствия 1);
стороны прямоугольника перпендикулярны , поэтому бимедианы перпендикулярны , тогда середины сторон прямоугольника являются вершинами ромба.
2) Диагонали ромба перпендикулярны , поэтому середины сторон ромба являются вершинами прямоугольника ( из следствия 2);
Стороны ромба равны, поэтому середины сторон ромба являются вершинами прямоугольника.
Задача 6
В выпуклом четырехугольнике ABCD отмечены середины противоположных сторон BC и AD — точки L и N соответственно . Диагональ AC проходит через середину отрезка LN . Найдите площадь четырехугольника ABCD , если площадь треугольника ACD равна S .
Решение : 1) Пусть K и M – середины сторон AB и CD. Тогда KNLM — параллелограмм Вариньона , поэтому отрезок KM содержит середину O отрезка LN. Стороны треугольника KOL – средние линии треугольника ACD , поэтому
SKOL=1/4SACD=1/4S.
Аналогично, SMON= 1/4SABC, а так как треугольники KOL и MON равны , то SADC=4SKOL=4SMON=SACD=S.
Следовательно, SABCD = SABC+SACD=S+S=2S
Ответ : SABCD=2S
Задача 7
Одна из средних линий четырехугольника ABCD равна а . Его диагонали равны 3/2а и 5/2а. Найдите площадь четырехугольника ABCD.
Решение : 1)Пусть в четырехугольнике ABCD LN =a, AC=3/2a,BD=5/2a.
Тогда , KL=1/2AC=3/4a и KN=1/2BD=5/4a
2) По формуле Герона площадь треугольника KLN = √3/2a*a/2*3a/4*a/4=3a²/8
Значит , SABCD=4SKLN=3a²/2
Ответ : SABCD=3a²/2
Задача 8
В четырехугольнике отрезки , соединяющие середины противоположных сторон , равны. Докажите , что диагонали исходного четырехугольника перпендикулярны.
Доказательство: для доказательства будем использовать теорему Вариньона
1) ▲ BEF ~ ▲BAC и ▲DHG ~ ▲DAC =) EF||HG||AC. Аналогично со сторонами EH и FG
2) Т.к. EG=FH, то из этого следует , что четырехугольник EFGH является параллелограммом Вариньона и прямоугольником (следствие2) =) EF⊥EH, FG⊥GH
3) Т.к. ▲ BEF ~ ▲BAC =) EF||AC и ▲AEH~ ▲ABD =)BD||EH
Поэтому EF⊥EH и AC⊥BD ч.т.д.
Задача 9
Докажите , что сумма длин двух отрезков , соединяющих середины противоположных сторон произвольного четырехугольника , меньше суммы длин его диагоналей
Доказательство:
1) Рассмотрим произвольный четырехугольник ABCD , где точки K,L,M,N – середины сторон AB,BC,CD,AD
2) NM является средней линией для▲ADC ,а LK средняя линия для▲ABC =)NM||CA||LK . Аналогично с ▲CDB и ▲ADB =) ML||DB||NK
3) NM=LK=1/2CA и ML=NK=1/2DB(по свойству средней линии ▲) =)
KLMN-параллелограмм Вариньона
4) т.к. сторона должна быть меньше суммы двух других=) KM<KL+LM и LN<LM+MN=) KM+LN<2NM+2LM=)KM+LN<AC+BD ч.т.д.
Задача 10
Дан выпуклый четырехугольник ABCD. Найдите площадь ABCD , если KL=6,KM=4√3 , ∠MKL=30°
Решение:1)Пусть точки K , L , M и N – середины AВ , BC , CD и AD, тогда получившийся четырехугольник KLMN – параллелограмм Вариньона =) SABCD=2SKLMN
2) Проведем высоту MF к основанию KL, тогда SKLMN = KL*MF
▲KMF – прямоугольный и имеет ∠MKL=30° =) катет , лежащий против ∠=30° равен половине гипотенузы =) ML=0,5KM=2√3
SKLMN=6*2√3=12√3
SABCD=12√3*2=24√3
Ответ:SABCD=24√3
6. Заключение.
В процессе исследования я узнала о Пьере Вариньоне, его достижениях, рассмотрела доказательство его теоремы для различных видов четырёхугольников. Я убедились в том, что теорема Вариньона помогает быстро и оригинально решать задачи, открывать и доказывать новые свойства четырёхугольников, что параллелограмм Вариньона может быть использован при решении геометрических задач различной сложности.
Таким образом, выдвинутая гипотеза: с помощью теоремы Вариньона решать планиметрические задачи будет намного легче и быстрее мною подтверждена, и цель работы: «Исследовать приемы решений планиметрических задач с использованием теоремы Вариньона и следствий из нее» была достигнута.
Проведенное исследование помогло мне систематизировать и углубить теоретические и практические знания по геометрии. Считаю выбранную тему актуальной и перспективной, т.к. геометрия важна в различных областях науки, а полученные знания могут быть применимы на олимпиадах, ОГЭ и ЕГЭ по математике, пользуясь теоремой Вариньона можно значительно сэкономить время на решение. В дальнейшем планирую поработать над утверждениями, обратными теореме Вариньона для различных видов четырёхугольников и изучить применение теоремы Вариньона при решении физических задач по теме «Механика».
7. Список использованных источников и литературы.
1. Атанасян, Л. С. Геометрия 7– 9 : учебник / Л .С. Атанасян. – М.: Просвещение, 2016. – 384 с.
2. Вавилов, В. Бимедианы четырехугольника//Математика / В. Вавилов, П. Красников.- 2006 — №22.
3. Зив, Б. Г. Задачи к урокам геометрии 7-11 кл / Б .Г. Зив. – СПб. : Изд-во АКАЦИЯ, 1995. – 624 с.
4. Глейзер, Г.И. История математики в школе 9-10 кл / Г.И.Глейзер. – М.: Просвещение, 1983. –351 с.
5. Ильин, В. Применение теоремы о средней линии треугольника к решению задач / В. Ильин // Газета Математика /. Объединение педагогических изданий 1 сентября. – 1998. – № 48.
6. Коксетер, Г. С. Новые встречи с геометрией / Г. С. Коксетр , С. Л. Грейтцер . – М.: Наука,1978.
7. Куланин, Е. Д. 3000 конкурсных задач по математике / Е .Д. Куланин. – М.: Рольф, 1997. – 608 с.
8. Нагибин, Ф.Ф. Математическая шкатулка / Ф. Ф. Нагибин , Е.С. Канин. – М.: Дрофа, 2006. – 270 с.
9. Прасолов, В.В. Задачи по планиметрии / В. В. Просолов. – М.: Наука, 1995.-Т.1,2.
10. Фарков, А.В. Учимся решать олимпиадные задачи. Геометрия. 5-11 кл. / А. В. Фарков – М.: Айрис-пресс, 2006. – 128 с.
11. Филипповский, Г.Б. Параллелограмм Вариньона решает задачи Г. Б. Филипповский // Журнал Математика в школе. – 2006. – № 4. – с. 45-49.
12. Энциклопедия Математика. – М.: Изд-во Аванта +, 2000.- Т.11. – 688 с.
13. Geretschlager, R. Kalinowski Jozef, Svrcek Jaroslav A Central European Olympiad, The Mathematical Duel [ электронный ресурс] / R. Geretschlager , J. Kalinowski , J. Svrcek .-2018.- Vol. 7. – Режим доступа : https://books.google.com. –Загл. с экрана.
14. Bits of Math [Электронныйресурс]. — community blogs ,2015-.- Режим доступа : https://artofproblemsolving.com, свободный.- Загл.с экрана.
15. Russia 2004 problem [Электронныйресурс]. — community blogs ,2011-.- Режим доступа : https://artofproblemsolving.com, свободный.- Загл.с экрана.
Просмотров работы: 2380




 Для печати
Для печати
 Предыдущая тема | Следующая тема
Предыдущая тема | Следующая тема