Нужно ли писать дано в егэ по математике геометрия

Глава 1. Вебинар по оформлению задач второй части ЕГЭ по математике (3 часа, 10 минут)

Почему важно начать учиться оформлять задачи второй части за 30 дней до ЕГЭ? Потому что вам нужно выработать привычку это делать.

Привычка формируется 30 дней (есть исследования). Если вы узнаете о том, как оформлять задачи за неделю до экзамена, будет поздно. 

Поэтому читайте материал первой главы, смотрите наше первый вебинар и потом применяйте на практике то, что вы узнаете при решении задач постоянно в течение 30 ДНЕЙ!

И прекратите терять баллы на ровном месте!

Научиться правильно оформлять задачи 2 части ЕГЭ по математике намного проще, чем научиться их решать!

Но тем не менее, каждый год огромное количество людей теряют десятки баллов из-за неправильного оформления.

Если вы посмотрите видео, вы научитесь оформлять задачи так, что гарантированно 100% экспертов ЕГЭ поставят вам полный балл (если вы правильно решите задачу, конечно же;) 

На этом видео мы очень подробно разберем все задачи второй части профильного ЕГЭ по математике, и вы узнаете все нюансы оформления: 

• Что такое критерии, как их понимать?
• Что считается опиской, что – арифметической ошибкой, а что – грубой «смысловой» ошибкой? 
• Нужно ли делать проверку ответов (да), и как её делать? 
• Тригонометрия: нужно ли писать разные буквы (n, m, k) в ответах или можно использовать одну для всех формул? 
• Какие способы отбора корней лучше использовать в задаче 13 б), а какие лучше не трогать?
• Как правильно показывать отбор на единичной окружности и не потерять при этом балл?
• В каких случаях предпочтительно пользоваться окружностью, а в каких – двойным неравенством?
• Насколько подробно нужно расписывать решения уравнений и неравенств?
• Нужно ли на чистовике полностью прописывать дискриминант и поиск корней, или достаточно вычислить их устно «по теореме Виета»?
• Как не запутаться в «значках»: где использовать равносильность, а где следствие, как не перепутать систему и совокупность и прочее?
• Можно ли использовать метод рационализации: мифы и реальность Вспомним, что такое ОДЗ, и всегда ли его нужно писать, и как его правильно писать?
• Экономическая задача – это вообще отдельная история. Как могут давать аж 3 первичных балла за простую задачу на проценты? А оказывается, что их за саму задачу и не дают: их дают за правильное оформление! И снимают за каждую мелочь. Многие получают 0 баллов, даже получив правильный ответ. Я очень подробно разберу, что же именно от нас нужно, и как не упустить халявные 3 балла.
• Задачи с параметром чаще всего тоже требуют довольно подробных объяснений, особенно, если мы выбираем графический метод решения. Геометрия.
• Можно ли не решать пункт а, но пользоваться им в решении пункта б? Обязательно ли делать рисунок? 
• Как в стереометрии показывать построение сечений? Какими теоремами можно пользоваться без доказательства? 
• Обязательно ли писать название каждой теоремы? Задача 19 – в каких случаях достаточно примера, а в каких – обязательно писать полное доказательство?
• И много других нюансов, которые уже не помещаются в этот длинный список! 

Если вам понравилось видео, подписывайтесь, ставьте лайки – это поможет тому, чтобы его увидели другие:

Тайм-коды для просмотра этого видео на YouTube:

Для тех, кто предпочитает смотреть видео на YouTube, вы можете перейти по этим тайм-кодам на наш канал на YouTube.

• 0:00 Вступление
• 2:52 Как выглядят критерии
• 4:09 Задача 13
• 5:59 ОДЗ
• 7:37 Можно ли не писать ОДЗ для логарифма?
• 9:00 Записали ОДЗ, но получили 0 баллов – как же так:(
• 12:23 Задача 13 (а)
• 14:00 Подписи осей единичной окружности
• 17:46 Разные или одинаковые буквы использовать в сериях корней (тригонометрия)?
• 26:30 Задача 13 (б) – первый способ, через двойное неравенство
• 32:35 Второй способ, через окружность
• 35:32 Система, совокупность – что это и что делать, если вы их путаете
• 37:11 Лайфхак – как быстро расставить корни на окружности
• 41:06 Третий способ – подбором
• 50:38 Замена переменных – как описывать
• 51:10 Квадратные уравнения – дискриминант или Виет?
• 58:13 Задача 15
• 1:02:26 Упрощаем себе вычисления ОДЗ
• 1:03:50 Пользуемся ОДЗ – упрощаем себе решение неравенства
• 1:04:55 Смешанное неравенство – первый способ (как лучше не делать)
• 1:07:47 Второй способ – обобщённый метод интервалов (и его подводные камни)
• 1:13:32 Метод рационализации – можно ли пользоваться и нужно ли доказывать?
• 1:18:50 Вывод по 15 задаче, критерии
• 1:21:35 Ответ, отличающийся на конечное число точек
• 1:25:42 Проверка ответов в неравенствах – как?
• 1:29:00 значок равносильности
• 1:40:30 Задача 17
• 1:49:50 Критерии; что такое мат. модель?
• 1:52:00 Четыре фразы, которые нужно обязательно написать
• 1:56:00 Умножать на проценты можно? А складывать?
• 2:03:28 Задача 18
• 2:09:46 Обязательно ли нужен красивый рисунок? Как потерять баллы из-за рисунка
• 2:14:05 Полностью обоснованное решение
• 2:15:40 Разбор критериев на 4, 3, 2 и 1 балл
• 2:20:11 Можно ли решать не через окружности, а аналитически?
• 2:21:13 Задача 19: подбор в пункте (а) и “оценка + пример” в пункте (в)
• 2:27:00 Задача 14
• 2:27:40 Координатный метод
• 2:30:33 Можно ли брать числа из пункта (б), когда решаем пункт (а)?
• 2:35:13 Построение сечения (с обоснованием)
• 2:39:05 Значки “лежит”, “принадлежит” – в чём отличие и важно ли не перепутать?
• 2:44:35 В пункте (б) пользуемся недоказанным пунктом (а) – в задачах 14 и 16
• 2:48:15 Использование “необычных” теорем – можно ли без доказательства?
• 2:51:30 Если забыл название теоремы
• 2:53:54 Элементарные вещи можно не выводить
• 2:57:05 Теорема Фалеса или обратная теорем Фалеса?
• 2:58:35 Что будет на Марафоне и кому он нужен
• 3:00:16 Призы

В задаче 16 ЕГЭ по математике (геометрия) пункт (а) – доказательство. Вот 30 полезных фактов, которые надо знать и уметь доказывать. Любой из них может быть таким «пунктом (а)» в задаче ЕГЭ №16. Доказательство таких полезных фактов – первый этап в освоении геометрии.

Углы, треугольники, четырехугольники

1. Биссектрисы смежных углов перпендикулярны.
2. Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.
3. Медианы треугольника пересекаются в одной точке и делятся в ней в отношении 2:1, считая от вершины.
4. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
5. Площадь любого четырехугольника равна половине произведения диагоналей на синус угла между ними.
6. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.
7. Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали – полусумме оснований.
8.Замечательное свойство трапеции. Точка пересечения диагоналей трапеции, точка пересечения продолжений ее боковых сторон и середины оснований лежат на одной линии.

Окружности

9. Диаметр, перпендикулярный хорде, делит ее пополам
10. Произведения отрезков пересекающихся хорд окружности равны.
11. Серединный перпендикуляр к хорде проходит через центр окружности
12. Равные хорды удалены от центра окружности на равные расстояния
13. Дуги окружности, заключенные между параллельными хордами, равны.
14. Теорема о касательной и секущей. Если из одной точки к окружности проведены секущая и касательная, то произведение всей секущей на ее внешнюю часть равно квадрату отрезка касательной.
15. Угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.
16. Угол между пересекающимися хордами равен полусумме противоположных дуг, высекаемых хордами.
17. Угол между двумя секущими равен полуразности дуг, высекаемых секущими на окружности.
18. Радиус окружности, вписанной в прямоугольный треугольник с катетами а и b и гипотенузой с, равен
19. Прямая, проходящая через точки пересечения двух окружностей, делит пополам общую касательную к ним.
20. Если расстояние между центрами окружностей радиусами R и r равно а и а > R+r, то отрезки общих внешних и общих внутренних касательных, заключенные между точками касания, равны соответственно и
21. Если четырехугольник можно вписать в окружность, то сумма его противоположных углов равна 180 градусов.
22. Если в четырехугольник можно вписать окружность, то суммы длин его противоположных сторон равны.
23. Если окружность вписана в равнобедренную трапецию, то боковая сторона трапеции равна ее средней линии.
24. Геометрическое место точек М, из которых отрезок АВ виден под прямым углом (угол АМВ = 90 градусов), есть окружность с диаметром АВ без точек А и В.
25. Геометрическое место точек М, из которых отрезок АВ виден под данным углом, есть две дуги равных окружностей с общей хордой АВ, без точек А и В.
26. Если М – точка касания со стороной АС окружности, вписанной в треугольник АВС, то АМ = р – ВС, где р – полупериметр треугольника АВС.
27. Если окружность касается стороны ВС треугольника АВС и продолжений сторон АВ и АС, то расстояние от вершины А до точки касания окружности с прямой АВ равно полупериметру треугольника АВС.
28. Если окружность, вписанная в треугольник АВС, касается сторон АВ, ВС и АС соответственно в точках K, L, M, а угол ВАС равен φ, то угол KLM равен
29. Если прямые, проходящие через точку А, касаются окружности S в точках В и С, то центр вписанной окружности треугольника АВС лежит на окружности S.
30. Если АМ и СК – высоты треугольника АВС, то треугольник МВК подобен треугольнику АВС, причем коэффициент подобия равен |cos В|.
31. Если площадь треугольника равна S, то площадь треугольника, составленного из его медиан, равна

Доказывайте полезные факты. Запоминайте картинки и схемы решения. Чем больше у вас таких ассоциативных связей – тем проще решаются задачи по геометрии.

При составлении списка полезных фактов использованы учебные пособия Р. К. Гордина.

Изменение требований к оформлению заданий с развернутым ответом

в ЕГЭ по математике.

Оформление номеров второй (письменной) части ЕГЭ по профильной математике – одна из наиважнейших тем, нюансы которой так важно освоить всем ученикам, претендующим на высокие баллы. На этом, казалось бы, не главнейшем моменте возможно как сильно «погореть», так и закрепить результат, получив максимально возможные баллы – разница может доходить до 10 первичных баллов за вторую часть – при более внимательном подходе. Рассмотрим основные пункты надлежащего оформления номеров 13, 15 и 17 – тех, которые входят в так называемую стратегию подготовки к ЕГЭ — «Ударим по нечетным».

Задание №13. Тригонометрические, показательные, логарифмические и иррациональные (последний вид был на досрочном тестировании в прошлом году) уравнения.

Под буквой (а) — решение, под буквой (б) — отбор корней на отрезке/интервале (по 1 баллу за каждый пункт, макс. — 2 балла).

Основные «подводные камни» — в оформлении пункта (б), а именно:

— Отбор корней нельзя назвать обоснованным, если перебор остановлен на корне, принадлежащем отрезку. В таком случае — 0 баллов за букву (б) номера 13 ДАЖЕ ПРИ ВЕРНОМ ОТВЕТЕ!

— Также очень придирчивы эксперты к методу отбора корней с помощью тригонометрической окружности. Особенно, если не обозначены границы «дуги», а в итоге также при правильном ответе его «нельзя считать достаточно обоснованным», а значит — 0 баллов за второй пункт. Обидно. Действительно, метод отбора по окружности не очень нагляден, поэтому мы и выбираем самый оптимальный — отбор с помощью двойного неравенства, что позволяет избежать вышеозначенных коллизий.

2. Задание №15. Дробно-рациональные, показательные, логарифмические и другие неравенства (макс. — 2 балла)

Первоочередной вопрос — ОДЗ:

— Аббревиатуры ОДЗ нет ни в одном учебнике федерального комплекта (Мордкович был из перечня исключен). Есть область допустимых значений ФУНКЦИИ, а вот ПЕРЕМЕННОЙ в федеральных программах мы не встретим.

— Есть большой риск указать не все допустимые значения, а значит сразу свести все усилия на нет, ведь написание слова ОДЗ обязывает нас учесть все ограничения, а значит — 0 баллов при идеальном решении основного неравенства, «четко и жестко», как нам объясняют на видео.
НО! Мне не хочется раньше времени «расхолаживать» своих учеников — мол, да не пишите вы слово ОДЗ, а значит — зачем вам знать, какие необходимые условия должны в нем содержаться.
Нет. Знать все ограничения можно и нужно, и на каждом занятии мы будем системно их оттачивать, но на самом экзамене, чтобы минимизировать риски ввиду нервов, ввиду появления номера, прототипов к которому не было и вы можете запутаться и учесть не всё, — вот на самом ЕГЭ слово ОДЗ мы писать НЕ БУДЕМ. Ограничения — приведем, это необходимо. Но связывать себе руки самим термином не станем.

Второй момент — использование рационализации и соответствующее оформление решения логарифмического неравенства данным методом.
Комиссия решила следующее: метод имеет место быть, даже если не всегда рассматривается в обычной школьной программе.
НО! Тогда эксперты предлагают упоминать в решении о монотонном возрастании логарифмической функции. На мой взгляд, наше оформление с приведением совокупности двух систем — двух случаев, на которые распадается исходное неравенство в зависимости от расположения основания относительно единицы и последующая фраза «данная совокупность равносильна неравенству» — представляется мне наиболее системным и понятным способом. По крайней мере, не встретилось еще ни одного случая, чтобы за это «отбирали» балл, напротив — всё проходит гладко. Вот и не будем менять курс. Методу рационализации официально дан «зеленый свет».

​​​​​​​ 3. Задание №17. Текстовая задача с экономическим содержанием (макс. — 3 балла):

— Если применять готовую формулу без ее выведения, решение считается недостаточно обоснованным даже если получен верный ответ. Лучшее — это построение т.н. математической модели (таблица, цепочка логических шагов в строчку в зависимости от вида задачи). В таком случае, даже если в конце допущена арифметическая ошибка, будет поставлено 2 балла из 3-х возможных, что имеет вес. И в конце. Не пренебрегайте оформлением. Не думайте, что проверяющий автоматически склониться в вашу сторону и будет искать логику в разрозненных кусках решений, в хаотическом нагромождении вычислений. Эксперты обязаны накладывать данные критерии оценки, принятые комиссией на федеральном уровне (!) для каждого абитуриента, какими бы строгими и абсурдными они вам не казались. Обидно получать 0 баллов за номер, на который вы потратили столько времени и сил, получили верный ответ, но не сочли важным оформить его должным образом. Будьте внимательнее и аккуратнее. Все полученные знания должны работать на вас, ведь другого случая уже не предоставится. Впереди финишная прямая.

ЕГЭ по математике профильного уровня — один из самых сложных экзаменов. Планируете сдавать его, но не знаете, с чего начать? Этот экзамен не покажется вам таким трудным, если вы узнаете про него побольше и грамотно подготовитесь. В этой статье обсудим, что нужно знать про ЕГЭ по математике 2023, из каких разделов он состоит и как к нему подготовиться.

Какие темы важно знать для ЕГЭ по математике 2023?

В математике, как и в любом предмете, есть опорные темы. Если вы их выучите, будет легче справиться с экзаменом.

Формулы тригонометрии

Очень важно знать формулы тригонометрии и уметь применять их. Хорошая новость: в справочных материалах можно найти несколько тригонометрических формул.

Но формул гораздо больше. Я советую не зубрить их, а научиться выводить: приходить к формулам шаг за шагом, опираясь на тождества. Кстати, мы учим выводить формулы на курсах подготовки к ЕГЭ: это полезно, чтобы оказаться на экзамене во всеоружии и ничего не перепутать.

Квадратные уравнения

Эти уравнения мы учимся решать еще в 7 классе. Они встречаются в ЕГЭ по математике постоянно: и как самостоятельные задания, и внутри более сложных уравнений или неравенств. Квадратные уравнения могут встретиться в математических моделях № 9 и № 15, в задачах на геометрию и стереометрию, в задании № 17 с параметром.

Самое главное — хорошо знать универсальные методы решения. Первый — через формулу дискриминанта, второй — через теорему Виета, которая может сэкономить время на экзамене.

Треугольники

Эта замечательная тема, которую проходят в 7 классе — основа основ всей геометрии. Она нужна и для решения стереометрии, и для простейших планиметрических задач. Еще треугольники необходимы, чтобы освоить огромное количество теорем. Выучите все, что с ними связано! Особое внимание обратите на прямоугольные треугольники, которые встречаются чаще остальных — тогда геометрические задачи сразу станут проще.

Проценты

Самая нелюбимая тема моих учеников после тригонометрии, которую необходимо хорошо знать. Проценты нужны для реальной математики — это № 9 (с кратким ответом) и № 15 (с развернутым ответом). Понимание этой темы может принести вам 3 первичных балла.

План успешной подготовки к ЕГЭ по математике 2023

Если вы хотите получить больше 80 баллов на ЕГЭ, нужно идеально решать часть с кратким ответом, а также справляться с большинством заданий с развернутым ответом.

Чтобы постепенно прорабатывать материал, воспользуйтесь кодификатором. В нем обратите внимание на таблицу 2, а именно на блоки:

• Алгебра
• Уравнения и неравенства
• Элементы комбинаторики, статистики и теории вероятностей
• Функции
• Начала математического анализа
• Геометрия

Ориентируйтесь на указанную последовательность, но геометрию изучайте параллельно с остальными блоками — на нее нужно больше времени.

Самое главное — ни в коем случае не ограничивайтесь теорией. Ее у вас не спросят на экзамене, а вот задания решать придется. Поэтому тренируйте практические навыки: актуальные задания вы сможете найти в открытом банке заданий на сайте ФИПИ или в нашем тренажере «Решутест».

Как решать часть с кратким ответом

Ни в коем случае не пренебрегайте частью с кратким ответом! Иначе будет обидно: например, вы наберете за экономическую задачу № 15 полные 2 балла, но потеряете их в двух заданиях первой части. Это актуально для всех ЕГЭ: подробнее о том, как идеально справляться с первой частью экзамена, читайте здесь.

Еще одно заблуждение: «часть с кратким ответом простая, к ней можно не готовиться». Даже в первой части иногда встречаются такие задания, которые ученики даже не решают, потому что не готовились к ним.

Как я уже говорила, часть с кратким ответом содержит 11 заданий. Начинать подготовку необходимо именно с заданий базового уровня сложности, потому что это та основа, на которую потом накладывается более сложная теория.

Что касается задач повышенного уровня сложности, то среди каждого номера есть лайфхаки, например, в этой статье я уже рассказывала про № 11, в котором нужно работать с производной.

Задания с развернутым ответом: немного статистики

Многие думают, что эта часть ЕГЭ по математике очень сложная. Поэтому ребята, которые не рассчитывают на высокие баллы, даже не приступают к ней. И очень зря! С помощью этих заданий можно заработать дополнительные баллы и побороться за высокое место в рейтинге.

Сейчас будет немного статистики. В среднем около 35% учеников получают полные 2 балла за решение № 12, а вот неравенство № 14 дается хуже, только около 12% с ним справляются на полный балл. Геометрия даётся ещё хуже: стереометрию № 13 полностью решают 2% выпускников, планиметрию (№ 16) менее 5%. А вот с экономической задачей (№ 15) справляются около 20%, а это целых 2 балла! Что касается № 17 и 18, то они даются ещё хуже, но на то они и самые сложные, хотя 1 балл за № 18 по статистике получают около 25% сдающих — там нужно просто привести пример.

Особенности уровней ЕГЭ по математике

В 2015 году ЕГЭ по математике разделили на базовый и профильный уровни. Это упростило жизнь выпускникам, которые не планируют поступать на специальности, связанные с математикой. Если ЕГЭ по математике нужен только для получения аттестата, можно сдать его облегченную версию, оставив время и силы для профильных экзаменов.

Базовый уровень ЕГЭ по математике

Как устроен базовый ЕГЭ по математике? Экзамен идет 180 минут, он состоит из 21 задания, за каждое из которых можно получить 1 балл. Этот экзамен единственный, который переводится не в 100-бальную систему, а в оценки.

В ЕГЭ по математике базового уровня 6 тематических блоков:

Также обратите внимание, что базовый ЕГЭ по математике не поменялся с точки зрения наполнения, изменился лишь порядок заданий. Вот что пишут ФИПИ:

Подробнее про базовый ЕГЭ по математике, включая разбор всех заданий, читайте здесь, а мы перейдём к профильному.

Профильный уровень ЕГЭ по математике

Данный экзамен, как и остальные ЕГЭ, переводится в 100-бальную систему:

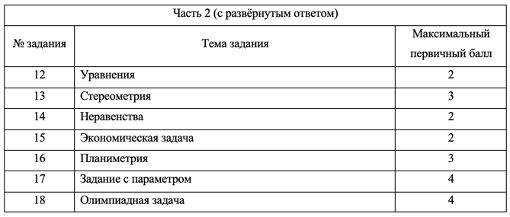
Экзамен состоит из двух частей: Часть 1 с кратким ответом, а Часть 2 — с развернутым. Длится он 235 минут. Всего есть 18 заданий, которые разделены на 3 блока: алгебра, геометрия и реальная математика. Максимальное количество первичных баллов — 31.

Структура ЕГЭ по математике 2023

Часть 1:

• Приносит 11 баллов, то есть 35% всего экзамена
• 11 заданий с кратким ответом

Часть 2:

• Приносит 20 баллов, то есть 65% всего экзамена
• 7 заданий с развернутым ответом

Внимание! Вся нумерация заданий в статье соответствует ЕГЭ 2023 года.

В заданиях с кратким ответом нужно лишь записать верное число в бланк. Заданий с развернутым ответом 7, в них нужно подробно расписать решение, которое должно соответствовать критериям оценивания.

ЕГЭ — стандартизированный экзамен, поэтому каждое задание всегда соответствует определенной теме.

Обратите внимание, что по сравнению с 2022 годом, в части 1 изменился только порядок заданий. Сами сотрудники ФИПИ говорят следующее:

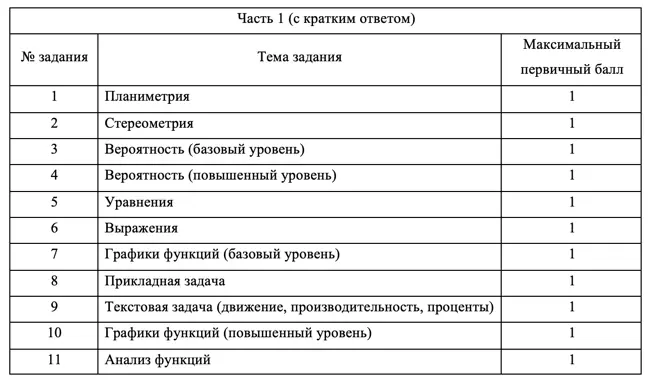
Задания с кратким ответом принесут вам до 11 первичных баллов (64 вторичных). Если не понимаете, что это за баллы и откуда они берутся, почитайте эту статью. Самая популярная цель на ЕГЭ по математике — набрать 80 баллов, для этого раньше было необходимо 19 первичных баллов. Ранее многие ученики пользовались рабочей стратегией — решить всю часть с кратким ответом, а также № 12, 14 и 15. Если хорошо разбирались в геометрии, выбирали № 13 и 16 — или использовали их как запасные задания. Сейчас стратегия должна быть другая, так как № 13 (стереометрия) стал стоить дороже — 3 балла вместо 2, а № 15 (экономическая задача) — подешевел с 3 баллов до 2. Изменилась также шкала перевода баллов, поэтому подумайте, какими заданиями вы сможете набрать необходимое количество первичных баллов.

Разделы ЕГЭ по математике

• Алгебра и начала анализа — 8 заданий, 13 первичных баллов
• Геометрия — 4 задания, 8 первичных баллов
• Реальная математика — 6 заданий, 10 первичных баллов

Какие задания входят в ЕГЭ по математике?

Здесь вам на помощь приходят документы с официального сайта ФИПИ: кодификатор, демоверсия и спецификация.

• Кодификатор — это краткий перечень всех блоков и тем, которые включены в экзамен.

  Сейчас кодификатор общий для обоих уровней экзамена, как базового, так и профильного. Он снова представляет собой единый документ, так что не запутаетесь.

• Демоверсия — типовой вариант ЕГЭ. Он показывает уровень экзамена и ориентировочную сложность заданий.
• Спецификация — это документ, описывающий структуру экзамена и разбалловку.

Что в итоге

Как правило, у большинства учеников самый нелюбимый блок в экзаменах — геометрия, потому что он тяжело даётся. А кто-то и вовсе его не понимает. А в геометрии есть самый нелюбимый тип заданий — это задачи на доказательство. Почему так происходит и как помочь ученику научиться их решать?

Что такое задача на доказательство

Задача на доказательство — это утверждение, которое нужно доказать, используя различные теоремы, аксиомы, следствия и признаки геометрии. Другими словами, нам нужно решить задачу и получить то же самое, что написано в условии, тогда задание будет выполнено. Поэтому задачи на доказательство на самом деле несильно отличаются от задач на нахождение чего-либо — просто то, что нужно найти, уже известно заранее. Звучит даже легче, не правда ли? Так почему же многие школьники всё равно намеренно пропускают эти задания и не решают их?

Всё дело в том, что задачи на доказательство очень похожи на то, как доказываются теоремы. А доказательство теорем начинается в 7 классе, когда происходит деление на Алгебру и Геометрию как отдельные предметы в школах. Однако обычно доказательство теорем выглядит следующим образом:

1. учитель доказывает теорему у доски,
2. ученики переписывают себе всё в тетрадь, иногда даже не понимая, что они пишут,
3. дальше звучит знакомая всем фраза «Выучите доказательство, потом ответите его на оценку»,
4. а дальше зачастую происходит зубрёжка переписанной теоремы.

Даже человек без педагогического образования догадается, что к пониманию, как осуществляется доказательство, это не приведёт. Да и зачем, если ни на одном экзамене не просят доказывать теоремы? Наоборот, нужно просто использовать уже готовые и доказанные формулировки. Но навык это очень полезный, и вот почему.

Где мы встречаемся с доказательствами

Умение доказывать геометрические задачи проверяют 2 главных школьных экзамена по математике — ОГЭ и ЕГЭ.

• В ОГЭ доказательство находится в № 24 как самостоятельная задача, которая приносит 2 балла максимум,
• в ЕГЭ доказательства встречаются в пунктах а) в № 13 (стереометрическая задача) и № 16 (планиметрическая задача), которые сами по себе приносят по 1 баллу, но без корректных доказательств практически невозможно перейти к пункту б) с решением, что в совокупности приносит по 3 балла за каждую задачу.

Как вы можете заметить, доказательства достаточно важны и приносят неплохие баллы сдающим экзамены. Но это не единственная их польза. Все задания на доказательство помогают ученикам выстраивать логические цепочки и учат рассуждать, а это пригодится не только на экзаменах, но и в жизни.

Так как помочь школьникам научиться их решать?

Как научить школьника решать задачи на доказательство

Доказательство, как я уже говорила, несильно отличается от решения всех геометрических задач. Алгоритм в обоих случаях такой:

1. построить чертеж,
2. отметить на чертеже, что дано,
3. отметить на чертеже, что нужно найти,
4. построить логическую цепочку от того, что нужно найти до того, что дано,
5. записать шаги доказательства.

Кроме того, в ходе решения или доказательства нужно не забывать выносить всю теорию на чертёж, а также строить чертеж, причем как можно большего размера — так будет лучше видно детали.

Но вернёмся к объяснению задач на доказательство ученикам. Самое главное — объяснить, как должно строиться доказательство, потому что именно здесь у учеников возникают проблемы. Обычно они двух видов:

• слабые ученики просто не берутся за доказательство, потому что не понимают, что делать,
• а сильные в ходе доказательства могут опускать и не расписывать некоторые важные пункты, потому что для них они кажутся очевидными, что приводит к нарушению логики и потере баллов.

Удобная аналогия для решения задач на доказательство

А секрет прост. Доказательство должно быть похоже на заплетание косички:

• три пряди, на которые мы делим все волосы — это то, что нам дано,
• готовая косичка — то, что должно получиться или то, что нужно доказать,
• процесс вплетания прядей — построение логической связи.

Заметили сходство с алгоритмом выше?

Если вы сможете донести это до учеников, то проблема с пропуском важных этапов решится. Ведь мы не можем пропустить прядь, пока плетём косичку? Тогда она у нас просто не получится.

Если пример с косичкой не поможет, то можно провести аналогию с объяснением доказательства очень-очень слабому ученику. Нужно посоветовать ему представить, что, записывая доказательство, он объясняет его другу, который ничего не понимает и всегда задаёт один и тот же вопрос «Почему?». Тогда «отвечая» каждый раз на «Почему?», ученик автоматически будет всё подробно расписывать, а у эксперта при проверке такого вопроса не возникнет.

Давайте объединим все вышеуказанные приёмы и алгоритм и разберём несложную задачу на доказательство. Я буду писать объяснение от первого лица, которое вы можете использовать на уроке, и к нему иногда добавлять поясняющие комментарии.

Разбор задачи на доказательство

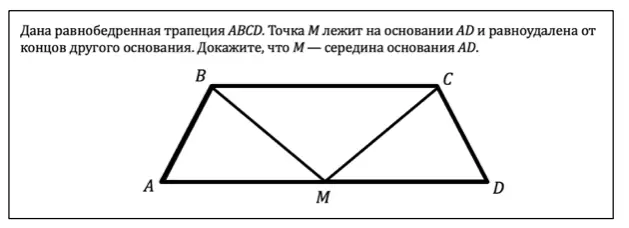
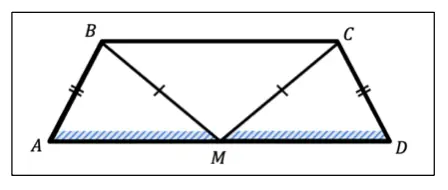
Шаг 1. Понять, что нам дано

К счастью, первый пункт алгоритма можно опустить, потому что чертёж нам уже дан. Далее нужно вынести на чертёж всё что дано, а именно:

• АВ = CD, так как по условию трапеция равнобедренная, а значит её боковые стороны равны,
• ВМ = СМ, так как точка М равноудалена концов основания ВС.

Шаг 2. Понять, что нужно доказать

Теперь отмечаем то, что нужно доказать:

• нужно доказать, что М — середина AD, а значит отрезки АМ и MD должны быть равны.

Итак, получается следующая картина:

А теперь нужно построить логическую цепочку от того, что нужно найти, до того, что дано.

Я не оговорилась, нужно идти от вопроса к тому, что есть. Скажите ученикам, чтобы они представили, будто раскручивают клубок с рассуждениями, а когда дойдут до точки начала, будут закручивать его обратно и записывать всё по порядку. Кстати, вот вам ещё один приём, который поможет научить учеников доказывать задачи.

Шаг 3. Выстроить логическую цепочку

• Итак, как мы можем доказать, что AM = MD? Верно, из треугольников ABM и MCD, ведь если мы докажем, что данные треугольники равны, то и все их элементы тоже будут равны. Сейчас мы раскрутили первый виток нашего клубочка.
• Как нам доказать, что треугольники ABM и MCD равны? Правильно, у нас уже есть две равные стороны, осталось доказать, что углы ABM DCM равны. Ещё виток раскрутили!
• А как доказать, что углы ABM DCM равны? Конечно, можно воспользоваться свойством равнобедренной трапеции, а также получившимся равнобедренным треугольником ВМС. Вот мы и раскрутили клубок! А теперь будем его закручивать, подробно всё расписывая.

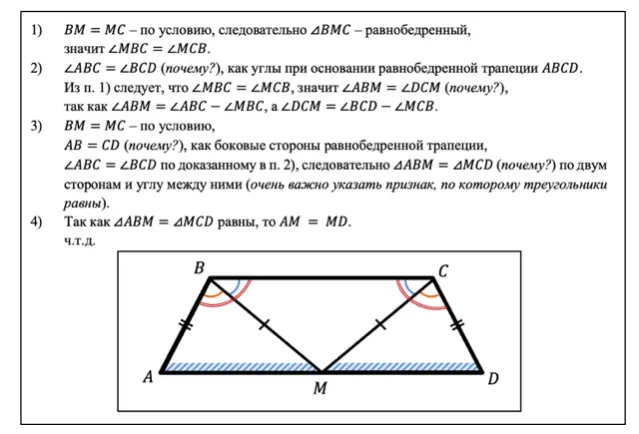
Не забывайте про ученика-почемучку, которому вы как будто объясняете доказательство. А также не забудьте в решение выписать всё то, что вы уже вынесли на чертёж, начинать нужно именно с этого.

1. ВМ = МС по условию, следовательно треугольник BMC — равнобедренный, значит углы МВС и МСВ равны.
2. Углы АВС и BCD равны (почему?), как углы при основании равнобедренной трапеции ABCD.
   Из п. 1) следует, что углы МВС и МСВ равны, значит углы АВM и DCM равны (почему?), так как АВM = АВС — МВС, а DCM = BCD — МСВ.
3. ВМ = МС по условию,
   АВ = CD (почему?), как боковые стороны равнобедренной трапеции,
   углы АВС и BCD равны по доказанному в п. 2), следовательно треугольники ABM и MCD равны (почему?) по двум сторонам и углу между ними (очень важно указать признак, по которому треугольники равны).
4. Так как треугольники ABM и MCD равны, то AM = MD.
   Что и требовалось доказать.

Вот так легко мы доказали задачу, используя:

• алгоритм решения геометрической задачи,
• косичку,
• ученика-почемучку
• и клубочек.

Теперь вы знаете, как объяснить доказательство самому слабому ученику, а также как подсказать сильному, чтобы он не упускал важные факты. И пусть мы разобрали задачу уровня ОГЭ, в ЕГЭ на более сложных примерах все эти принципы работают с таким же успехом.